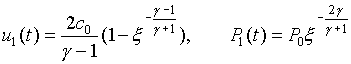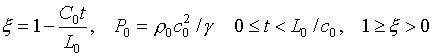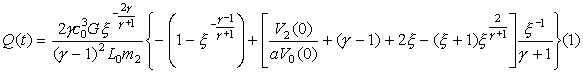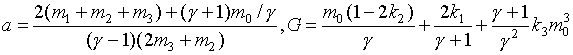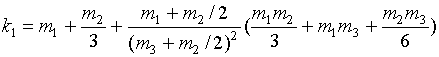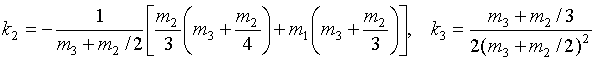Численное исследование реализации безударного сжатия и термоядерного горения несферической мишени тяжелоионного термоядерного синтеза

( Computational Investigation of Realization of Unshocked Compression and Thermonuclear Burn in Nonspherical Target of Heavy-Ion Driven Fusion
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Существенным затруднением при осуществлении безударного сжатия  является необходимость задания сложного внешнего граничного условия как функции (нормальная скорость или давление на поршне) с неограниченной величиной ее роста по времени. Нам неизвестны практические способы его возможной реализации.

Кроме общеизвестных причин, которые вынуждают использовать оболочечные конструкции при построении микромишеней  (усиление кумуляции, теплоизоляция топлива и др). при реализации неограниченного безударного сжатия требуется неограниченный рост энерговложения. Наличие тяжелой оболочки, окружающей топливо, позволяет накопить в ней в процессе движения необходимый запас кинетической энергии, который на заключительном этапе может быть достаточным для достижения в топливе необходимых параметров для зажигания. При этом не требуется доводить до бесконечных значений обострение вкладываемого импульса внешнего энерговложения.

До сих пор сохраняется большой интерес в связи с конструированием микромишени безударного сжатия управляемого термоядерного синтеза. Для достижения высокой степени плотности ДТ-газа, K.A.Brueckner [3] получил закон давления на границе ДТ-газа с помощью секвенцией ударной волны, так, что последовательные импульсы не нагоняют друг друга. Согласно теории автомодельных решений, R.E. Kidder[5] тоже получил закон давления, которое было связанно с лазерной мощностью при каком-то предположении о передаче внешней энергии. Профилированная лазерная мощность NIF (National Ignition Facility) тоже связана с низко-энтропийным сжатием.[4] Для микромишени прямого облучения тяжелыми ионами пока не известна похожая закономерность для осуществления   безударного сжатия. На основе  работы Г.В. Доголевой и А.В. Забродина[1], мы пытались конструировать микромишени безударного сжатия для реализации тяжелоионного термоядерного синтеза.

Известно, что энерговложение пучками тяжелых ионов, облучающих  микромишень, действительно является асимметричным. Симметрия исходной геометрии популярных мишеней противоречит асимметрии энерговложения, которая развивает (существует Релей-Тейлоровская неустойчивость) и в конце концов может нарушать кумуляцию энергии. В [2] представлена мишень, в которой форма внешней оболочки (Pb) подбиралась  так, чтобы пучки ионов останавливались  на внешней границе оболочки(Au), отдавая всю свою энергию в областях Pb и Be. Такое профилирование толщины внешнего слоя проводилось для компенсации указанной несферичности  энерговложения и обеспечения наиболее благоприятных условий сжатия, близких к условиям сферического сжатия.

В настоящей работе предполагается, что реальное асимметричное энерговложение для осуществления безударного сжатия может быть аппроксимировано функцией  . Если принять, что финальное обжатие топлива должно произойти в момент близкий к завершению одномерной кумуляции, то понятно, что движение внутренней границы тяжелой оболочки необходимо по возможности сохранить. Поэтому основную разнодинамичность ее движение из-за неодномерности энерговложения следует компенсировать разнотолщинностью за счет изменения формы наружной границы оболочки Au.

Предположение о возможности сохранения кумуляции ДТ- газа близкой к одномерному случаю позволяет рассмотреть поставленную задачу о возможности соответствующего профилирования тяжелой оболочки в секторном приближении. По аналогии с работой[1], было найдено приближенное решение, из которого следует, что компенсацию неодномерности энерговложения можно действительно осуществить через разнотолщинность тяжелой оболочки, и была приведена конкретная формула. Последующие численные расчеты в точной постановке подтвердили правильность подхода и сохранение кумуляции при движении ДТ.

1. Закономерность  энерговложения в микромишени  для осуществления безударного сжатия

На основе оболочечных слоистых систем воспроизводится безударное сжатие в одномерных конструкциях микромишеней. Существенным затруднением для получения такого безударного сжатия является необходимость осуществления на внешней границе ДТ смеси скорости или давления с неограниченной величиной их роста по времени. Нам неизвестны практические способы такой возможной реализации. Поэтому было проведено изыскание возможности осуществления безударного сжатия через профилированное энерговложение вне области энерговыделения ДТ смеси при тепловой изоляции последней.

Система состоит из следующих слоев:

                   m₀             m₁               m₂             m₃        

|---------------------|------|///////////////////////|------|

          0                          L₀      L₁                   L₂     L₃

Области m₁, m₃ с малой толщиной и большой плотностью по сравнению с областью m₂. При их движении, они приобретают малую внутреннюю энергию по сравнению с кинетической. В излагаемых ниже предложенных аналитических рассмотрениях они считаются несжимаемыми, а их скорости постоянными по пространству.

В области m₂, где осуществляется равномерное энерговложение, нужно учитывать пространственные градиенты скорости. Предполагаем, что распределение скорости в области m₂ представимо в виде:

Для воспроизведения безударного сжатия, в области m₀ на правой её границе скорость и давление должны удовлетворять соотношениям:

где c₀: начальная скорость звука, g: показатель адиабаты.

На правой границе области m₃ задано давление P(t)=0(свободная граница). Нужно найти зависимость энерговложения Q(t) такую, чтобы в области m₀ реализовать движение с заданной скоростью u₁(t) и давлением P₁(t).

Из одномерных уравнений газовой динамики с учетом принятых выше предположений, получена удельная мощность энерговложения в области m₂ [1]:

(2) (3)

(4)

a=1-плоская, a=2-цилиндрическая, a=3-сферическая симметрия.

Из формулы Q(t) видно, что при  Q(t) будет бесконечным. Учитывая, что обострение импульса на современных установках делать очень сложно и мощность энергии невозможно бесконечно увеличивать, была изменена закономерность энерговложения по сравнению с приведенной выше. До определенного времени t₁ энерговложение проходит по приведенной выше формуле Q(t), а далее оно остается постоянным Q(t)= Q(t₁) и затем Q(t)=0 при t>t₂ т.е. прекращается. Сильные ударные волны, формирующиеся в областях m₁,m₂, при изменении закона энерговложения дополнительно разогревает сжатую смесь ДТ. Температура  и плотность смеси ДТ достигает таких значений, что начинается горение смеси ДТ. Для регулирования величины энерговложения в формуле Q(t) можно ввести множитель k в качестве дополнительного параметра. До момента t₁ энерговложение по формуле k·Q(t). Подбором значений t₁,t₂ определяется достижение необходимой плотности ДТ-газа.

Расчетные результаты приводятся в следующей системе единиц: длина - 10^-2cm, время - 10^-8s, скорость- 10⁶ cm/s, температура - 10⁸K, удельная энергия - 10¹² erg/gm, плотность – gm/cm³.[g1] [g2] 

В наших расчетах выбраны C₀=0.1, L₀=10 и a=1.

На рис. 1 показаны профили энерговложения при  Q_max=9000TW/g, k=0.2, t₁=99.9385,k=0.6, t₁=99.9, k=1.0, t₁=99.874.

Рис.1 Профили энерговложения при некоторых значениях параметра k

2. Сферически-симметричная мишень

Микромишень состоит из таких областей: область I - топливо ДТ смеси, область II - сжимающий поршень(пушер), область III - приемник энергии тяжелых ионов излучения (абсорбер), и область IV - тампер.

          Основные параметры задачи:

                      r       0             10.0         10.5        19.3          21.8   

Надо отметить, распределение энерговложения следующее: 20% энергии вложено в области  III и 80% энергии в области IV. В расчетах М.М. Баско[6] предположено 25% в тампер и 75% в абсорбер для энергии ионов ²⁰⁹Bi 20Гэв. Реально пучок тяжелых ионов проходит большую часть длины мишени с небольшими изменениями характерного энерговложения, и только в конце пробега происходят более резкие изменения в области так называемого Брэгговского пика. Пока в наших расчетах предполагалось Q(t) постоянным по радиусу мишени. Первоначально в расчетах не включалась теплопроводность.

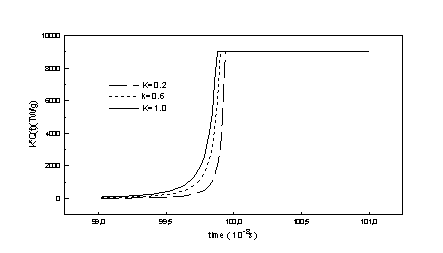
После оптимизации параметров в формуле энерговложения, были выбраны следующее значения: t₁=99.9, t₂=99.9999, k=0.6. Пиковая мощность тяжелоионного пучка составляет 227 TW при удельной мощности облучения 9000 TW/g. Сумма эерговложения:  E_in~0.43MJ.

Напомним, что формула была получена в предположении, что  только в область m₂ вкладывается энергия тяжелых ионов,  т.е. весь E_in~0.43MJ вложен в область m₂, а область m₃ получает энергию из области m_2. Ниже сравниваются численные  результаты двух вариантов.

I  - 20% энергии вложено в область m₃ и 80% энергии в область m_2.

II - 100% энергии вложено в область m₂.

< .. > - среднее значение в горячем пятне на момент достижения максимального сжатия.

- максимальная скорость имплозии,

r_min - минимальный радиус ДТ смеси,

- максимальная средняя плотность ДТ смеси,

- максимальная средняя плотность золотой оболочки,

E_abs , E_tamp , - энергия в абсорбер и тампер на момент достижения максимального сжатия,

W_DT - максимальная  внешняя работа над ДТ смесью,

G  -  коэффициент  термоядерного усилия(E_out/E_in).

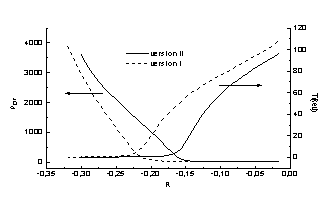
Из приведенной выше таблицы видно, что на момент достижения максимального сжатия в расчете I область тампер отобрала энергию больше, чем в расчете II, но его внешняя работа больше, и максимальная  температура в ДТ смеси тоже больше(рис.2). Несмотря на немного разные , коэффициенты  термоядерного усилия G очень  близкие. На рис. 2 показаны распределения температуры и плотности в области ДТ-газа на момент достижения максимального сжатия. Их характеры похожие, только существует перемещение положения внешней границы ДТ-газа по радиусу, который в расчете I больше, чем в расчете II. И так мы считаем, что возможно вложение энергии в двух областях (абсорбер и тампер) вместо одной области для осуществления безударного сжатия.

Рис.2 Распределения температуры и плотности в области ДТ-газа

Если в расчете задавалось постоянное энерговложение т.е. Q(t)=9000 TW/g, и сумма энерговложения тоже E_in~0.43MJ, то зажигание не возникало.  При коротком времени облучения (~1.9ns) процесс сжатия является высоко-энтропийнным. Хотя в самом центре максимальная  температура была 20.2kev, но плотность (=57.41) малая. Это значит, наша профилированная закономерность  энерговложения (формула 1) дает подход, который экономит энергию и представляется перспективным.

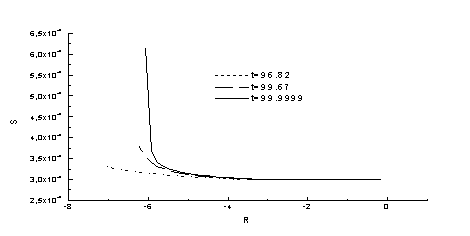
Надо отметить, что приведенная на рис. 3 зависимость энтропийной функции ДТ-газа от времени показывает, что отличие от начального уровня  не превышает двух раз. Сжатие является безударным при профилированном энерговложении.

В NIF, полная энергия лазеров 1.8MJ, пиковая мощность 500TW, время облучения 20ns и в оптимизированной микромишени обычно получается G_n=10 при . Наш результат близок к  мишени NIF.

Рис.3 Зависимость энтропийной функции в ДТ-газе от времени

3.   Двумерная микромишень на основе сферической задачи

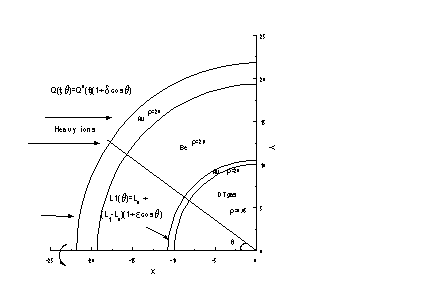
Рис.4 Сечение двумерной микромишени на основе

одномерной сферической мишени

Было предположено, что на основе одномерной сферической мишени можно компенсировать асимметрию энерговложения изменением толщины оболочки из тяжелого вещества при сохранении сферичности остальных оболочек(рис. 4), т.е. получить сжатие ДТ-газа близкое к сферическому. Но это верно только при малых асимметриях в энерговложении. От первоначального нарушения сферической симметрии энерговложения в процессе газодинамического сжатия будет нарастать развитие неустойчивости на границах золотой оболочки. При безударном сжатии согласованным выбором Q(t,q) и разнотолщинности золотой оболочки (при сохранении её внутреннего радиуса) оказывается возможно минимизировать развитие неустойчивости при схождении внутренней границы оболочки к центру.

Допустим, что формула асимметрического  энерговложения может писаться в следующем виде: ,и движение будет близким к радиальному; m₀, m₂ и m₃ не зависят от угла q, но только . Это значит, что к времени  весь газ ДТ фокусируется в центр. Поэтому нам нужно найти отношение между d и e, чтобы для данной микромешени осуществить безударное сжатие.

В конкретной задаче, m₀=0.5, m⁰₁=10.0, m₂=17.6, m₃=50.0, видно что  и , и получаем ,,.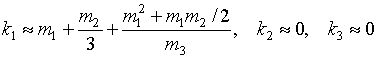

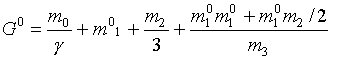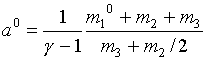Сравнив результатов точных решений G_точ=15.2307  a_точ=1.9897 и приближенных решений G_при=15.02 a_при=1.9796, считаем, что наше приближение справедливо. Q(t,q) имеет следующий вид: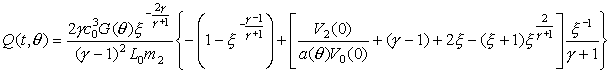

здесь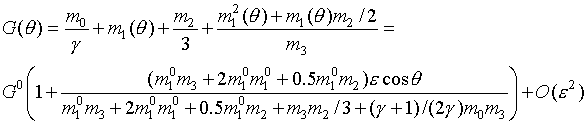(5)

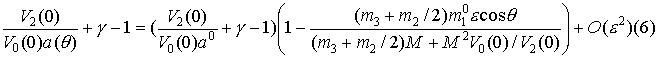
e<< 1.0, M=m₁+m₂+m₃, при  получены

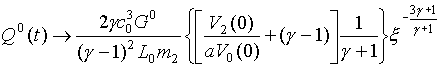
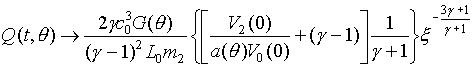
Подставив  (5)и (6) в формулу Q(t,q),  мы получим:

отсюда получено отношение между d и e,

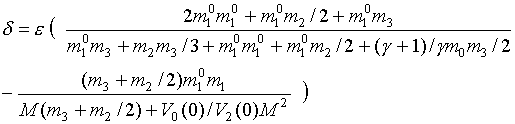    (7)

          В данной задаче:. Таким образом, получено соотношение между асимметрией энерговложения (d) в  и асимметрией геометрии мишени (e) в .

Ниже мы подробно рассмотрим для какой асимметрии в геометрии мишени (e) сжатие будет лучше сохранять сферичность при данной асимметрии энерговложения (d), т.е. какая степень изменения толщины золотой оболочки компенсирует асимметрию энерговложения. 

3.1 Расчеты при асимметрии энерговложения  d~1.27%.

В расчетах, числа узлов в областях по радиальному направлению от центра были 40,10,40,20 соответственно, а по угловому 30. В областях Au сетки равномерны. В области Be начальные 20 узлов сгущались к внутренней золотой области по геометрической прогрессии (l=1.05), а последние 19 узлов сгущались к внешней золотой области. В области ДТ сетки равномерны.

Прежде всего, мы рассмотрим как оптимизировать толщины при малой асимметрии. В этом случае касательный поток не сильный так, что предположение сохранения одномерного движения было справедливым. Асимметрия энерговложения задается d~1.27%. При t₁=99.9, t₂=99.9999, k=0.6, пиковая удельная мощность Q_max=9000TW/g и сумма энерговложения E_in~0.43MJ (одномерный результат был показан выше). Но не получается зажигания, потому что температура в центре не такая высокая, чтобы разогреть остальной ДТ-газ. При небольшом  увеличении энерговложения при t₁=99.9, t₂=100.05, k=0.6 E_in~0.55MJ   получается зажигание и удовлетворительное энерговыделение.

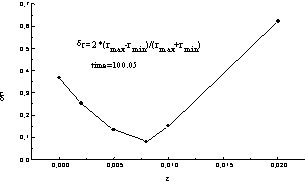
Ниже приводятся результаты расчетов при варьировании величины асимметрии в геометрии мишени (e). На рис.5 показана на момент времени t=100.05 зависимость от e относительной деформации  границы ДТ-газа. Здесь r_max, r_min максимальное и минимальное расстояние от границы до начала координат.

          Рис.5 Зависимость от e относительной деформации dr

Видно, что  достигает минимума 0.079% при e=0.008, т.е. сжатие остается близким к сферичному. Отметим, что аналитическое решение дает соответственно e=0.02 (по формуле 7) при d~1.27%. Отличие можно объяснить тем, что во-первых, действительно область m₁(пушер) и m₃ (тампер) были сжимаемыми, и во-вторых, существует касательный поток, который двигается от толстой стороны оболочки к тонкой. Тем не менее, до прекращения энерговложения при фиксированной асимметрии энерговложения d~1.27%, существует соответствующая начальная асимметрия в геометрии мишени (e=0.008), которая лучше компенсирует асимметрию энерговложения.

*_max - значение при  r_max.

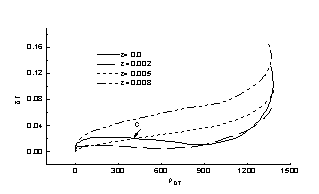
Рис.6 Зависимость от r_DT относительной деформации dr

При e=0.01 из-за большой деформации расчет в исходной постановке не удается довести до конце. При e=0.0 и 0.005 результаты близки к одномерному расчету(_max<11% и_max<20%). На рис. 6 приведена зависимость от r_DT относительной деформации dr при разных e. В процессе сжатия при e=0.002 деформация самая малая (до достижения максимального сжатия ДТ смеси dr ~8.44%), а при e=0.005 до r_DT~400 (точка C) деформация тоже меньше, чем при e=0.0. Приведенные расчеты  подтверждают, что под заданное угловое распределение интенсивности облучающего мишень потока можно по найденной выше формуле (7) подобрать разнотолщинность внутренней оболочки из Au, которая компенсирует асимметрию облучения, так, что практически сохраняется квазисферическая кумуляция.

3.2 Расчеты при асимметрии энерговложения  d~18%.

Сейчас мы переходим к большей асимметрии энерговложения d~18%. Сначала расчет проводится при параметрах  энерговложения Q_max=9000TW/g,k=0.6, E_in ~  0.4MJ.

Было выявлено натекание вещества оболочки на плоскость симметрии в окрестности ее угловой точки. Возмущение развивается так сильно что вещество двигается в сторону от оси быстрее, чем к оси, и в самом центре мишени существует сильный касательный поток. Из-за большой деформации расчет в исходной постановке завершить не удалось.(рис. 7)

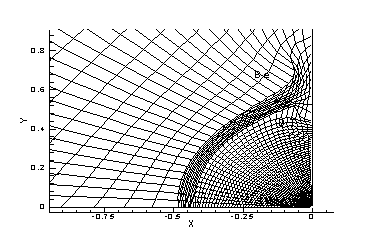
Рис.7 Локальные сетки в плоскости симметрии в окрестности угловой точки

Если увеличивается удельная мощность энерговложения, то уменьшается  время финального сжатия и наверное неустойчивость не успеет развиться. При увеличении энергии (t₁=99.94,t₂=99.9999, k=0.6, E_in~0.849MJ) деформация области Au и DT уменьшается, тем не менее зажигание практически не возникает от нарушения условия формирования «горячего пятна ». До момента максимального сжатия точка B двигается быстрее чем А (рис.8). В центре существует сильный касательный поток из D до C, и в точке O встречаются сильная отраженная волна из С и слабая волна сжатия из A.  Хотя в точке O максимальная температура была 60kev, но зажигание вообще не возникало.

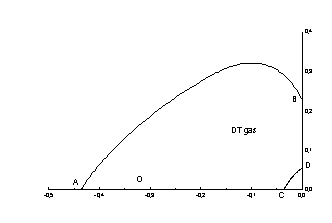
Рис. 8 Схема конфигурации ДТ области

В соответствии с полученными результатами при фиксированной пиковой удельной мощности энерговложения (Q_max=9000 TW/g) параметры были скорректированы так: t₁=99.9385, t₂=100.394, k=0.2.   Тогда при разных асимметриях геометрии мишени расчеты дают:

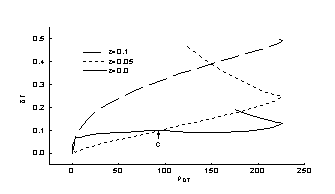
Рис.9 Зависимость от r_DT относительной деформации dr

Максимумы средней плотности ДТ-газа очень близкие. По формуле (7) при d~ 18% соответственно  e ~0.3. На рис. 9 показывается, что в процессе сжатия до r_DT~100 (точка C) деформация при e=0.05 меньше, чем при e=0.0. Далее от сильной отраженной волны из центра разница радиусов границы ДТ-смеси по направлению X и Y увеличивается. Но на момент достижения максимального  сжатия, общая форма при e=0.05 лучше, чем при e=0.0(рис.10). От сильного двумерного эффекта и неустойчивости при асимметрии энерговложения d~18% практически оптимальная асимметрия в начальной геометрии мишени меньше, чем в аналитическом решении. Но тем не менее, в расчетах получена асимметрия в начальной геометрии мишени, которая удовлетворительно  компенсирует асимметрию энерговложения.

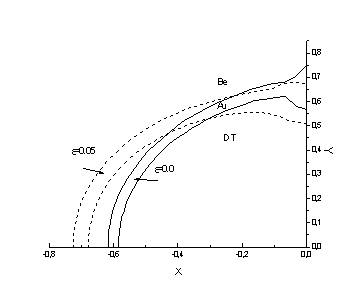
Рис.10 Формы на момент достижения максимального сжатия (e=0; 0.05)

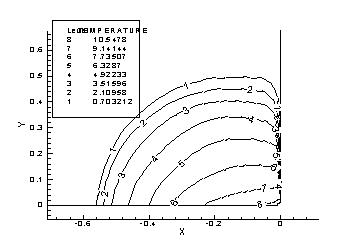
          Благодаря уменьшению параметра k до 0.2, остается мало времени, за которое деформация центральной области мишени не успевает сильно развиваться. Хотя в самом центре возникает зажигание, но распространение волны термоядерного горения уже не сохраняет  сферичность. Об этом можно судить из рис.11. Радиус ДТ смеси по направлению x ~0.584 а по направлению y~0.554.  Линия самой высокой температуры (метка 8) находится в центре. Но для осуществления зажигания ДТ-газа, необходимое суммарное энерговложения (~1.25MJ) в 3 раза больше, чем в одномерном сферическом расчете(~0.4MJ)

Рис.11 Изолинии температуры на момент достижения максимального сжатия (e=0)

4.   Заключение

     Изложенный подход об использовании безударного сжатия для осуществления тяжелоионного термоядерного синтеза с помощью профилированного энерговложения в области абсорбера и тампера представляется перспективным. В двумерном случае, при предположении  и компенсации асимметрии посредством изменения толщины пушера было получено двумерное профилированное энерговложение. При оптимизации параметров профилированного  энерговложения получены следующее выводы:

1.     До прекращения энерговложения сжатие безударное. 

2.     В одномерном случае после сравнения коэффициента термоядерного усилия и степени сжатия, наилучшая пиковая удельная мощность импульса равна 9000(TW/g) и  сумма  энерговложения равна ~0.43MJ. При этом получен и G ~12.5 при .

3.     В двумерном случае, для Q_max =9000(TW/g) при асимметрии энерговложения d~1.27% в процессе сжатия при начальной асимметрии геометрии e=0.002 деформация ДТ-газа остается малой. При d~18% и для множителя k = 0.6 горение не получается из-за сильной деформации. Для множителя k = 0.2, если сумма энерговложения равна ~1.2MJ, получены коэффициент термоядерного усиления и степени сжатия близкие к соответственным одномерным результатам, т.е. практически сохраняется квазисферическая кумуляция и происходит горение.

Литература

1.     Долголева Г.В., Забродин А.В. Воспроизведение безударного сжатия в оболочечных конструкциях микромишеней. //Препринт ИПМ, № 53, 1999г.

2.     Жуков В.Т., Забродин А.В., и др. Численное исследование процесса сжатия несферической мишени тяжелоионого термоядерного синтеза в приближении двухмерной теплопроводной газодинамики. //Вопросы атомной науки и техники. Серия: математическое моделирование физических процессов. Вып. 1,  С. 8-17, (1994).

3.     Brueckner K. A., Jorna S., Laser-driven fusion //Reviews of modern physics. V.46,№2,P.325-367,(1974)

4.     John Lindl,  Development of the indirect-drive approach to inertial confinement fusion  and the target physics basis for ignition and gain.// Phys. Plasmas. V. 2, P. 3933-4024, (1995).

5.     Kidder R.E. Theory homogeneous isentropic compression and its applications to laser fusion // Nucl. Fusion. Vol. 14, N 1. P. 53-60. (1974).

6.     Basko M.M., Imshennik V. S., and Churazov M.D. Overview of directly HIF target. //Particle Accelerators V.37-38, P.505-512, (1992).