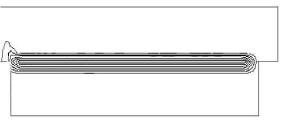
Моделирование тепловых процессов
при трении якоря о рельсы
в электродинамическом ускорителе
|
||||||||
|
a) |
б) |
|
в) |
|
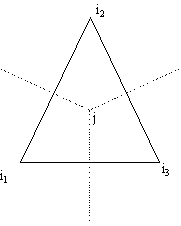
Рис. 1.2. Немонотонность распределения температуры по пространству (изотермы).
Необходимость во введении ИТ возникает, если условие h < k/r cv, где h – характерный линейный размер ячейки, не выполняется. Минимальное значение h ограничено методом генерирования ячеек (т.е. возможностями используемой ЭВМ). В описываемых расчетах оно составляло около 4.10-6 м, поэтому необходимо применять ИТ (правая часть последнего неравенства в данном случае около 10-7 м).
Введение ИТ в линейной форме (коэффициент ИТ пропорционален величине скорости якоря и не зависит от температуры), как это описано выше, привело к значительному расхождению между численным решением и аналитическим решением. Соответствующее распределение температуры представлено на рис.1.2.б. Видно, что тепло распределяется на всю глубину рельса.
Однако возможно выбрать нелинейную ИТ, величина которой зависит от решения в данном треугольнике, аналогично схеме с "лимитерами" из [10]. При этом принцип максимума в каждой ячейке остается справедливым. Данный подход, более подробно описанный в [4-6], позволяет избавиться от немонотонности решения корректным образом. Результат расчета решения с нелинейной ИТ представлен на рис. 1.2.в. Видно, что, с одной стороны, решение является монотонным, с другой – полоса распространения тепла соответствует расчету без ИТ.
§ 2. Приближенные
аналитические решения.
Несмотря на свою линейность и постоянство (возможное) коэффициентов, аналитическое решение задачи (0.1) получить не удается. Для понимания качественно – количественных характеристик решения полезны хотя бы приближенные аналитические решения, которые и представлены в данном параграфе. Рассмотрим различные приближения.
2.1.
Распределение температуры вдоль поверхности контакта.
В предположении о том, что теплопроводностью вдоль контакта можно пренебречь, можно найти аналитическое решение уравнения (0.1).
При таком допущении (0.1) может быть переписано в виде следующей системы:
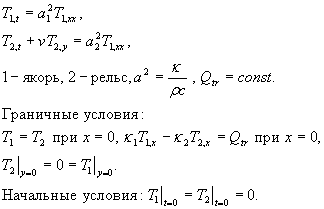 (2.1)
(2.1)
Применение интегрального преобразования Лапласа позволяет найти точное решение (2.1) для температуры вдоль поверхности контакта (y = 0). Оказывается, что такая температура равна:
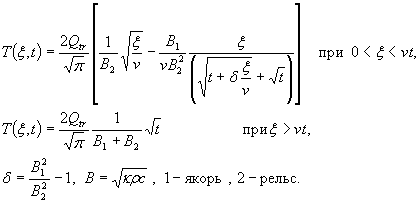 (2.2)
(2.2)
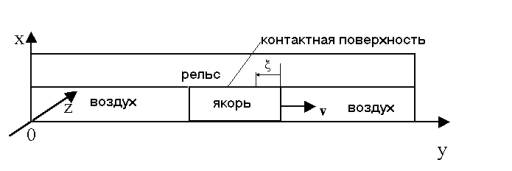
Линейная координата x (расстояние от начала якоря по направлению движения) показана на рис. 0.2.
Анализ данного соотношения показывает, что при малых временах от начала движения контактная температура зависит от продольной координаты лишь в окрестности передней кромки якоря, где присутствует влияние холодного рельса.
2.2.
Решение при наличии скачка теплового потока на контактной границе двух
бесконечных полупространств.
Данная постановка задача означает отсутствие в уравнении теплопроводности (0.1) производных температуры по координате вдоль поверхности контакта. В этом случае также можно получить точное решение:
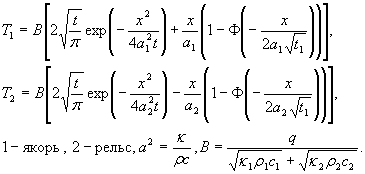 (2.3)
(2.3)
2.3.
Снос тепла от источника.
Для выделения роли конвективного переноса полезно рассмотреть исходную задачу в следующей постановке. Опустим в (0.1) слагаемые с производными по x (поперек контакта). При этом фактически имеем задачу о нахождении распределения тепла от источника мощностью q, находящегося на участке (0, l) контакта между двумя полупространствами. Иллюстрация рассматриваемой задачи приведена на рис. 2.1.
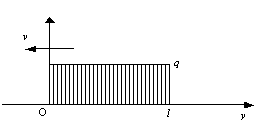
Рис. 2.1.
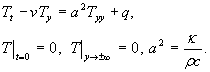 (2.4)
(2.4)
Точное решение (2.4) записывается следующим образом:
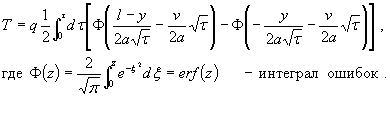 (2.5)
(2.5)
Для его исследования рассмотрим следующие упрощения.
А) Случай нулевой теплопроводности (a = 0).
Тогда имеем решение вида:
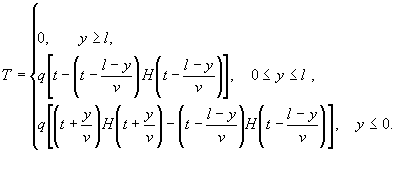 (2.6)
(2.6)
Здесь H(x) - функция Хевисайда.
Рис. 2.2 иллюстрирует пространственные распределения температуры для различных моментов времени в соответствии с приведенным решением. На данном рис. представлено решение (2.6) в двух пространственных точках в зависимости от времени (два верхних рисунка) и две картины распределения температуры по пространству в два характерных момента времени (два нижних рисунка).
Б) Случай малой теплопроводности.
Перепишем решение (2.5) в следующем виде:
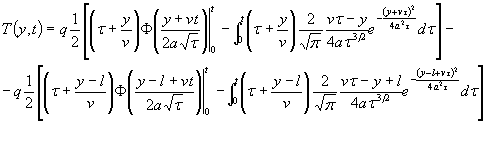
Его можно представить как сумму ![]() - главной части
решения - и двух интегралов I1
и I2:
- главной части
решения - и двух интегралов I1
и I2:
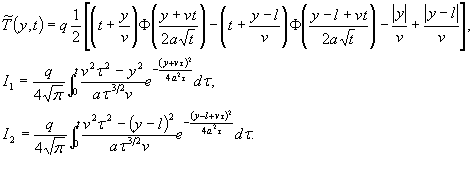 (2.7)
(2.7)
Для части решения I1 при малых значениях a может быть получена следующая асимптотическое соотношение:
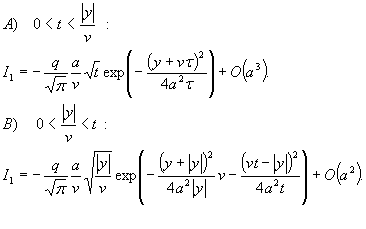 (2.8)
(2.8)
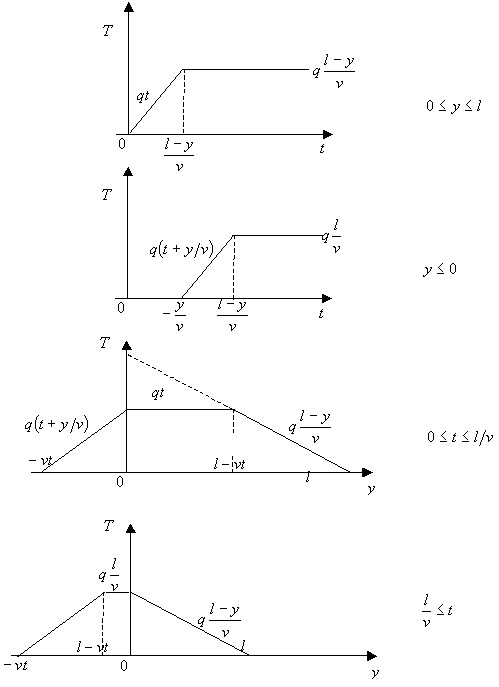
Рис. 2.2.
Для части решения I2 верно все то же самое с заменой y на y-l.
Видно, что при стремлении a к нулю главная часть решения (2.7) переходит в соотношение (2.6).
Асимптотика (2.8) получена в соответствии с методами [11].
§ 3. Численные расчеты
1. На рис. 3.1 сопоставлены продольные распределения температуры, полученные численно (с нелинейной ИТ) и аналитически (решение (2.2)), на момент времени 0.3 ms. При этом выбраны реальные физические параметры рельсотрона. Главные из них таковы: материал рельса - медь, материал якоря – алюминий, скорость якоря - 1000 м/с, тепловой поток, вызванный трением – 5.1010 Вт/м2.
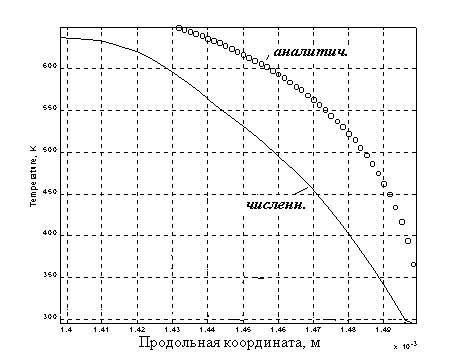
Рис. 3.1.
Рис. 3.1 демонстрирует превышение аналитическим решением численного, что свидетельствует о значительности теплопроводности в продольном направлении, которая не учитывается решением (2.2).
На рис. 3.2 представлены численная и аналитическая временные зависимости температуры в фиксированной точке на контакте (вблизи передней кромки якоря). Видно, что соответствующие численные кривые лежат ниже аналитических, но расхождение сравнительно небольшое. С одной стороны, это говорит о том, что численная модель дает физически корректный результат, с другой – тот факт, что аналитические профили температуры всегда лежат выше численных, свидетельствует о значимости продольной теплопроводности. Причины «насыщения» температуры контакта лучше всего ясны из решения (2.6).
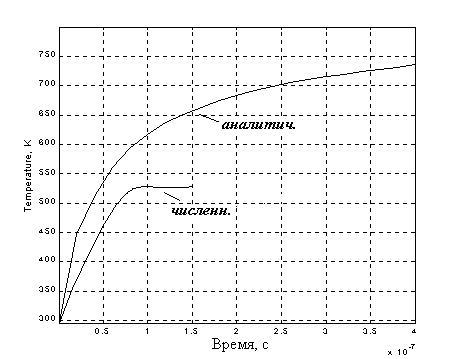
Рис. 3.2
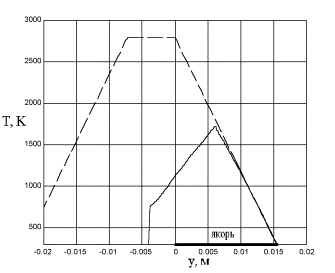
2. На рис. 3.3. сопоставлены результаты численных расчетов по двумерной модели с решением (2.6). На этом рисунке показаны распределения температуры вдоль поверхности контакта на два различных момента времени. Скорость движения якоря была постоянной и равнялась 1000 м/с. Теплофизические свойства якоря и рельса в численной модели, а также длина якоря, были взяты как в реальном рельсовом ускорителе. Величина q из уравнения (2.6) определялась через тангенс угла наклона правого фронта численной кривой распределения температуры на рис. 3.3.а. Якорь (зона источника тепла) занимает отрезок от 0.0 до 0.155 м. Зона, для которой численно решалась задача определения температуры, занимает отрезок от –0.004 м до 0.0165 м, поэтому численные кривые обрываются слева.
Видно, что теплопроводность, как в поперечном, так и в продольном направлениях, заметно влияет на картину распределения температуры. Близость углов наклона задних фронтов соответствующих численных и аналитических кривых, а также параллельность их передних фронтов, свидетельствуют о корректности учета конвективного теплопереноса при вычислениях по конечноэлементной модели.
|
а) t=12,3 мкс, (случай t<l/v) |
|
|
б) t=22,8 мкс, (t>l/v) |
|
Рис. 3.3. Сопоставление численно полученного распределения температуры на контакте со случаем чисто конвективного уноса тепла из зоны тепловыделения. Сплошные кривые – численный расчет, пунктир – решение (2.6).
С другой стороны, отличия расчетного и аналитического решений обусловлены различием численно решаемой задачи (0.1) и задачи (2.4). Главные из этих отличий: двумерность основной задачи (0.1) и присутствие теплопроводности во всех направлениях, различие источников тепла. В задаче (2.4) величина q есть мощность тепловыделения, в то время как в (0.1) Q – скачок теплового потока на границе раздела проводников.
При этом в зоне якоря в численных расчетах наблюдается тенденция к выходу распределения температуры контакта на стационарное распределение (см. численную кривую на рис. 3.3.б).
Заключение
В данной работе
представлена математическая модель процессов распространения тепла, источником
которого является механическое трение якоря о рельсы в электродинамическом
ускорителе типа рельсотрон. Показана необходимость введения нелинейной
искусственной теплопроводности в конечноэлементную схему для численного решения
соответствующего уравнения теплопроводности.
При определенных
допущениях, которые не привносят резких изменений в качественный характер
распределения температуры, получены аналитические решения. Данные аналитические
решения помогают объяснить картину распределения температуры, получаемую в вычислительных
экспериментах.
Аналитические и численные
результаты данной работы применены для сопоставления механического нагрева и
джоулева нагрева в рельсотроне. Показано, в частности, распространение зон
повышенной температуры, вызванных трением, от начала якоря по ходу движения.
Действие трения на всей контактной поверхности может привести к образованию
жидкой пленки значительно раньше, чем это произойдет за счет действия
скоростного скин – эффекта.
Литература
1. "Материалы I Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном поле" (Новосибирск, 10-13 апреля 1990 г.), под ред. М.Ф. Жукова, Новосибирск, изд. Инст. Теплофизики СО АН СССР, 1990, 350 с.
2. "Материалы II Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном поле" (Новосибирск, 4-6 декабря 1991г.), под ред. В.Е. Накорякова, Новосибирск, изд. Инст. Теплофизики СО РАН, 1992, 367 с.
3. М.П. Галанин, А.Д. Лебедев, А.П. Лотоцкий, К.К. Миляев. Тепловые и электромагнитные процессы на контактах электродинамического ускорителя // Препр. Ин. прикл. матем. им. М.В.Келдыша РАН. 2000. N 42. 32 с.
4. М.П. Галанин, Ю.П.
Попов. Квазистационарные электромагнитные поля в неоднородных средах.
Математическое моделирование. М., Наука. Физматлит. 1995. 320 с.
5. Галанин М.П. Нелинейная
квазимонотонная конечноэлементная схема для решения двумерных задач с
переносом. Задача о скоростном скин–слое // Дифференциальные уравнения. 1996. Т.
32. N 7. С.
935-942.
6. Галанин М.П. Задача о
скоростном скин - слое и квазимонотонная конечноэлементная схема для ее
численного решения. ускорителя // Препр. Ин. прикл. матем. им. М.В.Келдыша РАН.
1995. N 21. 29 с.
7. Г.И. Марчук, В.И.
Агошков. Введение в проекционно - сеточные методы. М., Наука, 1981, 416 с.
8. П. Сильвестер, Р.
Феррари. Метод конечных элементов для радиоинженеров и инженеров – электриков.
М., Мир, 1986, 229 с.
9. А.А. Самарский. Теория разностных схем. М., Наука, 1978, 656 с.
10. К.В. Вязников, В.Ф.
Тишкин, А.П. Фаворский, М.Ю. Шашков. Квазимонотонные разностные схемы повышенного
порядка для ее точности // Препр. Ин. прикл. матем. им. М.В.Келдыша АН СССР.
1987. N 36. 27 с.
11. М.В. Федорюк.
Асимптотика: Интегралы и ряды. М., Наука, 1987, 544 с.