Локальная обработка измерений радиосистемы межпланетных космических аппаратов

( Local measurement processing of the interplanetary spacecraft's radio system
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Введение

Определению орбит космических аппаратов предшествует первичная обработка траекторных измерений [1], которая решает следующие задачи:

-        небесно-механическую интерпретацию измерений;

-        идентификацию и удаление аномальных измерений;

-        сжатие результатов обработки траекторных измерений;

-        оценку качества измерений.

Прием и дешифровка траекторных измерений производятся автоматизированной системой баллистико-навигационного обеспечения управления полетами космических аппаратов (КА) [2]. Задача первичной обработки выбирает информацию из базы данных в структурированном виде, который соответствует содержанию информации, а не способу ее передачи по каналам связи.

Вопросы небесно-механической интерпретации траекторных измерений научных КА, в том числе межпланетных автоматических станций, рассмотрены в [3] и [4]. Настоящая работа посвящена вопросам оценки качества траекторных измерений, а также идентификации аномальных измерений.

Ошибки аномальных измерений могут быть обусловлены сбоями работы измерительной аппаратуры, либо большими искажениями при передаче результатов измерений по каналам связи, или другими причинами. Измерения с такими ошибками необходимо выявить и удалить до решения задачи определения параметров движения КА, поскольку отсутствие грубых ошибок измерений является одним из важнейших условий сходимости статистических методов оценивания параметров.

Алгоритм идентификации аномальных измерений использует априорную оценку точности траекторных измерений. Составляющие аппаратурных погрешностей измерений радиальной скорости и наклонной дальности радиосистемы дальних КА рассмотрены в [5]. В этой же работе приведены оценки этих составляющих, полученные в процессе работы с КА «Фобос-2».

Систематические ошибки измерений радиальной скорости определяются неточностью номинала частоты опорного генератора и фазовой нестабильностью приемопередающего тракта, каждая из которых составляет 0.15 мм/с. Составляющие флуктуационных ошибок, а также оценки их значений для 10-ти секундного интервала накопления показаны в таблице 1.

Таблица 1

Составляющие аппаратурной ошибки измерения наклонной дальности приведены в таблице 2.

Таблица 2

Флуктуационные ошибки измерений дальности определяются дискретом измерителя, составляющим 0.26 м и шумом, составляющим 1.4 м.

Ошибки, связанные с условиями распространения радиоволн в ионосфере и тропосфере, также имеют систематические составляющие [6],[7],[8],[9]. В процессе работы с КА «Фобос-2» учитывалась только тропосферная поправка измерений дальности, вычисляемая как функция влажности, давления и температуры [6]. Значения не учитываемых поправок приведены в таблице 3.

Таблица 3

При реализации проекта «Фобос-Грунт» на ответственных участках полета требуется обеспечить запросные измерения радиальной скорости с точностью 0.2 мм/c. Для достижения такой точности необходимо учитывать поправки к измерениям, вызванные условиями среды распространения. В первом разделе работы рассмотрен этот вопрос. Второй раздел посвящен вопросам идентификации аномальных измерений, сжатию информации и оценки качества измерений.

1.      Систематические погрешности измерений, обусловленные средой распространения

В работе [6] показано, что в сферически слоистой атмосфере поправка на фазовый путь  для сигнала, распространяемого с высоты до поверхности, может быть вычислена по формуле:

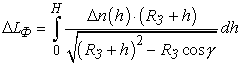
(1.1)

где

Используем это соотношение для получения поправок и оценок регулярных ошибок измерений дальности и скорости, вызванных тропосферой и ионосферой Земли.

1.1.       Систематические ошибки измерений, вызванные тропосферой Земли

Для тропосферы Земли справедлива следующая модель зависимости  от высоты:

 ,                                                                                                              (1.2)

где

Подставляя (1.2) в (1.1) и учитывая, что , преобразуем (1.1) к виду:

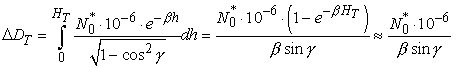
(1.3)

где

При работе с КА «Фобос-2» значение тропосферной поправки составляло от 2 до 22 м и учитывалось при обработке измерений.

Теперь, с использованием (1.1) и (1.2), получим соотношение для оценки систематической составляющей ошибки измерений скорости, вызванной тропосферой Земли:

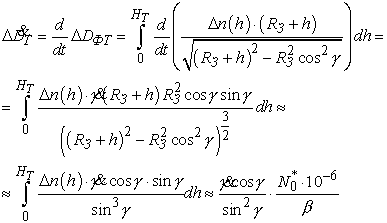
(1.4)

По данным, приведенным в [5], при работе с КА «Фобос-2» максимальное значение этой поправки составило 0.17 мм/с, но поправка не учитывалась при обработке измерений. При баллистико-навигационном обеспечении полета КА «Фобос-Грунт» эта поправка должна учитываться по формуле (1.4).

1.2.       Систематические ошибки измерений, вызванные ионосферой Земли

Для ионосферы Земли справедлива следующая модель для зависимости  от высоты:

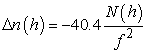
(1.5)

где

Подставляя (1.5) в (1.1), получим

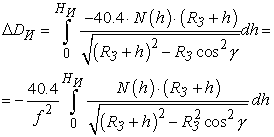
,                                                                                    (1.6)

где

Так как КА находится заведомо выше максимума электронной концентрации , можно воспользоваться следующей оценкой [6]:

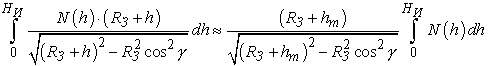
(1.7)

Используя (1.7), можно оценить :

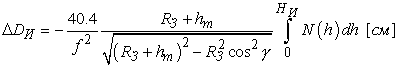
(1.8)

Значения ошибок, вносимых ионосферой, для различных углов места при интегральной электронной концентрации  и  показаны в таблице 4.

Таблица 4

Эти значения хорошо согласуются с данными, приведенными в [5]. Систематическая составляющая ошибки измерений радиальной скорости, вносимая ионосферой, определяется угловым перемещением луча ИП-КА по углу места. Поэтому соотношение для оценки можно получить дифференцированием (1.8) по времени. В результате получим:

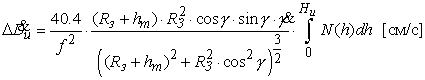
                                            (1.9)

Значения ошибок, обусловленных ионосферой, для различных углов места приведены в таблице 5. Интегральная электронная концентрация и  приняты такими же, как и при расчете таблицы 4.

Таблица 5

Значения ионосферных поправок для измерений дальности и скорости могут быть учтены, если на измерительных пунктах разместить приемник сигналов системы cпутниковой навигации, работающий на двух частотах. Используя соотношения (1.8) и (1.9), можно пересчитать поправку, полученную для частоты системы cпутниковой навигации, в поправку для частоты , на которой работает радиотехническая измерительная система.

2.      Идентификация аномальных измерений

Алгоритм идентификации аномальных измерений состоит из двух частей. Первая часть обеспечивает автоматическую идентификацию в случае, когда аномальных измерений не более 10%  от общего числа измерений, а вторая часть предназначена для автоматизированной работы в случае большого количества аномальных измерений.

В первой части алгоритма определяются коэффициенты линейной функции  от времени для аппроксимации невязок между измеренными и расчетными значениями. Анализируется среднеквадратичное отклонение построенной аппроксимации. Если среднеквадратичное отклонение аппроксимации меньше, чем априорно известное значение среднеквадратичной ошибки измерений, считается, что все измерения качественные. Если среднеквадратичное отклонение аппроксимации больше, чем априорно известная среднеквадратичная ошибка измерений, часть измерений должна быть удалена из последующей обработки. Измерения, для которых величина невязки между измеренным и расчетным значениями больше утроенного значения среднеквадратичного аппроксимации, удаляются из выборки. Процесс построения аппроксимации повторяется.

Если в результате работы первой части алгоритма не удалось идентифицировать и удалить некачественные измерения, включается вторая часть алгоритма. Этот алгоритм основан на предположении, что аппаратурная ошибка проявляется в добавлении к некоторой группе измерений значения, постоянного по величине. Искаженные измерения не обязательно следуют друг за другом. В одном сеансе может быть несколько групп измерений. В предположении, что разность между измеренными и расчетными значениями имеет линейный характер, измерения, попадающие в одну группу, должны лежать в определенных границах вокруг  некоторой прямой. Алгоритм определяет прямые и границы, а затем    формирует группы из исходной совокупности измерений. Допускается, что одно измерение может одновременно входить в несколько групп. Далее производится идентификация групп аномальных измерений. В разделе 2.2.5. рассмотрен алгоритм автоматического выделения групп аномальных измерений. Допускается автоматизированная работа, когда решение о том, какие группы соответствуют аномальным измерениям, принимает оператор.

2.1.       Критерий качества измерений на основе линейной аппроксимации невязок между измеренными и расчетными значениями

В данном разделе описан алгоритм отбраковки аномальных измерений, основанный на аппроксимации невязок между расчетными и измеренными значениями простой линейной регрессией.

2.1.1. Входная информация

Входной информацией алгоритма является:

-        множество пар ,

-        априорно известное среднеквадратическое значение флуктуационной составляющей ошибки измерений ,

где

Далее, не ограничивая общности, будем считать, что .

2.1.2. Результат работы алгоритма

Алгоритм может завершаться с положительным или отрицательным кодом ответа. В случае положительного кода ответа формируется подмножество качественных измерений, определяется оценка среднеквадратического значения флуктуационной составляющей ошибки измерений и другие параметры статистической модели. Отрицательный код ответа означает, что невозможно выбрать подмножество качественных  измерений.

2.1.3. Описание алгоритма

Алгоритм состоит из трех шагов.

Шаг 1. Преобразование входных данных

Измеренные значения преобразуются в невязки. Моменты времени отсчитываются от середины интервала .

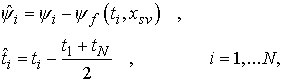                                                                                 (2.1)

здесь

Шаг 2. Построение линейной регрессии

Строится линейная регрессия  по множеству пар .

Определение значений , ошибок определения этих значений , а также среднеквадратического значения  величин . Значения  и  определяются по формулам:

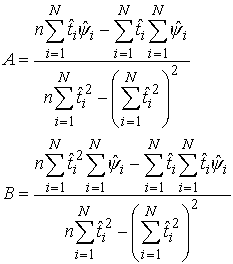                                                                                              (2.2)

Среднеквадратическое значение  величин вычисляется по формуле:

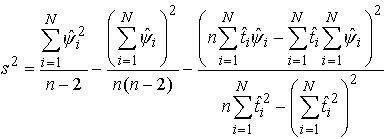                                                      (2.3)

Ошибки определения коэффициентов  и  вычисляются по формулам:

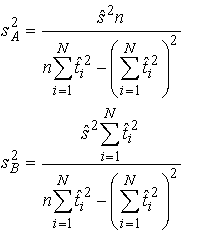                                                                                                     (2.4)

Шаг 3. Анализ результатов

Величина  сравнивается со среднеквадратическим значением флуктуационной составляющей ошибки измерений . Если , все измерения считаются качественными. Если , требуется исключить аномальные измерения. Исключаются измерения, для которых выполняется условие:

                                                                                                                (2.5)

Значение коэффициента  выбирается из диапазона  при условии, что количество исключаемых измерений не превосходит 50%. Если такое значение  выбрать можно, множество измерений корректируется и происходит переход к шагу 2. Если  выбрать нельзя, алгоритм завершается с отрицательным кодом.

2.1.4. Методическая погрешность, обусловленная применением линейной регрессии

Была проведена оценка методической погрешности, обусловленная применением линейной регрессии для аппроксимации невязок измеренных и расчетных значений, для орбиты спутника Марса, близкой к круговой, плоскость которой совпадает с плоскостью орбиты Фобоса, а полуось больше, чем полуось орбиты Фобоса, на ~300 км (орбита наблюдения КА «Фобос-2»). Расчеты показали, что если опорная и реальная орбиты различаются так, что невязки расчетных значений радиальной скорости не превосходят 15 мм/с, то на 10-ти минутном интервале их можно аппроксимировать линейной регрессией с точностью лучше, чем 0.01 мм/с.

2.2.       Критерий качества измерений на основе разбиения массива на группы

2.2.1. Входная информация

Входной информацией алгоритма является такая же информация, что и для алгоритма, рассмотренного в п 2.1.

2.2.2. Выходная информация

Выходной информацией алгоритма является список групп информации с указанием следующих параметров по каждой группе:

- максимальная невязка;

- минимальная невязка;

- начало базового набора;

- конец базового набора;

- число точек базового набора;

- общее число точек массива измерений, которые относятся к данной группе.

Здесь под базовым набором понимается подмножество пар исходного множества, моменты времени которых следуют друг за другом, и для которых выполняется критерий объединения в группы.

2.2.3. Статистическая модель

Рассмотрим случайные величины

 ,                                                                                      (2.6)

где

Можно показать, что

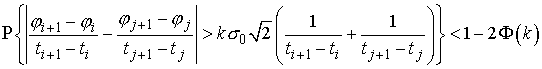,                (2.7)

где

Например, вероятности 0.995 соответствует , а вероятности 0.9995 — .

Условие (2.7) используется в алгоритме для разделения пар точек на группы по значению локального наклона.

2.2.4. Описание алгоритма

Алгоритм состоит из четырех шагов.

Шаг 1. Преобразование входных данных

Производится такое же преобразование, как и на первом шаге п. 2.1.3.

Шаг 2. Определение среднего значения локального наклона

На этом шаге алгоритма последовательно анализируются наклоны пар точек i, i+1 и формируется массив локальных наклонов. Каждый элемент массива локальных наклонов содержит 5 параметров:

Последовательно анализируются наклоны соседних точек i и i+1. Проверяется — соответствуют ли друг другу локальные наклоны соседних точек в рамках статистической модели ошибок измерений (условие 2.7). При этом проверяется, что

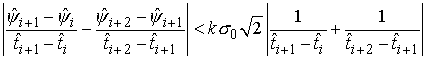,                                          (2.8)

где

Если условие (2.8) выполняется, модифицируется массив локальных наклонов. Если условие не выполняется, происходит переход к следующей паре точек.

Модификация массива локальных наклонов производится следующим образом. В начале ищется такой элемент m, для которого выполняется:

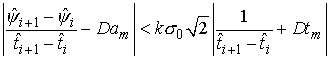.                                                                     (2.9)

Если такой элемент найден, модифицируются значения ,  и . При модификации  увеличивается на единицу, а

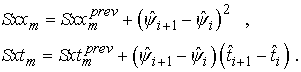                                                                           (2.10)

Здесь  и  — значения на предыдущем шаге. Если в массиве локальных наклонов имеется несколько наклонов, для которых выполняется условие (2.9), выбирается элемент с минимальным значением индекса m. Если в массиве локальных наклонов нет элемента, для которого выполняется условие (9), формируется новый элемент.

После завершения формирования массива локальных наклонов, определяется средний локальный наклон. Для этого выбирается элемент  массива локальных наклонов с максимальным числом точек. Среднее значение локального наклона определяется по формуле:

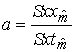.                                                                                                                                  (2.11)

Следует отметить, что вычисление среднего локального наклона по формуле (2.11) соответствует условию минимума функционала:

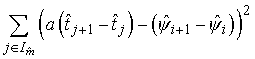,                                                                                     (2.12)

где

Шаг 3. Формирование групп

На этом шаге алгоритма формируется массив групп. Каждый элемент массива содержит 6 параметров:

Формирование массива групп происходит следующим образом. Последовательно просматриваются точки исходного массива. Проверяется условие

.                                                                                  (2.13)

Если условие (2.13) выполняется, корректируются параметры текущего m-го элемента массива: , , ,  и . В противном случае начинает формироваться новый элемент массива групп. После завершения формирования массива групп, для каждого элемента массива групп определяется число точек исходного массива, которое можно отнести к данной группе. Для  этого проверяется: попадает ли невязка проверяемой точки в интервал между минимальной и максимальной невязкой группы. Одна точка может быть отнесена к нескольким группам.

Шаг 4. Анализ результатов

Сначала исключаются точки, которые не относятся ни к какой группе. Как правило,  это отдельные аномальные точки. Затем анализируются группы и отмечаются те из них,  которые соответствуют аномальным измерениям. Затем исключаются точки, относящиеся к отмеченным группам.

Выделение групп аномальных измерений может производиться автоматически или вручную. При работе по проекту «Фобос-2» использовалась ручная технология. Алгоритм автоматического выделения групп аномальных измерений приведен в разделе 2.2.5.

2.2.5. Выделение групп аномальных измерений

Алгоритм состоит из 5 шагов.

Шаг 1. Построение линейных регрессий

Для каждой группы  выбираются точки, по которым была построена группа и по этим точкам строится линейная регрессия:

,                                                                                                           (2.14)

где

Наряду с параметрами линейной регрессии  и  определяются величины:

Шаг 2. Контроль по среднеквадратическим значениям

Из дальнейшего рассмотрения удаляются группы, у которых  .

Шаг 3. Установка веса группы

Для каждой группы определяется значение параметра  — число точек, которое может быть отнесено к данной группе.

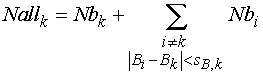,                                                                                   (2.15)

где

Шаг 4. Выбор основной группы

Выбирается группа , для которой значение  максимально. Если имеется несколько таких групп, выбирается группа с минимальным значением индекса.

Шаг 5. Выделение групп некачественных измерений

Исключаются все группы, точки которых не могут быть отнесены к группе, выбранной на шаге 4, т.е. если выполняется условие

,                                                                                                              (2.16)

группа исключается.

2.3.       Примеры работы алгоритмов

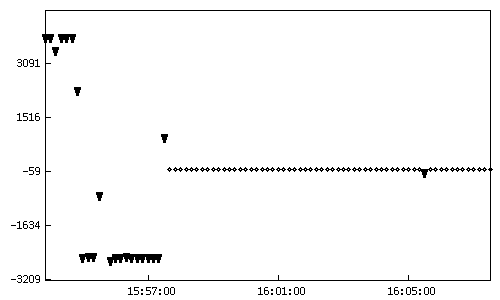
Примеры работы алгоритма на измерениях, полученных по КА «Фобос-2» в 1988-1989 гг, показаны на рисунках 1-4. В верхней части каждого рисунка показаны невязки измеренных и расчетных значений для всех измерений. Треугольными метками отмечены аномальные измерения. В нижней части рисунка показаны только измерения, оставшиеся после удаления аномальных измерений. Сплошной линией показана линейная функция, аппроксимирующая невязки и построенная по алгоритму 2.1. По оси ординат отложены невязки в м (рис. 1-3) и мм/с (рис. 4). По оси абсцисс отложено время в часах, минутах, секундах.

Результаты локальной обработки всех массивов измерений, проведенных в сантиметровом диапазоне по КА «Фобос-2», показаны в таблице 6.

        Таблица 6

.

Литература

1.      Э.Л. Аким, И.К. Бажинов, В.П. Павлов, В.Н. Почукаев. Поле тяготения Луны и движение ее искусственных спутников. М.: Машиностроение, 1984.

2.      Тучин А.Г., Шатаев В.В. Реализация реляционной СУБД с языком данных типа SQL // Препринт № 54, М.: ИПМ им. М.В. Келдыша РАН, 1990, 28 с.

3.      Небесно-механическая интерпретация и первичная обработка измерений КА "Гранат" и "Интербол". Э.Л. Аким, А.А. Горохова, И.П. Киселева, В.А. Степаньянц, А.Г. Тучин // Препринт № 83, М.: ИПМ им. М.В.Келдыша РАН, 1996, 21 с.

4.      Небесно-механическая интерпретация измерений радиосистемы межпланетных космических аппаратов «Квант-Д». Э.Л. Аким,  А.А. Горохова, И.П. Киселева, В.А. Степаньянц, А.Г. Тучин // Препринт №2, M.: ИПМ им. М.В. Келдыша РАН, 2002, 21с.

5.      Радиосистемы межпланетных космических аппаратов. Р.В.Бакитько, М.Б. Васильев, А.С. Виницкий и др. // М.: Радио и связь, 1993, 328 с.

6.      М.А. Колосов, Н.А. Арманд, О.И. Яковлев. Распространение радиоволн при космической связи // М.: Связь, 1969, 155 с.

7.      Космические траекторные измерения. Радиотехнические методы измерений и математическая обработка данных. Под ред. П.А. Агаджанова, В.Е. Дулевича, А.А. Коростелева // М.: Советское радио, 1969, 504 с.

8.      Ф.Б. Черный. Распространение радиоволн // М.: Советское радио, 1972, 464 с.

9.      А.Г. Квашнин, А.Г. Тучин. Баллистическое обеспечение радиоинтерферометрических измерений // Препринт № 98, М.: ИПМ им. М.В. Келдыша РАН, 1992, 26 с.

Приложение

До удаления аномальных измерений

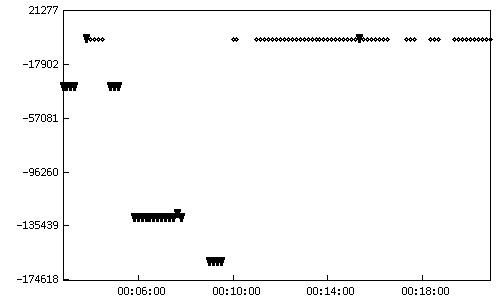
После удаления аномальных измерений

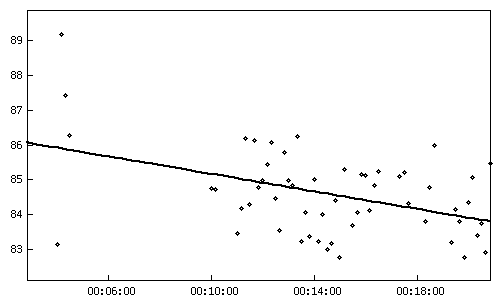
Рис.1. Невязки измеренных и расчетных значений до и после удаления аномальных измерений. По оси ординат — значения невязок в м, по оси абсцисс — время. Измерения наклонной дальности 1-го комплекта 292-го сеанса, проведенного из Евпатории 1988/08/19.

До удаления аномальных измерений

После удаления аномальных измерений

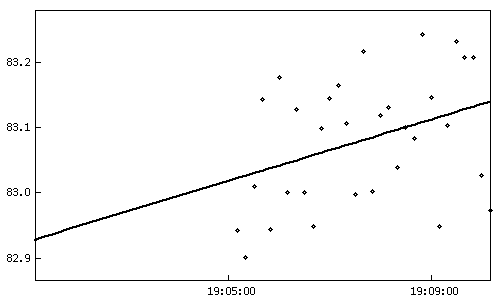
Рис.2. Невязки измеренных и расчетных значений: до и после удаления аномальных измерений. По оси ординат — значения невязок в м, по оси абсцисс — время. Измерения радиальной скорости 2-го комплекта 833-го сеанса, проведенного из Евпатории 1988/10/20.

До удаления аномальных измерений

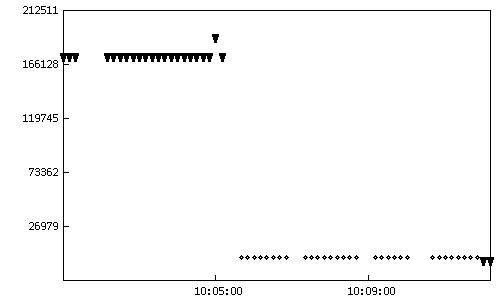
После удаления аномальных измерений

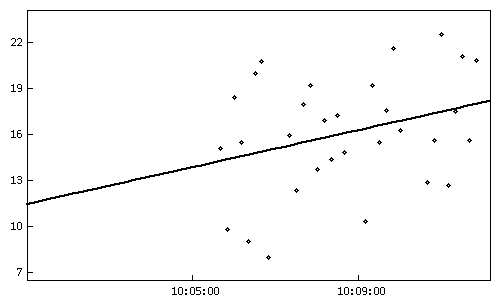
Рис.3. Невязки измеренных и расчетных значений: до и после удаления аномальных измерений. По оси ординат — значения невязок в м, по оси абсцисс — время. Измерения наклонной дальности 2-го комплекта 353-го сеанса, проведенного из Уссурийска 1988/12/06.

До удаления аномальных измерений

После удаления аномальных измерений

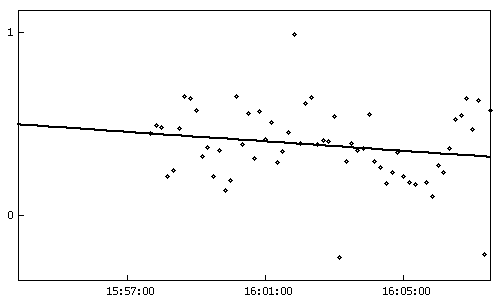
Рис.4. Невязки измеренных и расчетных значений до и после удаления аномальных измерений. По оси ординат — значения невязок в мм/с, по оси абсцисс — время. Измерения радиальной скорости 1-го комплекта 831-го сеанса, проведенного из Евпатории 1989/01/20.