Аннотация
Принцип Даламбера-Лагранжа распространяется на механические системы с односторонними связями.
Формулируются условия идеальности связей. Выводятся уравнения движения в форме уравнений
Лагранжа 1-го и 2-го рода, а также в форме уравнений Гамильтона.
Ключевые слова: механические системы с ударами, уравнения движения
Abstract
Dalamber-Lagrange principle expanded on to mechanics systems with one sided realations.
Ideal relations conditions are described. Equation of motion as Lagrange equations of
first and second kinds and Hamilton equations are derived.
Key words: Mechanical systems with impacts, equation of motion
Содержание
Введение
1. Уравнения
движения при однократном ударе.
2. Движение
вдоль ограничения.
3. Интеграл
Стилтьеса.
4. Формула
Лейбница.
5. Импульсные
дифференциальные уравнения.
6. Лемма об
аннуляторе.
7. Принцип
Даламбера-Лагранжа в интегральной фоме.
8. Уравнения
Лагранжа первого рода.
9. Гладкие
системы.
10. Уравнения
Лагранжа второго рода.
11. Канонические
уравнения Гамильтона.
Литература
В работе рассматриваются
механические системы с односторонними связями. Обзор работ по данной тематике
можно найти в [1,2]. Рассмотрим, например, склерономную систему с одной такой
связью. Для простоты будем предполагать, что удерживающие связи идеальны,
голономны и не зависят от времени, а действующие силы потенциальны. Пусть 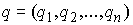 – вектор обобщенных
координат, и – вектор обобщенных
координат, и 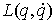 – лагранжиан системы.
Одностороннюю связь будем описывать как ограничение – лагранжиан системы.
Одностороннюю связь будем описывать как ограничение
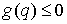 (1) (1)
где 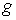 предполагается
гладкой (класса предполагается
гладкой (класса 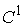 ) функцией обобщенных координат, причем ) функцией обобщенных координат, причем 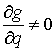 нигде на поверхности
удара нигде на поверхности
удара 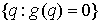 . .
При анализе движения системы материальных точек с
односторонними связями возникающие удары можно описывать, вводя реакции
односторонних связей в правые части уравнений Лагранжа второго рода. Если
траектория движения имеет конечное (или не более чем счетное) множество точек
удара, то реакции связей можно описать, используя дельта-функции Дирака. Однако
такое описание не подходит для участков
траектории, которые лежат на границе связи в течение некоторого отрезка
времени. На этом отрезке реакции односторонних связей являются гладкими
функциями времени.
В данной работе в качестве аппарата,
пригодного для описания движения систем с односторонними связями на любых
участках траектории, предлагается использовать теорию функций с ограниченной
вариацией (или, говоря иначе, мер Лебега-Стилтьеса). Остановимся на мотивах
именно такого выбора. В классической механике систем с идеальными удерживающими
связями движение механической системы представляет собой достаточно гладкую
кривую в конфигурационном пространстве. При наложении односторонних связей скорость
движения может уже претерпевать скачки. В большинстве случаев её
представляют в виде гладкой функции, к
которой добавляется кусочно-постоянная функция, называемая функцией скачков.
Таким образом, реальное движение систем с односторонними связями можно было бы
описывать в пространстве функций, которые представимы в виде такой суммы.
Однако такое пространство не является удобным для исследования свойств движения
аналитическими средствами. Например, в нем затруднительно решать вопрос о корректности
систем обыкновенных дифференциальных уравнений, описывающих движение. Удачным
пространством было бы, например, какое-либо банахово, т.е. полное метрическое
пространство функций. В самом деле, когда (при исследовании систем с
удерживающими связями) мы берем в качестве пространства возможных скоростей
движения банахово пространство непрерывных функций с естественной метрикой, то
оказывается, что решения дифференциальных уравнений (т.е. траектории)
существуют и, даже, являются гладкими.
Здесь уместно поставить вопрос о том,
каково минимальное пространство функций, которое объемлет гладкие функции и
функции скачков и при этом является банаховым. Естественной метрикой в
пространстве функций скачков является полная вариация. И минимальным подходящим
для нас банаховым пространством с этой метрикой является пространство функций с
ограниченной вариацией. Именно поэтому удобным представляется выбор
пространства возможных траекторий систем с односторонними связями в виде
пространства таких функций, производная (скорость) которых является функцией с
ограниченной вариацией. Сами траектории при этом, по крайней мере, являются абсолютно
непрерывными функциями. При таком описании движения реакции связей также
описываются как меры Лебега-Стилтьеса. Уравнения движения в этом случае
представляют собой обыкновенные дифференциальные уравнения, содержащие
импульсные члены в правой части.
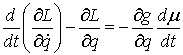 – в форме Лагранжа, (2) – в форме Лагранжа, (2)
или
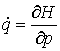 , , 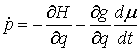 – в
форме Гамильтона. (3) – в
форме Гамильтона. (3)
Здесь 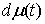 – некоторая
неотрицательная мера Лебега-Стилтьеса сосредоточенная на множестве тех точек
времени, в которые траектория движения
выходит на одностороннюю связь. Эта мера зависит от траектории и
характеризует реакцию односторонней связи. Следует заметить, что уравнения (2)
по форме совпадают с уравнения Аппеля для систем с непроинтегрированными связями. – некоторая
неотрицательная мера Лебега-Стилтьеса сосредоточенная на множестве тех точек
времени, в которые траектория движения
выходит на одностороннюю связь. Эта мера зависит от траектории и
характеризует реакцию односторонней связи. Следует заметить, что уравнения (2)
по форме совпадают с уравнения Аппеля для систем с непроинтегрированными связями.
Соображения, приводящие к
такому виду уравнений, могут быть следующими. Известно, что вариационные
принципы механических Лагранжевых систем с идеальными связями можно
эквивалентным образом формулировать в виде классической задачи оптимального
управления [3, 4]. При таком рассмотрении движение лагранжевых систем с
освобождающими связями можно описывать как решение классической задачи
оптимального управления с ограничениями на фазовые координаты. Для этих задач
известны необходимые условия экстремума Дубовицкого-Милютина в форме принципа
максимума [5]. Следует отметить, однако, что эти условия не означают обращения
в нуль вариации какого-либо функционала, а говорят о том, что соответствующие
конуса убывания, возможных и касательных направлений не пересекаются [6]. Переформулировка
этих необходимых условий в форме принятой для Лагранжевых и Гамильтоновых
систем дает приведенные выше дифференциальные уравнения движения (2-3),
содержащие в правой части члены с мерой Лебега-Стилтьеса.
Перейдем теперь к краткому
описанию работы. В первых двух разделах рассматриваются два простейших случая –
движение с однократным выходом на одностороннее ограничение и движение,
состоящее из участка свободного движения, который переходит в участок движения
по границе односторонней связи. Эти разделы служат иллюстрацией единообразного
описания движения импульсными дифференциальными уравнениями при наличии
односторонних связей.
В разделах 3 – 6 приводятся
необходимые сведения из функционального анализа, и доказывается несколько
небольших утверждений. В разделе 3 описываются основные факты из теории функций
с ограниченной вариацией и мер Лебега-Стилтьеса. В разделе 4 доказывается,
необходимая для дальнейшего, формула Лейбница для мер Лебега-Стилтьеса. В
разделе 5 рассматривается вопрос о том, как понимать обыкновенные
дифференциальные уравнения с импульсной правой частью. Даются строгие определения.
Формулируется (без доказательства) теорема о существовании и единственности
решения для таких уравнений. В разделе 6 формулируется лемма об аннуляторе ядра
регулярного оператора в банаховых пространствах и рассматривается один
конкретный пример описания такого аннулятора, который используется при выводе
уравнений Лагранжа первого рода.
В разделе 7 для механических систем с
двусторонними связями обычное условие идеальности связей, принцип
Даламбера-Лагранжа и уравнения Лагранжа первого рода формулируются в
интегральном виде. Это используется в дальнейшем для обоснования уравнений
движения систем с конфигурационными ограничениями. В разделе 8 формулируется
принцип Даламбера-Лагранжа, и выводятся уравнения Лагранжа первого рода для
механических систем с идеальными односторонними связями. Предварительно
формулируется условие идеальности при наличии односторонних связей. В локальной
формулировке принцип Даламбера-Лагранжа для таких систем известен уже давно
[7]. Однако, исходя из него, затруднительно получать уравнения движения
справедливые на всем отрезке движения, поскольку в его формулировке присутствуют
ускорения точек системы, которые могут быть неопределенными в моменты выхода на
границу односторонних связей (т.е. в точках удара). В данном разделе мы даём интегральную
формулировку принципа Даламбера-Лагранжа, которая позволяет избавиться от этих
трудностей.
В разделе 9 рассматривается
случай, когда все функции, входящие в определение нашей механической системы,
являются гладкими 2-го порядка по всем переменным. В этом случае и само
движение и уравнения движения имеют более простой вид. В разделах 10 и 11 выводятся уравнения движения механических
систем с односторонними связями в форме уравнений Лагранжа второго рода и
канонических уравнений Гамильтона.
Рассмотрим случай, когда траектория однократно
выходит на ограничение (1) в момент времени 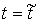 . Для случая, когда связь имеет простую форму . Для случая, когда связь имеет простую форму 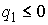 уравнения движения
можно написать, используя дельта-функцию Дирака (см. например [8]). уравнения движения
можно написать, используя дельта-функцию Дирака (см. например [8]).
 и и 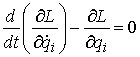 , при , при 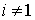 (1.1) (1.1)
где 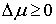 – некоторое
неотрицательное число, которое принято называть ударным импульсом. – некоторое
неотрицательное число, которое принято называть ударным импульсом.
Из (1.1) непосредственно вытекает теорема Аппеля о
сохранении обобщенных импульсов в касательной плоскости поверхности удара [9,
10]:
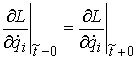 , ,  (1.2) (1.2)
При преобразованиях обобщенных координат левая
часть уравнений Лагранжа второго рода преобразуются как ковектор. Поэтому
правая часть уравнений (1.1) также преобразуется как ковектор. Остюда следует,
что в общем случае, когда уравнение связи имеет общий вид 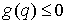 , уравнения (1.1) будут выглядеть следующим образом: , уравнения (1.1) будут выглядеть следующим образом:
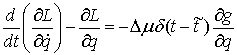 (1.3) (1.3)
а теорему Аппеля можно сформулировать так:
Теорема Аппеля.
Пусть траектория 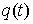 однократно выходит на
ограничение однократно выходит на
ограничение 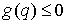 в некоторый момент
времени в некоторый момент
времени 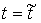 . Пусть . Пусть  – любой вектор касательный
поверхности удара в точке удара: – любой вектор касательный
поверхности удара в точке удара:  , тогда , тогда  . Т.е. проекция обобщенного импульса на касательную плоскость
поверхности удара не изменяется во время удара. . Т.е. проекция обобщенного импульса на касательную плоскость
поверхности удара не изменяется во время удара.
Для натуральных механических
систем величину ударного импульса 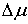 можно найти из закона
сохранения энергии. Пусть можно найти из закона
сохранения энергии. Пусть 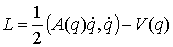 . Обозначим . Обозначим 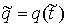 , , 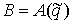 , , 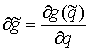 , , 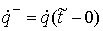 и и 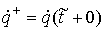 , тогда из (1.3) имеем , тогда из (1.3) имеем  или, или, 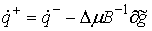 а из закона
сохранения энергии а из закона
сохранения энергии 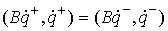 . Отсюда . Отсюда 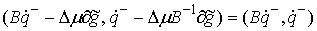 или или
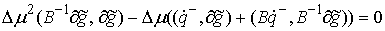 (1.4) (1.4)
Рассмотрим случай, когда траектория подходит к
поверхности удара под ненулевым углом, т.е. 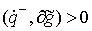 . Уравнение (1.4) допускает решение . Уравнение (1.4) допускает решение 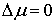 . Однако, в этом случае . Однако, в этом случае 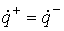 и и 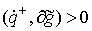 , Это противоречит, тому, что траектория однократно выходит
на ограничение. Таким образом, , Это противоречит, тому, что траектория однократно выходит
на ограничение. Таким образом, 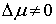 и из (1.4) находим и из (1.4) находим
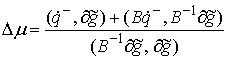
Рассмотрим случай, когда траектория движения нашей
системы в момент 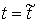 выходит на
ограничивающую поверхность выходит на
ограничивающую поверхность  и в дальнейшем двигается
по ней. Это означает, что в момент и в дальнейшем двигается
по ней. Это означает, что в момент 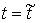 траектория движения
касается этой поверхности. траектория движения
касается этой поверхности.
До выхода на ограничение, т.е. при 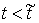 , уравнения движения имеют вид , уравнения движения имеют вид
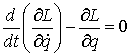 (2.1) (2.1)
При выходе на ограничение, т.е. при 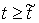 , к действующим силам добавляется реакция связи , к действующим силам добавляется реакция связи 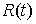 , направленная по ковектору , направленная по ковектору  в сторону области в сторону области 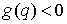 . Уравнения движения приобретут следующий вид . Уравнения движения приобретут следующий вид
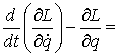 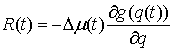 (2.2) (2.2)
где 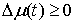 – некоторая
неотрицательная непрерывная (и даже дифференцируемая) функция, зависящая от
траектории движения. Введем теперь монотонно неубывающую функцию – некоторая
неотрицательная непрерывная (и даже дифференцируемая) функция, зависящая от
траектории движения. Введем теперь монотонно неубывающую функцию 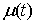 следующим образом: следующим образом:
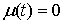 при при 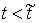 , и , и 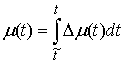 при при 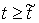 . .
Тогда уравнения движения (2.1-2.2) можно свести воедино:
 (2.3) (2.3)
Напомним,
несколько утверждений относящихся к интегралу Стилтьеса [11, 12]. Исходя из
нужд данной работы, начнем мы со случая неотрицательных мер.
Неотрицательные меры Лебега-Стилтьеса. Разбиением (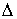 , , 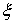 ) отрезка ) отрезка  называется его
представление в виде объединения конечного упорядоченного множества сегментов называется его
представление в виде объединения конечного упорядоченного множества сегментов 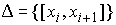 , , 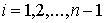 , , 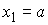 , , 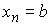 , , 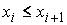 и выбор семейства
точек и выбор семейства
точек 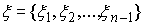 по одной в каждом сегменте по одной в каждом сегменте
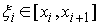 . Пусть . Пусть 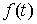 – непрерывная, а – непрерывная, а 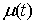 монотонно неубывающие
функции на отрезке монотонно неубывающие
функции на отрезке 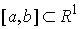 . Частной суммой для
разбиения ( . Частной суммой для
разбиения ( , , 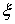 ) называется величина ) называется величина 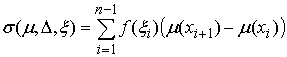 . Если эти частные суммы стремятся к конечному пределу . Если эти частные суммы стремятся к конечному пределу 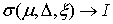 при при 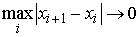 равномерно по равномерно по 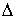 , ,  , то он называется интегралом Стилтьеса функции , то он называется интегралом Стилтьеса функции 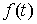 по функции по функции 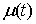 и обозначается и обозначается 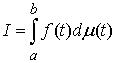 . .
Замечание. Пусть 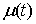 монотонно неубывающая
функция на отрезке монотонно неубывающая
функция на отрезке 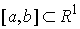 . С ее помощью можно определить меру . С ее помощью можно определить меру 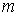 интервалов и полуинтервалов
на интервалов и полуинтервалов
на 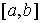 . Пусть . Пусть 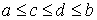 положим положим
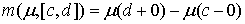 , , 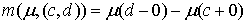 , ,
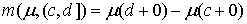 , , 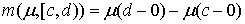 , ,
Эту меру
полуинтервалов можно расширить до меры Лебега на отрезке 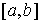 . Она называется неотрицательной мерой Лебега-Стилтьеса с
производящей функцией . Она называется неотрицательной мерой Лебега-Стилтьеса с
производящей функцией 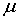 и обозначается и обозначается 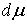 или или 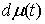 . Мера . Мера 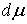 Лебега-Стилтьеса позволяет
определить интеграл Лебега суммируемой функции Лебега-Стилтьеса позволяет
определить интеграл Лебега суммируемой функции 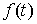 на отрезке на отрезке 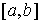 . Он обозначается . Он обозначается  и называется интегралом Лебега-Стилтьеса. и называется интегралом Лебега-Стилтьеса.
Если 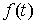 – непрерывная
функция, то интегралы Стилтьеса и Лебега-Стилтьеса совпадают. В дальнейшем мы
будем работать только с интегралами от непрерывных функций и поэтому не будем
различать интегралы Стилтьеса и Лебега-Стилтьеса. – непрерывная
функция, то интегралы Стилтьеса и Лебега-Стилтьеса совпадают. В дальнейшем мы
будем работать только с интегралами от непрерывных функций и поэтому не будем
различать интегралы Стилтьеса и Лебега-Стилтьеса.
Пример 1. Если 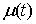 – абсолютно
непрерывная функция, то почти всюду на – абсолютно
непрерывная функция, то почти всюду на 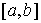 существует
производная существует
производная  и и 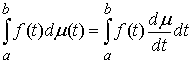 Неотрицательность
меры Неотрицательность
меры 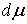 в этом случае
означает, что в этом случае
означает, что 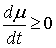 почти всюду. почти всюду.
Пример 2. Взяв
ступенчатую функцию 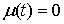 при при 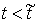 , и , и 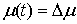 при при 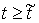 , мы получим , мы получим 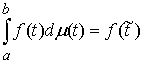 . В этом случае . В этом случае 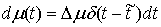 . Неотрицательность меры . Неотрицательность меры  означает, что означает, что  . .
Говорят,
что неотрицательная мера Лебега Стилтьеса сосредоточена на множестве 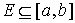 , если для любой непрерывной функции , если для любой непрерывной функции 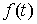 равной нулю на равной нулю на 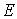 будет будет 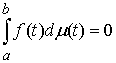 . В примере 1 мера сосредоточена на множестве точек, в
которых . В примере 1 мера сосредоточена на множестве точек, в
которых 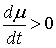 . В примере 2 мера сосредоточена в точке . В примере 2 мера сосредоточена в точке 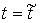 . .
Знакопеременные меры Лебега-Стилтьеса. Рассмотрим теперь знакопеременные меры. Пусть 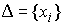 , , 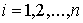 , , 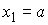 , , 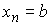 , , 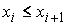 – разбиение отрезка – разбиение отрезка 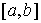 . Частной вариацией конечной функции . Частной вариацией конечной функции 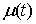 , заданной на отрезке , заданной на отрезке 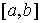 , для разбиения , для разбиения  называется величина называется величина
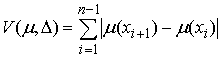
Функция 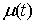 называется функцией с
ограниченной вариацией, если все ее частные вариации равномерно ограничены
сверху. Верхняя грань частных вариаций называется функцией с
ограниченной вариацией, если все ее частные вариации равномерно ограничены
сверху. Верхняя грань частных вариаций 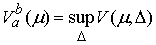 называется полной вариацией (или просто вариацией) функции называется полной вариацией (или просто вариацией) функции 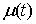 на отрезке на отрезке 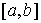 . Для монотонно неубывающей функции . Для монотонно неубывающей функции 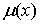 имеем имеем 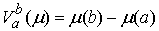 . .
Любую
функцию 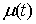 с ограниченной
вариацией на отрезке с ограниченной
вариацией на отрезке 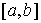 можно представить в
виде разности монотонно неубывающих функций: можно представить в
виде разности монотонно неубывающих функций: 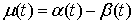 , где , где  , , 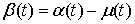 . Функции . Функции 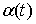 и и 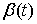 порождают
неотрицательные меры Лебега-Стилтьеса порождают
неотрицательные меры Лебега-Стилтьеса  и и 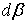 на на 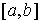 . Разность этих мер . Разность этих мер 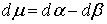 называется
(знакопеременной) мерой Лебега-Стилтьеса с производящей функцией называется
(знакопеременной) мерой Лебега-Стилтьеса с производящей функцией  . .
Как и выше можно определить интеграл Стилтьеса.
Пусть 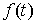 – непрерывная
функция, а – непрерывная
функция, а 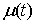 функция ограниченной
вариации на отрезке функция ограниченной
вариации на отрезке 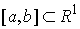 . Частной суммой для
разбиения ( . Частной суммой для
разбиения ( , ,  ) называется величина ) называется величина
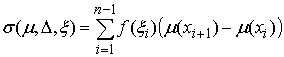
Если эти
частные суммы стремятся к конечному пределу 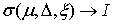 при при 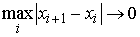 равномерно по равномерно по 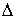 , , 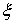 , то он называется интегралом Стилтьеса функции , то он называется интегралом Стилтьеса функции 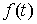 по функции по функции 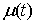 и обозначается и обозначается 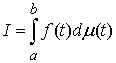 . Если . Если 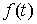 – непрерывная
функция, то интегралы Стилтьеса и Лебега-Стилтьеса совпадают. Если – непрерывная
функция, то интегралы Стилтьеса и Лебега-Стилтьеса совпадают. Если 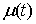 – абсолютно
непрерывная, а – абсолютно
непрерывная, а 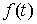 – непрерывная функции,
то – непрерывная функции,
то
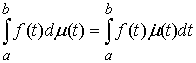
Особенности
мер Лебега-Стилтьеса. Любую монотонно неубывающую функцию 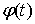 можно однозначным
образом разложить в сумму трех монотонно неубывающих функций можно однозначным
образом разложить в сумму трех монотонно неубывающих функций 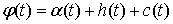 , где , где 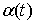 – абсолютно непрерывная
функция, – абсолютно непрерывная
функция, 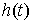 – ступенчатая функция
или функция скачков (это кусочно-постоянная функция с не более чем счетным
числом отрезков постоянства), – ступенчатая функция
или функция скачков (это кусочно-постоянная функция с не более чем счетным
числом отрезков постоянства), 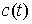 – непрерывная
функция, производная которой почти всюду равна нулю. Слагаемое – непрерывная
функция, производная которой почти всюду равна нулю. Слагаемое 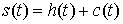 называется
сингулярной составляющей функции называется
сингулярной составляющей функции 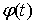 . Любая функция . Любая функция 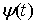 с ограниченной
вариацией единственным образом представима в виде с ограниченной
вариацией единственным образом представима в виде 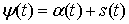 , где , где 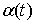 – абсолютно
непрерывная функция, – абсолютно
непрерывная функция, 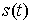 – сингулярная функция
(т.е. функция с ограниченной вариацией, производная которой почти всюду равна
нулю). – сингулярная функция
(т.е. функция с ограниченной вариацией, производная которой почти всюду равна
нулю).
Рассмотрим
теперь меру Лебега-Стилтьеса 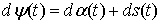 . Множество, на котором сосредоточена сингулярная мера . Множество, на котором сосредоточена сингулярная мера 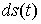 , называется множеством особенностей (сингулярностей) меры , называется множеством особенностей (сингулярностей) меры 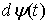 . .
Линейные функционалы.
Любая мера Лебега-Стилтьеса 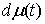 задает непрерывный
линейный функционал на пространстве задает непрерывный
линейный функционал на пространстве 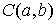 функций непрерывных
на отрезке функций непрерывных
на отрезке  . Для непрерывной функции . Для непрерывной функции 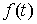 он определяется следующим
образом: он определяется следующим
образом:
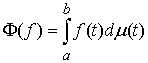 (3.1) (3.1)
Теорема Рисса. Верно и
обратное, если задан непрерывный линейный функционал 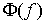 на пространстве на пространстве 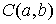 функций функций 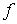 непрерывных на отрезке непрерывных на отрезке
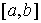 , то существует такая функция , то существует такая функция 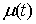 с ограниченной
вариацией, что функционал с ограниченной
вариацией, что функционал  задается соотношением
(3.1). Из теоремы Рисса следует, что, если задается соотношением
(3.1). Из теоремы Рисса следует, что, если 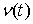 – непрерывная
функция, а – непрерывная
функция, а 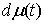 – мера Лебега-Стилтьеса, то существует мера
Лебега-Стилтьеса – мера Лебега-Стилтьеса, то существует мера
Лебега-Стилтьеса 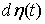 такая, что для любой
непрерывной функции такая, что для любой
непрерывной функции 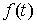 будет выполнено будет выполнено
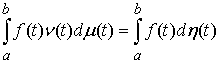 (3.2) (3.2)
Поэтому
выражение 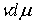 мы будем понимать как
соответствующую меру мы будем понимать как
соответствующую меру 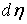 . .
Равенство
мер Лебега-Стилтьеса. В свете теоремы Рисса мы
будем считать две меры Лебега-Стилтьеса совпадающими, если совпадают соответствующие
им линейные функционалы. Например, (3.2) эквивалентно записи 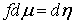 . .
При выводе уравнений Лагранжа второго
рода нам понадобится следующее утверждение.
Формула Лейбница. Если 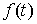 – абсолютно
непрерывная функция, а – абсолютно
непрерывная функция, а 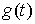 функция ограниченной
вариации на отрезке функция ограниченной
вариации на отрезке  , то , то
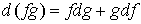 (4.1) (4.1)
Для доказательства этой формулы нам
понадобятся два утверждения - Теорема
Хелли и Лемма о приближении.
Теорема Хелли.[11] Пусть на отрезке 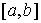 задана непрерывная
функция задана непрерывная
функция 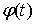 и последовательность
функций и последовательность
функций 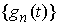 , которая в каждой точке , которая в каждой точке 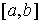 сходится к конечной
функции сходится к конечной
функции 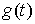 . Если вариации функций . Если вариации функций 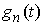 ограничены сверху ( ограничены сверху ( при всех при всех  ), то ), то  . .
Последовательность 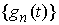 , удовлетворяющую условиям теоремы Хелли, будем называть последовательностью Хелли.
Заметим, что функции , удовлетворяющую условиям теоремы Хелли, будем называть последовательностью Хелли.
Заметим, что функции 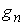 ограничены по модулю
равномерно по ограничены по модулю
равномерно по 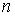 . В самом деле,
поскольку . В самом деле,
поскольку 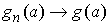 , то найдется , то найдется 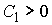 такое, что такое, что 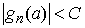 . Поэтому . Поэтому 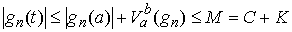 . .
Лемма о сглаживании. Если  – функция
ограниченной вариации на отрезке – функция
ограниченной вариации на отрезке 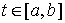 , то для нее найдется последовательность Хелли абсолютно
непрерывных функций , то для нее найдется последовательность Хелли абсолютно
непрерывных функций 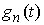 . Такую последовательность будем называть сглаживающей последовательностью Хелли. . Такую последовательность будем называть сглаживающей последовательностью Хелли.
Доказательство леммы. Любую функцию ограниченной вариации можно представить в виде разности двух
монотонно неубывающих функций. При этом
сумма их вариаций ограничивает сверху вариацию исходной функции. Поэтому
лемму достаточно доказать для случая, когда 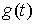 является монотонно
неубывающей. Не нарушая общности можно также считать, что является монотонно
неубывающей. Не нарушая общности можно также считать, что 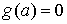 . Докажем для этого случая, что найдется последовательность
абсолютно непрерывных функций . Докажем для этого случая, что найдется последовательность
абсолютно непрерывных функций 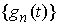 , сходящаяся к , сходящаяся к 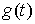 при всех при всех 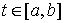 . Причем для любого . Причем для любого 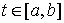 выполнено выполнено 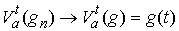 при при 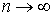 . Отсюда и будет вытекать утверждение леммы. Для
доказательства представим . Отсюда и будет вытекать утверждение леммы. Для
доказательства представим 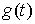 в виде суммы в виде суммы 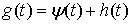 , где , где 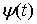 – непрерывная
неубывающая функция, а – непрерывная
неубывающая функция, а 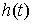 – неубывающая функция
скачков. Функцию скачков можно представить в виде конечного или бесконечного
ряда – неубывающая функция
скачков. Функцию скачков можно представить в виде конечного или бесконечного
ряда 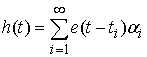 . Здесь . Здесь 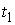 , , 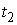 ,… – точки скачков, ,… – точки скачков, 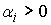 – величины скачков, – величины скачков, 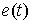 – функция единичного
скачка – функция единичного
скачка 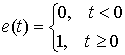 . Поскольку . Поскольку 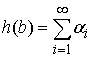 – сходящийся ряд, то – сходящийся ряд, то 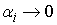 при при  . Пусть . Пусть 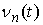 – последовательность
абсолютно непрерывных функций – последовательность
абсолютно непрерывных функций
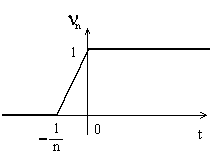 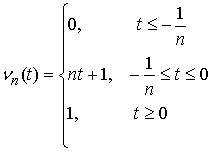
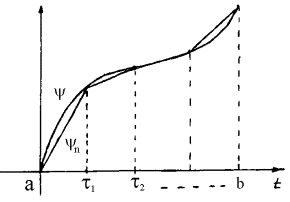 Обозначим Обозначим 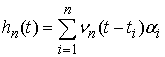 . Это неубывающие функции, причем . Это неубывающие функции, причем  при всех при всех  . Поэтому . Поэтому  . Разобьем отрезок . Разобьем отрезок 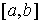 на на 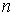 равных частей точками равных частей точками
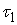 , , ,…, ,…, . Обозначим . Обозначим 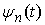 ломаную, соединяющую
точки ломаную, соединяющую
точки 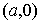 , , 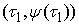 , , 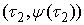 ,…, ,…, 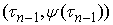 , , 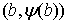 . Абсолютно непрерывные функции . Абсолютно непрерывные функции 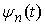 являются неубывающими
и являются неубывающими
и 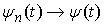 при всех при всех  . Значит, . Значит, 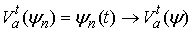 . Поэтому последовательность абсолютно непрерывных монотонно
неубывающих функций . Поэтому последовательность абсолютно непрерывных монотонно
неубывающих функций 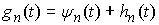 удовлетворяет всем
требуемым условиям. Для любого удовлетворяет всем
требуемым условиям. Для любого 
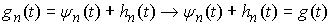 , и , и
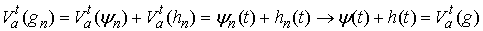 при при 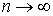
Доказательство Леммы о сглаживании завершено. Докажем теперь формулу
Лейбница.
Доказательство Формулы Лейбница. Пусть 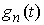 сглаживающая последовательность
Хелли для функции сглаживающая последовательность
Хелли для функции 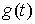 . Для любой непрерывной функции . Для любой непрерывной функции 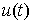 на отрезке на отрезке 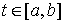 выполняется выполняется
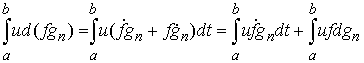 (4.2) (4.2)
Поскольку 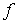 абсолютно непрерывна,
то последовательность функций абсолютно непрерывна,
то последовательность функций  – это сглаживающая
последовательность Хелли для функции – это сглаживающая
последовательность Хелли для функции 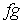 . Поэтому . Поэтому 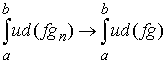 . Функция . Функция 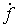 суммируема и суммируема и 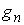 ограничена по модулю
равномерно по ограничена по модулю
равномерно по 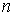 : : 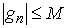 . Поэтому . Поэтому  . Поскольку . Поскольку 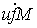 суммируема, то суммируема, то 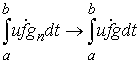 . Поскольку . Поскольку 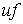 непрерывна, то непрерывна, то 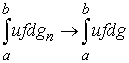 . Переходя теперь к пределу при . Переходя теперь к пределу при 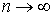 в левой и правой
частях (4.2) получаем в левой и правой
частях (4.2) получаем 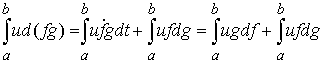 , что и завершает доказательство формулы Лейбница. , что и завершает доказательство формулы Лейбница.
Рассмотрим
теперь вопрос о том, как понимать обыкновенные дифференциальные уравнения с
импульсной правой частью. Рассмотрим сначала уравнение
 (5.1) (5.1)
Запишем его
немного иначе
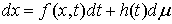 (5.2) (5.2)
где 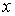 , , 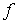 , , 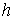 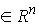 . Пусть . Пусть 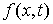 и и 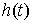 – непрерывные
вектор-функции, а – непрерывные
вектор-функции, а 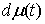 – одномерная мера
Лебега-Стилтьеса. Естественно
предположить, что решение этого уравнения мы ищем в классе вектор-функций – одномерная мера
Лебега-Стилтьеса. Естественно
предположить, что решение этого уравнения мы ищем в классе вектор-функций 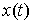 с ограниченной
вариацией. В этом случае и в левой и в правой частях (5.2) стоят векторные меры
Лебега-Стилтьеса и само уравнение надо понимать как их совпадение. Дадим теперь
строгое определение. Пусть на отрезке с ограниченной
вариацией. В этом случае и в левой и в правой частях (5.2) стоят векторные меры
Лебега-Стилтьеса и само уравнение надо понимать как их совпадение. Дадим теперь
строгое определение. Пусть на отрезке 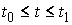 задана
вектор-функция задана
вектор-функция 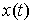 с ограниченной
вариацией. Она является решением уравнения (5.1) с начальными условиями с ограниченной
вариацией. Она является решением уравнения (5.1) с начальными условиями 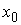 , если , если 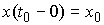 и для любой
непрерывной вектор-функции и для любой
непрерывной вектор-функции 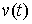 , заданной на отрезке , заданной на отрезке 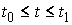 выполнено выполнено
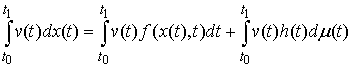 (5.3) (5.3)
Теорема о существовании и единственности решения. Если 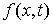 – гладкая по – гладкая по 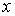 и непрерывная по и непрерывная по 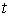 , то решение уравнения (5.2) с начальными условиями , то решение уравнения (5.2) с начальными условиями 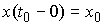 существует на
некотором отрезке времени и единственно (если существует на
некотором отрезке времени и единственно (если  ). Это можно доказать методом последовательных приближений
(см., например [13]). ). Это можно доказать методом последовательных приближений
(см., например [13]).
Заметим,
что (5.3) эквивалентно выполнению для каждого  следующего уравнения следующего уравнения
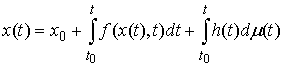 (5.4) (5.4)
Интеграл
здесь понимается как интеграл Стилтьеса на отрезке 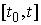 . .
В данной работе нас будут интересовать
несколько более сложные импульсные дифференциальные уравнения. В общем виде их
можно записать следующим образом.
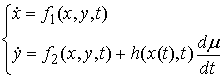 (5.5) (5.5)
где 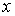 , , 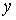 , , , , 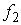 , , 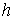 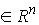 . Пусть . Пусть 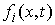 и и 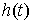 – непрерывные
вектор-функции, а – непрерывные
вектор-функции, а 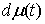 – одномерная мера
Лебега-Стилтьеса. Оно рассматривается совершенно аналогично уравнению (5.1).
Дадим строгое определение решения. Пусть на отрезке – одномерная мера
Лебега-Стилтьеса. Оно рассматривается совершенно аналогично уравнению (5.1).
Дадим строгое определение решения. Пусть на отрезке 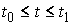 задана абсолютно
непрерывная вектор-функция задана абсолютно
непрерывная вектор-функция 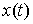 и функция с
ограниченной вариацией и функция с
ограниченной вариацией 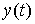 . Они являются решением уравнения (5.1) с начальными
условиями . Они являются решением уравнения (5.1) с начальными
условиями 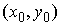 , если , если 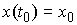 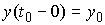 и для любой непрерывной
вектор-функции и для любой непрерывной
вектор-функции 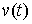 , заданной на отрезке , заданной на отрезке 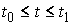 выполнено выполнено
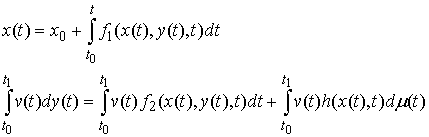 (5.6) (5.6)
Приведенные выше уравнения движения
(1.3) и (2.3) можно записать в единообразной форме. В обоих случаях существует
неотрицательная мера Лебега-Стилтьеса  , сосредоточенная на множестве тех
моментов времени, в которые траектория оказывается на поверхности удара: , сосредоточенная на множестве тех
моментов времени, в которые траектория оказывается на поверхности удара: 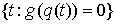 , такая, что траектория движения
удовлетворяет соответствующим уравнениям. Рассмотрим, например, уравнения в
форме Лагранжа , такая, что траектория движения
удовлетворяет соответствующим уравнениям. Рассмотрим, например, уравнения в
форме Лагранжа 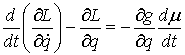 . Для данной кривой . Для данной кривой 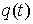 введем обобщенные
импульсы, т.е. вектор-функцию введем обобщенные
импульсы, т.е. вектор-функцию  . При достаточной гладкости лагранжиана . При достаточной гладкости лагранжиана 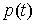 будет функцией
ограниченной вариации, поэтому наше уравнение можно записать в следующем виде будет функцией
ограниченной вариации, поэтому наше уравнение можно записать в следующем виде
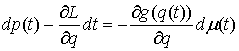
Для вывода
уравнений движения нам понадобится еще несколько фактов из функционального
анализа.
Банахово
пространство – это полное линейное пространство с нормой. Пусть 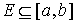 – непустое замкнутое
множество на числовом отрезке – непустое замкнутое
множество на числовом отрезке 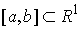 . Пространство . Пространство 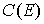 – функций – функций 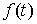 тождественно равных
нулю при тождественно равных
нулю при 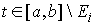 и непрерывных на и непрерывных на 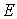 с нормой с нормой 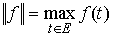 является банаховым.
Пусть теперь у нас есть семейство замкнутых непустых множеств является банаховым.
Пусть теперь у нас есть семейство замкнутых непустых множеств 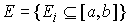 , , 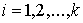 на числовом отрезке на числовом отрезке 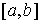 . Пространство . Пространство 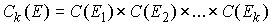 – это пространство вектор-функций – это пространство вектор-функций 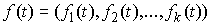 , каждая компонента которых , каждая компонента которых 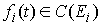 – это функция
непрерывная на множестве – это функция
непрерывная на множестве 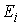 и тождественно равная
нулю вне него. Если ввести норму и тождественно равная
нулю вне него. Если ввести норму 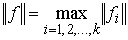 , то , то 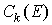 также станет
банаховым пространством. В частном случае, когда все также станет
банаховым пространством. В частном случае, когда все 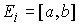 , пространство , пространство 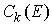 будем обозначать будем обозначать 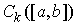 . .
Линейные функционалы.
Пусть 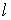 – линейный
непрерывный функционал на банаховом пространстве – линейный
непрерывный функционал на банаховом пространстве 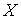 . Его значение на элементе . Его значение на элементе 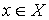 будем обозначать будем обозначать 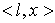 . В дальнейшем, для краткости, мы будем говорить просто о
линейных функционалах, подразумевая, что они непрерывны. . В дальнейшем, для краткости, мы будем говорить просто о
линейных функционалах, подразумевая, что они непрерывны.
Сопряженное пространство.
Пространство линейных непрерывных функционалов на банаховом пространстве 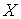 называется
пространством, сопряженным к называется
пространством, сопряженным к 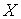 и обозначается и обозначается 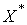 . Сопряженное пространство также является банаховым с нормой . Сопряженное пространство также является банаховым с нормой 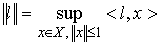 . .
Замечание о теореме Рисса. В соответствии с теоремой Рисса, пространство 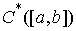 , сопряженное к , сопряженное к 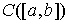 , представляет собой пространство функций с ограниченной
вариацией, или мер Лебега-Стилтьеса на отрезке , представляет собой пространство функций с ограниченной
вариацией, или мер Лебега-Стилтьеса на отрезке 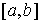 . Пространство . Пространство 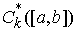 , сопряженное к , сопряженное к 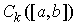 , представляет собой пространство векторных мер Лебега-Стилтьеса , представляет собой пространство векторных мер Лебега-Стилтьеса
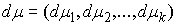 на отрезке на отрезке 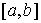 . Пространство . Пространство 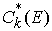 , сопряженное к , сопряженное к 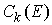 , представляет собой пространство векторных мер
Лебега-Стилтьеса , представляет собой пространство векторных мер
Лебега-Стилтьеса 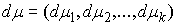 таких, что мера таких, что мера 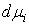 сосредоточена на
множестве сосредоточена на
множестве 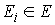 . .
Аннулятор подмножества.
Пусть 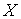 банахово пространство
и банахово пространство
и 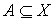 – некоторое
подмножество в нем. Аннулятором
множества – некоторое
подмножество в нем. Аннулятором
множества 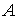 называется множество называется множество 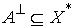 линейных функционалов
обращающихся в ноль на множестве линейных функционалов
обращающихся в ноль на множестве 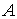 , т.е. , т.е. 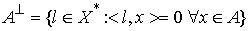 . .
Линейные
операторы. Пусть  и и 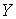 банаховы пространства
и банаховы пространства
и  – линейный
непрерывный оператор. Ядром оператора – линейный
непрерывный оператор. Ядром оператора 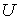 называется множество называется множество 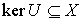 элементов
пространства элементов
пространства 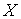 , отображающихся в ноль , отображающихся в ноль 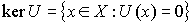 . .
Сопряженный
оператор. Пусть 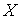 и и 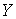 банаховы пространства
и банаховы пространства
и 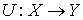 – линейный
непрерывный оператор. Он порождает сопряженный оператор – линейный
непрерывный оператор. Он порождает сопряженный оператор 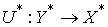 , определяемый следующим образом. Пусть , определяемый следующим образом. Пусть 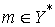 – линейный функционал
на – линейный функционал
на 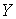 , тогда , тогда 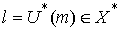 – это линейный
функционал на – это линейный
функционал на 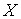 такой, что такой, что 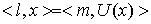 для для 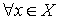 . .
Лемма об аннуляторе ядра регулярного оператора [14]. Пусть 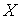 и и 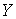 банаховы пространства
и банаховы пространства
и 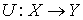 – линейный
непрерывный эпиморфизм (т.е., оператор, отображающий пространство – линейный
непрерывный эпиморфизм (т.е., оператор, отображающий пространство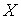 на все пространство на все пространство 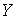 ). Тогда ). Тогда 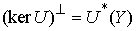 . .
Аннулятор в пространстве вариаций. Рассмотрим пример, который нам понадобится в дальнейшем. Пусть 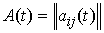 – матрица – матрица 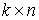 ( (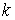 строк, строк, 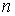 столбцов) определенная
на отрезке времени столбцов) определенная
на отрезке времени 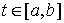 . Для каждой строки . Для каждой строки 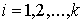 определено замкнутое
множество определено замкнутое
множество 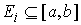 такое, что на множестве такое, что на множестве
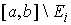 все элементы строки
тождественно равны нулю все элементы строки
тождественно равны нулю  , , 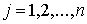 , а на самом множестве , а на самом множестве 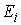 в любой момент
времени найдется хотя бы один ненулевой элемент. Потребуем также, чтобы каждая
функция в любой момент
времени найдется хотя бы один ненулевой элемент. Потребуем также, чтобы каждая
функция 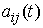 суженная на множество суженная на множество
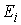 являлась непрерывной
функцией на нем. Будем обозначать являлась непрерывной
функцией на нем. Будем обозначать 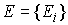 семейство множеств семейство множеств  , , 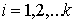 . .
Обозначим 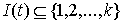 множество номеров множество номеров 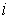 тех строк, для
которых тех строк, для
которых 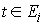 . Таким образом, если . Таким образом, если 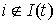 , то все элементы строки , то все элементы строки 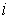 в момент времени в момент времени 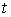 равны нулю. Если же равны нулю. Если же 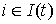 , то среди элементов строки , то среди элементов строки 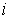 в момент времени в момент времени 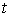 найдутся не равные
нулю. Будем обозначать найдутся не равные
нулю. Будем обозначать 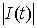 число элементов в число элементов в  , т.е. число ненулевых строк матрицы , т.е. число ненулевых строк матрицы 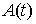 в момент в момент  . Пусть матрица . Пусть матрица 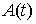 является
невырожденной в следующем смысле. Обозначим является
невырожденной в следующем смысле. Обозначим 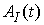 матрицу, составленную
из строк с номерами из матрицу, составленную
из строк с номерами из 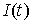 . Будем требовать, чтобы ранг этой матрицы был максимален. . Будем требовать, чтобы ранг этой матрицы был максимален.
Обозначим 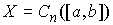 , , 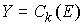 Определим линейный
оператор Определим линейный
оператор 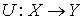 следующим образом.
Пусть следующим образом.
Пусть  – непрерывная
вектор-функция на отрезке – непрерывная
вектор-функция на отрезке 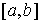 . Тогда . Тогда 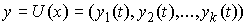 – это – это 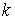 -мерная вектор функция определенная соотношением -мерная вектор функция определенная соотношением 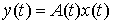 , или , или 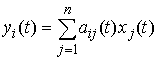 . В силу свойств матрицы . В силу свойств матрицы 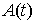 функции функции 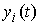 тождественно равны
нулю на множествах тождественно равны
нулю на множествах 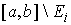 . .
Пусть 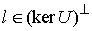 – линейный функционал
на – линейный функционал
на 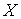 , принадлежащий аннулятору ядра оператора , принадлежащий аннулятору ядра оператора 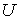 . Это значит, что для всех . Это значит, что для всех 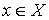 , таких, что , таких, что 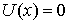 , выполнено , выполнено 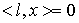 . Тогда найдется такой функционал . Тогда найдется такой функционал 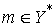 , что для любого , что для любого 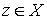 будет выполнено будет выполнено 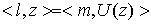 . В соответствии с замечаниями о теореме Рисса это можно
переформулировать следующим образом. . В соответствии с замечаниями о теореме Рисса это можно
переформулировать следующим образом.
Пусть  векторная мера Лебега
Стилтьеса на векторная мера Лебега
Стилтьеса на 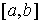 такая, что такая, что 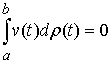 для любой
вектор-функции для любой
вектор-функции 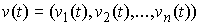 непрерывной на непрерывной на 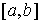 и такой, что и такой, что 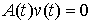 для всех для всех 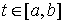 . Тогда найдется такая векторная мера Лебега-Стилтьеса . Тогда найдется такая векторная мера Лебега-Стилтьеса 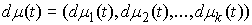 на на 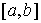 , у которой каждая компонента , у которой каждая компонента  сосредоточена на
множестве сосредоточена на
множестве 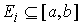 , и для любой вектор-функции , и для любой вектор-функции 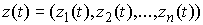 непрерывной на непрерывной на 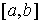 будет будет
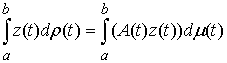
Поскольку 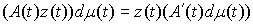 , где , где 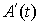 – транспонированная
матрица – транспонированная
матрица 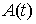 , то получаем отсюда , то получаем отсюда 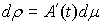 , или , или
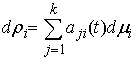 , , 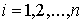
В данном разделе для механических
систем с двусторонними связями мы сформулируем условие идеальности связей и
принцип Даламбера-Лагранжа в интегральном виде [15, 16]. Это нам понадобится в
дальнейшем для обоснования уравнений движения систем с конфигурационными
ограничениями.
Сначала сформулируем принцип
Даламбера-Лагранжа в локальной форме. Рассмотрим систему из 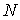 материальных точек,
перемещающихся в пространстве под действием приложенных к ним сил. Координаты
точек объединим в один вектор материальных точек,
перемещающихся в пространстве под действием приложенных к ним сил. Координаты
точек объединим в один вектор 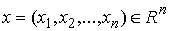 , где , где  . В отсутствие связей движение системы описывается вторым
законом Ньютона . В отсутствие связей движение системы описывается вторым
законом Ньютона
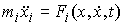 , , 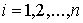 (7.1) (7.1)
где 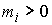 – массы точек, а – массы точек, а 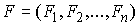 – вектор сил,
действующих на точки системы. Наложим на систему семейство – вектор сил,
действующих на точки системы. Наложим на систему семейство 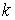 линейных удерживающих
связей: линейных удерживающих
связей:
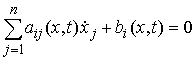 , , 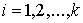 (7.2) (7.2)
где 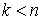 – число связей.
Запишем (7.2) в матричной форме. – число связей.
Запишем (7.2) в матричной форме.
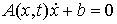 (7.3) (7.3)
где 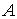 – матрица – матрица 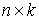 , ,  . .
Независимость связей. Удерживающие связи независимы, если 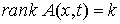 всюду. всюду.
Возможные перемещения. Возможным перемещением в точке  называется любой
вектор называется любой
вектор 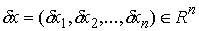 удовлетворяющий
условию удовлетворяющий
условию
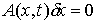 . (7.4) . (7.4)
Возможные перемещения образуют линейное пространство 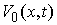 возможных перемещений
размерности возможных перемещений
размерности 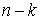 (если связи
независимы). (если связи
независимы).
Уравнения движения системы со связями выводятся из
следующих принципов.
Принцип освобождения от связей. Пусть 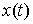 – траектория движения
системы со связями (7.3). Тогда систему
можно освободить от связей и добавить некую силу – реакцию связей – траектория движения
системы со связями (7.3). Тогда систему
можно освободить от связей и добавить некую силу – реакцию связей 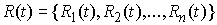 таким образом, что
кривая таким образом, что
кривая 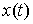 останется траекторией
освобожденной системы. Реакция связей при этом предполагается, по меньшей мере,
измеримой функцией. Для траектории останется траекторией
освобожденной системы. Реакция связей при этом предполагается, по меньшей мере,
измеримой функцией. Для траектории 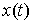 будут справедливы
следующие уравнения движения. будут справедливы
следующие уравнения движения.
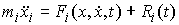 , ,  (7.5) (7.5)
Идеальность связей. Связи (7.3) являются идеальными, т.е.
для любого возможного перемещения 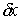 в любой точке в любой точке 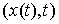 выполнено соотношение выполнено соотношение
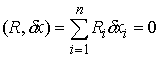 (7.6) (7.6)
или, как принято говорить, элементарная работа сил реакции связей на возможных
перемещениях равна нулю. Условие идеальности связей эквивалентно тому, что
найдется такая вектор-функция 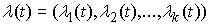 , что , что 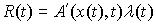 , где , где 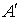 означает
транспонирование матрицы означает
транспонирование матрицы 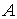 . Найдя . Найдя 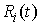 из (7.5) и, подставив
в (7.6) получим эквивалентную форму записи этого условия: из (7.5) и, подставив
в (7.6) получим эквивалентную форму записи этого условия: 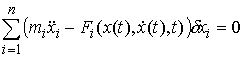 . .
Принцип Даламбера-Лаграгжа. Пусть кривая 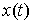 удовлетворяет уравнениям
связей (7.2-7.3). Кривая удовлетворяет уравнениям
связей (7.2-7.3). Кривая 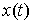 является траекторией
движения системы с идеальными связями (7.3) тогда и только тогда, когда для
любого возможного перемещения является траекторией
движения системы с идеальными связями (7.3) тогда и только тогда, когда для
любого возможного перемещения 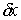 в любой точке в любой точке  выполнено соотношение выполнено соотношение
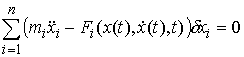 (7.7) (7.7)
Уравнения Лагранжа первого рода. Принцип Даламбера-Лагранжа
эквивалентен уравнениям Лагранжа первого рода. Пусть кривая 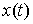 удовлетворяет
уравнениям связей (7.2-7.3). Кривая удовлетворяет
уравнениям связей (7.2-7.3). Кривая 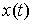 является траекторией
движения системы с идеальными связями (7.3) тогда и только тогда, когда
найдется такая вектор-функция является траекторией
движения системы с идеальными связями (7.3) тогда и только тогда, когда
найдется такая вектор-функция 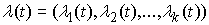 , что , что
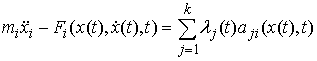 , , 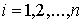 (7.8) (7.8)
Разложение реакций. Из уравнений Лагранжа видна справедливость
следующей аксиомы разложения реакций для удерживающих идеальных связей.
Разобьем связи (7.2-7.3) на две (или более) группы, например связи 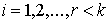 и связи и связи 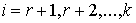 . Тогда реакции связей можно представить в виде суммы двух
слагаемых . Тогда реакции связей можно представить в виде суммы двух
слагаемых 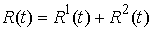 , которые мы будем называть соответственно реакциями первой и
второй группы связей. При этом для реакций первой группы будут выполнены
условия идеальности по отношению к первой группе связей , которые мы будем называть соответственно реакциями первой и
второй группы связей. При этом для реакций первой группы будут выполнены
условия идеальности по отношению к первой группе связей
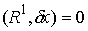 для всех для всех 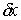 таких, что таких, что 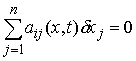 при при 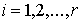
а для реакций второй группы будут выполнены условия идеальности по отношению
ко второй группе связей
 для всех для всех 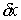 таких, что таких, что 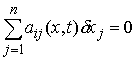 при при 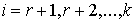
Если связи независимы, то такое разложение единственно.
Перейдем теперь к
формулировке принципа Даламбера-Лагранжа в интегральной форме. Мы будем
рассматривать движение на некотором отрезке времени 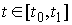 . .
Возможной вариацией кривой 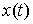 будем называть
гладкую вектор-функцию будем называть
гладкую вектор-функцию 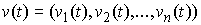 , для всех , для всех 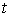 удовлетворяющую
условию удовлетворяющую
условию
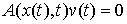 . (7.9) . (7.9)
По сути дела 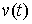 – это возможное
перемещение в точке – это возможное
перемещение в точке 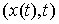 . .
Принцип освобождения от связей в интегральной форме. Пусть 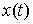 – траектория движения
системы со связями (7.3). Тогда систему
можно освободить от связей и добавить некую силу – реакцию связей – траектория движения
системы со связями (7.3). Тогда систему
можно освободить от связей и добавить некую силу – реакцию связей 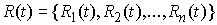 таким образом, что
кривая таким образом, что
кривая 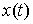 останется траекторией
освобожденной системы. Для траектории останется траекторией
освобожденной системы. Для траектории 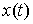 в любой момент
времени будут справедливы следующие уравнения. в любой момент
времени будут справедливы следующие уравнения.
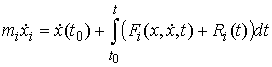 , , 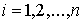 (7.10) (7.10)
или в импульсной форме
 , , 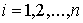 (7.11) (7.11)
где 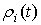 абсолютно непрерывные
функции такие, что абсолютно непрерывные
функции такие, что 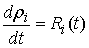 . .
Идеальность связей в интегральной форме. Связи (7.3)
являются идеальными, если для любой возможной вариации  траектории движения траектории движения  в любой момент
времени выполнено соотношение в любой момент
времени выполнено соотношение
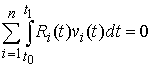 (7.11) (7.11)
мы будем говорить, что интегральная
элементарная работа сил реакции связей на возможных вариациях равна нулю. Найдя
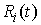 из (7.4) и подставив
в (7.11) получим эквивалентную форму записи этого условия: из (7.4) и подставив
в (7.11) получим эквивалентную форму записи этого условия:
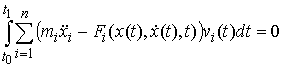
Принцип Даламбера-Лаграгжа в интегральной форме. Пусть
кривая 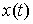 удовлетворяет
уравнениям связей (7.3). Кривая удовлетворяет
уравнениям связей (7.3). Кривая 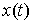 является траекторией
движения системы с идеальными связями (7.3) тогда и только тогда, когда для
любой возможной вариации является траекторией
движения системы с идеальными связями (7.3) тогда и только тогда, когда для
любой возможной вариации 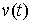 выполнено соотношение выполнено соотношение
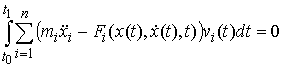 (7.12) (7.12)
Уравнения Лагранжа первого рода в интегральной форме. Принцип Даламбера-Лагранжа эквивалентен
уравнениям Лагранжа первого рода. Пусть кривая 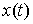 удовлетворяет уравнениям
связей (7.3). Кривая удовлетворяет уравнениям
связей (7.3). Кривая 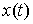 является траекторией
движения системы с идеальными связями (7.3) тогда и только тогда, когда
найдется такая вектор-функция является траекторией
движения системы с идеальными связями (7.3) тогда и только тогда, когда
найдется такая вектор-функция 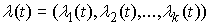 , что в любой момент времени , что в любой момент времени  выполнено выполнено
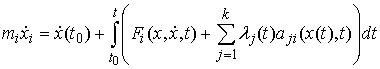 (7.13) (7.13)
или в импульсной форме
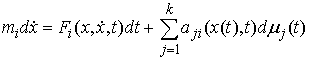 , , 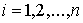 (7.11) (7.11)
где  абсолютно непрерывные
функции такие, что абсолютно непрерывные
функции такие, что 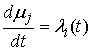 . Для безударных движений, когда траектории являются гладкими
(скорости непрерывны по времени), локальный и интегральный принципы
Даламбера-Лагранжа эквивалентны. Это можно показать, продифференцировав (7.10-7.12) по времени. . Для безударных движений, когда траектории являются гладкими
(скорости непрерывны по времени), локальный и интегральный принципы
Даламбера-Лагранжа эквивалентны. Это можно показать, продифференцировав (7.10-7.12) по времени.
В данном разделе, не
вдаваясь в подробное обоснование, мы сформулируем принцип Даламбера-Лагранжа, и
выведем уравнения Лагранжа первого рода для механических систем с
односторонними связями. В локальной формулировке принцип Даламбера-Лагранжа для
таких систем известен уже давно [7]. Однако, исходя из него, затруднительно
получать уравнения движения справедливые на всем отрезке движения, поскольку в
его формулировке присутствуют ускорения точек системы, которые могут быть
неопределенными в моменты выхода на границу односторонних связей (т.е. в точках
удара). В данном разделе мы даём интегральную формулировку принципа
Даламбера-Лагранжа, которая позволяет избавиться от этих трудностей.
Рассмотрим механическую
систему с линейными удерживающими связями (7.3). Добавим к ним семейство
односторонних голономных связей
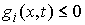 , , 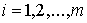 (8.1) (8.1)
Конфигурационное пространство. Множество точек 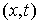 , удовлетворяющих связям (7.3, 8.1) будем называть
расширенным конфигурационным пространством или, иногда, для краткости просто
конфигурационным пространством. Внутренностью
конфигурационного пространства будем называть множество точек , удовлетворяющих связям (7.3, 8.1) будем называть
расширенным конфигурационным пространством или, иногда, для краткости просто
конфигурационным пространством. Внутренностью
конфигурационного пространства будем называть множество точек 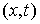 , в которых , в которых
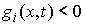 , , 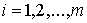 (8.2) (8.2)
Границей конфигурационного пространства или
поверхностью удара будем называть множество точек 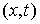 удовлетворяющих хотя
бы одному уравнению удовлетворяющих хотя
бы одному уравнению
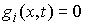 , ,  (8.3) (8.3)
Мы будем предполагать, что
удерживающие и односторонние связи являются непрерывными по 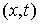 , а односторонние связи являются гладкими по , а односторонние связи являются гладкими по 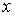 – первого класса
гладкости, так, что в каждой точке – первого класса
гладкости, так, что в каждой точке 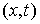 конфигурационного
пространства можно определить пространство возможных перемещений. конфигурационного
пространства можно определить пространство возможных перемещений.
Возможные перемещения удерживающих связей. Пространство
возможных перемещений удерживающих связей в точке 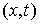 обозначается обозначается 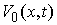 . Оно определяются так же, как и в предыдущем разделе. Возможным
перемещением удерживающих связей в точке . Оно определяются так же, как и в предыдущем разделе. Возможным
перемещением удерживающих связей в точке 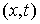 называется любой
вектор называется любой
вектор 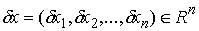 удовлетворяющий
условию удовлетворяющий
условию
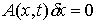 . (8.4) . (8.4)
Возможные перемещения. Пространство возможных перемещений
в точке 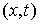 обозначается обозначается 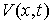 . Для точек, лежащих внутри области (8.1) оно определяется как пространство . Для точек, лежащих внутри области (8.1) оно определяется как пространство 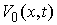 возможных перемещений
удерживающих связей. Для точек, лежащих на границе области (8.1), мы требуем
также, чтобы вектор возможного перемещения возможных перемещений
удерживающих связей. Для точек, лежащих на границе области (8.1), мы требуем
также, чтобы вектор возможного перемещения 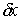 касался этой границы,
т.е. чтобы вдобавок к (8.4) выполнялось следующее условие: касался этой границы,
т.е. чтобы вдобавок к (8.4) выполнялось следующее условие:
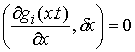 для тех для тех 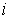 , для которых , для которых 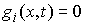
здесь 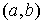 означает обычное
скалярное произведение векторов означает обычное
скалярное произведение векторов 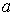 и и 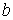 . .
Конус допустимых направлений. Мы также будем предполагать, что в каждой точке поверхности удара можно
определить конус  допустимых
направлений. Он представляет собой замыкание конуса возможных перемещений,
сдвигаясь вдоль которых мы попадаем внутрь области, допустимой связями (8.1).
Формально конус допустимых направлений, в добавление к условиям (8.4),
определяется системой неравенств допустимых
направлений. Он представляет собой замыкание конуса возможных перемещений,
сдвигаясь вдоль которых мы попадаем внутрь области, допустимой связями (8.1).
Формально конус допустимых направлений, в добавление к условиям (8.4),
определяется системой неравенств
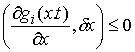 для тех для тех 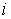 , для которых , для которых 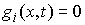
Также мы будем считать, что односторонние связи являются непротиворечивыми,
т.е. что конус допустимых направлений не пуст и содержит в себе пространство
возможных перемещений. Для внутренних точек конфигурационного пространства
конус 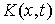 допустимых
направлений будем полагать совпадающим с пространством возможных перемещений допустимых
направлений будем полагать совпадающим с пространством возможных перемещений 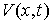 . .
Пример. Пусть, например, односторонняя связь задается одним
неравенством 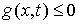 . Тогда мы предполагаем, что . Тогда мы предполагаем, что 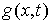 – гладкая функция, и
во всех точках – гладкая функция, и
во всех точках 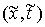 , в которых , в которых 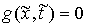 равномерно выполнено равномерно выполнено 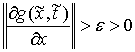 . Пространство возможных перемещений в точке . Пространство возможных перемещений в точке 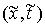 является пересечением
пространства является пересечением
пространства 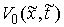 с гиперплоскостью с гиперплоскостью 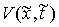 , задаваемой уравнением , задаваемой уравнением 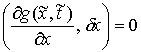 . Конус допустимых
направлений . Конус допустимых
направлений 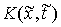 является пересечением
пространства является пересечением
пространства 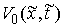 с полупространством
задаваемым неравенством с полупространством
задаваемым неравенством 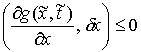 . .
Вернемся теперь к нашей системе. Мы будем
рассматривать движение на некотором отрезке времени 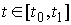 . .
Вариацией кривой 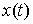 будем называть
непрерывную вектор-функцию будем называть
непрерывную вектор-функцию 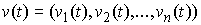 . .
Возможные вариации Вариацию 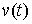 кривой кривой 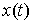 будем называть возможной,
если будем называть возможной,
если 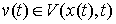 для всех для всех 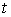 , т.е. вектор , т.е. вектор 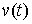 является возможным
перемещением в точке является возможным
перемещением в точке 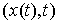 . Отличие от определения возможной вариации для случая только
удерживающих связей состоит в том, что во всех точках . Отличие от определения возможной вариации для случая только
удерживающих связей состоит в том, что во всех точках  , в которых кривая , в которых кривая 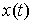 выходит на границу
односторонних связей, вектор выходит на границу
односторонних связей, вектор 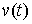 касается границы
односторонних связей. касается границы
односторонних связей.
Очевидно, что если перемещение 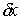 является возможным в
некоей точке является возможным в
некоей точке 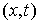 , то и перемещение , то и перемещение 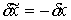 также является
возможным в этой точке. Поэтому если вариация также является
возможным в этой точке. Поэтому если вариация 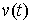 является возможной,
то и вариация является возможной,
то и вариация 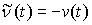 также является
возможной. также является
возможной.
Допустимые вариации. Вариацию 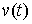 кривой кривой 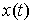 будем называть допустимой,
если будем называть допустимой,
если 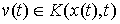 для всех для всех 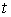 , т.е. вектор , т.е. вектор 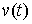 является допустимым
перемещением в точке является допустимым
перемещением в точке 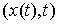 . Отличие от определения возможной вариации состоит в том, что во всех точках . Отличие от определения возможной вариации состоит в том, что во всех точках 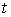 , в которых кривая , в которых кривая 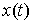 выходит на границу
односторонних связей, вектор выходит на границу
односторонних связей, вектор 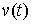 лежит в конусе
допустимых направлений лежит в конусе
допустимых направлений 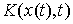 . Поскольку конус допустимых перемещений содержит
пространство возможных перемещений, то любая возможная вариация является
допустимой. . Поскольку конус допустимых перемещений содержит
пространство возможных перемещений, то любая возможная вариация является
допустимой.
Уравнения движения мы будем строить исходя из
следующих принципов.
Принцип освобождения от связей. Пусть 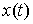 – траектория движения
системы со связями (7.3, 8.1). Тогда
систему можно освободить от связей и добавить некую силу – реакцию
связей – траектория движения
системы со связями (7.3, 8.1). Тогда
систему можно освободить от связей и добавить некую силу – реакцию
связей 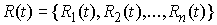 таким образом, что
кривая таким образом, что
кривая 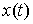 останется траекторией
освобожденной системы. При этом компоненты реакции связей представляют собой
меры Лебега-Стилтьеса останется траекторией
освобожденной системы. При этом компоненты реакции связей представляют собой
меры Лебега-Стилтьеса 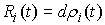 , имеющие особенности, сосредоточенные на множестве тех моментов
времени, в которые траектория , имеющие особенности, сосредоточенные на множестве тех моментов
времени, в которые траектория 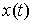 выходит на односторонние
ограничения. выходит на односторонние
ограничения.
Траектория системы представляет собой такую
дифференцируемую функцию 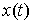 , производная которой, , производная которой, 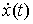 является функцией с
ограниченной вариацией. При этом будут
справедливы следующие уравнения. является функцией с
ограниченной вариацией. При этом будут
справедливы следующие уравнения.
 , , 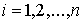 (8.5) (8.5)
Идеальность связей (полная). Связи (7.3, 8.1) называются (вполне) идеальными, если для любой траектории
системы 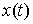 , для любой ее
допустимой вариации , для любой ее
допустимой вариации 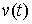 интегральная
элементарная работа сил реакции связей неотрицательна, т.е. интегральная
элементарная работа сил реакции связей неотрицательна, т.е.
 (8.6) (8.6)
Это условие означает, что при выходе действительной траектории системы на
границу удерживающих связей реакция связей направлена внутрь области, допустимой
этими связями.
Двусторонняя идеальность связей. Связи называются
двусторонне идеальными, если для любой траектории движения системы 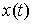 для любой ее
возможной вариации для любой ее
возможной вариации 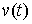 интегральная
элементарная работа сил реакции односторонних связей равна нулю, т.е. интегральная
элементарная работа сил реакции односторонних связей равна нулю, т.е.
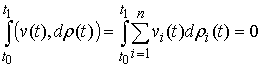 (8.7) (8.7)
Из полной идеальности связей
вытекает их двусторонняя идеальность. В самом деле, допустим противное, что
связи являются вполне, но не двусторонне идеальными. Тогда существует возможная
(и, следовательно, допустимая) вариация 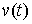 такая, что такая, что 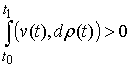 . Взяв возможную (и, следовательно, допустимую) вариацию . Взяв возможную (и, следовательно, допустимую) вариацию 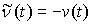 , получим , получим 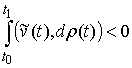 , что противоречит (8.6). Доказательство закончено. , что противоречит (8.6). Доказательство закончено.
Найдя 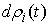 из (8.5) и подставив
в (8.6) получим эквивалентную форму записи условия полной идеальности связей. Для любой допустимой вариации из (8.5) и подставив
в (8.6) получим эквивалентную форму записи условия полной идеальности связей. Для любой допустимой вариации 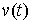 должно выполняться должно выполняться
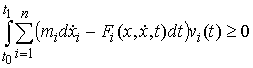 (8.8) (8.8)
Аналогично для условия двусторонней идеальности связей (8.7). Для любой
возможной вариации 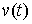 должно выполняться должно выполняться
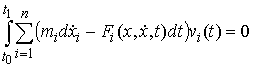 (8.9) (8.9)
Принцип Даламбера-Лаграгжа. Пусть непрерывная кривая 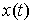 удовлетворяет
уравнениям связей (7.3, 8.1), а ее производная существует почти всюду и
является функцией ограниченной вариации. Кривая удовлетворяет
уравнениям связей (7.3, 8.1), а ее производная существует почти всюду и
является функцией ограниченной вариации. Кривая 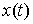 является траекторией
движения системы с идеальными связями (7.3, 8.1) тогда и только тогда, когда
для любой допустимой вариации является траекторией
движения системы с идеальными связями (7.3, 8.1) тогда и только тогда, когда
для любой допустимой вариации 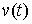 выполнены соотношения
(8.8) и, следовательно, для любой возможной вариации, соотношения (8.9). выполнены соотношения
(8.8) и, следовательно, для любой возможной вариации, соотношения (8.9).
Пользуясь леммой об
аннуляторе (см. п. 4) мы получаем уравнения Лагранжа первого рода.
Уравнения Лагранжа первого рода. Принцип Даламбера-Лагранжа эквивалентен следующим
уравнениям Лагранжа первого рода. Пусть непрерывная кривая 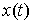 удовлетворяет
уравнениям связей (7.3, 8.1), а ее производная существует почти всюду и
является функцией ограниченной вариации. Кривая удовлетворяет
уравнениям связей (7.3, 8.1), а ее производная существует почти всюду и
является функцией ограниченной вариации. Кривая 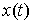 является траекторией
движения системы с (вполне) идеальными связями (7.3, 8.1) тогда и только тогда,
когда найдутся такие векторные меры
Лебега-Стилтьеса является траекторией
движения системы с (вполне) идеальными связями (7.3, 8.1) тогда и только тогда,
когда найдутся такие векторные меры
Лебега-Стилтьеса 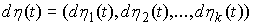 и и 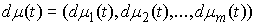 , что , что
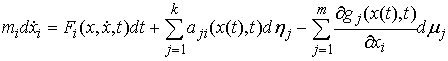 (8.10) (8.10)
При этом каждая мера 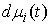 неотрицательна и
сосредоточена на множестве моментов времени, в которые неотрицательна и
сосредоточена на множестве моментов времени, в которые 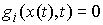 . Для безударных движений, когда траектории являются гладкими
(скорости непрерывны по времени), эти уравнения совпадают с обычными
уравнениями Лагранжа первого рода. . Для безударных движений, когда траектории являются гладкими
(скорости непрерывны по времени), эти уравнения совпадают с обычными
уравнениями Лагранжа первого рода.
Матричная форма уравнений. Пусть 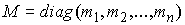 – диагональная
матрица, с элементами – диагональная
матрица, с элементами 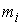 на диагонали, на диагонали, 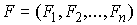 – сводный вектор сил, – сводный вектор сил,
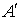 – транспонированная
матрица – транспонированная
матрица 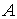 из (7.3), из (7.3), 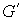 – транспонированная
матрица Якоби – транспонированная
матрица Якоби 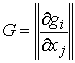 . Тогда уравнения (8.10) можно записать в более компактной
форме . Тогда уравнения (8.10) можно записать в более компактной
форме
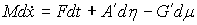 (8.11) (8.11)
Замечание о скачках. Любая функция ограниченной вариации
есть сумма непрерывной функции и функции скачков представляющей собой
ступенчатую функцию с не более чем счетным числом ступеней. В точках скачка
функций 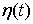 и и 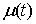 (и только в них)
траекторная скорость (и только в них)
траекторная скорость  также может иметь
скачок. Обозначим эти скачки соответственно также может иметь
скачок. Обозначим эти скачки соответственно 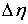 , , 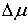 и и 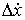 . В силу (8.10), они связаны следующим соотношением . В силу (8.10), они связаны следующим соотношением
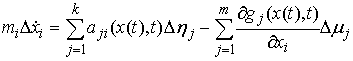 (8.12) (8.12)
или, более кратко
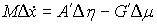 (8.13) (8.13)
Поскольку во все время движения выполнены уравнения удерживающих связей
(7.3), то 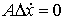 и из (8.13) получаем и из (8.13) получаем
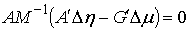 (8.14) (8.14)
Таким образом, скачки 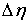 и и 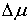 не являются
независимыми. Они связаны системой не являются
независимыми. Они связаны системой 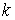 линейных соотношений. линейных соотношений.
Рассмотрим случай, когда все функции, входящие в
определение нашей механической системы, являются гладкими 2-й порядка по всем
переменным. Рассмотрим движение нашей системы на отрезке времени 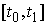 . Для него выполняются уравнения Лагранжа первого рода (8.10). Возьмем какую-либо
функцию . Для него выполняются уравнения Лагранжа первого рода (8.10). Возьмем какую-либо
функцию 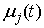 или или 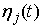 из этих уравнений и
обозначим ее для краткости из этих уравнений и
обозначим ее для краткости 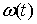 . Представим . Представим  в виде суммы трех
функций в виде суммы трех
функций 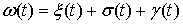 , где , где 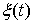 – абсолютно
непрерывная функция, – абсолютно
непрерывная функция, 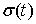 – функция скачков
представляющая собой ступенчатую функцию с не более чем счетным числом
ступеней, а – функция скачков
представляющая собой ступенчатую функцию с не более чем счетным числом
ступеней, а 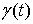 – сингулярная
непрерывная функция, производная которой почти всюду равна нулю. – сингулярная
непрерывная функция, производная которой почти всюду равна нулю.
Утверждение.
Докажем, что 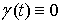 . Причем разрывы функции скачков . Причем разрывы функции скачков 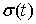 происходят только,
когда траектория находится на
односторонних ограничениях. происходят только,
когда траектория находится на
односторонних ограничениях.
Доказательство
будем вести индукцией по числу 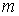 односторонних связей.
Итак, пусть односторонних связей.
Итак, пусть 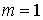 . .
Интервалы 1-го типа. Пусть на некоем отрезке времени 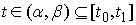 траектория траектория  находится во
внутренности конфигурационного пространства, т.е. выполнено неравенство (7.2): находится во
внутренности конфигурационного пространства, т.е. выполнено неравенство (7.2):
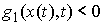 (9.1) (9.1)
тогда на этом отрезке времени происходит движение нашей системы стесненное
только удерживающими связями. Значит, 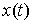 является гладкой
функцией. Кроме того, является гладкой
функцией. Кроме того, 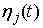 – тоже гладкие
функции, а – тоже гладкие
функции, а 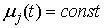 . Интервалы . Интервалы 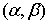 будем называть
интервалами первого типа. На этих интервалах будем называть
интервалами первого типа. На этих интервалах 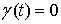 и нет разрывов
функции скачков. и нет разрывов
функции скачков.
Интервалы 2-го типа. Пусть на некоем отрезке времени 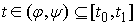 траектория траектория 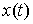 находится на границе
односторонних ограничений, т.е. выполнено равенство (7.3): находится на границе
односторонних ограничений, т.е. выполнено равенство (7.3):
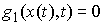 (9.2) (9.2)
тогда на этом отрезке времени происходит движение нашей системы стесненное
только удерживающими связями. Значит, 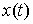 является гладкой
функцией. Кроме того, является гладкой
функцией. Кроме того, 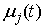 и и 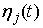 – тоже гладкие
функции. Причем – тоже гладкие
функции. Причем 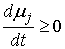 . Интервалы . Интервалы 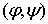 будем называть
интервалами второго типа. На этих интервалах будем называть
интервалами второго типа. На этих интервалах 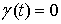 и нет разрывов
функции скачков. и нет разрывов
функции скачков.
Объединим все интервалы 1-го и 2-го типа в некое
открытое множество 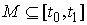 . Обозначим . Обозначим 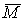 – замыкание – замыкание 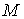 и докажем, что оно
совпадает со всем отрезком и докажем, что оно
совпадает со всем отрезком 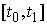 . Множество . Множество 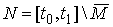 является открытым.
Докажем, что является открытым.
Докажем, что 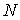 пусто. Допустим
противное и возьмем любое пусто. Допустим
противное и возьмем любое 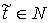 . Если точка . Если точка 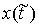 находится во
внутренности конфигурационного пространства, т.е. выполнено неравенство (9.1),
то, в силу непрерывности траектории движения, оно будет выполнено и на некоем
отрезке находится во
внутренности конфигурационного пространства, т.е. выполнено неравенство (9.1),
то, в силу непрерывности траектории движения, оно будет выполнено и на некоем
отрезке 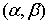 , содержащем , содержащем 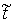 . Значит – это интервал 1-го типа. Но тогда . Значит – это интервал 1-го типа. Но тогда 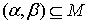 , чего не может быть. Таким образом, во всех точках , чего не может быть. Таким образом, во всех точках 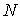 траектория траектория 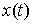 находится на границе
односторонних связей, т.е. выполнено (9.2). Но тогда любой открытый интервал находится на границе
односторонних связей, т.е. выполнено (9.2). Но тогда любой открытый интервал 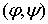 из из 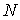 является интервалом
2-го типа и, поэтому, должен лежать в является интервалом
2-го типа и, поэтому, должен лежать в 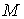 , чего тоже не может быть. Таким образом , чего тоже не может быть. Таким образом 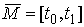 . .
На множестве 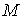 функция функция 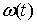 является гладкой и,
поэтому, является гладкой и,
поэтому, 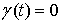 . Однако замыкание . Однако замыкание 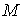 совпадает со всем
отрезком совпадает со всем
отрезком 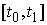 , а функция , а функция 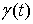 является непрерывной.
Поэтому является непрерывной.
Поэтому 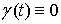 на на 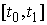 . Доказательство, для . Доказательство, для 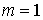 закончено. закончено.
Рассмотрим теперь случай 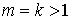 . Пусть утверждение верно для . Пусть утверждение верно для 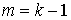 , докажем его для , докажем его для 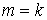 . Повторим те же рассуждения, что и для случая . Повторим те же рассуждения, что и для случая 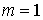 . Опять объединим все интервалы 1-го и 2-го типов в некое
открытое множество . Опять объединим все интервалы 1-го и 2-го типов в некое
открытое множество 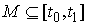 . На интервалах 1-го типа односторонняя связь . На интервалах 1-го типа односторонняя связь 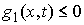 отсутствует. На
интервалах 2-го типа эта связь является удерживающей. Значит в обоих случаях
число односторонних связей равно отсутствует. На
интервалах 2-го типа эта связь является удерживающей. Значит в обоих случаях
число односторонних связей равно 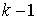 . Поэтому утверждение справедливо для . Поэтому утверждение справедливо для 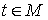 . Так же, как и для случая . Так же, как и для случая 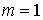 доказываем, что доказываем, что 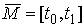 , откуда следует справедливость утверждения на всем отрезке , откуда следует справедливость утверждения на всем отрезке 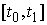 . Доказательство утверждения завершено. . Доказательство утверждения завершено.
Значит, любую функцию 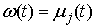 или или 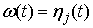 из уравнений Лагранжа
1-го рода можно представить в виде из уравнений Лагранжа
1-го рода можно представить в виде 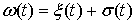 , где , где 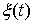 – абсолютно
непрерывная функция, а – абсолютно
непрерывная функция, а 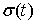 – функция скачков
представляющая собой ступенчатую функцию с не более чем счетным числом
ступеней. Причем разрывы функции скачков происходят только, когда траектория находится на односторонних
ограничениях. – функция скачков
представляющая собой ступенчатую функцию с не более чем счетным числом
ступеней. Причем разрывы функции скачков происходят только, когда траектория находится на односторонних
ограничениях.
Таким образом, в гладком
случае уравнения Лагранжа выглядят следующим образом.
Уравнения Лагранжа первого рода. В гладком случае уравнения движения системы
движения системы с (вполне) идеальными связями (7.3, 8.1) выглядят следующим
образом
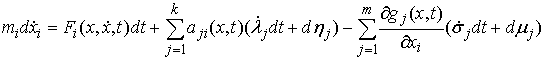 (9.3) (9.3)
где 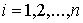 . Траектория . Траектория 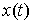 является абсолютно
непрерывной функцией, производная которой является абсолютно
непрерывной функцией, производная которой 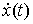 является функцией
ограниченной вариации, сингулярная компонента которой содержит только функцию
скачков. Величины является функцией
ограниченной вариации, сингулярная компонента которой содержит только функцию
скачков. Величины 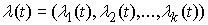 и и 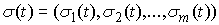 – некие
абсолютно-непрерывные вектор-функции. Величины – некие
абсолютно-непрерывные вектор-функции. Величины 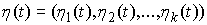 и и 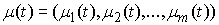 – некие функции
скачков. При этом все функции – некие функции
скачков. При этом все функции 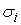 и и 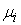 монотонно
неубывающие. Кроме того скачки функций монотонно
неубывающие. Кроме того скачки функций 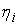 и и 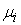 , а также точки, в которых функции , а также точки, в которых функции 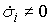 сосредоточены на
множестве моментов времени, в которые траектория находится на односторонних
ограничениях сосредоточены на
множестве моментов времени, в которые траектория находится на односторонних
ограничениях 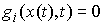 . .
Обсудим теперь вопрос определения неизвестных
функций 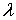 , , 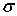 , , 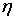 , , 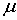 . .
Кратный удар. Мы
рассмотрим только случай, когда траектория движения не попадает в “угол”, т.е.
при выходе на односторонние ограничения выполняется только одно из уравнений
(7.3), например, первое: 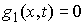 . В случае
попадания в “угол” для однозначного определения скачков скорости необходимо
введение дополнительных условий. Такая ситуация называется иногда кратным
ударом. Итак, пусть . В случае
попадания в “угол” для однозначного определения скачков скорости необходимо
введение дополнительных условий. Такая ситуация называется иногда кратным
ударом. Итак, пусть 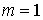 , т.е. на систему наложена только одна односторонняя связь , т.е. на систему наложена только одна односторонняя связь 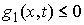 . Присоединим к уравнениям (9.3) уравнения удерживающих
связей (7.3), продифференцировав их по времени: . Присоединим к уравнениям (9.3) уравнения удерживающих
связей (7.3), продифференцировав их по времени:
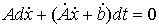 (9.4) (9.4)
Получим систему из  уравнений. Исключив
все уравнений. Исключив
все 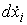 из (9.3, 9.4),
получим систему из уже из из (9.3, 9.4),
получим систему из уже из 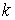 уравнений. уравнений.
Возьмем любой момент времени, когда траектория
находится внутри одностороннего ограничения (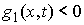 ), т.е. находится на интервале времени 1-го типа. Тогда ), т.е. находится на интервале времени 1-го типа. Тогда 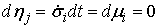 для всех индексов для всех индексов 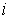 и и 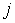 . И мы можем однозначно определить . И мы можем однозначно определить 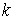 неизвестных величин неизвестных величин  . .
Пусть траектория находится на границе
одностороннего ограничения (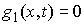 ). Почти для всех моментов времени существует траекторная
производная ). Почти для всех моментов времени существует траекторная
производная 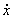 и для нее выполнено
соотношение и для нее выполнено
соотношение
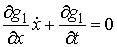 (9.5) (9.5)
В самом деле, если бы (9.5) не выполнялось, то траектория в некоторые моменты
времени оказалась бы вне одностороннего ограничения (т.е. было бы 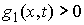 ). Поскольку здесь существует ). Поскольку здесь существует 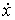 , то величины скачков не существенны (если они и есть, то они
компенсируют друг друга), поэтому можно положить , то величины скачков не существенны (если они и есть, то они
компенсируют друг друга), поэтому можно положить 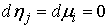 , и мы можем однозначно определить , и мы можем однозначно определить 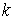 неизвестных величин неизвестных величин 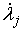 и одну величину и одну величину 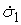 добавив (9.5) к (9.3,
9.4). добавив (9.5) к (9.3,
9.4).
Осталось рассмотреть только точки скачков
скорости. Множество этих точек имеет меру нуль. Пусть в момент времени 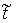 траектория находится
на одностороннем ограничении ( траектория находится
на одностороннем ограничении ( ), и произошел скачок скорости ), и произошел скачок скорости  . Добавим к (9.3,
9.4) . Добавим к (9.3,
9.4)  уравнений (8.14).
Теперь для однозначного определения уравнений (8.14).
Теперь для однозначного определения 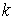 неизвестных величин неизвестных величин 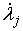 , одной величины , одной величины 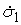 , , 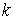 компонент скачка компонент скачка  и одной компоненты
скачка и одной компоненты
скачка 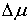 нам не хватает еще
одного уравнения. Оно появляется, если нам задан так называемый “коэффициент
восстановления” нам не хватает еще
одного уравнения. Оно появляется, если нам задан так называемый “коэффициент
восстановления” 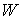 : : 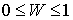 . Коэффициент
восстановления – это отношение
нормальных составляющих скоростей
движения нашей системы после и до удара
(в метрике, задаваемой матрицей кинетической энергии . Коэффициент
восстановления – это отношение
нормальных составляющих скоростей
движения нашей системы после и до удара
(в метрике, задаваемой матрицей кинетической энергии 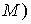 . Если обозначить . Если обозначить 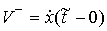 , , 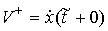 , и , и 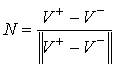 , то , то 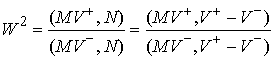
Зная коэффициент восстановления, мы получаем
недостающее уравнение: 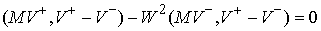 . Значение коэффициента восстановления определяет модель
удара. Величина . Значение коэффициента восстановления определяет модель
удара. Величина 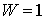 соответствует
абсолютно упругому удару, а величина соответствует
абсолютно упругому удару, а величина 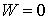 – соответствует
абсолютно неупругому удару. – соответствует
абсолютно неупругому удару.
В этом разделе мы выведем уравнения
движения механических систем с односторонними связями в форме уравнений
Лагранжа второго рода. Такие уравнения
можно получить, обычным образом, если удерживающие и односторонние связи
голономны. Пусть  обобщенные координаты
тогда обобщенные координаты
тогда
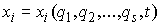 , , 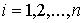 (10.1) (10.1)
Мы считаем, что функции 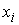 имеют, по крайней
мере, второй класс гладкости. Тогда траектория движения имеют, по крайней
мере, второй класс гладкости. Тогда траектория движения 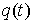 – это абсолютно
непрерывная вектор-функция, производная которой – это абсолютно
непрерывная вектор-функция, производная которой 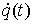 является функцией
ограниченной вариации. Односторонние связи в обобщенных координатах задаются
системой неравенств является функцией
ограниченной вариации. Односторонние связи в обобщенных координатах задаются
системой неравенств 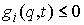 , ,  . Из (10.1) получаем . Из (10.1) получаем
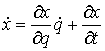 (10.2) (10.2)
отсюда
 (10.3) (10.3)
Кроме того
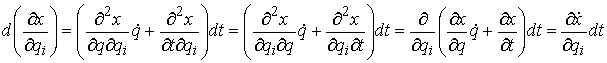
или, в матричной форме
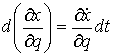 (10.4) (10.4)
Подставив (10.2) в уравнения удерживающих связей (7.3) получим систему 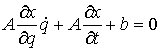 , которая должна тождественно выполняться при всех , которая должна тождественно выполняться при всех  . Отсюда . Отсюда
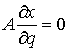 (10.5) (10.5)
Воспользуемся матричной формой уравнений Лагранжа 1-го рода (8.11). 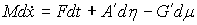 (10.6) (10.6)
Где 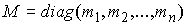 – диагональная
матрица, с элементами – диагональная
матрица, с элементами 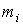 на диагонали, на диагонали, 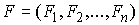 – сводный вектор сил, – сводный вектор сил,
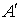 – транспонированная
матрица – транспонированная
матрица 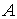 из (7.3), из (7.3), 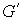 – транспонированная
матрица Якоби – транспонированная
матрица Якоби 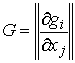 . Домножив обе части (10.6) слева на матрицу . Домножив обе части (10.6) слева на матрицу 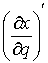 получим получим
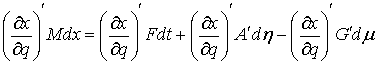
Матрица 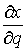 абсолютно непрерывна
поэтому, используя формулу Лейбница (4.1) получаем на действительной траектории абсолютно непрерывна
поэтому, используя формулу Лейбница (4.1) получаем на действительной траектории
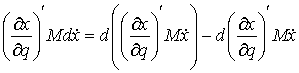
Использовав (10.3, 10.4), получаем отсюда
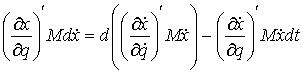
Введем кинетическую энергию системы 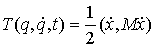 . Тогда . Тогда
 (10.8) (10.8)
Как обычно,
обозначим
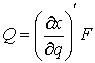 (10.9) (10.9)
вектор обобщенных сил 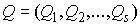 , , 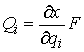 , ,  . Далее, в силу (10.5) имеем . Далее, в силу (10.5) имеем
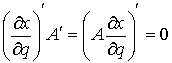 (10.10) (10.10)
Обозначим 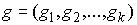 тогда тогда 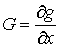 и и
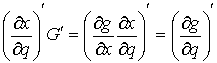 (10.11) (10.11)
Подставив
(10.8-10.11) в (10.6) получим
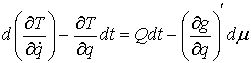 (10.12) (10.12)
или, в
покоординатном виде
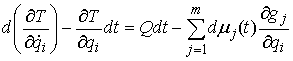 (10.13) (10.13)
Теорема Аппеля. Пусть в момент 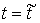 траектория движения
находится на границе односторонних ограничений, и скорость претерпевает скачок.
Тогда вектор обобщенных импульсов траектория движения
находится на границе односторонних ограничений, и скорость претерпевает скачок.
Тогда вектор обобщенных импульсов 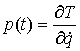 также имеет скачок.
Обозначим также имеет скачок.
Обозначим 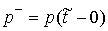 , , 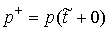 (для функции
ограниченной вариации эти величины всегда существуют). Тогда из (10.13) имеем (для функции
ограниченной вариации эти величины всегда существуют). Тогда из (10.13) имеем
 (10.14) (10.14)
Где 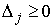 – некие
неотрицательные величины. Возьмем любой вектор – некие
неотрицательные величины. Возьмем любой вектор 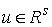 , касающийся границы односторонних ограничений в точке , касающийся границы односторонних ограничений в точке 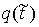 . Тогда из (10.14) имеем . Тогда из (10.14) имеем 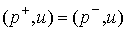 . Т.е. сохраняются проекции вектора обобщенного импульса на
плоскость касательную поверхности удара. Обычно это утверждение формулируется
для случая, когда в окрестности точки . Т.е. сохраняются проекции вектора обобщенного импульса на
плоскость касательную поверхности удара. Обычно это утверждение формулируется
для случая, когда в окрестности точки 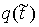 односторонние связи
имеют простейший вид: односторонние связи
имеют простейший вид: 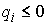 , , 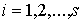 . Тогда сохраняются обобщенные импульсы . Тогда сохраняются обобщенные импульсы 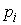 , , 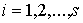
 , , 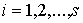
Потенциальный случай. Если силы потенциальны и имеют силовую функцию 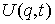 , то введем, как обычно, функцию Лагранжа , то введем, как обычно, функцию Лагранжа 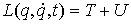 . И уравнения движения приобретут форму . И уравнения движения приобретут форму
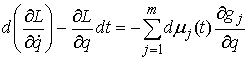 (10.15) (10.15)
Здесь везде 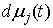 – неотрицательные
меры Лебега-Стилтьеса, каждая из которых сосредоточена на множестве моментов времени,
в которые траектория движения выходит на границу соответствующего
одностороннего ограничения – неотрицательные
меры Лебега-Стилтьеса, каждая из которых сосредоточена на множестве моментов времени,
в которые траектория движения выходит на границу соответствующего
одностороннего ограничения 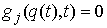 . .
Канонические уравнения Гамильтона
получаются из уравнений Лагранжа второго рода (10.5) обычным путем. Вводим
вектор обобщенных импульсов
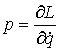 (11.1) (11.1)
разрешаем эту систему относительно 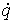 и составляем
гамильтониан и составляем
гамильтониан
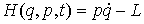 (11.2) (11.2)
Движение системы теперь описывается парой вектор-функций – абсолютно
непрерывной функцией 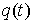 и функцией с
ограниченной вариацией и функцией с
ограниченной вариацией 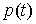 . Рассматривая . Рассматривая 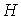 , , 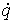 и и 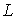 как гладкие функции
переменных как гладкие функции
переменных 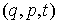 имеем из (11.2) имеем из (11.2) 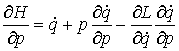 . Подставляя сюда (11.1) получаем первую группу канонических
уравнений Гамильтона . Подставляя сюда (11.1) получаем первую группу канонических
уравнений Гамильтона
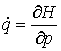 (11.3) (11.3)
Аналогично 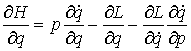 и из (11.1) получаем и из (11.1) получаем
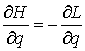 (11.4) (11.4)
Дифференцируя по  , получаем , получаем 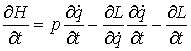 и из (11.1) и из (11.1) 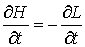 . Подставив (11.1, 11.4) в (10.5) получим вторую группу
канонических уравнений Гамильтона . Подставив (11.1, 11.4) в (10.5) получим вторую группу
канонических уравнений Гамильтона
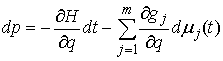 (11.6) (11.6)
Пусть теперь 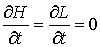 и и  – траектория нашей
системы. Тогда, в точках, где существует – траектория нашей
системы. Тогда, в точках, где существует 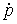 получаем получаем
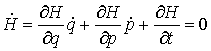
1.
Козлов В.В.,
Трещев Д.В. Биллиарды. Генетическое введение в динамику систем с ударами. М.,
МГУ, 1991 – 168с.
2.
Иванов А.П.
Динамика систем с механическими соударениями. М., “Международная программа
образования”, 1997 – 336с .
3.
Жуковский
Н.Е. О начале наименьшего действия. В кн. Вариационные принципы механики. М.,
Физматгиз, 1959, с. 425-429.
4.
Понтрягин
Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория
оптимальных процессов. М., Наука, 1969 – 384с.
5.
Дубовицкий
А.Я, Милютин А.А. Задачи на экстремум при наличии ограничений. “Журнал
вычислительной математики и математической физики”, 1965, 5, N 3, 395-453.
6.
Гирсанов
И.В. Лекции по математической теории экстремальных задач. М., МГУ, 1970 – 118с.
7.
Жуковский
Н.Е. Теоретическая механика. М., Гостехиздат, 1950 – 811с.
8.
Вильке В.Г.
Теоретическая механика. М., МГУ, 1998 – 271с.
9.
Аппель П.
Теоретическая механика. т. 2, М., Физматгиз, 1960 – 487с.
10.
Маркеев А.П.
Теоретическая механика. “Регулярная и хаотическая динамика”, 1999 – 569с .
11.
Натансон
И.П. Теория функций вещественной переменной. М., Наука, 1974 – 480с.
12.
Колмогоров
А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М., Наука,
1972 – 496с.
13.
Понтрягин
Л.С. Обыкновенные дифференциальные уравнения. М., Наука, 1965 – 332с.
14.
Алексеев
В.М. ,Тихомиров В.М., Фомин С.В. Оптимальное управление. М., Наука, 1979 –
432с.
15.
Козлов В.В.
Принципы динамики и сервосвязи. Вестник МГУ, сер. 1, математика, механика.
1989, N 5, с. 59-66.
16.
Голубев Ю.Ф.
Основы теоретической механики. М., МГУ, 2000 – 719с.
|