Аннотация
Устанавливается тип инвариантных многообразий для некоторых механических систем. Доказывается
несколько утверждений об эквивалентности фазовых потоков таких многообразий.
Abstract
Invariant manifolds of hamiltonian dynamic systems are investigated. In some cases the type
of such manifolds are established. Some statements are approved about the equvalenece of phase
flows of such manifolds.
Содержание
Введение.............................................................................................................. 3
1. Простой пример............................................................................................ 4
2. Многообразия уровня................................................................................... 6
3. Уровни и
накрытия....................................................................................... 9
4. Уровни и расслоения................................................................................... 11
5. Кинематическая независимость в механических
системах........................ 16
6. Несколько примеров.................................................................................... 17
7. Волчок Эйлера с эксцентриком................................................................... 21
8. Неголономная система................................................................................ 24
9. Эквивалентность инвариантных многообразий.......................................... 27
10. Интегралы, линейные по скоростям......................................................... 29
ЛИТЕРАТУРА................................................................................................... 32
Известно [1-4], что гамильтонова
система порядка 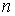 , имеющая независимую систему , имеющая независимую систему 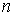 первых интегралов, образующих
конечномерную алгебру Ли относительно скобки Пуассона, интегрируема в
квадратурах, и компактная связная компонента инвариантного многообразия уровня
этой системы представляет собой инвариантный тор. При этом требуется, чтобы
размерность алгебры первых интегралов в сумме с ее рангом совпадала с размерностью инвариантного
многообразия. Такая система первых интегралов (и само инвариантное
многообразие) называется лиувиллевой. первых интегралов, образующих
конечномерную алгебру Ли относительно скобки Пуассона, интегрируема в
квадратурах, и компактная связная компонента инвариантного многообразия уровня
этой системы представляет собой инвариантный тор. При этом требуется, чтобы
размерность алгебры первых интегралов в сумме с ее рангом совпадала с размерностью инвариантного
многообразия. Такая система первых интегралов (и само инвариантное
многообразие) называется лиувиллевой.
В данной работе доказывается несколько
утверждений, об инвариантных многообразиях,
не являющихся лиувиллевыми, а также об эквивалентности фазовых потоков
на них. Результаты работы можно рассматривать как обобщение известных
утверждений о том, что для натуральных консервативных механических систем с
двухмерным, компактным конфигурационным многообразием, при достаточно больших
значениях константы интеграла энергии, его поверхность уровня представляет
собой гладкое расслоение с конфигурационным пространством в качестве базы и
слоем 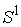 [5]. [5].
Для натуральных механических систем вводится
понятие кинематической независимости первых интегралов на многообразии их
уровней. Оно состоит в том, что естественная проекция касательного расслоения
фазового пространства является регулярной в каждой точке многообразия уровней. Оказывается, что если система n кинематически независимых первых интегралов высекает компактное
инвариантное многообразие 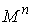 , то оно является конечнолистным накрытием конфигурационного
пространства. В окрестности , то оно является конечнолистным накрытием конфигурационного
пространства. В окрестности 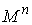 многие соседние
инвариантные многообразия диффеоморфны многие соседние
инвариантные многообразия диффеоморфны 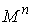 и фазовые
потоки на них эквивалентны. Аналогичные утверждения формулируются и для систем и фазовые
потоки на них эквивалентны. Аналогичные утверждения формулируются и для систем 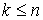 кинематически независимых
первых интегралов. кинематически независимых
первых интегралов.
Следует отметить, что условие кинематической
независимости является довольно сильным, и далеко не всегда имеет место. Тем не
менее, системы, удовлетворяющих рассматриваемым здесь условиям, имеются, и мы
приводим их примеры. Опишем кратко содержание работы.
В первом разделе, без использования понятия
кинематической независимости, рассматривается простой известный пример – волчок
Эйлера, у которого интегралы моментов высекают компактные трёхмерные
нелиувиллевые многообразия диффеооморфные конфигурационному пространству 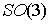 . Оказывается, среди этих многообразий довольно много
эквивалентных с точки зрения движения на них. . Оказывается, среди этих многообразий довольно много
эквивалентных с точки зрения движения на них.
Во втором разделе приводятся необходимые для
дальнейшего, известные утверждения о топологических свойствах многообразий
уровня системы функций, заданных на гладком многообразии, которое гладко
проектируется на некое другое гладкое многообразие.
В третьем разделе формулируются утверждения,
касающиеся кинематической независимости и топологических свойств многообразий 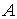 уровня системы
функций, заданных на гладком многообразии уровня системы
функций, заданных на гладком многообразии 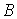 , которое гладко проектируется на некое другое гладкое
многообразие , которое гладко проектируется на некое другое гладкое
многообразие 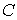 . При этом требуется, чтобы . При этом требуется, чтобы 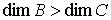 и и 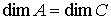 . Утверждения формулируются в терминах теории накрытий.
Результаты этого раздела, сформулированные через условие регулярности
отображений хорошо известны [6, 7]. В четвёртом разделе формулируются утверждения, касающиеся кинематической
независимости и топологических свойств многообразий . Утверждения формулируются в терминах теории накрытий.
Результаты этого раздела, сформулированные через условие регулярности
отображений хорошо известны [6, 7]. В четвёртом разделе формулируются утверждения, касающиеся кинематической
независимости и топологических свойств многообразий 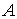 уровня системы
функций, заданных на гладком многообразии уровня системы
функций, заданных на гладком многообразии 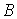 , которое гладко проектируется на некое другое гладкое
многообразие , которое гладко проектируется на некое другое гладкое
многообразие 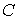 . При этом требуется, чтобы . При этом требуется, чтобы 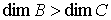 и и 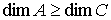 . Утверждения формулируются в терминах теории гладких расслоений. . Утверждения формулируются в терминах теории гладких расслоений.
В пятом разделе результаты предыдущих разделов
формулируются для специального случая многообразий, возникающих в механических
системах. В этом случае многообразия уровня системы функций располагаются в
фазовом пространстве, естественным образом проектирующемся на конфигурационное
пространство.
В шестом разделе рассматривается несколько
простых механических систем.
Первые два примера (тяжёлые точки на сфере и на горизонтальном торе) – это
системы с двумя степенями свободы, имеющие, кроме интеграла энергии, ещё один
первый интеграл. В соответствии с теоремой Лиувилля, в обоих случаях
многообразие уровня этих интегралов является двухмерным тором. Однако условие
кинематической независимости выполняется только в одном из них. Кроме того,
приводится общее утверждение о строении многообразия уровня
интеграла энергии. Рассматриваются многообразия уровня первых интегралов в
задаче о движении тяжёлого твёрдого тела с неподвижной точкой и в задаче о
движении волчка Эйлера. В седьмом разделе рассматриваются свойства многообразий
уровня первых интегралов движения для волчка Эйлера, к которому добавлен
одностепенной эксцентрик.
В восьмом разделе рассматриваются свойства
многообразий уровня первых интегралов движения неголономной системы,
представляющей собой динамически симметричный тяжёлый конёк, катающийся по
поверхности горизонтально лежащего тора.
В девятом разделе доказывается несколько простых
утверждений об эквивалентности фазовых потоков на многообразиях уровня первых
интегралов движения при различных значениях их констант.
В последнем разделе исследуется вопрос о кинематической независимости первых
интегралов линейных по скоростям. Показывается, что, если эти интегралы
порождаются независимыми полями симметрий, то при достаточно больших значениях
константы интеграла энергии полная система интегралов является кинематически
независимой.
В
данном разделе мы рассмотрим пример нелиувиллевой системы первых интегралов, и
покажем, что она высекает инвариантное многообразие диффеоморфное многообразию
конфигурационного пространства. И, что среди этих многообразий довольно много
эквивалентных с точки зрения движения на них. В следующих разделах результаты данного
раздела будут сформулированы в виде общих утверждений. Результаты этого раздела
являются общеизвестными (см. [8]), однако, мы сформулируем их в форме,
согласующейся с утверждениями следующих разделов.
Обратимся
к случаю Эйлера-Пуансо движения твёрдого
тела вокруг неподвижной точки (будем рассматривать основной случай, когда
тензор инерции твердого тела невырожден). Для простоты обозначений рассмотрим
эту задачу не в Гамильтоновом, а в Лагранжевом формализме. Конфигурационное
многообразие здесь – это пространство ориентаций твердого тела 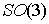 , а фазовое пространство – это касательное расслоение , а фазовое пространство – это касательное расслоение 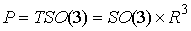 , т.е. пространство ориентаций и мгновенных угловых скоростей движения твердого тела с
неподвижной точкой. Поскольку в данном случае момент внешних сил относительно
неподвижной точки равен нулю, то система допускает три первых интеграла
движения – компоненты момента количества движения , т.е. пространство ориентаций и мгновенных угловых скоростей движения твердого тела с
неподвижной точкой. Поскольку в данном случае момент внешних сил относительно
неподвижной точки равен нулю, то система допускает три первых интеграла
движения – компоненты момента количества движения 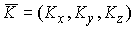 в абсолютном
пространстве. Эти интегралы не находятся в инволюции. Но, в совокупности с
интегралом энергии, они образуют лиувиллеву систему и, в общем случае, высекают
в фазовом пространстве двухмерные торы (см., например [1]). в абсолютном
пространстве. Эти интегралы не находятся в инволюции. Но, в совокупности с
интегралом энергии, они образуют лиувиллеву систему и, в общем случае, высекают
в фазовом пространстве двухмерные торы (см., например [1]).
Утверждение 1.1.
Рассмотрим инвариантное многообразие 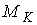 уровня компонент
момента количества движения уровня компонент
момента количества движения
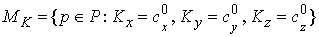
Докажем, что 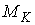 диффеоморфно
конфигурационному многообразию диффеоморфно
конфигурационному многообразию 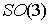 . .
Доказательство. Поскольку фазовое
пространство есть прямое произведение  и и 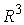 , то любую его точку , то любую его точку 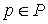 можно представить
парой можно представить
парой 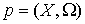 , где , где 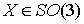 описывает ориентацию
твердого тела в пространстве, а описывает ориентацию
твердого тела в пространстве, а 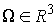 характеризует его
скорость движения (т.е. мгновенную угловую скорость). Обозначим характеризует его
скорость движения (т.е. мгновенную угловую скорость). Обозначим 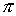 – естественную
проекцию фазового пространства на конфигурационное: – естественную
проекцию фазового пространства на конфигурационное: 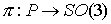 , ,  , и , и 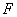 – сужение этого
отображения на – сужение этого
отображения на 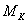 : : 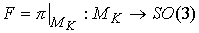 . Покажем, что . Покажем, что 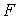 является диффеоморфизмом является диффеоморфизмом 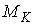 и и 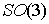 . Гладкость . Гладкость 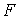 следует из гладкости
естественной проекции. Докажем его инъективность (т.е. взаимную однозначность),
и сюръективность (т.е. то, что оно является
отображением на все пространство следует из гладкости
естественной проекции. Докажем его инъективность (т.е. взаимную однозначность),
и сюръективность (т.е. то, что оно является
отображением на все пространство 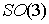 ). ).
Инъективность. Возьмём две любые
различные точки 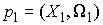 и и 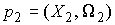 на на 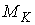 : : 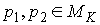 , , 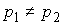 . Допустим противное – пусть . Допустим противное – пусть 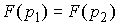 . Поскольку . Поскольку 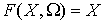 , то это означает, что , то это означает, что 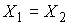 при том, что при том, что 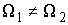 . В терминах нашей механической системы можно сказать, что
при заданной ориентации твердого тела . В терминах нашей механической системы можно сказать, что
при заданной ориентации твердого тела 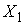 мы можем найти два
разных вектора мгновенной угловой скорости движения мы можем найти два
разных вектора мгновенной угловой скорости движения 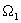 и и 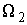 , которым будет отвечать один и тот же вектор кинетического
момента , которым будет отвечать один и тот же вектор кинетического
момента 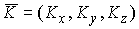 . Пусть . Пусть 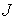 – матрица инерции
твердого тела в абсолютных осях при его ориентации – матрица инерции
твердого тела в абсолютных осях при его ориентации 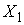 . Тогда . Тогда 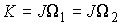 . И, поскольку тензор инерции невырожден, то . И, поскольку тензор инерции невырожден, то 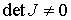 и и 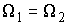 , т.е., мы приходим к противоречию. , т.е., мы приходим к противоречию.
Сюръективность. Пусть 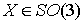 . Нам надо показать, что найдётся такой вектор мгновенной
угловой скорости движения твердого тела . Нам надо показать, что найдётся такой вектор мгновенной
угловой скорости движения твердого тела 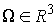 , что , что 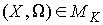 . Пусть опять . Пусть опять 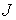 – матрица инерции
твердого тела в абсолютных осях при его ориентации – матрица инерции
твердого тела в абсолютных осях при его ориентации 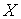 . Возьмем вектор . Возьмем вектор 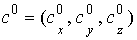 . Тогда . Тогда 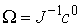 является искомым
вектором мгновенной угловой скорости. Доказательство закончено. является искомым
вектором мгновенной угловой скорости. Доказательство закончено.
Обозначим
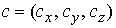 – вектор констант
интегралов момента количества движения. Каждому значению этого вектора
соответствует инвариантное многообразие уровня интегралов компонент момента
количества движения – вектор констант
интегралов момента количества движения. Каждому значению этого вектора
соответствует инвариантное многообразие уровня интегралов компонент момента
количества движения 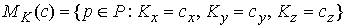 . Обозначим . Обозначим 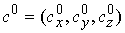 – некий выделенный
набор этих констант. Покажем теперь, что в окрестности многообразия – некий выделенный
набор этих констант. Покажем теперь, что в окрестности многообразия 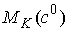 довольно много
инвариантных многообразий уровня, на которых движение устроено так же, как на довольно много
инвариантных многообразий уровня, на которых движение устроено так же, как на 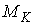 . .
Будем
говорить, что движение на многообразиях 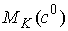 и и 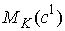 устроено, или, что
фазовые потоки на них эквивалентны, если существует диффеоморфизм устроено, или, что
фазовые потоки на них эквивалентны, если существует диффеоморфизм 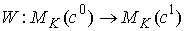 , при котором фазовый поток на , при котором фазовый поток на 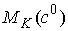 переходит в фазовый
поток на переходит в фазовый
поток на 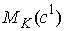 . .
Утверждение 1.2. В
окрестности константы 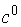 найдется гладкое двухпараметрическое
семейство констант найдется гладкое двухпараметрическое
семейство констант 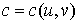 , такое, что потоки на , такое, что потоки на 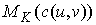 эквивалентны потоку
на эквивалентны потоку
на 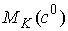 . .
Доказательство. В
нашем случае поворот абсолютной системы координат эквивалентен повороту вектора
момента количества движения в обратном направлении. При повороте системы
координат, инвариантное многообразие, соответствующее какому-либо вектору
констант 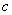 , перейдёт в многообразие соответствующее повёрнутому вектору
констант. Движения при этом, естественно совпадут. Поэтому двухпараметрическое семейство констант лежит на
поверхности двухмерной сферы с радиусом равным , перейдёт в многообразие соответствующее повёрнутому вектору
констант. Движения при этом, естественно совпадут. Поэтому двухпараметрическое семейство констант лежит на
поверхности двухмерной сферы с радиусом равным  . .
Сформулируем несколько общих утверждений, имея в
виду их дальнейшее применение к механическим системам. Рассмотрим гладкие связные
многообразия 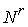 и и 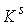 размерностей размерностей 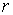 и и 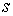 соответственно,
причем соответственно,
причем  . Пусть . Пусть 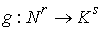 – гладкое отображение – гладкое отображение
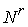 на на 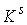 (сюръекция). Для
краткости будем здесь называть это отображение кинематическим. Пусть на (сюръекция). Для
краткости будем здесь называть это отображение кинематическим. Пусть на 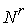 определена система из определена система из
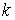 гладких функций гладких функций 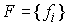 , , 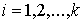 . Для вектора . Для вектора 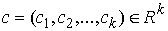 обозначим обозначим 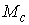 – множество уровня
системы – множество уровня
системы  , т.е. , т.е.
Ниже мы будем рассматривать не все множество,  а только какую-нибудь
его связную компоненту, обозначая ее также а только какую-нибудь
его связную компоненту, обозначая ее также 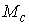 . .
Пусть
система 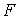 функционально
независима на функционально
независима на 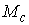 (т.е., в каждой точке (т.е., в каждой точке
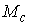 дифференциальные
формы дифференциальные
формы 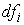 линейно независимы),
тогда линейно независимы),
тогда 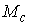 является замкнутым
подмногообразием. В некоторой ее открытой окрестности нет других точек этого
многообразия уровня. В локальной системе координат является замкнутым
подмногообразием. В некоторой ее открытой окрестности нет других точек этого
многообразия уровня. В локальной системе координат 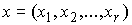 условие
функциональной независимости записывается в виде условия условие
функциональной независимости записывается в виде условия
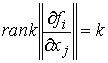 (2.1) (2.1)
Обозначим 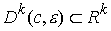 открытый шар радиуса открытый шар радиуса 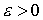 с центром в точке с центром в точке 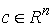 : : 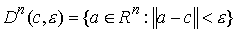 . .
Утверждение 2.1. Пусть 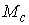 компактно. Существует
некоторое компактно. Существует
некоторое 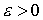 , такое, что для всех , такое, что для всех 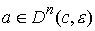 множество множество 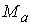 уровня системы
функций уровня системы
функций 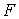 представляет собой
замкнутое компактное подмногообразие диффеоморфное представляет собой
замкнутое компактное подмногообразие диффеоморфное 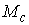 . Объединение всех . Объединение всех 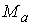 образует открытую
окрестность образует открытую
окрестность 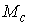 диффеоморфную прямому
произведению диффеоморфную прямому
произведению 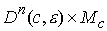 . .
Доказательство. Такое утверждение является одним из
основных в теории Морса (см., например, [9]). Приведём здесь схему
доказательства. Строим в окрестности
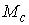 семейство гладких, ограниченных векторных
полей семейство гладких, ограниченных векторных
полей 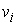 , , 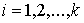 таких, что таких, что
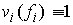 , и , и 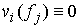 при при 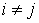 (2.2) (2.2)
Возьмём вектор констант 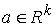 достаточно близким к достаточно близким к 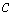 . Построим векторное поле . Построим векторное поле 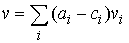 . Его траектории могут быть продолжены неограниченно во
времени. Сдвиг по ним за время равное единице диффеоморфно переводит . Его траектории могут быть продолжены неограниченно во
времени. Сдвиг по ним за время равное единице диффеоморфно переводит 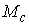 в в 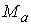 . Построение
векторных полей . Построение
векторных полей 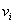 можно провести,
например, следующим образом. Покроем можно провести,
например, следующим образом. Покроем 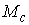 конечной системой
координатных окрестностей в конечной системой
координатных окрестностей в 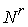 таких, что в каждой
из них условие (2.1) выполняется за счёт линейной независимости одного и того
же набора столбцов якобиевой матрицы. Для окрестности таких, что в каждой
из них условие (2.1) выполняется за счёт линейной независимости одного и того
же набора столбцов якобиевой матрицы. Для окрестности 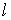 этот набор столбцов
обозначим этот набор столбцов
обозначим 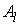 . Произведём разбиение единицы . Произведём разбиение единицы 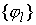 для этой системы
окрестностей. Внутри каждой окрестности для этой системы
окрестностей. Внутри каждой окрестности 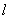 в локальных
координатах строим векторные поля в локальных
координатах строим векторные поля 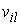 , удовлетворяющие (2.2). Для этого разрешаем систему , удовлетворяющие (2.2). Для этого разрешаем систему 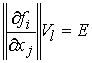 относительно набора столбцов относительно набора столбцов 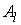 . Здесь . Здесь 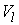 – матрица – матрица 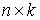 локальных координат
векторов локальных координат
векторов 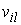 , а , а 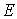 – единичная матрица – единичная матрица 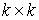 . Суммирование этих полей с весами . Суммирование этих полей с весами 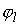 даст искомый
результат. даст искомый
результат.
Замечание 2.1. Разобьём
систему функциональных констант 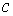 на две группы на две группы 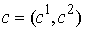 , , 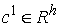 , ,  . Будем изменять теперь только константы . Будем изменять теперь только константы 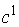 . Тогда из утверждения 2.1 следует, что существует некоторое . Тогда из утверждения 2.1 следует, что существует некоторое  , такое, что для всех , такое, что для всех 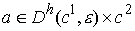 множество множество 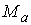 уровня системы
функций уровня системы
функций 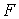 представляет собой
замкнутое компактное подмногообразие диффеоморфное представляет собой
замкнутое компактное подмногообразие диффеоморфное  . Объединение всех . Объединение всех 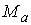 образует окрестность образует окрестность 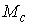 диффеоморфную прямому
произведению диффеоморфную прямому
произведению 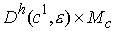 . .
Кинематическая независимость. Обозначим 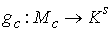 – сужение кинематического отображения – сужение кинематического отображения 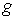 на на  . Дифференциал . Дифференциал
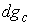 отображения отображения 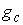 порождает отображение
касательных расслоений: порождает отображение
касательных расслоений: 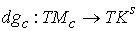 . Назовем систему функций . Назовем систему функций  кинематически
независимой на уровне кинематически
независимой на уровне 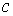 , если в каждой точке , если в каждой точке 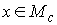 линейное отображение
соответствующих касательных пространств имеет максимально возможный ранг (т.е. линейное отображение
соответствующих касательных пространств имеет максимально возможный ранг (т.е. 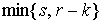 ). ).
Пусть теперь система функций  функционально и кинематически независима на уровне функционально и кинематически независима на уровне  . Множество уровня . Множество уровня  является замкнутым
подмногообразием размерности является замкнутым
подмногообразием размерности 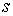 . Следуя [6] сформулируем несколько утверждений. . Следуя [6] сформулируем несколько утверждений.
Утверждение 2.2. Если 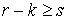 , то образ , то образ 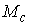 при отображении при отображении 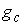 является открытым
множеством в является открытым
множеством в 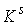 . .
Доказательство. Для
краткости обозначим 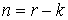 – размерность многообразия – размерность многообразия
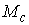 . Тогда . Тогда 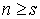 . Возьмём любую точку . Возьмём любую точку 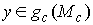 , и докажем, что у неё есть открытая окрестность в , и докажем, что у неё есть открытая окрестность в  . Пусть . Пусть 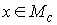 – любой прообраз
точки – любой прообраз
точки 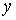 , т.е. , т.е.  . Выберем локальные координаты . Выберем локальные координаты 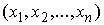 в окрестности точки в окрестности точки 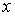 и и 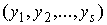 в окрестности точки в окрестности точки 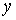 . В силу условия кинематической независимости ранг якобиевой
матрицы . В силу условия кинематической независимости ранг якобиевой
матрицы 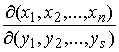 равен равен 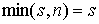 , поскольку , поскольку 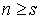 . Откуда, как следствие теоремы о неявных функциях, получаем,
что у точки . Откуда, как следствие теоремы о неявных функциях, получаем,
что у точки 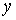 есть открытая
окрестность есть открытая
окрестность 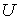 , каждая точка которой имеет прообраз. Значит , каждая точка которой имеет прообраз. Значит 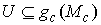 . Доказательство закончено. . Доказательство закончено.
Утверждение 2.3. Если многообразие  компактно, то образ компактно, то образ
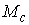 при отображении при отображении 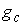 является замкнутым
множеством в является замкнутым
множеством в 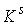 . .
Доказательство. Пусть 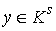 – любая предельная
точка множества – любая предельная
точка множества 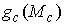 , докажем, что она лежит в , докажем, что она лежит в 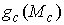 . Поскольку . Поскольку 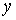 – предельная точка,
то найдётся последовательность точек из – предельная точка,
то найдётся последовательность точек из 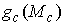 , сходящаяся к , сходящаяся к 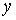 . Возьмём множество прообразов этих точек. Поскольку . Возьмём множество прообразов этих точек. Поскольку 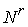 компактно, то у этого
множества есть предельная точка, образ которой и будет совпадать с компактно, то у этого
множества есть предельная точка, образ которой и будет совпадать с 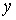 в силу непрерывности
отображения в силу непрерывности
отображения 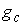 . Доказательство закончено. . Доказательство закончено.
Утверждение 2.4. Если 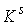 связно, связно, 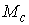 компактно и компактно и 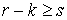 , то отображение , то отображение 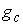 является сюръекцией,
т.е. отображением является сюръекцией,
т.е. отображением 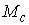 на всё на всё 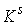 . При этом, как непрерывный образ компакта, . При этом, как непрерывный образ компакта, 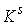 тоже компактно. тоже компактно.
Доказательство. Из предыдущих двух утверждений следует, что 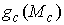 одновременно и
замкнуто и открыто. Следовательно, и его дополнение одновременно и
замкнуто и открыто. Следовательно, и его дополнение 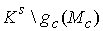 замкнуто. Тогда замкнуто. Тогда 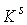 есть объединение двух
замкнутых множеств есть объединение двух
замкнутых множеств  и из его связности
следует, что и из его связности
следует, что 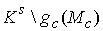 пусто. Доказательство
закончено. пусто. Доказательство
закончено.
Накрытие. Напомним кратко определение накрытия, следуя [7]. Пусть у нас есть два гладких
конечномерных связных многообразия 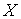 и и 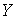 одинаковой
размерности. Гладкое отображение одинаковой
размерности. Гладкое отображение 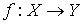 называется накрытием,
если для него выполняются следующие свойства. называется накрытием,
если для него выполняются следующие свойства.
a) Отображение является сюръекцией (т.е.
отображением на всё пространство 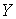 ). ).
b) Отображение регулярно в том смысле, что в
любой точке 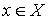 ранг отображения
равен размерности многообразий; ранг отображения
равен размерности многообразий;
c) У любой точки  найдётся (открытая)
окрестность найдётся (открытая)
окрестность 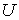 такая, что ее
прообраз состоит из конечного или счётного набора непересекающихся открытых
множеств такая, что ее
прообраз состоит из конечного или счётного набора непересекающихся открытых
множеств 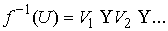 таких, что
отображение таких, что
отображение 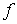 , суженное на любое , суженное на любое 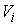 , является диффеоморфизмом , является диффеоморфизмом  и и 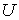 . .
Таким образом, прообраз любой точки 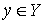 , который называется слоем накрытия, содержит конечное или счётное число
элементов. Число элементов в любом слое одинаково и называется числом листов
накрытия. Если оно, конечно, то накрытие называется конечнолистным.
Пространство , который называется слоем накрытия, содержит конечное или счётное число
элементов. Число элементов в любом слое одинаково и называется числом листов
накрытия. Если оно, конечно, то накрытие называется конечнолистным.
Пространство 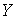 называется базой
накрытия, а называется базой
накрытия, а 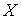 накрывающим
пространством. Из свойств накрытий нам понадобится лемма о поднятии пути. В ней утверждается, что всякий кусочно-гладкий
путь на базе накрытия, у которого задана одна точка прообраза, может быть однозначно поднят на накрывающее
пространство. Т.е. может быть однозначно определён кусочно-гладкий путь в
накрывающем пространстве, проходящий через заданную точку прообраза, и проекция
которого на базу совпадает с исходным путём. накрывающим
пространством. Из свойств накрытий нам понадобится лемма о поднятии пути. В ней утверждается, что всякий кусочно-гладкий
путь на базе накрытия, у которого задана одна точка прообраза, может быть однозначно поднят на накрывающее
пространство. Т.е. может быть однозначно определён кусочно-гладкий путь в
накрывающем пространстве, проходящий через заданную точку прообраза, и проекция
которого на базу совпадает с исходным путём.
Пусть мы находимся теперь в рамках определений
второго раздела.
Утверждение 3.1. Пусть 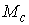 компактно, компактно, 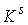 связно и размерности связно и размерности 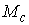 и и 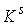 совпадают (т.е. совпадают (т.е. 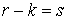 ). Если
отображение ). Если
отображение 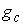 кинематически
независимо, то кинематически
независимо, то 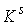 компактно и компактно и 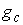 является конечнолистным накрытием с накрывающим пространством является конечнолистным накрытием с накрывающим пространством 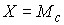 и базой и базой 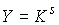 . Если же . Если же 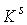 односвязно, то односвязно, то 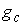 является диффеоморфизмом
многообразий является диффеоморфизмом
многообразий 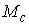 и и 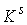 . .
Доказательство. Данное утверждение известно и обычно формулируется
в терминах регулярности отображений [7]. Тем не менее, мы приведём его
доказательство, для того, чтобы вывести из него следствие 3.1.
В силу
утверждения 2.4 кинематическое отображение 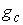 является сюръекцией.
А в силу условия кинематической независимости ранг отображения является сюръекцией.
А в силу условия кинематической независимости ранг отображения 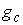 равен равен 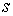 , поэтому нам надо доказать только свойство c). Докажем сначала, что у каждой точки , поэтому нам надо доказать только свойство c). Докажем сначала, что у каждой точки 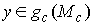 прообраз состоит из
конечного числа элементов. Допустим противное. Пусть прообраз состоит из
конечного числа элементов. Допустим противное. Пусть 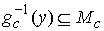 состоит из
бесконечного числа точек. Поскольку состоит из
бесконечного числа точек. Поскольку 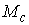 компактно, то из этих
точек можно выбрать последовательность, сходящуюся к некой точке компактно, то из этих
точек можно выбрать последовательность, сходящуюся к некой точке 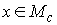 . При этом . При этом 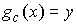 в силу непрерывности
отображения в силу непрерывности
отображения 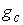 . Однако, из условия кинематической независимости и теоремы о
неявных функциях следует, что у каждой точки прообраза должна существовать
окрестность, в которой нет других точек прообраза. Это противоречит тому, что . Однако, из условия кинематической независимости и теоремы о
неявных функциях следует, что у каждой точки прообраза должна существовать
окрестность, в которой нет других точек прообраза. Это противоречит тому, что 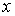 – предельная точка.
Докажем теперь свойство c).
Возьмём любую точку – предельная точка.
Докажем теперь свойство c).
Возьмём любую точку 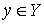 . Пусть . Пусть 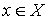 любой из её прообразов.
В соответствии с теоремой о неявных функциях найдутся шаровые окрестности любой из её прообразов.
В соответствии с теоремой о неявных функциях найдутся шаровые окрестности 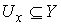 точки точки 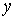 , и , и 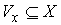 точки точки 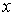 такие, что сужение такие, что сужение 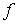 на на 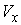 является
диффеоморфизмом является
диффеоморфизмом 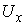 и и 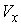 . Обозначим это сужение . Обозначим это сужение 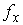 . Проделаем такое построение для каждого прообраза точки . Проделаем такое построение для каждого прообраза точки 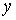 . Пусть . Пусть 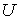 – шаровая окрестность
точки – шаровая окрестность
точки 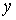 , лежащая в пересечении всех получившихся окрестностей , лежащая в пересечении всех получившихся окрестностей 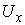 . Поскольку число прообразов точки . Поскольку число прообразов точки 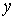 конечно, то она
существует. Тогда набор шаровых окрестностей конечно, то она
существует. Тогда набор шаровых окрестностей 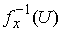 удовлетворяет
требованиям свойства с). удовлетворяет
требованиям свойства с).
Осталось рассмотреть случай односвязного
многообразия 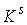 . Пусть . Пусть 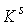 односвязно. Докажем,
что накрытие является однолистным. Допустим противное. Пусть у точки односвязно. Докажем,
что накрытие является однолистным. Допустим противное. Пусть у точки 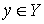 есть два прообраза есть два прообраза 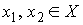 , , 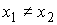 . Соединим их кусочно-гладким путём . Соединим их кусочно-гладким путём 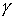 в в 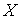 . Путь этот выберем таким, чтобы касательные к нему
проектировались в ненулевые вектора, касательные к базе. Это можно сделать,
поскольку выполнено условие кинематической независимости. Проекция этого пути
на . Путь этот выберем таким, чтобы касательные к нему
проектировались в ненулевые вектора, касательные к базе. Это можно сделать,
поскольку выполнено условие кинематической независимости. Проекция этого пути
на 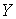 является
кусочно-гладким замкнутым путём в является
кусочно-гладким замкнутым путём в 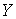 , начинающимся и кончающимся в точке , начинающимся и кончающимся в точке 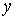 . Поскольку . Поскольку 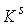 односвязно, то этот
путь можно гладко гомотопно стянуть в точку. Подняв промежуточные пути на односвязно, то этот
путь можно гладко гомотопно стянуть в точку. Подняв промежуточные пути на  , мы получим гомотопию пути , мы получим гомотопию пути 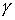 в путь с концами в в путь с концами в 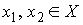 и весь проектирующийся
в точку и весь проектирующийся
в точку 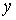 . Это противоречит тому, что число прообразов этой точки
конечно. . Это противоречит тому, что число прообразов этой точки
конечно.
Поскольку
накрытие однолистно, то накрывающее отображение взаимно однозначно и, поэтому,
существует обратное ему. Гладкость обратного отображения следует из условия
кинематической независимости и теоремы о неявных функциях. Доказательство
закончено.
Замечание 3.1. Из
доказательства утверждения 3.1 видно, что вместо односвязности базы можно
потребовать, чтобы число листов накрытия было равным единице. В этом случае так
же накрывающее отображение взаимно однозначно и, поэтому, существует обратное
ему. Аналогично гладкость обратного отображения следует из условия
кинематической независимости и теоремы о неявных функциях. Таким образом, и в данном
случае 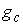 является диффеоморфизмом
многообразий является диффеоморфизмом
многообразий 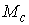 и и 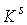 . .
Замечание 3.2.
Утверждение 3.1 можно обобщить. Пусть 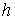 – число образующих
фундаментальной группы базы – число образующих
фундаментальной группы базы 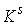 , тогда число листов накрытия не более чем , тогда число листов накрытия не более чем 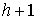 . Доказательство почти дословно повторяет рассуждения приведённые
в доказательстве утверждения 3.1. . Доказательство почти дословно повторяет рассуждения приведённые
в доказательстве утверждения 3.1.
Гладкое расслоение. Напомним кратко определение гладкого расслоения, следуя [7]. Пусть у нас
есть три гладких конечномерных многообразия 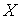 (расслоённое
пространство), (расслоённое
пространство), 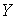 (база) и (база) и 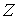 (слой), причём
суммарная размерность базы и слоя совпадает с размерностью расслоённого
пространства: (слой), причём
суммарная размерность базы и слоя совпадает с размерностью расслоённого
пространства: 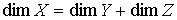 . Пусть также имеется гладкое отображение . Пусть также имеется гладкое отображение 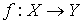 , называемое проекцией. Дифференциал проекции в каждой точке
должен быть невырожден (т.е. в локальных координатах якобиева матрица должна
иметь максимальный ранг равный , называемое проекцией. Дифференциал проекции в каждой точке
должен быть невырожден (т.е. в локальных координатах якобиева матрица должна
иметь максимальный ранг равный  ). Пусть имеется некая группа ). Пусть имеется некая группа 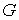 автоморфизмов слоя автоморфизмов слоя 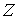 (т.е. диффеоморфизмов (т.е. диффеоморфизмов
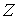 на себя). Эта группа
называется структурной группой
расслоения. Пусть задана структура
расслоения, т.е. база на себя). Эта группа
называется структурной группой
расслоения. Пусть задана структура
расслоения, т.е. база 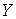 покрыта некоторым
семейством структурных окрестностей,
т.е. координатных окрестностей покрыта некоторым
семейством структурных окрестностей,
т.е. координатных окрестностей 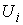 , для которых выполняются следующие условия. Обозначим , для которых выполняются следующие условия. Обозначим 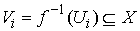 - полный прообраз
окрестности - полный прообраз
окрестности 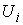 для проекции для проекции 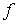 . Тогда . Тогда
1.
Для каждого 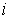 существует
расслаивающий диффеоморфизм существует
расслаивающий диффеоморфизм 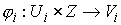 . .
2.
Отображение  - это тождественное
преобразование - это тождественное
преобразование 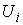 в в 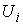 . Иначе говоря, если . Иначе говоря, если 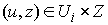 , то , то 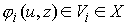 и и 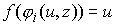 . .
3.
Расслаивающие
диффеоморфизмы попарно согласованы через структурную группу 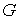 . А именно, пусть пересечение областей . А именно, пусть пересечение областей 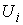 и и 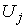 не пусто не пусто 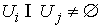 . Требуется, чтобы для любой точки . Требуется, чтобы для любой точки 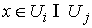 совпадали слои
проходящие через неё и соответствующие совпадали слои
проходящие через неё и соответствующие 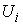 и и 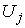 . Тогда . Тогда 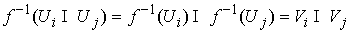 , и можно определить отображение , и можно определить отображение 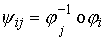 окрестности окрестности 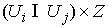 на себя на себя 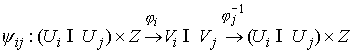 . Это отображение называется отображением склейки. Для любой
точки . Это отображение называется отображением склейки. Для любой
точки 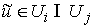 оно порождает некий
диффеоморфизм оно порождает некий
диффеоморфизм 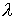 слоя слоя  на себя на себя 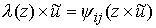 . Требуется, чтобы этот диффеоморфизм лежал в структурной
группе . Требуется, чтобы этот диффеоморфизм лежал в структурной
группе 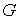 . .
Исходя из приложения к механическим системам, и для краткости изложения, мы
будем рассматривать только расслоения с максимальной структурной группой 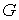 , которая включает все автоморфизмы слоя , которая включает все автоморфизмы слоя 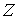 . Поэтому в дальнейшем структурную группу мы не будем
упоминать. . Поэтому в дальнейшем структурную группу мы не будем
упоминать.
Утверждение 4.1.
Пусть объемлющее многообразие 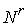 является гладким
расслоением с базой является гладким
расслоением с базой 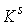 и некоторым слоем и некоторым слоем 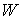 , причём кинематическое отображение , причём кинематическое отображение 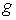 является проекцией
этого расслоения. Условие кинематической независимости состоит в том, что
многообразие уровня является проекцией
этого расслоения. Условие кинематической независимости состоит в том, что
многообразие уровня 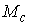 в каждой своей точке
максимально трансверсально слою в каждой своей точке
максимально трансверсально слою 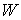 , проходящему через эту точку. В локальном координатном виде
это означает следующее. Возьмем любую точку , проходящему через эту точку. В локальном координатном виде
это означает следующее. Возьмем любую точку 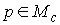 . Тогда существует её координатная окрестность в . Тогда существует её координатная окрестность в 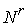 , в которой координаты слоя и базы разделены , в которой координаты слоя и базы разделены 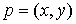 , , 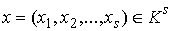 , , 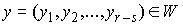 . Полное условие кинематической независимости выглядит
следующим образом . Полное условие кинематической независимости выглядит
следующим образом
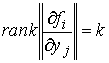 (4.1) (4.1)
на всём многообразии уровня  . Иначе говоря, это условие означает, что система функций . Иначе говоря, это условие означает, что система функций 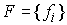 , ,  , высекающих , высекающих 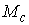 , функционально независима на каждом слое расслоения. , функционально независима на каждом слое расслоения.
Доказательство.
Будем обозначать касательные вектора приставкой 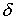 . Тогда вектора, касательные к . Тогда вектора, касательные к 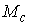 определяются в
локальной системе координат определяются в
локальной системе координат 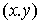 системой уравнений системой уравнений
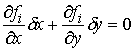 (4.2) (4.2)
Условие кинематической независимости эквивалентно тому, что для любого
вектора 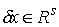 можно подобрать такой
вектор можно подобрать такой
вектор 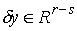 , что система (4.2) будет выполнена. Отсюда сразу следует,
достаточность условия (4.1). Докажем теперь его необходимость. Поскольку
система функций , что система (4.2) будет выполнена. Отсюда сразу следует,
достаточность условия (4.1). Докажем теперь его необходимость. Поскольку
система функций 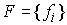 , , 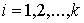 является
функционально независимой, то является
функционально независимой, то
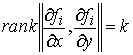 (4.3) (4.3)
Теперь можно воспользоваться следующим
известным утверждением линейной алгебры. Система 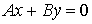 имеет решение относительно имеет решение относительно
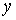 для любого заданного для любого заданного 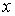 тогда и только тогда,
когда тогда и только тогда,
когда 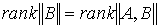 . Тем не менее, для полноты, приведём доказательство, не
опирающееся на этот факт. Допустим противное, что . Тем не менее, для полноты, приведём доказательство, не
опирающееся на этот факт. Допустим противное, что
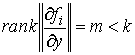 (4.4) (4.4)
Тогда из (4.3) следует, что в матрице 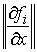 можно найти хотя бы
один столбец можно найти хотя бы
один столбец 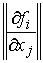 такой, что такой, что
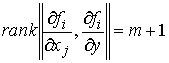 (4.5) (4.5)
Положив в (4.2) 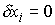 , при , при 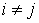 , и , и 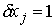 , получим, что система , получим, что система 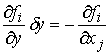 должна иметь решение
относительно должна иметь решение
относительно 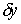 . По теореме Кронекера-Капелли [10] это возможно тогда и
только тогда, когда . По теореме Кронекера-Капелли [10] это возможно тогда и
только тогда, когда
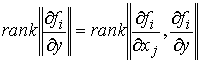
Мы пришли к противоречию с (4.4, 4.5). Доказательство закончено.
Утверждение 4.2. Пусть
объемлющее многообразие 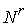 является гладким
расслоением с базой является гладким
расслоением с базой  , некоторым слоем , некоторым слоем 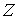 , причём кинематическое отображение , причём кинематическое отображение 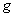 является проекцией
этого расслоения. Будем обозначать это расслоение символом является проекцией
этого расслоения. Будем обозначать это расслоение символом 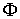 . Обозначим . Обозначим 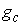 сужение сужение 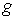 на на  . Пусть . Пусть 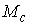 компактно, а компактно, а 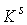 связно. Если отображение связно. Если отображение 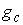 кинематически
независимо, то кинематически
независимо, то 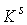 также компактно, а также компактно, а 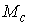 является гладким
расслоением с базой является гладким
расслоением с базой 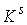 , некоторым слоем , некоторым слоем 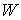 и проекцией и проекцией 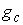 . Будем обозначать это расслоение символом . Будем обозначать это расслоение символом 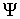 . При этом слой . При этом слой 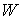 является компактным
многообразием соответствующей размерности является компактным
многообразием соответствующей размерности 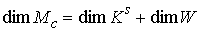 . .
Доказательство.
Компактность 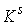 следует из
утверждения 2.4. Докажем остальное. Возьмем любую точку следует из
утверждения 2.4. Докажем остальное. Возьмем любую точку 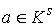 , и содержащую её структурную окрестность , и содержащую её структурную окрестность 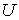 расслоения расслоения 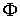 . Тогда . Тогда 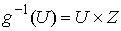 . Не нарушая общности можно считать, что . Не нарушая общности можно считать, что 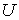 - это координатная окрестность точки - это координатная окрестность точки  , с локальными координатами , с локальными координатами 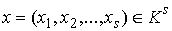 . Тогда слой . Тогда слой 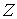 задаётся системой функциональных
уравнений задаётся системой функциональных
уравнений
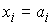 , , 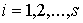 (4.6) (4.6)
где 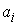 - координаты точки - координаты точки 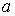 . Обозначим . Обозначим 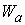 полный прообраз точки полный прообраз точки
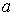 в пересечении с в пересечении с 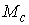 : : 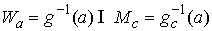 . Для его задания
в . Для его задания
в 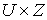 надо к (4.6) добавить систему уравнений надо к (4.6) добавить систему уравнений
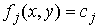 , , 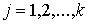 , , 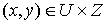 (4.7) (4.7)
Якобиева матрица системы (4.6-4.7) в
локальных координатах 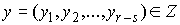 выглядит следующим
образом выглядит следующим
образом 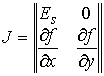 , где , где 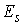 - единичная матрица - единичная матрица 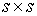 . В силу условия кинематической независимости . В силу условия кинематической независимости 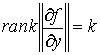 , поэтому , поэтому 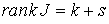 . Значит, . Значит, 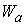 является замкнутым
компактным многообразием размерности является замкнутым
компактным многообразием размерности 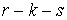 (см. утверждение
2.1). Из замечания 2.1 следует, что для некоторой окрестности (см. утверждение
2.1). Из замечания 2.1 следует, что для некоторой окрестности 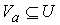 точки точки 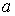 имеем имеем 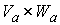 диффеоморфно диффеоморфно 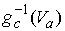 . .
Осталось показать
структурную согласованность расслаивающих диффеоморфизмов. Но она
непосредственно следует из структурной согласованности расслаивающих
диффеоморфизмов исходного расслоения.
Дадим ещё несколько
определений, следуя [7]. Гладким n-мерным распределением на многообразии  называется система называется система  независимых дифференциальных
форм независимых дифференциальных
форм 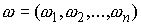 . В касательном пространстве . В касательном пространстве 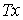 любой точки любой точки 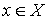 система уравнений система уравнений 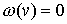 , , 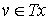 определяет
гиперплоскость размерности определяет
гиперплоскость размерности 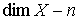 . Будем обозначать эту гиперплоскость . Будем обозначать эту гиперплоскость 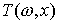 . Связность на
гладком расслоении - это гладкое распределение . Связность на
гладком расслоении - это гладкое распределение 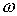 на пространстве
расслоения на пространстве
расслоения 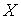 , размерность , размерность 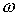 равна размерности
слоя равна размерности
слоя 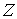 , и оно трансверсально слою в каждой точке. Это означает, что
размерность гиперплоскости , и оно трансверсально слою в каждой точке. Это означает, что
размерность гиперплоскости 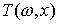 равна размерности
базы равна размерности
базы  и при естественной
проекции и при естественной
проекции 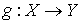 гиперплоскость гиперплоскость 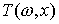 проектируется в
касательное пространство проектируется в
касательное пространство 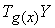 без вырождений.
Вектора без вырождений.
Вектора 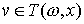 называются горизонтальными направлениями
связности называются горизонтальными направлениями
связности 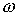 . Кусочно-гладкая кривая на . Кусочно-гладкая кривая на 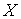 называется
горизонтальной, если вектора её скорости горизонтальны. В любом гладком расслоении
можно определить какую-нибудь риманову метрику называется
горизонтальной, если вектора её скорости горизонтальны. В любом гладком расслоении
можно определить какую-нибудь риманову метрику  , и она породит естественную связность , и она породит естественную связность  , в которой горизонтальными являются все вектора
ортогональные слою. Если слой , в которой горизонтальными являются все вектора
ортогональные слою. Если слой 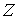 расслоения компактен,
то, как и в случае накрытий, верна лемма о поднятии пути. В ней
утверждается, что всякий кусочно-гладкий путь на базе расслоения, у которого
задана одна точка прообраза, может быть
однозначно поднят до горизонтального пути на пространстве расслоения расслоения компактен,
то, как и в случае накрытий, верна лемма о поднятии пути. В ней
утверждается, что всякий кусочно-гладкий путь на базе расслоения, у которого
задана одна точка прообраза, может быть
однозначно поднят до горизонтального пути на пространстве расслоения 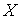 . Т.е., может быть однозначно определён кусочно-гладкий
горизонтальный путь в пространстве, расслоения, проходящий через заданную точку
прообраза, и проекция которого на базу совпадает с исходным путём. . Т.е., может быть однозначно определён кусочно-гладкий
горизонтальный путь в пространстве, расслоения, проходящий через заданную точку
прообраза, и проекция которого на базу совпадает с исходным путём.
Замечание 4.1.
Как и в случае накрытий, можно выделить отдельно ситуацию, когда база 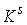 является односвязным
многообразием. В этом случае, если многообразие уровня является односвязным
многообразием. В этом случае, если многообразие уровня 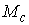 связно, то можно
добавочно утверждать, что слой связно, то можно
добавочно утверждать, что слой 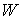 является связным
многообразием. Приведём схему доказательства. Сначала введём на гладком
расслоении является связным
многообразием. Приведём схему доказательства. Сначала введём на гладком
расслоении 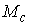 какую-нибудь риманову
метрику и соответствующую ей связность какую-нибудь риманову
метрику и соответствующую ей связность 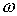 . Возьмём любую точку . Возьмём любую точку 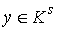 и лист и лист 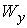 , проходящий через неё. Пусть у слоя , проходящий через неё. Пусть у слоя 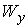 есть две связные
компоненты есть две связные
компоненты 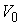 и и 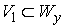 . Поскольку они лежат на связной компоненте многообразия
уровня . Поскольку они лежат на связной компоненте многообразия
уровня 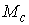 , то их можно соединить кусочно-гладким путём , то их можно соединить кусочно-гладким путём 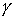 в в  . Проекция этого пути на . Проекция этого пути на 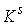 является
кусочно-гладким замкнутым путём является
кусочно-гладким замкнутым путём 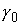 в в 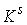 , начинающимся и кончающимся в точке , начинающимся и кончающимся в точке 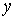 . Поднимем этот путь до горизонтального пути . Поднимем этот путь до горизонтального пути 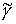 . Как и путь . Как и путь 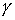 , он начинается на компоненте , он начинается на компоненте 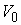 . Покажем, что оканчивается он на компоненте . Покажем, что оканчивается он на компоненте 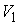 , возможно в другой точке, чем , возможно в другой точке, чем  . Пусть . Пусть 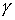 параметризован
параметром параметризован
параметром 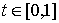 . В каждый момент точка . В каждый момент точка 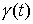 лежит в некоей
связной компоненте лежит в некоей
связной компоненте 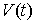 слоя, проходящего
через неё. Причём слоя, проходящего
через неё. Причём 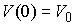 и и 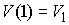 . Для любого . Для любого 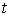 путь путь 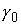 порождает
горизонтальное векторное поле на порождает
горизонтальное векторное поле на 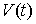 . Несложно убедиться в локальных координатах, что . Несложно убедиться в локальных координатах, что 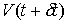 получается из получается из 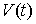 сдвигом вдоль этого
поля. Значит, сдвигом вдоль этого
поля. Значит, 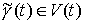 . .
Таким образом, мы получили
горизонтальный путь 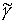 , соединяющий компоненты , соединяющий компоненты 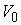 и и 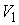 . Далее рассуждаем так же, как и в случае накрытий. Поскольку . Далее рассуждаем так же, как и в случае накрытий. Поскольку
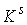 односвязно, то путь односвязно, то путь 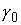 можно гладко
гомотопно стянуть в точку. Подняв горизонтально промежуточные пути, мы получим
гомотопию пути можно гладко
гомотопно стянуть в точку. Подняв горизонтально промежуточные пути, мы получим
гомотопию пути  в путь с концами на в путь с концами на 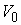 и и 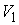 , и весь проектирующийся в точку , и весь проектирующийся в точку 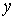 . Это противоречит тому, что . Это противоречит тому, что 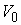 и и 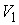 связные компоненты
слоя, и их нельзя соединить путём, который лежит в слое. связные компоненты
слоя, и их нельзя соединить путём, который лежит в слое.
Замечание 4.2. В условиях замечания 4.1, если размерность
слоя равна единице, то это - окружность 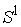 . Если размерность слоя равна двум, то это сфера с
ориентируемыми и неориентиремыми ручками. . Если размерность слоя равна двум, то это сфера с
ориентируемыми и неориентиремыми ручками.
Замечание 4.3.
Замечание 4.1 можно обобщить. Пусть 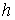 - число образующих
фундаментальной группы базы - число образующих
фундаментальной группы базы 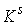 , тогда число связных компонент слоя , тогда число связных компонент слоя 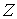 не более чем не более чем 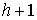 . Доказательство почти дословно повторяет рассуждения
приведённые в замечании 4.1. . Доказательство почти дословно повторяет рассуждения
приведённые в замечании 4.1.
Теперь рассмотрим лагранжеву механическую систему на
n-мерном связном конфигурационном многообразии 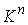 . Фазовое
пространство в этом случае представляет собой . Фазовое
пространство в этом случае представляет собой 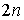 -мерное
многообразие касательного расслоения -мерное
многообразие касательного расслоения 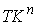 , точки которого
мы будем обозначать , точки которого
мы будем обозначать 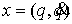 . В качестве
кинематического отображения . В качестве
кинематического отображения 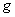 возьмем естественную
проекцию возьмем естественную
проекцию 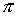 многообразия многообразия 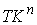 на на 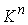 : : 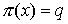 . Его дифференциал . Его дифференциал
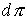 порождает отображение касательных пространств порождает отображение касательных пространств
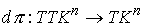 . .
Рассмотрим систему 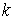 первых интегралов
движения первых интегралов
движения 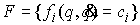 , , 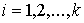 . Обозначим . Обозначим 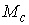 многообразие уровня
этих интегралов (предполагая, что они функционально независимы на многообразие уровня
этих интегралов (предполагая, что они функционально независимы на 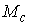 ). Будем говорить, что первые интегралы системы ). Будем говорить, что первые интегралы системы 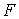 кинематически независимы на многообразии уровня кинематически независимы на многообразии уровня 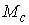 , если сужение отображения , если сужение отображения 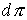 на на 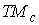 невырождено на невырождено на 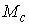 . Это означает, в частности, что в каждой точке . Это означает, в частности, что в каждой точке 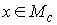 ранг соответствующего
линейного отображения касательных пространств равен ранг соответствующего
линейного отображения касательных пространств равен 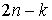 , однако, это всего лишь необходимое условие. , однако, это всего лишь необходимое условие.
Рассмотрим сначала случай 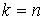 . .
Утверждение 5.1.
Условие кинематической независимости эквивалентно тому, что на всём
многообразии уровня 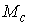 выполняется выполняется
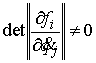 (5.1) (5.1)
Доказательство
сразу следует из утверждения 4.1. Однако, для большей ясности докажем это
утверждение непосредственно. Будем обозначать касательные вектора приставкой  . Тогда вектора, касательные к . Тогда вектора, касательные к 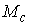 , определяются в локальной системе координат , определяются в локальной системе координат 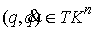 системой уравнений системой уравнений
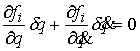 (5.2) (5.2)
Введём вектора 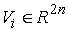 , , 
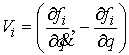 (5.3) (5.3)
Они удовлетворяют (5.2) и, поэтому касаются 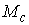 , т.е. , т.е. 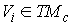 . Поскольку первые интегралы движения функционально
независимы, то система векторов . Поскольку первые интегралы движения функционально
независимы, то система векторов 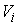 линейно независима.
Поэтому их линейная оболочка совпадает с пространством линейно независима.
Поэтому их линейная оболочка совпадает с пространством 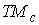 в каждой точке в каждой точке 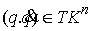 . При естественной проекции эти вектора проектируются в
вектора . При естественной проекции эти вектора проектируются в
вектора 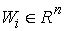 , касательные к конфигурационному многообразию в точке , касательные к конфигурационному многообразию в точке 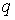 . В указанной локальной системе координат имеем . В указанной локальной системе координат имеем
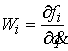 (5.4) (5.4)
Условие кинематической независимости означает, что линейная оболочка векторов
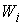 совпадает со всем
касательным пространством, и это эквивалентно условию (5.1). Доказательство
закончено. совпадает со всем
касательным пространством, и это эквивалентно условию (5.1). Доказательство
закончено.
Утверждение 5.2. Любая компактная связная компонента 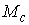 инвариантного
многообразия уровня системы инвариантного
многообразия уровня системы 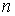 функционально и
кинематически независимых первых интегралов является конечнолистным накрытием
многообразия конфигурационного пространства функционально и
кинематически независимых первых интегралов является конечнолистным накрытием
многообразия конфигурационного пространства 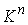 . Если же . Если же 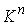 односвязно, то односвязно, то 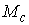 и и 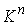 диффеоморфны. Если диффеоморфны. Если 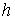 - число образующих
фундаментальной группы конфигурационного пространства - число образующих
фундаментальной группы конфигурационного пространства 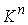 , то число листов накрытия не более, чем , то число листов накрытия не более, чем 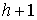 . .
Доказательство.
Непосредственно следует из утверждения 3.1 и замечаний к нему.
Рассмотрим теперь случай 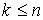 . .
Утверждение 5.3.
Полное условие кинематической независимости выглядит следующим образом
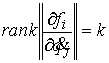 (5.1) (5.1)
на всём многообразии уровня  . .
Доказательство
сразу следует из утверждения 4.1.
Утверждение 5.4. Любая компактная связная компонента 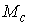 инвариантного
многообразия уровня системы инвариантного
многообразия уровня системы 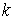 функционально и
кинематически независимых первых интегралов является расслоённым пространством
с базой функционально и
кинематически независимых первых интегралов является расслоённым пространством
с базой 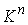 и некоторым слоем и некоторым слоем 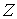 , который является гладким компактным многообразием размерности , который является гладким компактным многообразием размерности
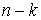 . Если . Если 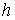 - число образующих
фундаментальной группы базы - число образующих
фундаментальной группы базы 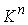 , то число связных компонент слоя , то число связных компонент слоя 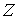 не более, чем не более, чем 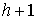 . .
Доказательство.
Непосредственно следует из утверждения 4.2 и замечаний к нему.
Замечание 5.1.
Утверждения этого раздела справедливы и для неголономных, систем. В таких
случаях к первым интегралам движения следует добавлять и сами неголономные
связи.
В данном разделе мы рассмотрим
несколько простых примеров. Первые два примера - это системы с двумя степенями
свободы, имеющие, кроме интеграла энергии, ещё один первый интеграл. В
соответствии с теоремой Лиувилля, в обоих случаях многообразие уровня этих
интегралов является двухмерным тором. Однако условие кинематической
независимости выполняется только в одном из них.
6.1. Тяжёлая точка на сфере. Рассмотрим движение тяжёлой точки массы 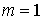 по гладкой сфере
радиуса по гладкой сфере
радиуса 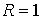 . Ускорение силы тяжести также будем считать единичным. В
данной задаче существуют два первых интеграла - энергии и вертикального момента
количества движения. Исследуем их кинематическую независимость. В сферических
координатах . Ускорение силы тяжести также будем считать единичным. В
данной задаче существуют два первых интеграла - энергии и вертикального момента
количества движения. Исследуем их кинематическую независимость. В сферических
координатах 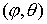 указанные интегралы
записываются следующим образом указанные интегралы
записываются следующим образом
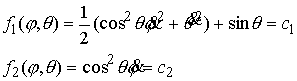 (6.1) (6.1)
Заметим, что для того, чтобы область возможного движения не была
пустой, необходимо, чтобы было 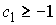 . Введём якобиеву матрицу . Введём якобиеву матрицу 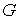 этих интегралов по
скоростям обобщённых координат этих интегралов по
скоростям обобщённых координат 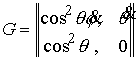 . В соответствии с утверждением 5.1, условие кинематической
независимости выглядит следующим образом . В соответствии с утверждением 5.1, условие кинематической
независимости выглядит следующим образом
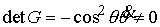 (6.2) (6.2)
Рассмотрим случай 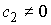 . Тогда из второго уравнения (6.1) имеем . Тогда из второго уравнения (6.1) имеем 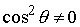 , и условие (6.2) эквивалентно условию , и условие (6.2) эквивалентно условию 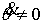 . Известно (см., например, [11]), что в этом случае движение
точки происходит между двумя горизонтальными параллелями, при выходе на которые . Известно (см., например, [11]), что в этом случае движение
точки происходит между двумя горизонтальными параллелями, при выходе на которые
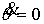 . Таким образом, условие кинематической независимости
нарушается. Пусть теперь . Таким образом, условие кинематической независимости
нарушается. Пусть теперь 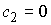 . Тогда несложно убедиться, что движение происходит в
вертикальной плоскости (т.е. в каждый момент времени . Тогда несложно убедиться, что движение происходит в
вертикальной плоскости (т.е. в каждый момент времени 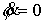 ). При этом точка обязательно будет проходить через нижний
полюс сферы, где ). При этом точка обязательно будет проходить через нижний
полюс сферы, где 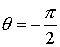 и и 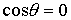 . И, значит, условие кинематической независимости (6.2) также
нарушается. . И, значит, условие кинематической независимости (6.2) также
нарушается.
Таким образом, в данной задаче при
любых значениях констант интегралов движения, условие кинематической
независимости не выполняется.
6.2. Тяжёлая точка на горизонтальном торе.
Рассмотрим движение тяжелой материальной точки единичной массы по гладкому
горизонтально лежащему тору. Радиус осевой окружности обозначим 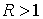 , а радиус окружности поперечного сечения будем считать
равным единице. Ускорение силы тяжести также будем считать единичным. В данной
задаче существуют два первых интеграла - энергии и вертикального момента
количества движения. Исследуем их кинематическую независимость. Пусть , а радиус окружности поперечного сечения будем считать
равным единице. Ускорение силы тяжести также будем считать единичным. В данной
задаче существуют два первых интеграла - энергии и вертикального момента
количества движения. Исследуем их кинематическую независимость. Пусть 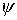 - угловая координата
на осевой (горизонтальной) окружности, а - угловая координата
на осевой (горизонтальной) окружности, а 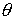 - угловая координата
на окружности поперечного сечения, отсчитываемая от внешней горизонтали. Будем
считать, что тор расположен симметрично в абсолютной системе координат - угловая координата
на окружности поперечного сечения, отсчитываемая от внешней горизонтали. Будем
считать, что тор расположен симметрично в абсолютной системе координат 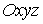 и декартовы
координаты точки на торе задаются следующими соотношениями и декартовы
координаты точки на торе задаются следующими соотношениями
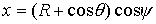 , ,  , , 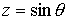
В выбранных координатах интегралы энергии и вертикального момента количества
движения записываются следующим образом
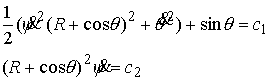 (6.3) (6.3)
Заметим, что
для того, чтобы область возможного движения не была пустой, необходимо, чтобы
было 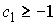 . Введём якобиеву матрицу . Введём якобиеву матрицу 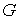 этих интегралов по
скоростям обобщённых координат этих интегралов по
скоростям обобщённых координат 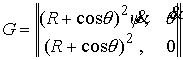 . В соответствии с утверждением 5.1, условие кинематической
независимости выглядит следующим образом . В соответствии с утверждением 5.1, условие кинематической
независимости выглядит следующим образом 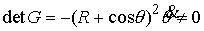 (6.4) (6.4)
Поскольку 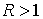 , то , то 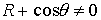 , и условие (6.4) эквивалентно условию , и условие (6.4) эквивалентно условию 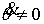 . Для достаточно больших значений константы энергии . Для достаточно больших значений константы энергии 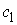 , это выполняется всегда. В самом деле, из второго уравнения
(6.3) находим , это выполняется всегда. В самом деле, из второго уравнения
(6.3) находим 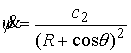 . Подставив это в первое уравнение (6.3) получаем . Подставив это в первое уравнение (6.3) получаем
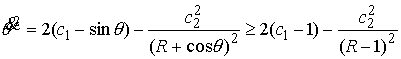 (6.5) (6.5)
откуда сразу
следует требуемое.
Таким образом, в данной задаче, при
достаточно больших значениях константы интеграла энергии 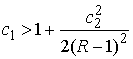 , условие кинематической независимости выполняется и, поэтому
инвариантное многообразие уровня (6.3) является конечнолистным накрытием
конфигурационного многообразия (т.е. двухмерного тора , условие кинематической независимости выполняется и, поэтому
инвариантное многообразие уровня (6.3) является конечнолистным накрытием
конфигурационного многообразия (т.е. двухмерного тора 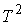 ). Поскольку фундаментальная группа двухмерного тора имеет
две образующие, то число листов накрытия не более чем два. Впрочем, поскольку
(6.5) имеет ровно два решения, то накрытие является двулистным. ). Поскольку фундаментальная группа двухмерного тора имеет
две образующие, то число листов накрытия не более чем два. Впрочем, поскольку
(6.5) имеет ровно два решения, то накрытие является двулистным.
6.3. Многообразие уровня интеграла энергии. Рассмотрим натуральную консервативную механическую
систему с компактным конфигурационным многообразием 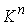 . Пусть в обобщенных координатах . Пусть в обобщенных координатах  интеграл энергии имеет
вид интеграл энергии имеет
вид 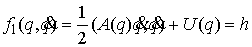 (6.6) (6.6)
Здесь 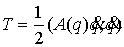 - кинетическая, а - кинетическая, а 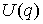 - потенциальная
энергии, - потенциальная
энергии, 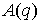 - невырожденная
положительно определённая - невырожденная
положительно определённая 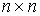 матрица. Все функции
предполагаем гладкими. В соответствии с утверждением 5.3, условие кинематической
невырожденности интеграла (6.6) выглядит следующим образом. матрица. Все функции
предполагаем гладкими. В соответствии с утверждением 5.3, условие кинематической
невырожденности интеграла (6.6) выглядит следующим образом.
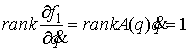 , или , или 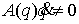
Поскольку  невырождена, то
последнее условие эквивалентно тому, что невырождена, то
последнее условие эквивалентно тому, что 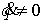 . Поскольку конфигурационное многообразие компактно, то
потенциальная энергия на нём достигает своего максимума . Поскольку конфигурационное многообразие компактно, то
потенциальная энергия на нём достигает своего максимума 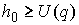 , , 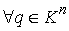 . Если константа . Если константа 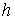 интеграла энергии
достаточно велика ( интеграла энергии
достаточно велика (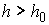 ), то на многообразии уровня интеграла энергии (6.6) везде ), то на многообразии уровня интеграла энергии (6.6) везде 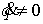 и, вследствие
утверждения 5.4, любая связная компонента этого многообразия представляет собой
расслоённое пространство с базой и, вследствие
утверждения 5.4, любая связная компонента этого многообразия представляет собой
расслоённое пространство с базой 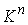 и некоторым слоем и некоторым слоем 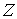 , который является гладким компактным многообразием
размерности , который является гладким компактным многообразием
размерности 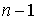 . В соответствии с замечанием 4.3, число связных компонент
слоя не превышает числа образующих фундаментальной группы конфигурационного
многообразия. При заданной точке . В соответствии с замечанием 4.3, число связных компонент
слоя не превышает числа образующих фундаментальной группы конфигурационного
многообразия. При заданной точке 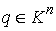 слой слой 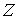 определяется
уравнением (6.6), т.е. представляет собой определяется
уравнением (6.6), т.е. представляет собой 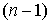 -мерную сферу -мерную сферу 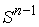 . .
6.4. Тяжёлое твёрдое тело с неподвижной точкой и любым гладким потенциалом. Интеграл энергии,
при достаточно больших своих значениях высекает многообразие уровня, являющееся
гладким расслоением с базой 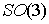 и двухмерным слоем.
Поскольку и двухмерным слоем.
Поскольку 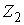 - фундаментальная
группа - фундаментальная
группа 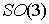 имеет одну
образующую, то, в соответствии с замечанием 4.3, число связных компонент слоя
не более чем две. В соответствии с примером 6.3, слой представляет собой
двухмерную сферу имеет одну
образующую, то, в соответствии с замечанием 4.3, число связных компонент слоя
не более чем две. В соответствии с примером 6.3, слой представляет собой
двухмерную сферу 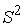
Если потенциал имеет вертикальную круговую
симметрию, то интеграл энергии, при достаточно больших своих значениях,
совместно с интегралом площадей, высекает многообразие уровня, являющееся
гладким расслоением с базой 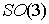 и одномерным слоем.
Одномерный слой, в силу компактности, является семейством не более чем двух
окружностей. Поскольку двухмерный слой - это и одномерным слоем.
Одномерный слой, в силу компактности, является семейством не более чем двух
окружностей. Поскольку двухмерный слой - это 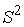 , то линейный по скоростям интеграл высекает из неё ровно
одну окружность, из которой и состоит одномерный слой. , то линейный по скоростям интеграл высекает из неё ровно
одну окружность, из которой и состоит одномерный слой.
6.5. Волчок Эйлера. Возьмём теперь волчок Эйлера, рассмотренный нами в первом разделе, и
исследуем многообразие уровня его первых интегралов, используя утверждения
доказанные выше. В данной задаче имеются три первых интеграла - проекции
момента количества движения на оси абсолютной системы координат 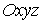 . Неявно эти интегралы можно записать следующим образом . Неявно эти интегралы можно записать следующим образом 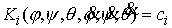 , , 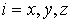 (6.7) (6.7)
где 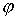 , , 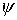 , , 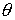 - углы Эйлера. Прежде
всего, отметим, что многообразие уровня (6.7) является ограниченным и,
следовательно, компактным, поскольку неограниченный рост какой-либо компоненты
угловой скорости - углы Эйлера. Прежде
всего, отметим, что многообразие уровня (6.7) является ограниченным и,
следовательно, компактным, поскольку неограниченный рост какой-либо компоненты
угловой скорости 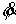 , , 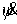 или или 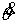 ведёт к
неограниченному росту вектора момента количества движения ведёт к
неограниченному росту вектора момента количества движения 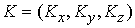 . Пусть . Пусть 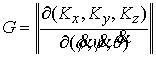 - якобиева матрица
этого вектора по скоростям. В соответствии с утверждением 5.1, условие
кинематической независимости здесь выглядит следующим образом: - якобиева матрица
этого вектора по скоростям. В соответствии с утверждением 5.1, условие
кинематической независимости здесь выглядит следующим образом: 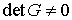 . .
Пусть 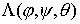 - матрица перехода от
подвижных осей твёрдого тела к неподвижным. Тогда - матрица перехода от
подвижных осей твёрдого тела к неподвижным. Тогда 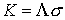 , где , где 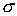 - вектор момента
количества движения в проекции на подвижные оси. Взяв в качестве подвижных осей
- главные оси инерции, будем иметь - вектор момента
количества движения в проекции на подвижные оси. Взяв в качестве подвижных осей
- главные оси инерции, будем иметь 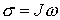 , где , где 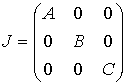 - матрица тензора
инерции, а - матрица тензора
инерции, а 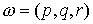 - вектор мгновенной
угловой скорости твердого тела в проекции на подвижные оси. Тогда - вектор мгновенной
угловой скорости твердого тела в проекции на подвижные оси. Тогда  и и  . Поскольку . Поскольку  и и 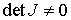 , то условие кинематической независимости (как это следует из
кинематических формул Эйлера) превращается в следующее , то условие кинематической независимости (как это следует из
кинематических формул Эйлера) превращается в следующее 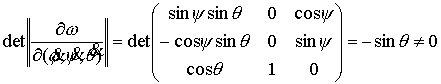
Поскольку
абсолютные оси можно
сориентировать произвольным образом, то условие кинематической независимости
выполняется всегда. Поэтому инвариантное многообразие уровня (6.7) является
конечнолистным накрытием конфигурационного многообразия (т.е. 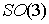 ). ).
Поскольку  , то угловые скорости однозначно определяются по константам
интегралов (6.7). Это означает, что число листов накрытия равно единице и,
вследствие замечания 3.1, инвариантное многообразие уровня (6.7) диффеоморфно
конфигурационному многообразию , то угловые скорости однозначно определяются по константам
интегралов (6.7). Это означает, что число листов накрытия равно единице и,
вследствие замечания 3.1, инвариантное многообразие уровня (6.7) диффеоморфно
конфигурационному многообразию 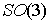 . .
Возьмём волчок Эйлера, т.е. твёрдое тело с неподвижной
точкой, в отсутствии моментов силы тяжести. Добавим к нему эксцентрик -
материальную точку массы 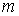 ,
вращающуюся вокруг первой главной
оси инерции тела на расстоянии ,
вращающуюся вокруг первой главной
оси инерции тела на расстоянии 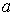 от неё в плоскости, и
отстоящей от начала координат на расстоянии от неё в плоскости, и
отстоящей от начала координат на расстоянии 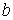 . Конфигурационное многообразие нашей системы - это . Конфигурационное многообразие нашей системы - это 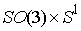 . Помимо углов Эйлера . Помимо углов Эйлера 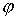 , ,
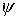 , ,  , определяющих
ориентацию твердого тела, введём также угол , определяющих
ориентацию твердого тела, введём также угол 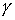 , задающий положение точки эксцентрика , задающий положение точки эксцентрика 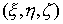 в
подвижной системе координат: в
подвижной системе координат: 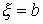 , , 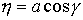 , , 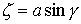 (7.1) (7.1)
Пусть 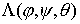 - матрица перехода от
подвижных осей твёрдого тела к неподвижным. Тогда - матрица перехода от
подвижных осей твёрдого тела к неподвижным. Тогда 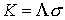 (7.2) (7.2)
где 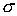 - вектор момента
количества движения в проекции на подвижные оси. Он представляет собой сумму
момента количества движения твердого тела и момента количества движения точки
эксцентрика: - вектор момента
количества движения в проекции на подвижные оси. Он представляет собой сумму
момента количества движения твердого тела и момента количества движения точки
эксцентрика:
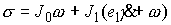 (7.3) (7.3)
здесь  - вектор мгновенной
угловой скорости твердого тела в проекции на подвижные оси, - вектор мгновенной
угловой скорости твердого тела в проекции на подвижные оси, 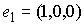 - направляющий вектор
первой главной оси инерции твёрдого тела в подвижных осях, - направляющий вектор
первой главной оси инерции твёрдого тела в подвижных осях, 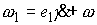 - вектор мгновенной
угловой скорости вращения эксцентрика в проекции на подвижные оси, - вектор мгновенной
угловой скорости вращения эксцентрика в проекции на подвижные оси, 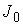 и и 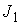 - матрицы тензоров
инерции твёрдого тела и эксцентрика в подвижных осях - матрицы тензоров
инерции твёрдого тела и эксцентрика в подвижных осях
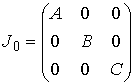 , , 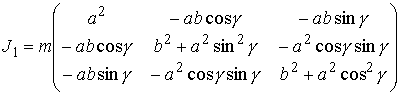 (7.4) (7.4)
Кинетическая энергия системы также представляет собой сумму кинетических
энергий твёрдого тела и точки эксцентрика:
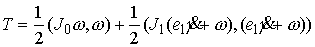 (7.5) (7.5)
Система допускает
четыре первых интеграла движения
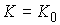 , ,  (7.6) (7.6)
Исследуем вид четырёхмерного многообразия уровней этих интегралов. Поскольку
в число интегралов движения входит интеграл энергии, представляющий собой
положительно определённую квадратичную форму по скоростям, то это многообразие
компактно. Условие кинематической независимости, как и в примере волчка Эйлера
6.5, будем рассматривать относительно угловых скоростей в проекции на подвижные
оси. Пусть 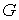 - якобиева матрица
интегралов (7.6) по угловым скоростям - якобиева матрица
интегралов (7.6) по угловым скоростям
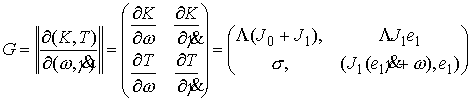 (7.7) (7.7)
Условием кинематической независимости интегралов (7.6) является условие 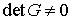 . Ввиду громоздкости формул мы проанализируем его, используя
геометрические соображения. . Ввиду громоздкости формул мы проанализируем его, используя
геометрические соображения.
Пусть у нас есть какое-либо положение твердого
тела и эксцентрика  , и какие-то мгновенные угловые скорости , и какие-то мгновенные угловые скорости 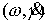 . Интегралы (7.6) кинематически независимы в точке . Интегралы (7.6) кинематически независимы в точке 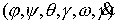 фазового
пространства, если бесконечно малыми изменениями мгновенных угловых скоростей фазового
пространства, если бесконечно малыми изменениями мгновенных угловых скоростей  можно добиться любого
бесконечно малого изменения момента количества движения и кинетической энергии можно добиться любого
бесконечно малого изменения момента количества движения и кинетической энергии  . Поскольку . Поскольку 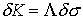 и и 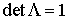 , то, эквивалентным образом, мы будем добиваться любого
бесконечно малого изменения , то, эквивалентным образом, мы будем добиваться любого
бесконечно малого изменения 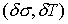 . Рассмотрим сначала случай . Рассмотрим сначала случай 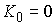 , , 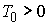 . Тогда . Тогда 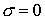 и из (7.3) имеем и из (7.3) имеем 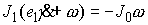 . Подставив это в (7.5) получим . Подставив это в (7.5) получим
 (7.8) (7.8)
Отсюда и из (7.7) имеем
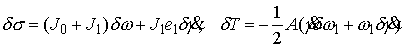 (7.9) (7.9)
Из (7.8) следует, что на всём многообразии
уровня интегралов 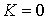 , , 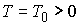 выполнено выполнено 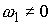 , , 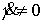 . А поскольку это многообразие компактно, то эти величины
ограничены снизу и сверху . А поскольку это многообразие компактно, то эти величины
ограничены снизу и сверху
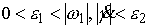 (7.10) (7.10)
Поэтому, из второго уравнения (7.9) находим
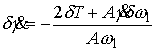 (7.11) (7.11)
и из первого уравнения (7.9)
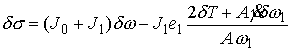 (7.12) (7.12)
Поскольку 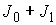 представляет собой
матрицу инерции совокупной системы тела и эксцентрика, то представляет собой
матрицу инерции совокупной системы тела и эксцентрика, то 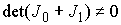 . Поскольку выполнено (7.10), то при достаточно малом модуле
матрицы . Поскольку выполнено (7.10), то при достаточно малом модуле
матрицы 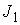 второй член в (7.12)
также достаточно мал и не нарушает невырожденности системы (7.12). Это
означает, что, при достаточно малых значениях второй член в (7.12)
также достаточно мал и не нарушает невырожденности системы (7.12). Это
означает, что, при достаточно малых значениях 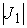 , система (7.12) всегда имеет решение относительно , система (7.12) всегда имеет решение относительно 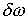 . Таким образом, при достаточно малых значениях массы эксцентрика,
система интегралов . Таким образом, при достаточно малых значениях массы эксцентрика,
система интегралов 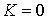 , , 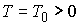 кинематически
независима. (Модуль матрицы оценивается неравенством кинематически
независима. (Модуль матрицы оценивается неравенством 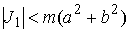 ). В силу компактности
многообразия уровня, кинематическая независимость сохранится и при ненулевых,
но достаточно малых значениях кинетического момента ). В силу компактности
многообразия уровня, кинематическая независимость сохранится и при ненулевых,
но достаточно малых значениях кинетического момента 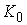 . .
Таким образом, при указанных
условиях, многообразие уровня интегралов (7.6) является конечнолистным
накрытием конфигурационного многообразия 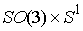 . Оценим число листов и их связность. Равенство . Оценим число листов и их связность. Равенство 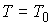 является квадратным
уравнением относительно является квадратным
уравнением относительно 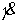 и может допускать два
решения. Система равенств и может допускать два
решения. Система равенств 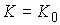 является линейной
относительно является линейной
относительно 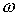 при заданном значении при заданном значении
 и имеет не более
одного решения при заданном значении и имеет не более
одного решения при заданном значении 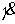 . Поэтому число листов накрытия не более чем два. Из (7.8)
видно, что при малых значениях момента количества движения мы всегда имеем два
решения (т.е. два листа), соответствующие двум комбинациям знаков: . Поэтому число листов накрытия не более чем два. Из (7.8)
видно, что при малых значениях момента количества движения мы всегда имеем два
решения (т.е. два листа), соответствующие двум комбинациям знаков: 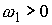 , , 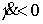 и и 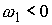 , , 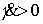 . Поскольку . Поскольку 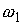 и и 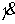 не могут обращаться в
ноль, то каждый лист представляет собой связную компоненту. не могут обращаться в
ноль, то каждый лист представляет собой связную компоненту.
Окончательно получаем
следующее утверждение. При достаточно малом значении массы эксцентрика и, при
достаточно малом значении констант интегралов момента количества движения,
многообразие уровня этих интегралов и интеграла энергии разбивается на две
связные компоненты, каждая из которых диффеоморфна конфигурационному
многообразию 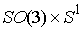 . .
Замечание 7.1.
Следует обратить внимание на то, что, воспользовавшись (7.8), мы заменили
интеграл (7.5) другой функцией, хотя и совпадающей с (7.5) при 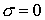 , но являющейся только лишь частным интегралом уравнений движения.
Однако многообразие уровня при этом не меняется, а в используемых утверждениях
из предыдущих разделов не требовалось, чтобы функции, уровни которых высекают
многообразие, были первыми интегралами движения. При малых шевелениях
компактного многообразия, естественно кинематическая независимость сохраняется. , но являющейся только лишь частным интегралом уравнений движения.
Однако многообразие уровня при этом не меняется, а в используемых утверждениях
из предыдущих разделов не требовалось, чтобы функции, уровни которых высекают
многообразие, были первыми интегралами движения. При малых шевелениях
компактного многообразия, естественно кинематическая независимость сохраняется.
Замечание 7.2. К
системе можно добавить потенциальные силы с 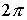 -периодический силовой функцией -периодический силовой функцией 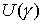 . Если константа интеграла энергии достаточно велика, то все
рассуждения, приведённые выше, останутся верными. . Если константа интеграла энергии достаточно велика, то все
рассуждения, приведённые выше, останутся верными.
В данном разделе мы
рассмотрим пример неголономной системы.
Тяжёлый круговой конёк на горизонтальном торе. Рассмотрим движение однородного круглого плоского диска, центр
которого касается поверхности гладкого, горизонтально лежащего двухмерного тора
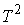 . Радиус осевой окружности тора обозначим . Радиус осевой окружности тора обозначим 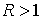 , а радиус окружности поперечного сечения будем считать
равным единице. Массу диска и ускорение силы тяжести также будем считать
единичными. Свяжем с диском сопутствующую систему координат с началом в центре
диска и направляющими векторами , а радиус окружности поперечного сечения будем считать
равным единице. Массу диска и ускорение силы тяжести также будем считать
единичными. Свяжем с диском сопутствующую систему координат с началом в центре
диска и направляющими векторами 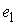 , , 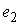 , , 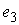 . Вектора . Вектора 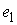 и и 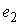 лежат в плоскости
диска, а вектор лежат в плоскости
диска, а вектор 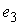 совпадает с внешней
нормалью к тору совпадает с внешней
нормалью к тору 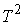 . В силу симметрии, оси сопутствующей системы является главными центральными осями инерции
диска. Главные моменты инерции диска
обозначим ( . В силу симметрии, оси сопутствующей системы является главными центральными осями инерции
диска. Главные моменты инерции диска
обозначим (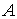 , , 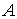 , , 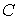 ). Рассматриваемая система имеет три степени свободы. Её
конфигурационное пространство представляет собой трёхмерный тор ). Рассматриваемая система имеет три степени свободы. Её
конфигурационное пространство представляет собой трёхмерный тор 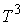 . Введём на нём естественные угловые координаты . Введём на нём естественные угловые координаты 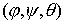 . Где . Где 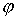 - угол собственного
вращения диска, отсчитываемый от горизонтальной параллели тора - угол собственного
вращения диска, отсчитываемый от горизонтальной параллели тора 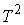 , на которой находится центр диска до вектора , на которой находится центр диска до вектора 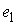 , , 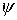 - угловая координата
на осевой (горизонтальной) окружности тора - угловая координата
на осевой (горизонтальной) окружности тора 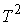 , а , а 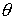 - угловая координата
на окружности его поперечного сечения, отсчитываемая от внешней горизонтали.
Будем считать, что тор расположен симметрично в абсолютной системе координат - угловая координата
на окружности его поперечного сечения, отсчитываемая от внешней горизонтали.
Будем считать, что тор расположен симметрично в абсолютной системе координат  , и декартовы координаты точки на торе задаются следующими соотношениями , и декартовы координаты точки на торе задаются следующими соотношениями 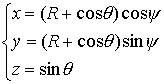 (8.1) (8.1)
Найдём координаты сопутствующих ортов 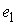 , , 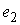 , , 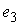 в абсолютной системе. Вектор в абсолютной системе. Вектор 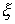 , касательный к горизонтальной параллели тора , касательный к горизонтальной параллели тора 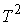 направлен по направлен по 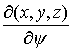 и равен и равен 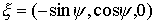 (8.2) (8.2)
Вектор  , касательный к меридиану тора , касательный к меридиану тора 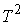 направлен по направлен по 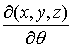 и равен и равен
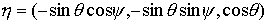 (8.3) (8.3)
Вектор 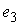 внешней нормали к
тору внешней нормали к
тору 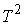 равен вектору равен вектору 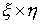 : :
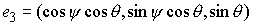 (8.4) (8.4)
Вектора 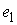 и и 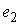 получаются из получаются из 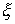 и и 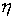 поворотом на угол поворотом на угол 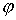 в плоскости в плоскости 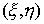 : :
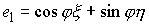 , , 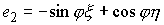 (8.5) (8.5)
или
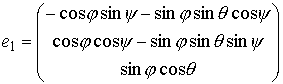 , , 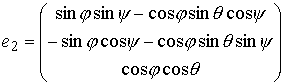 (8.6) (8.6)
На движение диска наложена следующая
дополнительная неголономная связь. Поместим в центр диска конёк, который
двигается по поверхности тора 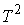 . Мы будем считать, что линия скольжения конька направлена по . Мы будем считать, что линия скольжения конька направлена по
 . Условие скольжения состоит в том, что скорость центра диска . Условие скольжения состоит в том, что скорость центра диска
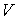 должна быть направлена
по линии скольжения должна быть направлена
по линии скольжения 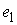 , т.е., должно быть выполнено , т.е., должно быть выполнено 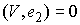 и и 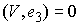 . В силу уравнений (8.1), последнее равенство выполняется
автоматически, поэтому остаётся только условие . В силу уравнений (8.1), последнее равенство выполняется
автоматически, поэтому остаётся только условие 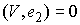 . Выразим его в обобщенных координатах . Выразим его в обобщенных координатах 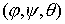 . Из (8.1) находим . Из (8.1) находим
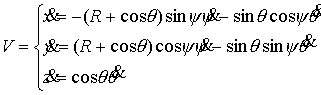 (8.7) (8.7)
Подставив 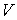 из (8.7) и из (8.7) и  из (8.6) в уравнение
неголономной связи из (8.6) в уравнение
неголономной связи 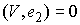 , и, приведя подобные члены, получаем , и, приведя подобные члены, получаем
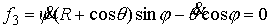 (8.8) (8.8)
Система допускает интеграл энергии 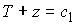 , где , где  - кинетическая, а - кинетическая, а 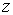 - потенциальные
энергия системы (напоминаем, что масса диска и ускорение силы тяжести равны
единице). Выразим кинетическую энергию в обобщенных координатах. По теореме
Кёнига - потенциальные
энергия системы (напоминаем, что масса диска и ускорение силы тяжести равны
единице). Выразим кинетическую энергию в обобщенных координатах. По теореме
Кёнига
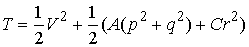 (8.9) (8.9)
где первое слагаемое - это кинетическая энергия центра масс. В примере 6.2
мы уже находили его: 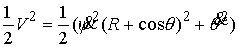 (8.10) (8.10)
Второе слагаемое в (8.9) - это кинетическая энергия вращения диска вокруг
центра масс. В нём 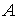 и и 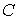 - главные моменты
инерции диска, а - главные моменты
инерции диска, а 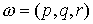 - его мгновенная
угловая скорость в проекции на подвижные оси. Вектор - его мгновенная
угловая скорость в проекции на подвижные оси. Вектор 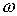 можно представить в
виде суммы можно представить в
виде суммы 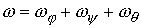 трёх мгновенных
угловых скоростей, возникающих при поворотах по углам трёх мгновенных
угловых скоростей, возникающих при поворотах по углам 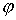 , , 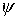 и и 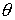 . Несложно убедиться в том, что . Несложно убедиться в том, что 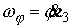 , , 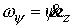 , , 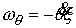 , где , где  - третий вектор подвижных
осей, - третий вектор подвижных
осей, 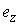 - вертикальный вектор
абсолютной системы, - вертикальный вектор
абсолютной системы, 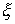 - вектор, касательный
к горизонтальной параллели тора - вектор, касательный
к горизонтальной параллели тора 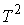 (см. 8.2). В
абсолютной системе координат (см. 8.2). В
абсолютной системе координат 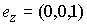 , а , а  задаётся формулами
(8.2). Воспользовавшись (8.4, 8.6) получим в проекции на подвижные оси задаётся формулами
(8.2). Воспользовавшись (8.4, 8.6) получим в проекции на подвижные оси
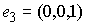 , , 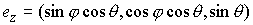 , , 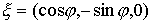
Отсюда находим
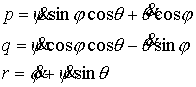 (8.11) (8.11)
Теперь можно выписать интеграл энергии в обобщённых координатах
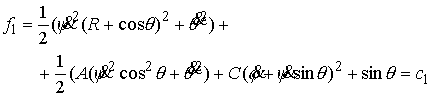 (8.12) (8.12)
Координата 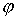 является циклической, т.к. она не входит в
кинетическую и потенциальную энергии, а её скорость не входит в уравнение
неголономной связи. Ей соответствует циклический интеграл момента собственного
вращения является циклической, т.к. она не входит в
кинетическую и потенциальную энергии, а её скорость не входит в уравнение
неголономной связи. Ей соответствует циклический интеграл момента собственного
вращения
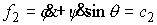 (8.13) (8.13)
Исследуем вид трёхмерного многообразия уровней
интегралов (8.12, 8.13, 8.8). Поскольку в число интегралов движения входит
интеграл энергии, представляющий собой положительно определённую квадратичную
форму по скоростям, то это многообразие компактно.
Исследуем кинематическую независимость интегралов.
Сначала подставим (8.13) в (8.12) и получим более простое выражение для
интеграла энергии
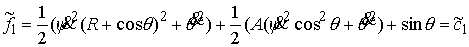 (8.14) (8.14)
Пусть  - якобиева матрица
интегралов (8.14, 8.13, 8.8) по угловым скоростям: - якобиева матрица
интегралов (8.14, 8.13, 8.8) по угловым скоростям:
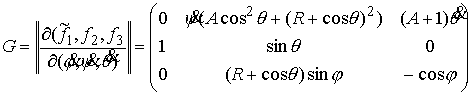 (8.15) (8.15)
Отсюда 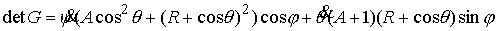 (8.16) (8.16)
Условием кинематической независимости наших интегралов является условие 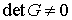 . Исследуем
обращение в ноль . Исследуем
обращение в ноль 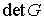 . Возьмём достаточно большую константу интеграла энергии . Возьмём достаточно большую константу интеграла энергии 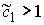 . Тогда из (8.14) следует, что всегда либо . Тогда из (8.14) следует, что всегда либо 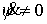 , либо , либо 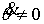 . .
Рассмотрим случай 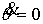 . Тогда . Тогда  и из (8.8), и того,
что и из (8.8), и того,
что 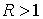 , получаем , получаем 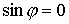 . Отсюда . Отсюда 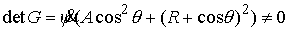 . .
Рассмотрим случай 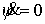 . Тогда . Тогда 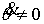 и из (8.8) получаем и из (8.8) получаем 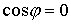 . Отсюда и того, что . Отсюда и того, что 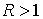 имеем имеем 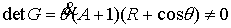 . .
Теперь проанализируем случай 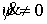 и и 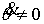 . .
Пусть 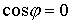 . Тогда . Тогда 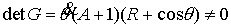 . .
Пусть 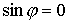 . Тогда . Тогда 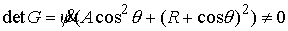 . .
Осталось рассмотреть случай 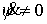 , , 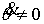 , , 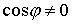 , ,  . Из (8.8) находим . Из (8.8) находим 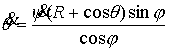 . Подставив это в (8.16) получим . Подставив это в (8.16) получим
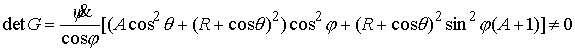
Таким образом, при достаточно большом значении константы интеграла энергии 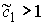 , система интегралов (8.12, 8.13, 8.8) кинематически независима. Поэтому при
указанных условиях многообразие уровня этих интегралов является компактным
конечнолистным накрытием конфигурационного многообразия , система интегралов (8.12, 8.13, 8.8) кинематически независима. Поэтому при
указанных условиях многообразие уровня этих интегралов является компактным
конечнолистным накрытием конфигурационного многообразия 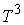 . Оценим число листов и их связность. Равенство . Оценим число листов и их связность. Равенство 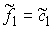 является квадратным
уравнением относительно является квадратным
уравнением относительно  или относительно или относительно  и всегда допускает
два решения. Система равенств (8.13,
8.8) является линейной относительно и всегда допускает
два решения. Система равенств (8.13,
8.8) является линейной относительно  , ,  , ,  и, при заданном
значении и, при заданном
значении  или или  имеет не более одного
решения. Поэтому число листов накрытия - два. имеет не более одного
решения. Поэтому число листов накрытия - два.
Рассмотрим нашу механическую систему в гамильтоновом формализме. Пусть у нас опять есть семейство
функционально независимых первых интегралов движения 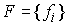 , , 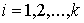 . И пусть . И пусть 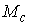 - связная компактная
компонента многообразия уровня этих интегралов. Её размерность обозначим - связная компактная
компонента многообразия уровня этих интегралов. Её размерность обозначим 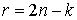 . Поскольку первые интегралы функционально независимы, то, в
соответствии с утверждением 2.1, в некоторой ее открытой окрестности нет других
точек этого многообразия, и существует некоторое . Поскольку первые интегралы функционально независимы, то, в
соответствии с утверждением 2.1, в некоторой ее открытой окрестности нет других
точек этого многообразия, и существует некоторое 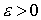 такое, что для всех такое, что для всех 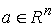 , таких, что , таких, что 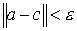 множество множество 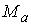 уровня системы
интегралов уровня системы
интегралов 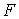 представляет собой
замкнутое компактное подмногообразие диффеоморфное представляет собой
замкнутое компактное подмногообразие диффеоморфное 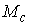 . Объединение всех . Объединение всех 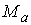 образует открытую
окрестность образует открытую
окрестность 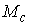 . .
Пусть система первых интегралов 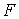 функционально
замкнута относительно канонической скобки Пуассона в фазовом пространстве, т.е. функционально
замкнута относительно канонической скобки Пуассона в фазовом пространстве, т.е.
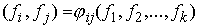 , где , где 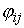 - некоторые гладкие
функции. Пусть - некоторые гладкие
функции. Пусть 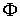 - система всех первых
интегралов из - система всех первых
интегралов из 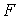 , пополненная линейными (или функциональными) операциями и
коммутированием до алгебры Ли. Тогда гамильтоновы векторные поля системы , пополненная линейными (или функциональными) операциями и
коммутированием до алгебры Ли. Тогда гамильтоновы векторные поля системы 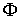 образуют алгебру Ли,
которую мы обозначим образуют алгебру Ли,
которую мы обозначим 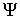 . .
Утверждение 9.1. Возьмем
какое-нибудь векторное поле 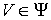 . Оно порождает локальную однопараметрическую группу . Оно порождает локальную однопараметрическую группу 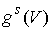 диффеоморфизмов
фазового пространства. Тогда локально эта группа диффеоморфно переводит каждое
многообразие диффеоморфизмов
фазового пространства. Тогда локально эта группа диффеоморфно переводит каждое
многообразие 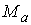 в некоторое
многообразие в некоторое
многообразие 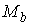 , сохраняя при этом исходный фазовый поток. , сохраняя при этом исходный фазовый поток.
Доказательство. В самом
деле, возьмем какой-нибудь первый интеграл
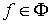 , порождающий , порождающий 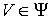 . Тогда по построению . Тогда по построению 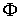 имеем имеем 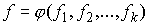 , где , где  - некоторая гладкая
функция. Пусть - некоторая гладкая
функция. Пусть 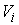 - гамильтоновы
векторные поля, порождаемые интегралами - гамильтоновы
векторные поля, порождаемые интегралами 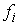 . Тогда . Тогда 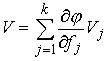 , и , и
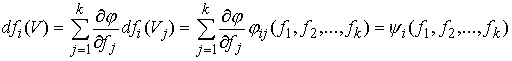 (9.1) (9.1)
где 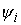 - гладкие функции.
Фактически (9.1) означает, что для всех точек - гладкие функции.
Фактически (9.1) означает, что для всех точек 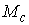 при движении по
векторному полю при движении по
векторному полю 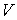 скорость изменения
константы скорость изменения
константы 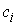 одна и та же. Если
обозначить одна и та же. Если
обозначить 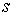 - групповой параметр
сдвига вдоль поля - групповой параметр
сдвига вдоль поля 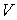 , то , то
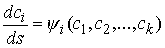 (9.2) (9.2)
Значит,
каждая поверхность уровня 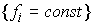 переходит в себя и,
следовательно, то же происходит и с переходит в себя и,
следовательно, то же происходит и с  . .
Осталось доказать, что
диффеоморфизм 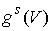 сохраняет гамильтонов
поток. Но это следует из того, что все функции сохраняет гамильтонов
поток. Но это следует из того, что все функции 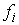 , будучи первыми интегралами движения, коммутируют с гамильтонианом. Значит и , будучи первыми интегралами движения, коммутируют с гамильтонианом. Значит и 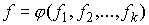 также коммутирует с
ним. также коммутирует с
ним.
В каждой точке 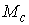 векторные поля из
алгебры векторные поля из
алгебры 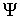 образуют линейное
пространство некоторой размерности образуют линейное
пространство некоторой размерности 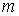 . Разность . Разность 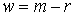 назовём корангом
алгебры векторных полей назовём корангом
алгебры векторных полей 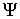 в данной точке в данной точке 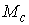 . Минимальное значение . Минимальное значение 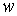 будем называть
корангом будем называть
корангом 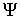 на на 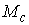 . На самом деле при определении коранга достаточно брать не
все векторные поля из . На самом деле при определении коранга достаточно брать не
все векторные поля из 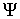 , а только систему гамильтоновых векторных полей , а только систему гамильтоновых векторных полей 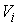 , порождаемых интегралами , порождаемых интегралами 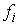 , поскольку на , поскольку на 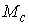 все поля из все поля из  являются линейными
комбинациями полей являются линейными
комбинациями полей 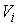 с коэффициентами
постоянными на с коэффициентами
постоянными на 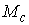 . .
Утверждение 9.2. Пусть 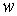 - коранг - коранг 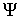 на на 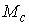 . Тогда в окрестности . Тогда в окрестности 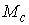 существует существует 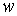 -параметрическое семейство инвариантных многообразий диффеоморфных -параметрическое семейство инвариантных многообразий диффеоморфных
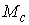 , и движение на которых эквивалентно движению на нём. , и движение на которых эквивалентно движению на нём.
Доказательство. Возьмём
какую-либо точку на 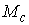 и найдём систему и найдём систему 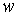 линейно независимых
векторов линейно независимых
векторов 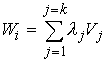 (9.3) (9.3)
не касающихся
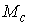 . Тогда и в любой другой точке . Тогда и в любой другой точке 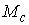 вектора, вычисленные
по (9.3)
будут линейно независимыми и трансверсальными вектора, вычисленные
по (9.3)
будут линейно независимыми и трансверсальными 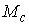 . Это следует из (9.2). Таким образом, мы получаем систему . Это следует из (9.2). Таким образом, мы получаем систему 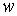 независимых векторных
полей трансверсальных независимых векторных
полей трансверсальных 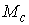 , и сохраняющих , и сохраняющих 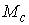 и гамильтонов поток
на нём при сдвиге вдоль этих полей. Сдвиги вдоль этих полей (хотя и не коммутирующие) образуют искомое и гамильтонов поток
на нём при сдвиге вдоль этих полей. Сдвиги вдоль этих полей (хотя и не коммутирующие) образуют искомое 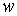 -параметрическое семейство диффеоморфизмов. -параметрическое семейство диффеоморфизмов.
Пример 9.1. В первом
разделе мы рассматривали инвариантное многообразие интегралов моментов
количества движения. Коранг алгебры векторных полей здесь равен двум (если
вектор момента не равен нулю).
Замечание 9.1. Если гамильтоновы векторные поля 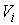 , порождаемые интегралами , порождаемые интегралами 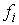 , не коммутируют, то распределение порождаемое ими неинволютивно.
Это означает, фактическая размерность семейства инвариантных многообразий
диффеоморфных , не коммутируют, то распределение порождаемое ими неинволютивно.
Это означает, фактическая размерность семейства инвариантных многообразий
диффеоморфных 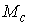 может оказаться выше,
чем та, которая объявлена в утверждении 9.2. Так, в примере 9.1 интегралы
момента количества движения не коммутируют, и поэтому все многообразия в окрестности может оказаться выше,
чем та, которая объявлена в утверждении 9.2. Так, в примере 9.1 интегралы
момента количества движения не коммутируют, и поэтому все многообразия в окрестности 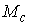 , при заданном уровне энергии эквивалентны ему. , при заданном уровне энергии эквивалентны ему.
В этом разделе мы исследуем вопрос о кинематической независимости первых
интегралов линейных по скоростям. Известно, что локально такие интегралы являются
циклическими [5]. Сначала повторим рассуждения примера 6.3.
Рассмотрим натуральную консервативную механическую систему с компактным
конфигурационным многообразием 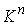 . Пусть в обобщенных координатах . Пусть в обобщенных координатах 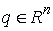 интеграл энергии имеет
вид интеграл энергии имеет
вид
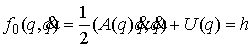 (10.1) (10.1)
Здесь 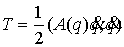 - кинетическая, а - кинетическая, а 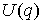 - потенциальная
энергии, - потенциальная
энергии, 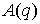 - невырожденная
положительно определённая - невырожденная
положительно определённая 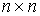 матрица. Все функции
предполагаем гладкими. В соответствии с утверждением 5.3, условие кинематической
невырожденности интеграла (10.1) выглядит следующим образом: матрица. Все функции
предполагаем гладкими. В соответствии с утверждением 5.3, условие кинематической
невырожденности интеграла (10.1) выглядит следующим образом: 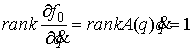 , или , или 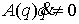 . Поскольку . Поскольку 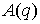 невырождена, то последнее
условие эквивалентно тому, что невырождена, то последнее
условие эквивалентно тому, что 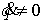 . Поскольку конфигурационное многообразие компактно, то
потенциальная энергия на нём достигает своего максимума . Поскольку конфигурационное многообразие компактно, то
потенциальная энергия на нём достигает своего максимума 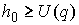 , , 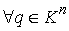 . Если константа . Если константа 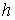 интеграла энергии
достаточно велика ( интеграла энергии
достаточно велика (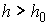 ), то на многообразии уровня интеграла энергии (10.1) везде ), то на многообразии уровня интеграла энергии (10.1) везде  и, вследствие
утверждения 5.4, любая связная компонента этого многообразия представляет собой
расслоённое пространство с базой и, вследствие
утверждения 5.4, любая связная компонента этого многообразия представляет собой
расслоённое пространство с базой 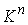 и некоторым слоем и некоторым слоем 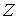 , который является гладким компактным многообразием размерности , который является гладким компактным многообразием размерности
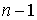 . При заданной точке . При заданной точке 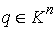 слой слой 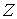 определяется
уравнением (10.6), т.е. представляет собой определяется
уравнением (10.6), т.е. представляет собой 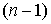 -мерную сферу -мерную сферу 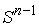 . .
Допустим, что у системы есть 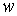 первых интегралов
линейных по скоростям. Локально, в любой координатной окрестности они имеют вид первых интегралов
линейных по скоростям. Локально, в любой координатной окрестности они имеют вид
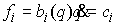 , ,  (10.2) (10.2)
где 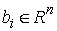 - гладкие
вектор-функция, самосогласованные в точках пересечения различных координатных
окрестностей. Пусть эти интегралы являются невырожденными, т.е. всюду на
конфигурационном многообразии - гладкие
вектор-функция, самосогласованные в точках пересечения различных координатных
окрестностей. Пусть эти интегралы являются невырожденными, т.е. всюду на
конфигурационном многообразии 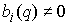 . Пусть, также, они независимы, т.е. всюду на
конфигурационном многообразии вектора . Пусть, также, они независимы, т.е. всюду на
конфигурационном многообразии вектора 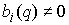 линейно независимы.
Заметим, что из независимости следует невырожденность. Если взять векторное
поле линейно независимы.
Заметим, что из независимости следует невырожденность. Если взять векторное
поле 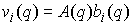 , то , то 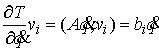 , т.е. интегралы (10.2) являются Нётеровыми для полей
симметрии , т.е. интегралы (10.2) являются Нётеровыми для полей
симметрии 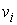 . Независимость интегралов, линейных по скоростям, эквивалентна
независимости соответствующих полей симметрии. . Независимость интегралов, линейных по скоростям, эквивалентна
независимости соответствующих полей симметрии.
Рассмотрим случай 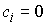 , , 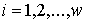 . Покажем, что система интегралов (10.1, 10.2) кинематически
независима. Пусть . Покажем, что система интегралов (10.1, 10.2) кинематически
независима. Пусть 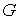 - якобиева матрица
интегралов (10.1, 10.2) по скоростям - якобиева матрица
интегралов (10.1, 10.2) по скоростям 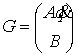 , где , где  - матрица, строками
которой являются вектора - матрица, строками
которой являются вектора  , ,  . Условием кинематической независимости является условие . Условием кинематической независимости является условие  . Пусть в какой-либо точке . Пусть в какой-либо точке 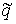 конфигурационного
многообразия условие кинематической независимости нарушается. Тогда найдётся такая
скорость конфигурационного
многообразия условие кинематической независимости нарушается. Тогда найдётся такая
скорость 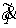 и числа и числа 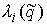 , , 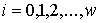 не все равные нулю,
что не все равные нулю,
что
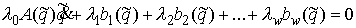
Поскольку  линейно независимы,
то линейно независимы,
то  (10.3) (10.3)
Напомним, что на всём многообразии уровня интеграла энергии  и, значит и, значит 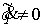 и и 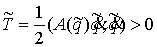 (10.4) (10.4)
Домножив обе части этого равенства справа на 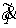 , получим , получим 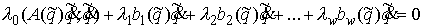
или 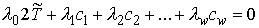 . Поскольку . Поскольку 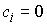 , , 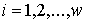 , то , то 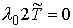 , и мы входим в противоречие с (10.3, 10.4). , и мы входим в противоречие с (10.3, 10.4).
Таким образом, интегралы
(10.1, 10.2) кинематически независимы при достаточно больших значениях
константы интеграла энергии и нулевых значениях констант интегралов, линейных
по скоростям.
Замечание 10.1.
Поскольку конфигурационное многообразие компактно, то кинематическая
независимость сохранится и при не слишком больших ненулевых значениях констант
интегралов, линейных по скоростям. В силу однородности по скоростям
кинетической энергии и линейных интегралов возможна замена времени, что
эквивалентно масштабированию констант линейных интегралов. Это означает, что
при формулировании достаточных условий кинематической независимости можно
ограничиться просто условием, что константа интеграла энергии является
достаточно большой. Тем самым, мы можем сформулировать следующее утверждение.
Утверждение 10.1. Если натуральная система с компактным конфигурационным многообразием 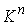 имеет имеет 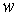 независимых первых
интегралов линейных по скоростям, то, для достаточно больших значений константы
интеграла энергии, многообразие совместного уровня этих интегралов и интеграла
энергии представляет собой гладкое расслоение с базой независимых первых
интегралов линейных по скоростям, то, для достаточно больших значений константы
интеграла энергии, многообразие совместного уровня этих интегралов и интеграла
энергии представляет собой гладкое расслоение с базой 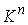 и слоем и слоем 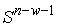 . .
Доказательство. В
силу замечания 10.1 нам надо только отметить, что слой представляет собой
совместное решение уравнений (10.1) и (10.2) в пространстве скоростей. Т.е.
слой - это сечение сферы 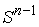 (точнее, эллипсоида) независимыми гиперплоскостями (10.2) в
количестве (точнее, эллипсоида) независимыми гиперплоскостями (10.2) в
количестве 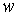 экземпляров. Это, очевидно,
сфера экземпляров. Это, очевидно,
сфера 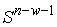 (эллипсоид). (эллипсоид).
Замечание 10.2. Рассмотрим теперь специальный случай, когда
число первых интегралов, линейных по скоростям на единицу меньше размерности
конфигурационного пространства, т.е. 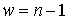 . В этом случае слой представляет собой две точки
(пересечение окружности и прямой), и многообразие уровня является двулистным
накрытием конфигурационного многообразия . В этом случае слой представляет собой две точки
(пересечение окружности и прямой), и многообразие уровня является двулистным
накрытием конфигурационного многообразия 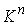 . Если же конфигурационное пространство односвязно, то
многообразие уровня представляет собой два его экземпляра, т.е. . Если же конфигурационное пространство односвязно, то
многообразие уровня представляет собой два его экземпляра, т.е. 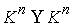 . .
Замечание 10.2.
Сказанное в данном разделе справедливо для систем с числом степеней свободы
большим единицы  . Для одномерных систем из равенства нулю линейного интеграла
следует, что скорость также равна нулю, и, значит, равна нулю кинетическая
энергия, т.е. при достаточно больших значениях интеграла энергии многообразие
уровня становится пустым. . Для одномерных систем из равенства нулю линейного интеграла
следует, что скорость также равна нулю, и, значит, равна нулю кинетическая
энергия, т.е. при достаточно больших значениях интеграла энергии многообразие
уровня становится пустым.
Замечание 10.3. Практическая значимость полученных здесь
результатов состоит в том, что для систем, включающих только интеграл энергии и
интегралы, линейные по скоростям, (при достаточно больших значениях интеграла
энергии) вместо проверки кинематической независимости полной системы интегралов
можно ограничиться проверкой независимости линейных интегралов или
соответствующих им полей симметрии.
Например, в задаче о
движении твёрдого тела с неподвижной точкой в осесимметричном потенциальном
поле сил, интеграл площадей всегда будет невырожден, поскольку поле поворотов
вокруг постоянной оси в  невырождено. Другой
пример - волчок Эйлера с эксцентриком (раздел 7). Тут независимость линейных
интегралов эквивалентна невырожденности отображения (7.3): невырождено. Другой
пример - волчок Эйлера с эксцентриком (раздел 7). Тут независимость линейных
интегралов эквивалентна невырожденности отображения (7.3): 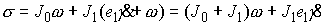 . Очевидно, это всегда имеет место. То же можно сказать и о
других примерах, приведённых в данной работе. . Очевидно, это всегда имеет место. То же можно сказать и о
других примерах, приведённых в данной работе.
Замечание 10.4. Из сказанного выше вытекает одно
геометрическое свойство. На 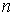 -мерном компактном односвязном гладком многообразии -мерном компактном односвязном гладком многообразии 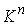 никакая риманова
метрика не может иметь никакая риманова
метрика не может иметь 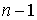 гладких попарно
коммутирующих свободно действующих однопараметрических групп симметрий. В самом
деле, допустим противное, и обозначим порождаемые указанными группами векторные
поля гладких попарно
коммутирующих свободно действующих однопараметрических групп симметрий. В самом
деле, допустим противное, и обозначим порождаемые указанными группами векторные
поля 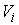 , , 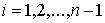 . Введём натуральную механическую систему с матрицей
кинетической энергии совпадающей с соответствующей матрицей римановой метрики.
Поля . Введём натуральную механическую систему с матрицей
кинетической энергии совпадающей с соответствующей матрицей римановой метрики.
Поля 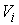 , , 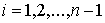 являются нётеровыми
для нашей системы, и порождают являются нётеровыми
для нашей системы, и порождают 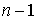 коммутирующих первых
интегралов, которые, совместно с интегралом энергии высекают коммутирующих первых
интегралов, которые, совместно с интегралом энергии высекают 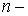 мерный инвариантный тор в фазовом пространстве. В силу же
односвязности мерный инвариантный тор в фазовом пространстве. В силу же
односвязности 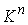 , при малых значениях констант нётеровых интегралов этот тор
должен быть диффеоморфен , при малых значениях констант нётеровых интегралов этот тор
должен быть диффеоморфен 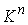 . Мы пришли к противоречию. В качестве примера - на . Мы пришли к противоречию. В качестве примера - на 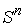 не следует ожидать
линейно интегрируемых систем, у которых интегралы линейные по скоростям нигде
не вырождаются. не следует ожидать
линейно интегрируемых систем, у которых интегралы линейные по скоростям нигде
не вырождаются.
[1]Арнольд В.И.
Математические методы классической механики. М., Эдиториал УРСС, 2000 - 408с. [2]Мищенко
А.С., Фоменко А.Т. Обобщенный метод Лиувилля интегрирования гамильтоновых
систем. Функциональный анализ, 1978, т. 12, вып. 2, с. 46-56. [3]Мищенко
А.С., Фоменко А.Т. Интегрирование гамильтоноовых систем с некоммутативными
симметриями. В кн: Труды семинара по векторному и тензорному анализу, вып. 20,
М., МГУ, 1980, с. 5-54. [4]Фоменко А.Т. Дифференциальная
геометрия и топология. Дополнительные главы. М., МГУ, 1983 - 217c. [5]Козлов
В.В. Симметрии, топология и резонансы в гамильтоновой механике. Ижевск, Изд-во
УдГУ, 1995 - 432с. [6]Громол Д., Клингенберг В., Мейер В. Риманова геометрия в
целом. М., Мир, 1971 - 343c. [7]Дубровин Б.А., Новиков С.П.,
Фоменко А.Т. Современная геометрия. М., Эдиториал УРСС, 1998, т.1 - 333с., т.2
- 278с. [8]Арнольд В.И., Козлов В.В., Нейштадт А.И. Математические
аспекты классической и небесной механики. М., Эдиториал УРСС, 2002 - 416с. [9]Милнор
Дж. Теория Морса. М., Мир, 1971. [10]Курош А.Г. Курс высшей алгебры.
М., Наука, 1965 - 431с. [11]Леви-Чивита Т., Амальди У. Курс
теоретической механики. т. 2, ч. 1, М., Иностранная литература, 1951 - 435с.
|