Небесно-механическая интерпретация измерений радиосистемы межпланетных космических аппаратов «Квант-Д»

( The celestial mechanics interpretation of measurements of the radio system "Kvant-D" for deep space spacecraft
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Введение

Для обеспечения полетов к Фобосу в 1988/1989 гг. и последующих полетов к Марсу в НИИ космического приборостроения была создана новая РТС «Квант-Д», работающая в диапазоне 5/6 ГГц [1],[2]. Возможности этой системы были использованы в полном объеме в работе по баллистико-навигационному обеспечению полетов космических аппаратов (КА) «Фобос-1,2». Траекторные измерения проводились на измерительных пунктах (ИП) в Евпатории и Уссурийске. Результаты показали, что РТС «Квант-Д» обеспечивает проведение траекторных измерений на порядок точнее систем предыдущего поколения. После завершения работ с КА «Фобос-2» РТС «Квант-Д» использовалась для баллистического обеспечения полета КА «Гранат» и «Интербол» [7]. Однако радиокомплексы этих КА были оборудованы передатчиком только дециметрового диапазона, что не позволило в полной мере использовать возможности измерительной системы «Квант-Д».

Проект «Фобос-Грунт», основной целью которого является доставка на Землю образцов грунта Фобоса, предусматривает, что основным типом измерительной системы для проведения траекторных измерений будет РТС «Квант-Д». В Институте прикладной математики им. М.В. Келдыша ведутся работы по баллистике и навигации проекта «Фобос-Грунт». В рамках этих работ проведен анализ возможностей измерительной системы «Квант-Д». В настоящей работе рассмотрена интерпретация измерений наклонной дальности и радиальной скорости  РТС «Квант-Д» в режимах, предусмотренных проектом «Фобос-Грунт». Новым по отношению к измерениям, проводимым при работе по КА "Фобос-2", является наличие 3-х путевых доплеровских измерений.

1.      Измерения наклонной дальности

Для измерения наклонной дальности используются фазовые методы, при которых дальность определяется измерением разности фаз излученного и принятого сигналов. Предусмотрено два режима измерения дальности, которые различаются структурой сигнала [1]. В первом режиме дальномерный сигнал представляет собой набор гармонических колебаний, наивысшая частота которых определяет аппаратную точность измерения. При частоте точной шкалы 300 КГц аппаратная точность равна 10м. Во втором режиме используется псевдошумовой код длиной 2047 элементов. Тактовая частота составляет 1.2 МГц, а аппаратная точность измерения - 5м. В обоих режимах для раскрытия неоднозначности используется измерение грубой шкалы. Для формирования дальномерных сигналов используется выходной сигнал синтезатора тактовой частоты

                                                                                                                    (1)

где

1.1.       Измеренные величины

Измеренными величинами являются:

Для получения измеренного значения дальности используются следующие величины:

1.2.        Интерпретация измерений дальности

В этом разделе будет описан алгоритм, позволяющий получить измеренное значение дальности в виде:

  ,                                                                                                                                  (2)

где

На первом шаге алгоритма вычисляется тропосферная поправка [3]:

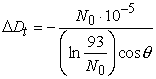
       ,                                                                                                          (3)

где

.                                                                                                               (4)

Затем раскрывается неоднозначность и вычисляется значение дальности в пределах зоны однозначного измерения

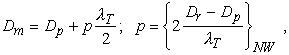                                                                                  (5)

где

Далее учитываются поправки и вычисляется значение  по формуле:

.                                                                                                      (6)

Вычисляется значение зоны однозначного измерения

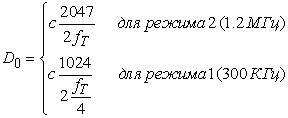                                                                                   (7)

Наконец, вычисляется измеренное значение наклонной дальности:

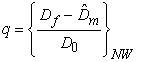,                                                                                                                       (8)

где

 — прогнозируемое (расчетное) значение дальности.

1.3.       Расчетный аналог измерения дальности

Для получения расчетного аналога измерения дальности представим измеренное значение в виде:

 ,                                                                                                             (9)

где

Время распространения сигнала dt на расстояние dr при удалении от Солнца на расстояние r равно [5]:

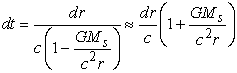,                                                                                             (10)

где  — гравитационная постоянная Солнца.

Соотношения для  получаются интегрированием (10) вдоль линии: передающая антенна - КА (КА - приемная антенна). Используя приближенную формулу Мойера для таких интегралов, получим:

,

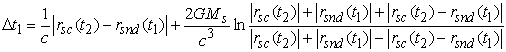
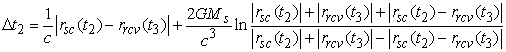,                     (11)

где

Подставляя (11) в (9), получим:

      ,                                            (12)

где

 ,

 .

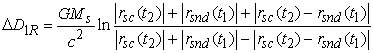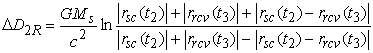Сумма  рассматривается как поправка. В качестве примера приведем два ее значения для КА «Фобос-2» на участке орбитального полета.

Измерительная система  обеспечивает только регистрацию момента  приема сигнала . Другие моменты времени  и  должны быть найдены из световых уравнений:

,

.                                                                         (13)

Эти уравнения решаются итерационным способом последовательно: cначала определяется , а затем - . А именно, для определения момента времени  необходимо выполнить следующие действия:

1) Принять .

2) Повторять вычисления для   по формуле

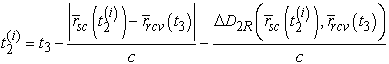                                     (14)

до выполнения условия при некотором i=k

,                                                                                                        (15)

где  является некоторой малой величиной. После этого можно положить . Для нахождения момента времени  нужно выполнить следующую последовательность действий:

3) ,

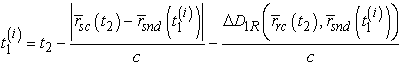                                                     (16)

до выполнения условия (15).  После этого следует положить .

При выполнении расчетов полагается, что  ~  сек. При этом для нахождения точных значений  необходимо делать в (14) и (16)   2-3 итерации.

2.      Запросные измерения радиальной скорости

2.1.       Измеряемый параметр

Радиотехническая система «Квант-Д» измеряет доплеровское смещение частоты принимаемого сигнала относительно излучаемого. Измеряемой величиной является полный набег нециклической, т.е. неограниченной значением 2p, фазы сигнала промежуточной частоты на интервале накопления. Частота этого сигнала равна разности частот принятого сигнала и сигнала, сформированного по прогнозу доплеровского сдвига [1]. Среднее значение набега фазы сигнала промежуточной частоты пересчитывается по конечным формулам в среднее значение отношения принимаемой частоты к передаваемой. Это отношение называют доплеровским множителем. Поэтому можно считать, что радиотехническая система проводит измерения среднего значения доплеровского множителя  на интервале времени . Получим соотношение, которое связывает  с моментами времени излучения и приема сигналов. Для этого рассмотрим (рис. 1) инерциальную систему координат К и мировые линии космического аппарата (КА) и измерительного пункта [6].

Пусть:

Тогда, среднее значение доплеровского множителя, измеренное системой, можно представить в виде:

.                                     (17)

Таким образом, среднее значение доплеровского множителя равно отношению интервала излучения к интервалу приема.

Так как погрешность, вносимая при переходе от отношения интервалов, отмеренных по часам ИПа, к отношению интервалов в системе К, пренебрежимо мала, вместо (17) будем рассматривать соотношение:

 .                                                                          (18)

2.2.       Интерпретация измерения в виде мгновенного значения радиальной скорости

В этом разделе будет показано, что мгновенное значение радиальной скорости на момент времени, соответствующий середине интервала накопления , определяется следующим соотношением:

   ,                                                                               

где

;

Для обоснования соотношения интерпретации найдем выражение для
 
через проекции скоростей на линии визирования: передающая антенна - КА и КА - приемная антенна.

Рассмотрим:

                                                             (19)

Откуда, учитывая, что  и , получим:

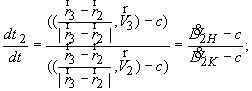
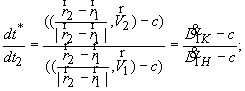
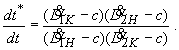                                                                                                            (20)

С точностью до членов, содержащих , выражение (20) может быть представлено в виде:

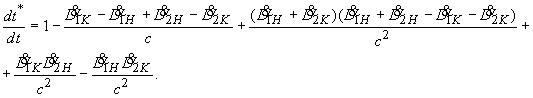
(21)

Следовательно,

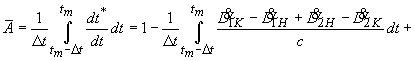
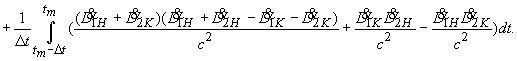                        (22)

Введем обозначение:

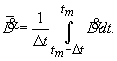
Рассмотрим выражение:

 .                                                                                                                                              (23)

После преобразований с точностью до членов, содержащих , получим:

                                                               (24)

Таким образом,

                                                                                                                                      (25)

с погрешностью:

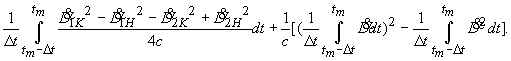
Получим соотношение между средним и мгновенным значениями радиальной скорости.

Представим зависимость от времени радиальной скорости в окрестности средней точки интервала в виде ряда Тейлора:

,                     (26)

где

После интегрирования по времени на интервале от () до  левой и правой частей соотношения (26) получим:

 .

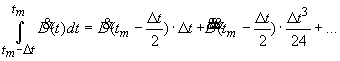Следовательно,

 .                                                          (27)

Откуда,

с погрешностью ~ .                                                                                           (28)

Получим, наконец, соотношение для небесно-механической интерпретации радиальной скорости, cоединяя соотношения (25) и (27):

                                                                                                                      (29)

с погрешностью:

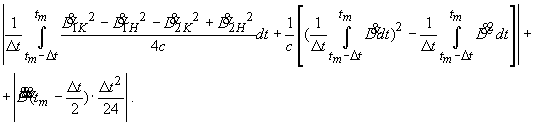
(30)

Проведенный численный анализ показал, что величина этой погрешности на траекториях, предусмотренных проектом «Фобос-Грунт», составляет

На интервале сеанса измерений протяженностью до 10 минут погрешность будет иметь характер систематической ошибки.

2.3.       Интерпретация измерения в виде приращения дальности

В этом разделе будет показано, что разность дальностей на  конец и началo интервала накопления по трассе: передающая антенна-КА-приемная антенна связана с измереным значением следующим соотношением:

,                                                                                                   (31)

где

Рассмотрим,

.                                                                       (32)

Из (31) следует (32), так как

 ,

 .                                                                                         (33)

2.4.       Компенсация методической ошибки интерпретации запросных доплеровских измерений

Интерпретация запросного измерения радиальной скорости в виде мгновенного значения в силу ее простоты более привлекательна, чем интерпретация в виде приращения дальности. Поэтому рассмотрим вопрос о внесении поправок, компенсирующих методическую погрешность интерпретации измеренного значения в виде мгновенного значения радиальной скорости. Вначале получим соотношение для методической ошибки интерпретации запросного доплеровского измерения в виде мгновенного значения радиальной скорости. Пусть — мгновенное значение радиальной скорости, соответствующее моменту регистрации , а  и — значения дальности по трассе: передающая антенна - КА - приемная антенна на моменты времени  и .

Тогда, используя (31), можно получить среднее значение доплеровского множителя на интервале  в виде

.

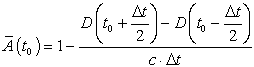
Этому среднему значению соответствует мгновенное значение радиальной скорости, вычисленное по формуле (23). Таким образом, для рассматриваемой методической ошибки справедливо соотношение:

.

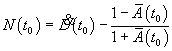Обозначим  значение методической ошибки, рассчитанное для опорной орбиты. Тогда, добавляя  к измеренному значению, можно компенсировать ошибку. Ответ на вопрос, насколько опорная орбита должна быть близка к реальной, чтобы поправка обеспечила необходимую точность дают частные производные по компонентам вектора состояния: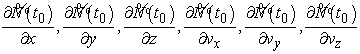

Максимальные значения производных для орбит, предусмотренных проектом «Фобос-Грунт» представлены в следующей таблице.

Таким образом, поправки, рассчитанные по опорной орбите, компенсируют методическую ошибку с необходимой точностью, если опорная орбита лежит в такой трубке, относительно уточненной, что невязки компонент вектора скорости не превосходят 1 м/сек, а компонент вектора положения — 1000 км.

3.      Беззапросные измерения радиальной скорости

3.1.        Измеряемый параметр

 РТС «Квант-Д» имеет возможность проводить доплеровские измерения по сигналу, излучаемому с борта КА. Также, как и в случае когерентных измерений, измеряется среднее значение доплеровского множителя:

 ,                                                                                                                                   (34)

где

После интегрирования (34), получим:

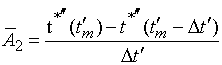     .                                                                                            (35)

Перейдем в гелиоцентрическую систему координат. Для этого преобразуем (35) к виду:

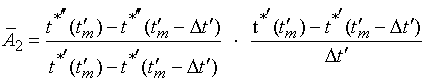 ,                                             (36)

где

Первый сомножитель в (36) представляет собой отношение интервалов времени между одними и теми же событиями, но в разных системах координат. Для наблюдателя, находящегося в гелиоцентрической системе координат, справедливо следующее соотношение [5],[6]:

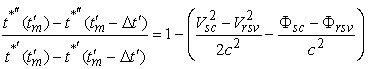,                                                           (37)

где

Рассмотрим более подробно второй сомножитель в (36). Так как за время распространения сигнала от КА до приемной антенны не изменились условия, определяющие параметры преобразования времени из системы координат ИПа в гелиоцентрическую систему координат, справедливо соотношение:

    ,                                                                                            (38)

где

Используя (37) и (38), преобразуем (36) к виду :

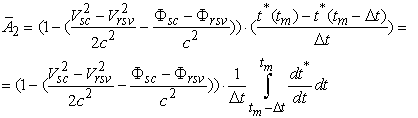
.                                (39)

3.2.       Расчетный аналог беззапросного измерения радиальной скорости

Как и в случае запросных доплеровских измерений, можно получить соотношение для
  через проекции скоростей на линию визирования КА-ИПов в гелиоцентрической системе координат

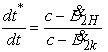,                                                                                                              (40)

где

С точностью до членов, содержащих , выражение (40) может быть представлено в виде:

,                                    (41)

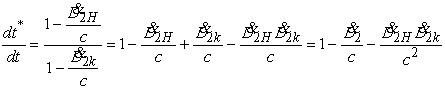
где

После подстановки (41) в (39) получим

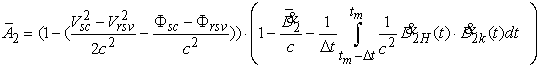
.              (42)

С точностью до членов, содержащих , выражение (42) может быть представлено в виде:

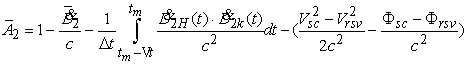
,                               (43)

где

.

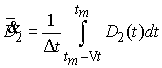
Разрешив (43) относительно , получим

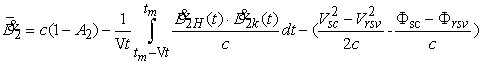
.                             (44)

Соотношение (44) может быть использовано как для интерпретации измеренных значений, так и для определения текущего значения частоты бортового задающего генератора по эталонной орбите.

4.      3-х путевой  доплер

Схема проведения измерений 3-х путевого доплера аналогична схеме 2-х путевого, которая рассмотрена во втором разделе, но прием сигнала осуществляется на двух различных измерительных станциях. Для определения параметров орбиты целесообразно использовать измерения 3-х путевого доплера как разность радиальных скоростей, полученных на каждой из этих станций. Измерения, полученные в результате такого вычитания, имеют большую информационную ценность, т.к. позволяют определить скорость измерения углового направления на КА. Ожидаемая точность измерений разности выше, чем точность обычных запросных доплеровских измерений (2-х путевых), поскольку при вычитании происходит взаимное уничтожение ряда составляющих ошибок, в частности:

-        ошибок, связанных с нестабильностью частоты излучаемого сигнала;

-        ошибок, возникающих при прохождении излученного сигнала через атмосферу;

-        ошибок, связанных с преобразованием сигнала в бортовом радиокомплексе.

Одним из вариантов проведения измерений 3-х путевого доплера, в проекте «Фобос-Грунт», рассматривается вариант проведения, при котором сигнал излучается из Евпатории¸ а принимается в Евпатории и Медвежьих Озерах [9].

Для обеспечения необходимой точности измерений необходимо учитывать ошибки измерения радиальной скорости, вызываемые атмосферой Земли. Эти ошибки имеют тропосферную и ионосферную составляющие. Так как при проведении измерений КА будет находиться за пределами атмосферы, эти ошибки определяются перемещением луча по углу места [4] и могут быть учтены по модели [8]. Тропосферная составляющая ошибки резко уменьшается с увеличением угла места. Лучший способ учета ионосферной составляющей — использование двух частот [2]. РТС «Квант-Д» имеет возможность проведения измерений на двух частотах, однако опыт работы по проекту полета к Фобосу в 1988/1989 гг. показал, что технологически это осуществить трудно. Следует отметить, что в наземной сети слежения за КА дальнего космоса США (DSN) для определения состояния атмосферы используются станции, принимающие сигнал на двух частотах от системы спутниковой навигации GPS. При реализации проекта «Фобос-Грунт» целесообразно воспользоваться этим опытом.

Литература

1.      Радиосистемы межпланетных космических аппаратов. Р.В.Бакитько, М.Б. Васильев, А.С. Виницкий и др. // М.: Радио и связь, 1993, 328 с.

2.      Космические траекторные измерения. Радиотехнические методы измерений и математическая обработка данных. Под ред. П.А. Агаджанова, В.Е. Дулевича, А.А. Коростелева // М.: Советское радио, 1969, 504 с.

3.      М.А. Колосов, Н.А. Арманд, О.И. Яковлев. Распространение радиоволн при космической связи // М.: Связь, 1969, 155 с.

4.      Ф.Б. Черный. Распространение радиоволн // М.: Советское радио, 1972, 464 с.

5.      А.Л. Зельманов, В.Г.Агаков. Элементы общей теории относительности // М.: Наука, 1989, 240 с.

6.      У. Берке. Пространство - время, геометрия, космология // М.: Мир, 1985, 411 с.

7.      Небесно-механическая интерпретация и первичная обработка измерений КА "Гранат" и "Интербол". Э.Л. Аким, А.А. Горохова, И.П. Киселева, В.А. Степаньянц, А.Г. Тучин // Препринт №83, М.: ИПМ им. М.В.Келдыша РАН,  1996, 21 с.

8.      А.Г. Квашнин, А.Г. Тучин. Баллистическое обеспечение радиоинтерферометрических измерений // Препринт № 98, М.: ИПМ им. М.В. Келдыша РАН, 1992, 26 с.

9.      Пространственно-временные соотношения при измерении дальности и скорости космических аппаратов. Технический отчет. М.Н. Мешков, Г.А. Соколов, В.А. Иванов // М.: Особое конструкторское бюро Московского энергетического института, 1997, 46 с.

Приложение

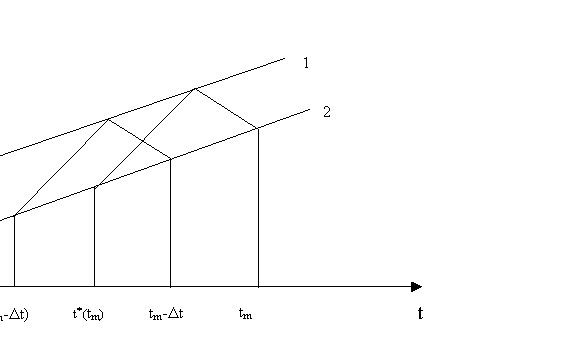
Рис. 1.

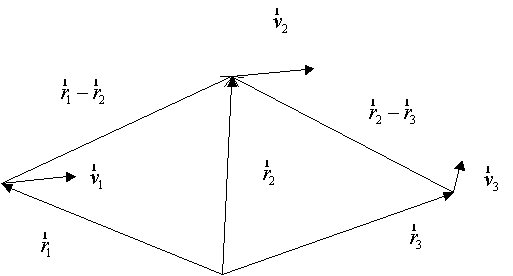
Рис. 2. Положение и скорость передающей антенны (), КА () и приемной антенны (), используемые в расчете мгновенного значения радиальной скорости. Линии визирования: передающая антенна - КА () и КА - приемная антенна ().