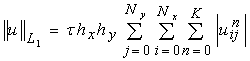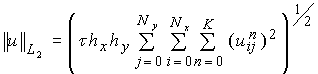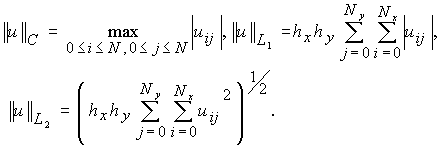Нелинейная монотонизация схемы К.И.Бабенко ("квадрат") для уравнения переноса
|
|
|
|
|
|
|
Локальная |
1.0 |
104.64 |
7.24 |
|
Интегральная |
1.0 |
12615.5 |
79.44 |
1. Монотонизованная
схема К. И. Бабенко.
Численное решение, полученное по предложенной схеме на конечный момент времени, «размазывается» на небольшое число узлов сетки. Наилучшим образом сохраняется форма начального профиля для третьего начального условия. Амплитуда численного решения практически неизменна. Для двух других начальных условий характерно некоторое понижение амплитуды численного решения.

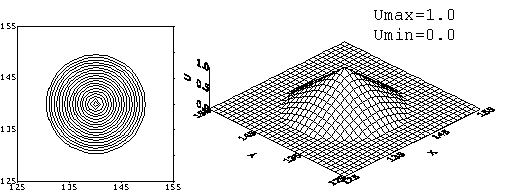
Рис. 1. Монотонизованная схема К. И. Бабенко. Решение
задачи с начальным профилем «конус» на момент времени ![]() = 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения.
= 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
0.4 |
33.68 |
2.37 |
|
Интегральная |
0.4 |
2038.98 |
14.61 |
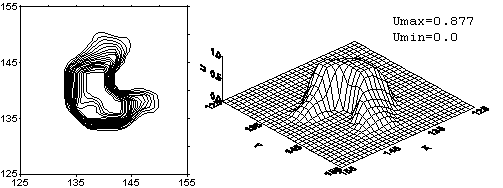
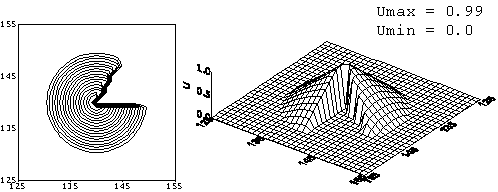
Рис. 2. Монотонизованная схема К. И. Бабенко. Решение
задачи с начальным профилем «конус без сектора» на момент времени ![]() = 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения.
= 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
0.88 |
32.43 |
2.55 |
|
Интегральная |
0.88 |
2217.37 |
18.78 |
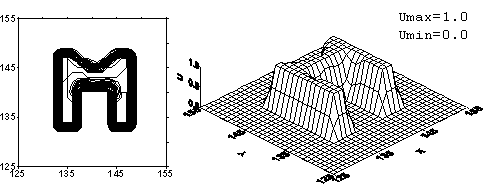
Рис. 3. Монотонизованная схема К. И. Бабенко. Решение
задачи с начальным профилем «М» на момент времени ![]() = 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения.
= 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
1.0 |
35.56 |
3.7 |
|
Интегральная |
1.0 |
5023.53 |
48.28 |
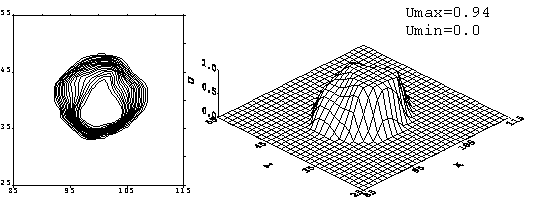
Рис. 1.1. Монотонизованная схема К. И. Бабенко. Решение
задачи с начальным профилем «конус» на момент времени ![]() = 480. Начальный
профиль переместился на 17 своих длин (траектория движения в приложении 2) без
вращения.
= 480. Начальный
профиль переместился на 17 своих длин (траектория движения в приложении 2) без
вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
0.94 |
104.64 |
8.74 |
|
Интегральная |
1.0 |
23661.86 |
118.61 |
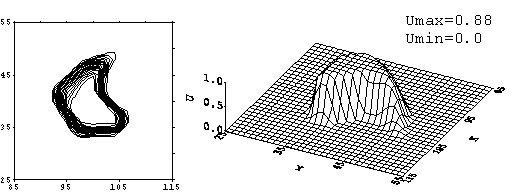
Рис. 2.1. Монотонизованная схема К. И. Бабенко. Решение
задачи с начальным профилем «конус без сектора» на момент времени ![]() = 480. Начальный профиль переместился на 17 своих длин
(траектория движения в приложении 2) без вращения.
= 480. Начальный профиль переместился на 17 своих длин
(траектория движения в приложении 2) без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
0.88 |
85.23 |
7.9 |
|
Интегральная |
1.0 |
19501.45 |
107.3 |
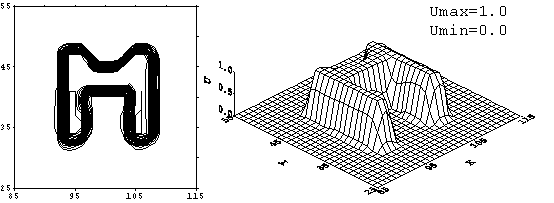
Рис. 3.1. Монотонизованная схема К. И. Бабенко. Решение
задачи с начальным профилем «М» на момент времени ![]() = 480. Начальный профиль переместился на 17 своих длин
(траектория движения в приложении 2) без вращения.
= 480. Начальный профиль переместился на 17 своих длин
(траектория движения в приложении 2) без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
1.0 |
11.28 |
170.18 |
|
Интегральная |
1.0 |
148.0 |
34202.93 |
2. Схема с «лимитерами»
[8].
Для численного решения, полученного по данной схеме, характерно некоторое понижение амплитуды, более сильно выраженное, чем в предыдущем случае. Линии уровня начальных профилей «конус» и «конус без сектора» приобретают более ярко выраженную «квадратную» форму, по сравнению с формой в начале расчета. Наилучшим образом передано численное решение задачи с начальным профилем «М».
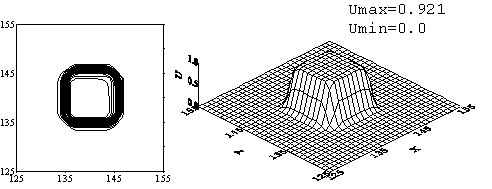
Рис. 4. Схема с «лимитерами». Решение задачи с начальным
профилем «конус» на момент времени ![]() = 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения.
= 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
0.43 |
54.47 |
3.67 |
|
Интегральная |
0.45 |
5704.77 |
35.73 |
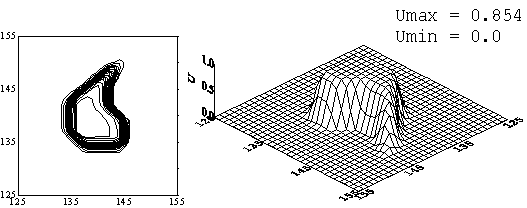
Рис. 5. Схема с «лимитерами». Решение задачи с начальным
профилем «конус без сектора» на момент времени ![]() = 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения.
= 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
0.85 |
48.29 |
3.67 |
|
Интегральная |
0.87 |
4719.94 |
33.28 |
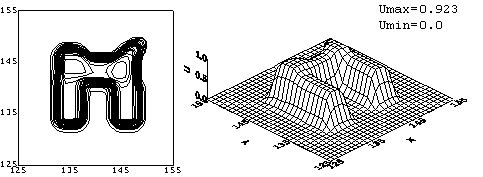
Рис. 6. Схема с «лимитерами». Решение задачи с начальным
профилем «М» на момент времени ![]() = 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения.
= 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
0.91 |
72.48 |
5.35 |
|
Интегральная |
0.96 |
7914.47 |
56.87 |

Рис. 6.1. Схема с «лимитерами». Решение задачи с начальным
профилем «М» на момент времени ![]() = 480. Начальный профиль переместился на 17 своих длин
(траектория движения в приложении 2) без вращения.
= 480. Начальный профиль переместился на 17 своих длин
(траектория движения в приложении 2) без вращения. ![]() .
.
Ошибка численного решения.
|
«М» |
|
|
|
|
Локальная |
0.91 |
10.01 |
158.66 |
|
Интегральная |
1.0 |
148.0 |
35337.29 |
3. Схема с направленными разностями.
При любых формах поверхности начального условия и любых
способах задания поля скоростей со временем численное решение «размазывается»
на достаточно большое число интервалов разностной сетки и его амплитуда
уменьшается. На финальный момент времени численное решение для любого
допустимого значения ![]() приобретает
характерный колоколообразный вид, не имеющий ничего общего с формой начального
распределения
приобретает
характерный колоколообразный вид, не имеющий ничего общего с формой начального
распределения ![]() .
.
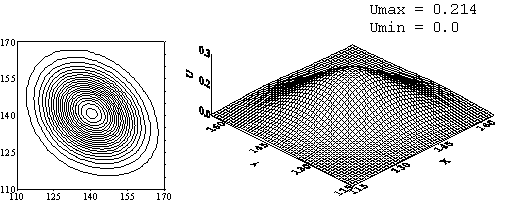
Рис. 7. Схема с направленными разностями. Решение задачи с
начальным профилем «М» на момент времени ![]() = 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения.
= 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
0.89 |
243.51 |
10.56 |
|
Интегральная |
0.89 |
23676.5 |
98.95 |
4. Схема
П. Лакса [9].
Качество численного решения в этом случае близко по своим характеристикам к качеству решения, полученного по схеме с направленными разностями (начальный профиль «размазывается», амплитуда решения уменьшается). Вдобавок к негативным характеристикам появляются характерные коротковолновые осцилляции. Сравнение норм численных решений, представленных в таблицах к рис.7 и рис.8, показывает, что метод Лакса дает худший результат по всем показателям.
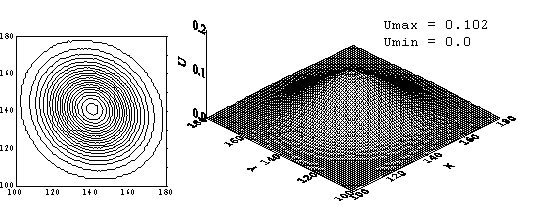
Рис. 8. Схема П. Лакса. Решение задачи с начальным профилем
«М» на момент времени ![]() = 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения.
= 120. Начальный профиль переместился на 9 своих длин по
диагонали квадрата без вращения. ![]() .
.
Ошибка численного решения.
|
|
|
|
|
|
Локальная |
0.92 |
268.51 |
11.32 |
|
Интегральная |
0.92 |
27014.8 |
107.66 |
Заключение.
1. Предложенная
монотонизованная схема К. И. Бабенко («квадрат») показала наилучшие результаты
среди всех рассмотренных в работе схем (при движении начального профиля без
вращения), в особенности, в случае
негладкого начального профиля «М».
2. Численные решения,
полученные по схеме с направленными разностями и схеме П. Лакса, существенно
уступают по точности решениям, полученным с помощью новой монотонизованной
схемы К. И. Бабенко и схемы с «лимитерами».
Приложение 1.
1) Схема с направленными разностями.
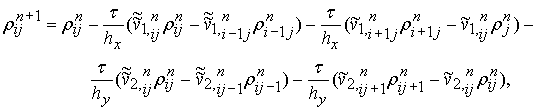
где ![]()
![]()
2)
Схема Лакса. [9]
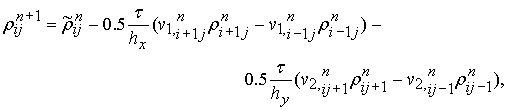
где ![]() .
.
Для решения двумерной задачи с помощью схемы с «лимитерами»
применялся алгоритм расщепления по координатам ![]() ,
, ![]() [4] и решались соответственно
одномерные задачи по каждому направлению. Поэтому ниже приведен вариант этой
схемы для одномерного уравнения переноса, записанного в дивергентной форме:
[4] и решались соответственно
одномерные задачи по каждому направлению. Поэтому ниже приведен вариант этой
схемы для одномерного уравнения переноса, записанного в дивергентной форме:
![]() ,
, ![]() .
.
3) Схема с «лимитерами». [8]
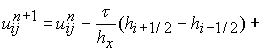
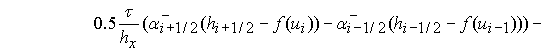
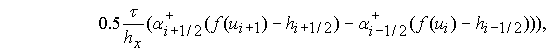
где 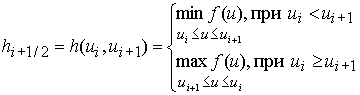 ,
, ![]() ,
,
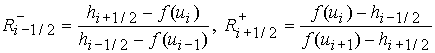 ,
,
функция ![]() определяется
следующим образом:
определяется
следующим образом:
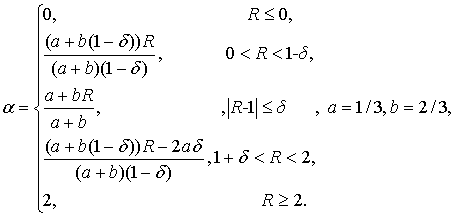
Приложение 2.
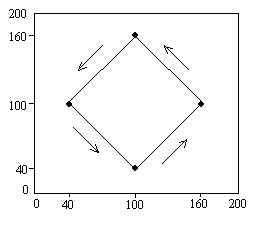
Траектория движения начального профиля, по
которой он проходит 17 своих длин:
Литература.
1. Галанин М. П., Еленина Т. Г. Сравнительный
анализ разностных схем для линейного уравнения переноса. // Препринт ИПМ им. М.
В. Келдыша РАН, № 52, 1998 г., 33 с.
2. Галанин М. П., Еленина Т. Г. Тестирование
разностных схем для линейного уравнения переноса. // Препринт ИПМ им. М. В. Келдыша РАН, № 40, 1999 г., 42 с.
3. Галанин М. П., Еленина Т. Г. Нелинейная
монотонизация разностных схем для линейного уравнения переноса. // Препринт ИПМ
им. М. В. Келдыша РАН, № 44, 1999 г., 30 с.
4. А. А. Самарский. Теория разностных схем. М.:
Наука, 1977, 656 с.
5. К. И. Бабенко, Г. П. Воскресенский. Численный метод
расчета пространственного обтекания тел сверхзвуковым потоком газа. // ЖВМиМФ,
1961, т. 1, № 6, с. 1051 - 1060.
6. С. К. Годунов.
Уравнения математической физики. М. : Наука, Физматлит, 1979, 392 с.
7. Еленина Т. Г. Решение нелинейной
монотонизированной схемы К.И.Бабенко («квадрат»). // Препринт ИПМ им. М. В.
Келдыша РАН, 2001 г., в печати.
8. К. В. Вязников, В. Ф. Тишкин, А. П. Фаворский, М. Ю.
Шашков. Квазимонотонные разностные схемы повышенного порядка точности. // М.:
Препринт ИПМ АН СССР, 1987, №36, 27 с.
9. Ю. Н. Днестровский, Д. П. Костомаров. Математическое
моделирование плазмы. М.: Наука, 1982, 319 с.
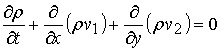 ,
, 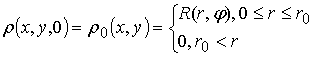 ,
,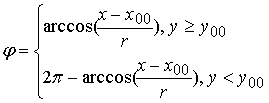 ,
, 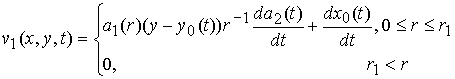 ,
,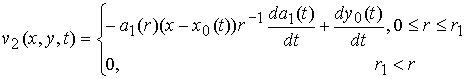 ,
,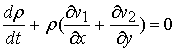 ,
, 
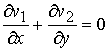 , начальный профиль решения сохраняется.
, начальный профиль решения сохраняется.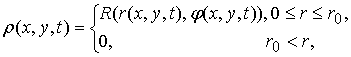
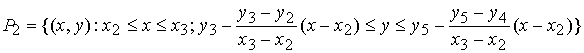 ,
, 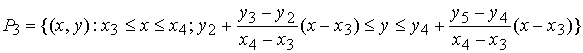 ,
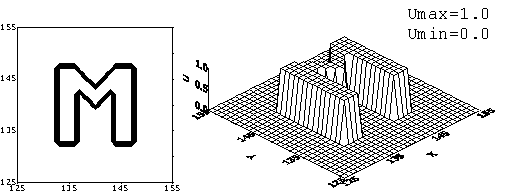
, 
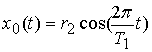 ,
, 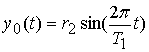 ,
, 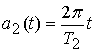 ,
, 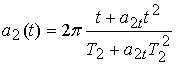 ,
, 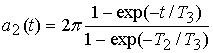 ,
, 
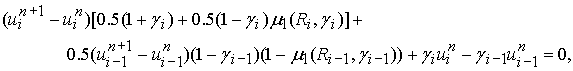
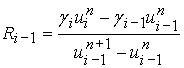 ,
, 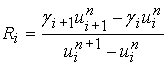 ,
, 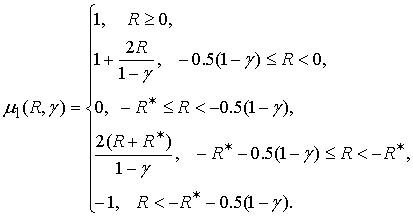
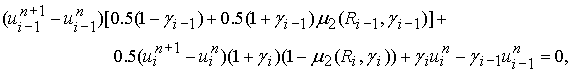
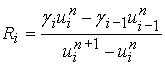 ,
, 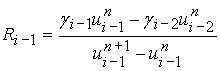 ,
,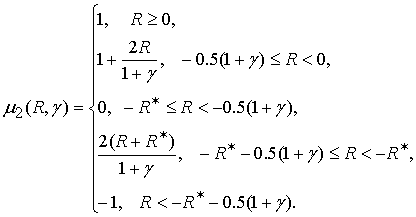
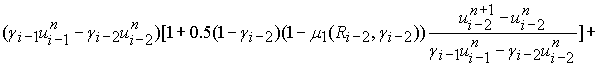
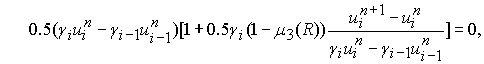
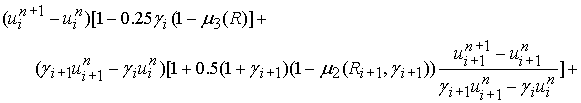
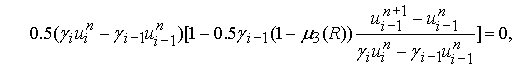
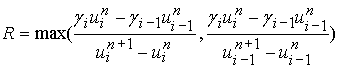 ,
, 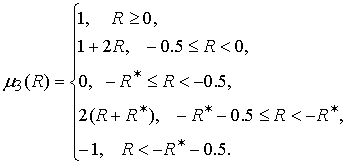
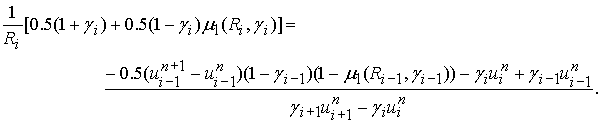
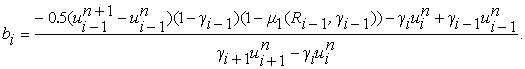
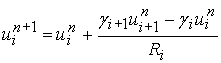 , а
, а 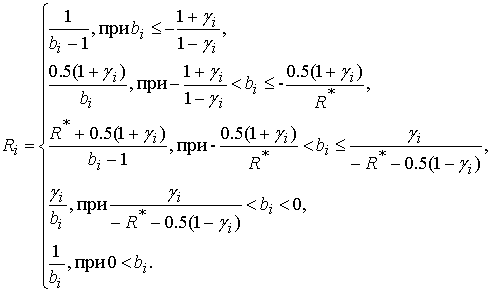
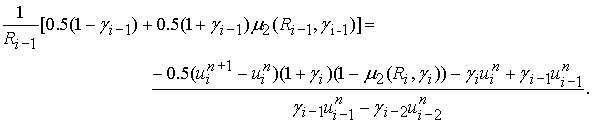
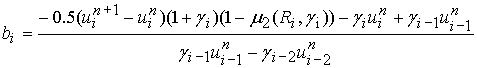 .
.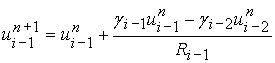 , а
, а 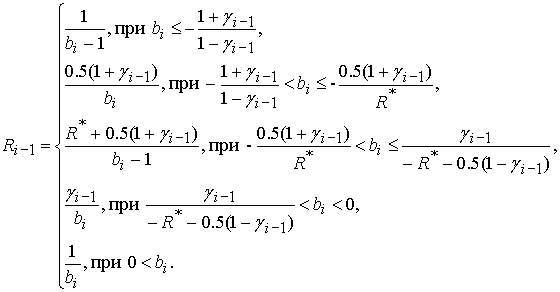 (13)
(13)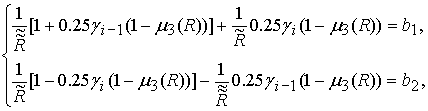
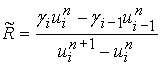 ,
, 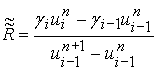 ,
,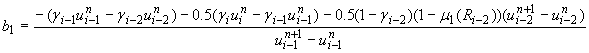 ,
,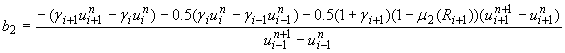 .
.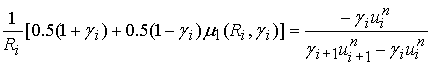 ,
, 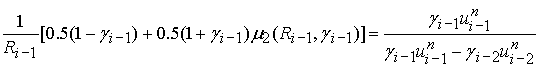 ,
, 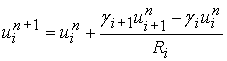 , где
, где 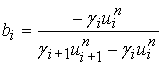 .
.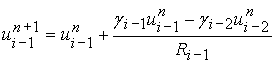 , где
, где 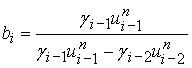 .
.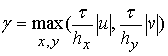 ) было ограничено сверху величиной
) было ограничено сверху величиной