Теоретические аспекты организации интерпретирующей навигации мобильного робота

( Theoretical Aspects of Mobile Robot Interpreting Navigation
Preprint, Inst. Appl. Math., the Russian Academy of Science)

1. Введение.

         Организация двигательного поведения мобильного робота  (МР) может  осуществляться  тремя способами: координатным, интерпретирующим, смешанным. Эти способы кратко охарактеризованы в таблице 1.

Таблица 1. Способы задания и реализации пути.

                   Суть рассматриваемой в работе  интерпретирующей  навигации  (ИН) [1,2] заключается в том, что положение МР на местности определяется не в декартовой системе координат (ДСК) [3],  а на основе описаний окружающего пространства на языке видимых особенностей среды - ориентиров и его изменений в процессе движения.  При этом аналогом количественной модели ДСК  выступает иная,  качественная модель, - граф информационной эквивалентности (Г.И.Э.).  В таком описании вершинам графа  соответствуют связные  районы  местности с одинаковым информационно-визуальным содержанием - районы информационной эквивалентности (И.Э.),  а ребрам - изменение этих описаний при переходе из района в район.  В этом случае организация передвижения МР основывается  на  фиксированном  наборе   информационно-двигательных действий (ИДД).

         Основные понятия, используемые в ИН, даны в приложении 1 - словаре терминов.

2. ОРГАНИЗАЦИЯ ИНФОРМАЦИОННОГО СЛЕЖЕНИЯ.

         Основой рассматриваемого  подхода для анализа задач и алгоритмов информационного обеспечения  мобильных  роботов  является отношение видимости [5,6]. Это отношение является частным и специфическим случаем отношения толерантности, т.е. его можно определить рефлексивным и сим- метричным, но в общем случае транзитивным оно не будет.

         Качественная навигация (quolitative navigation), предложенная в [4],  заключается в следующем.  Основой  навигации  служат ориентиры  L1...Ln, которым на нижнем (физическом) уровне может соответствовать и значительно протяженный объект.  Эти ориентиры разбивают линиями действия,  каждая из которых проходит через два ориентира, всю доступную область - плоскость движения МР на выпуклые многоугольники, которые мы будем  называть районами информационной эквивалентности (и.э.) - см.  рис. 1.

                                             L₂

           L₁

                                                                           L₃

                                                                L₄  G

                            L₆                             L₅

                                                     S

Рис. 1. Качественная навигация - пример разбиения плоскости движения МР на районы информационной эквивалентности, определяемые ориентирами L1- L6. S,...,G - точки траектории перемещения МР (в интерпретирующей навигации траектория задается последовательностью районов И.Э., через которые она проходит).

В этом случае положение МР определяется с точностью до  характерного размера района  и.э.  и эта точность значительно возрастает при увеличении числа ориентиров. На такой основе возможно осуществление выбора пути по связной цепочке районов и.э. от начального до целевого положения (см. рис. 1). Следует отметить, что в данном случае каждому району и.э. соответствует абсолютное описание - упорядоченная по углу наблюдения последовательность видимых ориентиров - кольцо.

         Каждому ориентиру приписывается абсолютный признак (например, номер или координаты в ДСК) и относительный,  который вычисляется с помощью локально действующей информационной системы (ИС) с учетом  затенения.  На одном физическом объекте может быть расположено несколько ориентиров,  и,  кроме того,  видимые признаки ориентиров (относительные, а не абсолютные) могут совпадать.

         2.1. Основные понятия.

              Используется модель среды в виде террайна [29,30]. В общем случае под МР будем понимать ориентированную точку, способную перемещаться на местности -  области плоскости,  ограниченной препятствиями - многоугольниками (постановка 2D). При этом,  если ориентация МР для навигации несущественна (и ее можно считать постоянной),  то будем  говорить,  что робот снабжен “компасом”.  Если ориентация существенна,  то будем полагать, что скорость изменения ориентации МР ограничена величиной w. Скорость движения МР на местности также будем полагать ограниченной величиной v.

         Предполагается, что   МР  снабжен  информационной  системой (ИС), конкретизация работы которой будет дана ниже, и некоторым вычислителем  для реализации алгоритмов сбора и обработки информации и планирования движения.

         Примем следующие обозначения:

         V - “местность” -  множество  доступных  для  МР точек (включая граничные точки препятствий);

         Г=dV - множество граничных точек препятствий;

         P - множество вершин препятствий.

         Последнее множество всегда будем полагать состоящим из  конечного числа элементов.

         Также будем полагать,  что V ограничено  некоторой  прямоугольной рамкой. Все рассматриваемые ниже множества точек суть подмножества V, если не оговорено противное.

         Введем на  множестве V отношение видимости x~y,  если [x,y] входит в V (при этом может быть x=y).  Отношение видимости  есть отношение толератности, т.к. здесь отсутствует транзитивность.

         Пусть А - множество  точек.  Через  А(x)  будем  обозначать подмножество  точек А,  видимых из точки x,  а через V(A) - множество точек местности, видимых хотя бы из одной точки множества А.

         Отношение видимости  или  видимости  в  пределах  заданного расстояния (радиуса действия ИС) продуцирует понятие локальности или локального описания (см. ниже).

     Выделим следующие классы сред:

     (П0) - если стороны  многоугольников  ориентированы  только соответственно сторонам прямоугольной граничной рамки;

     (П1) - если углы в многоугольниках равны 90 или 270  градусов, но ориентация сторон не фиксирована;

     (П2) - если ни на углы, ни на ориентацию многоугольников не накладывается никаких ограничений.

         Лемма 1. Для любой точки местности х число видимых из х точек-вершин препятствий P(x) ограничено снизу величиной

                  3 - для (П1), (П2)

                  4 - для (П0).

         Доказательство леммы следует из простых геометрических соображений.

         Множество точек плоскости, из которых видны все точки местности, называется навигационным множеством.

         Таким образом, Р является навигационным множеством по край-

ней мере третьего порядка (т.е. из каждой точки местности видно не менее 3-х точек Р).  В дальнейшем изложении мы предположим,  что  ориентиры  суть элементы Р.  В этом случае мы можем ввести простую классификация видимых из точки  х  вершин  -  см. Рис. 2.

                                     Х

                                                         Р₁                                            Р₄

                                                       Р₃

                            Р₂

Рис. 2. Классификация видимых из точки Х вершин:

           1 - выпуклый угол; 2 - вогнутый угол; 3 - скачок “к”; 4 - скачок “от”.

         Соответствующее значение принимает и классификационный признак, который может быть определен с помощью ИС МР.

         2.2. Абсолютные и относительные локальные описания.

         При помощи ИС МР можно выделить локальные признаки видимых вершин. Эти  признаки могут  быть  упорядочены  в кольцевую структуру по азимутальному углу. Описания окружающей среды в виде кольца признаков будут служить основой для анализа  МР  среды в наших постановках. Элементом такого кольца служат признак или наборы локально вычислимых признаков.  В состав набора признаков могут входить:

- указанный выше классификационный признак вершины,

- ряд других локально вычислимых признаков, таких как набор расстояний от вершины до других наблюдаемых вершин и др.

- азимутальный угол наблюдения ориентира и его координаты в

собственной (связанной с МР) системе координат (ССК).

         Все указанные  выше признаки являются локально вычислимыми.

Такие признаки мы будем называть также  относительными.  Но  для каждого  ориентира  (вершины) существует еще абсолютный признак, отличающий эту точку от других точек местности в глобальной  модели, например, - координаты этого ориентира в некоторой ДСК или абсолютный номер,  абсолютное “имя” и т.п. Абсолютный признак в общем случае не является локально вычислимым: одинаковым относительным признакам могут соответствовать разные абсолютные и наоборот.

         Будем полагать, что абсолютный признак у всех наблюдаемых ориентиров различен.

         В дальнейшем, мы будем рассматривать и кольца, в состав наборов признаков которых входит  и  абсолютный  признак.  Такие  описания будем называть абсолютными локальными описаниями в отличие от относительных локальных описаний, которые получаются на основе только локально вычислимых признаков.

         Абсолютный признак и абсолютное описание  следует  понимать как  “ключи” к возможности использования имеющейся у робота глобальной модели местности  того  или  иного  типа,  гарантирующие адекватную интерпретацию его положения по отношению к среде.

               2.3. Структурный признак в кольце.

         Под структурным (дополнительным) признаком данного элемента кольца в случае локального относительного описания  будем  понимать  упорядоченную  последовательность  признаков  (или  набора признаков),  начиная от данного элемента и кончая предыдущим  по кольцу.  В  общем  случае  структурный признак представим в виде матрицы. Мы будем полагать, что любой из рассматриваемых признаков представим целым числом из некоторого диапазона. В этом случае,  в связи с тем, что нас будет интересовать лишь факт совпадения  или  несовпадения  структурных признаков элемента кольца, каждый структурный признак данного описания можно  “свернуть”  в одно число.

         Если структурные признаки хотя бы у двух  элементов  кольца совпадают, то кольцо называется самоналожимым. Очевидно, что абсолютное кольцо самоналожимым быть не может. Самоналожимость означает  возможность изоморфного отображения кольца в себя с сохранением отношения соседства.  В  случае  относительного  кольца структурный  признак может способствовать разделению ориентиров, имеющих одинаковые начальные наборы признаков, например, в кольце признаков

C --- A

   |           \

      |             B

  |           /

B --- A

элементы с признаками В имеют разные  структурные  признаки:

“BABCA” и “BCABA”, а в кольце

A

/    \

B      B

\   /

A

структурные признаки этих элементов одинаковы (последнее  кольцо является самоналожимым).

         2.4. Классы и районы информационной эквивалентности.

         Под термином  “описание”  будем  понимать  в зависимости от обстоятельств две взаимосвязанные вещи:

     1. Общие  характеристики  описания,  в том числе и алгоритм его вычисления, а также множество опорных ориентиров А.

     2. Конкретное описание видимой местности в данной точке х - А(х).

         Если задано описание А, то оно продуцирует разбиение исходной местности V на области, для которых значение описания постоянно. Такое множество точек, в котором описание принимает одно и то же значение, мы будем называть классом информационной эквивалентности. 

         Всюду определенное описание задает, таким образом,  некоторое отношение эквивалентности. Классы и.э. в общем случае  представляют собой несвязные множества.  при этом каждый класс разбивается на односвязные области  -  районы  и.э.  (рис.  3).

                                              R₁                                   R₂

Рис. 3. Несвязные районы и.э., входящие в один класс и.э. Два района и.э. R₁ и R₂ одного класса и.э. абсолютного описания Р(х) или К(х): видимые множества ориентиров и их упорядочивания в виде колец совпадают при хÎR₁ и хÎR₂.

         Районы  и.э.  являются  основой глобальной модели местности, представляемой в виде Г.И.Э. Каждой вершине этого графа соответствует определенный район с некоторым описанием Аk, а выходящему из вершины направленному ребру  -  описание  перехода  из данного района в соседний (см.  ниже). Этот граф, таким образом, позволяет задавать трассу не в конфигурационном пространстве,  а на языке описаний и инструкций по переходу из района в район.

         Навигационное описание среды в точке х в общем случае - это некая информация о видимой окрестности точки х - V(x). Возможны различные типы навигационных описаний. Любое множество выделенных ориентиров А задает некоторое навигационное описание - подмножество данного множества А,  видимое из точки х - А(х). В частности, V(x), P(x) будут описаниями.

         Описание может быть числом. Примеры такого описания - число видимых  ориентиров  из  заданного множества в точке х и площадь видимой окрестности в точке х.

         Навигационное описание может быть функцией. Простейший пример - функция D_x(j) - измеряемой дальности из точки x в  направлении j.

         Назовем P(x) основным ориентирным описанием.

         Хорошее навигационное  описание  должно  обладать свойством

непрерывности в том смысле, что описания в двух последовательных точках x и y, в которых решается навигационная задача, не должны изменяться резко (или должны иметь общую часть).  Это дает  возможность привязать измерения в новой точке y к измерениям в предыдущей точке x.  Для рассматриваемого  типа  описаний,  который продуцируется  исходным множеством ориентиров А можно ввести два определения непрерывности описания А(х):

         (1) e -непрерывность:  для любого x, принадлежащего V, найдется eтакое, что как только расстояние между x и y меньше e, то множества A(x) и A(y) имеют непустое пересечение.

         (2) Информационная непрерывность:  если x и y связаны отношением видимости (х~у),  то множества A(x) и A(y) имеют непустое пересечение (А(x) Ç A(y) ¹ Æ).

         Ниже мы будем всегда полагать,  что исходное множество ориентиров всегда является навигационным. Справедливы следующие утверждения.

     Лемма 2.  Если точки объединения множеств А и Р находятся в общем положении (т.е.  никакие три точки указанного  объединения множеств не лежат на одной прямой), то А(х) является e-непрерывным описанием.

         Доказательство заключается в том, что при указанных обстоятельст- вах всегда найдется e такое,  что при расстоянии между x и y меньше e отрезок [x,y] пересекает только одну прямую, проходящую через точки a_k, p_i; a_k ÎA, p_i ÎP, т.е.  только один ориентир может исчезнуть или появиться.  Если он появляется,  то условие непрерывности выполняется. Если он исчезает, то число элементов в множестве A(x) больше 1, т.к. в противном  случае А не было бы навигационным множеством и опять наблюдается непустота пересечений двух соседних описаний.

         Лемма 3. Р(х) информационно непрерывно.

         Доказательство. Если на линии,  проходящей через точки  x,y расположена вершина p~x, то p~y и утверждение доказано. Если это не так,  то с каждой стороны от этой прямой найдется ориентир  р~x такой, что угол pxy минимален, тогда p~y.

         Кроме этих  характеристик непрерывности описания Р справедлива

         Лемма 4. Из P(x)=P(y) следует, что x~y.

         Доказательство проводится методом от противного.  Утверждение следует из того факта,  что в  рассматриваемых  постановках, когда  контуры ненулевых по толщине препятствий задаются многоугольниками, из x/~y следует Р(х) не совпадает с P(y).

         Таким образом,  Р-описание (абсолютное!) определяет точку с точностью  до  отношения видимости,  при этом остается возможной несвязность класса и.э. - см. рис. 3.

         Схему построения районов и.  э. для Р-описания иллюстрирует рис. 4. Вершины разбиваются на пары источник-затенитель (i,z): z есть затенитель i, если из i в направлении z есть видимые точки, не  принадлежащие  границе препятствий и находящиеся за вершиной z. Соответствующая часть луча источник-затенитель называется линией действия. Линии действия и участ- ки границы разбиваются точками пересечения на образующие,  объединения которых в непересекающиеся (за исключением общих границ) выпуклые многоугольники и дает районы и.э. по Р-описанию.

         Существует простая связь между Р-описанием и К-описанием, с которым мы будем работать дальше.  К-описание строится на основе Р-описа-ния путем упорядочивания видимых ориентиров в кольцо.

         Лемма 5. Район и.э. по Р-описанию есть район и.э. по К-описанию.

         Доказательство достаточно очевидно:  для изменения К-описания в районе и.э.  по Р-описанию  необходимо  пересечение  линии действия  по  ориентирам из Р,  что невозможно исходя из способа построения районов и.э. по Р-описанию, изложенного выше.

         Назовем два кольца абсолютных признаков,  К1 и К2,  эквивалентными, если они содержат одинаковые наборы признаков и преобразуются  одно  в  другое путем вращения.  Для проверки подобной эквивалентности полезна следующая лемма.

         Лемма 6. Содержащие один и тот же набор признаков кольца К1 и К2 будут эквивалентными в том и только в том случае,  если для любой тройки признаков a,b,c из общего набора  подпоследовательности  включения этих элементов в К1 и К2 будут образовывать эквивалентные элементарные кольца.  С  другой  стороны,  К1  и  К2 представляют  собой неэквивалентные кольца тогда и только тогда, когда существуют три элемента a,b,c из общего  набора  признаков такие, что подпоследовательности включения этих элементов в К1 и К2 образуют элементарные неэквивалентные кольца.

         Доказательство производится простым перебором по индукции.

         2.5. Задача абсолютной интерпретации.

         Под задачей  абсолютной интерпретации мы будем понимать вычисление абсолютного признака для каждого видимого ориентира  и определение положения МР в глобальной модели (см.  ниже).

         Сеансом  измерений назовем построение с помощью ИС МР локального относительного описания в некоторой текущей точке местности. Время сеанса будем считать пренебрежимо малым по отношению ко времени исполнения двигательных действий.

         Задача абсолютной интерпретации разделяется на две задачи:

     (1). Задача информационного слежения, т.е. построения абсолютной интерпретации текущего локального относительного описания в случае,  если задана абсолютная интерпретация локального относительного описания в начальный момент.

     (2). Задача определения начального положения МР, т.е. определение  абсолютной  интерпретации для локального относительного описания некоторого положения МР без помощи “извне”.

         Задача (2)  в общем случае для произвольной местности рассматриваемых классов решения не имеет [2]. В то же время для каждой  местности  существует  некоторая частота сеансов измерений, гарантирующая решение задачи информационного слежения.

         Как уже было сказано выше,  районы и.э.  служат основой для представления глобальной модели местности типа графа  и.э..  При использовании моделей этого типа (см.  ниже) СУ МР должна быть в состоянии определять свое положение на этой модели (при работе с локальными относительными описаниями),  т.е.  в каком из районов и.э. МР находится в данный момент. Соответствующая навигационная задача называется задачей информационной привязки. Ее необходимо решать, например, при организации информационного слежения.

         3. Особые точки и особые ситуации.

         3.1. Особые точки.

         3.1.1. Особые точки первого рода.

         Дадим определение особой точки:  особая точка - это

такая точка на местности,  что сколь  угодно  малое  перемещение

вблизи нее может приводить к пересечению нескольких линий действия.

         Отметим, что в случае особой точки типа “клещи” (Рис. 4) определение остается  в силе,  поскольку здесь происходит как бы слияние двух линий действия: ориентир-источник появляется и сразу же исчезает.

         Алгоритм информационного слежения работает при достаточно общих предположениях  о структуре местности указанного типа.  Мы будем считать запрещенными только ситуации типа “клещи” (Рис. 4).

         При пересечении МР во время движения нескольких кратных линий действия возникает ситуация типа “навал” (рис. 5). При этом могут появляться или исчезать сразу несколько источников на данной линии действия.

                                                                                                        i

                                                     Z₂                                         Z₁  

                 W

 Рис. 4. Ситуация типа “клещи”: источник i в W виден только на линии.

                                                                                                       i_n

                                                                                  i₂

                                                                        i₁   

                                                          Z

Рис. 5. Ситуация типа “навал”: кратная линия по данному затенетилю.

         В случае  пересечения  в одной точке нескольких линий действия,  эту точку будем называть узлом соответствующей  кратности (минимальная кратность равна 2) - рис. 6.

         Особо выделим выпуклые вершины (угол в  вершине  90  градусов).  Небольшое  смещение  вблизи  такой вершины также способно сильно изменить видимую картину (рис. 7). Ситуацию, возникающую при пересечении МР вблизи видимой вершины нескольких линий действия,  которые она порождает в качестве затенителя,  будем называть ситуацией типа “веер”.

         Нетрудно видеть, что лишь в ситуации типа “веер” наблюдается изменение типа наблюдаемого на данной вершине скачка.  Для простоты изложения мы полагаем,  что МР  не  производит сеансов на линиях действия ориентиров.

                                                                           i₂

                    i₃                                                     Z₂                                               i₁

                           Z₃                                         Z₁

Рис. 6. Ситуация типа “узел”: пересечение линий действия по разным затенителям.

                                   i₂                                      i₄

                           Z

 i₁

     i₃

Рис. 7. Ситуация типа “веер”: пересечение нескольких линий действия при движении вблизи выпуклой вершины.

         Справедлива

         Теорема 1.  Все  возможные типы особых точек для постановки 2D сводятся к перечисленным выше четырем случаям.

         Доказательство.  Особая точка, по определению, существует в случае наличия общих точек у линий действия.  Здесь могут быть два случая:

     (1). Линии  действия совпадают на каком-то участке.  В этом случае может получиться только особая точка типа  “навал”,  т.к.  затенитель и источник расположены на одной линии.

     (2). Линии действия (более двух) пересекаются  в  некоторой точке. Здесь возможны два подслучая:

     (2.1). Эта многократная точка пересечения совпадает с затенителем. Тогда  получается особая ситуация типа “веер” (передвижение МР вблизи затенителя).

     (2.2). Точка пересечения не совпадает с затенителем - получается точка типа “узел”.

         Наконец, особая точка типа “клещи” возникает в случае, если источник и два затенителя с различными признаками “скачка”  расположены на одной прямой. Таким образом, перебор по всем возможным ситуациям расположения источников и затенителей дает  только описанные выше типы особых точек.

         Все перечисленные  выше типы особых точек первого рода и их влияние на алгоритмы ИН приведены в таблице 3.

3.1.2. Особые точки второго рода.

         Эти типы особых точек возникают в случае, если особые точки первого рода (описанные выше) совпадают друг с  другом.  Естественно, что  совпадать могут только точки различных типов.  Таким образом, максимум может совпасть четыре особые  точки  различных типов.

3.2. Особые ситуации.

         Все особые ситуации при интерпретации видимой картины  ориентиров в двухмерном случае можно свести в таблицу 4, которую иллюстрируют Рис. 8-10.

         Таблица 3. Типы особых точек для описаний на основе видимых ориентиров в                              интерпретирующей навигации.

Таблица 4. Особые ситуации при абсолютной интерпретации описаний на основе ориен-                        тиров.

                   Х                                                                                 У

Рис. 8. Особая ситуация типа “ирония судьбы” - несвязность классов и.э. локального описания на основе относительных признаков ориентиров. Локальные относительные описания видимой части среды в точках Х и У совпадают, эти точки принадлежат одному и тому же классу и.э., но разным районам и.э.

                                                          Х

Рис. 9. Особая ситуация типа “буриданов осел” - описание видимой части среды в точке Х на основе относительных признаков ориентирв-вершин является самоналожимым, т.е. переходит в себя при повороте кольца С(х).

                III                                                            IV

                       Р

                 II                   I

Рис. 10. Особая ситуация типа “хамелеон” - локальный относительный признак ориентира-вершины в точке Р зависит от точки зрения (х): хÎI - “скачок от”; хÎII-“выпуклый угол”; хÎIII-“скачок к”; хÎIV-“ориентир невидим”.

4. Алгоритм информационного слежения.

         Основой анализа текущей навигационной ситуации служит описание окрестности МР в виде упорядоченного списка видимых ориентиров с их  признаками  (например,  тип  наблюдаемого вблизи ориентира скачка азимутальной дальности,  величина наблюдаемого угла между гранями,  высота или длина грани  и  т.п.).  В процессе анализа эти признаки ориентиров (они определяются на основе видимых особенностей среды)  получают  абсолютную  интерпретацию путем использования Г.И.Э.  Абсолютную интерпретацию получает и район, в котором находится МР. Основой этого процесса и других алгоритмов ИН служит алгоритм информационного слежения.

         Районы И.Э. для 2D постановки порождаются разбиением плоскости движения “линиями действия”,  которые проходят через “ориентир-источник” и “ориентир-затенитель”.

Ориентир-источник - это такой ориентир, который либо появляется, либо исчезает при выходе за пределы данного района И.Э.  (при пересечении линии действия).

Ориентир-затенитель, актуальный для данного ориентира-источника, находится на некоторой части границы видимого  контура  препятствия, ответственного за затенение ориентира-источника (см. Рис. 11).

                              i₂

    Рис. 11. Схема построения районов и.э. по линии действия источник-затенитель.

         Z - затенитель для источников i₁ ¸ i₄;

         (Z,g) - линия действия по i₁ , Z;

                R₁¸R₅ -районы информационной эквивалентности по описаниям Р, К;

         R₁ и R₃ , R₁ и R_4,  R₁ и R₅ - касающиеся районы;

         “Пояс” R₁ есть расстояние от (Z,g) до точечной ломаной.

         Ориентиры обоих типов входят  в  “навигационное  множество” ориентиров.  Размер  этого множества равен минимально возможному количеству видимых ориентиров,  необходимых  для  навигационного описания местности.

         Алгоритм информационного слежения состоит из четырех действий. 

1°Строится локальное описание среды (например,  в виде кольца признаков видимых ориентиров С(x)).

2° Выделяется “ориентирная  база”  - общая часть данного и предыдущего сеансов измерений. Для ориентиров, попавших в эту базу, абсолютная  интерпретация предполагается проведенной на предыдущем сеансе.  В случае, если произошел переход в новый район И. Э., производятся еще два действия.

3° Выделяются актуальные затенители, т.е.  ориентиры, расположенные на участках среды (“выступах”), ответственных за исчезновение или появление ориентиров.

4° На основе использования разметки ребер Г.И.Э., которая определяет изменения в описаниях видимой части среды при переходах в соседние районы, происходит абсолютная интерпретация ориентиров. Подобные описания  изменений в видимой части среды задаются тройками (актуальный ориентир-затенитель, ориентир-источник, признак появления или исчезновения ориентира-источника).

         Таким образом производится абсолютная интерпретация  ориентиров  при  информационном слежении в случае априорно известного Г.И.Э. (который достаточно  просто может быть построен по известной модели (карты) среды).  В условиях отсутствия карты этот граф  строится  поэтапно  в  процессе движения.

         Как уже было сформулировано  выше,  задача  информационного слежения  состоит в том,  чтобы в случае задания в начальный момент абсолютной интерпретации видимых ориентиров-вершин (их  абсолютного  признака) в любой последующий момент движения определять абсолютную интерпретацию видимых ориентиров.

         Отметим очевидный факт:  для абсолютной интерпретации  всех

видимых ориентиров в полученном локальном относительном описании типа кольца в случае известной информационной привязки в  данный момент  достаточно знать абсолютную интерпретацию хотя бы одного видимого ориентира и описание данного района в виде простого абсолютного кольца.

         Соседние районы и.э.,  имеющие общую границу только в  точках, будем называть касающимися - см.  рис. 11. Часть границы района и.э.,  не принадлежащую границе препятствий, будем называть свободным контуром района. Рассмотрим свободные контуры соседних к R районов и выделим в них те отрезки, которые не входят одновременно  в  свободные контуры каких-либо двух соседних к R районов. Такие отрезки образуют “пояс” района (см.  рис. 11).

         Пусть d(R) - расстояние между свободным контуром данного района R и “поясом”  этого района. Пусть, далее,  e1=min d(R), где минимум берется по всем районам и.э.  по Р-описанию для данной местности; e2 - половина минимального расстояния между вершинами из Р.

         Определим видимый диаметр местности L как максимальное

     L = max  // x-y //

                  x~y

         Положим e < min( e1,e2).  Излагаемый ниже алгоритм информационного слежения гарантирует абсолютную интерпретацию и  информационную привязку (в случае, если они заданы в начальный момент времени) при частоте сеансов

     f > (v+wL) / e, где v - ограничение сверху на скорость передвижения робота,  w  -  максимальная  угловая скорость вращения ориентации робота

При этом для МР с “компасом” полагаем w=0.

         Через R(t) будем обозначать район, в котором МР находится в момент t.

         Теорема 2. Алгоритм  информационного  слежения гарантирует  абсолютную  интерпретацию и информационную привязку (в случае,  если они заданы в начальный момент времени) при частоте сеансов,  не превышающей величину ( v + wL)/e, при условии, что на местности не наблюдается ситуация типа “клещи” (источник  виден  только на линии (см. Рис. 10)).

         Доказательство этой теоремы следует из излагаемого далее алгоритма информационного слежения.

         4.1. Общая схема алгоритма.

         Существенной чертой излагаемого алгоритма является его  автономность от других систем управления МР.

        Схема такта работы алгоритма на каждом сеансе приведена  на рис. 12.

         Рис. 12. Такт работы алгоритма информационного слежения.

         Опишем работу указанных на схеме блоков.

1. Построение текущего локального относительного описания С(t) -

строится  простая модель типа относительного кольца,  которая была описана выше. Проводимая далее абсолютная интерпретация делает эту модель эквивалентной абсолютному кольцу К (кольцу абсолютных признаков).

2. В этом блоке описание С(t) сравнивается с  полученным на предыдущем сеансе описанием С(t-dt),  dt=1/f. На основе сравнения этих двух описаний выделяется текущая ориентирная база Е = P(t) ÇP(t-dt),  где Р(t) - множество ориентиров-вершин,  видимых в момент t. Для ориентиров из Е проводится абсолютная интерпретация.

         Отметим, что указанная выше частота сеансов  измерений  гарантирует /Е/ >=1 (число элементов в Е больше или равно 1).

         Если Е=P(t)=P(t-dt),  то в силу выбора данной частоты сеансов R(t)=R(t-dt) и алгоритм кончает работу.

         Если это условие не выполняется,  то необходимо определить, в какой из соседних районов и.э.  перешел МР и, в случае необходимости,  провести абсолютную интерпретацию  для  ориентиров  из P(t)\E.

         При  этих  процедурах используется соответствующая глобальная модель.  Для адекватного ее использования необходимо  предварительно выделить в Е множество актуальных затенителей,  т.е. затенителей, породивших линии действия, которые пересекает один раз траектория МР между двумя сеансами.

         Схема  выделения актуальных затенителей приводится в п. 4.4.

         4.2. Используемые модели.

         В качестве локальной относительной модели  С(t)  будем  использовать относительное кольцо,  где каждому видимому ориентиру (вершине) ставятся в соответствие его  координаты  в  ССК  МР  и классификационный признак, введенный выше (см. п. 2). Последний используется лишь при интерпретации двусмысленностей типа  “двойной  веер” (см. п. 3.).

         Используемая глобальная модель типа Г.И.Э.,  которую мы будем обозначать (ГИЭ)1, имеет следующую структуру.

         Вершинам соответствуют районы и.э.  по  Р-описанию,  причем вершинам  соответствуют  ссылки на их абсолютные описания в виде простого кольца. Следует, однако, отметить, что в случае задания начального абсолютного описания эти ссылки могут быть опущены после начального расчета ребер перехода.

         Направленному ребру между соседними ( в том числе и  касающими-ся) районами соответствует информация об изменении локального абсолютного описания при соответствующем переходе.  Это изменение в (ГИЭ)1 кодируется следующим образом.

         Рассмотрим ребро,  соответствующее переходу из района с абсолютным описанием К1 в район с описанием К2.  При этом переходе появляются или исчезают определенные источники. Каждое такое событие  описывается  тройкой (z,i,j),  где z - абсолютный признак затенителя, i - абсолютный признак источника, j=0, если источник исчезает и j=wk,  если источник появляется.  При этом w=1,  если источник появляется слева от затенителя и w=-1,  если он появляется  справа,  а  k=n(z,i)+1,  где n(z,i) - число видимых вершин между z и i в К2 при просмотре кольца в направлении w.

         На рис. 13 приведен пример подобной разметки ребер в (ГИЭ).

                  3

                                                                                              4

                                  1                                               2    

                                      R₄                       R₃                         R₅

                                                                                              5           6

                                         R₁                 R₀                 R₂

Карта районов.

         Рис. 13. Разметка ребер в графе информационной эквивалентности.

         Следующие леммы легко доказываются исходя из определений.

         Лемма 7.  Если ребру перехода соответствует тройка (z,i,w_k)

и  k  >  1,  то  этому  же ребру соответствуют тройки (z,i_l,w_l), l=1,...k-1.

         Лемма 8. Если заданному ребру перехода соответствуют тройки (z,i1,j1), (z,i2,j2), то i1#i2 и если j#0, то j1#j2.

         Лемма 9.  Пусть данному ребру перехода соответствуют тройки (z,i1,0) и (z,i2,j), где j#0. Тогда при соответствующем переходе наблюдается ситуация типа “веер” (см. п.3).

         Индексом актуального  затенителя  по данному ребру перехода назовем  число  Ind(z)=max(k),  где  max  берется   по   тройкам (z,i,wk). Он равен числу появившихся источников по данному затенителю.

         Очередные две леммы указывают простой способ информационной привязки  при переходе в соседний район.

         Лемма 10.  Пусть  индексы  затенителя для двух разных ребер перехода одинаковы.  Возьмем тройки по z c одинаковым k для этих ребер. Тогда в эти тройки входит один и тот же источник.

         Лемма 11.  Поставим каждому ребру перехода  в  соответствие множество  троек (z,Ind(z),N(z)),  где z - актуальный затенитель по данному переходу,  Ind - его индекс,  N - число троек c j=0 и данным затенителем, приписанных данному ребру (индекс “исчезновения”).  Тогда указанные множества для разных ребер перехода будут различны.

         Из этих лемм вытекает способ абсолютной интерпретации новых появившихся источников по модели (ГИЭ)1.

         Если известен абсолютный признак актуального затенителя для данного источника,  индекс перехода в новый район по данному затенителю Ind(z) и признак появившегося источника j=wk,  то абсолютный признак источника i восстанавливается по  тройке  (z,i,w_k), соответствующей любому ребру перехода с данным индексом.

         Таким образом,  описание перехода,  соответствующее данному ребру,  можно трактовать как набор “редакторских команд” для перехода от К1 к К2.

         4.3. Выделение ориентирной базы.

         Пусть p принадлежит E,  где Е - текущая  ориентирная  база.

Обозначим  через  r_p(t) - координаты вершины p в ССК МР в момент

t.  Тогда указанная выше частота сеансов гарантирует  выполнение

неравенств

     //rp(t) - rp(t-dt)// < e2,

     //rp(t) - rq(t-dt)// > 2e2

при p#q. Отсюда вытекает алгоритм выделения в С(t) ориентиров из Е  и их абсолютной интерпретации.  При этом будут также выделены Pout=P(t-dt)\E - множество абсолютных признаков исчезнувших  источников,  а  также множество Cin=P(t)\E - множество появившихся источников, для которых абсолютная интерпретация неизвестна.

         Каждому источнику  из Pout и Cin - i - поставим в соответствие два ближайших к нему в C(t-dt) или C(t) соответственно ориентира из Е: p+ - в положительном направлении от i и p- (в отрицательном).  Актуальным затенителем,  ответственным за появление или исчезновение источника i может быть либо p+, либо p-.

         В общем случае /Е/ >=1.  Очевидно, что при принятой частоте сеансов не может быть /E/=0,  т.к. при переходе в соседний район всегда должен быть хотя бы один актуальный затенитель.

         Возможный случай  /Е/=1 для постановок (П1) и (П2) иллюстрирует рис.  14.

х

           Р

          у

Рис. 14. Пример с /E/=1. Навигационная база между сеансами (количество общих ориентиров) принимает минимальное значение, равное 1, при любом достаточно малом смещении х ® у в близи вершины Р.

         Если /Е/=1, то образующий Е ориентир есть актуальный  затенитель  (при этом на нем реализуется ситуация типа “веер”). Тогда его индекс равен /P(t)/-1 и по соответствующему ребру  (единственному!) (ГИЭ)1 однозначно определяется информационная привязка и абсолютная интерпретация  появившихся  источников (w в этом случае произвольно).

     Пусть /E/ >= 2.  Тогда можно определить параметры  перехода от  ССК МР в момент t-dt к ССК в момент t - вектор перехода dr и матрицу поворота T(da),  где a - азимутальный угол. Действительно, преобразование системы координат на плоскости задается тремя скалярными величинами, а знание координат ориентирной базы Е дает 4 уравнения (зависимых).

         4.4. Выявление актуальных затенителей.

Пусть /Е/ >=2.  Рассмотрим два идущих подряд (в положительном направлении) в кольце С(t) ориентира из базы  Е:  p1  и  p2.  Пусть p1 выступает в качестве p-, а p2 - в качестве p+ для некоторых подмножеств источников Iout из Pout и Iin из Cin. Глобальная  модель (ГИЭ)1 позволяет выявить множество потенциальных актуальных затенителей, т.е. множество всех актуальных затенителей по всем ребрам перехода из данного района R(t-dt).

         Если только один из ориентиров p1 или p2 входит в Q,  то он и  будет  актуальным  затенителем для множеств источников Iout и Iin.

         Если оба ориентира входят в Q,  то возможны “двусмысленные” ситуации типа изображенной на рис.  15. В этом случае для каждого из источников определим актуальный затенитель следующим образом.

                                           i₂                                        i₁₁

                        i₁₂

                            Z₂                      Z₁

                     ?                      R                        ?

                                            x

Рис. 15. Пример “двусмысленности” при интерпретации. Какой переход из точки х района R был реализован, если между ориентирами-затенителями Z₁ и Z₂ исчез источник i₂ и появился источник i₁₁ или i₁₂?

         Если хотя бы на одном из потенциальных затенителей p1 и  p2 сохраняется  скачок одного и того же типа,  то каждый источник i из Iout и Iin обработаем следующим образом.  Если  он  входит  в Iout, вычислим

     r_i(t) = T(da)(r_i(t-dt)+dr), а если в Iin, то r_i(t-dt) = T^т(da)r_i(t) - dr, где T^т

- обратная матрица.

         Таким образом  будут получены координаты источника на сеансе, когда он невидим.  Пусть r_k обозначает координаты  ориентира p_k, e_k(t)  -  обозначает единичный вектор,  перпендикулярный rk; положим

     a_ki = (r_i(t),e_k(t))(r_i(t-dt)e_k(t-dt))

(в скобках стоят скалярные произведения векторов; выражение для a_ki позволяет  определить, может  ли  p_k быть актуальным затенителем для i).  Тогда в силу определения частоты сеансов p_k есть актуальный затенитель для i в том и только том случае,  если a_ki < 0  и  не является таковым, если a_ki >=0.

         Если же на обоих потенциальных затенителях  тип  скачка  не сохраняется, то получается ситуация типа “двусмысленность с веером” (см. п.3), при которой источники из Iin обрабатываются также,  как выше, а источники из Iout приписываются той же вершине, на которой в С(t) наблюдается скачок соответствующего типа.

         Обработав подобным образом все источники из Iout и Iin,  мы

определим для каждого из них актуальный затенитель, а для каждого актуального затенителя подобным образом (при полной обработке списков  исчезнувших  и появившихся источников) определяется индекс перехода и индекс исчезновения.  Признак wk при этом тривиально  определяется по С(t).  После этого на основе (ГИЭ)1 будут проведена абсолютная  интерпретация  всех  новых  источников  из С(t).

         На основе  полученного таким способом описания перехода однозначно определяется район R(t).

         Здесь мы  может поставить вопрос:  является ли обязательным представление глобальной модели в виде графа районов, а не графа классов? Ведь в последнем случае для Р-описаний вторая часть алгоритма информационной привязки не является необходимой. Рис. 16 иллюстрирует, что для изложенного алгоритма представление в виде графа районов является принципиальным,  а “свертывание” всех районов данного класса может привести к неадекватной интерпретации.

                                                                                     i₂           i₁

                                                                           Z

                                                          R₁

                                                                   R₂

Рис. 16. Иллюстрация к вопросу о принципиальности представления графа районов для адекватной интерпретации. Районы R₁ и R₂ принадлежат одному классу по К-описанию: К(R₁) = К(R₂), но при переходе из R₁  по линии действия Z появляется i₂, а при соответствующем переходе из R₂ - i₂ .

         5. Управление движением.

                   5.1. Типы ориентиров для различных постановок.

         Типы ориентиров приведены в таблице 5.

         Следует отметить,  что для каждой  из  этих постановок возможно  доказательства теорем аналогичных теореме 1 и теореме 2, но это дело будущего.  Ниже, в п. 5.2. будет приведен пример планирования движения  на основе алгоритмов ИН для случая протяженных ориентиров.

Таблица 5. Основные типы постановок задач для интерпретирующей навигации.

         Следует сделать  следующее существенное замечание.  В общем случае для постановки типа 2D можно ввести параметры - характерные расстояния  между  препятствиями (или от МР до препятствий): R1 и R2. Если r - текущее расстояние от МР до препятствий, то при r < R1 - ориентирами служат особенности контуров препятствий (например, вершины многоугольников, как было рассмотрено выше); при r > R2 - ориентирами служат контура препятствий,  как это рассмотрено в [4]; при R1 < r < R2 возможны оба подхода. Возможны также и смешанные  типы постановок.

         5.2. Алгоритмы управления движением.

         Основные разработанные алгоритмы интерпретирующей навигации можно свести в таблицу 5.

         Базой для всех этих алгоритмов является организация информационного слежения, описанная в п.4 для точечных ориентиров. В работе [2] были выявлены группы ИДД, которые позволяют МР осуществлять  произвольное  перемещение в среде на основе ИН.  В этот набор,  в частности,  входят:  движение по  линии  действия (прямой, определяемой  источником  и затенителем) и движение по окружности с центром в заданном ориентире.  В случае, если необходимо прийти в точку с заданными координатами,  на заключительном этапе реализуется движение с координатной привязкой  видимых ориентиров в целевом районе.

Таблица 5. Алгоритмы интерпретирующей навигации (ИН) и  их аналоги для коорди                  натного способа задания пути.

         В общем случае команда перемещения робота осуществляется  в виде  предложения  типа  “осуществлять данное ИДД с привязкой по видимым ориентирам до наступления заданного события”. В качестве события выступают в основном появление или исчезновение ориентиров в видимой картине среды при  движении,  истечение  заданного интервала времени  или  достижение  заданного расстояния до препятствия или ориентира.

         Для согласования с координатным способом управления  движением  существует алгоритм трансляции ломаной,  задающей движение МР,  в последовательность предложений языка ИН  указанного выше типа. Разработанные  алгоритмы  управления движением в режиме ИН иллюстрирует таблица 5.  Магистральное движение осуществляется в три этапа:  достижение ближайшей “станции”, движение по “маршрутам-магистралям” до станции, ближайшей к целевому району, достижение целевого района от конечной станции.  В этом случае достигается  существенная  экономия  памяти  для  хранения Г.И.Э.

         Теорема 3.  Пусть  в набор информационно-двигательных действий МР входят движение по окружности с центром  в  ориентире  - некоторой вершине  препятствий и движение по линии действия “источник-затени-тель”.  Пусть,  кроме того,  МР способен определять свои  координаты относительно видимых ориентиров (которых в данном районе должно быть не менее 3 в данной постановке). Тогда:

     (а) МР способен осуществлять перемещение из данного района и.э. в любой другой по априорно известной карте.

     (б) МР способен осуществлять перемещение из любой заданной точки в любую заданную точку по априорно известной карте.

         Доказательство. Утверждение (а) прямо следует из  результатов [2].  Утверждение (б) следует из того, что вначале МР способен осуществить перемещение к району и.э.,  где находится конченная  точка,  а  затем выйти в положение на границе этого района, характеризующееся тем,  что расстояние от конечной точки и расстояние  от  текущей точки до некоторой вершины будет одинаковым.

         Использование локальных относительных и абсолютных (при организации информационного слежения) описаний  позволяет  существенно упростить задание пути МР в супервизорном режиме.  А именно,  при планировании пути в частично известной местности,  этот путь можно задавать не в терминах последовательности узловых координат, а на языке, предложения которого имеют форму:

• получить  локальное  относительное описание видимой части среды и провести его абсолютную интерпретацию;

• производить  данное ИДД (информационно-двигательное действие) до наступления данного фиксированного события.

         Пример подобного подхода приведен на рис.  17, где приведен фрагмент трассы движения,  реализованной в результате выполнения следующих команд:

     1. Двигаться вперед  до  наступления  события  “препятствие близко”, после чего повернуть направо.

     2. Двигаться,  пока в точке А не  будет наблюдаться  значение  “выпуклый угол” (значение “скачок” исчезнет).

     3. Двигаться к вершине B до события “препятствие близко”.

     4. Повернуть налево и двигаться вдоль стены до ее конца.

     5. Двигаться к “скачку” С до события “препятствие близко”.

     6. Двигаться до вершины D.

         В данной  последовательности команд опущены команды на проведение абсолютной интерпретации вершин в  процессе  движения  с частотой, указанной выше (в теореме 1).

                                                                                                  D

                                                                                                       С

                                                                                       В

                                                                 А

         Рис. 17. Планирование пути на основе интерперетирующей навигации.

      При расширении указанного подхода возможны различные варианты.

      Рассмотрим следующий набор ИДД.

     1. Движение в данном направлении,  определяющимся как среднее направление между данными видимыми вершинами.

     2. Движение в направлении данной видимой вершины.

     3. Движение по контуру препятствия, обход данной вершины до появления вершины с заданным абсолютным признаком.

         Предположим, что в известной местности для данной постановки построен путь в данную точку,  например,  по графу видимости.

Тогда справедлива:

         Теорема 4. Путь, построенный по графу видимости, траслируется,  за исключением последнего отрезка в путь на данном наборе ИДД,   причем   последовательность  команд  представима  в  виде А,В,А,В,А,В..., где А - ИДД типа 1 или 2, а В - ИДД типа 3.

         Доказательство теоремы  подтверждается непосредственной проверкой. Последнее звено пути, также как и при доказательстве теоремы 3,  может  быть достигнуто движением в конечную точку пути с подкорректировкой по ориентирам-вершинам в ДСК.

         5.3. Организация возврата в пройденное положение.

         При организации возврата в пройденное положение следует обратить внимание на изменение локальных  относительных  признаков

опорных (т.е. задающих ИДД) ориентиров.  Для этого случая справедлива:

         Теорема 5.  При организации возврата относительные признаки ориентиров трансформируются следующим образом:

     “скачок к” -> “скачок от” ;

     “скачок от” -> “скачок к “ ;

     “выпуклый угол” -> “скачок от”, если препятствие при прямом

                        движении обходилось справа;

     “выпуклый угол” -> “скачок к”,  если препятствие при прямом

                        движении обходилось слева;

     “вогнутый угол” -> “вогнутый угол”.

         Доказательство теоремы состоит из прямых проверок указанной трансляции признаков.

         На рис. 18 приведен пример работы алгоритма трансляции прямого пути в обратный (возврат в пройденное положение) на  основе относительных признаков.

         Рис. 19 иллюстрирует пример организации магистрального движения для постановки с протяженными ориентирами.  В этом  случае линии действия как бы “размываются”.  Организация магистрального движения для координатного представления рассмотрена в [7].

                                                                                               6

                                                                                               1

                                              3                  4                5

                                              4                  3                2

                  1                2

                  6                5

         Рис. 18. Пример работы алгоритма трансляции прямого пути в обратный (организация возврата в пройденное положение) на основе относительных признаков.

         Прямой путь:

1. Движение к ближайшему ориентиру с признаком “скачок к”.

2. Обход этого ориентира справа до появления ориентира с признаком “выпуклый угол”.

3. Движение к этому новому ориентиру (на этот ориентир до задонного расстояния).

4. Обход препятствия справа - движение вдоль препятствия на заданном расстоянии, движение до появления ориентира с признаком “скачок от”.

5. Обход этого ориентира справа до появления ориентира с признаком “скачок к”.

6. Движение к ориентиру с признаком “скачок от”.

                   Обратный путь:

1. Движение к ближайшему ориентиру с признаком “скачок от”.

2. Обход этого ориентира слева до появления ближайшего ориентира с признаком “скачок от”.

3. Движение к этому новому ориентиру (на этот ориентир до задонного расстояния).

4. Обход препятствия слева - движение вдоль препятствия на заданном расстоянии, движение до появления ориентира с признаком “скачок от”.

5. Обход этого ориентира слева ( до появления ориентира с признаком “скачок к”).

6. Движение вдоль препятствия до исходной точки.

6. Заключение.

         Разработана теория интерпретирующей навигации (ИН) для  мобильных роботов  (МР),  позволяющая эффективно производить адекватную интерпретацию наблюдаемых ориентиров и района местоположения МР на основе динамики изменения описания наблюдаемой видимой окрестности среды. 

         Особенности данного подхода в области качественной навигации заключается в том, что

 -  в качестве ориентиров могут выступать как точечные,  так и протяженные  объекты;

 -  аналитичеcки показаны “пределы роста” алгоритмов качественной навигации на основе ориентирных описаний:  построены  основные  типы  особых  точек среды для описаний на основе видимых ориентиров и особых ситуаций при интерпретации;

 -  предлагаемые алгоритмы ИН покрывают более широкий (по сравнению с известными алгоритмами качественной навигации) спектр задач обеспечения целенаправленного перемещения МР;

 -  задание и реализация пути МР на языке ИН  допускает  эффективное согласование с традиционным координатным способом (например, трансляция пути, заданного координатным способом, на язык ИН и наоборот), что позволяет в перспективе увеличить живучесть  системы  управления МР;

 -  в перспективе, наряду с 2D постановкой возможны 2¹/₂ D и 3D постановки.

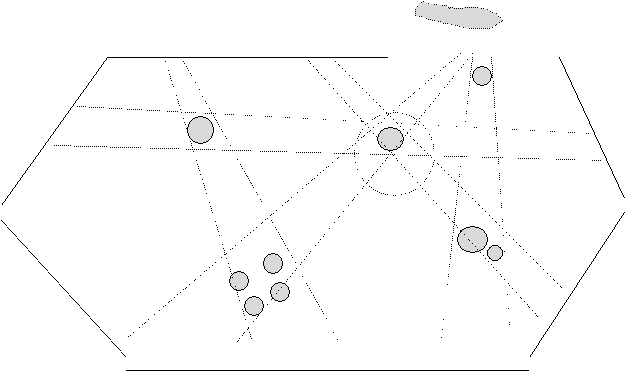
                         R₇      St8            R₆           St7        R₅     St6

                                                                                p₄              p₃       R₄ 

                St9

                                                                                                          St5

                                          p₅                   R₉

                                                                               St10

                      R₈                                                                                         R₃

                                                            p₁

                                                                                               p₂          St4

                                                                            R₁

                                       St1              St2                                  St3   R₂

                                                         а)    

                                                                          Ý Вход и выход в структуру полигона

б)

         Рис. 19. Организация магистрального движения (постановка с протяженными ориентирами).

а) - исходная карта полигона с протяженными ориентирами - камнями и холмами;

б) - Граф магистралей для исходной карты.

Обозначения:

p_i   - “станции пересадок” вблизи ориентиров-камней;

StI - “станции пересадок” в областях затенения одного ориентира-камня другим (StI расположены вблизи холмов)

R_i   - районы карты, привязанные к определенным станциям (на рисунке указаны только основные районы).

7. ЛИТЕРАТУРА

1. Платонов А.К.,  Кирильченко А.А., Кугушев Е.И. Использование локальных ориентиров для определения положения  мобильного робота. //”Проблемы машинного видения в робототехнике”, М.: Ин-т прикл. матем. АН СССР, 1981, с. 31-47.

2. Кирильченко  А.А.  Интерпретация локальных относительных описаний среды подвижным роботом. //М.: Препринт Ин-та прикл. ма-тем. им. М.В.Келдыша АН СССР, 1983, # 149, 28 с.

3. Соколов С.М. Использование фотометрической информации в комплексе интегрального локомоционного робота.  - В кн. Управление робототехническими системами и их очувствление. М., Наука, 1983, сс. 150-163.

4. Levitt T.S.,  Lawton D.T. Qualitative navigation for mo-bile robots. //”Artif. Intell.”, 1990, v. 44, pp.305-360.

5. Zeeman E.C. The topology of the brain and visual percep-tion.  //”The topology of 3-Manifolds, M.K.Fort (ed.), 1962, pp.  240-256.

6. Кирильченко А.А.  О  представлении  информационно-двигательного  взаимодействия  мобильного  робота со средой на основе отношения видимости.  //Препринт  Ин-та  прикл. матем.  АР  СССР, 1987, # 235, 28 с.

7. Барбашова Т.Ф., Кирильченко А.А., Павловский В.Е. Исследование и выбор эффективных алгоритмов маршрутизации. //Препринт Ин-та прикл. матем. им. М.В.Келдыша АН СССР, 1987, # 4, 32 с.

8. Соколов С.М. Определение ориентира и его смещений в поле зрения фотометрической системы. //Препринт Ин-та прикл. матем. им. М.В.Келдыша АН СССР, 1980, № 98, 30 с.

9. Sgouros N.M., Papakonstntinou G., Tsanakas P. Localized qualitative navigation for indoor environments. // Proc. 1996 IEEE Conf. on Robotics and Automation, v.1, pp.921-926.

Приложение 1.

СЛОВАРЬ ТЕРМИНОВ

         Абсолютный признак вершины-ориентира  -  абсолютный  “номер” или “имя” ориентира, которые отличают его от других вершин-ориенти- ров.

         Абсолютное описание - описание видимой части среды,  использующее абсолютные признаки вершин-ориентиров.

         Актуальный затенитель - затенитель, ответственный за переход в соседний район информационной эквивалентности.

         Граф информационной эквивалентности - модель местности в виде графа,  вершинам которого поставлены в соответствие абсолютные описания районов информационной эквивалентности,  а ребрам приписаны изменения в описании соседних вершин.

         Затенитель - вершина-ориентир,  из-за которой появляются или за которой исчезают новые ориентиры-источники.

         Информационное слежение - абсолютная интерпретация всех  видимых ориентиров-вершин.

         Информационная привязка - определение местоположения мобильного робота на графе информационной эквивалентности.

         Источник - вершина-ориентир,  появляющаяся или исчезающая за вершиной-затенителем.

         Класс информационной эквивалентности - область на местности, где данное локальное абсолютное или относительное описание принимает постоянное значение.

         Линия действия источник затенитель - часть отрезка, проходящего через источник и затенитель, при пересечении которой появляется или исчезает источник при переходах между районами информационной эквивалентности.

         Описание - описание видимой части среды на основе последовательности признаков (локальных или абсолютных) видимых  в  данной точке среды ориентиров-вершин.

         Относительный признак  вершины  ориентира  - признак вершины ориентира, который может быть вычислен исходя из видимых  особенностей ориентира.

         Относительное описание  - описание видимой части среды,  использующее относительные признаки вершин-ориентиров.

         Район информационной эквивалентности - связная область класса информационной эквивалентности.