Аннотация
Рассматриваются системы ориентации для
обеспечения заданного углового движения малых спутников, создающие управляющий
момент за счет взаимодействия с геомагнитным полем. В зависимости от целевой
функции спутника и его возможностей они могут быть пассивными или активными.
Относительно невысокая точность ориентации, достигаемая с помощью таких систем,
либо является вполне приемлемой с точки зрения целевой функции спутника, либо
компенсируется дополнительной обработкой информации. Представлены магнитные
системы ориентации малых спутников, разработанные в последние годы.
Ключевые слова: малый спутник, магнитная система ориентации, алгоритм управления
Abstract
Attitude control systems which provide small
satellites with a required angular motion developing the control torque through
interaction with the geomagnetic field are considered. They can be passive or
active in regard with the purpose of a satellite. Relatively low accuracy of
orientation achieved by such systems can be ether accepted due to the purpose
of the satellite or can be compensated through preprocessing the payload data.
Next, the magnetic attitude control systems developed for the latest years are
presented.
Key words: small satellite, magnetic attitude control system, algorithm of control
E-mail: ovchinni@keldysh.ru
СОДЕРЖАНИЕ
Введение и размышления
Гравитационная система ориентации со сферическим магнитным демпфером
Гравитационная система ориентации с гистерезисными стержнями
Магнитная система ориентации с постоянным магнитом и гистерезисными стержнями
Активное управление угловым движением спутника с помощью токовых катушек
Заключение
Список литературы
ВВЕДЕНИЕ И РАЗМЫШЛЕНИЯ
Одними из наиболее простых, экономичных и
надежных систем ориентации, обеспечивающих заданное угловое движение
наноспутников, стесненных ограничениями на массу, габариты и энергетику,
являются системы, создающие управляющие моменты за счет взаимодействия
актюаторов с геомагнитным полем. В зависимости от целевой функции спутника и
его возможностей они могут быть пассивными или активными. Обычно пассивные
системы обеспечивают ориентацию спутника относительно градиента силового поля (например,
магнитного или гравитационного). Активные системы способны обеспечить его
ориентацию относительно заданного, не обязательно фиксированного, направления в
инерционном пространстве. Относительно невысокая точность ориентации,
достигаемая с помощью таких систем (обычно не превышающая нескольких градусов),
либо является вполне приемлемой с точки зрения целевой функции спутника, либо
компенсируется дополнительной обработкой информации. Примером последнего
является системы дистанционного зондирования Земли и астрономических наблюдения
с использованием малоинерционных чувствительных элементов на основе
микроканальных пластин и пьезоакустических фильтров, включая гиперспектрометр
высокого разрешения. В настоящей работе, представленной на конференции «Проблемы
развития и использования микротехнологий в авиации и космонавтики» в рамках VII
Ежегодной международной выставки-конгресса «Высокие технологии. Инновации.
Инвестиции», Санкт-Петербург, 4-7 июня, 2002, объединены результаты разработки
магнитных систем ориентации наноспутников Munin,
REFLECTOR
и других, которые были успешно выведены на орбиту в последние годы.
Достижения в области электроники,
вычислительной техники, материаловедения сделали возможным создание
малоразмерных спутников, способных решать задачи, до недавнего времени бывшие
по силам лишь большим и, как правило, дорогостоящим аппаратам. Снижение требований
к отдельным элементам спутника позволяет пойти по пути их упрощения и, тем
самым, снижения стоимости и, иногда, повышения надежности. Одним из наиболее
дорогостоящих служебных систем спутника является его система ориентации.
Поэтому их упрощение с одновременным усилением роли математических методов
бортовой обработки информации может привести к снижению общей стоимости спутника.
Различные типы систем ориентации, использующих взаимодействие с геомагнитным
полем, будут рассмотрены в настоящей статье.
Одной из причин, по которой малые
спутники получили широкое распространение в последние десятилетие, является их
относительная простота реализации и, как следствие, относительно короткий срок
разработки и изготовления и низкая стоимость как самого спутника, так и его
вывода на орбиту [1,2]. Сокращение финансирования космических разработок
практически во всех странах - лидерах космической индустрии привело к тому, что
заметная часть разрабатываемых новых проектов базируются теперь на идеологии
малых спутников. Достаточно, например, просмотреть труды регулярно проходящего
в Берлине Симпозиума Международной астрономической академии по малым спутникам
для наблюдения Земли из космоса (IAA
International
Symposium
“Small Satellites for Earth
Observation”)
[3], чтобы убедиться в этой тенденции.
Можно выделить два основных направления,
по которым развиваются малые спутники. Первое направление (условно назовем его
«университетским») базируется на идее «проще, быстрее, дешевле». Спутники,
разработанные с учетом такой идеологии, действительно становятся малыми по
массе и габаритам (обычно – это 10¸100
кг и несколько десятков сантиметров соответственно). При их изготовлении
используются самые распространенные элементы, как правило, не проходящие
сертификации для использования в условиях космоса и это - при обычно
негерметичном исполнении корпуса спутника. Основная экономия происходит из-за
трех «составных частей»: дешевые комплектующие, дешевые студенческие рабочие
руки и, при малой массе спутника, – дешевый, а зачастую и бесплатный вывод на
орбиту. Правда, в зарубежной литературе для описания таких спутников
используется термин low
cost,
а не cheap,
подчеркивающий, что это «не дешевка», а спутники низкой стоимости. Такие
спутники в основной своей массе не решают серьезные научные или технологические
задачи. Впрочем, для них такие задачи и не формулируются. Зачастую полезная
нагрузка предоставляется ее создателями даже бесплатно с целью, в свою очередь,
бесплатной проверки ее работоспособности в условиях космоса. Бремя
финансирования разработки и создания полезной нагрузки несет
фирма-изготовитель. Пожалуй, основным результатом такого подхода является
обучение специалистов через непосредственное участие в реальном проекте, пусть
и не сложном, но содержащем все основные этапы реальных проектов чего не
удается достигнуть при любом, сколь угодно изощренном аудиторном обучении. В
России примером такого подхода являются проекты малых спутников,
разрабатывавшиеся в недалеком прошлом [4] и разрабатываемые сейчас, например, в
МАИ, МВТУ, МЭИ, САКУ, ВИКИ. Безусловно, заслуживает внимание опыт НАСА
финансирования более сорока студенческих проектов малых спутников в
университетах США, в частности, в Стэнфордском университете. Но это, как
говорится, другая песня. Примером результата успешного развития работ по линии
студенческих проектов является английская коммерческая фирма SSTL (Small Satellite
Technology
Ltd),
выросшая из университета графства Surrey
что под Лондоном, движущей силой которой является ее коммерческий директор
Мартин Свитинг (Martin
Sweeting).
Мартин в 80-х годах начинал с обучения своих студентов, а в настоящее время на
примере изготавливаемых его фирмой малых спутников производит обучение
иностранных специалистов из развивающихся стран, вводя эти страны формально в
разряд космических [5]. Европейское Космическое Агенство организовало
международный студенческий проект малого спутника ESEO
(European
Student
Earth Orbiter) в рамках программы SSETI (Student Space Exploration
and Technology Initiative), целью которого
является обучение студентов работать в распределенной команде, состоящей из
групп более чем из 20-ти европейских университетах, по стандартам Агенства [6].
Суммируя сказанное выше, инвестиции в такого рода студенческие проекты со
стороны промышленности и государственных структур (Минпромнауки,
Минобразования) могут привести к прямым (отработка новых технологий и
технологических решений) и непрямым (обучение молодых специалистов, способных к
активному участию в реальных космических проектах) результатам.
Второе направление (условно назовем его
«промышленным») инициируется космическими фирмами и агенствами с целью создания
«серьезных» проектов в отличие от «студенческих». Используемые современные
технологии конечно же не способствуют удешевлению самого спутника. Иногда сами
спутники становятся даже дороже. Ибо прямое, уменьшающее габариты
масштабирование лишь увеличивает трудоемкость изготовления, например, малогабаритных
приводов или реактивных двигателей, при очевидном снижении лишь затрат на
материалы. Однако, применяя последние достижения в электронике,
материаловедении и нетрадиционные подходы к конструированию, удается создать
спутники, отличающие по массе на порядок в меньшую сторону от традиционных. При
массе спутника в несколько сот килограмм значительная экономия достигается при
его выводе на орбиту. Здесь умышленно не обсуждается тема удешевления вывода
путем использования конверсионных носителей. Эйфория, вызванная наличием
большого количества боевых ракет, подлежащих уничтожению в соответствие с
международными договоренностями, которые можно было бы использовать для вывода
малых спутников, пошла на убыль. Требующиеся инвестиции для переоборудования таких ракет и пусковых
установок, их адаптации к требованиям, предъявляемыми условиями вывода
спутника, и другие факторы практически сводят на нет преимущества, порождаемые
количеством имеющихся в наличии ракет.
Сейчас наблюдается процесс, при котором
международное сообщество не в состоянии аккумулировать достаточные для этого
материальные ресурсы и вынуждено сворачивать интересные и перспективные
проекты. В этой статье мы не пытаемся анализировать причины таких изменений,
однако, следует обратить внимание, что это коснулось всех без исключения
ведущих космических держав. Включая и тех держав, где имеется богатый опыт
«убеждения» общества в необходимости инвестировать средства в новые технологии
или в разработку способов достижения таких технологий. Однако, «вовремя»
появились технологии, позволяющие во многих случаях отказаться от больших и
дорогостоящих космических аппаратов и соответственно избежать значительных
расходов на их вывод в космос. Конечно, далеко не все малые с точки зрения веса
и размеров спутники можно отнести к малым по стоимости и не все задачи могут
быть решены малыми спутниками. Поэтому догматический подход в виде попытки
решить все задачи, стоящие перед космической отраслью, опираясь только на малые
аппараты, приведет к дискредитации этого направления в космической индустрии.
Однако преимущества, которые дает их применения, должны, где это можно,
безусловно использоваться. К счастью, есть положительные сдвиги в этом
направлении не только в учебных заведениях и небольших коммерческих фирмах, но
и в солидных организациях космической индустрии. Ведущие отечественные
предприятия заявили о разработке проектов малых спутников. Видимо, длительное
ожидание солидного бюджетного финансирования для дорогих больших проектов
вынудило их «повернуться лицом» к созданию недорогих аппаратов в попытке
решения с их помощью текущих задач. Более того, сейчас прослеживается понимание
необходимости использования этих возможностей не только у непосредственных
создателей космической техники, но и у заказчиков из различных министерств и
ведомств. Пока из российских малых аппаратов, фактически реально функционируют
в космосе только несколько спутников Гонец-Д.
Остальные выведенные на орбиту малые спутники, как это не прискорбно, можно
только условно назвать спутниками – скорее это их макеты. Гонец-Д создан на базе хорошо отработанного аппарата,
функционировавшего на орбите не один десяток лет. По-видимому, это и
предопределило успешную работу тех аппаратов этой серии, которые удалось
вывести на орбиту. Из успешно летающих или летавших микроспутников, которые
были сделаны целиком в России именно по идеологии малых аппаратов, можно
выделить микроспутник Колибри (СКБ
космического приборостроения ИКИ, Таруса) и REFLECTOR (НИИ
прецизионного приборостроения, Москва).
Но вернемся к заявленным в названии
статьи системам ориентации. Жесткие ограничения, налагаемые на
массово-габаритные и энергетические характеристики систем малых спутников,
диктуют особые подходы к реализации служебных систем, в частности, систем
ориентации. С развитием мощности бортовых вычислительных машин и повышения
точности и миниатюризации датчиков ориентации удалось переложить «тяжесть»
проблемы обеспечения заданного углового движения спутника на алгоритмы и
математическое обеспечение бортовых компьютеров. Наиболее простыми, дешевыми и
надежными исполнительными органами системы ориентации являются токовые катушки,
создающие механический момент при их взаимодействии с геомагнитным полем.
Определение текущей ориентации может осуществляться по показаниям бортового магнитометра
с использованием статистических методов или с привлечением измерений других датчиков.
Несмотря на широкое использование
вычислительной техники на борту спутника и вместе с ней и активных методов
обеспечения ориентации, в последнее время вновь проявляется интерес к
использованию систем, принцип работы которых основан на использовании пассивных методов, в частности, магнитных и
гравитационных систем ориентации с магнитным гистерезисным демпфером. Начнем с
рассмотрения пассивных систем.
ГРАВИТАЦИОННАЯ СИСТЕМА
ОРИЕНТАЦИИ
СО СФЕРИЧЕСКИМ МАГНИТНЫМ ДЕМПФЕРОМ
В настоящее время наибольшее распространение получила гравитационная
система ориентации, в качестве демпфирующих элементов которой используются
токовые катушки. Существенным недостатком такой системы на пути ее упрощения
является наличие активного органа с элементами определения текущей ориентации в
контуре управления. При повышении требований к точности ориентации введение активных
элементов в контур управления является необходимым условием. Однако при
упрощении системы в свете приведенных выше обстоятельств становится возможным
возврат к пассивной системе, к которой демпфирующим элементом служит, например,
сферический магнитный демпфер. Такой демпфер содержит сильный постоянный
магнит, относительное движение внешней, соединенной со спутником проводящей
сферы в поле которого приводит к наведению в ней токам Фуко и, как следствие, к
рассеиванию энергии возмущенного вращательного движения спутника. Сферический
магнитный демпфер широко применялся на отечественных спутниках в 70-х – 80-х
годах прошлого столетия на спутниках серии Интеркосмос, разработки КБ «Южное»,
спутниках связи, разрабатывавшихся в КБ Прикладной механики и НПО «Полет», а
также многих их «двойниках» прикладного назначения. Не обошли своим вниманием
такие демпферы и создатели малых спутников – Искра-5, Старт-1, СПС-спутник и других, разрабатывавшихся
в начале 90-х годов. Рассмотрим динамически осесимметричный спутник с
достаточно вытянутым эллипсоидом инерции, снабженный сферическим магнитным
демпфером. Спутник движется в центральном гравитационном поле по круговой
орбите. Геомагнитное поле аппроксимируется полем диполя, помещенного в центре
Земли антипараллельно оси ее вращения. Пусть характерная величина демпфирующего
момента 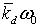 , действующего на спутник со стороны демпфера, значительно
меньше характерной величины восстанавливающего гравитационного момента , действующего на спутник со стороны демпфера, значительно
меньше характерной величины восстанавливающего гравитационного момента 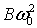 , действующего на спутник из-за градиента гравитационного
поля. Здесь , действующего на спутник из-за градиента гравитационного
поля. Здесь 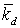 - коэффициент демпфирования, - коэффициент демпфирования, 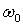 угловая скорость
орбитального движения спутника, угловая скорость
орбитального движения спутника, 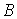 - экваториальный момент
инерции спутника. Тогда вынужденное установившееся движение спутника на
круговой орбите в окрестности положения равновесия в орбитальной системе
координат может быть записано в приближенном виде - экваториальный момент
инерции спутника. Тогда вынужденное установившееся движение спутника на
круговой орбите в окрестности положения равновесия в орбитальной системе
координат может быть записано в приближенном виде
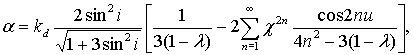 (1) (1)
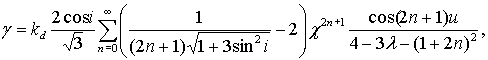
где 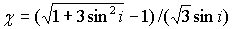 , с точностью до , с точностью до 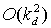 . Здесь a, g - углы тангажа и крена, l - инерционный параметр
спутника, равный отношению его осевого момента инерции к экваториальному, kd= . Здесь a, g - углы тангажа и крена, l - инерционный параметр
спутника, равный отношению его осевого момента инерции к экваториальному, kd=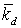 /(Bw0) - безразмерный коэффициент
демпфирования, i - наклонение орбиты, u – аргумент широты. /(Bw0) - безразмерный коэффициент
демпфирования, i - наклонение орбиты, u – аргумент широты.
Для сравнения эффективности системы по быстродействию, то есть скорости
выхода на установившееся движение, приведем усредненные по собственным
колебаниям и аргументу широты уравнения для амплитуд малых колебаний оси
симметрии спутника по тангажу (A1)
и крену (A2) и скорости
осевого вращения, совпадающей при малых A1, A2 с w3, с точностью до 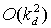
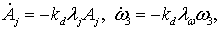 (2) (2)
где с уменьшением
наклонения орбиты от p/2 до 0 показатель
экспоненты l1 убывает, обращаясь
в нуль на экваториальной орбите, а показатели l2 и lw возрастают, увеличиваясь
соответственно в полтора и три раза. При этом сохраняется периодический
колебательный характер движения вокруг оси симметрии спутника. Точкой
обозначено дифференцирование по u.
Численный анализ периодических движений осесимметричного спутника
показывает, что колебательный характер его устойчивых движений сохраняется не
всегда. При весьма малых l на смену ему приходит
устойчивое медленное вращение вокруг оси симметрии, по крайней мере, с периодом
вращения центра масс спутника по орбите.
Как следует из выражений (1) и (2) требования на точность и быстродействие
системы являются противоречивыми. Так как быстродействие системы ориентации не
является в большинстве случаев критичным, то при выборе параметров
гравитационной системы ориентации спутника можно исходить из заданной амплитуды
отклонения его оси симметрии. Естественно, следует принять во внимание наличие
устойчивого вращения спутника при малых значениях инерционного параметра l. Полный цикл исследования
динамики спутника с гравитационной системой ориентации на этапе выбора
параметров системы приведен, например, в работе [7].
ГРАВИТАЦИОННАЯ СИСТЕМА
ОРИЕНТАЦИИ
С ГИСТЕРЕЗИСНЫМИ СТЕРЖНЯМИ
Другой способ использования геомагнитного поля для демпфирования
возмущенных движений спутника состоит в использовании эффекта гистерезисного
рассеяния энергии, возникающего при перемагничивании в геомагнитном поле
магнитомягкого материала, размещенного на спутнике в виде удлиненных стержней.
Оставляя за пределами этой работы рассмотрение достаточно сложной проблемы
выбора магнитного материала, формы, количества и способов размещения стержней в
теле спутника, акцентируем внимание на его динамике.
Основная сложность, которую приходится преодолевать при моделировании
динамики спутника со стержнями из магнитомягкого материала и определении их
параметров, состоит в выборе адекватной модели гистерезиса. Несмотря на эти
сложности, гистерезисные стержни обладают несомненными конструктивными
достоинствами - простотой и
надежностью, малой массой, высокой стабильностью характеристик и поэтому
находят свое применение и на современных малых спутниках. Используемая модель
должна допускать компромисс, учитывая основные свойства гистерезиса и допуская
получение достаточно наглядных и обозримых результатов.
Воспользуемся моделью
параллелограмма для получения простых соотношений между основными
параметрами системы ориентации и динамическими характеристиками спутника. Эта
модель отражает, пожалуй, основное свойство гистерезиса - слабую зависимость индукции
стержня от величины скорости перемагничивания, но существенную зависимость от
знака скорости. Кроме того, эта модель допускает использование ее как в
аналитических, так и в численных расчетах. Она позволяет сделать скорее
качественные выводы, чем количественные. Для получения количественных
характеристик потребуется использовать модели, реализованные на ЭВМ, например,
описанную в [8].
Вначале необходимо решить вопрос о минимально необходимом количестве
стержней. Рассмотрим частный случай - движение спутника в
плоскости полярной круговой орбиты. Пусть на спутнике установлены два
идентичных по своим магнитным характеристикам гистерезисных стержня. Пусть
коэрцитивная сила Hc равна нулю. В рамках модели параллелограмма в
этом случае петля гистерезиса вырождается в прямую линию, проходящую через
начало координат, и при совпадении в каждый момент времени суммарного
наведенного магнитного момента стержней с H геомагнитное поле не влияет на движение
спутника. Следует сразу заметить, что уже в рамках модели Релея для
аппроксимации петли, в отсутствие гистерезиса наблюдается возникновение
возмущающего момента даже при установке идентичных взаимно ортогональных
стержней. Отличие выводов в рамках модели параллелограмма и модели Релея тем
больше, чем больше отличие текущей магнитной проницаемости от ее начального значения.
Уравнение малых колебаний спутника в плоскости орбиты после усреднения
по собственным колебаниям и аргументу широты [9] имеет решение
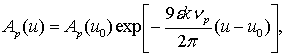 (3) (3)
где Ap - амплитуда малых колебаний
спутника, e - безразмерный коэффициент
демпфирования, k - безразмерная коэрцитивная
сила материала стержня, np - безразмерный
коэффициент, зависящий от ориентации стержней относительно главных осей инерции
спутника. Максимум np равный 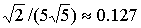 достигается при
расположении «креста» из двух взаимно ортогональных идентичных стержней под
углом 45° к главным осям
инерции спутника, лежащим в плоскости орбиты. Именно такое расположение
стержней мы применили в наноспутнике REFLECTOR. достигается при
расположении «креста» из двух взаимно ортогональных идентичных стержней под
углом 45° к главным осям
инерции спутника, лежащим в плоскости орбиты. Именно такое расположение
стержней мы применили в наноспутнике REFLECTOR.
При расположении стержней параллельно этим осям np=0 и демпфирования в
первом приближении нет. Учет слагаемых более высокого порядка малости по углу a показал [9], что в этом
случае расположение стержней параллельно главным осям инерции приводит к смене
вида зависимости амплитуды от времени. Численное исследование динамики спутника
при произвольных начальных отклонениях спутника с использованием как модели
параллелограмма, так и достаточно адекватной модели гистерезиса [8] показало
удовлетворительное соответствие приведенным выше результатам.
В случае пространственного движения на спутнике должно быть установлено
три взаимно ортогональных стержня. Выводы о расположении двух стержней в
плоскости осей среднего и минимального моментов инерции сохраняются. Третий
стержень, расположенный параллельно оси максимального момента инерции,
обеспечивает эффективное демпфирование малых колебаний. При этом колебания по
крену и рысканию затухают за конечное время [10] в рамках используемой модели.
Примером использования гистерезисных стержней в составе пассивной
гравитационной системы ориентации служит наноспутник REFLECTOR, успешно выведенный на
солнечно-синхронную орбиту попутно с основным спутником Метеор-3М 10 декабря 2001г. Cпутник предназначен для
проведения экспериментов по оптическому сопровождению космических объектов.
Обычно при выполнении таких экспериментов наиболее существенным мешающим
фактором является мерцание атмосферы. Для изучения способов компенсации
мерцания в реальном времени требуется объект с известными оптическими
свойствами. Спутник REFLECTOR представляет собой
предварительно тарированный объект для выполнения экспериментов с лазерными
источниками излучения. Следует отметить, что спутник представляет собой
полностью пассивное устройство. Какое-либо изменение его геометрической конфигурации
можно выполнить только одновременно с отделение спутника от носителя. В
дальнейшем из-за отсутствия на спутнике приемо-передающего устройства,
источника энергии, датчиков, вычислительного устройства, таймера и вообще
чего-либо за исключение рефлекторов не представляется возможным изменение конфигурации
и использование активных методов управления его угловым движением. По этой
причине было предложено использовать пассивную систему ориентации, состоящую из
надлежащим образом распределенных грузов, формирующих необходимый трехосный
тензор инерции, и 18-ти гистерезисных стержней диаметром 0.3 мм (!),
изготовленных из магнитомягкого материала. Спутник разработан и изготовлен
Научно-исследовательским институтом прецизионного приборостроения при участие Института
прикладной математики им.М.В.Келдыша РАН (г.Москва) [11,12] в части обеспечения
его требуемого углового движения. Вид спутника с выдвинутой гравитационной
штангой и дополнительными грузами приведен на рис.1. На рисунке видны места
крепления гистерезисных стержней но правой панели (точки, едущие под углом к
продольной оси спутника).
В настоящее время (2002г.) спутник успешно наблюдается созданной под
эгидой ЮНЕСКО Международной службой лазерной дальнометрии (ILRS) (в нее входит и Российская лазерная сеть),
которая на основе обмена получаемой информацией работает со всеми КА, оснащенными
ретрорефлекторами. В частности, на рис.2 представлены результаты сеанса
наблюдения от 23 ноября 2001г., проведенного станцией слежения NERC Space
Geodesy Facility, расположенной в Herstmonceux Castle, Hailsham, East Sussex,
UK [13]. По оси абсцисс показано время наблюдения (в минутах), а по оси ординат
– расстояние (в метрах) отражающего рефлектора от картинной плоскости,
проходящей через центр масс спутника и перпендикулярной направлению лазерного
луча, сканирующего спутник. Наличие нескольких точек в один и тот же момент
времени означает, что наблюдается сразу несколько рефлекторов и по форме кривых
удается определить скорость вращения спутника вокруг оси, перпендикулярной
лазерному лучу, угол, который образует гравитационная штанга с этой осью и
скорость вращения спутника вокруг штанги [14].
МАГНИТНАЯ СИСТЕМА
ОРИЕНТАЦИИ
С ПОСТОЯННЫМ МАГНИТОМ
И ГИСТЕРЕЗИСНЫМИ СТЕРЖНЯМИ
Пожалуй, наиболее простой системой ориентации с точки зрения создания и
эксплуатации является пассивная магнитная система. Как правило, объектом ее
применения являются небольшие научные спутники. Первым таким спутником был
американский Transit-1B (1960г.). Обзор
пассивных магнитных систем ориентации, спутников, снабженных ими, и методов
моделирования динамики таких спутников приведен в [4].
При использовании постоянного магнита для обеспечения восстанавливающего
момента одним из основных факторов при выборе параметров системы ориентации
является возможный резонанс между частотами собственных колебаний спутника и
частотами, кратными частоте его орбитального движения. Приведенное в работе
[15] соотношение
h»pan2+r0+r1l, (n=2,3,...), (4)
полученное
асимптотическими методами для динамически осесимметричного спутника,
вращающегося в плоскости круговой полярной орбиты, позволяет определить
значения дипольного момента магнита m,
при которых наступает резонанс. Здесь h=mmm/(Bmg) - безразмерный магнитный
момент постоянного магнита, установленного на спутнике; mm, mg - магнитный и гравитационный
параметры Земли. Резонанс между собственными колебаниями спутника в плоскости
орбиты и его орбитальным движением
определяется выражением (4) при pa»2.63, r1»0.51, r0»-0.49. Резонанс между
собственными колебаниями относительно плоскости орбиты и орбитальным движением
определяется этим же выражением при pa»2.63, r1»1.25, r0»-4.25.
Аналогичная по своей структуре, но более громоздкая формула приведена в
[15] для орбит с произвольным наклонением. Это позволяет определить ”опасные”
области значений дипольного момента магнита с точки зрения увеличения амплитуды
установившихся колебаний спутника при различных наклонениях орбиты. Почувствовать
влияние резонанса можно на следующих цифрах: при амплитуде установившегося
движения 10¸15° попадание в ближайшую
область резонанса приводит к увеличению амплитуды до 30¸50°.
Наиболее простым демпфирующим устройством, образующим вместе с
постоянным магнитом пассивную магнитную систему ориентацию, является набор
гистерезисных стержней. При установке на спутнике двух идентичных взаимно
ортогональных стержней в плоскости, проходящей через середину магнита и
перпендикулярной ему, амплитуда R
малых пространственных колебаний ориентируемой оси спутника относительно
вектора H определяется после усреднений
по нескольким переменным и малосущественных упрощений в рамках модели параллелограмма
в соответствии со следующей формулой [16]:
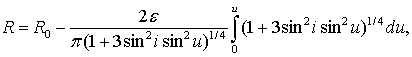
R0 - постоянная интегрирования, e - безразмерный коэффициент
демпфирования. Отсюда видно, что затухание колебаний происходит в среднем по
орбитальному движению линейно по времени с наложенными колебаниями, которые обусловлены
изменением модуля вектора H.
Примером использования методики расчета, изложенной в [16], является
пассивная магнитная система ориентации шведского наноспутника Munin, в разработке системы ориентации которого мы
принимали участие. Внешний вид спутника на испытательном столе перед установкой
на основный спутник приведен на рис.3. Munin был успешно выведен на орбиту 21 ноября 2000 года с помощью ракеты Delta-II попутным запуском. Описание спутника и
полезные задачи, решаемые им, приведены в [17]
Для функционирования пассивной системы ориентации спутника Munin датчики углового положения не нужны, однако
для интерпретации измерений, выполненных полезной нагрузкой, в частности,
измерений потоков нейтральных и заряженных частиц впоследствии потребовалось
знать его положение относительно магнитной силовой линии. Эта задача решалась в
отсутствие датчиков ориентации с использованием лишь измерений токосъема
солнечных батарей, покрывающих все шесть граней кубического корпуса спутника.
Решение задачи усложнялась также, в частности, отсутствием предварительной
калибровки каждой батареи и отсутствием информации о режиме зарядки
аккумуляторной батареи («по току» или «по напряжению») в моменты проведения
измерений токосъема. Пример сеанса определения ориентации от 18 января 2001г.,
выполненного с использованием метода наименьших квадратов, приведен на рис.4,
где изображена зависимость угла отклонения ориентируемой оси спутника
относительно касательной к магнитной силовой линии. К этому времени спутник
практически уже вышел на режим установившегося движения.
Пассивная магнитная система ориентации остается предпочтительной для
наноспутников, масса которых лежит в пределах 10 кг, используемых в
образовательных целях. В таблице 1 [18] приведена информация о системах
ориентации, используемых для наноспутников, которая подтверждает этот тезис.
Несмотря на свою привлекательность в силу простоты и надежности, пассивные
системы, как правило, не в состоянии обеспечить точность ориентации, требуемую
для решения задач, например, связанных с наблюдением Земли из космоса. Для
решения проблемы повышения точности и мобильности в угловом движении вводятся
частично или полностью активные элементы в систему ориентации. При этом для
долгоживущих спутников целесообразно использовать возобновляемые источники
энергии. Таковым является электрическая энергия, возобновляемая посредством
солнечных батарей. В этом случае в качестве исполнительных органов могут
выступать один из двух типов актюаторов – токовые катушки, взаимодействующие с
геомагнитным полем, и электродвигатели-маховики, создающие либо
гироскопический, либо реактивный момент. Точность и быстродействие, достигаемые
при использовании электродвигателей, оказываются выше, чем при использовании
токовых катушек, но за это приходится платить большей массой и сложностью
конструкции, а также более низкой надежностью. Токовые катушки занимают промежуточное
место между пассивными и активными системами, зачастую входя в состав
комбинированных систем ориентации, в которых сочетаются пассивные и активные
элементы. Рассмотрим некоторые способы и примеры использования токовых катушек
в составе систем ориентации спутника.
АКТИВНОЕ УПРАВЛЕНИЕ УГЛОВЫМ ДВИЖЕНИЕМ
СПУТНИКА С ПОМОЩЬЮ ТОКОВЫХ КАТУШЕК
Активное
управление с помощью токовых катушек является, пожалуй, наиболее
распространенным методом обеспечения углового движения малых и особенно
микроспутников. При этом обычно реализуются следующие режимы. Магнитная
ориентация вдоль вектора местной индукции геомагнитного поля (катушки
используются для создания восстанавливающего и демпфирующего моментов). Гравитационная
ориентация вдоль местной вертикали (катушками обеспечивается демпфирующий момент).
Трехосная ориентация (одна из главных осей удерживается вдоль нормали к
плоскости орбиты с помощью тангажного маховика, а поворот в плоскости орбиты
контролируется токовыми катушками либо используются только катушки без
маховика).
Собственно говоря,
просматриваются два основных подхода в реализации магнитного управления
(назовем их «дифференциальным» и «интегральным»). При дифференциальном подходе
восстанавливающий и демпфирующий моменты формируются по информации о текущем
фазовом состоянии спутника, в направлении и с величиной, уменьшающими текущие отклонение осей спутника от
заданных направлений в пространстве и уменьшающими относительную угловую
скорость. При интегральном подходе на основе текущего состояния спутника
формируется необходимая величина и знак производной функции, задающие скорость
убывания функционала, характеризующего отклонение спутника от требуемого
положения или движения по заранее выбранной метрике. Это – локально оптимальное
управление, когда минимизируемый функционал в каждый момент времени не
возрастает. Обычно в качестве функционала выбирается функции Ляпунова, которая
характеризует энергию относительного движения спутника. В теории безусловной
минимизации этот метод носит название второго метода Ляпунова.
В качестве примера
использования дифференциального метода рассмотрим алгоритм управления малым
спутником BADR-B [19] (эскиз приведен
на рис.5), выведенным на орбиту 10 декабря 2001г. совместно с основным
спутником Метеор-3М. На этапе
предварительной ориентации по магнитному полю был использован следующий алгоритм
[Разработка Space Innovation Ltd (UK).]:
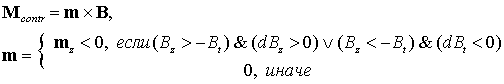
Здесь
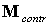 - управляющий момент, - управляющий момент,
 - магнитный дипольный
момент спутника, создаваемый управляющими токовыми катушками, - магнитный дипольный
момент спутника, создаваемый управляющими токовыми катушками, 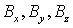 - проекции вектора - проекции вектора 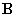 местной индукции
геомагнитного поля на оси связанной со спутником системы координат Oxyz, ось Oz должна быть
ориентирована вдоль вектора местной индукции
геомагнитного поля на оси связанной со спутником системы координат Oxyz, ось Oz должна быть
ориентирована вдоль вектора 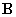 ; ; 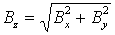 . Пример переходного процесса, полученного с использованием
приведенного выше алгоритма при некоторых заданных параметрах релейного
дипольного магнитного момента спутника и подобранных нужным образом временных
константах, приведен на рис.6. Здесь по оси абсцисс отложено время (в оборотах
вокруг Земли), а по оси ординат – угол между положительным направлением оси Oz спутника и вектором . Пример переходного процесса, полученного с использованием
приведенного выше алгоритма при некоторых заданных параметрах релейного
дипольного магнитного момента спутника и подобранных нужным образом временных
константах, приведен на рис.6. Здесь по оси абсцисс отложено время (в оборотах
вокруг Земли), а по оси ординат – угол между положительным направлением оси Oz спутника и вектором 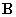 (в градусах). График
описывает положение спутника, близкое к перевернутому. Такое положение
требуется по условию финального движения, предъявляемому к системе предварительной
ориентации. Дифференциальный алгоритм чувствителен к величине дипольного
момента катушек и продолжительности движения с включенными катушками, когда не
удается проводить измерения магнитного поля и спутник фактически управляется с
использованием «устаревшей» информации. (в градусах). График
описывает положение спутника, близкое к перевернутому. Такое положение
требуется по условию финального движения, предъявляемому к системе предварительной
ориентации. Дифференциальный алгоритм чувствителен к величине дипольного
момента катушек и продолжительности движения с включенными катушками, когда не
удается проводить измерения магнитного поля и спутник фактически управляется с
использованием «устаревшей» информации.
Для обеспечения
одноосной ориентации спутника вдоль фиксированного направления в инерциальном
пространстве с помощью токовых катушек предлагается использовать
дифференциальный алгоритм, сводящийся к следующему. Управление осуществляется в
двух взаимно перпендикулярных плоскостях, а собственное вращение,
препятствующее разделению пространственного движения на два плоских,
поддерживается в допустимых пределах.
Рассмотрим задачу
магнитного управления ориентацией спутника, когда требуемое направление
отлично, от направления вектора индукции B
магнитного поля Земли. Будем считать, что спутник – осесимметричный, орбита его
центра масс полярная; на спутник действует только управляющий магнитный момент;
а направление, вдоль которого спутник должен быть ориентирован свой продольной
осью (осью симметрии) с ортом n фиксировано в
инерциальном пространстве и параллельно плоскости экватора Земли. Введем систему координат Oxyz с началом в центре
масс спутника; ось Ox параллельна направлению ориентации спутника; Oz параллельна оси
вращения Земли; ось Oy дополняет систему координат до правой. Положение оси симметрии
спутника n относительно системы координат Oxyz будем задавать при
помощи двух углов 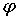 , , 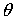 (рис.7). Требуемая
ориентация спутника соответствует (рис.7). Требуемая
ориентация спутника соответствует 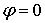 , , 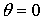 . Введем также величину . Введем также величину 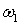 ‑ проекцию
угловой скорости на направление оси симметрии спутника n. Главные моменты инерции спутника обозначим ‑ проекцию
угловой скорости на направление оси симметрии спутника n. Главные моменты инерции спутника обозначим 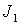 и и 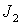 , где , где 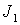 ‑ момент
инерции вокруг оси симметрии спутника, а ‑ момент
инерции вокруг оси симметрии спутника, а  - вокруг двух других
взаимно-перпендикулярных друг другу и вектору n осей.
Будем использовать наиболее простую модель магнитного поля Земли, в которой
конец вектора индукции B на полярной орбите
равномерно вращается по окружности. В этом случае, если имеется возможность
создать управляющий дипольный магнитный момент m
фиксированной величины в любом направлении, то к спутнику может быть приложен
механический момент также постоянной величины M в
любом направлении перпендикулярном вектору индукции B
геомагнитного поля. Далее будем считать, что магнитные катушки на спутнике
постоянно включены, а переменной управления является угол - вокруг двух других
взаимно-перпендикулярных друг другу и вектору n осей.
Будем использовать наиболее простую модель магнитного поля Земли, в которой
конец вектора индукции B на полярной орбите
равномерно вращается по окружности. В этом случае, если имеется возможность
создать управляющий дипольный магнитный момент m
фиксированной величины в любом направлении, то к спутнику может быть приложен
механический момент также постоянной величины M в
любом направлении перпендикулярном вектору индукции B
геомагнитного поля. Далее будем считать, что магнитные катушки на спутнике
постоянно включены, а переменной управления является угол 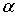 , который задает направление механического момента M в плоскости перпендикулярной вектору B. , который задает направление механического момента M в плоскости перпендикулярной вектору B.
Для описания
вращательного движения спутника воспользуемся уравнениями
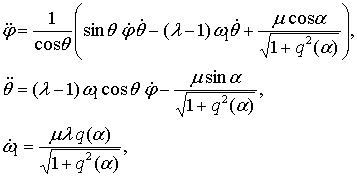
где
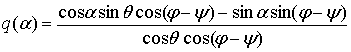 , ,
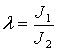 , , 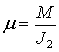 . .
Анализ приведенных
выше уравнений показывает, что можно осуществить поочередное управление углами 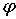 и и 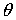 . При желании управлять только углом . При желании управлять только углом  следует выбирать следует выбирать  . Если . Если 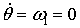 , то уравнения для углов принимают вид: , то уравнения для углов принимают вид:
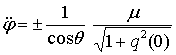 , , 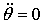 . .
Откуда,
если предположить, что справедливо равенство 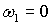 , следует , следует 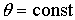 . Аналогично, для управления по углу . Аналогично, для управления по углу 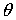 следует выбирать следует выбирать 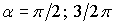 . Если . Если 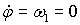 , то уравнения для углов принимают вид: , то уравнения для углов принимают вид:
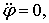 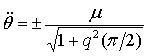 , ,
и,
следовательно 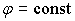 . Однако управления углами . Однако управления углами 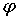 и и 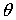 имеют одно
существенное различие. При управлении углом имеют одно
существенное различие. При управлении углом 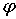 величина величина 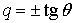 , и, следовательно, если величина угла , и, следовательно, если величина угла  не близка к не близка к 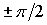 , то управление углом , то управление углом 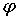 всегда возможно
независимо от положения спутника на орбите. При управлении углом всегда возможно
независимо от положения спутника на орбите. При управлении углом 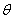 величина величина 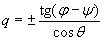 и, если разность и, если разность 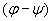 приближается к приближается к 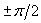 , то возможность управления углом , то возможность управления углом 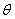 исчезает. Таким
образом, эффективность управления углом исчезает. Таким
образом, эффективность управления углом 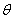 в отличие от угла в отличие от угла 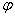 существенно зависит
от положения спутника на орбите. Это создает трудности при корректировке угла,
то есть возможна ситуация, когда момент импульса, сообщенный спутнику системой
управления для изменения величины угла существенно зависит
от положения спутника на орбите. Это создает трудности при корректировке угла,
то есть возможна ситуация, когда момент импульса, сообщенный спутнику системой
управления для изменения величины угла 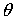 , не может быть нейтрализован в нужный момент, и спутник как
бы «проскакивает» требуемое значение угла , не может быть нейтрализован в нужный момент, и спутник как
бы «проскакивает» требуемое значение угла 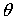 . .
Описанную
трудность можно преодолеть, выбирая специальным образом интервалы времени
поочередного управления углами 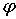 и и 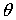 в зависимости от
положения спутника на орбите. Такой выбор производится на основании величины в зависимости от
положения спутника на орбите. Такой выбор производится на основании величины 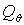 ‑ слагаемого в
правой части дифференциального уравнения для угла ‑ слагаемого в
правой части дифференциального уравнения для угла 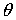 , определяющего величину управляющего воздействия на поворот
по этому углу, , определяющего величину управляющего воздействия на поворот
по этому углу,
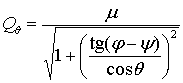 . .
Если величина 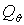 возрастает, то
управление углом возрастает, то
управление углом 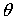 допускается. В случае
же убывания допускается. В случае
же убывания 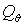 требуется остановить
изменение угла требуется остановить
изменение угла 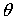 и, если это
необходимо, перейти к управлению углом и, если это
необходимо, перейти к управлению углом 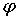 . .
Во время работы
предлагаемого алгоритма корректировки углов 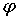 и и 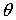 необходимо
поддерживать выполнение соотношения необходимо
поддерживать выполнение соотношения 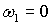 . Это также можно осуществить за счет магнитных катушек.
Эффективность управления компонентой угловой скорости . Это также можно осуществить за счет магнитных катушек.
Эффективность управления компонентой угловой скорости 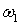 тем выше, чем больше
угол между вектором индукции геомагнитного поля B и осью
симметрии спутника или, что то же самое, чем меньше величина (B/B, n). тем выше, чем больше
угол между вектором индукции геомагнитного поля B и осью
симметрии спутника или, что то же самое, чем меньше величина (B/B, n).
Запишем
предложенный алгоритм магнитного управления ориентацией одноосного
невращающегося спутника на полярной орбите:
·
ЕСЛИ  И (B/B, n) < И (B/B, n) < 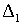 , ,
ТО ПРОЗВЕСТИ КОРРЕКТИРОВКУ 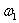
·
ИНАЧЕ
·
ЕСЛИ 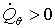 И И 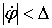
ТО ПРОИЗВЕСТИ КОРРЕКТИРОВКУ 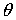
·
ЕСЛИ 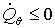 И И 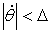
ТО ПРОЗВЕСТИ КОРРЕКТИРОВКУ 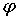
·
ЕСЛИ (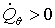 И И 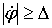 ) ИЛИ ( ) ИЛИ (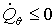 И И 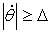 ) )
ТО
·
ЕСЛИ 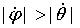
ТО ОСТАНОВИТЬ ИЗМЕНЕНИЕ 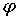
·
ИНАЧЕ
ОСТАНОВИТЬ ИЗМЕНЕНИЕ 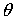
На рис.8
представлен результат моделирования работы предложенного алгоритма при
следующих значениях параметров: высота орбиты спутника 800 км; управляющий
магнитный дипольный момент 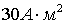 ; угловая скорость вращения спутника вокруг Земли ; угловая скорость вращения спутника вокруг Земли 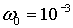 рад/с, моменты
инерции спутника рад/с, моменты
инерции спутника 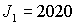 , , 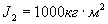 ; индукция магнитного поля Земли ; индукция магнитного поля Земли 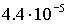 Т; параметры алгоритма Т; параметры алгоритма 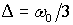 рад/с; рад/с; 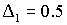 . Видно, что по углу . Видно, что по углу 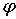 спутник довольно быстро выходит на требуемое нулевое значение
(верхний график). По углу спутник довольно быстро выходит на требуемое нулевое значение
(верхний график). По углу 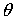 выход на его нулевое значение осуществляется значительно
медленнее, прерываясь сеансами уменьшения скорости осевого вращения. выход на его нулевое значение осуществляется значительно
медленнее, прерываясь сеансами уменьшения скорости осевого вращения.
Один из подходов к
обеспечению ориентации спутника токовыми катушками на круговой орбите на основе
интегрального подхода изложен в [20]. Для интеграла Якоби 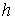 , существующего для твердого тела в центральном
гравитационном поле при движении его центра масс по круговой орбите, , существующего для твердого тела в центральном
гравитационном поле при движении его центра масс по круговой орбите,
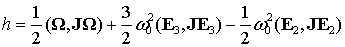 , ,
где
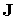 - тензор инерции
спутника, - тензор инерции
спутника, 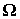 - угловая скорость
вращения спутника относительно орбитальной системы координат, - угловая скорость
вращения спутника относительно орбитальной системы координат, 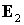 и и 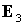 - орты нормали к
плоскости орбиты и местной вертикали, заданные своими проекциями на оси
связанной системы координат Oxyz соответственно, его производная по времени в силу уравнений движения
спутника имеет вид - орты нормали к
плоскости орбиты и местной вертикали, заданные своими проекциями на оси
связанной системы координат Oxyz соответственно, его производная по времени в силу уравнений движения
спутника имеет вид
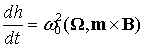 . .
Тогда для
локально-оптимальной минимизации интеграла Якоби управляющий магнитный момент
необходимо выбирать, сообразуясь с условием
 , ,
если
смешанное произведение меньше некоторой, наперед заданной отрицательной
величины и магниный момент полагается равным нулю в противном случае. Проблема
стабилизации спутника в окрестности положения равновесия решается на основе
стандартной задачи оптимального управления линеаризованной системы уравнений с
периодическими коэффициентами. Определение текущего фазового вектора
осуществляется на базе статистической обработки измерений, например, местного
вектора напряженности геомагнитного поля и вектора направления на Солнце.
Иной подход к
обеспечению ориентации спутника с помощью токовых катушек как относительно
магнитной силовой линии, так и местной вертикали при наличии только текущих
измерений проекций на связанные оси вектора индукции геомагнитного поля изложен
в [21]. Особенностью изложенного в этой статье метода является то, что не
требуется создания восстанавливающего гравитационного момента при ориентации
вдоль местной вертикали. Более того, показано, что гравитационный момент
является даже возмущающим, снижая эффективность алгоритма.
Планируется также
использование активного магнитного управления и на малом спутнике Вулкан-Астрогон (эскиз спутника приведен
на рис.9) [22] для наблюдения Земли из космоса, разрабатываемого в рамках
Федеральной космической программы при поддержке Российского
авиационно-космического Агенства (головные исполнители НТЦ «Реагент» и НИИЭМ),
в совокупности с управляющими маховиками для обеспечений прецизионного
управления его угловым движением. Особенностью спутника является полезная
нагрузка, в состав которой входит гиперспектрометр высокого разрешения
разработки НТЦ «Реагент», позволяющий в
реальном масштабе времени строить детальную карту подстилающей поверхности
с распознаванием и выделением цветом состава почв, и идентификации объектов и
материалов, в том числе и подповерхностных. Принцип его действия основан на
использовании не только линейных, но и спектральных
измерений со статистической (когда распознаваемое вещество однокомпонетное)
или субпиксельной (когда распознаваемое вещество многокомпонетное) обработкой
входного сигнала. Прототип АГСМТ–1, работающий в оптическом диапазоне 0.3 – 2.5
мкм, бортового гиперспектрометра был испытан в натурных условиях на борту
летающей лаборатории ИЛ-20 на территории Ямбургского газоконденсатного
месторождения (объекты ОАО «Газпром») в сентябре 2000 года подтвердили
правильность основных научных и технических решений, принятых при создании
системы [23]. Пример карты местности в условных цветах, соответствующих
различным породам и составам грунта приведен на рис.10.
ЗАКЛЮЧЕНИЕ
Рассмотренные системы ориентации могут
быть использованы в качестве основных для недорогих спутников
«университетского» типа и как вспомогательные для более сложных спутников.
Выбор алгоритмов управления определяется целевой функцией спутника и
возможностями системы определения ориентации и имеющимися в наличии на борту
актюаторами, а также вычислительными и энергетическими мощностями.
СПИСОК
ЛИТЕРАТУРЫ
1. M.Yu.Ovchinnikov.
Small Satellites in Russia and in the World: Current State, Journal for Space Communications, 1995,
V.13, N 1, pp.45-50.
2. M.Yu.Ovchinnikov.
Small Satellites in Russia (Economical and Management Aspects), Actual Problems of Aviation and Aerospace
Systems Journal, Kazan Technical University (Kazan, Russia) and
Aeronautical University (Daytona Beach, USA) Publisher, 1998, N 1(5), pp.13-25.
3. http://sensorsystems.dlr.de/SE/IAA.SYMP/
4. В.А.Сарычев,
М.Ю.Овчинников. Магнитные системы
ориентации ИСЗ, Итоги науки и техники,
Серия: Исследование космического пространства, М.: ВИНИТИ, 1985, Т.23, 104
с.
5. http://www.sstl.co.uk/Default_java.html
6. http://www.sseti.net/home/WSW/index.php
7. M.Yu.Ovchinnikov.
Gravity-Gradient Attitude Control System for Small Communication Satellite, Advances in Astronautical Science, V.84,
1993, 16p.
8. В.А.Сарычев,
В.И.Пеньков, М.Ю.Овчинников. Математическая модель гистерезиса, основанная на
магнитомеханической аналогии. Математическое
моделирование, 1989, Т.1, No.4, с.122-133.
9. В.А.Сарычев,
В.И.Пеньков, М.Ю.Овчинников, А.Д.Герман. Движение
гравитационно-ориентированного спутника с гистерезисными стержнями в плоскости
полярной орбиты. Космические исследования,
1988, Т.26, No 5, с.654-667.
10. В.А.Сарычев,
В.И.Пеньков, М.Ю.Овчинников, А.Д.Герман. Влияние гистерезисного стержня,
установленного вдоль оси максимального момента инерции спутника, на его
движение в режиме гравитационной ориентации. Космические исследования, 1989, Т.27, No 6, с.849-860.
11. М.Ю.Овчинников,
В.И.Пеньков, С.А.Мирер. Пассивная
гравитационная система ориентации нано-спутника REFLECTOR. Препринт Института прикладной математики
им.М.В.Келдыша РАН, 1999, No.30, 35с.
12. V.Shargorodsky,
V.Shevchenko, M.Ovchinnikov, V.Pen'kov, S.Mirer, R.Nemuchinsky. Nanosatellite REFLECTOR for Optical
Calibrations: Attitude Control and Determination Aspects, Advances in Space Research J. July
2002, V.30, Issue 2, pp.337-343.
13. http://nercslr.nmt.ac.uk/
14. Р.Б.Немучинский.
Использование Signal Processing для получения характеристик вращательного
движения искусственного спутника Земли. Сб.
статей: Обработка информации и моделирование. М.: МФТИ, 2002, 6 с. (в
печати).
15. В.А.Сарычев,
М.Ю.Овчинников. Движение спутника с постоянным магнитом относительно центра
масс. Космические исследования, 1986,
Т.24, N 4, с.527-543.
16. М.Ю.Овчинников,
В.И.Пеньков. Пассивная магнитная система ориентации наноспутника, Космические исследования, 2002, т.40, N 2, с.1-16.
17. M.Ovchinnikov, V.Pen’kov, O.Norberg, S.Barabash. Attitude Control System for the First Swedish Nanosatellite MUNIN, Acta Astronautica, 2000, V.46, Issue 2-6, pp.319-326.
18. M.Ovchinnikov,
Attitude Control Systems for Nanosatellites, ZAMM Z. angew. Math. Mech., Berlin, 81 (2001) Suppl.4, S1027-S1030.
19. M.Yu.Ovchinnikov.
Methods to Control the Attitude Motion of a Satellite by the Earth’s Magnetic
Field Usage, Proceedings of the Euro-Asian Space Week on Cooperation in Space
– “Where East & West Finally Meet”, 23-27 November, 1998, Singapore,
(ESA SP-430, February 1999, pp.475-483).
20. М.Ю.Овчинников,
Г.В.Смирнов. Стабилизация спутника в режиме гравитационной ориентации с помощью
катушек с током, Препринт Института
прикладной математики им.М.В.Келдыша РАН, 1994, N 111.
21. V.A.Bushenkov,
M.Yu.Ovchinnikov, G.V.Smirnov. Attitude
Stabilization of a Satellite by Magnetic Coils, Acta Astronautica, 2002, V.50, Issue 12, pp.721-728.
22. E.Dedikov,
N.Khrenov, V.Lukjaschenko, R.Salikhov, A.Ponomarev, M.Ovchinnikov, I.Rodionov.
Russian Hyperspectral Small Satellite for Gaz Pipelines Monitoring, Digest of the 3rd International
Symposium of IAA “Small Satellites for Earth Observation”,
2-6 April, 2001, Berlin, Germany, IAA-B3-0801, pp.235-239.
23. Н.Н.Хренов,
А.Н.Дмитриевский, А.Г.Ананенков, В.В. Шеремет, А.А. Пономарев, И.Д.Родионов.
Гиперспектральный аэрокосмический мониторинг трасс трубопроводов и территорий
месторождений, Наука и техника в газовой
промышленности, №2-3, с. 37-46, 2001.
|