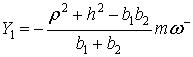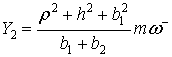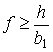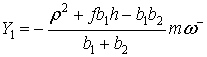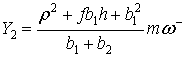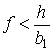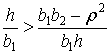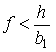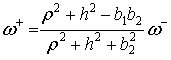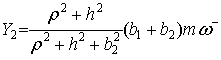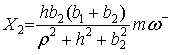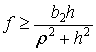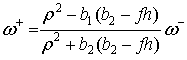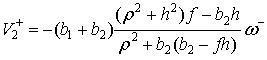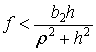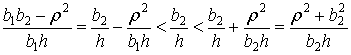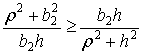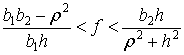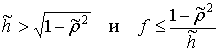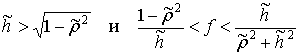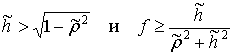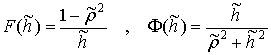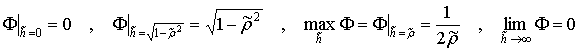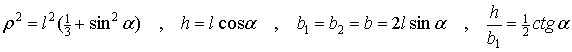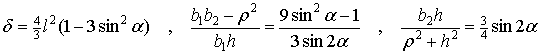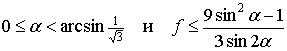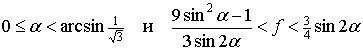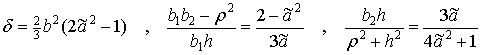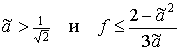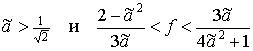Удар тела о поверхность при наличии дополнительной точки соприкосновения

(A body collision with a surface in the presence of an additional point of contact
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Введение

Исследована плоская задача об абсолютно неупругом ударе тела о шероховатую поверхность. При этом предполагается, что до удара тело имело дополнительную неподвижную точку контакта с поверхностью. Показано, что в результате удара возможны различные типы движения тела:

§     останов тела;

§     скольжение на двух точках опоры;

§     вращение вокруг неподвижной новой точки опоры;

§     скольжение на новой точке опоры и вращение вокруг нее.

Ранее эта задача исследовалась в работах [1–3] в случае абсолютно шероховатой поверхности (бесконечного коэффициента трения). Интерес к данной задаче обусловлен изучением движения шагающих машин [1, 3-5] движения мебели и незакрепленных предметов при землетрясении и корабельной качке [6].

§ 1. Постановка задачи и исследование процесса удара.

Твердое тело, совершающее плоское движение, (рис. 1) опирается на опорную поверхность в точке , которая имеет нулевую скорость. В результате вращения твердого тела вокруг этой точки происходит удар об опорную поверхность в новой точке контакта . При этом удар предполагается абсолютно неупругим и после удара, новая точка соприкосновения остается на опорной поверхности. Ударные импульсы реакции опорной поверхности возникают как в точке соударения , так и в точке опоры . В результате удара первоначальная точка опоры может остаться на опорной поверхности, либо покинуть ее, в силу того, что связь является неудерживающей. Кроме того, в результате удара, может начаться скольжение тела по опорной поверхности. Определим условия, при которых имеет место тот или иной тип движения после удара.

Назовем виртуальной ногой отрезок, соединяющий центр масс тела  корпуса с концом ноги. В дальнейшем для описания движения тела будем использовать только центр масс, и виртуальные ноги. Последние будем называть ногами, опуская слово виртуальные. Тем самым сведем задачу об ударе тела (рис. 1) к задаче об ударе плоского двуногого устройства (рис. 2), состоящего из массивного корпуса и двух невесомых ног. Конец ноги, соприкасающийся с опорной поверхностью, будем называть стопой.

Введем обозначения  (рис. 2). Центр масс тела  C. Масса равна  m  ,    –  момент инерции относительно центра масс,    –  радиус инерции относительно центра масс. Стопы опорных ног:   –  стопа передней ноги,   –  стопа задней ноги. Ось Ox совпадает с опорной поверхностью, ось  Oy  направлена вертикально вверх. Точка  H  –  проекция центра масс на горизонтальную поверхность. Вертикальная координата центра масс равна  h. Передний вынос передней ноги  –  , задний вынос задней ноги  –  . Скорость центра масс обозначим через  . Предположим, что центр масс находится между точками опоры или .

Замечание. Решение задачи об ударе не изменится, если опорная поверхность не является горизонтальной. В силу того, что при ударе не учитывается действие конечных сил, в том числе и силы тяжести.

В момент удара возникают ударные импульсы в точках опоры ног (ударные реакции опорной поверхности) их проекции на оси координат обозначим    в стопе    и    в стопе    (рис. 2).

Наложенные на координаты стоп опорных ног связи являются неудер­живающими ( стопы опорных ног могут оторваться от опорной поверхности и двигаться вверх). Следовательно, вертикальные составляющие ударных реакций в точках опоры ног являются не отрицательными

Если стопа  i-й ноги (i = 1, 2) в результате удара отрывается от опорной поверхности, то после удара скорость стопы направлена вверх

Кроме того, примем гипотезу, что ударные реакции в точке опоры этой ноги равны нулю [1–3]

Это предположение равносильно отсутствию импульсных управлений в степенях подвижности ног, которые могли бы дополнительно “подтолкнуть” тело ногой, которая оторвется от опорной поверхности.

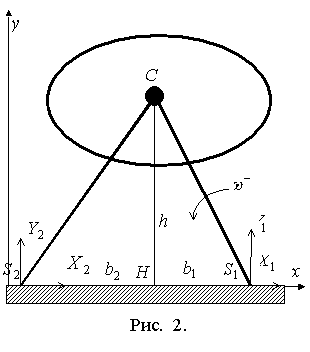
Обозначим    ,    ,    ,    скорость центра масс  C  и угловую скорость тела, соответственно, до удара и после удара. Здесь и далее за положительное направление угловой скорости принимается направление против часовой стрелки.

До удара тело вращалось вокруг неподвижной стопы    и в момент соприкосновения стопы    с опорной поверхностью (до удара) имело угловую скорость

Тогда

Предположим, что удар стопы об опорную поверхность является абсолютно неупругим, тогда в силу теорем о движении центра масс и изменении кинетического момента системы относительно центра масс имеем

Примем гипотезу Рауса [1-3] о том, что при ударе трение сводится к сухому трению с коэффициентом трения   f

До удара скорость центра масс  направлена налево, а скорость новой точки соприкосновения вертикально вниз. Если, в результате удара начинается скольжение тела на одной или двух ногах, то имеет место скольжение налево. При скольжении ударные реакции в точках опоры ног удовлетворяют условию

Возможны четыре различных режима движения замороженной конфигурации машины после удара:

1. Обе ноги остаются на опорной поверхности. Возникают ударные реакции в точках опоры обеих ног. После удара тело останавливается

2. Обе ноги остаются на опорной поверхности. Возникают ударные реакции в точках опоры обеих ног. После удара тело скользит на обеих ногах. Ниже будет показано, что имеет место скольжение налево

3.     После удара начинается вращение тела вокруг неподвижной стопы   с угловой скоростью 

4.     После удара начинается вращение тела вокруг стопы    с угловой скоростью  и скольжение на этой стопе влево со скоростью

Определим, при каких условиях имеет место каждый из этих случаев.

Замечание. Невозможность скольжения тела направо на одной или двух ногах в результате удара вполне очевидна и легко проверяется формально. Также невозможно изменение направления скольжения в процессе удара, по-видимому, в связи с тем, что скорость стопы  в начале удара направлена вертикально вниз. Подобный весьма нетривиальный тип удара с изменением направления скольжения возможен при одноточечном ударе тела о шероховатую поверхность [7-8].

Удар двумя ногами и останов.  Подставляя (9) в (6), имеем

Тогда

Условие не отрицательности вертикальных составляющих ударных реакций (1) в силу (4) и (16) равносильно условию

Из уравнений удара (15) невозможно определить горизонтальные составляющие ударных реакций, но из первого этих уравнений определяется их сумма. Условие остановки тела в результате удара (7), запишем в виде

Это условие в силу (4), (15), (16) равносильно

Скольжение на двух ногах.  Подставляя (10) в (6), имеем

Тогда

В силу (1), (4), (10), (20) данный случай имеет место тогда и только тогда, когда

Из  следует . Из  следует

Тогда условие (21) эквивалентно совокупности (объединению) двух условий

и

Вращение вокруг неподвижной стопы. Подставляя (13), (14) в (6) , имеем

Тогда

Вращение вокруг стопы    возникает в результате удара тогда и только тогда, когда  ,      и   . В силу (4) и (25) получаем, второе из этих условий выполнено всегда, а первое и третье равносильны условиям

Скольжение на стопе и вращение вокруг нее. Подставляя (13), (14) в (6) , имеем

Тогда

Скольжение на стопе    и вращение вокруг нее возникает в результате удара тогда и только тогда, когда  ,   ,   . В силу (4) и второго из уравнений (27) получаем, что третье из этих условий выполнено всегда, когда выполнено первое. Первое и третье условия равносильны, соответственно, условиям

Легко видеть, что первое из этих условий всегда не пусто

и

так как .

В результате скольжение на стопе    и вращение вокруг нее имеет место тогда и только тогда, когда

Это условие не пусто тогда и только тогда, когда правая граница коэффициента трения  больше, чем левая

или

Обозначим

Объединяя (17-18), (22-23), (26), (29-31) получаем, что характер движения после удара стопой    об опорную поверхность определяется следующим утверждением.

Утверждение 1. При    после удара тело либо останавливается при 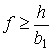; либо начинает скользить на двух ногах при  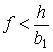. При    после удара тело либо скользит на двух ногах при 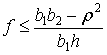 ; либо скользит на стопе  и вращается вокруг нее при 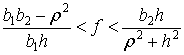; либо вращается вокруг неподвижной стопы  при .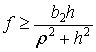

Следствие. В случае абсолютно шероховатой поверхности характер движения после удара определяется знаком . При    после удара начинается вращение вокруг стопы   , а при    в результате удара тело останавливается.

2. Частные случаи

Рассмотри несколько частных случаев, для которых удалось построить графически области, в которых имеет место тот или иной тип удара.

Стопы ног расположены симметрично относительно центра масс или  . Введем безразмерные параметры

В силу утверждения 1 после удара тело

§     останавливается, если

§     скользит на двух ногах, если либо

либо

§     скользит на стопе  и вращается вокруг нее, если

§     вращается вокруг неподвижной , если

Покажем графически области, соответствующие этим условиям на плоскости безразмерных параметров  и коэффициент трения  при фиксированном значении . Введем функции ограничивающие значения этих параметров

При  функция  является гиперболой монотонно убывающей  и

Функция  имеет локальный максимум в точке , точку перегиба при  и

График функции  показан на рис. 3.

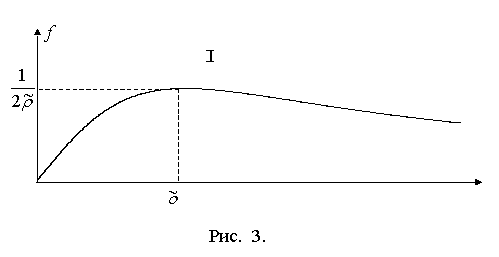
Если , то функция  и  причем  только при . Следовательно, удар двумя ногами с последующим остановом тела или скольжением на двух ногах невозможны. Функция  делит множество допустимых значений параметров  и  на две области (рис. 3). В области I после удара тело скользит на стопе  и вращается вокруг нее, а в области II – вращается вокруг неподвижной стопы .

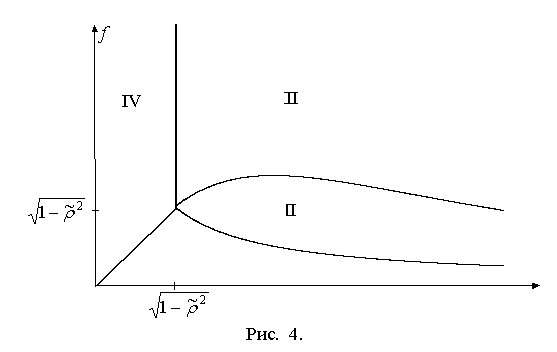
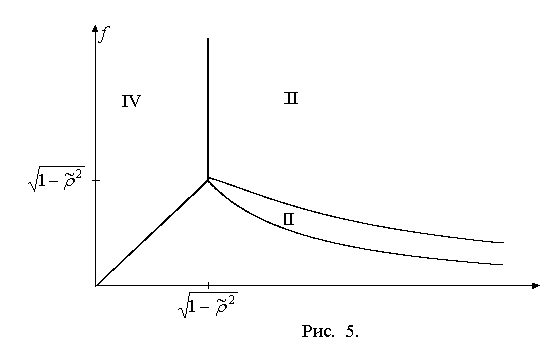
Если , то возможны все четыре типа удара. Графические картинки немного отличаются для случаев  (рис. 4)и  (рис. 5). В первом случае максимум функции  лежит справа от точки ветвления (бифуркации) , а втором случае – слева от нее и поэтому он отсутствует на границе разделяющей области I и II. В области I после удара тело скользит на двух ногах, в области II – скользит на стопе  и вращается вокруг нее, в области III – вращается вокруг неподвижной стопы , в области IV – останавливается.

Во всех этих случаях решение задачи является корректным с точки зрения непрерывной зависимости решения от параметров. На границах пределы из каждой из этих областей совпадают, и решение можно определять по любой из формул соответствующих граничным областям, а в точке бифуркации по формулам соответствующим любому из четырех случаев.

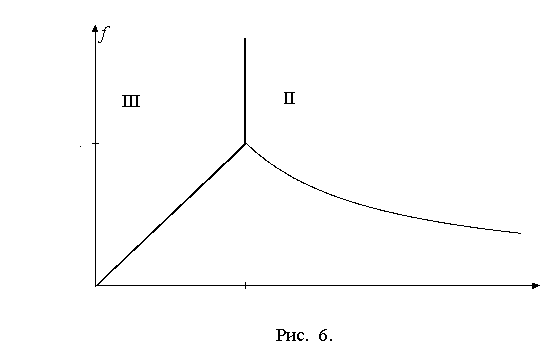
Если тело является материальной точкой  (рис. 6), то . Становится невозможным случай скольжения на стопе  и вращения вокруг нее, что ранее отмечалось в [4]. На рис. 6 в области I после удара тело скользит на двух ногах, в области II – вращается вокруг неподвижной стопы , в области III – останавливается. При этом решение задачи становится некорректным. На границе областей I и II решение меняется скачкообразно.

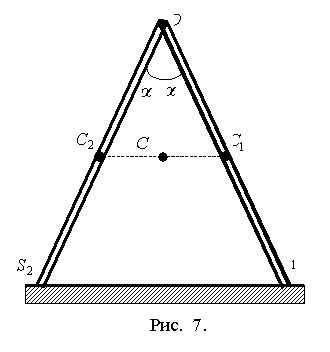
Циркуль. Рассмотрим тело состоящее из двух одинаковых однородных стержней, скрепленных за концы под углом  (рис. 7). Масса каждого стержня равна , длина – . Центр масс тела расположен в точке , причем ,   . Удар циркуля об абсолютно шероховатую поверхность рассмотрен в [1]. Определим области, соответствующие различным типам удара, на плоскости параметров , где угол  .

Для циркуля

В силу утверждения 1 после удара тело

§     останавливается, если

§     скользит на двух ногах, если либо

либо

§     скользит на стопе  и вращается вокруг нее, если

§     вращается вокруг неподвижной , если

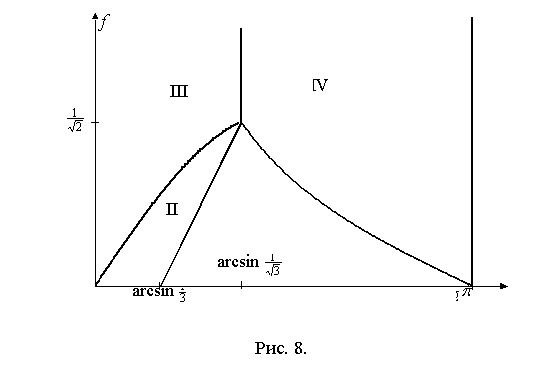
На плоскости безразмерных параметров угол   и коэффициент трения  (рис. 8) в области I после удара тело скользит на двух ногах, в области II – скользит на стопе  и вращается вокруг нее, в области III – вращается вокруг неподвижной стопы , в области IV – останавливается. Точка бифуркации имеет координаты ,  .

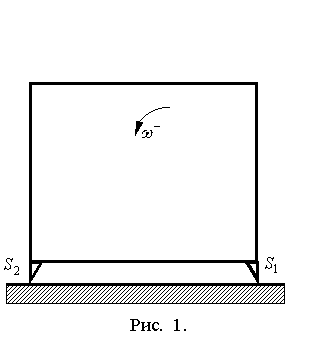
Однородная прямоугольная пластина на ножках размерами, которых можно пренебречь (рис. 1). Ширина пластины равна , высота – . Определим области соответствующие различным типам удара на плоскости параметров , где  безразмерный параметр – отношение высоты пластины к ее ширине

Тогда

В силу утверждения 1 после удара тело

§     останавливается, если

§     скользит на двух ногах, если либо

либо

§     скользит на стопе  и вращается вокруг нее, если

§     вращается вокруг неподвижной , если

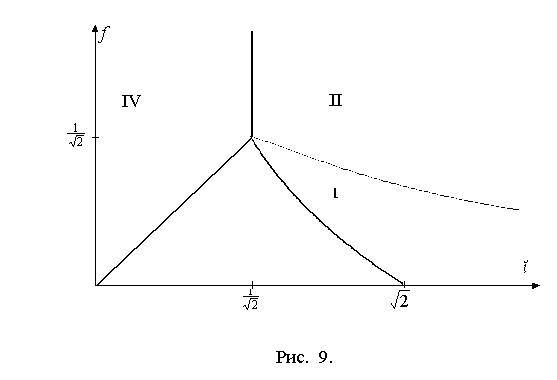
На плоскости безразмерных параметров отношение высоты пластины к ее ширине   и коэффициент трения  (рис. 9) в области I после удара тело скользит на двух ногах, в области II – скользит на стопе  и вращается вокруг нее, в области III вращается вокруг неподвижной стопы , в области IV – останавливается. Точка бифуркации имеет координаты .

Литература

1. Формальский А.М. Перемещение антропоморфных механизмов. М., Наука, 1982.

2. Формальский А.М., Шевальро К., Перра Б. Об ударном взаимодействии тела с опорой. Вестник Московского ун-та, серия “Математика, механика”, 2000, № 1, с. 27-32.

3. Лапшин В.В. Экстренный останов шагающей машины на абсолютно шероховатой поверхности. Препринт Ин-та прикл. мат. РАН, 1996, № 85.

4. Lapshin V. Model problem of a walking machine emergency stop. In: 5th IFAC Symposium on Robot Control, Vol. 3, Nantes, France, 1997, pp. 807-812.

5. Охоцимский Д.Е., Голубев Ю.Ф. Механика и управление движением автоматического шагающего аппарата. М., Наука, 1984.

6. Нагаев Р.Ф. Механические процессы с повторными затухающими соударениями. М., Наука 1985.

7. Плявниекс В.Ю. Расчет косого удара о препятствие. В кн.: Вопросы динамики и прочности, № 18. Рига, Зинатне, 1969, с. 87-109.

8. Лапшин В.В. Плоский удар тела о шероховатую поверхность. Препринт Ин-та прикл. мат. РАН, 2001, № 10.