Исследование режима одноосной солнечной ориентации спутника
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
15 |
|
|
|
|
|
|
18 |
|
|
|
|
|
|
21 |
|
|
|
|
|
|
24 |
|
|
|
|
|
|
27 |
|
|
|
|
|
|
30 |
|
|
|
|
|
Как показывают значения величин ![]() в таблице, формула
(2) оказалась достаточно точной. Однако хотя эти величины малы, коэффициент
в таблице, формула
(2) оказалась достаточно точной. Однако хотя эти величины малы, коэффициент ![]() при изменении
при изменении ![]() от нуля до
от нуля до ![]() меняется примерно на
1.3%. Таким изменением можно пренебречь, но интересно заметить, что найденные
значения
меняется примерно на
1.3%. Таким изменением можно пренебречь, но интересно заметить, что найденные
значения ![]() достаточно точно
аппроксимируются формулой
достаточно точно
аппроксимируются формулой ![]() , где
, где ![]() и
и ![]() – постоянные
коэффициенты. Определение этих коэффициентов методом наименьших квадратов дает
– постоянные
коэффициенты. Определение этих коэффициентов методом наименьших квадратов дает ![]() Нм,
Нм, ![]() Нм. Ошибки
аппроксимации
Нм. Ошибки
аппроксимации ![]() приведены в последнем
столбце таблицы.
приведены в последнем
столбце таблицы.
Зависимость
коэффициентов ![]() и
и ![]() от
от ![]() иллюстрируется
таблицей 2. Для сравнения укажем, что в рамках рассмотренной выше простейшей
модели тепловой деформации паруса момент светового давления также выражается
формулой (2) с коэффициентом (при
иллюстрируется
таблицей 2. Для сравнения укажем, что в рамках рассмотренной выше простейшей
модели тепловой деформации паруса момент светового давления также выражается
формулой (2) с коэффициентом (при ![]() 1/град.)
1/град.) ![]()
![]() Нм.
Нм.
Таблица 2
|
|
|
|
|
20 |
|
3.253 |
|
40 |
|
3.319 |
|
80 |
|
3.340 |
Приведенные
результаты показывают, что в рамках принятой модели влияние тепловой деформации
приводит в основном к увеличению модуля коэффициента ![]() . Новое значение этого коэффициента лежит в пределах, рассмотренных
в [1]. В [1]
параметры
. Новое значение этого коэффициента лежит в пределах, рассмотренных
в [1]. В [1]
параметры ![]() и
и ![]() в формуле (2) парметризовались углом
в формуле (2) парметризовались углом ![]() :
: ![]() ,
, ![]() . Рассматривались несколько значений этого угла из диапазона
. Рассматривались несколько значений этого угла из диапазона ![]() . При
. При ![]() имеем
имеем ![]() Нм. Таким образом,
учет тепловой деформации паруса не повлиял даже на количественные выводы работы
[1]. Заметим,
что точность одноосной солнечной
ориентации при этом новом значении
Нм. Таким образом,
учет тепловой деформации паруса не повлиял даже на количественные выводы работы
[1]. Заметим,
что точность одноосной солнечной
ориентации при этом новом значении ![]() увеличивается. Даже если
учесть зависимость
увеличивается. Даже если
учесть зависимость ![]() от
от ![]() , то структура момента светового давления не изменится – он
по-прежнему будет потенциальным. Это значит, методы и выводы работы [1] применимы и в рассматриваемой
ситуации.
, то структура момента светового давления не изменится – он
по-прежнему будет потенциальным. Это значит, методы и выводы работы [1] применимы и в рассматриваемой
ситуации.
1.4. Интерполяция момента сил светового давления. Аппроксимация поверхности паруса системой треугольников и расчет
действующего на парус момента сил светового давления по формулам (2)
универсальны и практичны. Однако в случае паруса сложной формы или
использования достаточно детальной модели паруса работа компьютерной
программы, основанной на этих формулах, требует сравнительно больших затрат
процессорного времени. В процессе интегрирования уравнений вращательного
движения спутника желательно вообще не обращаться к такой программе. Следует
один раз насчитать функцию ![]() на некоторой сетке и
хранить насчитанные данные в отдельном файле. Перед интегрированием уравнений
движения эти данные следует считать в массив и в процессе интегрирования
вычислять по ним
на некоторой сетке и
хранить насчитанные данные в отдельном файле. Перед интегрированием уравнений
движения эти данные следует считать в массив и в процессе интегрирования
вычислять по ним ![]() с помощью интерполяционных
формул [2, 3].
с помощью интерполяционных
формул [2, 3].
Интерполяционные
формулы составим исходя из факта, что орт ![]() в процессе
ориентированного движения спутника не отклоняется от оси
в процессе
ориентированного движения спутника не отклоняется от оси ![]() более чем на
более чем на ![]() . Пусть в системе координат
. Пусть в системе координат ![]()
![]() . Введем параметры
. Введем параметры ![]() ,
, ![]() ,
, ![]() и будем рассматривать
и будем рассматривать
![]() как функцию
как функцию ![]() , заданную в квадрате
, заданную в квадрате ![]() . В плоскости
. В плоскости ![]() введем сетку с узлами
в точках
введем сетку с узлами
в точках ![]()
![]() и вычислим массив
и вычислим массив ![]() . Интерполяция функции
. Интерполяция функции ![]() осуществляется так.
Для произвольной точки
осуществляется так.
Для произвольной точки ![]() выбираются целые
числа
выбираются целые
числа ![]() и
и ![]() , удовлетворяющие неравенствам
, удовлетворяющие неравенствам ![]() ,
, ![]() , и находятся
, и находятся ![]() ,
, ![]() . В качестве интерполяционного значения
. В качестве интерполяционного значения ![]() принимается [4]
принимается [4]
![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Функция ![]() непрерывно
дифференцируема, причем
непрерывно
дифференцируема, причем ![]() .
.
В данной работе описанный способ интерполяции применялся только в случае, когда учитывалась тепловая деформация паруса. В остальных случаях формулы (3) использовались непосредственно.
1.5. Модели паруса, использованные в расчетах. При численном моделировании режима одноосной ориентации спутника
рассматривались четыре варианта задания момента сил светового давления. В
вариантах 1 – 3 лепестки паруса считались одинаковыми равнобедренными
треугольниками с углом при вершине ![]() и высотой, опущенной
на основание,
и высотой, опущенной
на основание, ![]() м. Каждая такая
высота лежит в плоскости, содержащей ось
м. Каждая такая
высота лежит в плоскости, содержащей ось ![]() и составляет с ней
угол
и составляет с ней
угол ![]() . Эти плоскости образуют между собой углы, кратные
. Эти плоскости образуют между собой углы, кратные ![]() . Вершины треугольников, противоположные основанию, лежат на
оси
. Вершины треугольников, противоположные основанию, лежат на
оси ![]() . При этом вершины двух соседних треугольников сдвинуты друг
относительно друга на 0.5 м, и если треугольники занумеровать последовательно,
то вершины всех треугольников с номерами одинаковой четности совпадают. Если
основания всех треугольников параллельны плоскости
. При этом вершины двух соседних треугольников сдвинуты друг
относительно друга на 0.5 м, и если треугольники занумеровать последовательно,
то вершины всех треугольников с номерами одинаковой четности совпадают. Если
основания всех треугольников параллельны плоскости ![]() , то такой парус в точности совпадает с парусом идеальной
формы, рассматривавшемся в [1]. В данной работе такой вариант модели паруса называется вариантом 3. Полагаем при этом, что
центр масс спутника совпадает с вершинами, имеющими меньшее значение координаты
, то такой парус в точности совпадает с парусом идеальной
формы, рассматривавшемся в [1]. В данной работе такой вариант модели паруса называется вариантом 3. Полагаем при этом, что
центр масс спутника совпадает с вершинами, имеющими меньшее значение координаты
![]() .
.
Повернем
каждый треугольник на одинаковый угол ![]() вокруг высоты,
опущенной на основание. Знак этого угла считаем положительным, если для
наблюдателя на вершине треугольника поворот выполняется против часовой стрелки.
Полученный парус представляет собой парус с пропеллерным эффектом из работы [1]. Этот вариант модели
паруса назовем вариантом 1.
вокруг высоты,
опущенной на основание. Знак этого угла считаем положительным, если для
наблюдателя на вершине треугольника поворот выполняется против часовой стрелки.
Полученный парус представляет собой парус с пропеллерным эффектом из работы [1]. Этот вариант модели
паруса назовем вариантом 1.
Вариант 2 получается из варианта 3, если
в парусе идеальной форме повернуть на одинаковые по модулю, но противоположные
по знаку углы только два противоположных лепестка одинаковой четности. Для
определенности лепестки паруса занумеруем числами 1, 2, …, 8 и будем считать,
что вершины лепестков 1, 3, 5, 7 (напомним, они совпадают и лежат на оси ![]() ) имеют координату
) имеют координату ![]() больше той же координаты вершин лепестков 2, 4, 6, 8.
Поворачиваются лепестки 1 и 5. Угол поворота основания лепестка 1 обозначим
больше той же координаты вершин лепестков 2, 4, 6, 8.
Поворачиваются лепестки 1 и 5. Угол поворота основания лепестка 1 обозначим ![]() . Тогда угол поворота лепестка 5 будет
. Тогда угол поворота лепестка 5 будет ![]() . Как нетрудно видеть, при
. Как нетрудно видеть, при ![]() варианты 1 и 2
совпадают с вариантом 3. Вариант 2 рассматривается для иллюстрации того факта,
что повороты лепестков паруса вокруг высоты, опущенной на основание, могут не
вызывать пропеллерного эффекта.
варианты 1 и 2
совпадают с вариантом 3. Вариант 2 рассматривается для иллюстрации того факта,
что повороты лепестков паруса вокруг высоты, опущенной на основание, могут не
вызывать пропеллерного эффекта.
Вариант 4 – это по существу вариант 3,
подверженный описанной выше тепловой деформации. Детальное описание этого
варианта приведено в п. 1.3. Деформация труб рассчитывалась при аппроксимации
их ломаными с 40 звеньями (![]() . Для расчета момента светового давления
при интегрировании уравнений движения спутника использовался способ
интерполяции описанный в п. 1.4. Интерполяция строилась при
. Для расчета момента светового давления
при интегрировании уравнений движения спутника использовался способ
интерполяции описанный в п. 1.4. Интерполяция строилась при ![]() , погрешность интерполяции не превышала
, погрешность интерполяции не превышала ![]() Нм.
Нм.
2. ОДНООСНАЯ СОЛНЕЧНАЯ ОРИЕНТАЦИЯ СПУТНИКА
1. Уравнения движения
спутника относительно центра масс. Будем использовать
две системы таких уравнений. Первая система предназначена для непосредственного
численного интегрирования, вторая служит отправной точкой при получении с
помощью метода усреднения так называемых эволюционных уравнений, которые
описывают вековое изменение наиболее существенных параметров вращательного
движения спутника. Расчет правых частей эволюционных уравнений и их
интегрирование выполняются численно. Возможность применения этих уравнений
обусловлена специальным видом изучаемых движений.
Спутник считаем динамически симметричным
твердым телом. Для записи указанных систем его уравнений движения введем три
правые декартовы системы координат. Система ![]() образована главными
центральными осями инерции спутника. Тензор инерции спутника в этой системе
имеет матрицу diag
образована главными
центральными осями инерции спутника. Тензор инерции спутника в этой системе
имеет матрицу diag![]() . Оси системы
. Оси системы ![]() сохраняют неизменные
направления в абсолютном пространстве. Плоскость
сохраняют неизменные
направления в абсолютном пространстве. Плоскость ![]() параллельна плоскости
земного экватора, оси
параллельна плоскости
земного экватора, оси ![]() и
и ![]() направлены в точку
весеннего равноденствия и северный полюс мира. Система
направлены в точку
весеннего равноденствия и северный полюс мира. Система ![]() связана с вектором
связана с вектором ![]() кинетического момента
спутника в его движении относительно центра масс; ось
кинетического момента
спутника в его движении относительно центра масс; ось ![]() направлена по
направлена по ![]() , ось
, ось ![]() лежит в плоскости
лежит в плоскости ![]() .
.
Положение системы координат ![]() относительно системы
относительно системы ![]() будем
задавать при помощи углов
будем
задавать при помощи углов ![]() и
и ![]() . Первый из этих углов образован осями
. Первый из этих углов образован осями ![]() и
и ![]() , второй – осями
, второй – осями ![]() и
и ![]() . Направления отсчета этих углов согласованы с направлениями
осей
. Направления отсчета этих углов согласованы с направлениями
осей ![]() и
и ![]() соответственно. Матрицу перехода от системы
соответственно. Матрицу перехода от системы ![]() к системе
к системе ![]() обозначим
обозначим ![]() , где
, где ![]() – косинус угла между
осями
– косинус угла между
осями ![]() и
и ![]() . Элементы этой матрицы имеют вид
. Элементы этой матрицы имеют вид
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]()
Положение системы координат ![]() относительно системы
относительно системы ![]() зададим углами
зададим углами ![]() ,
, ![]() и
и ![]() , определив их следующим образом. Система
, определив их следующим образом. Система ![]() может быть переведена
в систему
может быть переведена
в систему ![]() тремя
последовательными поворотами: 1) на угол
тремя
последовательными поворотами: 1) на угол ![]() вокруг оси
вокруг оси ![]() , 2) на угол
, 2) на угол ![]() вокруг новой оси
вокруг новой оси ![]() , 3) на угол
, 3) на угол ![]() вокруг новой оси
вокруг новой оси ![]() , совпадающей с осью
, совпадающей с осью ![]() .
Матрицу перехода от системы
.
Матрицу перехода от системы ![]() к системе
к системе ![]() обозначим
обозначим ![]() , где
, где ![]() – косинус угла между
осями
– косинус угла между
осями ![]() и
и ![]() . Элементы этой матрицы выражаются формулами
. Элементы этой матрицы выражаются формулами
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]()
![]()
Матрицу
перехода от системы ![]() к системе
к системе ![]() обозначим
обозначим ![]() ,
, ![]() – косинус угла между
осями
– косинус угла между
осями ![]() и
и ![]() . Введенные матрицы связаны между собой формулой
. Введенные матрицы связаны между собой формулой ![]() .
.
Пусть ![]() – вектор
– вектор ![]() ,
, ![]() ,
, ![]() –
его компоненты в одной из введенных систем координат. Если эти компоненты
относятся к системе
–
его компоненты в одной из введенных систем координат. Если эти компоненты
относятся к системе ![]() , то будем писать
, то будем писать ![]() . Если же они указаны в системе
. Если же они указаны в системе ![]() или
или ![]() , то соответственно напишем
, то соответственно напишем ![]() или
или ![]() .
.
В
уравнениях движения спутника относительно центра масс будем учитывать
гравитационный момент и момент сил светового давления. Первая система этих
уравнений имеет вид
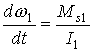 ,
, 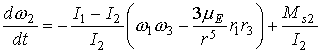 ,
,
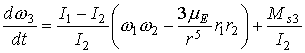 ,
(1)
,
(1)
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Здесь ![]() –
время,
–
время, ![]() – абсолютная угловая
скорость спутника,
– абсолютная угловая
скорость спутника, ![]() – гравитационный
параметр Земли,
– гравитационный
параметр Земли, ![]() – геоцентрический
радиус-вектор точки
– геоцентрический
радиус-вектор точки ![]() ,
, ![]() ,
, ![]() – действующий на
спутник момент сил светового давления. Гравитационный момент в выписанных
уравнениях задан явными выражениями.
– действующий на
спутник момент сил светового давления. Гравитационный момент в выписанных
уравнениях задан явными выражениями.
Первые
три уравнения (1) представляют собой динамические уравнения Эйлера
вращательного движения твердого тела, остальные уравнения этой системы –
кинематические уравнения Пуассона для направляющих косинусов осей ![]() и
и ![]() в системе координат
в системе координат ![]() . В силу последнего замечания переменные
. В силу последнего замечания переменные ![]() и
и ![]() не являются
независимыми – они связаны соотношениями (некоторые из условий ортогональности
матрицы
не являются
независимыми – они связаны соотношениями (некоторые из условий ортогональности
матрицы ![]() )
)
![]() ,
, ![]() ,
, ![]() ,
,
являющимися интегральными
соотношениями системы (1). Эти соотношения должны быть выполнены при задании
начальных условий вычисляемых решений.
В
процессе интегрирования уравнений (1) величины ![]() рассчитывались по
формулам
рассчитывались по
формулам ![]() ,
, ![]() и
и ![]() , движение точки
, движение точки ![]() задавалось формулами
задачи двух тел, в которых учитывались вековые изменения элементов орбиты,
обусловленные главным членом сжатия Земли. Необходимое для расчета момента
задавалось формулами
задачи двух тел, в которых учитывались вековые изменения элементов орбиты,
обусловленные главным членом сжатия Земли. Необходимое для расчета момента ![]() геоцентрическое движение
Солнца находилось по формулам [5]. При этом в качестве орта
геоцентрическое движение
Солнца находилось по формулам [5]. При этом в качестве орта ![]() направления “спутник
– Солнце” (см. предыдущий раздел) использовался орт “Земля – Солнце”.
направления “спутник
– Солнце” (см. предыдущий раздел) использовался орт “Земля – Солнце”.
Переходим
ко второй системе. Для реализации одноосной солнечной ориентации спутника на длительных
интервалах времени предлагается использовать движения с достаточно большим
собственным кинетическим моментом [1]. Эти движения близки
регулярной прецессии Эйлера осесимметричного твердого тела, и при изучении этих
движений внешние моменты можно рассматривать как малые возмущения.
Приближенное исследование движения спутника в такой ситуации можно провести
методом усреднения. Такое исследование проведено в [1], но там принято,
что парус имеет номинальную форму и для момента сил светового давления
использованы простые аналитические выражения. В частности, в большинстве
рассмотренных в [1] задач момент светового давления оказался
потенциальным. Основное внимание в [1] уделено получению приближенных аналитических
оценок, характеризующих точность одноосной солнечной ориентации и время ее
существования.
В случае произвольной формы
солнечного паруса детальное исследование движения спутника можно провести
только численными методами. Непосредственное численное интегрирование уравнений
(1) позволяет решить эту задачу, но для надежности полученные таким способом
результаты следует подтвердить другим методом. В качестве альтернативного
метода использовалось численное интегрирование так называемых эволюционных
уравнений. Эволюционные уравнения выводятся в рамках той же схемы усреднения по
регулярной прецессии Эйлера [6], которая применялась в [1], но записаны они в
других переменных, имеют более высокий порядок и дают возможность изучить более
широкий класс движений. Использованная в данной работе методика численного
расчета правых частей этих уравнений является частным случаем методики [2,3].
Пусть ![]() ,
, ![]() –
вычисленный относительно точки
–
вычисленный относительно точки ![]() главный момент
внешних сил, действующих на спутник. Уравнения движения спутника вокруг центра
масс запишем в виде
главный момент
внешних сил, действующих на спутник. Уравнения движения спутника вокруг центра
масс запишем в виде
![]() ,
, ![]() ,
, 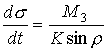 ,
,
 , (2)
, (2)
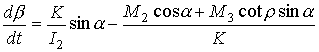 ,
,
 .
.
Вывод первых трех из этих уравнений приведен
в [6],
уравнения для углов ![]() ,
, ![]() и
и ![]() можно вывести по
схеме, которая использованна в [6] для вывода аналогичных уравнений для углов
Эйлера, задающих положение системы координат
можно вывести по
схеме, которая использованна в [6] для вывода аналогичных уравнений для углов
Эйлера, задающих положение системы координат ![]() относительно системы
относительно системы ![]() .
.
В
общем случае использованные в [6] углы Эйлера более удобны для описания регулярной
прецессии твердого тела и вывода эволюционных уравнений. Однако при совпадении
оси собственного вращении спутника с вектором его кинетического момента (осью
прецессии) эти углы вырождаются, и именно такие движения планируется использовать для
реализации режима одноосной солнечной ориентации [1].
Указанное вырождение делает невозмож-ным применение углов Эйлера в численных
расчетах представляющих интерес движений. Чтобы избежать вырождения, в
данной работе введены углы ![]() ,
, ![]() и
и ![]() , хотя это несколько усложнило вывод эволюционных уравнений.
, хотя это несколько усложнило вывод эволюционных уравнений.
Поясним
смысл переменных системы (2). Величины ![]() ,
, ![]() и
и ![]() задают вектор
задают вектор ![]() в абсолютном
пространстве, углы
в абсолютном
пространстве, углы ![]() ,
, ![]() и
и ![]() характеризуют движение
спутника относительно этого вектора. Главный момент
характеризуют движение
спутника относительно этого вектора. Главный момент ![]() внешних сил полагаем
суммой гравитационного момента и момента сил светового давления. Тогда
внешних сил полагаем
суммой гравитационного момента и момента сил светового давления. Тогда ![]()
![]() суть функции
суть функции ![]() , элементов
, элементов ![]() и
и ![]() введенных матриц
перехода, а также положений Солнца и спутника в системе
координат
введенных матриц
перехода, а также положений Солнца и спутника в системе
координат ![]() . Геоцентрические движения Солнца и спутника будем задавать так же, как
в уравнениях (1). В результате придем к функциям
. Геоцентрические движения Солнца и спутника будем задавать так же, как
в уравнениях (1). В результате придем к функциям ![]() , периодически зависящим от угла
, периодически зависящим от угла ![]() с периодом
с периодом ![]() . Получили замкнутую систему уравнений вращательного
движения.
. Получили замкнутую систему уравнений вращательного
движения.
2.2. Эволюционные уравнения. Влияние
внешних моментов на вращательное движение спутника будем считать малым. Это
допущение позволяет воспользоваться для приближенного интегрирования уравнений
(2) методом усреднения. Сначала приведем основные формулы невозмущенного
движения.
При ![]() первые три уравнения
(2) переходят в уравнения
первые три уравнения
(2) переходят в уравнения ![]() ,
, ![]() ,
, ![]() и означают, что
вектор кинетического момента спутника сохраняет свой модуль и направление в
абсолютном пространстве. Остальные уравнения системы (2) переходят в уравнения
и означают, что
вектор кинетического момента спутника сохраняет свой модуль и направление в
абсолютном пространстве. Остальные уравнения системы (2) переходят в уравнения
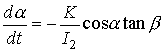 ,
,  , (3)
, (3)
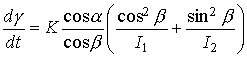 , (4)
, (4)
в которых ![]() – параметр. Уравнения
(3) не содержат
– параметр. Уравнения
(3) не содержат ![]() и образуют замкнутую
подсистему с первым интегралом
и образуют замкнутую
подсистему с первым интегралом ![]() const. Замена переменных
const. Замена переменных ![]() ,
, ![]() переводит систему (3)
в систему
переводит систему (3)
в систему
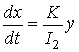 ,
, 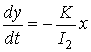 ,
,
общее решение которой запишем в виде
![]() ,
, ![]() ,
, ![]() ,
, 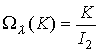 .
.
Здесь ![]() и
и ![]() – произвольные
постоянные,
– произвольные
постоянные, ![]() . Задание переменных
. Задание переменных ![]() и
и ![]() не определяет углов
не определяет углов ![]() и
и ![]() единственным образом.
Ниже будем рассматривать движения, в которых эти углы близки к нулю. В этом случае
указанный выше первый интеграл системы (3) принимает вид
единственным образом.
Ниже будем рассматривать движения, в которых эти углы близки к нулю. В этом случае
указанный выше первый интеграл системы (3) принимает вид ![]() .
.
Подставив
найденное решение системы (3) в уравнение (4), получим
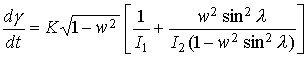 .
.
Поскольку ![]() , из последнего соотношения следует
, из последнего соотношения следует
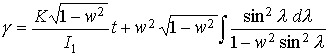 .
.
Полученное
выражение для ![]() можно представить
следующим образом
можно представить
следующим образом
![]() ,
,
где ![]() – произвольная
постоянная,
– произвольная
постоянная,
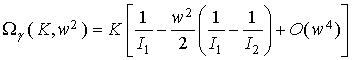 ,
,
![]() ,
, ![]() ,
,
![]() .
.
При ![]() выписанное решение
принимает вид
выписанное решение
принимает вид ![]() ,
, ![]() и описывает
стационарное вращение спутника вокруг оси
и описывает
стационарное вращение спутника вокруг оси ![]() , совпадающей с осью
, совпадающей с осью ![]() .
.
Регулярную прецессию спутника будем задавать величинами ![]() ,
, ![]() ,
, ![]() и
и ![]() . В случае
. В случае ![]() изменение
изменение ![]() описывается
уравнением
описывается
уравнением
![]() .
(5)
.
(5)
При![]() переменные
переменные ![]() ,
, ![]() ,
, ![]() и
и ![]() являются медленными,
переменные
являются медленными,
переменные ![]() ,
, ![]() и
и ![]() – быстрыми.
Зависимость компонент внешнего момента
– быстрыми.
Зависимость компонент внешнего момента ![]()
![]() от времени при
фиксированных значения остальных переменных выражается квазипериодическими
функциями времени, наибольшая частота которых равна орбитальной частоте
(среднему движению спутника)
от времени при
фиксированных значения остальных переменных выражается квазипериодическими
функциями времени, наибольшая частота которых равна орбитальной частоте
(среднему движению спутника) ![]() . Поскольку для представляющих интерес движений
. Поскольку для представляющих интерес движений ![]() ,
, ![]() , время в рассматриваемой задаче также является медленной переменной.
, время в рассматриваемой задаче также является медленной переменной.
Движение спутника можно рассматривать как медленную эволюцию регулярной
прецессии. Дифференциальные уравнения, приближенно описы-вающие в нерезонансном
случае вековое изменение (эволюцию) медленных переменных, так называемые
эволюционные уравнения [6], получаются усреднением правых частей первых трех
уравнений (2) и уравнения (5) по регулярной прецессии
Эйлера при фиксированных значениях всех медленных переменных. Усреднение
проведем следуя рецепту [7],
первоначально предло-женному для усреднения по более сложному движению Эйлера –
Пуансо. С помощью указанного выше решения системы (3) тригонометрические
функции углов ![]() и
и ![]() выразим через
величины
выразим через
величины ![]() и
и ![]() , элементы матрицы перехода
, элементы матрицы перехода ![]() выразим через
выразим через ![]() ,
, ![]() и
и ![]() . В результате компоненты внешнего момента
. В результате компоненты внешнего момента ![]() станут функциями величин
станут функциями величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() , периодическими по
, периодическими по ![]() и
и ![]() с периодом
с периодом ![]() . Уравнение (5) при этом перейдет в уравнение
. Уравнение (5) при этом перейдет в уравнение
![]() .
.
В нерезонансном случае (при иррациональном
отношении частот ![]() и
и ![]() ) эволюционное уравнение для
) эволюционное уравнение для ![]() получается
усреднением правой части последнего уравнения по
получается
усреднением правой части последнего уравнения по ![]() и
и ![]()
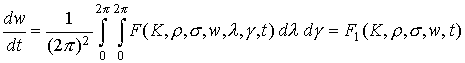 .
.
Аналогичным образом
получаются эволюционные уравнения относительно ![]() ,
, ![]() и
и ![]() . Операцию усреднения, определяемую правой частью последнего
уравнения, будем обозначать символом
. Операцию усреднения, определяемую правой частью последнего
уравнения, будем обозначать символом ![]() . С использованием этого обозначения эволюционные уравнения
можно записать так
. С использованием этого обозначения эволюционные уравнения
можно записать так
![]() ,
, 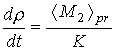 ,
, 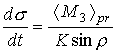 ,
, ![]() (6)
(6)
Формально условие отсутствия резонанса означает, что отношение ![]() должно быть
иррациональным числом. На самом деле эволюционные уравнения (6) могут быть
неадекватны лишь в тех областях изменения переменных
должно быть
иррациональным числом. На самом деле эволюционные уравнения (6) могут быть
неадекватны лишь в тех областях изменения переменных ![]() и
и ![]() , в которых это выражение приближенно равно отношению
небольших натуральных чисел.
, в которых это выражение приближенно равно отношению
небольших натуральных чисел.
Поскольку правые части уравнений (6) линейны по моменту ![]() , при их вычислении операцию усреднения
, при их вычислении операцию усреднения ![]() можно выполнить над
каждым учитываемым внешним моментом по отдельности, а затем полученные
результаты сложить. Для некоторых моментов, например, для гравитационного,
усреднение
можно выполнить над
каждым учитываемым внешним моментом по отдельности, а затем полученные
результаты сложить. Для некоторых моментов, например, для гравитационного,
усреднение ![]() быть проведено аналитически
[6], но в общем случае момента сил светового давления приходится применять
численные методы. Указанное свойство линейности позволяет выбирать при
усреднении каждого момента наиболее удобный способ.
быть проведено аналитически
[6], но в общем случае момента сил светового давления приходится применять
численные методы. Указанное свойство линейности позволяет выбирать при
усреднении каждого момента наиболее удобный способ.
В случае рассматриваемого спутника с солнечным парусом слагаемые правых
частей уравнений (6), отвечающие гравитационному моменту, рассчитывались по
формулам [6]
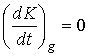 ,
, 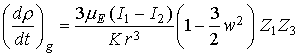 ,
,
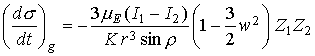 ,
, 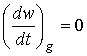 ,
,
где ![]() ; слагаемые, отвечающие моменту сил светового давления,
находились численно.
; слагаемые, отвечающие моменту сил светового давления,
находились численно.
Опишем численное выполнение операции ![]() . Оно заключается в вычислении двойного интеграла по квадрату
. Оно заключается в вычислении двойного интеграла по квадрату
![]() от функции двух
переменных, причем по каждой переменной эта функция – периодическая с периодом
от функции двух
переменных, причем по каждой переменной эта функция – периодическая с периодом ![]() . При вычислении таких интегралов в случае достаточно гладкой
подынтегральной функции весьма эффективны теоретико-числовые квадратур- ные
формулы [8]. Для функции двух переменных оптимальная по
точности формула выглядит следующим образом. Пусть функция
. При вычислении таких интегралов в случае достаточно гладкой
подынтегральной функции весьма эффективны теоретико-числовые квадратур- ные
формулы [8]. Для функции двух переменных оптимальная по
точности формула выглядит следующим образом. Пусть функция ![]() – периодическая по
– периодическая по ![]() и
и ![]() с периодом 1,
с периодом 1, ![]() и
и ![]() – соседние члены последовательности
чисел Фибоначчи 1, 1, 2, 3, 5, …Тогда принимается
– соседние члены последовательности
чисел Фибоначчи 1, 1, 2, 3, 5, …Тогда принимается
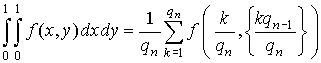 ,
(7)
,
(7)
где символ ![]() означает дробную
часть числа. В расчетах, результаты которых описаны ниже, результат практически
не зависел от
означает дробную
часть числа. В расчетах, результаты которых описаны ниже, результат практически
не зависел от ![]() при
при ![]() .
.
При
изучении эволюции вращательного движения спутника на интервалах времени,
существенно превышающих орбитальный период, правые части уравнений (6)
целесообразно дополнительно усреднить по орбитальному движению спутника. В
случае момента светового давления такое усреднение сводится к умножению
соответствующих членов в (6) на коэффициент ![]() , определяемый выражениями [1]
, определяемый выражениями [1]
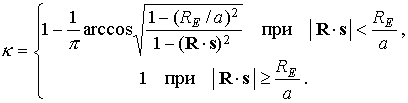
Здесь ![]() –
орт орбитального кинетического момента спутника (нормаль к плоскости орбиты),
–
орт орбитального кинетического момента спутника (нормаль к плоскости орбиты), ![]() – орт направления
“Земля – Солнце”,
– орт направления
“Земля – Солнце”, ![]() км – радиус Земли,
км – радиус Земли, ![]() – большая полуось
орбиты спутника. Коэффициент
– большая полуось
орбиты спутника. Коэффициент ![]() представляет собой
отношение длины отрезка орбиты, освещенного Солнцем, к длине всей орбиты. При
выводе выражения для
представляет собой
отношение длины отрезка орбиты, освещенного Солнцем, к длине всей орбиты. При
выводе выражения для ![]() орбита спутника
считалась круговой радиуса
орбита спутника
считалась круговой радиуса ![]() . В данном случае это допущение оправдано, поскольку
эксцентриситет орбиты мал.
. В данном случае это допущение оправдано, поскольку
эксцентриситет орбиты мал.
Слагаемые правых частей уравнений (6), отвечающие гравитационному
моменту и усредненные по орбитальному моменту, рассчитывались по формулам [2]
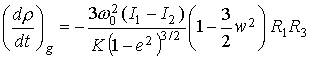 ,
,
 ,
,
где ![]() – эксцентриситет
орбиты.
– эксцентриситет
орбиты.
Ниже, говоря о
системе (6), усредненной по орбитальному движению, будем называть ее системой
(6![]() ). Именно система (6
). Именно система (6![]() ) имелась в виду, когда в начале данного раздела упоминались
эволюционные уравнения, выводимые из второй системы. Система (6) использовалась
только для проверки программы численного интегрирования системы (6
) имелась в виду, когда в начале данного раздела упоминались
эволюционные уравнения, выводимые из второй системы. Система (6) использовалась
только для проверки программы численного интегрирования системы (6![]() ).
).
2.3. Результаты численных
расчетов. Исследование движения спутника в режиме одноосной солнечной ориентации
сводилось к численному интегрированию уравнений (1), (6) и (6![]() ), причем основное внимание уделялось системам (1) и (6
), причем основное внимание уделялось системам (1) и (6![]() ).. Начальный момент
).. Начальный момент ![]() вычисляемых решений
был отнесен к
вычисляемых решений
был отнесен к ![]() декретного
московского (зимнего) времени 22.09.2001. Принималось, что спутник в этот
момент находился в восходящем узле орбиты. Параметры орбиты были взяты
следующие (ср. [1]): большая полуось –
декретного
московского (зимнего) времени 22.09.2001. Принималось, что спутник в этот
момент находился в восходящем узле орбиты. Параметры орбиты были взяты
следующие (ср. [1]): большая полуось – ![]() км, эксцентриситет –
км, эксцентриситет – ![]() , наклонение –
, наклонение – ![]() , начальное значение аргумента широты перигея –
, начальное значение аргумента широты перигея – ![]() . Начальное значение долготы восходящего узла –
. Начальное значение долготы восходящего узла – ![]() . Значения моментов инерции спутника
. Значения моментов инерции спутника ![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() . Момент сил светового давления рассчитывался для четырех
вариантов модели паруса, описанных в разделе 1.
. Момент сил светового давления рассчитывался для четырех
вариантов модели паруса, описанных в разделе 1.
Примем, что в начальный
момент времени ось ![]() спутника направлена
по орту
спутника направлена
по орту ![]() , ось
, ось ![]() лежит в плоскости
лежит в плоскости ![]() (положение оси
(положение оси ![]() при
при ![]() может быть
произвольным, указанное положение выбрано из соображений удобства). В этом
случае начальные значения элементов
может быть
произвольным, указанное положение выбрано из соображений удобства). В этом
случае начальные значения элементов ![]() имеют вид
имеют вид
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Начальные
значения угловой скорости: ![]() ,
, ![]() ,
, ![]() . Выписанные соотношения задают начальные условия для системы
(1). Начальные условия для систем (6) и (6
. Выписанные соотношения задают начальные условия для системы
(1). Начальные условия для систем (6) и (6![]() ) находились из соотношений
) находились из соотношений
![]()
![]() ,
, ![]() , (8)
, (8)
которые легко разрешить относительно ![]() ,
, ![]() ,
, ![]() и
и ![]() . Правые части этих соотношений в данном случае должны быть
выражены через начальные значения переменных системы (1).
. Правые части этих соотношений в данном случае должны быть
выражены через начальные значения переменных системы (1).
Сначала
опишем результаты интегрирования систем (1), (6) и (6![]() ) с согласованными начальными условиями, чтобы оценить
точность
систем (6) и (6
) с согласованными начальными условиями, чтобы оценить
точность
систем (6) и (6![]() ) Вычисляемые решения будем представлять графиками
зависимости от времени величин
) Вычисляемые решения будем представлять графиками
зависимости от времени величин ![]() ,
, ![]() ,
, ![]() и
и ![]() . В случае системы (1) эти величины находились из соотношений
(8) на каждом шаге численного интегрирования. Полученные результаты
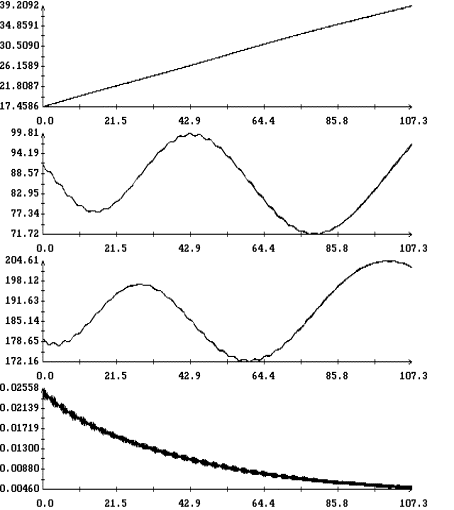
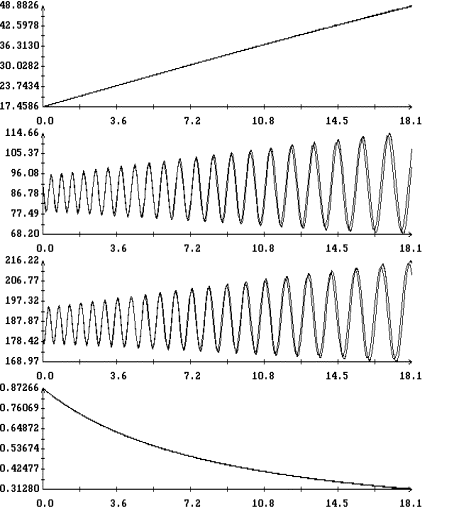
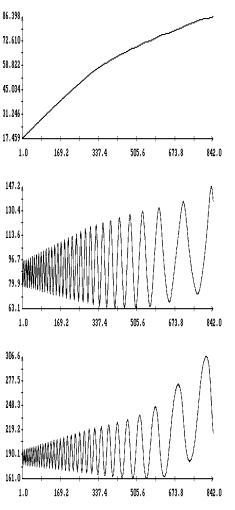
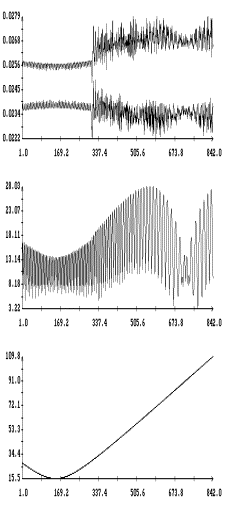
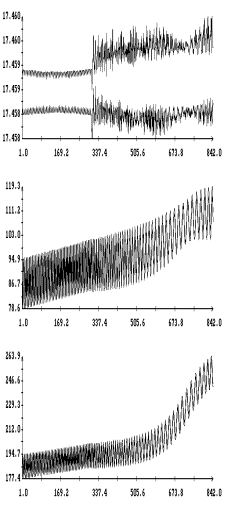
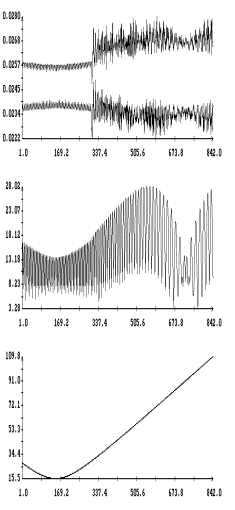
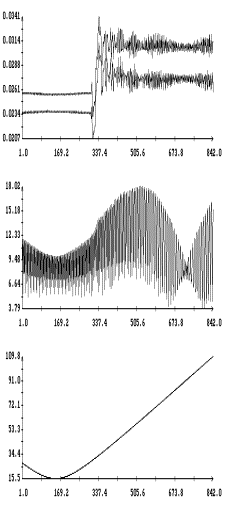
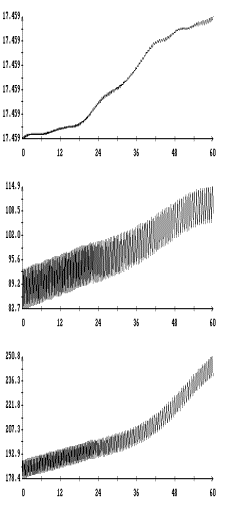
представлены на рис. 1 – 8. На рис. 1 – 4 в одних и тех же
координатных осях изображены графики решений системы (6) и графики, построенные
по решениям системы (1). Как видно из этих графиков, решения обеих систем
достаточно точно согласуются между собой на интервале времени около полутора
суток. Точность согласования не зависит от использованной модели паруса.
. В случае системы (1) эти величины находились из соотношений
(8) на каждом шаге численного интегрирования. Полученные результаты
представлены на рис. 1 – 8. На рис. 1 – 4 в одних и тех же
координатных осях изображены графики решений системы (6) и графики, построенные
по решениям системы (1). Как видно из этих графиков, решения обеих систем
достаточно точно согласуются между собой на интервале времени около полутора
суток. Точность согласования не зависит от использованной модели паруса.
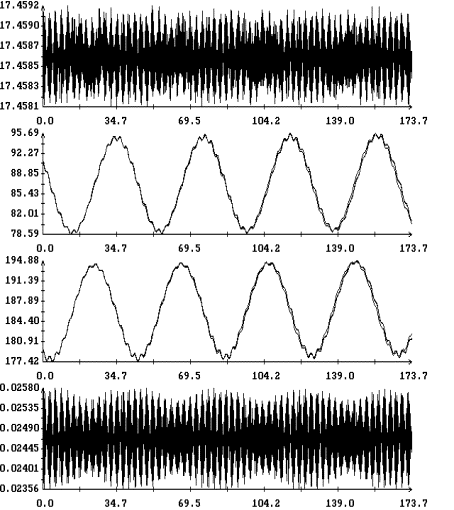
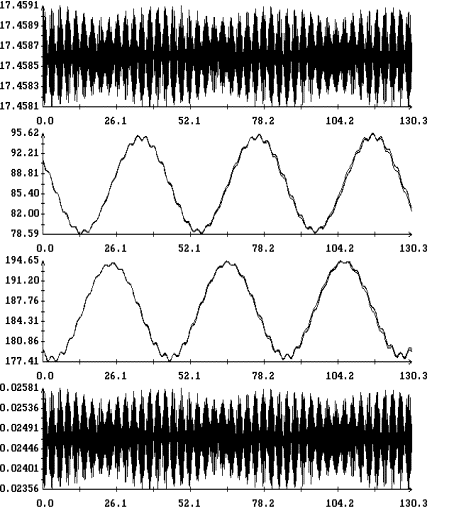
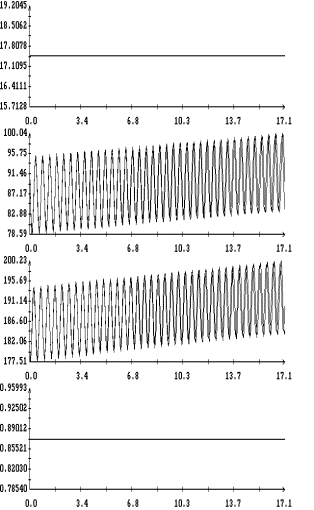
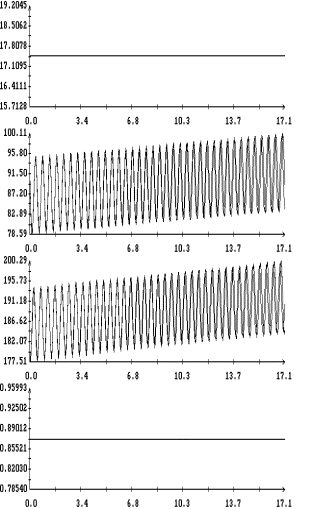
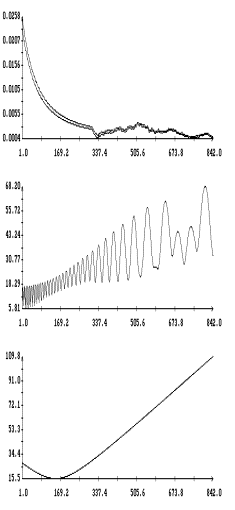
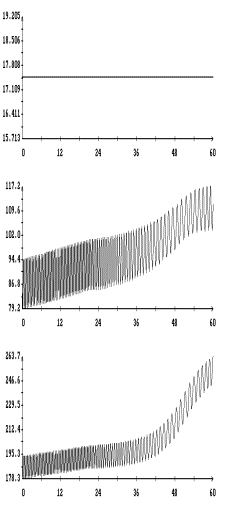
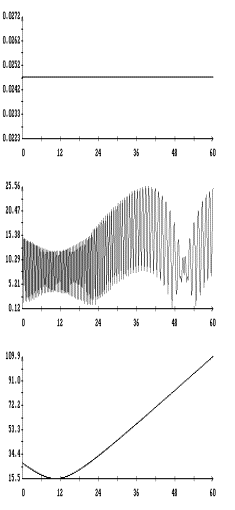
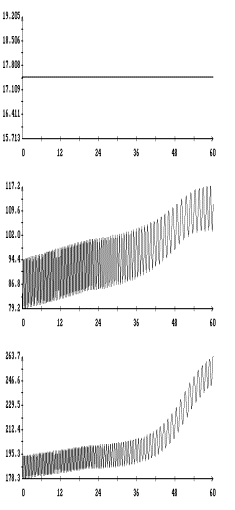
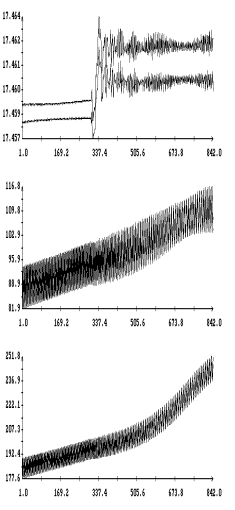
На рис. 5 – 8 в одних и тех же
координатных осях приведены графики решений систем (6) и (6![]() ) на интервале времени 2 – 3 недели. Эти решения достаточно хорошо
совпадают по переменным
) на интервале времени 2 – 3 недели. Эти решения достаточно хорошо
совпадают по переменным ![]() ,
, ![]() и вековому изменению
амплитуд углов
и вековому изменению
амплитуд углов ![]() и
и ![]() , но фазы двух последних углов в конце интервала
интегрирования в этих решениях заметно отличаются. Полученные результаты
согласуются с типичными оценками погрешности метода усреднения. Анализ рис. 5 – 8
свидетельствует о приемлемой точности систем (6) и (6
, но фазы двух последних углов в конце интервала
интегрирования в этих решениях заметно отличаются. Полученные результаты
согласуются с типичными оценками погрешности метода усреднения. Анализ рис. 5 – 8
свидетельствует о приемлемой точности систем (6) и (6![]() ) на интервалах времени в несколько десятков суток. Особенно
удобна в этом отношении система (6
) на интервалах времени в несколько десятков суток. Особенно
удобна в этом отношении система (6![]() ), которая позволяет вычислять движение спутника с весьма
малыми затратами процессорного времени и оперативно проводить анализ большого
числа вариантов движения.
), которая позволяет вычислять движение спутника с весьма
малыми затратами процессорного времени и оперативно проводить анализ большого
числа вариантов движения.
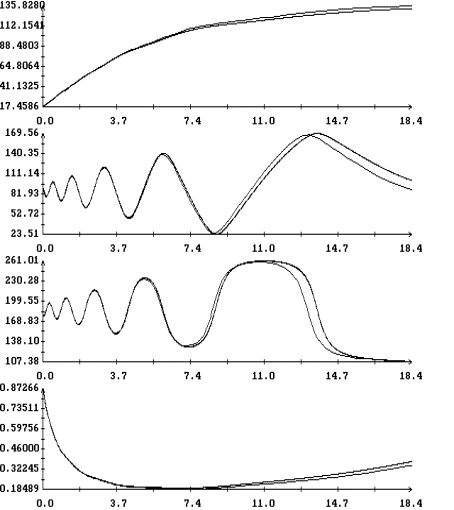
Рис.
1 и 5 иллюстрируют сильноое влияние пропеллерного эффекта на движение спутника.
Чтобы этот эффект не очень сильно проявлялся на длительных интервалах времени,
в первой модели паруса на длительных интервалах принималось ![]() . Рис. 2 и 6 показвают, что сбалансирован- ный поворот
лепестков паруса (вариант 2) не вызывает пропеллерного эффекта.
. Рис. 2 и 6 показвают, что сбалансирован- ный поворот
лепестков паруса (вариант 2) не вызывает пропеллерного эффекта.
Перейдем
к результатам исследования движения спутника на длительных интервалах времени.
Представление решений системы (6![]() ) на интервале времени в 60 сут не требует каких-либо
дополнительных усилий. С решениями системы (1) дело обстоит сложнее. Решения системы (1)
на продолжительных интервалах времени будем представлять следующим образом.
Введем обозначения:
) на интервале времени в 60 сут не требует каких-либо
дополнительных усилий. С решениями системы (1) дело обстоит сложнее. Решения системы (1)
на продолжительных интервалах времени будем представлять следующим образом.
Введем обозначения: ![]() – драконический
период спутника (промежуток времени между двумя его последовательными
прохождениями восходящего узла орбиты, в данном случае
– драконический
период спутника (промежуток времени между двумя его последовательными
прохождениями восходящего узла орбиты, в данном случае ![]() const),
const), ![]()
![]() – временные отрезки,
соответствующие орбитальным виткам спутника,
– временные отрезки,
соответствующие орбитальным виткам спутника, ![]() – угол между осью
– угол между осью ![]() и ортом
и ортом ![]() ,
, ![]() – угол между ортами
– угол между ортами ![]() и
и ![]() . Введенные углы можно найти по формулам
. Введенные углы можно найти по формулам
![]() ,
, ![]() .
.
На решении системы (1) определим последовательности чисел
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() (
(![]() ).
).
Члены этих последовательностей суть
минимальные и максимальные на каждом орбитальном витке значения некоторых
переменных и функций. Введенные последовательности будем представлять
графически ломаными. Например, последовательности ![]() и
и ![]() будем изображать
ломаными, проходящими соответственно через точки
будем изображать
ломаными, проходящими соответственно через точки ![]() и
и ![]()
![]() в плоскости
в плоскости ![]() и т. д. Такие ломаные
наглядно и сжато характеризуют границы изменения выбранных величин на каждом
витке и позволяют получить представление о движении спутника.
и т. д. Такие ломаные
наглядно и сжато характеризуют границы изменения выбранных величин на каждом
витке и позволяют получить представление о движении спутника.
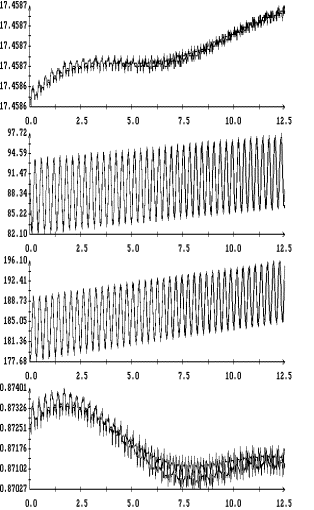
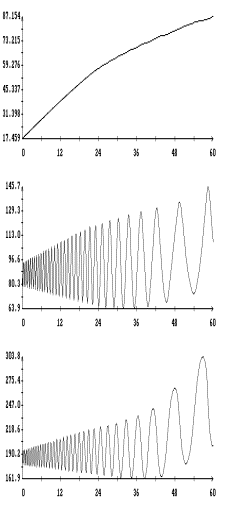
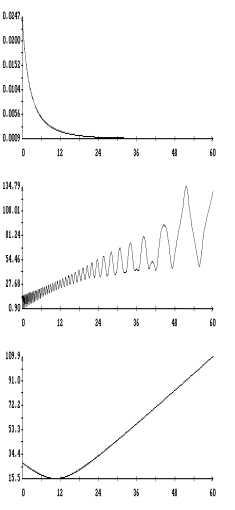
Примеры указанных
ломаных приведены на рис. 9, 11, 13 и 15. На рис. 10, 12, 14 и 16 представлены
графики описывающих те же движения спутника решений системы (6![]() ). Для удобства сравнения разных способов описания движения
спутника при использовании одной и той же модели паруса рисунки разбиты на
пары. На одной странице рядом помещены ломаные, построенные по решениям системы
(1), и графики решений системы (6
). Для удобства сравнения разных способов описания движения
спутника при использовании одной и той же модели паруса рисунки разбиты на
пары. На одной странице рядом помещены ломаные, построенные по решениям системы
(1), и графики решений системы (6![]() ). Налицо достаточно точное (но несколько хуже, чем на рис. 1
– 9) совпадение результатов, полученных с использованием разных систем. На
некоторых графиках ломаные сливаются друг с другом и выглядят как гладкие
кривые. В решениях на рис. 11 и 13 последовательности
). Налицо достаточно точное (но несколько хуже, чем на рис. 1
– 9) совпадение результатов, полученных с использованием разных систем. На
некоторых графиках ломаные сливаются друг с другом и выглядят как гладкие
кривые. В решениях на рис. 11 и 13 последовательности ![]() и
и ![]() при
при ![]() заметно изменяют свое
поведение. Это связано с появлением на орбите спутника теневого участка.
Заметим, что с увеличением угловой скорости спутника эффективность
(процессорное время, точность и т. п.) использования системы (1) уменьшается, а
эффективность использования системы (6
заметно изменяют свое
поведение. Это связано с появлением на орбите спутника теневого участка.
Заметим, что с увеличением угловой скорости спутника эффективность
(процессорное время, точность и т. п.) использования системы (1) уменьшается, а
эффективность использования системы (6![]() ) увеличивается.
) увеличивается.
Полученные
результаты показывают, что использование эволюционных уравнений для
исследования движения спутника в режиме одноосной солнечной ориентации
приемлемо по точности. Показано также, что усложнение модели паруса не приводит
к каким-либо новым эффектам в динамике этого режима и выводы работы [1]
сохраняют свою силу.
Данная работа выполнена при финансовой поддержке РФФИ
(грант 02-01-00323).
Литература
1. Лихачев В.Н., Сазонов
В.В., Ульяшин А.И. Режим одноосной солнечной ориентации искусственного спутника
Земли. Препринт ИПМ им. М.В.Келдыша РАН, № 15, 2001.
2. Комаров М.М.,
Сазонов В.В. Расчет сил и моментов светового давления, действующих на астероид
произвольной формы. Астрономический вестник, 1994, т. 28, № 1, с. 21- 30.
3. Сазонов В.В.
Движение астероида относительно центра масс под действием момента сил светового
давления. Астрономический вестник, 1994, т. 28, № 2, с. 95- 107
4. Maude
A.D.
Interpolation – mainly for graph plotters. Computer Journal, 1973, v. 16, № 1,
p. 64-65.
5. Меес Ж.
Астрономические формулы для калькуляторов. М., Мир, 1988.
6. Белецкий В.В.
Движение искусственного спутника относительно центра масс. М., Наука, 1965.
7. Черноусько Ф.Л. О
движении спутника относительно центра масс под действием гравитационных
моментов. Прикладная математика и механика. 1963, т. 27, № 3, с. 474-483.
8. Коробов Н.М.
Теоретико-числовые методы в приближенном анализе. М., Физматгиз, 1963.
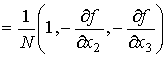 ,
,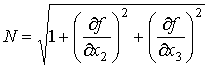 .
.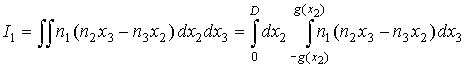 .
.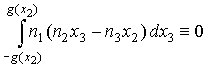 .
.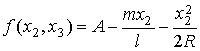 ,
,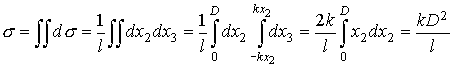 ,
,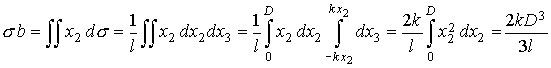 ,
,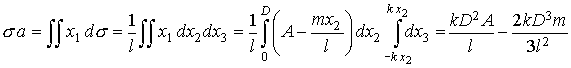 .
.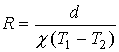 .
.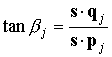 ,
,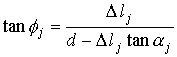 .
.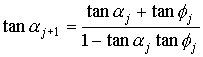 ,
, .
. ,
, ,
, ,
, .
.