ДВУХГРУППОВАЯ МОДЕЛЬ АССИМИЛЯЦИИ МИГРАНТОВ

( THE TWO-GROUP MODEL OF MIGRANT ASSIMILATION PROCESS
Preprint, Inst. Appl. Math., the Russian Academy of Science)

ВВЕДЕНИЕ

Проблема математического прогноза изменения численности народонаселения имеет более чем двухвековую историю и открывается работой Мальтуса [1], в которой было получено уравнение экспоненциального роста человечества в условиях неограниченности ресурса и постоянных коэффициентах рождаемости и смертности: , где  – численность пар, – коэффициент воспроизводства. Уточнение этой модели сделал в 1907г. Лотка [2], введя в нее член, отвечающий конкурентной борьбе за жизненные ресурсы: , где – плотность жизненных мест. Однако то обстоятельство, что модель Лотка достаточно хорошо описывает биоценозы в квазиравновесном состоянии, но плохо согласуется с данными о человеческом обществе, привело к разработке более детального подхода к описанию эволюции людской численности, используя распределение по возрастам для женской части населения . В 1911г. Лотка и Шарп [3] получили интегральное уравнение воспроизводства населения в терминах  при постоянных возрастных коэффициентах рождаемости и смертности (т.н. линейная модель стабильного населения). Позднее [4-7] с разной степенью строгости исследовались частные решения этого уравнения. В дальнейшем этот подход развивался во многих работах по математической демографии (см., напр., [8] и цитируемую там литературу). Подробный обзор математических моделей, применяющихся в демографии, содержится в книге [9]. Существование решений для класса линейных интегральных уравнений воспроизводства, обобщающих модель [3], исследовалось в [10]. В настоящее время существует несколько теорий, пытающихся объяснить закономерности демографических процессов с помощью определенных фундаментальных идей [11-17]. Мы не будем здесь сравнивать различные подходы, поскольку фактического материала еще недостаточно для полноценного анализа. Обратим только внимание на то, что развитие технологий, обусловленных, в свою очередь, удельной мощностью потребления энергии, по-видимому, влияет на рождаемость и смертность, причем одинаковым образом – снижая оба демографических показателя. Для стран Европы характерной величиной является мощность энергопотребления 3.5кВт/чел., по достижении которой рождаемость начинает падать и опускается примерно в 2 раза ниже уровня простого воспроизводства. Возможно, что именно в окрестности этой цифры находится то значение энергии, которое решает проблемы выживания человека в сообществе в отсутствие семьи, но мы не хотели бы делать далеко идущие выводы из этого наблюдения. Оно приведено здесь только для того, чтобы можно было высказать предположение о сохранении таких тенденций в ближайшие десятилетия. В связи с этим представляется особенно важным исследовать эволюцию сообществ, в которых происходит смешивание (или замещение) групп людей с различными коэффициентами воспроизводства. Актуальность этой задачи иллюстрирует следующая

Таблица 1. Распределение стран мира по уровню рождаемости, приходящейся на одну женщину за весь репродуктивный период. 1998г. Данные [18].

Основная особенность представленного распределения в том, что страны с высокой и низкой рождаемостями относятся к разным этническим группам, между которыми происходит не только естественная конкуренция за выживание, но и столь же естественная кооперация, сопровождаемая миграционными потоками и последующими затем смешанными браками. Модели прогнозирования такой ситуации опираются на некоторые точные результаты теории интегральных уравнений типа свертки, которые кратко описываются ниже.

Мы приведем здесь обобщение классического подхода [3, 5, 11] к прогнозированию демографической ситуации (в частности, в России) с использованием метода кинетических уравнений для математического моделирования эволюции возрастных характеристик и численности населения, а также для  решения задач демографии, в которых учитывается разбиение социума на различные группы и страты. В заключение мы приведем результаты прогноза численности населения России к 2050г. в рамках нелинейной модели рождаемости [19-21] с учетом смешанных браков и миграционных потоков для пессимистичного и оптимистичного сценариев развития демографической ситуации. Описанная в [20] модель дополняется в настоящей работе уточнениями, связанными с вариацией приоритетов вступления в смешанные браки. В рамках этой модели исследуется задача о замещающей миграции в России. Начальные условия определяются по данным [22-23].

ТОЧНОЕ РЕШЕНИЕ ДЕМОГРАФИЧЕСКОГО УРАВНЕНИЯ

Получим сначала точное аналитическое решение [21] линейного уравнения воспроизводства для неоднородной популяции со стабильным распределением внутри страт. В этом случае средние коэффициенты рождаемости и смертности для всего населения не постоянны, но, тем не менее, кинетическое уравнение для функции распределения населения по возрастам имеет точное решение. Это расширяет область применимости уравнения Мак-Кендрика – фон Ферстера [5, 11] на случай неоднородных сообществ, если они состоят из нескольких групп однородных стабильных популяций, между которыми может происходить обмен членами в виде линейных потоков. Разделение сообщества на стабильные группы происходит не обязательно по национальному признаку, но, например, по уровню образования, доходам, способу питания и пр.

          Введем следующие обозначения:

 – текущее время;

 – текущий возраст;

 – функция распределения населения -ой группы, как мужчин «M», так и женщин «F», по возрастам  в момент времени , нормированная на полное число людей соответствующей группы;

 – возрастной коэффициент рождаемости, так что  есть число детей («M» или «F»), рождаемых женщинами -ой группы в условиях классической линейной модели рождаемости для случая однородной стабильной популяции;

 – возрастной коэффициент смертности;

– темп миграции населения (человек в год);

– фертильная численность мужчин и женщин -ой группы;

– полная фертильная численность -ой группы;

В [21] показано, что уравнения для функций распределения мужчин и женщин по возрастам могут быть преобразованы так, что соответствующие распределения находятся независимо. Поэтому для краткости не будем пока различать мужчин и женщин, и запишем уравнение для возрастного распределения популяции в целом, чтобы сосредоточить внимание на структуре точного решения. Подчеркнем, что модель рассматривает чисто демографические причины изменения коэффициентов рождаемости и смертности населения в целом за счет того, что меняются доли составляющих его стабильных групп. Эти изменения следует уметь отделять от других, вызываемых изменением условий существования.

Итак, если имеется  стабильных групп и задана матрица переходов  людей возраста  из -ой группы в -ую в единицу времени, а также постоянная матрица  вероятности рождения ребенка в -ой группе от женщины из -ой группы (учитывая возможность последующей групповой самоидентификации детей), то уравнение эволюции для группового распределения  по возрастам в линейном приближении интеграла рождаемости имеет вид

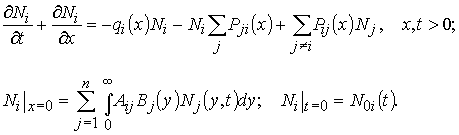
(1)

Введем матрицу

.                         (2)

Тогда в векторной форме система (1) примет вид

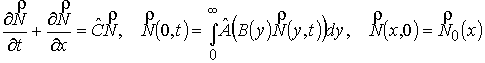.           (3)

Будем рассматривать случай, когда система (3) приводима по Ляпунову, т.е. когда существует такая матрица , что  – постоянная матрица. Тогда преобразование  приводит систему (3) виду

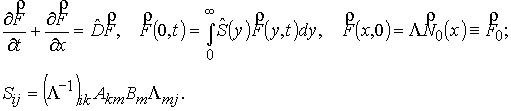               (4)

Обозначим теперь через  невырожденное преобразование, приводящее  к диагональному виду: . (Для простоты считаем, что собственные значения матрицы  простые). Тогда компоненты величин  находятся независимо: . Введем матрицу дожития

.                                                         (5)

Обозначим через  корни уравнения

.                              (6)

Тогда решение системы (4) в случае простых корней имеет вид

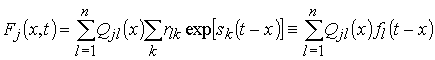,                              (7)

где  – вычеты подынтегрального выражения в обратном преобразовании Лапласа для решения алгебраической системы в образах:

(8)

Выражение для  получается из (7) с учетом того, что  . Для конкретных моделей функций рождаемости можно вычислить значения корней  и соответствующих вычетов в (8). Такое решение описывает суперпозицию демографических волн и мальтусовский рост. Если корни  кратные, то решение (7) представляет собой суперпозицию квазимногочленов по  степени, равной кратности корней.

          В нелинейной модели интегральное уравнение воспроизводства населения в (1) заменяется на следующее [1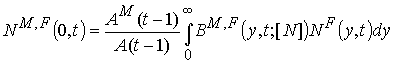9]:

.                                       (9)

Функция рождаемости  учитывает смешанные браки между различными группами, а также включает возможность последующей групповой самоидентификации детей [23].

МОДЕЛЬ АССИМИЛЯЦИИ

Будем считать, что имеются две основные группы: аборигены и пришельцы (т.е. титульное население и этники). В каждой из групп, обозначаемых соответственно индексами 0 и 1, имеется доля (в дальнейшем предполагаемая постоянной) населения  соответственно мужчин и женщин, которые ориентированы на вступление в брак только с представителями своей группы. Кроме того, имеется постоянная доля   тех, кто желает иметь партнера из другой этнической группы, и остальные, которые не имеют таких предпочтений. Пусть  – численность фертильного населения -ой группы,  – полная численность фертильного населения, вычисляемая как интеграл от возрастного распределения населения на интервале от 15 до 55 лет. Для простоты предполагаем, что вероятность рождения ребенка от родителей данного типа пропорциональна вероятности их встречи при условии равномерного распределения населения по регионам проживания. Тогда, например, доля детей категории 0, родившихся от браков родителей с мононациональным предпочтением, равна отношению благоприятных исходов  к общему возможному числу таких исходов  (т.е. рождению ребенка категории 0 в мононациональном браке) . Будем считать, что дети, рожденные в мононациональных браках, с вероятностью 1 идентифицируют себя с тем же этносом. В браке типа  мальчик выбирает национальность 0 с вероятностью , а девочка – с вероятностью , и аналогично в браке типа . Это, конечно, упрощенная модель, поскольку вероятности этнической самоидентификации в смешанных браках зависят не только собственно от национальности родителей, но и от предпочтения родителей при вступлении в брак, а также от окружающих условий, в том числе и политической ситуации. В силу отсутствия достоверных данных мы не будем загромождать модель обилием соответствующих коэффициентов, однако учтем, что в смешанных браках, образованных из подгрупп с предпочтением другой национальности, вероятности выбора национальной группы детьми отличаются от случая брака без группового предпочтения, и равны  для брака типа  и  для брака .  Наконец, возрастные коэффициенты рождаемости в смешанных браках будем считать равными среднему арифметическому от коэффициентов чистых групп , а доли мальчиков и девочек среди родившихся – постоянными, равными соответственно 0.513 и 0.487. Тогда, в частности, для мальчиков категории 0 получаем следующее уравнение рождаемости (для девочек оно аналогично с заменой коэффициента 0.513 на 0.487 и индекса M на F):

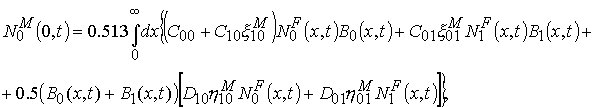
                                                                                                                          (10)

где

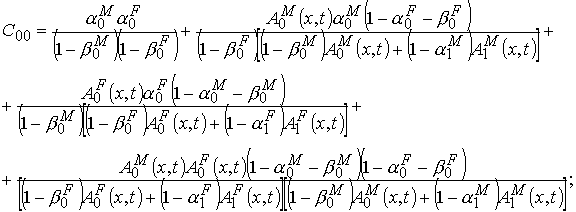
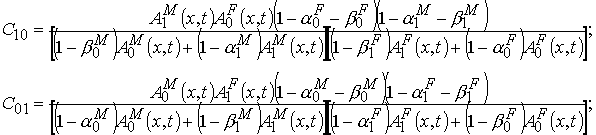
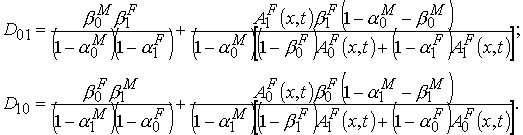
Аналогично записывается уравнение рождаемости мальчиков категории 1, с заменой в соответствующих местах индексов 0 на 1 и коэффициентов  на . Эти уравнения рождаемости дополняются уравнениями эволюции населения -го типа с учетом миграционных потоков , возрастное распределение в которых принято в соответствии с данными [18]:

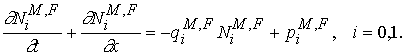
Результаты расчетов по этой модели приведены ниже.

ПРОГНОЗНЫЕ СЦЕНАРИИ

Расчеты по модели [21] показывают, что при сохранении тенденций рождаемости и смертности населения России в целом на уровне 2000г. примерно к 2025г. ожидается рост численности в самой продуктивной когорте (19-24 года). Это приведет к небольшому всплеску рождаемости и, возможно, станет определенным поворотным пунктом в демографическом процессе. Однако даже такой вариант приводит к значительному сокращению населения в долгосрочном прогнозе, поскольку только для простого воспроизводства необходим коэффициент рождаемости, равный  для России 2.15, тогда как в настоящее время он приблизительно равен 1.2. По-видимому, в ближайшее время такая необходимая фертильность достигнута не будет. При сохранении же имеющихся тенденций к 2050г. ожидается катастрофическая диспропорция возрастной пирамиды, которая фактически обращена (поставлена на «вершину»), что означает сильнейшую социально-экономическую напряженность в стране из-за скачкообразного нарастания численности населения в нетрудовом возрасте и уменьшения работающих. Этой проблемой (в социально-экономическом плане, поскольку собственно на демографическую ситуацию повлиять трудно) необходимо заниматься уже сейчас, тем более что характерный «двугорбый» вид сегодняшней возрастной пирамиды означает первую волну кризиса такого рода приблизительно через 15 лет.

Отдельный интерес вызывает прогноз численности населения России в двухгрупповой этнической модели (народы, традиционно принадлежащие к христианской культуре, и остальные – ислам, буддизм, иудаизм). Разумеется, отождествление культуры с принадлежностью к этнической группе не может быть абсолютно точным, и здесь рассматривается как рабочее приближение. По данным, приведенным в [24], можно определить численность населения России, принадлежащего к определенной языковой группе и традиционному вероисповеданию (т.е. культурной группе). Так, в 1989г. из 147.0 млн. чел. официально русских было 119.8 млн. чел. (или 81.5%), к славянской языковой группе принадлежали 126.4 млн. чел. (или 85.9%), к православной культуре – 131.7 млн. чел. (89.6%), к христианской культуре – 132.6 млн. чел. (90.2%). В 1926г. доля представителей христианской культуры в России была 94.1% (84.2 млн.чел.) [18], а в 1999г. – 89.3% (130.1 млн.чел.). В то же время в приближении несмешивающихся сообществ в отсутствие миграции известные данные по коэффициентам рождаемости и смертности среди отдельных этнических групп приводят к тому, что вышеуказанная доля населения в 1999г. была бы 88.5%. Это означает, что при составлении прогноза на долгосрочную перспективу необходимым является не только составление миграционного сценария, но и учет смешанных браков между мигрантами и коренным населением. Описанная выше модель (9-10) позволяет исследовать влияние ассимиляции при различных коэффициентах предпочтений вступления в смешанные (или, напротив, в мононациональные) браки.

Демографический прогноз рассматривается как сочетание, по крайней мере, трех сценариев – рождаемости, смертности и миграции. Применительно к российской ситуации сценарий миграции распадается на три сценария: внутренней миграции (которая не участвует в прогнозе всего населения России), миграции русскоязычного населения между Россией и другими странами ближнего зарубежья, и миграцией между Россией и всем миром. Наконец, четвертый поток, который сегодня не влияет на миграционную ситуацию, но может стать весьма существенным в будущем – миграция в Россию нерусскоязычного населения стран СНГ и из-за пределов территории бывшего СССР.

При расчетах принята гипотеза, что рождаемость в «странах-экспортерах» будет снижаться, экспоненциально приближаясь к минимуму простого воспроизводства, темпы снижения фертильности – 2% в год на протяжении с 1990г. по 2000г. Коэффициент рождаемости (на 1 женщину) в 2000г. составил: в России – 1.17, в Грузии – 1.16, в Армении – 1.30, в Казахстане – 1.86, в Азербайджане – 1.88, в Киргизии – 2.80, в Узбекистане – 2.82, в Таджикистане – 3.70, в Туркменистане – 4.09.

В основу большинства демографических прогнозов положена трехвариантная схема. Сценарии обычно называют «высоким», «средним» и «низким». В данной работе мы рассматриваем также сверхнизкий и сверхвысокий сценарии, которые  призваны ограничить поле возможных значений показателей, так что будущие параметры воспроизводства населения России не выйдут за границы, очерченные этими вариантами. При разработке сценариев мы постарались обосновать гипотезы о динамике рождаемости, смертности и миграции на ближайшие годы, а далее просто экстраполировали сформулированные гипотезы.

В используемой модели прогноза к числу сценарных переменных относятся следующие индикаторы:

Сверхвысокий сценарий рождаемости допускает, что наметившийся в 2001 г. подъем рождаемости – долговременное явление. Тогда уровень рождаемости к 2050 г. достигнет 2,15 рождений на 1 женщину, что обеспечивает положительный естественный прирост. Сверхвысокий вариант означает, что уровень рождаемости в 2012 г. будет совпадать с желаемым числом детей поколений женщин 1965-1974 годов рождения (1,71) согласно всероссийской микропереписи 1994 года.

В период после 2050 г. предполагается, что рост суммарного коэффициента рождаемости продолжится и к 2100 г. поднимется до 2,5 рождений.

Сверхнизкий сценарий предполагает сохранение тенденции 1993–1999 г. примерно до 2010 г., когда, при этом предположении, уровень рождаемости сократится до 0,95 рождений.

Рисунок 1. Сценарии рождаемости в России после 2000г.

Абсолютный минимум коэффициента суммарной рождаемости в городском или сельском населении регионов России в 1999 г. был 0,87, а 2001 г. - 0,96. Выбранный уровень 0,95 рождений на женщину – это минимальный уровень из фиксировавшихся в одном регионе (в данном случае – в Санкт-Петербурге) в течение нескольких лет. Уровень рождаемости 0,95 означает, что 30% женщин вообще бездетны, причем для 25% отказ от рождения детей – сознательное решение. Согласно данному сценарию такой уровень сохранится на весь период прогноза.

Из тех же соображений выбираются сценарии изменения среднего возраста матери при рождении ребенка. Согласно сверхвысокому сценарию он к 2025 г. возрастет до 30,6 года и стабилизируется, а согласно сверхнизкому – к 2006 г. сократиться до 25 лет, что соответствует уровню коэффициента суммарной рождаемости 0,95, а далее меняться не будет.

Рассмотрим теперь сценарии изменения смертности. Сверхнизкий сценарий предполагает, что в России в XXI веке продолжительность жизни будет снижаться с тем же темпом, что в 1965-1980 гг. до уровня, когда разрыв продолжительности жизни мужчин и женщин достигнет 15 лет (примерно в 2008 г.). При этом продолжительность жизни мужчин снизится до 57 лет и станет ниже, чем в 1955 г.

В дальнейшем рост смертности взрослых продолжится, но очень медленно, а смертность детей продолжит свое снижение, так что продолжительность жизни меняться не будет. В конце XXI века продолжительность жизни мужчин составит 57 лет, женщин – 71,5 лет, а коэффициент младенческой смертности сократится до 1,7 на 1000 новорожденных.

Социальные различия по коэффициентам смертности связаны главным образом с тем, что факторы риска неравномерно распределены по социальным группам; этнические различия реализуются в основном через различия в уровне образования, которые являются наиболее значимыми для продолжительности жизни.

Рисунок 2. Сценарии изменения ожидаемой продолжительности жизни мужчин.

Сверхвысокий сценарий изменения продолжительности жизни предполагает, что в ближайшие годы произойдет ее рост до уровня 1994-1998 гг., а затем продолжительность жизни для мужчин и женщин суммарно будет расти тем же темпом, что и в странах ЕС в 1970-1999 годах (на 0,23-0,24 года за 1 год). Предполагается, что темп роста продолжительности жизни у мужчин будет несколько выше, а у женщин – несколько ниже, чем в странах ЕС, с тем, чтобы к 2050 г. разрыв в продолжительности жизни между мужчинами и женщинами не превосходил 10 лет. В таком сценарии к 2100г. продолжительность жизни составит более 87 лет у мужчин и более 95 – у женщин. Коэффициент младенческой смертности сократится до 0,4 на 1000 новорожденных.

Сценарии миграции. Три основных потока определяют в настоящее время российскую международную миграцию:

-       миграция в Россию русскоязычного населения из стран СНГ и Балтии;

-       миграция из России в страны СНГ и Балтии;

-       миграция из России в страны дальнего зарубежья.

В настоящее время Россия формально практически не принимает иных категорий мигрантов. Однако нельзя исключить из рассмотрения нелегальную миграцию, которая может существенно изменить фактическое положение дел. Поэтому важной задачей является установление  величины замещающей миграции, при которой полностью компенсируется убыль населения. Кроме того, при долгосрочных прогнозах необходимо учитывать различную фертильность этнических групп, а также процесс образования смешанных браков, дети от которых с некоторой долей вероятности принадлежат к одной из групп (жесткая модель ассимиляции). Соответствующая модель и была построена выше.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

          Поскольку сокращение населения России составляет в среднем 770 тыс. чел. в год, то без учета ассимиляции естественно считать, что миграционный поток порядка 800 тыс. в год достаточен для возмещения естественной убыли населения. Однако при долгосрочных расчетах нельзя считать, что мигранты мгновенно становятся этнически неотличимы от коренного населения. Это может дать определенные преимущества в долгосрочном прогнозе, т.к. средний коэффициент рождаемости будет повышен. В то же время в модели независимого сосуществования двух групп населения приток пришельцев с более высокой рождаемостью эффективно понизит долю коренного населения, т.е. будет способствовать еще более быстрому его сокращению. Учет же смешанных браков имеет обратный эффект – повышается фертильность коренного этноса за счет примыкания к нему части пришельцев. Для иллюстрации влияния этих процессов приведем несколько модельных расчетов при начальной доле коренного населения 90%.

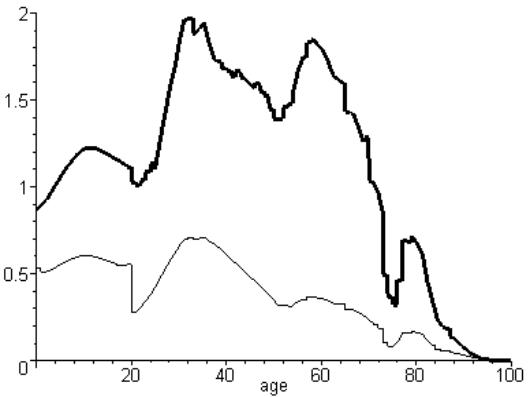
Рисунок 3. Распределение аборигенов (жирная кривая) и пришельцев (тонкая кривая) к 2020г. Миграция представителей второй группы (т.е. не репатриация) составляет 100 тыс. чел. (находится на уровне миграции нерусскоязычного населения в 1998г.). Коэффициенты предпочтений (согласно обозначениям (9-10)) следующие:

смертность предполагается одинаковой среди обеих категорий населения.

          Ниже приведен график изменения полной численности, когда фертильность пришельцев равна 4.1.

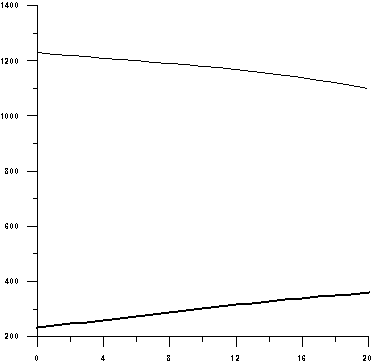
Рисунок 4. Численности населения (сто тыс. чел.): M0 (убывает), M1 (растет), M0+M1=146млн. чел. (постоянна).

          В следующем варианте расчета пришельцы имеют более высокий коэффициент образования мононациональных браков, что приводит при тех же условиях, что и выше, к росту населения в целом.

Рисунок 5. Распределение аборигенов (жирная кривая) и пришельцев (тонкая кривая) к 2020г. Коэффициенты предпочтений:

          Динамика численности обеих групп населения приведена ниже:

Численность, 100 тыс. чел.

   годы

Рисунок 6. Для расчета, представленного на Рис.5, население в целом растет примерно со скоростью 400тыс. в год.

          Эти расчеты показывают, что модель довольно чувствительна к параметрам ассимиляции мигрантов. Если рассматривать ситуацию по среднему сценарию, когда имеется постоянный поток мигрантов на уровне 100 тыс. чел. в год с реальной динамикой фертильности, снижающейся за 20 лет со среднего значения 3.5 до 2.1 и далее остающейся постоянной, то при выбранных на Рис. 3 параметрах будет снижение общей численности со скоростью 550 тыс. чел. в год с замедлением по 8 тыс. чел. в год.

          Автор приносит глубокую благодарность проф. С.П. Капице за внимание к работе и ценные указания.

ЛИТЕРАТУРА

1. Malthus T.R. An Essay on the Principle of Population. Printed for J. Johnson in St. Paul’s Churchyard, London, 1798.

2. Lotka A.J. Model of growth of material aggregates // Am. J. of Sc. 1907. V.24. P. 199-216.

3. Sharpe F.R., Lotka A.J. A problem in age-distribution // Phil. Mag., 1911. V.21. P. 435-438.

4. Lotka A. J., Dublin L.I. On the true rate of natural increase // J. American Stat. Association. 1925. V. 20. №150.

5. McKendrick A.G. Applications of Mathematics to Medical Problems // proc. Edinburg Math. Soc. 1926. V. 44. No 1. P. 98-130.

6. Feller W. On the integral equation of renewal theory // Annals of Mathematical Statistics. 1941. V.12. P. 243-267.

7. Lotka A. J. Elements of mathematical biology. N.-Y.: Dover, 1956.

8. Моран П. Статистические процессы эволюционной теории. М.: Наука, 1973.

9. Pollard J.H. Mathematical models for the growth of human populations. Cambridge University press. London, N.-Y., Melbourne. 1973.

10. Хмелевский Ю.И. Самовоспроизводящиеся системы. Математическая теория. М.: Наука, 1991.

11. Forster H. von. Some Remark on Changing Population // The Kinetics of Cellular Proliferations. 1959. P. 382-407.

12. Стешенко В.С. Демография в современном мире. М.: 1979.

13. Вишневский А. Г. Воспроизводство населения и общество. М.: 1982.

14. Лискин Л. Планирование семьи: международная перспектива // Планирование семьи.    1996. №2. С.

15. Капица С.П., Курдюмов С.П., Малинецкий Г.Г. Синергетика и прогнозы будущего. М.: Наука, 1997.

16. Капица С. П. Общая теория роста человечества. М.: Наука, 1999.

17. Новая парадигма развития России. Москва – Иркутск: «Academia», 2000.

18. Население России. 2000. Под ред. А.Г. Вишневского. М.: ЦДЭЧ, 2001.

19. Орлов Ю.Н., Суслин В.М. Кинетический подход к описанию нелинейных демографических процессов. Препринт ИПМ им. М.В. Келдыша РАН, №47, 2001.

20. Орлов Ю.Н., Суслин В.М. Кинетические уравнения для нестационарных демографических моделей. Препринт ИПМ им. М.В. Келдыша РАН, №53, 2001.

21. Орлов Ю.Н., Суслин В.М. Кинетические уравнения для некоторых моделей демографии. // Мат. Мод. 2002. (в печати).

22. Российский статистический ежегодник. М.: Госкомстат, 1999.

23. Комарова О.Д. Население России сквозь призму этнических процессов. В сб. «Мир России».1999. Т. VIII. №4. С.71-80.

24. Школьников В., Андреев Е., Малеева Т. Неравенство и смертность в России. М.: Сигналъ, 2000.