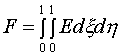,
Вариационные методы расчета двумерных сеток при решении нестационарных задач
|
Настоящая работа является
непосредственным продолжением и развитием [1], в которой были рассмотрены
вопросы применения для построения двумерных сеток некоторых вариационных
функционалов универсального характера. Они позволяют получить любую
невырожденную сетку при соответствующем задании входящих в них параметров. При
этом остались без обсуждения вопросы построения сеток в ходе расчета
нестационарных задач с подвижными границами расчетных областей. Между тем
расчет подвижных сеток имеет свою специфику и предъявляет дополнительные
требования к алгоритмам их построения. Это отмечалось неоднократно различными
авторами. Не претендуя ни в какой мере на обзорный характер настоящей работы,
упомянем [2]-[3], на которые придется ссылаться по существу обсуждаемых вопросов.
Если речь идет о задаче построения сетки в заданной области с
фиксированными границами (для краткости будем говорить о стационарной задаче,
хотя это не совсем точно), то у исполнителя имеется возможность предпринять,
если нужно, не одну, а несколько попыток расчета сетки. Знакомясь (например,
визуально) с их результатами (даже на уровне «нравится - не нравится») и имея определенный арсенал
разработанных методов построения сеток, исполнитель может надеяться на благополучный
исход поисков приемлемой сетки.
Такая ситуация совершенно неприемлема при
решении нестационарных задач с подвижными границами, где сетку нужно строить на
каждом шаге по времени, а число этих шагов в современных задачах и при
современных вычислительных системах может достигать сотен тысяч и миллионов.
Особая трудность состоит еще и в том, что
деформацию подвижных границ зачастую трудно предвидеть заранее. А если и можно
предвидеть (например, с помощью предварительных «грубых» расчетов), то удачно
принятое в начальный момент времени решение о выборе алгоритма построения сеток
может привести к нежелательному или даже катастрофическому («авостному»)
развитию событий в расчете.
Это влечет за собой необходимость что-то
менять. Даже если новое решение сразу окажется удачным, сам процесс перехода
осложняется из-за больших скоростей узлов сетки, перестраивающейся с одних
уравнений на другие (даже, если это одни и те же уравнения, но отличающиеся
управляющимися параметрами).
Еще одна аналогичная трудность, связанная
с большими скоростями движения узлов сетки, порождается тем, что итерационные
процессы для ее построения, как правило, нереально (да и практически
нецелесообразно) доводить до нужного уровня сходимости, т.е. до получения
достаточно малых значений невязок решаемых уравнений. Между тем скорость узлов
сетки в используемых алгоритмах напрямую или опосредованно связана именно с
величинами невязок. Поэтому, в случае, если в решаемой основной нестационарной
задаче по какой-то причине резко уменьшается величина шага по времени (неважно,
происходит это по каким-то содержательным физическим причинам или в этом
повинна сама сетка), происходит резкое увеличение скоростей узлов сетки и далее
«цепная реакция» неприятностей, приводящих решение к печальному исходу.
«Лечение» описанных трудностей в
настоящее время осуществляется разными «фельдшерскими» методами (это «удачное»
название фигурирует в предисловии к монографии [2]). Предлагаемый подход должен
решить, по крайней мере, описанные проблемы, связанные с регулированием скоростей
движения узлов сетки.
В ходе изложения будет прослеживаться
также стремление по возможности автоматизировать назначение управляющих
параметров.
Для упрощения описания математического
содержания алгоритмов построения сеток избран простейший вариант регулярной
сетки, упорядоченной по двум индексам, применительно к изолированной области,
которая рассматривается как четырехугольник с криволинейными границами.
Поскольку описываемые алгоритмы носят локальный характер, очевидно, что они
переносятся на произвольную «карту», составленную из таких областей.
§ 1. Вариационные функционалы.
В упомянутом случае изолированной области
Ω, рассматриваемой как
четырехугольник с криволинейными границами, задача построения сетки может быть
осуществлена как дискретная реализация невырожденного отображения единичного
квадрата Q: (0£x£1, 0£h£1) на эту область W плоскости пространственных переменных (х,у).
В
[4] для этой цели предложено использовать функционал вида
(1.1) ,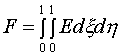
в котором
подынтегральная функция Е, названная
плотностью энергии отображения, задается формулой
(1.2)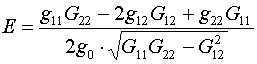 
.
Элементы симметричной и
положительно определенной матрицы
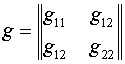
представляют метрические
параметры отображения:
(1.3)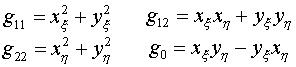 
Невырожденность
отображения и положительная определенность матрицы g взаимосвязаны ввиду очевидного тождества:
(1.4) 
.
- элементы
аналогичной симметричной и положительно определенной матрицы G, заданной в каждой точке единичного
параметрического квадрата Q.
Функционал минимизируется на классе
функций 
, 
, являющихся гладким продолжением внутрь квадрата Q заданных на его границе функций хг,уг. Эти последние осуществляют гладкое взаимно
однозначное отображение границы квадрата Q на границу области W, в которой должна быть построена сетка.
Легко доказывается, что Е³1.
Доказательство представлено и в [4] и непосредственной выкладкой в
[1] на стр.9-10. Следовательно, абсолютный минимум функционала 
.
Пусть 
, 
- произвольное
гладкое невырожденное отображение квадрата Q на область W. Положим
(1.5) 
, 
, 
Тогда, в силу тождества
(1.4), получаем Еº1, F=1. Следовательно, это
произвольное отображение реализуется как решение задачи минимизации функционала
(1.1)-(1.2) с матрицей (1.5).
Удобно ввести матрицу 
с нормированными
элементами:
(1.6) 
, 
, 
Нормирующий коэффициент G0 определим формулой:
(1.7) 
.
Рассмотрим вариационный
функционал, отличающийся от (1.1) только тем, что в качестве области
интегрирования вместо параметрического единичного квадрата Q используется сама физическая область W:
(1.8) 
.
Поскольку 
, для плотности энергии отображения E* получаем:
(1.9)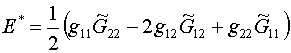 
Таким образом, функционал (1.8)-(1.9)
отличается от (1.1)-(1.2) только отсутствием в знаменателе якобиана
отображения. Как отмечалось в [1], такое решение было принято авторами работы [5], в
которой (см. стр. 1034) был предложен функционал (1.8)-(1.9), сознательно,
чтобы упростить проблему решения возникающих уравнений Эйлера-Лагранжа.
Если сделать назначение метрических параметров
G согласно (1.5), то минимизация
функционала (1.8)-(1.9) приводит к абсолютному минимуму F*, равному площади области W.
Следовательно, посредством назначения
(1.5) функционал (1.8)-(1.9) тоже воспроизводит любое отображение. Таким
образом, функционалы F и F* можно считать универсальными
генераторами сеток.
В частности, если полагать
(1.10) 
, 
,
то реализуются
отображения, обычно называемые гармоническими, как и соответствующие им сетки.
В функционале F тогда
плотность энергии отображения 
, а в функционале F* величина
. В качестве вариационных уравнений Эйлера-Лагранжа для
функционала F* в этом
частном случае (1.10) очевидно получаются уравнения Лапласа
(1.11) 
, 
.
Для функционала F после некоторых преобразований (см., напр., [3], стр. 7-8) в качестве
следствия вариационных уравнений получаются обращенные уравнения Лапласа:
(1.12) 
Принято считать, что применение уравнений
(1.12) в практике расчета сеток восходит к работе [6].
Для уравнений (1.11) автором построен
пример, в котором для области простой формы получается вырожденное отображение
(см., напр., [1], стр. 8). Ранее более громоздкий пример был описан в [3], стр.
5-6. Поэтому при произвольном назначении матрицы 
функционал
(1.8)-(1.9) невырожденности отображения не гарантирует.
В свою очередь для функционала
(1.1)-(1.2) в дискретной форме в работе [7] доказано, что он дает невырожденное
отображение при произвольных положительно определенных матрицах 
. Это его несомненное преимущество. Однако и функционал
(1.8)-(1.9) имеет ряд других преимуществ по сравнению с (1.1)-(1.2). Поэтому
считаем целесообразным в дальнейшем рассматривать оба этих функционала.
Для наглядности будем называть
(1.1)-(1.2) функционалом с якобианом, а (1.8)-(1.9) – функционалом без
якобиана.
Вариационные уравнения Эйлера-Лагранжа
для функционала без якобиана имеют вид:
(1.13)
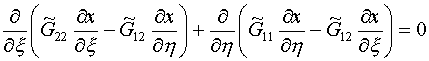
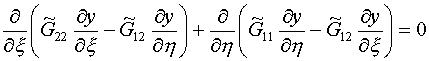
Назовем их системой S*[G]. Она является линейной при заданных 
. Аналогичная, но гораздо более громоздкая нелинейная система
уравнений получается для функционала с якобианом. В качестве ее следствия в
работе [7] на стр. 49 получены нелинейные уравнения, обобщающие (1.12) на случай
произвольных матриц 
. Для полноты изложения приведем их вид в наших обозначениях:
(1.14) 
,
где
, 
, 
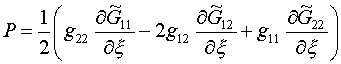
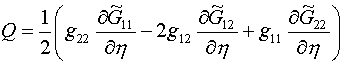
Назовем их системой S[G].
Интересно отметить, что по своей
структуре они похожи на уравнения, приведенные в [3] на стр. 8, которые
получаются после введения дополнительной замены переменных в уравнениях (1.12).
Относительная простота и линейность
вариационных уравнений (1.13) по сравнению с (1.14) является существенным
преимуществом функционала без якобиана.
§ 2. Нестационарная задача для сетки.
Перейдем теперь к вопросу о
конструировании сеток при расчетах нестационарных задач с подвижными границами.
Пусть N – номер очередного шага по времени t, 
- величина шага по
временной координате t, 
- сетка, полученная
на предыдущем шаге. Вектор 
содержит две
пространственные координаты (х,у) и,
в дискретном варианте, о котором речь пойдет в § 3, значения этих координат во
всех узлах расчетной сетки.
Для определенности пусть рассматривается
некоторая газодинамическая задача без конкретизации ее содержания. В
соответствии с общепринятой схемой расщепления расчет очередного шага состоит
из нескольких этапов.
На I этапе осуществляется движение
границ расчетных областей. Оно обусловлено теми или иными физическими законами
и конкретным распределением физических величин в окрестности границы на текущий
момент времени. Абстрагируясь от них, будем предполагать, что
последовательности 
определяют положение границ на предыдущем шаге и превращаются
в последовательности 
для очередного
рассчитываемого шага. Очевидно можно полагать, что
(2.1) 
Условимся подразумевать,
что (2.1) и аналогичные равенства в дальнейшем выполнены для каждой из
координат вектора 
.
По соображениям, изложенным в [8], в
качестве II этапа расчета целесообразно вычислить величины сдвига граничных узлов
сетки
(2.2)
,
затем по
интерполяционным формулам рассчитать значения сдвига 
для внутренних узлов
сетки и получить начальное приближение
(2.3)
для узлов сетки N-го
шага. Граничные узлы при этом занимают правильное положение, которое при
дальнейшем расчете сетки текущего шага изменяться не будет.
Обсуждение интерполяционных формул
отложим до § 6.
Из них будет очевидно, что
(2.4)
Перейдем теперь к III этапу
– назначению матриц коэффициентов G для описанных выше
функционалов.
Предлагается использовать для этого
метрические параметры сетки, полученной на предыдущем шаге по времени:
(2.5)
.
Как описано выше в § 1,
такое назначение будет воспроизводить
сетку предыдущего шага, т.е.
(2.6)
для функционала
(1.1)-(1.2),
для функционала
(1.8)-(1.9).
В силу (2.4), можно полагать,
что
(2.7)
и аналогично для второго
функционала.
Конечно, строго говоря, при этом
необходимо формулировать требования, которые нужно накладывать на гладкость
границ области, гладкость текущей сетки и т.п. Мы их опускаем, тем более, что
практически эти требования необходимо формулировать для дискретного варианта,
который будет описан позже в § 3.
При хорошей обусловленности систем
уравнений можно было бы полагать также, что искомые сетки 
, определяемые из уравнений:
или 
, удовлетворяют
условию:
(2.8)
.
Это полностью решало бы проблему
конструирования сеток при расчете нестационарных задач. К сожалению, на
практике дело обстоит хуже. При назначении (2.5) рассматриваемые функционалы
обнаруживают «равнодушие» к судьбе конструируемой сетки, поскольку для любой сетки значение функционала близко
к абсолютному минимуму, отличаясь от него лишь на величину порядка 
из-за отклонения
граничных условий (2.1). При отсутствии обратной связи ухудшение качества сетки
постепенно может приводить к необратимым последствиям, вплоть до «авостных».
Поэтому назначение (2.5) необходимо корректировать.
В работе [1] при расчете стационарных сеток
(для областей с фиксированными границами) рассматривался один из возможных
вариантов такой корректировки метрических параметров (см.[1],
стр.25):
(2.9) 
Она гарантирует
выполнение условия 
для 
, 
. Оказалось, что, в силу нормировки (1.6)-(1.7), формулы
(2.9) эквивалентны таким:
, 
, 
,
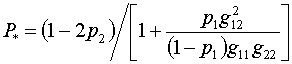
При условии сохранения хорошей
обусловленности для корректированной системы уравнений тоже можно надеяться на выполнение
условия (2.8), если 
. От вычурного вида формулы для 
можно отказаться и в
качестве корректировки принять:
(2.10) 
, 
, 
,
где p>0 –
управляющий параметр. Эти формулы представляют, конечно, лишь один из возможных
вариантов корректировки. Этот вариант отражает стремление «приблизить» сетку к
«квазиортогональной».
Однако более эффективным оказался вариант
корректировки самого функционала. Для функционала (1.1)-(1.2) с якобианом
предлагается:
(2.11)
,
Для функционала
(1.8)-(1.9) без якобиана:
(2.12) 
, 
Для реализации (2.11)
или (2.12) достаточно изменить формулы нормировки (1.6)-(1.7):
(2.13)
, 
, 
,
сохранив 
и назначение (2.5)
: 
.
Интересно отметить, что при назначении
(1.5) корректирующие функционалы 
и 
приобретают вид
соответственно:
(2.14) 
, 
Первый из них
рассматривался в работе [9] в качестве «функционала ортогональности», а второй –
автором в работе [10]
– в качестве одного из вариантов для получения
«квазиортогональных» сеток. В обоих случаях их прямое использование для расчета
сеток обнаружило некорректность, которую пришлось преодолевать подключением
дополнительных «регуляризующих» средств. Предлагаемый вариант их реализации в
качестве такого средства использует «опорные» функционалы (1.1)-(1.2) или
(1.8)-(1.9), к которым они подключаются с
коэффициентом 
.
Возникает также общее предложение:
использовать для корректировки опорных функционалов произвольные «хорошие
функционалы» со своими управляющими коэффициентами 
. Термин «хорошие
функционалы» предполагает обеспечение
хорошей обусловленности для корректированного функционала и целенаправленное
воздействие на рассчитываемую сетку для обеспечения ее качества, требуемого при
решении основной задачи. Обратим внимание на необходимость согласования
размерности используемых функционалов по переменным (х,у).
Отметим также, что с точки зрения
размерности по t
представляется целесообразным вместо управляющих коэффициентов 
задавать для
корректирующих функционалов весовые коэффициенты формулами:
(2.15)
, где 
В частности, например, подключение
функционала, реализующего гармонические сетки, с коэффициентом 
достигается заменой
(2.13) на следующие формулы:
,
(2.16)
.
§ 3. Дискретизация.
Следующим этапом работы по созданию
алгоритма расчета сеток является переход от дифференциальной формы
вариационного функционала к дискретной. Простейшим и экономным способом его
реализации была бы замена дифференциальных выражений разностными в уравнениях
Эйлера-Лагранжа (1.13) для функционала (1.8)-(1.9) и следствий из таких
уравнений (1.14) для функционала (1.1)-(1.2). Однако, как уже отмечалось,
например, в [1], мнение о том, что этот этап сводится к механической замене
дифференциальных выражений разностными, является ошибочным. При такой замене
могут быть утеряны важные свойства дифференциальной модели.
Для рассматриваемой задачи крайне важным
является обеспечение для дискретной
модели условий (2.6), т.е. тождественного равенства нулю невязок
разностных уравнений, возникающих после назначения (2.5) коэффициентов G, при
подстановке в эти уравнения сетки
предыдущего временного шага. Нарушение этого требования в надежде, что
погрешности аппроксимации окажутся достаточно малыми, может приводить к
неконтролируемым значениям для скоростей узлов сетки. Гарантию достижения этой
цели дает тщательная реализация специальной процедуры, известной под названием
вариационного
барьерного метода.
Впервые она была изложена в работе [11] для
расчета гармонических сеток, хорошо известна и многократно описана.
Изложение окончательного результата,
имеющего непосредственное отношение к рассматриваемым функционалам, в нужных
нам обозначениях представлено в [1] на стр. 16-17. Для полноты
изложения и некоторых дополнительных замечаний целесообразно его повторить.
Дискретный аналог функционала (1.1)-(1.2)
записывается в виде:
(3.1)
,
где суммирование
производится по всем ячейкам сетки расчетной области. Обычно им присваивают
«полуцелые» номера (
). Нормирующий коэффициент на число ячеек сетки в формуле
(3.1) опущен как не влияющий на дальнейший результат.
Разностные уравнения для узла сетки с
номером (n,m) имеют
вид:
(3.2) 
, 
Для их получения достаточно рассмотреть
«шаблон», в котором участвуют 4 ячейки, примыкающие к этому узлу. Он изображен
на рис.1. Для упрощения описания расчетных формул входящим в него узлам
присвоены более простые номера, а четырем ячейкам – номера 
. Тогда уравнения (3.2) можно записать так:
(3.3)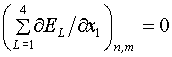 
, 
.
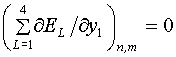В свою очередь, каждую
из ячеек L, вершины которой имеют
номера (1,2L,2L+1,2L+2), разделим
на две пары треугольников, проведя ее диагонали (1,2L+1) и (2L,2L+2). Образующимся треугольникам присвоим номера 
, как на рис. 2, относя их к соответствующим вершинам ячейки.
Вершинам треугольника с номером k присвоим свои номера k-1, k,
k+1 (см.
рис.3а). Доопределение недостающих номеров очевидно и останавливаться на нем не
будем. Полагаем далее:
(3.4)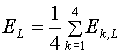 
, 
(3.5)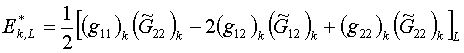 
Здесь и в дальнейшем индекс (k,L) означает, что соответствующая величина
определяется в треугольнике с номером k ячейки с номером L.
Отметим весьма важное
обстоятельство. Описываемая конструкция интегральной суммы (3.1) предполагает,
что
(3.6) 
для всех k,L.
Как будет следовать из
дальнейшего, величины 
представляют
удвоенные площади соответствующих треугольников, и тогда требование (3.6)
предполагает выпуклость всех ячеек сетки. Практика расчетов требует ослабления
этого требования, и этот вопрос будет обсуждаться в §5. Пока же будем
предполагать условия (3.6) выполненными.
Для вычисления метрических параметров в
треугольнике с номером k
применяются формулы, которые после введения обозначений:
(3.7)
, 
, 
имеют вид:
(3.8)
, 
, 
Для них тождественно выполнен разностный аналог
формулы (1.4):
(3.9)
Кроме того, имеют место
равенства:
(3.10)
, 
,
где 
- угол, образованный
отрезками сетки в вершине с номером k ячейки L (см.
рис.3б).
Величины 
определяются такими
же формулами с использованием координат узлов сетки на предыдущем шаге по
времени, а затем подвергаются корректировке, например, по формулам (2.16).
Для функционала (1.8)-(1.9) без якобиана
разностные уравнения (3.3) в узле 1 шаблона могут быть записаны в виде:
(3.11)
,
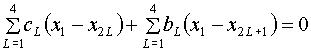
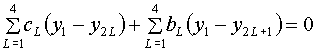где коэффициенты 
вычисляются по
следующим формулам:
(3.12)
(3.13)
Обратим внимание, что в
этих формулах отсутствуют величины с
индексом (3,L),
отвечающие треугольнику с номером k=3. Это
не случайно, поскольку «вклад» этого треугольника в сумму (3.1) не будет
изменяться при вариации узла 
. Поэтому расчет треугольника с номером k=3 можно не производить.
Отметим далее, что в случае 
присутствие в
формулах (3.12)-(3.13) отрицательных коэффициентов является обычным явлением.
Следовательно, для получаемой системы линейных уравнений принцип максимума не
выполняется. Это еще одна из причин тщательного подхода к конструированию
системы разностных уравнений на основе положительно определенной квадратичной
формы в случае работы с функционалом без якобиана.
При получении коэффициентов 
для нормировки
используются величины 
. В силу формулы (3.10) они прямо зависят от значений величин
для углов, образуемых
отрезками сетки предыдущего шага по времени во всех ее узлах. Следовательно,
конструируемая система уравнений «реагирует» на малые значения любого из этих
углов или на их приближение к значению 
, т.е. должна препятствовать вырождению соответствующих
ячеек. Это существенный аргумент в пользу усложнения алгоритма, связанного с
разрезанием ячейки на треугольники.
Если этого не делать, в формулах (3.12)-(3.13) будут участвовать лишь некоторые
«усредненные» значения 
и площадь всей ячейки
сетки, «смазывая» эффект ее вырождения.
Заслуживает специально быть отмеченным
случай 
. Тогда 
, и система (3.11)
превращается в более простую:
(3.14)
, 
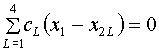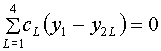
Более того, из (3.11)
будем иметь
(3.15)
.
Следовательно, такая
система будет удовлетворять принципу максимума.
При этом в формулах (1.6) 
, 
.
Следовательно, разрезание ячеек на
треугольники становится ненужным.
Поэтому так привлекательны для построения
сеток в областях с фиксированными границами алгоритмы конструирования
«квазиортогональных» сеток. К сожалению, в случае нестационарной задачи
назначение 
противоречит
изложенной в § 2 идеологии, допускающей только вариации коэффициентов 
. Поэтому оно обсуждаться не будет, хотя и не закрывает
возможности использования таких алгоритмов для расчета стационарных сеток.
Обратимся теперь к функционалу
(1.1)-(1.2) с якобианом в знаменателе. Соответствующая ему система сеточных
уравнений (3.3) будет нелинейной из-за наличия знаменателя в формуле (3.4) и
имеет существенно более громоздкий вид. Она описана в работе [4] вместе
с итерационным процессом. Соответствующие расчетные формулы будут представлены
в следующем параграфе.
§ 4. Итерационные процессы.
Начнем с обсуждения метода
решения системы разностных уравнений (3.11) для функционала без якобиана.
Заметим, что имеется хорошее начальное приближение 
для искомого решения,
определяемое формулой (2.3), и, в силу (2.4) и (2.8), отличающееся от искомого
решения на величины 
. Это обстоятельство и сама структура уравнений (3.11)
вызывают естественное желание воспользоваться простейшим итерационным
процессом:
(4.1)
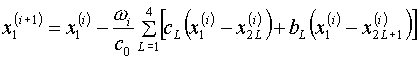
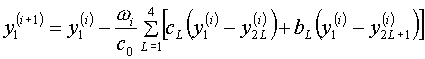
В этих формулах коэффициенты 
на итерациях не
меняются.
(4.2)
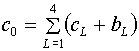
Управляющий параметр 
может меняться от
итерации к итерации. Вопрос о его назначении будет рассмотрен ниже. Для
обеспечения численной устойчивости итерационного процесса 0<w0<1.
Для функционала (1.1)-(1.2)
с якобианом, в соответствии с изложенным в конце § 3, расчетные формулы
итерационного процесса имеют вид:
(4.3)
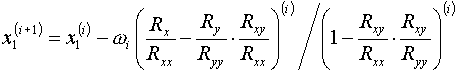
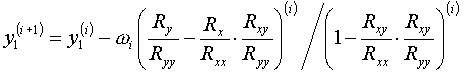
В этих формулах 
представляют
соответствующие первые и вторые производные разностного функционала 
для центральной точки
шаблона, описанного
ранее в § 3, вычисленного на сетке, полученной на предыдущей итерации. Он использует так же значения матрицы
коэффициентов 
, вычисленные с
помощью сетки предыдущего шага по
времени и с учетом корректировки (2.16), которые остаются неизменными на всех
итерациях. Каждая из величин 
представляет сумму 12
слагаемых, отвечающих в каждой из четырех ячеек с номерами 
трем треугольникам с
номерами k=1,2,4. Получение
расчетных формул для этих величин представляет кропотливое, но несложное
упражнение по дифференцированию, и мы их приводить не будем. Тем более, что эти
формулы будут различными для треугольников k=1,2,4
из-за различной роли в них узла (x1,y1).
С точки зрения практической
организации вычислений возможны два варианта. Первый состоит в том, что
отбираются все величины, входящие в шаблон отдельного внутреннего узла сетки, и
вычисления проводятся полностью до получения результата (x1,y1)(i+1). Второй вариант предусматривает специальный массив для
накапливания величин 
посредством
последовательной обработки всех ячеек сетки, как это описывалось в работах [11]
и [4]. С точки зрения объема вычислительной работы второй вариант
предпочтительнее. Однако с точки зрения многопроцессорных вычислительных систем
это далеко не очевидно и требует проверки в численном эксперименте.
В § 3 было избрано
изложение, опирающееся на первый из указанных вариантов, прежде всего, для
того, чтобы представить суть алгоритма и получить структуру коэффициентов
(3.12)-(3.13) в уравнениях (3.11).
Как отмечалось в работах
[11], [4] и других, итерационный процесс (4.3) представляет вариант метода
Ньютона-Рафсона, отличающийся от стандартного тем, что в расчете участвует
только блочная диагональ матрицы вторых производных. Благодаря этому удается
обойтись явными итерациями, избежав решения сложной нелинейной системы
уравнений. Такой процесс применялся для расчета гармонических сеток.
Заслуживает быть отмеченным
следующее обстоятельство. Поскольку для функционала (1.8)-(1.9) без якобиана
будем иметь:
(4.9) 
, 
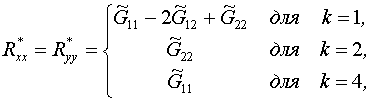
формулы (4.3) принимают вид:
(4.10)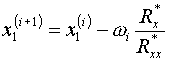 
, 
Легко убедиться, что с учетом (4.9) формулы (4.10) тождественны
формулам (4.1), поскольку 
.
Следовательно, итерационный
процесс (4.1)тоже представляет аналогичный вариант метода Ньютона-Рафсона
применительно к функционалу без якобиана, представляющему в дискретной форме
положительно определенную квадратичную форму от координат узлов искомой сетки.
Попутно отметим, что сумма с0 коэффициентов в формуле (4.2)
положительна, поскольку в соответствии с (4.9) каждый из 12 треугольников дает
положительный «вклад» в нее. В самом деле, 
, поскольку 
.
Теперь обратимся к вопросу
о назначении управляющего параметра 
. Специфика рассматриваемой задачи состоит в том, что главной
заботой в ходе итерационного процесса является обеспечение невырожденности
сетки, т.е. недопущение образования самопересекающихся ячеек. Для функционала с
якобианом в знаменателе это требование
еще строже: необходимо обеспечивать сохранение выпуклости всех ячеек сетки. Как
уже отмечалось в § 3, пока предполагается, что
требование (3.6) для исходной сетки выполнено.
Поэтому после каждой
итерации сетка 
подвергается
контролю: проверке на выпуклость ячеек. Для каждой ячейки по координатам ее
вершин вычисляются 4 величины 
, используя формулы (3.7)-(3.8). Если 
для всех 
, ячейка выпукла.
Нарушение этого условия
хотя бы в одной ячейке влечет за собой пересчет всей сетки с уменьшенным
значением параметра 
. Если уменьшить 
вдвое, то нужный
результат получается, если взять полусумму сеток:
(4.10) 
, 
.
Полученная сетка 
подвергается
повторной проверке, и в случае необходимости процедура уменьшения 
и пересчет сетки
повторяется. (Во избежании «зацикливания» этого процесса в программах
предусматривается ограничение числа таких «урезаний»).
Жесткая процедура пересчета
всей сетки в случае появления хотя бы одной «плохой» ячейки имеет практической
целью сохранение гладкости сетки. Исправление ситуации посредством «лечения»
отдельных «плохих» ячеек, как показывает практика, может приводить к
неблагоприятным последствиям.
При расчете следующей
итерации целесообразно начинать со значения параметра 
, на котором закончилась предыдущая итерация, или этого
значения, умноженного на коэффициент
больший 1.
Последняя мера диктуется
соображением «не задерживать процесс», который по здравому смыслу должен
улучшаться по мере сходимости итераций с
уменьшением невязки решаемых уравнений.
Вопрос об исходном значении
параметра 
для первой итерации
сложнее, поскольку (опять же по здравому смыслу) оно может зависеть от формы
расчетной области на рассматриваемый момент времени. Одним из возможных решений
является использование значения, на котором закончился расчет сетки в этой
области на предыдущем шаге по времени, или этого значения, умноженного на
коэффициент несколько больший 1 (тогда эти значения нужно сохранять в числе
«областных» управляющих параметров).
Тогда вопрос сводится к заданию этого пара-метра только на исходном шаге
расчета, что не так уж и существенно.
Теперь обратимся к вопросу
о скорости сходимости описанных итерационных процессов. Несмотря на
обнадеживающие слова о том, что эти процессы представляют модифицированные
варианты метода Ньютона-Рафсона, практически скорость их сходимости крайне
медленная. Положение спасают следующие два обстоятельства. Во-первых, на каждом
очередном шаге система уравнений конструируется так, что при значениях
корректирующих параметров, равных нулю, сетка предыдущего шага ей удовлетворяет
точно, с нулевой невязкой (в дискретном варианте). Поэтому в соответствии с
(2.4) и (2.8) итерациями предстоит погасить невязку 0(t). Этим предлагаемые алгоритмы расчета сеток принципиально
отличаются от других, тянущих за собой
шлейф «недоитерированности» уравнений, которые практически до сходимости
довести не удается. Во-вторых, задача итерационного процесса, наряду с
погашением невязки 0(t), состоит в том, чтобы обеспечить гладкость сетки,
привязанной к слегка изменившим свое
положение новым границам, и в том, чтобы направить изменение сетки в приемлемое
(хотелось бы, нужное) русло, не допуская ухудшения ее качества, необходимого
для решения на этой сетке основной задачи. Это должно достигаться подключением
соответствующих корректирующих функционалов. Если упомянутые две цели достигаются, то вопрос о том, будет ли полностью погашена
упомянутая невязка 0(t), не так уж и важен. Следующий шаг начнется с «белого
листа» – конструирования новой системы разностных уравнений. Поэтому можно
рассчитывать, что необходимое число итераций (пусть и очень медленно
сходящихся), как правило, не придется назначать большим. Естественно, здесь существенную роль играет форма
конкретной области. Кроме того, очевидно, что существенную роль играет и
величина управляющих параметров p(t), с которыми подключаются
корректирующие функционалы.
Существует ли альтернатива,
позволяющая улучшить ситуацию со сходимостью итераций? В монографии [12],
стр. 263, читаем:
«В общей теории итерационных методов рассматриваются методы двух типов:
использующие априорную информацию об операторах итерационные схемы и не
использующие (методы вариационного типа). В методах первого типа качество
начального приближения не используется. В методах вариационного типа
итерационные параметры выбираются из условия минимума некоторых функционалов,
связанных с исходным уравнением. В этом случае итерационные параметры обладают
свойством учитывать качество начального приближения».
Таким образом, рекомендации
явно склоняются в пользу вариационных методов. С точки зрения создания автоматизированных
систем расчета сеток такой подход может показаться перспективным. Однако в силу
специфики задачи, уже описанной выше, нельзя игнорировать и опасение, что
вычисленный итерационный параметр окажется непригодным, поскольку приведет к
«плохой» сетке. К тому же (с учетом дополнительной вычислительной работы) нет
уверенности и в том, что использование более сложных методов обеспечит заметный
выигрыш при реализации алгоритмов.
§ 5. О вырождении сетки и невыпуклых ячейках.
До сих пор обсуждаемые
алгоритмы расчета сеток исходили из предположения, что все ячейки сетки
являются выпуклыми, как было оговорено в § 3 условием (3.6). К сожалению,
практика расчетов требует ослабления этого ограничения.
В качестве иллюстрации на
рис.4 представлены ситуации, когда требуется допустить в расчетной области,
наряду с четырехугольниками, и ячейки, которые вырождаются (или почти
вырождаются) в треугольники (см. рис.4а,б,в). Более того, на рис.4г изображена
ситуация, когда одна ячейка в исходной постановке является невыпуклой.
(Заметим, что рис.4 носит эскизный иллюстративный характер – фактически
восполнение линий сетки осуществляется, как правило, отрезками прямых).
Вырождение (или почти вырождение) четырехугольных ячеек в треугольники может
происходить и в процессе расчета нестационарной задачи при усложнении границ
расчетных областей, которые приходится аппроксимировать ограниченным
количеством узлов сетки, зафиксированным в исходных данных.
Для реального осуществления
расчета в условиях вырождения ячейки в треугольник предусматривается коррекция
алгоритма.
Как уже было отмечено,
величина 
, определяемая формулами (3.7)-(3.8), представляет удвоенную
площадь треугольника с номером k. Тогда для ячейки
будем иметь:
(5.1)
Коррекция алгоритма состоит в следующем: пусть
(5.2)
, где 
.
Тогда треугольник с номером k исключается из расчета.
Фактически это означает,
что в дискретном варианте формул для (1.1) и (1.8) исключается некоторая
(незначительная) часть области интегрирования, отвечающая таким выродившимся
треугольникам. (Заметим, что она покрывается другой парой треугольников).
Отметим также, что предлагаемые различными авторами «безавостные» модификации
(например, замена обращающегося в нуль якобиана в знаменателе функционала на нечто иное),
по-видимому, вполне работоспособные при расчете стационарных сеток, приводят к
неконтролируемым значениям скоростей узлов сетки при расчетах нестационарных сеток.
Описанный выше прием (5.2)
исчерпывает меры, связанные с вырождением четырехугольных ячеек в треугольники.
Значительно сложнее обстоит
дело с учетом возможного появления невыпуклых ячеек. Их появление
обнаруживается в случае, если окажется, что для некоторого («плохого»)
треугольника
(5.3)
.
Гипотетически возможны следующие альтернативные варианты разрешения
таких ситуаций.
а) Не обращать внимание (ничего не менять в расчетных формулах).
Например, в случае, изображенном на рис.4г, если единственная «плохая»
(невыпуклая) ячейка является «угловой» для расчетной области, соответствующий
«плохой» треугольник получит номер k=3 и не будет
участвовать в расчетных формулах, как уже отмечалось в § 3.
Заметим, что придется
позаботиться о том, чтобы программа контроля сетки на выпуклость пропустила
«провинившуюся» ячейку, не провоцируя появление новых невыпуклых ячеек.
б) «Плохой» треугольник исключается, т.е. не участвует в описанных
расчетных формулах. Такой вариант в принципе допустим. Например, для расчета
гармонических сеток в работе [13] рассматривался алгоритм, при котором
разрезание невыпуклых ячеек осуществлялось только с помощью одной («хорошей»)
диагонали, и даже для выпуклых ячеек выбиралась одна диагональ – та, при
которой реализуется меньшее значение функционала. Работоспособность такого
алгоритма подтверждалась практическими расчетами.
в) В формуле (1.2) заменяем
величину g0 на 
. Очевидно, что при этом будет сохранена положительная
определенность всех матриц Gk. Для функционала с
якобианом в соответствии с упоминавшейся теоремой из работы [7], существование
невырожденной сетки для такого набора матриц Gk гарантировано. Проблема состоит в том, как одолеть
вариационный барьер, за которым оказался соответствующий из узлов сетки, и
какая скорость его движения будет при этом выработана.
г) Принимаются меры по исключению возможности появления невыпуклой
ячейки сетки. В качестве такой меры предлагается, например, использовать
следующий прием. В случае (5.3) узел с номером
k проектируется на отрезок, соединяющий
узлы с номерами
(k-1) и (k+1), и точка с полученными координатами
заносится вместо 
. Невыпуклая ячейка превращается при этом в треугольник. Для
полноты изложения приведем соответствующие расчетные формулы. Полагаем
, 
.
Согласно уравнению прямой, соединяющей узлы 
и 
:
(5.4) 
, 
.
Согласно уравнению перпендикуляра через точки 
и 
:
.
Отсюда получаем формулу для 
:
(5.5)
.
После этого вычисляем 
по формулам (5.4).
Конечно, следует иметь в
виду, что такое волевое превращение невыпуклой ячейки в треугольник может
привести к бесконтрольному увеличению скорости соответствующего узла сетки.
Тем не менее, исходя из
практического опыта, заметим, что допущение в расчете сеток невыпуклых ячеек
может приводить к весьма неблагоприятным последствиям, поскольку они могут
приобретать очень «плохую» форму. При этом вряд ли можно ожидать разумной
аппроксимации даже первых производных, необходимых для последующего решения
основной задачи.
Поэтому, исходя из
обсуждения возможных альтернативных вариантов действий в случае появления
невыпуклых ячеек, по-видимому, целесообразно остановиться на последнем. А
именно, необходимо уже в исходных данных
избавиться от невыпуклых ячеек (например, описанным приемом) и в дальнейшем
не допускать их появления.
Соответствующая технология, опирающаяся на подбор в итерационном процессе значений параметров 
, была описана в § 4.
Отметим также, что
рекомендуемое решение исходит из интересов расчета газодинамических задач на
регулярных четырехугольных сетках. Оно может быть другим, например, в случае,
если основная задача решается на
треугольных сетках или в ситуациях б)
и в), когда присутствие невыпуклых
четырехугольных ячеек вполне допускается.
§ 6. Проблема контроля скоростей узлов сетки.
В работе [14,
стр.17] С.К.Годунов написал: «… расчет выделенных ударных волн, движение которых
вызывает перемещение точек двумерной или трехмерной сетки, также не изучен до
сих пор ни теоретически, ни экспериментально с исчерпывающей подробностью.
Заведомо не исследована обратная связь такого перемещения точек на движение
волны, нет ясности в том, какие эффекты эта обратная связь вызывает».
В подтверждение этих слов
стоит сказать, что накопленный отрицательный опыт связан в первую очередь с
недопустимыми скоростями узлов сетки, появляющимися в расчетах из-за
несовершенства алгоритмов конструирования сеток. Безусловно, скорость движения
сетки весьма существенно влияет на расчет основной решаемой задачи. Это можно
видеть уже на примере элементарной задачи о распаде разрыва, являющейся идейным
стержнем методики расчета газодинамических задач, как описано в монографии [2].
В случае подвижных
границ алгоритм построения сеток должен непрерывно обеспечивать адекватное изменение положения узлов
сетки внутри области. Казалось бы естественным требование, чтобы скорости
«внутренних» узлов сетки были заключены в пределах, в которых изменяются
скорости «граничных» узлов. (Это аналогично известному «принципу максимума» для
решений эллиптических уравнений). Однако, несмотря на кажущуюся его естественность,
легко могут быть придуманы примеры, когда такое требование не выполнено,
например, при применении для расчета сеток интерполяционных формул.
Сейчас уместно более
подробно осветить этот вопрос, как было обещано выше в § 2. В работе [15] представлены результаты
сравнения нескольких вариантов построения двумерных разностных сеток посредством интерполяционных формул.
В качестве одного из
«оправдавших ожидания» алгоритмов можно рекомендовать использование так
называемой трансфинитной интерполяции. В простейшем двумерном варианте
интерполяционная формула для функции 
на единичном квадрате
, 
, по ее значениям на контуре квадрата, имеет вид:
(6.1) 
Здесь 
- монотонно
возрастающие функции своих аргументов на отрезке [0,1], причем
, 
.
Легко проверить, что для произвольных функций 
, удовлетворяющих этим условиям, будем иметь равенство интерполянты 
заданным граничным
значениям.
Рассматривая
последовательности координат узлов сетки, заданных на границах области, как
значения в точках 
, 
некоторых непрерывных
функций, и применяя формулу (6.1) независимо для каждой из двух
пространственных координат х и у, получаем интерполяционные формулы для
расчета координат внутренних узлов сетки.
Для задания управляющих
функций 
в практике расчетов успешно
используются так называемые законы расстановки узлов сетки вдоль границ,
описанные в монографии [2] на стр. 180-182:
; 
.
В работе [15] на простом
методическом примере построения сетки для выпуклого четырехугольника с прямолинейными границами обнаружились
некоторые (в чем-то неожиданные) результаты при (специально придуманных)
неравномерных расстановках узлов сетки на граничных отрезках.
Например, оказалось, что
задание в качестве значений управляющих функций
(6.2)
, 
дает для рассматриваемой области
(четырехугольник с прямолинейными
границами) невырожденную сетку при произвольных
расстановках узлов на контуре. А вот в случае задания
(6.3) 
, 
, 
, 
,
казалось бы, более естественного, чем (6.2), строятся примеры таких
расстановок узлов, при которых сетка оказывается вырожденной. Тем более
неудовлетворительный результат могут давать
формулы:
(6.4) 
, 
.
Заметим, что в случае
произвольных областей и формулы (6.2) могут давать неудовлетворительный
результат (поэтому и приходится конструировать сложные алгоритмы построения
сеток). Однако «живучесть» интерполяционных формул, использующих (6.2),
существенно выше, чем использующих (6.3) и (6.4).
Что касается скоростей
движения узлов сетки, рассчитываемой по интерполяционным формулам с
использованием (6.1), то очевидно следующее. Наличие в формуле (6.1), наряду с
положительными, отрицательных весовых коэффициентов для угловых точек,
позволяет легко строить примеры, когда скорости внутренних узлов сетки выходят
за пределы, в которых изменяются скорости граничных узлов. Это может иметь
место для каждой из двух координат х
и у и, тем более, для полной скорости
узла. В § 3 обращалось внимание на аналогичную ситуацию в системе линейных
уравнений (3.11).
Это обстоятельство
затрудняет автоматизацию контроля скоростей сетки в практических расчетах.
Можно, например, в ходе расчета вычислять максимальную скорость узлов сетки на
границах расчетной области Wгр и максимальную скорость внутренних узлов Wвн . Но какое отклонение Wвн от Wгр можно считать
допустимым?
Обратим внимание, что
описанные алгоритмы построения сеток могут использоваться также для перестройки
сетки при зафиксированных границах области (в целях получения сетки, более
приемлемой для расчета основной задачи.
В процессе перестройки Wгр=0, а Wвн¹0.
Заключение
Подведем итог изложенному.
Для конструирования сеток в нестационарных двумерных расчетах предлагается
использовать в качестве опорных функционалов (1.1)-(1.2) или (1.8)-(1.9).
Входящие в них коэффициенты вычисляются как метрические параметры сетки,
полученной на предыдущем временном шаге нестационарного расчета.
При тщательно выполненной
дискретизации этих функционалов удается получить систему уравнений, которая при
подстановке в нее сетки предыдущего шага в качестве невязки будет давать
тождественный нуль. Поэтому при граничных условиях, отвечающих новому моменту
времени, невязки будут величинами порядка шага по времени t. Следовательно, можно ожидать, что и скорости
узлов сетки окажутся лежащими в разумных пределах по отношению к скоростям
движения границ. В силу изложенного в предыдущем § 6 более четкое утверждение
сделать трудно.
Использование «чистых»
опорных функционалов при отсутствии обратной связи может приводить к тому, что
в ходе нестационарного расчета сетка будет необратимо портиться, становясь
непригодной для расчета основной задачи, для которой она и конструируется.
Чтобы этому препятствовать, к опорным функционалам могут подключаться со своими
весовыми коэффициентами 
другие функционалы.
В простейшем варианте это
реализуется посредством формулы (2.16) для корректировки коэффициентов 
. Условно можно говорить, что с помощью коэффициента p0
подключается
функционал «ортогональности», а коэффициента pГ – гармонический.
В случае функционала
(1.8)-(1.9) без якобиана реализуется система разностных уравнений (3.11) с
коэффициентами (3.12)-(3.13). Из этих формул видно, что корректировка (2.16)
сводится к увеличению коэффициентов cL в системе уравнений
(3.11). Вопрос о том, какие функционалы подключать для корректировки и с какими
весовыми коэффициентами, должен стать предметом специальных экспериментальных
исследований.
Теперь уместно обсудить
вопрос о том, какой из двух функционалов (с якобианом или без) стоит
предпочесть. Как уже отмечалось, функционал с якобианом гарантирует невырожденность
сетки при любом задании положительно определенных симметричных матриц
коэффициентов G, а функционал без
якобиана этого не гарантирует. Однако следует заметить, что при малых
коэффициентах корректирующих функционалов фактически работа будет происходить в
окрестности опорных функционалов. А они оба дают практически тождественные
результаты, воспроизводя сетку предыдущего временного шага, которая
предполагается невырожденной. Следовательно, при достаточно малых значениях
параметров p* можно надеяться,
что и функционал без якобиана обеспечит получение невырожденной сетки.
Весьма важную роль при этом
играет присутствие в знаменателе функционала (1.8)-(1.9) якобиана G0 для сетки предыдущего шага
по времени. Кроме того, в процессе
расчета на каждой итерации контролируется, чтобы сетка не стала вырожденной.
Эти аргументы дополняются
преимуществами функционала без якобиана.
Прежде всего, таким является линейность уравнений (3.11), благодаря чему
коэффициенты (3.12) остаются неизменными на всех итерациях. Матрицу этих
коэффициентов (8 чисел в каждом внутреннем узле сетки) можно вычислить на
каждом шаге один раз и использовать на всех итерациях. При этом расчет итерации
сводится к простым формулам (4.1) и контролю получающейся сетки на выпуклость.
В такой ситуации необременительным будет и большое число итераций, если в этом
возникнет необходимость. Для функционала с якобианом расчетные формулы
существенно сложнее, а следовательно возрастают и затраты времени расчета.
Практически, по-видимому,
целесообразно иметь в арсенале алгоритмов построения сеток оба функционала, но
прибегать к использованию функционала с якобианом только после того, как
исчерпаны возможности функционала без якобиана.
Заметим, что на практике
этому, как правило, предшествует этап, когда сетка рассчитывается просто по
интерполяционным формулам. Он используется до тех пор, пока дает приемлемые
сетки.
Важным принципиальным
отличием предлагаемой технологии является то, что переход от интерполяционного
этапа к использованию функционалов должен проходить относительно безболезненно
(без возникновения недопустимых
скоростей узлов) благодаря изложенной выше идеологии опорного функционала.
Также обстоит дело и в случае необходимости смены управляющих параметров в
самих функционалах.
Однако, как показывает
практика расчетов, этот тезис реализуется только в том случае, если такая
перестройка начинается «заблаговременно», чтобы иметь достаточный «запас
времени», не приводящий к катастрофическим последствиям для основной задачи.
С точки зрения «живучести»
алгоритмов построения сеток и, самое главное, пригодности получающихся сеток
для последующего решения основной задачи весьма важен вопрос о том, допускать
или не допускать невыпуклость ячеек сетки. Этот вопрос обсуждался в § 5. Представляется целесообразным (если такое
решение допустимо) уже в исходных данных избавиться от невыпуклых ячеек и в
дальнейшем не допускать их появления (предусмотрев это в программе контроля
качества сетки). В § 4 были описаны возможности реализации такого предложения
путем автоматизированного подбора итерационного параметра 
.
Несмотря на все сказанное,
автор далек от того, чтобы претендовать на создание полностью
автоматизированных алгоритмов построения сеток, позволяющих считать
нестационарные задачи без вмешательства исполнителя. Допустим, что удастся
экспериментально отработать технологию подключения корректирующих функционалов,
упомянутых выше. Заметим, что это должно быть реализовано в виде конкретных
рекомендаций, которые обеспечили бы работу методики не в руках ее создателя, а
в руках исполнителя расчетов. (Конечно, идеальным было бы автоматизированное
назначение управляющих параметров на каждом шаге расчета, исходя из конкретной
сложившейся ситуации).
Останутся ситуации, когда
расчет невозможно провести до конца из-за необходимости изменять топологическую
карту задачи (менять «раскрой» задачи на расчетные области), менять число узлов
сетки для того, чтобы адекватно отразить возникающие особенности (например,
проявляющиеся в искажении формы границ) и т.д. Автоматизация решения таких
вопросов была и остается актуальной проблемой, нерешенной с приемлемой для
практики полнотой.
Содержание настоящей работы
докладывалось автором на IX Всероссийском совещании по проблемам построения
сеток для решения задач математической физики, посвященном памяти академика
А.Ф.Сидорова (Новороссийск, Абрау-Дюрсо, 16-21 сентября 2002 г.).
Автор выражает
благодарность Г.Б.Алалыкину за реализацию описанных алгоритмов на ЭВМ и участие в проведении численных
экспериментов по их апробации, а также М.С.Гавреевой за помощь в оформлении
настоящей работы.
Литература
1.
Прокопов Г.П. Универсальные вариационные функционалы для построения
двумерных сеток.// М, Препринт ИПМ им. М.В.Келдыша РАН, 2001, №1, 36
стр.
2. Численное решение многомерных задач газовой динамики. Под общей редакцией
С.К.Годунова.//М., «Наука», 1976, 400 стр.
3. Прокопов Г.П. Некоторые общие вопросы конструирования алгоритмов построения
разностных сеток.// Вопросы атомной науки и техники (ВАНТ), Сер.: Мат.моделир.физ.процессов,
1988, вып.1, 3-13.
4.
Иваненко С.А. Управление формой ячеек в процессе построения сеток.//
ЖВМ и МФ, 2000, т.40, № 11, 1662-1684.
5. Годунов С.К., Прокопов Г.П. О расчетах конформных отображений и построения
разностных сеток.// ЖВМ и МФ, 1967, т.7, №5, 1031-1059.
6. Winslow A.M. Numerical
solution of the quasi-linear Poisson
equation in a non uniform triangle mesh.// J. Comp. Phys. 1966, vol.1, №2,
149-172.
7. Иваненко С.А. О существовании уравнений для описания классов невырожденных
криволинейных координат в произвольной области //ЖВМ и МФ, 2002, т.42, №1,
47-52.
8. Антонова Р.Н., Прокопов Г.П., Софронова О.И. Расчет подвижных разностных
сеток и проблема начального приближения для расчета сетки в сложной области.//ВАНТ,
Сер.: Мат. моделир. физ. процессов, 1996, вып.1-2, 84-90.
9. Сидоров А.Ф., Шабашова Т.И. Об одном методе расчета оптимальных разностных
сеток для многомерных областей.// Численные методы механики сплошной среды.
Новосибирск, ИТПМ СО АН СССР, 1981, т.12, №5, 106-124.
10.
Прокопов Г.П. Методология вариационного подхода к
построению квазиортогональных сеток.// ВАНТ, 1998, вып.1, 37-46.
11.
Иваненко
С.А., Чарахчьян А.А. Криволинейные сетки из выпуклых четырехугольников.//ЖВМ и
МФ, 1988, т.28, №4, 503-514.
12.
Самарский А.А., Николаев Е.С. Методы решения
сеточных уравнений.//М, «Наука», Гл. ред. физ.-мат. лит., 1978.
13.
Уськов В.М. Построение сеток из невырожденных
четырехугольников с использованием критерия Делоне.//ВАНТ,
Сер.: Мат. моделир. физ. процессов, 1994, вып.2, 12-18.
14.
Годунов С.К. Воспоминания о разностных схемах.
Доклад на Международном симпозиуме «Метод Годунова в газовой динамике».
Мичиганский университет (США). Май 1997//Новосибирск, Научная книга, 1997, 40
стр.
15.
Антонова Р.Н., Прокопов Г.П. Сравнение нескольких
вариантов построения двумерных разностных сеток посредством интерполяционных
формул.//ВАНТ, Сер.: Мат. моделир. физ. процессов, 1994, вып.1, 78-84.