Аннотация
Разработана феноменологическая макроскопическая модель стационарно-неравновесной трехмерной
турбулентности в сжимаемой жидкости с учетом происходящих в ней нелинейных кооперативных
процессов. Представление турбулизованного континуума в виде термодинамического комплекса,
состоящего из двух подсистем * подсистемы осредненного движения и подсистемы турбулентного
хаоса, рассматриваемого, в свою очередь, как конгломерат вихревых структур различных
пространственно-временных масштабов, позволило получить методами статистической неравновесной
термодинамики определяющие соотношения для турбулентных потоков и сил, которые наиболее полно
описывают процессы переноса и самоорганизации в квазистационарном случае. Введение в модель
внутренних параметров среды, характеризующих возбуждаемые макроскопические степени свободы
дало возможность обобщить теорию Онзагера таким образом, чтобы она описывала и турбулентные
пульсации относительно средних, что, в частности, позволило смоделировать термодинамическими
методами колмогоровский каскадный процесс и получить разнообразные кинетические уравнения
(типа Фоккера-Планка в конфигурационном пространстве) для функций распределения мелкомасштабных
характеристик турбулентности. В силу распространенности турбулентного режима течения в природе,
можно ожидать, что предложенный синергетический подход к вопросам моделирования развитой
турбулентности найдет применение в различных астро- и геофизических приложениях.
Abstract
The phenomenological macroscopic model of a stationary- nonequilibrium three-dimensional
turbulence in compressible fluid with allowance for of nonlinear cooperative processes,
happening in her designed. Representation of a turbulized continuum by the way of
thermodynamic complex consisting of two subsystems * of a subsystem of an average motion and
a subsystem of turbulent chaos, viewed, in turn, as conglomeration of vortex structures of
different time-space gauges, has allowed to receive by methods of statistical nonequilibrium
thermodynamics defining relations for turbulent flows and forces, which one fullestly feature
processes of transport and self-organizing in a quasistationary case. The introduction in model
of interior parameters of medium describing provoked macroscopic degrees of freedom has enabled
to extend the theory Онзагера so that she featured also turbulent fluctuations concerning
medial, that, in particular, has allowed to simulate by thermodynamic methods Kolmogorov
cascade process and to receive the manifold kinetic equations for distribution functions of
the small-scale performances of a turbulence. By virtue of abundance of a turbulent flow regime
in the nature, it is possible to expect, that offered the synergeti approach to problems of
model operation of a developed turbulence will find a use in different астро- and geophysical
appendices.
Введение.
Турбулентность без
преувеличения является самым распространенным видом движения “космической
жидкости” во Вселенной и, вместе с тем, принадлежит к числу наиболее сложных
природных явлений, связанных с возникновением и развитием организованных
диссипативных структур (вихрей различного пространственно-временного масштаба,
вихревых колец, вихревых трубок, неоднородностей в концентрациях,
представляющих собой геометрические формы с высокой степенью симметрии и т.п.)
при определенных режимах течения жидкости в существенно неравновесной открытой
системе. Процессы самоорганизации на
фоне турбулентного движения являются важнейшим механизмом, формирующим свойства
астро- и геофизических объектов на разных стадиях их эволюции, включая
возникновение галактик и галактических скоплений, рождение звезд из диффузной
среды газопылевых облаков, образование протопланетных дисков )
и последующую аккумуляцию планетных систем, формирование газовых оболочек
планет (атмосфер), разномасштабные течения в атмосферах и околопланетной
плазме и т.д. К сожалению прямое
численное моделирование турбулентных движений на основе точных (мгновенных) гидродинамических
уравнений сопряжено с большими математическими трудностями, а построение общей
теории турбулентности, из-за сложности механизмов возникновения и эволюции
взаимодействующих когерентных структур, вряд ли возможно. Все это требует
развития новых модельных макроскопических подходов к описанию
турбулентности, введения осредненных
физических параметров среды, установления
(для их определения) универсальных и частных соотношений, дополняющих уже известные соотношения типа законов
сохранения массы, энергии, количества движения и т.п. Именно на этом пути
открываются действительно реальные возможности эффективно преодолевать
проблемы, с которыми связаны перспективные постановки и численные решения
разнообразных и сложных задач астро- и геофизики.
Новый взгляд на
турбулентность. Согласно почти что
общепринятым представлениям, турбулентность является процессом хаотическим.
Однако существует и иная точка зрения на турбулентность, высказанная впервые,
по-видимому, Пригожиным (1986). Согласно ей
переход от ламинарного течения к турбулентному является процессом
самоорганизации, при котором часть энергии теплового хаоса (связанного с
произвольными флуктуациями, происходящими на молекулярном уровне) переходит в
макроскопически организованное движение упорядоченных диссипативных структур. Это обстоятельство повышает
внутреннюю упорядоченность системы по сравнению с молекулярным хаосом. В
частности, каскадный процесс дробления вихрей, имеющий место в развитой
турбулентности, можно трактовать как неограниченную последовательность
процессов самоорганизации. При этом множество пространственно-временных
масштабов, на которых разыгрывается этот процесс, соответствует когерентному
поведению огромного числа частиц, выражающемуся в форме подобной
супермолекулярной организации (молекулы участвуют в коллективных,
согласованных, взаимозависимых, вращательных движениях, соответствующих вихрям).
Итак, феномен турбулентности
дает позитивный материал для разработки новых идей, касающихся соотношения
порядка и хаоса в пульсационных течениях жидкости, простоты и сложности в
поведении открытых нелинейных гидродинамических систем, которые могут без
специфического воздействия извне путем самоорганизации образовывать
макроскопические диссипативные пространственно-временные структуры
(осуществлять вдали от равновесия «порядок через флуктуации»). К сожалению, нужно отметить, что хотя со
времени понимания синергетической природы турбулентности, как процесса
самоорганизации, прошло уже более двадцати лет, однако до сих пор представления
о возникающих в потоке когерентных структурах не материализовались в разработки
модельных подходов, направленных на создание практических инженерных методов
расчета турбулентности, основанных, как
правило, на осредненных гидродинамических уравнениях. Вместе с тем, известное в литературе (см., например,
Пригожин, 1960) расширение формализма неравновесной термодинамики на среды с
возбужденными макроскопическими степенями свободы (которые служат внутренними
параметрами, описывающими макроструктуру среды) позволяет, по-видимому,
распространить подобный подход и на макроскопическое описание каскадного
процесса переноса турбулентной энергии вихрями разного размера, образующихся в
результате каскадного процесса их последовательных дроблений. Таким образом, цель данной работы состоит в том, чтобы, при
использовании методов статистической
термодинамики необратимых процессов, столь хорошо зарекомендовавших себя в
последнее время при изучении всевозможных неравновесных диссипативных структур
вдали от термодинамического равновесия (см., например, Эбелинг и др., 2001),
попытаться построить феноменологически макроскопическую модель стационарно-
неравновесной турбулентности с учетом
происходящих в ней нелинейных кооперативных процессов, т.е. сформулировать
замкнутую систему осредненных гидродинамических уравнений, описывающих развитую
трехмерную турбулентность.
1.
два Уровня феноменологических моделей
Далее будем следовать
классическому подходу к феноменологии развитой турбулентности, который
основывается на идее Рейнольдса об осреднении мгновенных уравнений
движения жидкости для случайных
гидродинамических переменных  (дающих сжатое
описание однокомпонентной среды) по пространству и времени, или посредством
другой эквивалентной процедуры, например, посредством принятой в статистической
гидродинамике (Монин, Яглом, 1992) теоретико-вероятностной процедуре осреднения
по соответствующему физическому ансамблю – множеству систем,
«тождественно приготовленных» (в одинаковых внешних условиях) с точки зрения их
сжатого описания. Все подобные осреднения (при учете обычного для статистической физики предположения об эргодичности))
отфильтровывают те моды движения, масштаб которых меньше
пространственно-временного интервала осреднения. Эти мелкомасштабные движения,
представленные пульсациями физических параметров по отношению к соответствующим
осредненным значениям, в дальнейшем будем именовать турбулентными. Таким
образом, разделение (для целей
математического моделирования) реального течения на осредненное и турбулентное
полностью зависит от выбора пространственно-временной области (дающих сжатое
описание однокомпонентной среды) по пространству и времени, или посредством
другой эквивалентной процедуры, например, посредством принятой в статистической
гидродинамике (Монин, Яглом, 1992) теоретико-вероятностной процедуре осреднения
по соответствующему физическому ансамблю – множеству систем,
«тождественно приготовленных» (в одинаковых внешних условиях) с точки зрения их
сжатого описания. Все подобные осреднения (при учете обычного для статистической физики предположения об эргодичности))
отфильтровывают те моды движения, масштаб которых меньше
пространственно-временного интервала осреднения. Эти мелкомасштабные движения,
представленные пульсациями физических параметров по отношению к соответствующим
осредненным значениям, в дальнейшем будем именовать турбулентными. Таким
образом, разделение (для целей
математического моделирования) реального течения на осредненное и турбулентное
полностью зависит от выбора пространственно-временной области  , для которой установлены осредненные значения (детерминированные и регулярные функции
макрокоординат , для которой установлены осредненные значения (детерминированные и регулярные функции
макрокоординат  ) гидродинамических переменных, т.е. имеет до некоторой
степени условный характер. Масштаб неоднородности регулярного течения ) гидродинамических переменных, т.е. имеет до некоторой
степени условный характер. Масштаб неоднородности регулярного течения  (масштаб наблюдения
по Обухову (1941)), определяемый размером (масштаб наблюдения
по Обухову (1941)), определяемый размером  ~ ~ области осреднения области осреднения
 , предполагается
далее малым по сравнению с характерным масштабом , предполагается
далее малым по сравнению с характерным масштабом  для всей системы в
целом. В этом случае все вихри
большего масштаба вносят вклад в регулярное движение, описываемое одновременными средними значениями
(математическими ожиданиями) для всей системы в
целом. В этом случае все вихри
большего масштаба вносят вклад в регулярное движение, описываемое одновременными средними значениями
(математическими ожиданиями)  случайных
гидродинамических переменных случайных
гидродинамических переменных  , являющихся функциями векторнозначного стохастического
процесса , являющихся функциями векторнозначного стохастического
процесса  (здесь
совокупность случайных экстенсивных переменных (здесь
совокупность случайных экстенсивных переменных  , характеризующих простую гидродинамическую
систему, собрана в вектор состояния , характеризующих простую гидродинамическую
систему, собрана в вектор состояния  ). В дальнейшем, как правило, черта над буквой будет обозначать
осреднение вышеописанного типа по ансамблю гидродинамических систем. Все вихри
меньшего масштаба, исключенные в процессе осреднения, вносят вклад в
турбулентное движение, определяемое соответствующими пульсациями ). В дальнейшем, как правило, черта над буквой будет обозначать
осреднение вышеописанного типа по ансамблю гидродинамических систем. Все вихри
меньшего масштаба, исключенные в процессе осреднения, вносят вклад в
турбулентное движение, определяемое соответствующими пульсациями  тех же самых
переменных от их средних. Для получения репрезентативных (детерминированных)
средних значений будем считать, что пространственно-временная область
осреднения тех же самых
переменных от их средних. Для получения репрезентативных (детерминированных)
средних значений будем считать, что пространственно-временная область
осреднения  включает в себя весь
ансамбль реализаций гидродинамических полей. включает в себя весь
ансамбль реализаций гидродинамических полей.
В случае использования
физического ансамбля требуется знание статистического распределения тех
переменных, которые выбраны для сжатого описания. Будем далее предполагать, что
для полного описания рассматриваемого здесь стохастического процесса  достаточно знать
функцию достаточно знать
функцию  (плотность вероятности найти (плотность вероятности найти  в интервале ( в интервале ( , ,  + + ) в пространственно-временной точке ( ) в пространственно-временной точке ( )) и двухточечную функцию )) и двухточечную функцию  (совместную плотность
распределения вероятности). Процессы, полностью описываемые только этими
функциями являются, как известно, марковскими процессами. Далее будем также
использовать двухточечную плотность условной вероятности (совместную плотность
распределения вероятности). Процессы, полностью описываемые только этими
функциями являются, как известно, марковскими процессами. Далее будем также
использовать двухточечную плотность условной вероятности  , которая дает вероятность найти значение , которая дает вероятность найти значение  в точке ( в точке ( ), если с вероятностью равной единице ), если с вероятностью равной единице  в точке ( в точке ( ). Связь между средними
значениями по условному подансамблю и всему ансамблю неявно содержится в
соотношении ). Связь между средними
значениями по условному подансамблю и всему ансамблю неявно содержится в
соотношении   , которое собственно и вводит, так называемую, вероятность
перехода , которое собственно и вводит, так называемую, вероятность
перехода  . Для стационарного стохастического процесса не только . Для стационарного стохастического процесса не только  не зависит от времени,
но и плотности совместных вероятностей зависят лишь от попарных разностей
времени; имея это ввиду, мы при рассмотрении стационарного
ансамбля будем опускать в выражениях для не зависит от времени,
но и плотности совместных вероятностей зависят лишь от попарных разностей
времени; имея это ввиду, мы при рассмотрении стационарного
ансамбля будем опускать в выражениях для
 и и  начальный момент
времени. Следует отметить, что для
стационарного ансамбля только условные средние начальный момент
времени. Следует отметить, что для
стационарного ансамбля только условные средние  зависят от времени.
Именно эти, зависящие от времени величины, связаны с макроскопическими
уравнениями переноса. зависят от времени.
Именно эти, зависящие от времени величины, связаны с макроскопическими
уравнениями переноса.
Напомним теперь кратко (на
примере несжимаемой температурно-однородной однокомпонентной жидкости ( ) те основные идеи феноменологической теории мелкомасштабной вихревой
турбулентности, которые существенным
образом будут использованы в данной
работе при построении макроскопической модели развитой трехмерной
турбулентности для одноточечных моментов. ) те основные идеи феноменологической теории мелкомасштабной вихревой
турбулентности, которые существенным
образом будут использованы в данной
работе при построении макроскопической модели развитой трехмерной
турбулентности для одноточечных моментов.
Микроструктура
развитой турбулентности. Согласно теории Колмогорова (см., например,
Ландау, Лифшиц, 1988), мелкомасштабная структура турбулентности в
изотермической жидкости ( ), рассматриваемой
как сплошная среда, определяется
каскадным характером передачи энергии по спектру вихрей (турбулентных
пульсаций) различных пространственно-временных масштабов ).
Качественная схема каскада Ричардсона состоит в следующем. Мелкие вихри получают
энергию в результате последовательного дробления крупных вихрей при росте управляющего параметра течения в целом –
числа Рейнольдса ), рассматриваемой
как сплошная среда, определяется
каскадным характером передачи энергии по спектру вихрей (турбулентных
пульсаций) различных пространственно-временных масштабов ).
Качественная схема каскада Ричардсона состоит в следующем. Мелкие вихри получают
энергию в результате последовательного дробления крупных вихрей при росте управляющего параметра течения в целом –
числа Рейнольдса  , соответствующего крупномасштабным движениям в
потоке (здесь , соответствующего крупномасштабным движениям в
потоке (здесь  – характерный размер крупномасштабных вихрей
(интегральный масштаб турбулентности), – характерный размер крупномасштабных вихрей
(интегральный масштаб турбулентности),  –
характерная скорость течения (разность
гидродинамических скоростей на расстояниях –
характерная скорость течения (разность
гидродинамических скоростей на расстояниях  ), ),  – кинематическая молекулярная вязкость). Самые
большие энергонесущие вихри образуются в результате потери устойчивости
исходного ламинарного течения (обладающего одной степенью свободы), и их
размеры – кинематическая молекулярная вязкость). Самые
большие энергонесущие вихри образуются в результате потери устойчивости
исходного ламинарного течения (обладающего одной степенью свободы), и их
размеры  (прандтлевский путь перемешивания) в значительно меньше
характерного масштаба (прандтлевский путь перемешивания) в значительно меньше
характерного масштаба  самой области течения самой области течения
 . Эти возмущения первого порядка из-за слишком большого числа
Рейнольдса . Эти возмущения первого порядка из-за слишком большого числа
Рейнольдса  , соответствующего их масштабу , соответствующего их масштабу  и относительной
скорости и относительной
скорости  , также оказываются неустойчивыми и, разрушаясь, порождают
возмущения второго порядка ( , также оказываются неустойчивыми и, разрушаясь, порождают
возмущения второго порядка ( ), которые в свою очередь по той же причине вызывают
появление еще более мелких вихрей и т.д. Процесс последовательных бифуркаций
(дробления вихрей) останавливается, когда силы молекулярной вязкости в жидкости начинают играть существенную
роль, что происходит для вихрей с
числами Рейнольдса ), которые в свою очередь по той же причине вызывают
появление еще более мелких вихрей и т.д. Процесс последовательных бифуркаций
(дробления вихрей) останавливается, когда силы молекулярной вязкости в жидкости начинают играть существенную
роль, что происходит для вихрей с
числами Рейнольдса  . При этом происходит непрерывное перераспределение
удельной кинетической энергии . При этом происходит непрерывное перераспределение
удельной кинетической энергии  несущего
потока от крупномасштабных вихрей к более мелким вплоть до самых мелких с
характерным размером порядка внутреннего масштаба турбулентности несущего
потока от крупномасштабных вихрей к более мелким вплоть до самых мелких с
характерным размером порядка внутреннего масштаба турбулентности  , который характеризует влияние вязких эффектов на структуру
мелкомасштабной турбулентности. В
пределе очень больших чисел , который характеризует влияние вязких эффектов на структуру
мелкомасштабной турбулентности. В
пределе очень больших чисел  устанавливается
квазистационарный режим инерционного
переноса кинетической энергии от больших вихрей к меньшим, при котором
энергия в конце концов из-за вязкости устанавливается
квазистационарный режим инерционного
переноса кинетической энергии от больших вихрей к меньшим, при котором
энергия в конце концов из-за вязкости  превращается в
тепло в гидродинамически устойчивых
мелких вихрях масштаба превращается в
тепло в гидродинамически устойчивых
мелких вихрях масштаба  (вязкий
интервал). Колмогоров предположил, что существует так называемый инерционной
интервал ( (вязкий
интервал). Колмогоров предположил, что существует так называемый инерционной
интервал ( ) масштабов вихрей, в
которых не происходит заметного продуцирования и диссипации энергии, точнее
диссипация в них мала по сравнению с
той энергией, которую они получают от более крупных вихрей и передают более
мелким. Важно подчеркнуть, что если число ) масштабов вихрей, в
которых не происходит заметного продуцирования и диссипации энергии, точнее
диссипация в них мала по сравнению с
той энергией, которую они получают от более крупных вихрей и передают более
мелким. Важно подчеркнуть, что если число  велико, то,
несмотря на анизотропность, неоднородность и нестационарность осредненного течения,
случайный характер дробления вихрей и
хаотичность передачи их энергии по
каскаду приводят к тому, что статистический режим мелкомасштабных пульсаций,
лежащих в пространственно-временной области велико, то,
несмотря на анизотропность, неоднородность и нестационарность осредненного течения,
случайный характер дробления вихрей и
хаотичность передачи их энергии по
каскаду приводят к тому, что статистический режим мелкомасштабных пульсаций,
лежащих в пространственно-временной области  , является локально изотропным, т.е. однородным, изотропным
и квазистационарным (меняющимся в
зависимости лишь от характеристик осредненного движения). Квазистационарный режим турбулентного
течения, при котором реализуется поток энергии в область малых масштабов,
предполагает, разумеется, определенные граничные условия на границе , является локально изотропным, т.е. однородным, изотропным
и квазистационарным (меняющимся в
зависимости лишь от характеристик осредненного движения). Квазистационарный режим турбулентного
течения, при котором реализуется поток энергии в область малых масштабов,
предполагает, разумеется, определенные граничные условия на границе  рассматриваемой
области течения рассматриваемой
области течения  , создающие накачку и сток. Формула , создающие накачку и сток. Формула  для диссипационного масштаба длины для диссипационного масштаба длины  является следствием
первой гипотезы подобия Колмогорова (1941), согласно которой статистический
режим мелкомасштабной локально
изотропной турбулентности однозначно
определяется двумя размерными параметрами – средней скоростью
диссипации энергии является следствием
первой гипотезы подобия Колмогорова (1941), согласно которой статистический
режим мелкомасштабной локально
изотропной турбулентности однозначно
определяется двумя размерными параметрами – средней скоростью
диссипации энергии  и вязкостью и вязкостью  . .
Величина  (ключевая
характеристика локально изотропной турбулентности) представляет собой
осредненную по ансамблю возможных реализаций течения среды диссипацию
турбулентной энергии (в единице массы жидкости в единицу времени) и
одновременно характеризует скорость передачи кинетической энергии пульсационного
движения по иерархии вихрей в каскадном процессе: (ключевая
характеристика локально изотропной турбулентности) представляет собой
осредненную по ансамблю возможных реализаций течения среды диссипацию
турбулентной энергии (в единице массы жидкости в единицу времени) и
одновременно характеризует скорость передачи кинетической энергии пульсационного
движения по иерархии вихрей в каскадном процессе:    –
следствие второй гипотезы подобия Колмогорова
(1941), согласно которой в инерционном
интервале ( –
следствие второй гипотезы подобия Колмогорова
(1941), согласно которой в инерционном
интервале ( ) статистический
режим турбулентности определяется единственным параметром ) статистический
режим турбулентности определяется единственным параметром  . Здесь . Здесь   - удельная
кинетическая энергия, получаемая в единицу времени вихрями - удельная
кинетическая энергия, получаемая в единицу времени вихрями  -го порядка от вихрей -го порядка от вихрей  -го порядка и передаваемая ими вихрям -го порядка и передаваемая ими вихрям  -го порядка; -го порядка;  , ,  - соответственно порядок скорости
и времени пульсаций в вихрях колмогоровского диссипационного масштаба - соответственно порядок скорости
и времени пульсаций в вихрях колмогоровского диссипационного масштаба  . В теории
Колмогорова предполагается также, что на каждом масштабе (шаге каскада) вихри заполняют всю область . В теории
Колмогорова предполагается также, что на каждом масштабе (шаге каскада) вихри заполняют всю область  непрерывно. непрерывно.
Количественное описание
мелкомасштабной локально изотропной турбулентности в области  (далее везде
предполагается, что (далее везде
предполагается, что  ) основано на использовании структурных функций ) основано на использовании структурных функций  и их спектров и их спектров  , где , где  , ,  –волновое число (Колмогоров, 1941; Обухов,
1941). Из первой гипотезы подобия и
предположения о том, что параметры крупномасштабной турбулентности слабо
меняются на расстояниях порядка –волновое число (Колмогоров, 1941; Обухов,
1941). Из первой гипотезы подобия и
предположения о том, что параметры крупномасштабной турбулентности слабо
меняются на расстояниях порядка  , если , если  , вытекает что , вытекает что    , где , где  и и  – произвольные функции безразмерного аргумента – произвольные функции безразмерного аргумента
 . Согласно второй гипотезе подобия структурная функция в
инерционном интервале . Согласно второй гипотезе подобия структурная функция в
инерционном интервале  не зависит от
вязкости не зависит от
вязкости  , т.е. , т.е.  , ,  при при  . Отсюда следует один из важнейших законов мелкомасштабных
турбулентных движений (закон двух третей): в любом турбулентном течении с
достаточно большим числом Рейнольдса . Отсюда следует один из важнейших законов мелкомасштабных
турбулентных движений (закон двух третей): в любом турбулентном течении с
достаточно большим числом Рейнольдса  средний квадрат
разности скоростей в двух точках на
расстоянии средний квадрат
разности скоростей в двух точках на
расстоянии  друг от друга при не
слишком малых, но и не слишком больших значениях друг от друга при не
слишком малых, но и не слишком больших значениях  (сравнимых с масштабом длины (сравнимых с масштабом длины  соответствующего
осредненного течения) должен быть пропорционален соответствующего
осредненного течения) должен быть пропорционален  , ,
 , (1) , (1)
где  – универсальная постоянная. Эквивалентное
«закону двух третей» для структурной функции поля скорости утверждение,
сформулированное в терминах спектров,
принимает вид: – универсальная постоянная. Эквивалентное
«закону двух третей» для структурной функции поля скорости утверждение,
сформулированное в терминах спектров,
принимает вид:  при при  (Обухов, 1941). Этот
закон в настоящее время хорошо подтвержден экспериментально для самых
разнообразных турбулентных течений (см. Монин, Яглом, 1996). Что касается структурных
функций (Обухов, 1941). Этот
закон в настоящее время хорошо подтвержден экспериментально для самых
разнообразных турбулентных течений (см. Монин, Яглом, 1996). Что касается структурных
функций  -порядка, то теория подобия Колмогорова приводит к соотношению -порядка, то теория подобия Колмогорова приводит к соотношению
 , (где , (где  ), которое, вообще говоря, не подтверждается экспериментально,
в особенности для ), которое, вообще говоря, не подтверждается экспериментально,
в особенности для  . .
 Как известно, это обстоятельство связано с тем, что гипотезы подобия для локально изотропной
турбулентности в их первоначальной форме предполагали постоянство притока
энергии к мелкомасштабным возмущениям, лежащим в инерционном интервале, т.е.
постоянство параметра Колмогорова Как известно, это обстоятельство связано с тем, что гипотезы подобия для локально изотропной
турбулентности в их первоначальной форме предполагали постоянство притока
энергии к мелкомасштабным возмущениям, лежащим в инерционном интервале, т.е.
постоянство параметра Колмогорова  (точное определение
которого (точное определение
которого
 ; (2) ; (2)
здесь и далее везде по повторяющимся индексам
производится суммирование), а также что совместные многомерные функция
плотности распределения вероятностей  для пульсаций поля
скоростей в достаточно малой пространственно-временной области для пульсаций поля
скоростей в достаточно малой пространственно-временной области  с диаметром с диаметром  зависят только от
параметра зависят только от
параметра  . Однако,
для реальных турбулентных течений
диссипация энергии . Однако,
для реальных турбулентных течений
диссипация энергии  меняется не только при переходе от одной точки меняется не только при переходе от одной точки  (области (области  ) течения к
другой, но является случайной величиной
от координат ) течения к
другой, но является случайной величиной
от координат  и времени и времени  , пульсируя вместе с мгновенным полем скоростей , пульсируя вместе с мгновенным полем скоростей  . Распределения вероятностей диссипации энергии . Распределения вероятностей диссипации энергии  (зависящие в общем
случае от изменения гидродинамических характеристик осредненного движения
среды, в частности, от числа Рейнольдса (зависящие в общем
случае от изменения гидродинамических характеристик осредненного движения
среды, в частности, от числа Рейнольдса  ) оказывают влияние на безусловные распределения вероятностей для
мелкомасштабных характеристик развитой турбулентности, которые по этой причине
в общем случае не могут быть вполне универсальными. Известное замечание Ландау
(см., например, Ландау, Лифшиц, 1988) относительно первоначальных гипотез
подобия Колмогорова касалось именно этого
влияния. ) оказывают влияние на безусловные распределения вероятностей для
мелкомасштабных характеристик развитой турбулентности, которые по этой причине
в общем случае не могут быть вполне универсальными. Известное замечание Ландау
(см., например, Ландау, Лифшиц, 1988) относительно первоначальных гипотез
подобия Колмогорова касалось именно этого
влияния.
В связи с этими
затруднениями, представления Колмогорова о случайном каскаде были уточнены в
работе Обухова (1962), который предложил отказаться от условия  в области в области  (с центром в
точке (с центром в
точке  и характерным
масштабом и характерным
масштабом  ) и исходить из того, что статистические
характеристики мелкомасштабных движений (например, структурные функции) определяются
не теоретико-вероятностным средним значением ) и исходить из того, что статистические
характеристики мелкомасштабных движений (например, структурные функции) определяются
не теоретико-вероятностным средним значением случайной величины случайной величины  , а зависят от значений диссипации , а зависят от значений диссипации 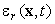 , осредненной по некоторому объему , осредненной по некоторому объему  с характерным
размером с характерным
размером  , малым по сравнению с типичным масштабом неоднородности осредненного
течения, , малым по сравнению с типичным масштабом неоднородности осредненного
течения,  . Если в качестве
области осреднения, лежащей в пределах . Если в качестве
области осреднения, лежащей в пределах  , выбрать
шар радиуса , выбрать
шар радиуса  (получаемые
результаты слабо зависят от формы области осреднения), то (получаемые
результаты слабо зависят от формы области осреднения), то
 . (3) . (3)
Статистическая изменчивость
параметра  потребовала
следующего уточнения понятия физического ансамбля систем, по которому осуществляется теоретико-вероятностное осреднение
(Обухов,1962): Статистический ансамбль,
параметрически зависящий от потребовала
следующего уточнения понятия физического ансамбля систем, по которому осуществляется теоретико-вероятностное осреднение
(Обухов,1962): Статистический ансамбль,
параметрически зависящий от  и и  («чистый»
ансамбль), позволяет рассчитать лишь условные средние значения любых
статистических характеристик мелкомасштабных движений, определяемых при
фиксированном значении диссипации
энергии («чистый»
ансамбль), позволяет рассчитать лишь условные средние значения любых
статистических характеристик мелкомасштабных движений, определяемых при
фиксированном значении диссипации
энергии  . Однако на практике всегда приходится иметь дело с
некоторым смешанным ансамблем, в котором величина . Однако на практике всегда приходится иметь дело с
некоторым смешанным ансамблем, в котором величина  изменяется
согласно некоторому общему статистическому закону. Поэтому для вычисления
безусловного среднего значения какой-либо характеристики мелкомасштабной
турбулентности (например, тензора Рейнольдса изменяется
согласно некоторому общему статистическому закону. Поэтому для вычисления
безусловного среднего значения какой-либо характеристики мелкомасштабной
турбулентности (например, тензора Рейнольдса  )
необходимо осреднять
условное значение соответствующего
момента по возможным значениям параметра )
необходимо осреднять
условное значение соответствующего
момента по возможным значениям параметра  . В частности, для определения тензора Рейнольдса нужно
вычислить интеграл . В частности, для определения тензора Рейнольдса нужно
вычислить интеграл   (где (где  – плотность распределения вероятности для – плотность распределения вероятности для  , определяемая, вообще говоря, крупномасштабными регулярными движениями; , определяемая, вообще говоря, крупномасштабными регулярными движениями;   ; ;  –
условная функция плотности вероятности пульсаций скорости, т.е. вероятность
попадания –
условная функция плотности вероятности пульсаций скорости, т.е. вероятность
попадания  в интервал от в интервал от  до до  в подансамбле,
относительно которого известно, что в подансамбле,
относительно которого известно, что  при всех при всех  ). Значения подобных интегралов могут быть, вообще говоря,
различными у разных типов течений и, в частности, зависящими от числа ). Значения подобных интегралов могут быть, вообще говоря,
различными у разных типов течений и, в частности, зависящими от числа  . .
Используя параметр  , Колмогоров
(1962) переформулировал первую и вторую гипотезы подобия (установив, так
называемые, уточненные гипотезы, в которых величина , Колмогоров
(1962) переформулировал первую и вторую гипотезы подобия (установив, так
называемые, уточненные гипотезы, в которых величина  заменена на заменена на  ) и, кроме этого,
дополнил их еще и третьей гипотезой, постулирующей (при большом
отношении масштабов ) и, кроме этого,
дополнил их еще и третьей гипотезой, постулирующей (при большом
отношении масштабов  ) нормальное распределение плотности вероятности величины ) нормальное распределение плотности вероятности величины  и линейность
зависимости дисперсии и линейность
зависимости дисперсии  от от  : :
 , (4) , (4)
 , ,  , , 
где  - дисперсия величины - дисперсия величины  , ,  - медиана распределения, - медиана распределения,  - универсальная постоянная (” 0.5), - универсальная постоянная (” 0.5),  - слагаемое, зависящее от
характеристик осредненного регулярного движения. Распределение (4) позволило
рассчитать важные статистические характеристики стационарной мелкомасштабной
турбулентности, в частности, моменты - слагаемое, зависящее от
характеристик осредненного регулярного движения. Распределение (4) позволило
рассчитать важные статистические характеристики стационарной мелкомасштабной
турбулентности, в частности, моменты  : :

(коэффициенты  зависят от
макроструктуры турбулентного течения). Отсюда для структурной функции зависят от
макроструктуры турбулентного течения). Отсюда для структурной функции  -го порядка -го порядка  следует
выражение следует
выражение  , которое, в случае , которое, в случае  (формула (1)), оказывается
близким к пределам точности имеющихся экспериментальных данных, а в применении
к структурным функциям высших порядков сильно отличается от зависимости,
предсказываемой первоначальной теорией Колмогорова для изотропной
турбулентности (но в то же время неплохо согласуется с имеющимися экспериментальными
данными). Аналогичным образом была поправлена теория локальной структуры
пульсационных полей температуры и концентрации химически активной примеси,
перемешиваемых турбулентностью (см., например, Монин, Яглом, 1996). (формула (1)), оказывается
близким к пределам точности имеющихся экспериментальных данных, а в применении
к структурным функциям высших порядков сильно отличается от зависимости,
предсказываемой первоначальной теорией Колмогорова для изотропной
турбулентности (но в то же время неплохо согласуется с имеющимися экспериментальными
данными). Аналогичным образом была поправлена теория локальной структуры
пульсационных полей температуры и концентрации химически активной примеси,
перемешиваемых турбулентностью (см., например, Монин, Яглом, 1996).
Обратимся теперь еще к одной причине, по которой важно использование параметра  при
феноменологическом описании турбулентности. Отметим, что первоначальная (не
уточненная) теория каскада не
является абсолютно точной еще и потому,
что в ней не учитываются в явном виде
какие-либо мелкомасштабные когерентные диссипативные структуры, которыми может обладать турбулентное поле, за
исключением допустимого в ее рамках
макроструктурирования потока на больших масштабах ~ при
феноменологическом описании турбулентности. Отметим, что первоначальная (не
уточненная) теория каскада не
является абсолютно точной еще и потому,
что в ней не учитываются в явном виде
какие-либо мелкомасштабные когерентные диссипативные структуры, которыми может обладать турбулентное поле, за
исключением допустимого в ее рамках
макроструктурирования потока на больших масштабах ~ . Между тем, в последние годы стало ясно, что любая
адекватная теория турбулентности обязана учитывать наличие и динамику подобных
диссипативных структур и неравномерность их пространственно-временного
распределения в хаотическом потоке (Кроу, Чампагне, 1971; Браун, Рожко, 1974).
С хаотическим характером передачи кинетической энергии по каскаду, вызываемым
неустойчивостью диссипативных структур, связано в свою очередь явление
гидродинамической внутренней перемежаемости, при которой области, занятые так
называемыми турбулентными пятнами (в которых наблюдаются интенсивные пульсации
градиентов скорости, . Между тем, в последние годы стало ясно, что любая
адекватная теория турбулентности обязана учитывать наличие и динамику подобных
диссипативных структур и неравномерность их пространственно-временного
распределения в хаотическом потоке (Кроу, Чампагне, 1971; Браун, Рожко, 1974).
С хаотическим характером передачи кинетической энергии по каскаду, вызываемым
неустойчивостью диссипативных структур, связано в свою очередь явление
гидродинамической внутренней перемежаемости, при которой области, занятые так
называемыми турбулентными пятнами (в которых наблюдаются интенсивные пульсации
градиентов скорости,  ), тесно переплетаются с областями со слабо турбулизованной или полностью безвихревой
жидкостью (в которых такие пульсации практически отсутствуют, ), тесно переплетаются с областями со слабо турбулизованной или полностью безвихревой
жидкостью (в которых такие пульсации практически отсутствуют,  ). Наличие
перемежаемости отвечает режиму течения
(при малом числе ). Наличие
перемежаемости отвечает режиму течения
(при малом числе  ), когда мощности постоянно действующего механизма
турбулизации среды, передающего энергию потоку на больших масштабах, еще
недостаточно для формирования полностью развитой турбулентности во всей области ), когда мощности постоянно действующего механизма
турбулизации среды, передающего энергию потоку на больших масштабах, еще
недостаточно для формирования полностью развитой турбулентности во всей области  , занятой жидкостью. Таким образом, значения величины , занятой жидкостью. Таким образом, значения величины  (или
родственных ей величин, квадратичных по градиентам скорости), могут служить
индикатором перемежаемости. (или
родственных ей величин, квадратичных по градиентам скорости), могут служить
индикатором перемежаемости.
Следует отметить, что
статистические модели случайного каскада, в которых перемежаемость
турбулентности в инерционном интервале
описывается в терминах пульсаций  , в настоящее время развиты во многих работах
отечественных и зарубежных (см.,
например, Новиков, Стюарт, 1964; Фриш,
1978,1998; Монин, Яглом, 1996). Разработаны
и другие подходы к моделированию гидродинамической перемежаемости,
основанные, в частности, на понятии о
странных аттракторах (см., например,
сб. пер. «Странные аттракторы», 1981). Однако, в так называемых, полуэмпирических моделях турбулентности, которые
получили в последнее время широкое распространение в инженерной практике (см.,
например, Турбулентность: Принципы и применение, 1980), понятие перемежаемости, как правило, не используется. , в настоящее время развиты во многих работах
отечественных и зарубежных (см.,
например, Новиков, Стюарт, 1964; Фриш,
1978,1998; Монин, Яглом, 1996). Разработаны
и другие подходы к моделированию гидродинамической перемежаемости,
основанные, в частности, на понятии о
странных аттракторах (см., например,
сб. пер. «Странные аттракторы», 1981). Однако, в так называемых, полуэмпирических моделях турбулентности, которые
получили в последнее время широкое распространение в инженерной практике (см.,
например, Турбулентность: Принципы и применение, 1980), понятие перемежаемости, как правило, не используется.
Вместе с тем,
приведенные результаты Колмогорова-
Обухова феноменологического моделирования мелкомасштабной структуры
турбулентности позволяют пересмотреть
макроскопические подходы к описанию развитой турбулентности, в частности, термодинамические методы,
используемые при построении полуэмпирических моделей для одноточечных моментов.
В подобных моделях определяющие связи
между термодинамическими потоками и силами носят исключительно локальный
характер, например, тензор напряжений Рейнольдса  зависит только от кинетической
энергии турбулентности, диссипации и
градиента средней скорости в той же пространственно-временной точке зависит только от кинетической
энергии турбулентности, диссипации и
градиента средней скорости в той же пространственно-временной точке  . При этом теория Колмогорова- Обухова в полуэмпирических
моделях турбулентности до последнего времени никак не применялась. Однако,
введение в гидродинамическую модель внутренних параметров среды,
характеризующих возбуждаемые макроскопические степени свободы, дает возможность
описать методами статистической неравновесной термодинамики колмогоровский
каскадный процесс (стационарно-неравновесный процесс), задействовать в уравнениях движения в
качестве индикатора перемежаемости, зависящий от глобального числа Рейнольдса . При этом теория Колмогорова- Обухова в полуэмпирических
моделях турбулентности до последнего времени никак не применялась. Однако,
введение в гидродинамическую модель внутренних параметров среды,
характеризующих возбуждаемые макроскопические степени свободы, дает возможность
описать методами статистической неравновесной термодинамики колмогоровский
каскадный процесс (стационарно-неравновесный процесс), задействовать в уравнениях движения в
качестве индикатора перемежаемости, зависящий от глобального числа Рейнольдса
 , параметр Колмогорова , параметр Колмогорова  , и получить
разнообразные кинетические уравнения типа Фоккера-Планка (в
соответствующем конфигурационном пространстве) для функций распределения важных характеристик мелкомасштабной
турбулентности. , и получить
разнообразные кинетические уравнения типа Фоккера-Планка (в
соответствующем конфигурационном пространстве) для функций распределения важных характеристик мелкомасштабной
турбулентности.
Перейдем теперь
непосредственно к построению макроскопической модели развитой трехмерной
турбулентности в однокомпонентной жидкости, как процесса самоорганизации в
открытой системе при стационарных граничных условиях.
Макроскопическое
описание развитой турбулентности. Для составления осредненных уравнений
движения турбулизованной жидкости, характеризуемой двумя линейными масштабами
движений  (внешним) и (внешним) и  (внутренним), удобно ввести две координатные системы:
микромасштаба (внутренним), удобно ввести две координатные системы:
микромасштаба   и макромасштаба и макромасштаба   . Эти системы координат подразделяют пространство на элементарные
объемы . Эти системы координат подразделяют пространство на элементарные
объемы  и и  соответственно. Будем далее считать, что соответственно. Будем далее считать, что  и и  . Здесь величина . Здесь величина  есть интегральный
масштаб турбулентности (характерный масштаб движения среды), величина есть интегральный
масштаб турбулентности (характерный масштаб движения среды), величина  (размер турбулентного
«моля») есть масштаб внутреннего движения или состояния системы, а величина (размер турбулентного
«моля») есть масштаб внутреннего движения или состояния системы, а величина  есть молекулярный
почти нулевой микромасштаб. Можно поставить задачу нахождения уравнений
движения среды в макромасштабе есть молекулярный
почти нулевой микромасштаб. Можно поставить задачу нахождения уравнений
движения среды в макромасштабе  по известным
уравнениям Навье-Стокса в микромасштабе по известным
уравнениям Навье-Стокса в микромасштабе  . .
Связанная с этой задачей проблема осреднения является одной из
центральных в механике сплошных сред, а в случае такой сложной системы, как турбулизованная жидкость, часто именно
от способа осреднения зависит само построение макроскопической модели. Приведем
здесь некоторые итоговые результаты работ автора (см. также Колесниченко, Маров, 1999), посвященных выводу осредненных гидродинамических
уравнений, отвечающему переходу от уравнений движения малых элементов сплошной
среды к описанию тех же движений в макромасштабе. В классических теориях
турбулентности, обычно для всех без исключения физических параметров,
осреднения вводятся некоторым одинаковым образом, причем, как правило, без весовых
коэффициентов. Вместе с тем подобное идентичное для всех физических параметров
осреднение в общем случае жидкости с переменной массовой плотностью  )
приводит не только к громоздким уравнениям масштаба среднего движения, но и к
затруднениям физической интерпретации некоторых отдельных членов в них. Поэтому
при построении модели турбулентности в
сжимаемой жидкости удобно использовать, наряду с теоретико-вероятностным
средним значением )
приводит не только к громоздким уравнениям масштаба среднего движения, но и к
затруднениям физической интерпретации некоторых отдельных членов в них. Поэтому
при построении модели турбулентности в
сжимаемой жидкости удобно использовать, наряду с теоретико-вероятностным
средним значением  какого-либо
гидродинамического параметра какого-либо
гидродинамического параметра  , так называемое, среднемассовое значение этого параметра, задаваемое соотношением , так называемое, среднемассовое значение этого параметра, задаваемое соотношением
 ; (5) ; (5)
при этом:   ; ;   , ,  ; ;  - соответствующие турбулентные
пульсации. - соответствующие турбулентные
пульсации.
Система «регулярных»
гидродинамических уравнений масштаба среднего движения ),
полученная путем теоретико-вероятностного осреднения, справедливых в
микромасштабе мгновенных уравнений движения, имеет вид (см., например, Колесниченко,
1998):
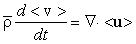 , ( , ( ), (6) ), (6)
 , (7) , (7)
 . (8) . (8)
Здесь  , ,   - соответственно мгновенные значения скорости, давления, удельного объема ( - соответственно мгновенные значения скорости, давления, удельного объема ( ) и удельной
внутренней энергии жидкой частицы; ) и удельной
внутренней энергии жидкой частицы;  - осредненная
(средневзвешанная) гидродинамическая скорость среды; - осредненная
(средневзвешанная) гидродинамическая скорость среды;  –
осредненное давление; –
осредненное давление;  - полная производная по
времени относительно осредненного поля скоростей; - полная производная по
времени относительно осредненного поля скоростей;  - внешняя сила, действующая
на единицу массы (в данной работе пульсациями массовой силы для простоты будем
пренебрегать); - внешняя сила, действующая
на единицу массы (в данной работе пульсациями массовой силы для простоты будем
пренебрегать);  - тензор турбулентных
(рейнольдсовых) напряжений; - тензор турбулентных
(рейнольдсовых) напряжений;  - полный тензор напряжений в
турбулентном потоке; - полный тензор напряжений в
турбулентном потоке;  , ,  - соответственно турбулентные
потоки удельного объема и тепла (где - соответственно турбулентные
потоки удельного объема и тепла (где  - мгновенное значение удельной энтальпии среды); - мгновенное значение удельной энтальпии среды);  - суммарный поток тепла
в подсистеме среднего движения
(где - суммарный поток тепла
в подсистеме среднего движения
(где  - осредненный молекулярный
поток тепла); - осредненный молекулярный
поток тепла);    - средневзвешенное значение
удельной скорости диссипации турбулентной кинетической энергии в тепло под
влиянием молекулярной вязкости - средневзвешенное значение
удельной скорости диссипации турбулентной кинетической энергии в тепло под
влиянием молекулярной вязкости  (соотношение
обобщающее формулу Обухова (3) на случай сжимаемой жидкости); (соотношение
обобщающее формулу Обухова (3) на случай сжимаемой жидкости);  - единичный тензор; - единичный тензор;  , ,  , ,  , ,  - соответственно осредненный
тензор вязких напряжений, тензор скоростей деформации для осредненного континуума и их части с нулевым следом, определяемые соотношениями: - соответственно осредненный
тензор вязких напряжений, тензор скоростей деформации для осредненного континуума и их части с нулевым следом, определяемые соотношениями:
  , ,  , (9) , (9)
где  ; ;  – оператор Гамильтона; символы – оператор Гамильтона; символы  и и  означают соответственно
внутреннее произведение двух тензоров
и внешнее произведение двух
векторов (диада); символ означают соответственно
внутреннее произведение двух тензоров
и внешнее произведение двух
векторов (диада); символ  означает обобщенную
дивергенцию, поскольку означает обобщенную
дивергенцию, поскольку  не всегда является вектором. Из
системы уравнений (6)-(8) видно, что осредненное движение среды характеризуется: во- первых,
осредненными молекулярными термодинамическими потоками не всегда является вектором. Из
системы уравнений (6)-(8) видно, что осредненное движение среды характеризуется: во- первых,
осредненными молекулярными термодинамическими потоками  и и  , для которых необходимы определяющие соотношения (см,
Колесниченко, 1985); и во-вторых, в эти уравнения входят неопределенные смешанные одноточечные
корреляции –
моменты второго порядка , для которых необходимы определяющие соотношения (см,
Колесниченко, 1985); и во-вторых, в эти уравнения входят неопределенные смешанные одноточечные
корреляции –
моменты второго порядка   и и  , представляющие собой перенос гидродинамических
характеристик среды турбулентными
пульсациями. Корреляционные члены, включающие
пульсации давления , представляющие собой перенос гидродинамических
характеристик среды турбулентными
пульсациями. Корреляционные члены, включающие
пульсации давления  и и  , а также осредненную величину вязкой диссипации турбулентной
энергии , а также осредненную величину вязкой диссипации турбулентной
энергии  также необходимо уметь находить. также необходимо уметь находить.
При
термодинамическом построении модели развитой турбулентности, выбор линейных
определяющих соотношений, замыкающих
систему (6)-(8), может быть проведен в соответствии с реологическими правилами
континуальной механики методом Онзагера, в основу которого положено
представление о том, что за линейную релаксацию осредненных переменных к
устойчивому стационарному состоянию ответственны соответствующие
термодинамические силы (см, например, Пригожин, 1960). Вместе с тем,
разрабатываемый в данной работе термодинамический подход, при котором
турбулизованный континуум считается сплошной средой с некоторой внутренней
структурой, позволяет обобщить теорию
Онзагера таким образом, чтобы она описывала и турбулентные пульсации
относительно средних. Следует отметить, что, в рамках полной макроскопической
модели турбулентности, система (6)-(8) описывает крупномасштабную структуру
турбулентного поля.
2.
балансовые Уравнения для энтропии
в
турбулизированной
жидкости
Будем далее
предполагать, что турбулизованный жидкий континуум является
термогидродинамическим комплексом, состоящим из двух взаимодействующих между
собой подсистем (Колесниченко, 1985). Такими подсистемами являются: подсистема среднего движения, которая получается в
результате теоретико-вероятностного осреднения мгновенного движения жидкости, и
подсистема турбулентного хаоса (турбулентная
надструктура), которая связана с пульсационным движением среды. Каждая
подсистема в отдельности является (в физически бесконечно малом объеме  ) открытой
термодинамической системой, обменивающейся
с другой энергией и энтропией
(но не веществом). Поля скоростей внутри указанных подсистем полагаем совпадающими, поскольку в процессе
турбулентного движения жидкости не
происходит разделения
соответствующих лагранжевых объемов (эффекта диффузии) - подсистема “турбулентного
хаоса” не имеет гидродинамической скорости относительно подсистемы осредненного
движения. В соответствии с принятой в данной работе точкой зрения Пригожина на
турбулентность, как на течение макроскопически высокоорганизованное,
подсистему турбулентного хаоса, в свою очередь, будем рассматривать, как
континуум с внутренней структурой, состоящий из вихревых образований
всевозможных пространственно-временных масштабов, лежащих в интервале
равновесия (сумма инерционного и вязкого интервалов спектра турбулентности);
кроме этого будем полагать, что на каждом масштабе (шаге каскада) вихри
заполняют все пространство непрерывно. Для каждой из указанных подсистем
для любого элементарного объема среды определим (указанным ниже способом)
локальные «крупнозернистые» переменные (являющиеся непрерывными функциями
координат и времени), такие как плотность, давление, температура, внутренняя
энергия, энтропия и т.д. ).
Будем кроме этого считать, что обобщенные параметры состояния, характеризующие
турбулентный хаос, связаны обычными для локально-равновесной термодинамики
соотношениями типа тождеств Гиббса, Гиббса-Дюгема и т.п. Другими словами будем
считать, что такого рода соотношения остаются справедливыми и вдали от
локального термодинамического равновесия, если в качестве состояния отсчета
выбрать подходящее устойчивое стационарно-неравновесное состояние (Пригожин,
1960). Подобное предположение
составляет своего рода новый постулат, на котором базируются термодинамический
подход к описанию развитой турбулентности. ) открытой
термодинамической системой, обменивающейся
с другой энергией и энтропией
(но не веществом). Поля скоростей внутри указанных подсистем полагаем совпадающими, поскольку в процессе
турбулентного движения жидкости не
происходит разделения
соответствующих лагранжевых объемов (эффекта диффузии) - подсистема “турбулентного
хаоса” не имеет гидродинамической скорости относительно подсистемы осредненного
движения. В соответствии с принятой в данной работе точкой зрения Пригожина на
турбулентность, как на течение макроскопически высокоорганизованное,
подсистему турбулентного хаоса, в свою очередь, будем рассматривать, как
континуум с внутренней структурой, состоящий из вихревых образований
всевозможных пространственно-временных масштабов, лежащих в интервале
равновесия (сумма инерционного и вязкого интервалов спектра турбулентности);
кроме этого будем полагать, что на каждом масштабе (шаге каскада) вихри
заполняют все пространство непрерывно. Для каждой из указанных подсистем
для любого элементарного объема среды определим (указанным ниже способом)
локальные «крупнозернистые» переменные (являющиеся непрерывными функциями
координат и времени), такие как плотность, давление, температура, внутренняя
энергия, энтропия и т.д. ).
Будем кроме этого считать, что обобщенные параметры состояния, характеризующие
турбулентный хаос, связаны обычными для локально-равновесной термодинамики
соотношениями типа тождеств Гиббса, Гиббса-Дюгема и т.п. Другими словами будем
считать, что такого рода соотношения остаются справедливыми и вдали от
локального термодинамического равновесия, если в качестве состояния отсчета
выбрать подходящее устойчивое стационарно-неравновесное состояние (Пригожин,
1960). Подобное предположение
составляет своего рода новый постулат, на котором базируются термодинамический
подход к описанию развитой турбулентности.
Термодинамика подсистемы осредненного движения. Начнем с анализа балансовых
уравнений для осредненной энтропии  турбулизованной
среды. Теоретико-вероятностное
осреднение справедливого по предположению для микродвижений тождества
Гиббса турбулизованной
среды. Теоретико-вероятностное
осреднение справедливого по предположению для микродвижений тождества
Гиббса  (где (где   - соответственно мгновенные
значения температуры и удельной энтропии в жидкой частице), приводит к фундаментальному тождеству
Гиббса для подсистемы осредненного движения (Колесниченко, 1998). Это
тождество, записанное вдоль осредненной траектории движения центра масс
физически элементарного объема, имеет вид - соответственно мгновенные
значения температуры и удельной энтропии в жидкой частице), приводит к фундаментальному тождеству
Гиббса для подсистемы осредненного движения (Колесниченко, 1998). Это
тождество, записанное вдоль осредненной траектории движения центра масс
физически элементарного объема, имеет вид
 . (10) . (10)
Тождеству (10) можно придать вид уравнения локального
баланса энтропии  , если исключить из него субстанциональные производные
по времени от параметров , если исключить из него субстанциональные производные
по времени от параметров  и и  с помощью
осредненных гидродинамических уравнений (6) и (8); в результате получим: с помощью
осредненных гидродинамических уравнений (6) и (8); в результате получим:
 , (11) , (11)
где
 , (12) , (12)
 . (13) . (13)
Здесь положительная величина
 определяет
скорость локального производства энтропии определяет
скорость локального производства энтропии  , обусловленного необратимыми процессами переноса
внутри подсистемы осредненного движения;
величина , обусловленного необратимыми процессами переноса
внутри подсистемы осредненного движения;
величина  (сток или
приток энтропии ) как будет ясно из
дальнейшего, отражает обмен энтропией
между подсистемами турбулентного хаоса и осредненного движения. Важно отметить,
что величина (сток или
приток энтропии ) как будет ясно из
дальнейшего, отражает обмен энтропией
между подсистемами турбулентного хаоса и осредненного движения. Важно отметить,
что величина  может быть
разной по знаку в зависимости от конкретного режима турбулентного
движения. Действительно, скорость
диссипации турбулентной энергии может быть
разной по знаку в зависимости от конкретного режима турбулентного
движения. Действительно, скорость
диссипации турбулентной энергии  является
положительной величиной. Однако скорость перехода энергии является
положительной величиной. Однако скорость перехода энергии  (представляющая собой работу,
совершаемую над турбулентными вихрями за единицу времени в единице
объема окружающей средой, как следствие существования пульсаций давления и расширения ( (представляющая собой работу,
совершаемую над турбулентными вихрями за единицу времени в единице
объема окружающей средой, как следствие существования пульсаций давления и расширения ( ) или сжатия ( ) или сжатия ( ) вихрей) может быть разной по знаку. Величина ) вихрей) может быть разной по знаку. Величина  положительна в
случае мелкомасштабной турбулентности, однако для крупномасштабных вихрей она
может быть как положительной, так и отрицательной (Колесниченко, Маров 1999).
Таким образом, из уравнения (11) следует, что в общем случае осредненная
энтропия положительна в
случае мелкомасштабной турбулентности, однако для крупномасштабных вихрей она
может быть как положительной, так и отрицательной (Колесниченко, Маров 1999).
Таким образом, из уравнения (11) следует, что в общем случае осредненная
энтропия  может как возрастать, так и уменьшаться, что
является характерной чертой открытых термодинамических систем. может как возрастать, так и уменьшаться, что
является характерной чертой открытых термодинамических систем.
Отсюда следует, что одной только
осредненной энтропии  не достаточно
для адекватного описания всех особенностей турбулизированной жидкости в физически элементарном объеме не достаточно
для адекватного описания всех особенностей турбулизированной жидкости в физически элементарном объеме  , поскольку она не
связана с какими-либо параметрами, характеризующих внутреннюю структуру подсистемы турбулентного хаоса, в частности,
с таким ключевым параметром, как энергия турбулентности (осредненная
пульсационная кинетическая энергия единицы массы среды) , поскольку она не
связана с какими-либо параметрами, характеризующих внутреннюю структуру подсистемы турбулентного хаоса, в частности,
с таким ключевым параметром, как энергия турбулентности (осредненная
пульсационная кинетическая энергия единицы массы среды)
 . (14) . (14)
В связи с этим, введем в рассмотрение термодинамику «турбулентной надструктуры»,
связанной с пульсационным движением среды (Блекейдер, 1955). Более того, для
макроскопического описания структурной турбулентности и, в частности, каскадного
процесса переноса турбулентной энергии вихрями разного размера, используем
известное обобщение формализма термодинамики необратимых процессов на среды с
внутренней структурой.
Термодинамика
подсистемы “турбулентного хаоса”. Итак, с макроскопической точки зрения квазистационарное состояние
физически элементарного объема  в окрестности точки в окрестности точки  в момент времени в момент времени  будем
охарактеризовать следующими характеристическими переменными, определяющими
структуру “хаоса”, – экстенсивными
переменными будем
охарактеризовать следующими характеристическими переменными, определяющими
структуру “хаоса”, – экстенсивными
переменными  (плотность
внутренней энергии турбулизации), (плотность
внутренней энергии турбулизации),  (удельный объем
среды) и (удельный объем
среды) и  (локальная
энтропия турбулизации). Обобщенная энтропия (локальная
энтропия турбулизации). Обобщенная энтропия связана с флуктуациями и динамическими изменениями в
квазистационарном состоянии так же, как локальная равновесная энтропия в квазиравновесном
состоянии. Поскольку, согласно принятой в данной работе концепции, основной чертой развитого турбулентного
движения является наличие большого числа
возбужденных макроскопических степеней свободы, то, кроме характеристических
переменных связана с флуктуациями и динамическими изменениями в
квазистационарном состоянии так же, как локальная равновесная энтропия в квазиравновесном
состоянии. Поскольку, согласно принятой в данной работе концепции, основной чертой развитого турбулентного
движения является наличие большого числа
возбужденных макроскопических степеней свободы, то, кроме характеристических
переменных  и и  , «сжатое» описание
подсистемы турбулентного хаоса будем
дополнительно охарактеризовать еще и некоторым
дискретным набором внутренних
параметров) , «сжатое» описание
подсистемы турбулентного хаоса будем
дополнительно охарактеризовать еще и некоторым
дискретным набором внутренних
параметров)  ( ( ), которые могут пульсировать около значения ), которые могут пульсировать около значения  , соответствующего устойчивому стационарному состоянию
(в некоторых случаях , соответствующего устойчивому стационарному состоянию
(в некоторых случаях  ). Будем предполагать, что набор локальных случайных
переменных ). Будем предполагать, что набор локальных случайных
переменных  (множество всех (множество всех
 составляет
векторнозначный стохастический процесс составляет
векторнозначный стохастический процесс   ), характеризующих структуру мелкомасштабной турбулентности внутри лагранжевого объема ), характеризующих структуру мелкомасштабной турбулентности внутри лагранжевого объема  , достаточен для полного описания состояния турбулентного
поля (вихревых образований в каскадном процессе взаимодействия турбулентных
движений разного масштаба, вихревых колец типа деформированного тора, вихревых
трубок, вихревых слоев и т.п.). В качестве параметров , достаточен для полного описания состояния турбулентного
поля (вихревых образований в каскадном процессе взаимодействия турбулентных
движений разного масштаба, вихревых колец типа деформированного тора, вихревых
трубок, вихревых слоев и т.п.). В качестве параметров  могут, в частности,
фигурировать пульсирующая скорость ( могут, в частности,
фигурировать пульсирующая скорость ( ), квадрат разности скоростей (температур) в двух достаточно
близких точках пространства, кинетическая энергия вихрей ( ), квадрат разности скоростей (температур) в двух достаточно
близких точках пространства, кинетическая энергия вихрей ( , скорость
диссипации энергии в вихрях ( , скорость
диссипации энергии в вихрях ( ), скорость
вырождения дисперсии температуры ( ), скорость
вырождения дисперсии температуры ( ; величина ; величина  определяет меру
неоднородности температурного поля, исчезающей в единицу времени за счет
молекулярной температуропроводности определяет меру
неоднородности температурного поля, исчезающей в единицу времени за счет
молекулярной температуропроводности  ), квадрат любой пространственной производной от
пульсационного поля скорости ( ), квадрат любой пространственной производной от
пульсационного поля скорости ( ), или размеры (волновые числа ), или размеры (волновые числа  ) вихрей. В данной работе для простоты будем считать,
что отдельные стохастические процессы ) вихрей. В данной работе для простоты будем считать,
что отдельные стохастические процессы  являются
статистически некоррелированными, тогда
не нарушая общности рассмотрения, можно ограничиться одним скалярнозначным
стохастическим процессом являются
статистически некоррелированными, тогда
не нарушая общности рассмотрения, можно ограничиться одним скалярнозначным
стохастическим процессом  ). ).
Следуя методу Гиббса (см., например, Мюнстер, 2002), выберем в качестве
локальной характеристической функции (содержащей все термодинамические сведения
о подсистеме турбулентного хаоса в стационарном состоянии) следующее фундаментальное
уравнение Гиббса (в интегральном виде) для обобщенной энтропии
 (15) (15)
это функциональное соотношение считается заданным a priori. Здесь параметр    представляет
собой удельную плотность, а величина представляет
собой удельную плотность, а величина  –
число вихревых структур (в единице объема), для которых характеризующий их набор внутренних координат лежит в интервале от –
число вихревых структур (в единице объема), для которых характеризующий их набор внутренних координат лежит в интервале от  до до  . Предполагая, что вихревые образования каким-то
образом локализованы как в координатном пространстве . Предполагая, что вихревые образования каким-то
образом локализованы как в координатном пространстве  , так и в конфигурационном пространстве , так и в конфигурационном пространстве  , будем считать, что
величины , будем считать, что
величины  можно
рассматривать как непрерывные функции координат и времени ( можно
рассматривать как непрерывные функции координат и времени ( ). Примем теперь, как это делается обычно в обобщенной
локально-равновесной термодинамике,
следующие определения сопряженных переменных ). Примем теперь, как это делается обычно в обобщенной
локально-равновесной термодинамике,
следующие определения сопряженных переменных  , ,  и и  (считая, что
все указанные производные положительны): (считая, что
все указанные производные положительны):
 , ,  , ,
  . .
Тогда, интенсивным переменным  и и  можно приписать смысл соответственно
обобщенных температуры и давления
(турбулизации), а величине можно приписать смысл соответственно
обобщенных температуры и давления
(турбулизации), а величине   - обобщенного химического потенциала для внутренних степеней свободы - обобщенного химического потенциала для внутренних степеней свободы  (Пригожин,
1960). Соответствующая дифференциальная форма фундаментального
уравнения Гиббса (15), записанная вдоль траектории движения центра масс
физически элементарного объема, принимает вид (Пригожин, Кондепуди, 2002) (Пригожин,
1960). Соответствующая дифференциальная форма фундаментального
уравнения Гиббса (15), записанная вдоль траектории движения центра масс
физически элементарного объема, принимает вид (Пригожин, Кондепуди, 2002)
   . (15*) . (15*)
Очевидно, что различные соотношения для
интенсивных переменных  , ,  и и  , которые могут быть получены обычным для термодинамики
способом из (15), допустимо интерпретировать
как “уравнения состояния” рассматриваемой подсистемы. , которые могут быть получены обычным для термодинамики
способом из (15), допустимо интерпретировать
как “уравнения состояния” рассматриваемой подсистемы.
Далее будем отождествлять
величину  с энергии турбулентности с энергии турбулентности
 , (16) , (16)
и полагать, что подсистема турбулентного
хаоса в термодинамическом смысле является идеальным классическим газом (с тремя
степенями свободы, по которым энергия распределена равномерно) – ключевые
гипотезы модели. Тогда, в частности,
имеем
 , ,  , (17) , (17)
где  - “газовая постоянная” для
вихревого конгломерата, - “газовая постоянная” для
вихревого конгломерата,  - постоянная Больцмана, - постоянная Больцмана,  - полное число вихревых
образований в единичном объеме конфигурационного пространства, - полное число вихревых
образований в единичном объеме конфигурационного пространства,  – так
называемая потенциальная энергия по внутренней координате – так
называемая потенциальная энергия по внутренней координате  , зависящая в
общем случае и от давления турбулизации , зависящая в
общем случае и от давления турбулизации  . Из (17) можно определить . Из (17) можно определить  как функцию переменной как функцию переменной  , если задано a
posteriori какое-либо распределение , если задано a
posteriori какое-либо распределение  , например, соответствующее статистически стационарному
состоянию турбулентного поля , например, соответствующее статистически стационарному
состоянию турбулентного поля  ). В этом случае, для постоянных ). В этом случае, для постоянных  и и  , энтропия
турбулизации , энтропия
турбулизации  должна быть
минимальной ), так что должна быть
минимальной ), так что  Поскольку
полное число вихревых молей Поскольку
полное число вихревых молей  постоянно,
справедливо также постоянно,
справедливо также  . Из этих двух условий следует, что стационарный
химический потенциал для конфигурации . Из этих двух условий следует, что стационарный
химический потенциал для конфигурации  не зависит от
координаты не зависит от
координаты  ( ( ); учитывая это, легко получить следующее
выражение ); учитывая это, легко получить следующее
выражение
 , (18) , (18)
которое может быть переписать в виде
 , ,  , (18*) , (18*)
являющемся
обобщением известной формулы Эйнштейна (для статистически равновесного
состояния) на стационарные состояния в пространстве конфигураций. Функция
 ( ( ) имеет смысл
плотности условной вероятности обнаружить систему в интервале ( ) имеет смысл
плотности условной вероятности обнаружить систему в интервале ( ) в момент времени ) в момент времени  , если в начальный момент (при , если в начальный момент (при  ) она с вероятностью,
равной единице, находилась в состоянии ) она с вероятностью,
равной единице, находилась в состоянии  . .
Для наших целей понадобится основное кинетическое уравнение
для скорости изменения числа вихревых молей  в каскадном
процессе взаимодействия турбулентных движений разного масштаба. Так как в
случае развитой турбулентности (при конечном, но большом числе в каскадном
процессе взаимодействия турбулентных движений разного масштаба. Так как в
случае развитой турбулентности (при конечном, но большом числе  ) имеется континуум
возбужденных степеней свободы, то далее будем предполагать, что ) имеется континуум
возбужденных степеней свободы, то далее будем предполагать, что  - параметр, принимающий
непрерывные значения. Это соответствует такому каскадному процессу разрушения
больших и образования мелких вихрей (на
языке химии этот процесс можно рассматривать как ряд последовательных реакций,
выражаемых схемой - параметр, принимающий
непрерывные значения. Это соответствует такому каскадному процессу разрушения
больших и образования мелких вихрей (на
языке химии этот процесс можно рассматривать как ряд последовательных реакций,
выражаемых схемой  ), при
котором в единичном акте взаимодействия
происходят только бесконечно малые изменения величин ), при
котором в единичном акте взаимодействия
происходят только бесконечно малые изменения величин  , тогда как конечные изменения возникают благодаря
кумулятивному действию большого числа
вихревых взаимодействий. Кроме этого будем считать, что механизм каскадного дробления вихрей, связанный с переходом
кинетической энергии от крупных вихрей
ко все более мелким, таков, что среда
“сохраняет память” только лишь о последнем переходе (марковский процесс). Тогда
кинетическое уравнение для скорости изменения числа вихревых молей может
быть записано в форме уравнения
неразрывности (в координатном пространстве и
пространстве внутренней координаты , тогда как конечные изменения возникают благодаря
кумулятивному действию большого числа
вихревых взаимодействий. Кроме этого будем считать, что механизм каскадного дробления вихрей, связанный с переходом
кинетической энергии от крупных вихрей
ко все более мелким, таков, что среда
“сохраняет память” только лишь о последнем переходе (марковский процесс). Тогда
кинетическое уравнение для скорости изменения числа вихревых молей может
быть записано в форме уравнения
неразрывности (в координатном пространстве и
пространстве внутренней координаты  ) следующим образом ) следующим образом
 ,
(19) ,
(19)
или для одного
стохастического процесса  , с учетом (6), в виде , с учетом (6), в виде
 , (19*) , (19*)
где  – термодинамический поток в пространстве
внутренней координаты – термодинамический поток в пространстве
внутренней координаты  (точнее поток
вероятности в состоянии (точнее поток
вероятности в состоянии  ). ).
Используя (19*), преобразуем тождество Гиббса (15) путем интегрирования по частям (и в предположении, что поток  обращается в нуль на обеих границах обращается в нуль на обеих границах  и и  области определения
переменной области определения
переменной  –
следствие условия –
следствие условия  ) к виду: ) к виду:
 . (20) . (20)
Последний член этого уравнения
 . (21) . (21)
описывает суммарный рост энтропии турбулизации,
обусловленный необратимыми процессами образования вихревых структур «сорта»  . Из выражения (21) видно, что локальное производство
пульсационной энтропии . Из выражения (21) видно, что локальное производство
пульсационной энтропии  , соответствующее каждой части пространства внутренней
координаты , соответствующее каждой части пространства внутренней
координаты  , имеет
обычную термодинамическую форму , имеет
обычную термодинамическую форму   , где , где

 (22) (22)
– обобщенное химическое сродство для конфигурации  (функция
состояния подсистемы турбулентного хаоса),
записанное здесь с учетом (17) для обобщенного химического потенциала (функция
состояния подсистемы турбулентного хаоса),
записанное здесь с учетом (17) для обобщенного химического потенциала  . .
Уравнение переноса для
энтропии турбулизации  получим из
(20), используя тот же образ действий,
который привел к уравнению (11). Исключая из (20) субстанциональные производные
от удельного объема получим из
(20), используя тот же образ действий,
который привел к уравнению (11). Исключая из (20) субстанциональные производные
от удельного объема  и турбулентной
энергии и турбулентной
энергии  («точное»
уравнение для определения которой
имеет вид («точное»
уравнение для определения которой
имеет вид
 , (23) , (23)
(см., например, Колесниченко, 1998)), в
результате будем иметь:
 , (24) , (24)
где
 , (25) , (25)

 . (26) . (26)
Здесь  - диффузионный поток
турбулентной энергии; - диффузионный поток
турбулентной энергии;  - часть с нулевым следом тензора турбулентных напряжений, определяемая соотношением - часть с нулевым следом тензора турбулентных напряжений, определяемая соотношением
 , ,  , ,
а величины  и и  имеют смысл,
соответственно, локального производства и стока энтропии имеют смысл,
соответственно, локального производства и стока энтропии  подсистемы
турбулентного хаоса. Отметим, что работа турбулентных напряжений подсистемы
турбулентного хаоса. Отметим, что работа турбулентных напряжений  приводит к
росту энтропии хаоса, в то время как вязкая диссипация приводит к
росту энтропии хаоса, в то время как вязкая диссипация  уменьшает
энтропию турбулизации уменьшает
энтропию турбулизации  . .
Балансовое уравнение для суммарной энтропии. Суммируя (11) и
(24), найдем уравнение баланса для суммарной энтропии  системы системы
 ,
(27) ,
(27)
где
  (28) (28)
- локальное производство энтропии, связанное с необратимыми процессами внутри всего турбулизованного континуума. Величина  , записанная с учетом формул (12), (13) и (25), (26)
имеет структуру билинейной формы , записанная с учетом формул (12), (13) и (25), (26)
имеет структуру билинейной формы  : :

  . (29) . (29)
Согласно основному постулату термодинамики неравновесных процессов, в случае
системы, находящейся вблизи локально равновесных или устойчивых стационарных
состояний, термодинамические потоки можно представить в виде линейных функций
от сопряженных макроскопических сил:   (де Гроот, Мазур, 1964). Таким образом,
формула (29) позволяет найти замыкающие градиентные соотношения для трех
основных областей турбулизованного
течения: для ламинарной области; для зоны развитого турбулентного течения, в
которой турбулентные потоки намного эффективнее соответствующих осредненных
молекулярных потоков ( (де Гроот, Мазур, 1964). Таким образом,
формула (29) позволяет найти замыкающие градиентные соотношения для трех
основных областей турбулизованного
течения: для ламинарной области; для зоны развитого турбулентного течения, в
которой турбулентные потоки намного эффективнее соответствующих осредненных
молекулярных потоков ( , ,  и т.п.); для
буферного слоя – промежуточной области, в которой эффективности осредненного
молекулярного и турбулентного переноса сравнимы по значимости (см. Колесниченко,
1998; Маров, Колесниченко, 2001). Важно подчеркнуть, что матрица феноменологических
коэффициентов и т.п.); для
буферного слоя – промежуточной области, в которой эффективности осредненного
молекулярного и турбулентного переноса сравнимы по значимости (см. Колесниченко,
1998; Маров, Колесниченко, 2001). Важно подчеркнуть, что матрица феноменологических
коэффициентов  для
турбулизованного континуума будет
зависеть не только от осредненных параметров состояния (температуры, плотности
и т.п.), но и от характеристик самой турбулентной надструктуры, т.е. от
параметров для
турбулизованного континуума будет
зависеть не только от осредненных параметров состояния (температуры, плотности
и т.п.), но и от характеристик самой турбулентной надструктуры, т.е. от
параметров  , ,  , ,  и т.п. Подобная
ситуация (функциональная зависимость и т.п. Подобная
ситуация (функциональная зависимость  от самих термодинамических потоков от самих термодинамических потоков  , например, от
скорости диссипации , например, от
скорости диссипации  ), типичная, как известно, для самоорганизующихся систем (Хакен, 1985; 1991), может привести, вообще говоря, к тому, что отдельные слагаемые ), типичная, как известно, для самоорганизующихся систем (Хакен, 1985; 1991), может привести, вообще говоря, к тому, что отдельные слагаемые  в сумме в сумме  не будут
положительно определенными, хотя вся
сумма не будут
положительно определенными, хотя вся
сумма  . Для этого
случая суперпозиция различных потоков в
принципе может приводить к отрицательным значениям отдельных диагональных
элементов матрицы . Для этого
случая суперпозиция различных потоков в
принципе может приводить к отрицательным значениям отдельных диагональных
элементов матрицы  , чем,
вероятно, и объясняется эффект отрицательной вязкости, в некоторых турбулентных
течениях (см. ниже). , чем,
вероятно, и объясняется эффект отрицательной вязкости, в некоторых турбулентных
течениях (см. ниже).
Как видно из (29),
спектр возможных перекрестных эффектов для
турбулентного режима течения расширяется по сравнению с ламинарным
режимом. Так, например, поток тепла  в
турбулизованном континууме возможен не только под влиянием сопряженной
с ним термодинамической силы в
турбулизованном континууме возможен не только под влиянием сопряженной
с ним термодинамической силы  , но и силы , но и силы  , сопряженной с потоком , сопряженной с потоком  (описывающим “диффузионный”
перенос турбулентной кинетической
энергии). Однако в настоящее время нет
надежных экспериментальных данных, количественно описывающих перекрестные
эффекты подобного рода. Кроме этого, обычно вклад любых перекрестных эффектов в
общую скорость процесса на порядок меньше по сравнению с прямыми эффектами (де
Гроот, Мазур, 1964). Учитывая это
обстоятельство, будем далее пользоваться требованиями положительности
интенсивностей (описывающим “диффузионный”
перенос турбулентной кинетической
энергии). Однако в настоящее время нет
надежных экспериментальных данных, количественно описывающих перекрестные
эффекты подобного рода. Кроме этого, обычно вклад любых перекрестных эффектов в
общую скорость процесса на порядок меньше по сравнению с прямыми эффектами (де
Гроот, Мазур, 1964). Учитывая это
обстоятельство, будем далее пользоваться требованиями положительности
интенсивностей  , ,  независимо друг от друга, а также, без специальных
оговорок, опускать ряд перекрестных эффектов в линейных конститутивных
соотношениях. независимо друг от друга, а также, без специальных
оговорок, опускать ряд перекрестных эффектов в линейных конститутивных
соотношениях.
Закончим
настоящий раздел следующим замечанием:
последнее слагаемое в правой части (29), описывающее производство энтропии внутри полной системы за счет необратимого обмена энтропией между
подсистемами турбулентного хаоса и осредненного движения, в силу второго закона термодинамики всегда положительно
 . (30) . (30)
Поэтому, “направление”
термодинамического потока  определяется
знаком функции состояния определяется
знаком функции состояния  , которую
следует рассматривать как сопряженную термодинамическую силу
(макроскопическую причину), вызывающую этот поток энтропии. Известно, что подобный обмен энтропией между
двумя взаимно открытыми подсистемами является
непременным условием структурированного коллективного поведения,
т.е. может быть источником
самоорганизации в одной из них (Пригожин, Стенгерс, 1994). , которую
следует рассматривать как сопряженную термодинамическую силу
(макроскопическую причину), вызывающую этот поток энтропии. Известно, что подобный обмен энтропией между
двумя взаимно открытыми подсистемами является
непременным условием структурированного коллективного поведения,
т.е. может быть источником
самоорганизации в одной из них (Пригожин, Стенгерс, 1994).
Покажем теперь, что
диссипативная активность подсистемы турбулентного хаоса в случае
стационарно-неравновесного состояния как раз и определяется притоком
отрицательной энтропии ( ) от подсистемы осредненного движения. ) от подсистемы осредненного движения.
3.
Стационарно-неравновесное состояние.
эволюционные уравнения в конфигурационном пространстве
Рассмотрим методами
статистической термодинамики необратимых процессов важнейший режим развитого
турбулентного движения жидкости – линейный )
режим стационарно-неравновесной турбулентности. Ясно, что для его реализации должен
существовать какой-то постоянно действующий механизм турбулизации среды
(проволочная решетка, установленная перпендикулярно к вынужденному течению жидкости, производящая турбулентность; стационарные граничные условия, вызывающие,
например, крупномасштабный сдвиг скорости течения или термоконвективную
крупномасштабную неустойчивость), передающий энергию вихревому движению на
больших масштабах и не позволяющий системе достигнуть полного термодинамического
равновесия. Мощность подобного источника энергии должна быть такой, чтобы скомпенсировать расход турбулентной
энергии, рассеиваемой за счет молекулярной вязкости. Для этого режима практически вся расходуемая
энергия без сколько-нибудь существенных (но, вообще говоря, имеющих место быть) потерь будет передаваться
через инерционный интервал от энергетического к вязкому интервалу, причем
процесс передачи энергии от крупномасштабных вихрей к малым, может быть наглядно представлен как процесс дробление
вихрей. Очевидно, что тогда в структуре подсистемы турбулентного хаоса устанавливается такое неравновесное
стационарное состояние, при
котором  (Пригожин, Кондепуди, 2002). Это означает ),
что производство (Пригожин, Кондепуди, 2002). Это означает ),
что производство  энтропии энтропии  в такой степени
компенсируется ее оттоком в такой степени
компенсируется ее оттоком  , что суммарное возникновение энтропии , что суммарное возникновение энтропии  отсутствует ( отсутствует ( ); поток энтропии турбулизации в стационарном случае
постоянен ( ); поток энтропии турбулизации в стационарном случае
постоянен ( ). Так как ). Так как  , то справедливо выражение , то справедливо выражение  , т.е. подсистема турбулентного хаоса должна
экспортировать энтропию во “внешнюю среду” (отдавать подсистеме осредненного
движения), чтобы скомпенсировать производство энтропии за счет внутренних
необратимых процессов. Другими словами для поддержания стационарного состояния
внутри подсистемы турбулентного хаоса необходим приток отрицательной
энтропии (негэнтропии) от “внешней
среды” (подсистемы осредненного движения), , т.е. подсистема турбулентного хаоса должна
экспортировать энтропию во “внешнюю среду” (отдавать подсистеме осредненного
движения), чтобы скомпенсировать производство энтропии за счет внутренних
необратимых процессов. Другими словами для поддержания стационарного состояния
внутри подсистемы турбулентного хаоса необходим приток отрицательной
энтропии (негэнтропии) от “внешней
среды” (подсистемы осредненного движения),
  (эта поступающая в
подсистему негэнтропия расходуется на поддержание и совершенствование
внутренней структуры подсистемы турбулентного хаоса). Но тогда справедливо
соотношение (эта поступающая в
подсистему негэнтропия расходуется на поддержание и совершенствование
внутренней структуры подсистемы турбулентного хаоса). Но тогда справедливо
соотношение   , и уравнение (11) баланса осредненной энтропии системы , и уравнение (11) баланса осредненной энтропии системы  принимает
вид принимает
вид
 , (31) , (31)
где для локального
рассеяния энергии  справедливо
выражение справедливо
выражение
 . (32) . (32)
Здесь  - суммарный поток тепла
в подсистеме среднего движения для
режима развитой турбулентности. - суммарный поток тепла
в подсистеме среднего движения для
режима развитой турбулентности.
Поскольку в
стационарно-неравновесном состоянии величина оттока энтропии из подсистемы
осредненного движения положительна ( ) , то скорость ) , то скорость  обмена
энтропией (теплом) между осредненным и
турбулентным движениями также положительна, обмена
энтропией (теплом) между осредненным и
турбулентным движениями также положительна,  . Но тогда из неравенства (30) следует, что температура турбулизации . Но тогда из неравенства (30) следует, что температура турбулизации  выше осредненной температуры турбулизованного
континуума ( выше осредненной температуры турбулизованного
континуума ( ), что находится в полном согласии с основным синергетическим принципом о
самоорганизации диссипативной системы. В соответствии с этим принципом,
образование упорядоченных структур (в нашем случае разномасштабных вихревых
образований в подсистеме турбулентного хаоса) при отводе тепла из системы, т.е.
при переходе к более низким температурам, является универсальным свойством материи. ), что находится в полном согласии с основным синергетическим принципом о
самоорганизации диссипативной системы. В соответствии с этим принципом,
образование упорядоченных структур (в нашем случае разномасштабных вихревых
образований в подсистеме турбулентного хаоса) при отводе тепла из системы, т.е.
при переходе к более низким температурам, является универсальным свойством материи.
Исходя из (32), можно записать в линейном приближении и при
использовании принципа Кюри-Пригожина (согласно которому связь между тензорами
различного ранга в изотропной среде невозможна (де Гроот, Мазур, 1974)), следующие обобщенные реологические
соотношения для турбулентных потоков и сопряженных им термодинамических сил:
 , (33) , (33)
 , (34) , (34)
 , (35) , (35)
соответствующие
режиму стационарно-неравновесного состояния турбулентного поля. Феноменологические коэффициенты
(коэффициенты турбулентного обмена)    в этих
соотношениях являются скалярными величинами, поскольку сильная турбулентность,
является локально однородной и изотропной. Как было отмечено выше, эти
величины, в отличие от коэффициентов молекулярного обмена, не являются материальными константами. Это
обстоятельство связано с тем, что в турбулизованном континууме разнообразные
процессы переноса (вещества, импульса и энергии) из одной области системы в
другую, определяются коллективными движениями молекул (вихревыми образованиями), и, следовательно, должны зависеть от параметров интенсивности
турбулентности, в частности, от
параметров в этих
соотношениях являются скалярными величинами, поскольку сильная турбулентность,
является локально однородной и изотропной. Как было отмечено выше, эти
величины, в отличие от коэффициентов молекулярного обмена, не являются материальными константами. Это
обстоятельство связано с тем, что в турбулизованном континууме разнообразные
процессы переноса (вещества, импульса и энергии) из одной области системы в
другую, определяются коллективными движениями молекул (вихревыми образованиями), и, следовательно, должны зависеть от параметров интенсивности
турбулентности, в частности, от
параметров  и и  (или (или  ). Так, например, в
инерциальном интервале масштабов вихрей ( ). Так, например, в
инерциальном интервале масштабов вихрей ( ), коэффициент турбулентной вязкости ), коэффициент турбулентной вязкости  , отвечающий эмпирическому “закону четырех третей” Ричардсона-Обухова (этот закон следует,
в частности, из соображений теории
размерности и подобия) имеет вид: , отвечающий эмпирическому “закону четырех третей” Ричардсона-Обухова (этот закон следует,
в частности, из соображений теории
размерности и подобия) имеет вид:   . .
Таким образом, при
моделировании стационарно-неоднородной турбулентности в тех приложениях, когда
важны процессы диссипации энергии в
системе, необходимо привлекать к рассмотрению
уравнение переноса тепла для
осредненного движения в виде (31); это уравнение должно быть дополнено
линейными определяющими соотношениями (33)-(35).
Применение
пригожинского принципа. Согласно
формуле (35), феноменологическое соотношение
для термодинамического потока  в
пространстве внутренней координаты в
пространстве внутренней координаты  и
соответствующего «мгновенного» сродства и
соответствующего «мгновенного» сродства  (формула
(22)) имеет в общем случае
интегральный вид. Вслед за
Пригожиным (1960), будем теперь
считать, что в каждой части внутреннего
координатного пространства необратимые
процессы идут в таком направлении, что происходит только положительное
приращение энтропии. Это означает, что положительным будет не только интеграл
(21), но и величина (формула
(22)) имеет в общем случае
интегральный вид. Вслед за
Пригожиным (1960), будем теперь
считать, что в каждой части внутреннего
координатного пространства необратимые
процессы идут в таком направлении, что происходит только положительное
приращение энтропии. Это означает, что положительным будет не только интеграл
(21), но и величина  , представляющая собой рассеяние энергии на единицу
объема внутреннего пространства конфигураций. Тогда определяющее соотношение,
связывающее поток вероятности , представляющая собой рассеяние энергии на единицу
объема внутреннего пространства конфигураций. Тогда определяющее соотношение,
связывающее поток вероятности  и сродство и сродство  состояния состояния  , соответствующее протеканию одного эквивалента
процесса распада вихрей есть просто , соответствующее протеканию одного эквивалента
процесса распада вихрей есть просто
 , (36) , (36)
где  - онзагеровский коэффициент. - онзагеровский коэффициент.
Покажем теперь, что
предположение (36) позволяет
находить нелинейные определяющие соотношения для суммарных потоков,
связанных с внутренним параметром, а также
может служить основой для получения эволюционных уравнений в частных
производных (уравнений Фоккера-Планка в конфигурационном пространстве  ) для функций распределения различных статистических
характеристик мелкомасштабной турбулентности,
если относительно последних приняты какие-то гипотезы распределения в
стационарно-неравновесном состоянии. Следует, однако, иметь в виду, что почти
всегда подобного рода гипотезы не вполне строги и являются идеализацией или
упрощением турбулентного движения в естественных условиях (Монин, Яглом, 1996). ) для функций распределения различных статистических
характеристик мелкомасштабной турбулентности,
если относительно последних приняты какие-то гипотезы распределения в
стационарно-неравновесном состоянии. Следует, однако, иметь в виду, что почти
всегда подобного рода гипотезы не вполне строги и являются идеализацией или
упрощением турбулентного движения в естественных условиях (Монин, Яглом, 1996).
Эволюция вихрей в пространстве пульсирующих
скоростей. Применим сначала пригожинский принцип (36) к выводу кинетического
уравнения, описывающего изменение
во времени функции плотности условной вероятности распределения вихревых скоростей  . Эта функция рассматривается далее, как внутренняя
переменная подсистемы турбулентного хаоса, а пульсирующая скорость . Эта функция рассматривается далее, как внутренняя
переменная подсистемы турбулентного хаоса, а пульсирующая скорость  - как внутренняя координата - как внутренняя координата  . Из физической кинетики ясно, что эволюция подобной функции распределения в приближении
непрерывного взаимодействия вихрей должна описываться в конфигурационном
пространстве . Из физической кинетики ясно, что эволюция подобной функции распределения в приближении
непрерывного взаимодействия вихрей должна описываться в конфигурационном
пространстве  уравнением типа
Фоккера-Планка. Получим его здесь термодинамически. уравнением типа
Фоккера-Планка. Получим его здесь термодинамически.
Известно, что функция распределения вероятностей пульсирующей скорости не является
универсальной в случае развитой турбулентности, поскольку она зависит от механизма,
порождающего турбулентное поле. Тем не менее, следуя Миллионщикову (1941),
используем далее гипотезу о нормальном распределении пульсирующих скоростей
(для локально изотропного турбулентного поля) в стационарном случае
 . (37) . (37)
Подобное распределении Миллионщиков применил в теории
турбулентности для специальных целей, которые здесь мы обсуждать не будем.
Заметим только, что есть много примеров, когда функция распределения скорости
приближенно оказывается гауссовской, например в турбулентности, порождаемой
решетками в аэродинамических трубах, или для турбулентности в атмосферном
пограничном слое (см., например, Бэтчелор, 1955; Фриш, 1998). Для
рассматриваемой нами подсистемы
турбулентного хаоса постоянную  в (37) можно связать с температурой
турбулизации в (37) можно связать с температурой
турбулизации  точно таким
же способом, как это делается в кинетической теории газов. Используя (17)
и (37), легко найти, что точно таким
же способом, как это делается в кинетической теории газов. Используя (17)
и (37), легко найти, что   , откуда для , откуда для  следует
другое эквивалентное выражение следует
другое эквивалентное выражение
  (37*) (37*)
Подставляя это
распределение в (17), получим следующее
выражение химического потенциала  для
конфигурации для
конфигурации  : :
 . (38) . (38)
С
учетом этой формулы, феноменологическое уравнение (36)) для потока
вероятности  принимает
вид принимает
вид
 . (39) . (39)
где  . Здесь введен коэффициент . Здесь введен коэффициент  , который
может быть интерпретирован, как «подвижность»
в пространстве внутренней координаты , который
может быть интерпретирован, как «подвижность»
в пространстве внутренней координаты  на единицу
объема; в первом приближении этот коэффициент не зависит от на единицу
объема; в первом приближении этот коэффициент не зависит от  и по
предположению от величины и по
предположению от величины  . При подстановке (39) в (19), получим искомое кинетическое уравнение
Фоккера-Планка для функции плотности условной вероятности пульсационной
скорости . При подстановке (39) в (19), получим искомое кинетическое уравнение
Фоккера-Планка для функции плотности условной вероятности пульсационной
скорости  : :

 (40) (40)
Это динамическое уравнение,
дополненное начальным условием   (справа
стоит (справа
стоит  -функция, сосредоточенная в точке -функция, сосредоточенная в точке  ), описывает временную эволюцию функции плотности
распределения условной вероятности ), описывает временную эволюцию функции плотности
распределения условной вероятности  пульсирующей
скорости пульсирующей
скорости  , в частности, для затухающей (вырождающейся) турбулентности. Следует
отметить, что величина , в частности, для затухающей (вырождающейся) турбулентности. Следует
отметить, что величина  (коэффициент
трения в соответствующем уравнении Ланжевена) играет роль коэффициента дрейфа в
стандартной записи уравнения Фоккера-Планка, а величина (коэффициент
трения в соответствующем уравнении Ланжевена) играет роль коэффициента дрейфа в
стандартной записи уравнения Фоккера-Планка, а величина  имеет смысл
коэффициента диффузии. имеет смысл
коэффициента диффузии.
Нормальное
распределение (37), являющееся стационарным решением одномерного по параметру 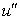 уравнения
Фоккера-Планка (40), можно принять за начальное статистическое
состояние поля пульсирующих скоростей для целого класса различных движений
вырождающейся турбулентности. Тогда
нестационарное решение этого уравнения
удается построить в аналитически замкнутом виде (см., например, Хакен, 1985): уравнения
Фоккера-Планка (40), можно принять за начальное статистическое
состояние поля пульсирующих скоростей для целого класса различных движений
вырождающейся турбулентности. Тогда
нестационарное решение этого уравнения
удается построить в аналитически замкнутом виде (см., например, Хакен, 1985):
 , (41) , (41)
где
 , ,  ; (42) ; (42)
 и и  - начальные условия. Это решение позволяет рассчитать различные - начальные условия. Это решение позволяет рассчитать различные  –точечные моменты (корреляционные функции) –точечные моменты (корреляционные функции)  –го порядка, описывающие статистическую связь
между случайными скоростями в различных точках пространства-времени. В
частности, для величин –го порядка, описывающие статистическую связь
между случайными скоростями в различных точках пространства-времени. В
частности, для величин  (условная
средняя скорость ансамбля вихрей в момент времени (условная
средняя скорость ансамбля вихрей в момент времени  ) и ) и  (двух
временная одноточечная корреляционная функция) имеем: (двух
временная одноточечная корреляционная функция) имеем:
 , (откуда , (откуда
 ), (43) ), (43)

 ,
(44) ,
(44)
где среднее берется по стохастическому
процессу. Здесь  - совместная плотность
вероятности, которая в силу марковости процесса зарождения новых мод пульсационного движения (дробления вихревых
образований) представляется в виде произведения плотности вероятности в момент - совместная плотность
вероятности, которая в силу марковости процесса зарождения новых мод пульсационного движения (дробления вихревых
образований) представляется в виде произведения плотности вероятности в момент  , ,  , и условной
вероятности , и условной
вероятности  (сводящейся
в момент (сводящейся
в момент  к к  -функции -функции  ): ):  . .
Так как  , то из (44) следует, во-первых, правильное соотношение , то из (44) следует, во-первых, правильное соотношение  , которое согласуется с предположением о
локальной изотропности вихревого поля скоростей в случае развитой турбулентности, и, во вторых, эффективная формула
для одной из наиболее важных величин в
теории статистической турбулентности , которое согласуется с предположением о
локальной изотропности вихревого поля скоростей в случае развитой турбулентности, и, во вторых, эффективная формула
для одной из наиболее важных величин в
теории статистической турбулентности
 , (45) , (45)
которая определяет, как быстро пульсационная
скорость «забывает свое прошлое» (согласно (45) - за время порядка  ). ).
Решение (41) при нулевых значениях параметров  и и  принимает
вид принимает
вид
 , (46) , (46)
позволяющий проследить временную
эволюцию функции распределения условной вероятности для пульсирующей скорости, если при стационарном режиме турбулентности
распределение по скоростям было гауссовским.
В заключение следует
отметить, что некоторые предположения,
используемые при выводе формулы (46), сделаны лишь для упрощения и вовсе не
являются необходимыми. Более того,
выбор пульсирующей скорости  в качестве
подходящей характеристики вихрей (внутренней координаты подсистемы
турбулентного хаоса), очевидно, не
всегда себя оправдывает, поскольку гауссовское распределение вероятностей пульсирующей скорости в качестве
подходящей характеристики вихрей (внутренней координаты подсистемы
турбулентного хаоса), очевидно, не
всегда себя оправдывает, поскольку гауссовское распределение вероятностей пульсирующей скорости  не
подтвердилась с достаточной степенью надежности ни экспериментально
(установлено, например, что за решеткой
отклонение от нормальности возрастают с ростом числа Рейнольдса не
подтвердилась с достаточной степенью надежности ни экспериментально
(установлено, например, что за решеткой
отклонение от нормальности возрастают с ростом числа Рейнольдса  ), ни теоретически (для этого распределения законы
“двух и пяти третей” нарушаются). ), ни теоретически (для этого распределения законы
“двух и пяти третей” нарушаются).
Ранее мы уже
указывали, что наиболее приемлемыми характеристиками мелкомасштабной
турбулентности на роль внутренней координаты являются, по-видимому,
неотрицательные макроскопические переменные (– четные функции скоростей), типа
кинетической энергии вихрей,
скорости диссипации энергии и
т.п. Подобные случайные характеристики, согласно гипотезе Колмогорова,
асимптотически удовлетворяют логарифмически нормальному распределению
вероятностей. Это объясняется тем, что процесс последовательного дробления
вихревых образований подобен процессу коагуляции твердых частиц (а последний приводит, как
известно, к логнормальному распределению частиц по размерам (см.,
например, Монин, Яглом, 1996). Вместе с
тем, важно подчеркнуть, что логнормальное распределение не описывает аккуратно
края истинного распределения данной
случайной переменной и поэтому с
большой осмотрительностью может быть использовано для вычисления старших
моментов.
Применим теперь
пригожинский принцип (36) к выводу
кинетического уравнения, описывающего временную эволюцию функции распределения вихрей в пространстве
кинетической энергии.
Каскадный процесс (термодинамическое рассмотрение, соответствующее первоначальным гипотезам
подобия Колмогорова). Итак, будем описывать каскадный процесс
Ричардсона-Колмогорова (крупные вихри мелкие вихри мелкие вихри теплота) аналогично процессу последовательных
химических реакций. В этом случае исходное кинетическое уравнение (19) для
функции распределения теплота) аналогично процессу последовательных
химических реакций. В этом случае исходное кинетическое уравнение (19) для
функции распределения  вихрей в
пространстве энергии ( вихрей в
пространстве энергии ( ) может быть переписано в виде ) может быть переписано в виде
 , (47) , (47)
где
  . (48) . (48)
– скорость реакции перехода из состояния  в состояние в состояние  , соответствующая потоку вероятности , соответствующая потоку вероятности  в состоянии в состоянии  . Другими словами соотношение (48) определяет параметр . Другими словами соотношение (48) определяет параметр  , который в рассматриваемом случае можно
интерпретировать, как скорость передачи кинетической энергии , который в рассматриваемом случае можно
интерпретировать, как скорость передачи кинетической энергии  по иерархии вихрей
вдоль координаты по иерархии вихрей
вдоль координаты  ;
одновременно эта величина определяет и среднее значение диссипации кинетической энергии в вихрях сорта ;
одновременно эта величина определяет и среднее значение диссипации кинетической энергии в вихрях сорта  .
Действительно, уравнение для первого момента .
Действительно, уравнение для первого момента   , получаемое из (47)
в результате интегрирования по частям (и в предположении, что на границах области интегрирования поток , получаемое из (47)
в результате интегрирования по частям (и в предположении, что на границах области интегрирования поток  равен нулю,
имеет вид равен нулю,
имеет вид
 , (49) , (49)
(здесь условное среднее берется по
стохастическому процессу  ). Параметр ). Параметр  в этом уравнении определяет
скорость диссипации турбулентной энергии в точке ( в этом уравнении определяет
скорость диссипации турбулентной энергии в точке ( (см., например, Ландау, Лифшиц, 1988). Поэтому и
возможна интерпретация величины (см., например, Ландау, Лифшиц, 1988). Поэтому и
возможна интерпретация величины  , как скорости диссипации энергии в вихрях сорта , как скорости диссипации энергии в вихрях сорта  (в точке (в точке  конфигурационного
пространства). Но тогда, для той части
энергии рассеяния конфигурационного
пространства). Но тогда, для той части
энергии рассеяния  (см. формулу
(32)), которая обусловлена передачей турбулентной энергии по каскаду, имеем (см. формулу
(32)), которая обусловлена передачей турбулентной энергии по каскаду, имеем
 . (50) . (50)
Отсюда следует локальное феноменологическое
уравнение пригожинского типа:
 ,
(51) ,
(51)
в котором
 (52) (52)
– химическое
сродство процесса дробления вихрей
(функция состояния подсистемы турбулентного хаоса);  – так называемая сила трения; – так называемая сила трения;  - коэффициент подвижности,
который по предположению не зависит от - коэффициент подвижности,
который по предположению не зависит от  . .
Если в турбулизованной среде
устанавливается такой стационарно-неравновесный режим течения, при котором скорость передачи энергии
по каскаду постоянна,  (предположение, принятое в первоначальной формулировке гипотез
Колмогорова), то неравенство (50) принимает вид (предположение, принятое в первоначальной формулировке гипотез
Колмогорова), то неравенство (50) принимает вид
 , (53) , (53)
где  – так называемое
глобальное сродство процесса образования турбулентных структур, которое с
учетом (52) может быть записано в виде – так называемое
глобальное сродство процесса образования турбулентных структур, которое с
учетом (52) может быть записано в виде
 (54) (54)
поскольку на
границах области интегрирования  обращается в нуль. Таким образом,
производство обращается в нуль. Таким образом,
производство  осредненной
энтропии в подобном стационарном
процессе имеет вид произведения общей скорости передачи энергии по каскаду осредненной
энтропии в подобном стационарном
процессе имеет вид произведения общей скорости передачи энергии по каскаду  и суммарного
сродства и суммарного
сродства  , относящегося ко всему каскадному
процессу в целом. В этом случае справедливо линейное феноменологическое
соотношение , относящегося ко всему каскадному
процессу в целом. В этом случае справедливо линейное феноменологическое
соотношение
 (55) (55)
в полном соответствии с результатами
необратимой термодинамики для последовательных (консекутивных) химических реакций (см., например, Пригожин, Кондепуди,
2002).
С другой стороны, условие квазистационарности (независимости
от параметра  ) термодинамического потока кинетической энергии по иерархии вихрей ) термодинамического потока кинетической энергии по иерархии вихрей  ,
рассматриваемое совместно с линейным соотношением (51), приводит к более общей, чем (55), нелинейной
связи между величиной ,
рассматриваемое совместно с линейным соотношением (51), приводит к более общей, чем (55), нелинейной
связи между величиной  и химическим сродством для каскадного процесса в целом,
определяемым формулой и химическим сродством для каскадного процесса в целом,
определяемым формулой   . Это нелинейное определяющее соотношение легко
может быть получено при применении второй
формулы (22) для величины “локального сродства” . Это нелинейное определяющее соотношение легко
может быть получено при применении второй
формулы (22) для величины “локального сродства”  ; в
результате будем иметь: ; в
результате будем иметь:
 , где , где  . (56) . (56)
(здесь  –
локальное значение колмогоровского микромасштаба). –
локальное значение колмогоровского микромасштаба).
Таким образом, использование двух интерпретаций параметра Колмогорова  , как величины, описывающей скорость диссипации энергии в тепло, и
одновременно являющейся скоростью
передачи турбулентной энергии по каскаду вихрей, позволило получить при термодинамическом моделировании
стационарно-неравновесной турбулентности определяющие соотношения (55) и (56)
для скорости диссипации , как величины, описывающей скорость диссипации энергии в тепло, и
одновременно являющейся скоростью
передачи турбулентной энергии по каскаду вихрей, позволило получить при термодинамическом моделировании
стационарно-неравновесной турбулентности определяющие соотношения (55) и (56)
для скорости диссипации  . Эти соотношения, замыкающие систему осредненных
гидродинамических уравнений (6)-(8), делают термодинамический подход к
моделированию развитой турбулентности самодостаточным. . Эти соотношения, замыкающие систему осредненных
гидродинамических уравнений (6)-(8), делают термодинамический подход к
моделированию развитой турбулентности самодостаточным.
В заключение отметим
следующее: На первый взгляд, условие возрастания энтропии суммарного континуума
(32) должно было бы, по аналогии с ламинарным движением жидкости, накладывать
определенные ограничения на коэффициенты турбулентного переноса в определяющих
соотношениях (33), (34) и (55).
Известно, что именно из условий подобного рода вытекает положительная
определенность прямых коэффициентов молекулярного обмена; при этом перекрестные
коэффициенты могут быть разными по знаку (Ландау, Лифшиц, 1988). Подставляя
соотношения (33), (34),(55) в выражение
(32) для производства суммарной энтропии турбулизованной системы, получим:
  (57) (57)
Как отмечалось выше, особенность специфики взаимодействия (связанная с функциональной зависимостью
турбулентных коэффициентов переноса
от параметров  и и  ) различных
диссипативных процессов в
турбулизованном континууме такова, что «отключение» одной из термодинамических
сил (например, сродства ) различных
диссипативных процессов в
турбулизованном континууме такова, что «отключение» одной из термодинамических
сил (например, сродства  ) может привести к изменению (или даже «отключению»)
каких-либо других процессов (например, вязких). Это означает, что второй закон термодинамики, требующий
положительности всей суммы (57) в целом,
не может, вообще говоря, быть
применен к отдельным ее слагаемым. Таким образом, может случиться, что, например, величина ) может привести к изменению (или даже «отключению»)
каких-либо других процессов (например, вязких). Это означает, что второй закон термодинамики, требующий
положительности всей суммы (57) в целом,
не может, вообще говоря, быть
применен к отдельным ее слагаемым. Таким образом, может случиться, что, например, величина
 , при
условии, что сумма , при
условии, что сумма  . А это указывает на возможность появления в
конкретных условиях таких турбулентных режимов течения, для которых коэффициент
турбулентной вязкости отрицателен, . А это указывает на возможность появления в
конкретных условиях таких турбулентных режимов течения, для которых коэффициент
турбулентной вязкости отрицателен,  . .
Термодинамическое рассмотрение каскада,
соответствующее уточненным гипотезам подобия Колмогорова. Наиболее важной
мелкомасштабной переменной является параметр Обухова  , определяемый формулой (3). Выше рассмотрен случай,
когда скорость передачи энергии по каскаду вихрей в пределах лагранжева объема , определяемый формулой (3). Выше рассмотрен случай,
когда скорость передачи энергии по каскаду вихрей в пределах лагранжева объема  постоянна (именно по
этой причине можно было не делать различия между постоянна (именно по
этой причине можно было не делать различия между  , ,  и и  ). Однако,
осредненная по малому (в пределах ). Однако,
осредненная по малому (в пределах  ) объему ) объему  , скорость диссипации , скорость диссипации  для
реального турбулентного движения является случайной функцией, пульсирующей
вместе с градиентом поля скоростей для
реального турбулентного движения является случайной функцией, пульсирующей
вместе с градиентом поля скоростей  . Используем
эту характеристику мелкомасштабной турбулентности в качестве внутренней координаты
подсистемы турбулентного хаоса ( . Используем
эту характеристику мелкомасштабной турбулентности в качестве внутренней координаты
подсистемы турбулентного хаоса ( ) и применим пригожинский принцип (36) к выводу кинетического уравнения
Фоккера-Планка, описывающего временную
эволюцию функции распределения условной вероятности ) и применим пригожинский принцип (36) к выводу кинетического уравнения
Фоккера-Планка, описывающего временную
эволюцию функции распределения условной вероятности  диссипации
турбулентной энергии диссипации
турбулентной энергии  . Это вероятностное уравнение будет содержать
параметры (в частности, число Рейнольдса), от значений которых зависит, в каком
состоянии находится система. . Это вероятностное уравнение будет содержать
параметры (в частности, число Рейнольдса), от значений которых зависит, в каком
состоянии находится система.
Итак, по современным представлениям случайная величина  в
стационарном состоянии имеет логарифмически нормальное распределение
вероятностей (Колмогоров, 1962), задаваемое формулой (4). Подставляя распределение (4) в (17), получим нужную для наших целей формулу
для химического потенциала в
стационарном состоянии имеет логарифмически нормальное распределение
вероятностей (Колмогоров, 1962), задаваемое формулой (4). Подставляя распределение (4) в (17), получим нужную для наших целей формулу
для химического потенциала  по внутренней
координате по внутренней
координате  : :
 , (58) , (58)
где
 (59) (59)
– потенциал силы трения  , фигурирующей также и в соответствующем
стохастическом уравнении Ланжевена , фигурирующей также и в соответствующем
стохастическом уравнении Ланжевена  ( ( –случайная «сила»).
Тогда локальное феноменологическое уравнение (36) для потока вероятности –случайная «сила»).
Тогда локальное феноменологическое уравнение (36) для потока вероятности  принимает
вид: принимает
вид:
 .
(60) .
(60)
Здесь  – коэффициент подвижности
в пространстве внутренней координаты – коэффициент подвижности
в пространстве внутренней координаты
 (который в
первом приближении не зависит от (который в
первом приближении не зависит от  и по предположению
от величины и по предположению
от величины  ), а
величина ), а
величина
 (61) (61)
определяет обобщенное химическое сродство
состояния  . .
Используя теперь формулу
Колмогорова (4) для дисперсии  , а также известные соотношения , а также известные соотношения  и и  для среднего
значения и медианы логнормального
распределения, найдем явное выражение для
силы трения для среднего
значения и медианы логнормального
распределения, найдем явное выражение для
силы трения  . В результате получим следующее выражение . В результате получим следующее выражение

 , (62) , (62)
зависящее, в частности, как от
параметра  , управляющего режимом движения в целом, так и от специфических особенностей крупномасштабных движений жидкости (через соотношение
Колмогорова , управляющего режимом движения в целом, так и от специфических особенностей крупномасштабных движений жидкости (через соотношение
Колмогорова   ; см. формулу (4)). ; см. формулу (4)).
Наконец, подставляя (60) в
(19), получим искомое кинетическое
уравнение для функции распределения вероятностей  в виде в виде
 . (63) . (63)
Здесь  - коэффициент
диффузии в конфигурационном пространстве - коэффициент
диффузии в конфигурационном пространстве  , отражающий наличие вихревой структуры подсистемы
турбулентного хаоса и являющейся источником так называемого “естественного
шума”. Специфика уравнения (63) такова, что влияние этого шума, а также
управляющих параметров (через , отражающий наличие вихревой структуры подсистемы
турбулентного хаоса и являющейся источником так называемого “естественного
шума”. Специфика уравнения (63) такова, что влияние этого шума, а также
управляющих параметров (через  ) на относительное увеличение флуктуаций скорости
передачи энергии по каскаду, существенно возрастает при приближении к
различного рода критическим точкам (Хакен, 1985, 1991) ).
В зависимости от численной величины числа Рейнольдса ) на относительное увеличение флуктуаций скорости
передачи энергии по каскаду, существенно возрастает при приближении к
различного рода критическим точкам (Хакен, 1985, 1991) ).
В зависимости от численной величины числа Рейнольдса  флуктуации
переменной флуктуации
переменной  (а вместе с ними и
величина (а вместе с ними и
величина  ) могут достигать таких
критических значений, при которых происходит определенная перестройка
турбулентного поля, связанная с образованием новых относительно устойчивых коллективных
движений (диссипативных вихревых структур), меняющих макроскопическое поведение
системы в целом; с подобной перестройкой связан, в частности, переход от течения с перемежаемостью к полной турбулизации потока. Однако, детальный
разбор механизма образования мелкомасштабных вихревых структур на основе
уравнения (62) лежит вне рамок настоящей работы. ) могут достигать таких
критических значений, при которых происходит определенная перестройка
турбулентного поля, связанная с образованием новых относительно устойчивых коллективных
движений (диссипативных вихревых структур), меняющих макроскопическое поведение
системы в целом; с подобной перестройкой связан, в частности, переход от течения с перемежаемостью к полной турбулизации потока. Однако, детальный
разбор механизма образования мелкомасштабных вихревых структур на основе
уравнения (62) лежит вне рамок настоящей работы.
Уравнение для первого
момента
 , (64) , (64)
легко получаемое путем интегрирования (63) по частям (в предположении, что на границах области интегрирования потоки  равны
нулю), полностью замыкает осредненную
гидродинамическую систему (6)-(8). равны
нулю), полностью замыкает осредненную
гидродинамическую систему (6)-(8).
Таким образом, глубокая аналогия,
существующая между консекутивными химическими реакциями (А В В С С и т.д.) )
и каскадным процессом Ричардсона-Колмогорова
дробления вихрей с соответствующими химическим потенциалом и химическим
сродством, позволила провести методами
термодинамики необратимых процессов макроскопическое описание развитой
турбулентности, как процесса самоорганизации в открытой системе. Введение в
рассмотрение непрерывных внутренних
параметров, характеризующих возбуждаемые
макроскопические степени свободы, дало возможность получить кинетические
уравнения для функций распределения различных мелкомасштабных
характеристик турбулентного поля. При последующей конкретизации в задачах численного моделирования разнообразных астро- и геофизических
явлений, развитый выше синергетический подход к описанию стационарно-неравновесной
турбулентности несомненно получит свое дальнейшее уточнение и развитие. и т.д.) )
и каскадным процессом Ричардсона-Колмогорова
дробления вихрей с соответствующими химическим потенциалом и химическим
сродством, позволила провести методами
термодинамики необратимых процессов макроскопическое описание развитой
турбулентности, как процесса самоорганизации в открытой системе. Введение в
рассмотрение непрерывных внутренних
параметров, характеризующих возбуждаемые
макроскопические степени свободы, дало возможность получить кинетические
уравнения для функций распределения различных мелкомасштабных
характеристик турбулентного поля. При последующей конкретизации в задачах численного моделирования разнообразных астро- и геофизических
явлений, развитый выше синергетический подход к описанию стационарно-неравновесной
турбулентности несомненно получит свое дальнейшее уточнение и развитие.
Заключение
Кратко суммируем основные
результаты работы. В рамках синергетического подхода к сложным системам
проведено термодинамическое рассмотрение
стационарно-неравновесной трехмерной турбулентности с учетом процессов образования упорядоченных
диссипативных структур (вихревых пространственно-временных образований). Представление турбулизованного континуума в
виде термодинамического комплекса, состоящего из двух взаимно открытых
подсистем - подсистемы осредненного движения и подсистемы турбулентного хаоса, рассматриваемого, в свою
очередь, как ансамбль вихрей различных
пространственно-временных масштабов, позволило
получить методами неравновесной термодинамики определяющие соотношения
для турбулентных потоков и сил, которые наиболее полно описывают процессы
переноса и структурирования в нем. В развитие работ (Колесниченко, 1985, 1998;
Маров, Колесниченко, 2001) проведено построение гидродинамической модели стационарно-неравновесной
турбулентности, как процесса самоорганизации в открытой системе. Введение в
рассмотрение дополнительных случайных параметров среды, характеризующих
возбужденные макроскопические степени свободы сильно турбулизованного
континуума, дало возможность, при использовании постулата Пригожина
(касающегося направления необратимых процессов, локализованных в пространстве
конфигураций), термодинамически описать колмогоровский каскадный процесс и
получить разнообразные кинетические
уравнения Фоккера-Планка для функций распределения мелкомасштабных
характеристик турбулентности. Использование двух интерпретаций параметра Колмогорова, как скорости диссипации кинетической энергии в тепло под
влиянием молекулярной вязкости, и, одновременно
с этим, как скорости передачи
энергии по каскаду вихрей, позволило
найти нелинейные определяющие соотношения
и для этой величины, сделав тем
самым термодинамическое моделирование турбулентности самодостаточным.
Более глубокое понимание
феноменологии каскада Колмогорова, возможное на пути учета большого числа
статистически коррелированных стохастических процессов  (характеризующих вихревые пространственно-временные
образования), служит, в первую очередь, задаче создания
репрезентативных моделей сильно турбулизованных астро-геофизических сред и
выполнения на их основе соответствующих численных экспериментов. Вместе с тем,
проведенный уже здесь упрощенный термодинамический анализ стационарной
турбулентности и построенная на
его основе адекватная макроскопическая
модель, позволяют расширить наши представления о свойствах открытых
диссипативных гидродинамических систем, являющихся объектом изучения одного из
важнейших и быстро развивающихся направлений нелинейной динамики, включающего в
себя эволюцию хаотических движений и формирование упорядоченных диссипативных
структур. (характеризующих вихревые пространственно-временные
образования), служит, в первую очередь, задаче создания
репрезентативных моделей сильно турбулизованных астро-геофизических сред и
выполнения на их основе соответствующих численных экспериментов. Вместе с тем,
проведенный уже здесь упрощенный термодинамический анализ стационарной
турбулентности и построенная на
его основе адекватная макроскопическая
модель, позволяют расширить наши представления о свойствах открытых
диссипативных гидродинамических систем, являющихся объектом изучения одного из
важнейших и быстро развивающихся направлений нелинейной динамики, включающего в
себя эволюцию хаотических движений и формирование упорядоченных диссипативных
структур.
Двойственный характер
необратимых процессов, приводящих и к беспорядку вблизи равновесия и к
упорядоченности вдали от равновесия,
наглядно проявляется при анализе современных проблем турбулентности
макромира во всем разнообразии пространственно-временных масштабов, от вопросов
происхождения и нелинейной эволюции Вселенной, звездной и планетной космогонии,
до процессов в газовых оболочках небесных тел и формирования экосистем, в
которых возможны каскады пространственно-временных конфигураций. При таком
подходе гораздо более емким и глубоким становится понятие энтропии. Процитируем
в этой связи небольшой фрагмент из книги (Пригожин, Стенгерс, 1994): “Ясно, что сказанное - не более чем начало, но оно
очень существенно, поскольку иллюстрирует, сколь широкое поле исследований
открывает перед нами понятие хаоса, т.е. конструктивной роли необратимости. Мы
убеждены, что эти исследования приведут к новому облику науки, в центре которой
будет находиться проблема становления. Но каково бы ни было будущее науки, один
вывод ясен: без необратимых процессов невозможно описать окружающий нас мир”.
Основной задачей настоящей работы было
найти дополнительное подтверждение данному утверждению на пути исследования
стационарных турбулентных движений с использованием методов неравновесной
термодинамики, показав теоретически
возможность самоорганизации в такого рода открытых системах.
Работа выполнена при
финансовой поддержке Российского фонда фундаментальных исследований (гранты №
03-01-00032; № 02-02-16165)
Список литературы
де Гроот С., Мазур П. Неравновесная
термодинамика. М.: Мир, 1964. 456 с.
Браун, Рожко (Brown
G. L., Roshko A.) On density effects and large structures in turbulent
mixing layers// J. Fluid Mech. 1974. V.
64. P. 775-816.
Блекейдер (Blackadar
A.K.).
Extension of the laws of thermodynamics to turbulent system//J. Meteorology.
1955. V.12. P.165-175.
Бэтчелор
Дж.
Теоория однородной турбулентности. М.: Ин. лит., 1955. 197 с.
Колесниченко А.В. Соотношения
Стефана-Максвелла и поток тепла для турбулентных многокомпонентных сплошных
сред//В
сб. “Проблемы современной механики (к юбилею Л.И. Седова)”, под ред. С.С.
Григоряна. М.: МГУ.
1998. С. 52-74.
Колесниченко (Kolesnichenko
A.V., Marov
M.Ya.).
Methods of nonequilibrium thermodynamics for description of multicomponent turbulens gas mixture//Arch.Mech.(Warszawa), 1985.V.37. №1-2. P, 3-19.
Колесниченко А.В., Маров
М.Я.
Турбулентность многокомпонентных сред. М.: Наука, 1999.336 с.
Колмогоров А.Н. Локальная структура
турбулентности в несжимаемой жидкости при очень больших числах Рейнольдса//ДАН СССР. 1941. Т.
30. С. 299-303.
Колмогоров А.Н. Уточнение представлений о
локальной структуре турбулентности в несжимаемой вязкой жидкости при больших
числах Рейнольдса//In: Mecanique de la turbulence: Colloq. Intern.
CNRS, Marseille, aout - sept. 1961/ На рус. и фр. яз. Paris. 1962. P.
447-458.
Кроу, Чaмпагне (Crow
S.C., Champagne F.H.) Orderly structures in jet turbulence//J.Fluid Mech.
1971. V. 48. P. 547-591.
Ландау Л.Д., Лифшиц В.М. Гидродинамика. М.: Наука.
1988. 733 с.
Маров, Колесниченко (Marov M.Ya., Kolesnichenko
A.V.) Mechanics of turbulence of multicomponent gases. Kluwer Academic
Publishers, Dordrecht, Boston,London, 2001. 375 c.
Миллионщиков М.Д. К теории однородной и
изотропной турбулентности//Изв.АН СССР.
Сер.геогр. и геофиз. 1941. Т.5. № 4-5.
С. 433-446.
Монин А.С., Яглом А.М. Статистическая
гидромеханика. Т.1. Санкт-Петербург: Гидрометеоиздат. 1992. 694 с.
Монин А.С., Яглом А.М. Статистическая
гидромеханика. Т.2. Санкт-Петербург:
1996. 742 с.
Мюнстер А. Химическая термодинамика. М.: Едиториал
УССР, 2002. 295 с.
Новиков Е.А.,
Стюарт Р.У. Перемежаемость турбулентности и спектр флюктуаций диссипации энергии.
Изв. АН СССР, сер. Геофиз. 1964, № 3. С. 408-413.
Обухов (Obukhov А.М.) Some specific features of
atmospheric turbulence// J. Fluid Mech. 1962. V.13 Pt. 1. P.77-81.
Обухов А.М. О распределении энергии в
спектре турбулентного потока// Изв. АН СССР. Сер. геогр. и геофиз. 1941. Т.5. № 4.
С. 453-466.
Онзагер (Onsager L.) Statistical hydrodynamics//
Nuovo Cimento (Supplement). 1949. V.6. P.279-287.
Пригожин И. Введение в термодинамику необратимых
процессов. М. ИЛ, 1960. 160 с.
Пригожин И., Стенгерс И. Порядок из хаоса. Новый
диалог человека с природой. М.:
прогресс, 1986, 310 с.
Пригожин И., Стенгерс И. Время.Хаос. Квант. К решению парадокса времени. М.: Издательская группа «Прогресс», 1994.
240 с.
Пригожин И. Кондепуди Д. Современная
термодинамика. От тепловых двигателец до диссипативных структур. Москва: Мир,
2002, 461.
Турбулентность: Принципы и применение/Под ред. У.Фроста и
Т.Моулдена М.: Мир.1980, 535 с.
Фриш и др.(Frisch
U., Sulem P.L., Nelkin M.) A simple dynamical model of intermittent fully developed
turbulence// J. Fluid Mech. 1978. V.87. P.719-736.
Фриш У. Турбулентность.
Наследие Колмогорова. М.: Фазис, 1998.
343 с.
Странные
аттракторы: Сб.пер. с анг./Под ред.
Я.Г. Синая и Л.П. Шильникова. М.: Мир. 1981.
Хакен Г.
Синергетика. Иерархии неустойчивостей в самоорганизующихся системах и
устройствах. М. : Мир.
1985. 419 с.
Хакен Г. Информация и самоорганизация.
Макроскопический подход к сложным системам. М. : Мир. 1991. 240 с.
Эбелинг
В., Энгель А, Файстель Р. Физика процессов эволюции. Синергетический
подход. М.: Эдиториал УССР, 2001. 386 с.
|