Содержание

Введение. 3

1. Фрактальные и предфрактальные графы.. 3

2. Предфрактальные графы в анализе и проектировании структур. 4

3. Некоторые топологические характеристики. 6

4. Диаметр структуры.. 7

5. Связность. 8

6. Распараллеливание. 17

Выводы и результаты.. 22

Литература. 23

Введение

Задача построения структур с заданными характеристиками появляется там, где требуется объединить элементы, часто различной природы, в целостную функционирующую систему. В настоящее время, в эпоху “больших задач”, создание структур с большой размерностью (с большим числом элементов) имеет особое значение.

Проследить за сохранением (или, наоборот, отсутствием) определенных качественных характеристик при проектировании сложных структур – сложная и важная задача для многих организационных структур [1] и структур “естественных”, возникающих в геологии [2], геофизике [2], астрофизике [3] и т.д.

В настоящей работе предлагает новый метод проектирования и анализа сложных многоэлементных структур. В основе метода лежит свойство самоподобия фрактальных графов [4]. Предфрактальный граф, конечный аналог фрактального графа, - есть симбиоз графа и фрактала. Использование свойства самоподобия дает возможность “программирования” предфрактального графа требуемыми характеристиками и свойствами. Немаловажно и то, что алгоритмы обработки предфрактальных графом легко распараллеливаются с заметным снижение вычислительной сложности.

1. Фрактальные и предфрактальные графы

Предфрактальный граф будем обозначать через , где - множество вершин графа, а  - множество его ребер. Определим его рекуррентно, поэтапно, заменяя каждый раз в построенном на предыдущем этапе  графе  каждую его вершину связной затравкой  [4]. Такая операция называется замещение вершины затравкой (ЗВЗ). На первом этапе предфрактальному графу соответствует затравка. При этом об описанном процессе говорят, что предфрактальный граф  порожден затравкой . На рис. 1 показаны предфрактальные графы  и  порожденные затравкой . Ребра, появившиеся на этапе , , порождения предфрактального графа, будем называть ребрами ранга . Новыми ребрами предфрактального графа  назовем – ребра ранга  (на рис. 1В, они изображены самыми тонкими линиями), а все остальные ребра назовем старыми.

Предфрактальный граф  условимся называть  - графом, если он порожден -вершинной -реберной связной затравкой .

Обобщением определенного ранее процесса порождения предфрактального графа  является такой случай, когда вместо единственной затравки  используется множество затравок , . Суть этого обобщения состоит в том, что при переходе от графа  к графу  каждая вершина замещается некоторой затравкой , которая выбирается случайно или согласно определенному правилу, отражающему специфику моделируемого процесса. Предфрактальные графы полученные подобным образом называются каноническими. В случае же, когда, в процессе порождения предфрактального графа, затравками замещается только часть его вершин, то предфрактальный граф называется неканоническим. Процесс построения предфрактального графа, по существу, есть процесс построения последовательности предфрактальных графов, которую и назовем траекторией. На рис. 1 последовательность предфрактальных графов , ,  - есть траектория предфрактального графа .

Если процесс порождения продолжать бесконечно, то получим фрактальный граф, который, очевидно, имеет бесконечную траекторию.

Фрактальные графы могут служить моделью такого явления как структурный хаос. Несмотря на строгие правила построения (порождения), точно предсказать структуру связей между вершинами предфрактального графа, на очередном этапе порождения, невозможно. Но можно выявить характеристики, которые остаются неизменными на всей траектории фрактального графа или изменяются по определенным правилам.

2. Предфрактальные графы в анализе и проектировании структур

Современные средства передачи информации делают несущественными физические расстояния (соизмеримые с размерами Земли) между узлами информационных систем. В такой ситуации важную роль играет структура связей между узлами системы. Это, вообще говоря, касается любой системы, не только информационной. Моделью структуры связей между узлами системы является граф. На практике одинаково значимы и анализ и проектирование структур. Существует ряд параметров [5], которые принято использовать в анализе и проектировании структур.

(а) Чтобы провести анализ структуры и выяснить соответствует ли она требуемым параметрам, в первую очередь, необходимо построить граф – абстрактную модель исследуемой структуры. Сделать это довольно просто – достаточно обозначить элементы структуры вершинами графа, а связи между элементами структуры – ребрами графа. Обычно графы задаются в виде матриц смежности или инцидентности, но при решении задач, связанных со сложными структурами, возникают определенные трудности с быстрым анализом структуры. Под сложностью структуры будем понимать большой набор элементов структуры (возможно различной природы) и нетривиальность связей между ними. Сложные структуры естественного происхождения, такие как инфраструктура, коммуникации, сети , обладают особым свойством иерархичности, т.е. элементы (или связи между элементами) структуры упорядочены по времени их появления. В начальный момент структура представляет собой “несложный” граф. В следующий момент времени появляются элементы, имеющие связи, как между собой, так и с элементами структуры, возникшими в предыдущий момент времени, причем количество новых элементов и связей оптимизировано в зависимости от среды, где строится структура. Рост структуры продолжается до тех пор, пока этого требует среда.

Наиболее ярким примером иерархической структуры является структура связей между нейронами нервной системы живого организма. Согласно [6], эволюционное формирование структуры нервной системы происходит по описанному нами принципу. Если рассмотреть эволюцию в дискретном времени, то в начальный момент времени структура нервной системы будет представлять собой звезду (см. рис 2А), вершины которой соответствуют нейронам, а ребра – связям между нейронами. Звезда – это первый уровень иерархии структуры нервной системы. Таких звезд у “ранних” организмов могло быть несколько.

В следующий момент времени “разрозненные звезды” объединяются, образуя двухуровневую иерархическую структуру (см. рис. 2Б). Объединение происходит по средствам “промежуточных” нейронов, наиболее выгодным для организма образом. Число уровней в иерархии нервной системы определяется средой обитания организма.

Формализацией описанного процесса служит процесс построения неканонического предфрактального графа (фрактального графа – в случае бесконечного времени роста структуры), который в фиксированный момент времени точно отражает состояние исследуемой структуры. А именно, в начальный момент времени  структуре соответствует затравка  (первый этап порождения предфрактального графа). В момент времени , после появления новых элементов и связей в структуре (это говорит о проведении операции ЗВЗ) структуре соответствует предфрактальный граф  (второй этап порождения предфрактального графа). Далее, на этапе  получим предфрактальный граф  отражающий порядок связей элементов структуры в последний момент времени исследуемого промежутка.

Уточним, что построить предфрактальный граф соответствующий некоторой структуре – значить определить множество затравок, порождающее предфрактальный граф, и правила замещения вершин затравками на разных этапах порождения предфрактального графа.

Построить предфрактальный граф, соответствующий исследуемой структуре, можно двумя способами.

Первый. Рассмотрев эволюцию структуры, т.е. ее развитие в дискретном времени, можно составить множество затравок , , порождающее предфрактальный граф и определить его траекторию.

Второй. Использовать алгоритмы распознавания [4].

Отметим, что первый способ эффективен в случае построения неканонических предфрактальных графов низкого уровня, порожденных множеством затравок. Второй же способ, наоборот, более эффективен при идентификации канонических предфрактальных графов высокого уровня, порожденных одной затравкой.

В параграфах 4 – 6 будут доказаны теоремы, которые дают оценки для ряда характеристик предфрактального графа по характеристикам затравки. Благодаря этому анализ всего предфрактального графа сводится к анализу затравки. В свою очередь анализ затравки можно провести известными методами [5].

(б) Проблемы проектирования структур с малым числом элементов и связей решаются известными методами [5]. Однако развитие систем с многоэлементными структурами требуют разработку “быстрых” подходов в проектировании структур с заданными характеристиками. Подход, предлагаемый в настоящей работе, основан на непосредственном использование определения предфрактального графа [4]. Используя известные эвристические методы, заложить необходимые характеристики в затравку (затравки), и построить требуемый предфрактальный граф. Интересно, что предфрактальный граф, в процессе порождения, может приобрести и те характеристики, которыми не обладает сама затравка. При необходимости, уточнив порядок связей между ребрами (сохранение или, наоборот, нарушение смежности старых ребер), можно наделить предфрактальный граф характеристиками, которыми не обладает затравка.

3. Некоторые топологические характеристики

Целесообразно, установить точное соответствие между свойствами исследуемой структуры и топологическими характеристиками соответствующей ей графа. За основу возьмем характеристики, предложенные в работе [5].

Иерархичность – свойство структуры, которое проявляется в связях между элементами. Эта характеристика позволяет распределить элементы структуры в порядке их значимости. Значимость элемента определяется связями и расположением соответствующей ему вершины в графе по отношению к другим вершинам. На предфрактальном графе, к примеру, значимость ребер убывает с ростом их ранга. Чем “старее” ребра, т.е. чем ниже ранг ребер, тем больше вершин в подграфах, которые они соединяют.

Диаметр структуры – диаметр графа [7], метрическая характеристика, введенная для определения кратчайшего расстояния между наиболее удаленными вершинами. По значению диаметра можно косвенно судить о ряде предельных параметров системы, в частности о ее надежности, пропускной способности и т.д. [5]. Пропускная способность структуры [5] определяется максимальным потоком сообщений, который можно организовать между ее элементами. При равной пропускной способности элементов, пропускная способность всей структуры обратно пропорциональна ее диаметру [5]. Поэтому при проектировании структур с высокой пропускной способностью естественно стремиться к структуре с минимальным диаметром.

Связность – способность “противостоять” разбиению, разделению структуры на части. Теория графов оперирует реберной и вершинной связностью [7]. Они позволяют оценить топологию структуры на “крепость”, и поэтому важны в проектировании структур. К характеристикам, оценивающим связность графов, можно отнести так же число точек сочленения и мостов [7]. К ним прибегают, когда граф имеет связность равную единицы.

Распараллеливание – возможность обработки исследуемой структуры несколькими процессорами (процессами) [8,9]. Это свойство трудно недооценить в сложных структурах.

В порождении предфрактального графа важное место занимает случайный характер связей между старыми ребрами. Именно, это не позволяет нам рассматривать точные количественные значения его характеристик. В таком случае разумнее рассматривать интервалы, в которых варьируются значения тех или иных характеристик. На практике, для анализа и проектирования сложных структур с использованием предфрактальных графов, достаточными могут быть интервалы (или количественные оценки), а не точные значений этих характеристик. Ниже будут даны оценки рассмотренных в этом параграфе характеристик, и описаны условия достижимости их концов.

4. Диаметр структуры

Представленные в этом параграфе теоремы необходимы для полноты раскрытия темы настоящей работы. В их обоснованности можно убедится в [4].

Теорема 1. Для всякого предфрактального графа  ранга , порожденного n-вершинной затравкой, величина диаметра  удовлетворяет неравенству .

Оценка является достижимой в случае, когда предфрактальный граф порождается полной затравкой. Полной затравкой называется граф, любые две вершины которого имеет общее ребро. Более того, величина  представляет собой точное значение нижней достижимой оценки диаметра в классе всех предфрактальных графов, порождаемых одной затравкой.

Теорема 2. Для всякого предфрактального графа  ранга , порожденного какой-либо затравкой , справедлива следующая оценка величины диаметра : , где  - диаметр затравки.

Можно указать неограниченное множество  затравок, каждая из которых в случае выполнения условия непересечения старых ребер в текущих графах ,  порождает предфрактальный граф, для которого верхняя оценка будет достижимой. В частности, этому множеству принадлежат такие графы, как цепь или звезда.

5. Связность

(а) Числом реберной связности  графа  назовем наименьшее число ребер, удаление которых приведет к нарушение связности графа .

Теорема 3. Для всякого предфрактального графа , порожденного затравкой , справедливо равенство .

Доказательство. Следуя условиям теоремы, выделил произвольно на затравке  число  ребер , , удаление которых приводит к распадению графа  на компоненты  и . Не будем заострять внимание на доказательстве невозможности появления более чем двух компонент. Фактически, удаление ребер  приводит к нарушению любых связей между множествами вершин  и , где . По этой причине и происходит распад затравки  на компоненты. Рассмотрим процесс порождения и траекторию предфрактального графа . На протяжении всей траектории, как следует из определения предфрактального графа, старые ребра первого ранга , , будут инцидентны образам вершин  и . Поэтому удаление всех ребер , , в любом предфрактальном графе , , из траектории приведет к нарушении связностей между образами вершин  и . А это повлечет за собой разделение предфрактального графа  на две компоненты. Тем самым мы доказали, что . Докажем, что  - наименьшее число ребер, удаление которых приведет к разрушению предфрактального графа  на компоненты.

Число реберной связности  предфрактального графа  из траектории не может уменьшаться при продвижении по траектории, , по двум причинам. Во-первых, операция ЗВЗ на этапе , не влияет на число старых ребер ранга , . Во-вторых, предфрактальный граф , , состоит из множества затравок, соединенных старыми ребрами различных рангов. Отсюда верно равенство .

(б) Числом вершинной связности  графа  назовем наименьшее число вершин, удаление которых приведет к несвязному или тривиальному графу.

Теорема 4. Для всякого предфрактального графа  число вершинной связности , если смежность старых ребер не нарушается.

Доказательство. Фактически, теорема гласит, что при сохранении условия смежности старых ребер число вершинной связности предфрактального графа не зависит от числа вершинной связности его затравки. А именно, смежность старых ребер приводит к появлению точек сочленения на предфрактальном графе. Точкой сочленения графа назовем вершину, удаление которой приведет к нарушению связности графа.

Рассмотрим два графа  и . Выделим произвольно на графе  вершину  (рис. 3А) и множество инцидентных ей ребер . На графе  аналогичным образом выделим вершину  (рис. 3Б) и множество инцидентных ей ребер . Заместим вершину  графом . Получим граф  (рис. 3В), в котором множество вершин , а множество ребер  определим следующим образом. Смежность вершин в подграфах  и  не меняется, а для вершины  множество инцидентных ей ребер представляет собой множество .

Ясно, что при таком замещении вершины  любая простая цепь, содержащая одновременно вершины множеств  и  в графе  будут содержать и вершину . Поэтому ввиду [7], можно утверждать, что вершина  есть точка сочленения графа . А значит . Таким образом, мы доказали, что сохранив смежность ребер в замещенной вершине  графа , превратили вершину  в точку сочленения для графа .

Процесс порождения предфрактального графа  представляет собой последовательное использование операций ЗВЗ. Поэтому на основе доказанного выше утверждения можно сделать вывод. Сохранение смежности старых ребер в процессе порождения предфрактального графа приведет к появлению точек сочленения. А значит, и к уменьшению числа вершинной связности до . Так для предфрактального графа  на рис. 1 вершины  и  - точки сочленения. Поэтому число вершинной связности , в то время как для затравки  оно равно .

Из доказанных теорем вытекают несколько важных для приложений следствий.

Регулярным называется граф, все степени вершин которого равны между собой.

Лемма 1. Для всякого предфрактального графа , порожденного затравкой , справедливо неравенство .

Доказательство. Для любого графа  верно неравенство  [7], где  - наименьшая степень вершин графа . Тогда непосредственно из теоремы 3 следует, что . Важно, что достижимость  осуществляется при непересечении старых ребер на протяжении всей траектории предфрактального графа .

Лемма 2. Для всякого предфрактального графа , порожденного регулярной затравкой , справедливо равенство , где  - натуральное число, если смежность старых ребер не сохраняется.

Доказательство. Поэтому для регулярного графа  справедливо  [7]. Согласно лемме 1, непересечение старых ребер предфрактального графа обеспечивает невозрастание его минимальной степени вершин  и . А значит, на всей траектории предфрактального графа сохраняется равенство .

Лемма 3. Для любого натурального числа  можно построить предфрактальный граф  такой, что .

Доказательство. Для того, чтобы построить предфрактальный граф  с заданными характеристиками , достаточно использовать для его порождения регулярную затравку  степени вершин . Конечно, в процессе порождения смежность старых ребер не сохраняется.

(в) Число точек сочленения графа обозначим через .

Теорема 5. Для всякого предфрактального -графа , порожденного затравкой , справедливы следующие верхняя и нижняя оценки для числа точек сочленения: , если затравка  - дерево.

Доказательство. Очевидно, что на затравке , как и на любом другом дереве, все вершины, за исключением висячих (ее степень равна единице), являются точками сочленения. А поскольку  - дерево, то максимальное число точек сочленения достигается, если в траектории старые ребра соединяют затравки таким образом, что число висячих вершин наименьшее. Найдем условия, при которых это может произойти.

Рассмотрим предфрактальный граф  порожденный затравкой - деревом . На этапе  при ЗВЗ старые ребра могут принять два положения, относительно вершин затравок:

1)     старые ребра инцидентны невисячим вершинам затравок, т.е. точкам сочленения затравок;

2)     старые ребра инцидентны висячим вершинам затравок.

В первом случае число точек сочленения для графа  равно , где  - число затравок в графе , а во втором , где  - число старых ребер.

Разница числа точек сочленения в первом и во втором случае составляет , это говорит о том, что каждое старое ребро в графе  соединенное вторым способом дает две новые точки сочленения. Ясно, что если старые ребра соединены произвольно, то число точек сочленения ограничивается двойным неравенством: .

Предположим теперь, что теорема верна для предфрактального дерева , т.е. , это значит, что наименьшее число точек сочленения в графе   возможно только лишь при инцидентности старых ребер невисячим вершинам затравок, а максимальное - , при инцидентности старых ребер висячим вершинам затравок. На следующем  этапе порождения графа , при выполнении условия 1) на всей траектории, число точек сочленения увеличится ровно в  раз, т.е. нижняя оценка имеет вид . А верхняя оценка, достигаемая при выполнении условия 2) на всей траектории, отличается от нижней на удвоенное число всех старых ребер - .

При произвольном соединении старых ребер на  этапе порождения число точек сочленения оценивается неравенством .

Теорема 6. Для всякого предфрактального -графа , порожденного затравкой  без точек сочленения, справедливы верхняя и нижняя оценки для числа точек сочленения , если смежность старых ребер одного ранга не нарушается.

Доказательство. Рассмотрим предфрактальный граф . Поскольку затравка  не имеет точек сочленения, то на графе  они появятся только в том случае, если старые ребра первого ранга подходящие к затравкам остаются смежными, т.е. инцидентными одной вершине. Удаление каждой такой вершины неизбежно приведет к распадению графа  на компоненты. Тогда число точек сочленения предфрактального графа  равно , т.е. числу затравок.

На следующем этапе порождения , старые ребра одного ранга не нарушая смежности между собой, могут быть смежны еще и со старыми ребрами других рангов. И в этом случае число точек сочленения будет равно числу затравок графа , . В случае же смежности ребер только лишь одного ранга, число точек сочленения равно общему числу всевозможных подграфов ,  из траектории ; количество подграфов  равно , а число  равно  т.е. . Ясно, что при смежности ребер одного ранга и необязательной при этом смежности старых ребер различных рангов, число точек сочленения графа  будет ограничено неравенством .

Продолжая рассуждения аналогичным образом, предположим, что число точек сочленения  графа  оценивается неравенством . По индукции переходя в траектории от графа  к графу , как и ранее, при выполнении условий теоремы, возможны два случая. Первый - достижение нижней оценки числа точек сочленения возможно, если старые ребра предыдущего ранга смежны как между собой так со старыми ребрами следующего ранга; в этом случае число точек сочленения графа  равно числу затравок этого графа - . При достижении же верхней оценки смежность только лишь ребер одного ранга, добавляет в граф  число точек сочленения равное числу затравок этого графа, т.е. , это значит что каждая операция ЗВЗ при порождении графа  дает по одной точке сочленения. В случае же произвольной смежности ребер различных рангов число точек сочленения  ограничивается двойным неравенством , .

Следствие 1. Предфрактальный граф  порожденный затравкой  без точек сочленения, не имеет точек сочленения, если старые ребра не пересекаются в траектории.

Теорема 7. Для всякого предфрактального -графа , порожденного затравкой , справедливы верхняя и нижняя оценки для числа точек сочленения , если смежность старых ребер одного ранга не нарушается.

Доказательство. Рассмотрим траекторию предфрактального графа , порожденного затравкой , имеющей  - точек сочленения. На этапе  порождения все точки пересечения старых ребер (первого ранга) могут совпасть с точками сочленения затравок и в этом случае , где  - число затравок графа . При выполнении условий теоремы меньше чем  точек сочленения быть не может. В случае же несовпадения всех точек пересечения старых ребер с точками сочленения затравок, число точек сочленения  графа  будет определено равенством , поскольку каждая пара смежных старых ребер в инцидентной им вершине дадут по точке сочленения графа . А в общем, при произвольном размещении смежных старых ребер, число точек сочленения  графа  ограничивается неравенством .

Продолжая рассуждения аналогичным образом, на  - ом этапе, , порождения в траектории графа , получим, что число точек сочленения  графа  равно , при совпадении инцидентности смежных старых ребер с точками сочленения затравок. В противном случае, если каждая смежная пара старых ребер одного ранга не инцидентна ни одной из точек сочленения затравок, а значит каждая из таких пар дает по одной точке сочленения для графа , то, как уже стало ясно, верхняя оценка достижима и равна .

В целом при произвольной инцидентности пар старых смежных ребер с точками сочленений затравок или другими точками сочленения, полученных в результате смежности старых ребер одного ранга, число точек сочленения  графа  оценивается двойным неравенством , .

(г) Мостом графа назовем ребро, удаление которого приводит к нарушению связности графа. Число мостов графа  обозначим через .

Теорема 8. Для всякого предфрактального -графа  порожденного затравкой , справедливы верхняя и нижняя оценки для числа мостов: .

Доказательство. Рассмотрим траекторию предфрактального графа  порожденного затравкой . На затравке  выделим мост  (см. рис. 4А), удаление которого приводит к разделению затравки на две компоненты. На этапе  порождения предфрактального графа , после замещения всех вершин затравки, выделенное нами ребро (уже старое ребро 1-го ранга)  (см. рис. 4Б) случайным образом соединит вершины двух подграфов-затравок предфрактального графа .

Но удаление ребра  приведет к распадению графа  на компоненты, поскольку, как требует определение, мост  - единственная цепь соединяющая концы ребра , независимо от того какие вершины  и  или же  и  оно соединяет. Из этих рассуждений вытекает, что все мосты затравки  остаются мостами на всей траектории графа , поэтому  -мостов предфрактального -графа  не меньше числа - мостов затравки , .

Рассмотрим теперь произвольный предфрактальный граф , , выделим на нем подграф-затравку , который, в отдельном от графа виде, имеет  мостов. На рис 5 ребра затравки изображены “тонкими” линиями, а старые ребра предфрактального графа  - “жирными”. Возникает вопрос - останутся ли мостами для графа  ребра являющиеся мостами на отдельно взятой затравке . Пусть при удалении моста , как следует из определения, затравка  распадается на две компоненты  и  (см. рис. 5). Значит, для того чтобы ребро  перестало быть мостом на самом графе , достаточно, чтобы подграфам и  были инцидентны хотя бы по одному старому ребру  -го ранга, тем самым нейтрализуя мост  и сохраняя связность графа , при удалении ребра . Описанное отражено на рис. 5А.

В случае же, если старые ребра -го ранга сохраняют смежность, то ребро  - будет мостом и для всего графа . Поскольку при его удалении связность предфрактального графа  нарушается. Этот случай проиллюстрирован на рис. 5Б.

Теперь стало ясно, что число мостов  предфрактального графа , порожденного затравкой , зависит от того, как часто сохраняется смежность старых ребер графа . Если старые ребра -го ранга предфрактального графа ,  из траектории предфрактального графа  подходят к подграфам-затравкам таким образом, что каждый их   мостов образует с какими-либо двумя из старых ребер одного ранга простую цепь, то мосты отдельно взятой затравки не будут мостами графа , т.к. при их удалении из подграфа - затравки , компоненты, на которые должна была бы распасться отдельная затравка, будут инцидентными старым ребрам, тем самым сохраняя связность самого графа . В случае выполнения этого правила для всех графов ,  из траектории предфрактального графа  получим, что все мосты затравок, появляющихся в процессе порождения графа , нейтрализуются старыми ребрами, кроме тех  мостов, которые существовали изначально на графе , поскольку для этих мостов не существует старых ребер меньшего ранга. Отсюда следует, что нижняя граница для числа мостов графа  определяется неравенством .

Для нахождения верхней границы достаточно рассмотреть случай, когда в предфрактальном графе  сохраняется смежность старых ребер любого ранга. Действительно, при сохранении смежности старых ребер -го ранга предфрактального графа , , все старые ребра, подходящие к затравке , будут смежными одной из компонент, полученных при удалении одного из мостов. А следовательно все  мосты затравки  останутся мостами и на графе . Учитывая, что на графе  число затравок равно , замечаем, что число его мостов по сравнению с графом  увеличится на :

.

Итак, в процессе порождения графа , двигаясь по его траектории, замечаем, что, в случае сохранения смежности старых ребер, число мостов растет по геометрической прогрессии, а ее сумма равна достижимой верхней границе ; .

Обобщим полученные результаты. При произвольном построении фрактального графа  число его мостов  ограничивается неравенством , что и требовалось доказать.

Примечание. Возможны случаи, когда не все мосты затравки можно нейтрализовать старыми ребрами.

Первый случай. Затравка  имеет висячие вершины, т.е. наименьшая степень вершин затравки равна . Это позволяет предположить наличие висячих вершин у предфрактального графа . При висячих вершин затравками на шаге , , к самой затравке  подойдет лишь одно старое ребро  - ранга и все -мостов затравки останутся мостами и для графа . Так на рис. 6 изображена затравка , ее ребра нарисованы “тонкими” линиями. Затравка  имеет два моста  и , причем мост  инцидентен висячей вершине. Затравке  инцидентно одно старое ребро (на рис. 1 оно выделено “жирной” линией), которое не может нейтрализовать ни один из мостов затравки.

Второй случай. На затравке  число мостов  больше наименьшей степени вершин затравки. В процессе порождения предфрактального графа, при замещении затравкой вершины с наименьшей степенью, затравке станут инцидентны старые ребра, число которых меньше числа  мостов затравки. Поэтому некоторое число мостов не будет нейтрализовано старыми ребрами, при любом их расположении относительно затравки.

На рис. 7, где “тонкими” линиями отмечены ребра затравки , а “жирными” – старые ребра предфрактального графа, показано, что мосты  и  нейтрализованы, а ребро  остается мостом и для всего предфрактального графа.

Описанные случаи наглядно доказывают невозможность достижения точной нижней оценки числа мостов предфрактального графа  в теореме 8, если предфрактальный граф порожден затравкой , число мостов которой не удовлетворяет неравенству .

6. Распараллеливание

Для задач большой размерности применение известных последовательных алгоритмов требует больших временных затрат. Современные одиночные вычислительные машины, даже самые мощные, не могут справляться с поставленными задачами за приемлемо короткое время. Решением этой проблемы может служить одновременное использование многих вычислительных машин. Но для этого необходимо “правильное” распараллеливание известных алгоритмов или создание новых. В настоящее время ведется огромная исследовательская работа по разработке параллельных алгоритмом и программ их реализации для поставленных задач [8,9].

Предфрактальные графы, как было сказано ранее, обладают свойством самоподобия. Используя это свойство, для задач на предфрактальных графах можно строить параллельные алгоритмы, трудоемкость которых на порядки ниже, чем у известных последовательных алгоритмов. Отметим, что решение задач на предфрактальных графах, независимо от того представлен ли алгоритм как последовательный (использование одного процессора) или параллельный (использовании нескольких процессоров), вычислительная сложность этого алгоритма ниже чем у известных последовательных алгоритмов.

В подтверждение приведем параллельный алгоритм  поиска кратчайшего пути на предфрактальном графе, смежность старых ребер которого не нарушается. Вообще говоря, поиск кратчайшего пути между элементами структуры – важная в практике задача [5].

Пусть дан предфрактальный -граф , смежность старых ребер которого на всей его траектории не нарушается, и два процессора  и . Необходимо найти кратчайший путь между двумя вершинами  и .

(а) Введем некоторые определения и обозначения. s-ой затравкой ранга  назовем s-ую "новую" затравку предфрактального графа , , из траектории. И обозначим ее через , где  - порядковый номер затравки, использовавшейся на -ом этапе порождения предфрактального графа . Таким образом, на -ом этапе порождения предфрактального графа  появится ровно  затравка  ранга . Т.е., на графе  затравок 1-ого ранга – одна, затравок 2-ого ранга – n,…, затравок L-ого ранга - .

На рис. 8 изображен предфрактальный граф , порожденный треугольной затравкой , причем смежность старых ребер предфрактального графа  не нарушается. Самыми “толстыми” линиями нарисованы ребра затравки первого ранга . Линиями “средней толщины” нарисованы ребра затравок  второго ранга, их количество равно трем - . И наконец, “тонкими” линиями изображены ребра затравок  третьего ранга.

s -ым блоком  ранга , , , предфрактального графа  назовем его связный подграф состоящий из ребер рангов от  до  включительно. Согласно определения, предфрактальный граф  совпадает со своим блоком . В свою очередь, затравки  ранга  предфрактального графа , также совпадают с блоками  ранга .

Вообще говоря, для того чтобы на предфрактальном графе  выделит все блоки  ранга , достаточно удалить из него все старые ребра от первого до -го ранга включительно. Такое удаление приведет к появлению  компонент, каждая из которых будет блоком  ранга , с присвоенным ему порядковым номером .

Вернемся к рис. 8. На нем изображен предфрактальный граф , совпадающий со своим блоком . Пунктирными окружностями на рис. 8 очерчены один блок  второго ранга и один блок  третьего ранга.

(б) Опишем основные принципы работы алгоритма .

Лемма 4. Для любых двух вершин , предфрактального -графа , смежность старых ребер которого не нарушатся, существует такой блок , что кратчайший путь между вершинами v и u будет принадлежать этому блоку.

Доказательство проведем конструктивно. Пусть заданы две вершины . Найдем общий блок для этих вершин. Каждая из этих двух вершин принадлежат затравкам L-го ранга, которые являются и блоками L-го ранга. Если эти две вершины принадлежат одному и тому же блоку, то найден общий блок . В противном случае, рассматриваем блоки -ого ранга, которым принадлежат вершины v и u. Если вершины v и u принадлежат одному блоку -ого ранга, тогда общий блок найден. Если не найден общий блок -ого ранга, тогда продолжаем процедуру уменьшения рангов блоков, в которые входят вершины v и u до тех пор, пока не будет найден общий блок .

Таким образом, в начале алгоритму необходимо находит один общий блок , в пределах которого и будет осуществляться поиск кратчайшего пути между двумя заданными вершинами предфрактального графа.

Работа алгоритма заключается в следующем. Каждая затравка рассматривается как отдельный подграф, и два процессора  параллельно независимо друг от друга находят кратчайшие пути, переходя от одной затравки к другой. Цель такого подхода уменьшить, на сколько это возможно высоту алгоритма, т.е. его вычислительную сложность [8].

Процессор  назначается вершине v, основная цель которого найти кратчайший путь от вершины v до затравки наименьшего ранга, принадлежащей общему блоку . Процессор  назначается вершине u, основная цель которого найти кратчайший путь от вершины u до затравки наименьшего ранга, принадлежащей общему блоку . Затравка наименьшего ранга одна, и имеет ту же индексацию, что и найденный блок , т.е.  - также является "общей" затравкой для заданных вершин v и u. Последним шагом алгоритма будет поиск кратчайшего пути между двумя вершинами  и  на затравки , найденными в процессе работы алгоритма.

Опишем теперь работу одного процессора . Вершины предфрактального графа могут одновременно принадлежать затравкам разных рангов. Пусть вершина v принадлежит затравке наименьшего ранга, тогда обозначим ее через , а затравку которой она принадлежит через . Если затравка  и есть общая затравка , тогда работа процессора останавливается и вершина  обозначается через . В противном случае просматриваются все вершины затравки . Вершину принадлежащую затравке наименьшего ранга, обозначим через , а саму затравку - . Далее осуществляется поиск кратчайшего пути от вершины  до . Если затравка  и есть общая затравка , тогда работа процессора останавливается и вершина  обозначается . В противном случае процессор продолжает свою работу, находя кратчайшие пути на затравках меньших рангов ,, пока не будет найден кратчайший путь до одной из вершин затравки .

Работа процессора  будет аналогичной, при этом вершины и затравки будут обозначаться через ,и  соответственно.

После того, как будут найдены вершины  и , на последнем этапе алгоритм находит кратчайший путь между этими двумя вершинами на общей затравке .

(в) Поиск кратчайшего пути на затравках ведется с помощью алгоритма Дейкстры [5], который заложен в алгоритм в виде вызываемой процедуры. Следует отметить, что затравка, на которой ведется поиск кратчайшего пути, рассматривается как отдельный подграф и за пределы затравки процедура не выходит.

Процедура поиска кратчайшего пути (ПКП), основанная на алгоритме Дейкстры.

(Вход: вершины s и t, затравка z)

Шаг 1. Все вершины и ребра не окрашены. Каждой вершине затравки z в ходе выполнения алгоритма присваивается число , равное длине кратчайшего пути из s в x, включающего только окрашенные вершины.

Положить  и  для всех х, отличных от s. Окрасить вершину s и положить у = s (у - последняя из окрашенных вершин).

Шаг 2. Для каждой неокрашенной вершины х пересчитать величину :

Если , для всех неокрашенных вершин х, закончить процедуру алгоритма: в исходном графе отсутствуют пути из вершины s в неокрашенные вершины. В противном случае окрасить ту из вершин х, для которой величина  является наименьшей. Кроме того, окрасить ребро, ведущее в выбранную на данном шаге вершину х. Положить у = х.

Шаг 3. Если у = t, закончить процедуру: кратчайший путь из вершины s в вершину t найден (это единственный путь из s в t, составленный из окрашенных ребер). В противном случае перейти к шагу 2.

(Выход: кратчайший путь из s в t)

Конец процедуры.

(г) Алгоритм .

Шаг 1. Найти общий блок  для заданных вершин v и u предфрактального графа. Пусть в начале каждая из двух вершин v и u принадлежат блокам L-го ранга.

Шаг 1.1. Если вершины v и u принадлежат одному и тому же блоку, то найден общий блок . Тогда перейти шагу 2.

В противном случае, если общий блок не найден, перейти к шагу 1.2.

Шаг 1.2. Уменьшить ранги блоков, которым принадлежат вершины v и u. Перейти к шагу 1.1.

Шаг 2. Одновременно два процессора , для вершин v и u выполнять следующие шаги.

Работа процессора :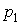

Шаг 2.1. Затравку наименьшего ранга, среди всех затравок, которым принадлежит вершина v, определить как , а саму вершину как . Инициировать циклическую переменную: .

Шаг 2.2. Если затравка  и есть общая затравка , вершина  обозначить , перейти к шагу 3. В противном случае перейти к шагу 2.3.

Шаг 2.3. Просмотреть все вершины затравки . Найти вершину принадлежащую затравке наименьшего ранга, обозначить через , а саму затравка - . Найти кратчайший путь от вершины  до  с помощью процедуры поиска кратчайшего пути:

Процедура ПКП (, , );

Увеличить итерационную переменную: .

Перейти к шагу 2.2.

Работа процессора :

Шаг 2.1. Затравку наименьшего ранга, среди всех затравок, которым принадлежит вершина u, определить как , а саму вершину как . Инициировать циклическую переменную: .

Шаг 2.2. Если затравка  и есть общая затравка , вершина  обозначить , перейти к шагу 3. В противном случае перейти к шагу 2.3.

Шаг 2.3. Просмотреть все вершины затравки , Найти вершину принадлежащую затравке наименьшего ранга, обозначить через , а саму затравку - . Найти кратчайший путь от вершины  до  с помощью процедуры поиска кратчайшего пути:

Процедура ПКП (, , );

Увеличить итерационную переменную: .

Перейти к шагу 2.2.

Шаг 3. На выходе шага 2 получаем кратчайший путь от вершины v до  и кратчайший путь от u до . Найти кратчайший путь от вершины  до вершины  на общей затравке : Процедура ПКП (,,);

Конец алгоритма .

(д) Теорема 9. Вычислительная сложность [8] алгоритма  для предфрактального -графа , , порожденного затравкой , , равна , если смежность старых ребер не нарушается.

Доказательство. Основная вычислительная нагрузка алгоритма  ложится на шаг 2. Каждый процессор находит кратчайшие пути на L затравках, т.е. выполняет эту операцию L раз. Перед тем как начать поиск кратчайшего пути, на каждой затравке просматриваются все ее n вершин. Т.е. для просмотра всех вершин каждому процессору понадобится выполнить  операций.

Согласно [5], поиск кратчайшего пути на отдельно взятой затравку занимает  операций, а в целом для всех затравок .

Таким образом вычислительная сложность шага 2 для одного процессора равна , а для двух процессоров - .

Отсюда, для , вычислительная сложность алгоритм  .

Примечание. Вычислительная сложность параллельного алгоритма  для предфрактального -графа , смежность старых ребер которого не нарушается, меньше вычислительной сложности алгоритма Дейкстры:

, в  раз.

Теорема 10. Временная сложность параллельного алгоритма  для предфрактального -графа , смежность старых ребер которого не нарушается, равна .

Выводы и результаты

(а) В настоящей работе описан новый метод проектирования сложных структур. В основе этого метода лежат предфрактальные графы. Доказан ряд теорем позволяющий наделить затравки предфрактальных графов такими топологическими и метрическими характеристиками, образы которых требуемы для проектируемых структур, моделями которых и являются предфрактальные графы.

(б) На примере параллельного алгоритма поиска кратчайшего пути на предфрактальном графе наглядно продемонстрирована возможность распараллеливания известных графовых алгоритмом. Распараллеливание алгоритма проводится благодаря свойству самоподобия предфрактального графа. Вычислительная сложность этого алгоритма, при определенных правилах порождения исследуемого предфрактального графа, на порядок ниже, чем у алгоритма Дейкстры поиска кратчайшего пути на обычных графах.

Авторы считают приятным долгом выразить глубокую признательность профессору Малинецкому Г.Г. за оказанную помощь и поддержку в выполнении работы.

Литература

1.     Г.Г. Малинецкий, М.С. Шакаева. Модель иерархической организации. Препринт ИПМ им. М.В. Келдыша РАН, 1995

2.     Б. Мандельброт. Фрактальная геометрия природы. – М.: ИКИ, 2002

3.     А.А. Потапов. Фракталы в радиофизике и радиолокации. – М.: Логос, 2002

4.     А.М. Кочкаров. Распознавание фрактальных графов. Алгоритмический подход. - Нижний Архыз: РАН САО, 1998

5.     Г.Т. Артамонов, В.Д. Тюрин. Топология сетей ЭВМ и многопроцессорных систем. - М: Радио и связь, 1991

6.     В.Ф. Турчин. Феномен науки. Кибернетический подход к эволюции. – М.: ЭТС, 2000

7.     Ф. Харари. Теория графов. - М: Мир, 1973

8.     В.В. Воеводин. Математические модели и методы в параллельных процессах. - М.: Наука, 1986

9.     В.В. Воеводин, Вл.В. Воеводин. Параллельные вычисления. С.-П.: БХВ-Петербург, 2002