Аннотация
Проведено сравнение двух методов определения квазистатической компоненты микроускорения,
возникающего на борту Международной Космической станции. В первом методе микроускорение
рассчитывалось по относительному движению станции, которое реконструировалось на основе
телеметрической информации. Второй метод состоял в прямом измерении микроускорения
низкочастотным акселерометром и сглаживании полученных данных. Используемые измерения были
выполнены американским акселерометром MAMS. Сопоставление значений микроускорений, полученных
разными способами, выполнялось по результатам решения задачи аппроксимации измеренных
значений микроускорения их расчетными значениями. Эта задача решалась методом наименьших
квадратов. Уточняемыми параметрами служили компоненты радиуса-вектора акселерометра в системе
координат, связанной с центром масс станции, и постоянные смещения в данных измерений.
Как оказалось, оба метода дают близкие результаты. Результаты решения указанной задачи можно,
в принципе, использовать для уточнения положение центра масс станции относительно ее корпуса.
Abstract
Two methods of determining a quasi-steady acceleration component arising on board the
International Space Station were compared. The first method was based on the calculation
of the accelerations by telemetry information about station attitude motion. The second method
consisted in direct measuring the accelerations by a thriaxial low frequency accelerometer
and subsequent smoothing measurement data. The measurement data were produced by MAMS.
Comparison of the acceleration values, obtained by different ways, was carried out as a result
of constructing the approximation of the measured acceleration values by their calculated
values. The approximation was constructed by the least squares method. Ajustable parameters
were the constant biases in measurement data and coordinates of the accelerometer position
in the coordinate system, connected to the centre of mass of the station. Both methods
gave similar results. The received estimations of the accelerometer coordinates can be used
for the more precise definition of the position of the station centre of inertia.
Расчет квазистатической компоненты микроускорения
по телеметрической информации
В данной работе
продолжено описание результатов, полученных в ходе выполнения технического
эксперимента “Изгиб”. Этот эксперимент состоит в изучении остаточных
микоускорений на борту Международной космической станции. Его первые результаты
опубликованы в [1], где приведены оценки уровня квазистатической и вибрационной
компонент микроускорения на Российском сегменте МКС. Данная работа посвящена
более частной задаче. В ней сравниваются два метода определения квазистатической компоненты микроускорения.
Первый метод заключается в расчете этой компоненты по движению станции, которое
реконструируется на основе телеметрической информации. Второй метод состоит в
прямом измерении микроускорения низкочастотным акселерометром и сглаживании
полученных данных.
Опишем сначала результаты,
полученные первым методом. Для расчета квазистатической составляющей
микроускорения известна простая формула. Пусть станция представляет собой
твердое тело, и точка 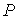 жестко с ней связана.
Из негравитационных сил, приложенных к станции, учтем только сопротивление
атмосферы. Тогда микроускорение жестко с ней связана.
Из негравитационных сил, приложенных к станции, учтем только сопротивление
атмосферы. Тогда микроускорение 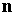 в точке в точке 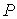 имеет вид [2, 3] имеет вид [2, 3]
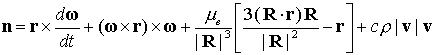 . (1) . (1)
Здесь 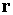 – радиус-вектор точки – радиус-вектор точки
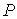 относительно центра
масс станции, относительно центра
масс станции, 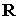 и и 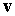 – геоцентрический
радиус-вектор этого центра масс и его скорость относительно поверхности Земли, – геоцентрический
радиус-вектор этого центра масс и его скорость относительно поверхности Земли, 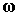 – абсолютная угловая
скорость станции, – абсолютная угловая
скорость станции, 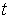 – время, – время, 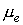 гравитационный
параметр Земли, гравитационный
параметр Земли, 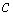 – баллистический
коэффициент станции, – баллистический
коэффициент станции, 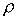 – плотность
набегающего на станцию аэродинамического потока. Формула (1) дает приближенное
выражение для разности между напряженностью гравитационного поля в точке – плотность
набегающего на станцию аэродинамического потока. Формула (1) дает приближенное
выражение для разности между напряженностью гравитационного поля в точке 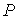 и абсолютным
ускорением этой точки. Если по какой-либо информации восстановить фактическое
движение станции, то с помощью формулы (1) можно найти реальную
квазистатическую составляющую микроускорения в любой заданной точке борта в
функции времени [2, 3]. Такой подход к определению микроускорения удобен еще и
тем, что в некоторых задачах математического моделирования гидродинамических
процессов на борту станции необходимо знать также квазистатические составляющие
величин и абсолютным
ускорением этой точки. Если по какой-либо информации восстановить фактическое
движение станции, то с помощью формулы (1) можно найти реальную
квазистатическую составляющую микроускорения в любой заданной точке борта в
функции времени [2, 3]. Такой подход к определению микроускорения удобен еще и
тем, что в некоторых задачах математического моделирования гидродинамических
процессов на борту станции необходимо знать также квазистатические составляющие
величин 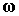 и и 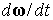 [3]. [3].
Аппроксимация
фактического вращательного движения станции выполнялась по значениям
кватерниона, задающего ее ориентацию относительно инерциальной системы
координат. Пусть на каком-либо временном интервале моменты со значениями такого
кватерниона расположены достаточно часто. Эти значения сглаживаются
кватернионной функцией времени, имеющей непрерывную вторую производную.
Дифференцированием этой функции находятся 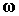 и и 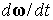 , в результате получается аппроксимация вращательного движения
станции. Движение центра масс последней считается кеплеровым. Элементы этого
движения определяются по данным траекторных измерений. Знание движения центра
масс станции и ее движения относительно центра масс позволяет рассчитать первые
три слагаемых формулы (1). Вычисление четвертого слагаемого требует еще задания
способов вычисления , в результате получается аппроксимация вращательного движения
станции. Движение центра масс последней считается кеплеровым. Элементы этого
движения определяются по данным траекторных измерений. Знание движения центра
масс станции и ее движения относительно центра масс позволяет рассчитать первые
три слагаемых формулы (1). Вычисление четвертого слагаемого требует еще задания
способов вычисления 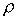 и и 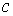 . Первая из этих величин рассчитывается согласно модели
атмосферы [4], вторая считается постоянной и определяется по данным траекторных
измерений. . Первая из этих величин рассчитывается согласно модели
атмосферы [4], вторая считается постоянной и определяется по данным траекторных
измерений.
В качестве инерциальной
системы координат, по отношению к которой задается ориентация станции,
используется правая система 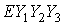 , связанная с земным экватором. Точка , связанная с земным экватором. Точка  – центр Земли, оси – центр Земли, оси 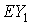 и и 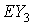 направлены в точку
весеннего равноденствия и северный полюс мира эпохи 2000.0. Под ориентацией
станции понимается ориентация жестко связанной с ее корпусом строительной
системы координат направлены в точку
весеннего равноденствия и северный полюс мира эпохи 2000.0. Под ориентацией
станции понимается ориентация жестко связанной с ее корпусом строительной
системы координат 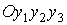 . Эта система также правая. Точка . Эта система также правая. Точка 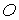 центр масс станции,
ось центр масс станции,
ось  параллельна
продольной оси Служебного модуля и направлена от его переходного отсека к
агрегатному отсеку, ось параллельна
продольной оси Служебного модуля и направлена от его переходного отсека к
агрегатному отсеку, ось 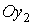 перпендикулярна оси
вращения солнечных батарей СМ. Положение системы перпендикулярна оси
вращения солнечных батарей СМ. Положение системы 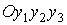 относительно системы относительно системы 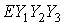 задается с помощью
кватерниона задается с помощью
кватерниона 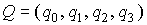 , имеющего единичную норму: , имеющего единичную норму: 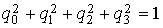 . Матрицу перехода от системы . Матрицу перехода от системы 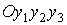 к системе к системе 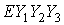 обозначим обозначим 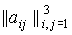 , где , где 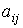 – косинус угла между
осями – косинус угла между
осями 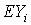 и и 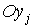 . Элементы этой матрицы выражаются через компоненты . Элементы этой матрицы выражаются через компоненты 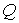 с помощью формул с помощью формул
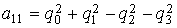 , , 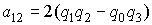 , , 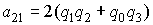
и формул, которые получаются из выписанных
циклической перестановкой индексов 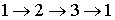 . Ниже, если не оговорено особо, компоненты векторов и
координаты точек указываются в системе . Ниже, если не оговорено особо, компоненты векторов и
координаты точек указываются в системе  . .
Значения
кватерниона ориентации, используемые для аппроксимации фактического
вращательного движения станции, берутся из телеметрической информации. Эта
информация собирается в течение нескольких часов и содержит последовательность
моментов времени и кватернионов
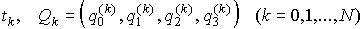 .
(2) .
(2)
Здесь 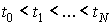 , , 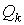 – значение кватерниона – значение кватерниона
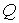 , вычисленное на момент , вычисленное на момент 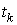 . Как правило, . Как правило, 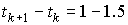 мин, мин, 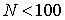 . Кватернион, задающий ориентацию станции, определен с
точностью до знака. Знаки . Кватернион, задающий ориентацию станции, определен с
точностью до знака. Знаки 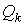 и момент и момент 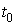 в (2) выбираются из
условия в (2) выбираются из
условия
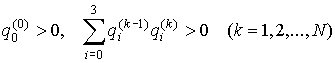 . .
Сглаживание
последовательности кватернионов (2) выполняется покомпонентно с использованием
решения следующей задачи. Пусть в точках 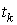 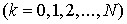 , , 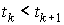 , известны приближенные значения гладкой функции , известны приближенные значения гладкой функции 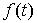 : : 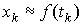 . Требуется приближенно восстановить эту функцию на отрезке . Требуется приближенно восстановить эту функцию на отрезке 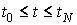 . .
В [5] отыскание 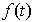 в предположении, что
эта функция дважды непрерывно дифференцируема, сводится к решению вариационной
задачи в предположении, что
эта функция дважды непрерывно дифференцируема, сводится к решению вариационной
задачи
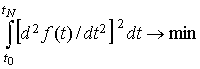 , , 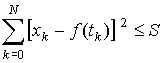 . (3) . (3)
Здесь 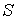 – заданное
положительное число. Решением задачи (3) является кубический сплайн. В [5]
приведена программа на алголе-60 вычисления коэффициентов этого сплайна по
величинам – заданное
положительное число. Решением задачи (3) является кубический сплайн. В [5]
приведена программа на алголе-60 вычисления коэффициентов этого сплайна по
величинам 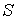 , , 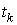 , , 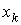  . Эта программа, переписанная на турбо-паскаль, применялась в
данной работе. . Эта программа, переписанная на турбо-паскаль, применялась в
данной работе.
Норма кватерниона,
который образован сплайнами, сглаживающими компоненты кватернионов (2), уже не
равна единице, но мало отличается от нее. Полученная кватернионная функция
нормируется на единицу и служит аппроксимацией вращения системы 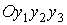 относительно системы относительно системы 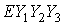 на отрезке на отрезке 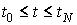 . Проекции абсолютной угловой скорости . Проекции абсолютной угловой скорости 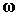 системы системы 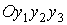 на ее собственные оси
находятся с помощью производной этой функции и кинематических уравнений на ее собственные оси
находятся с помощью производной этой функции и кинематических уравнений
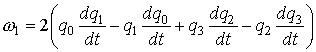 , ,
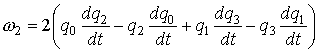 , ,
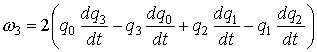 . .
Продифференцировав последние уравнения по времени и
подставив в полученные выражения первую и вторую производные нормированной
кватернионной функции, можно найти 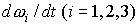 . Теперь все готово для расчета микроускорения по формуле
(1). . Теперь все готово для расчета микроускорения по формуле
(1).
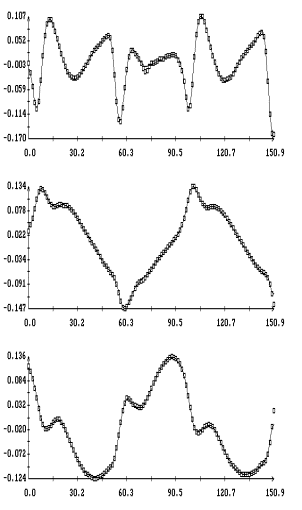
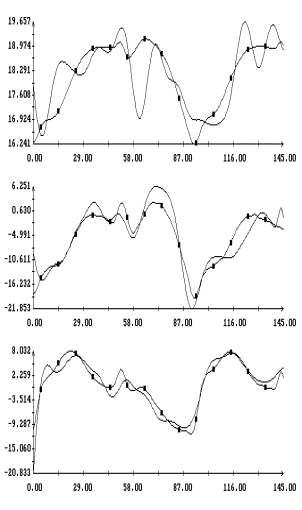
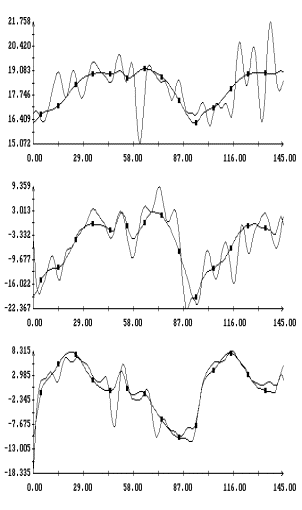
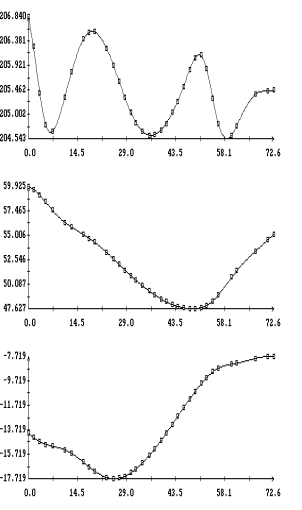
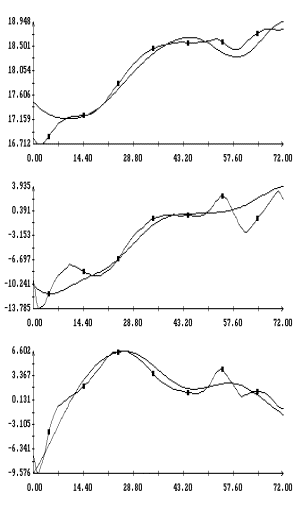
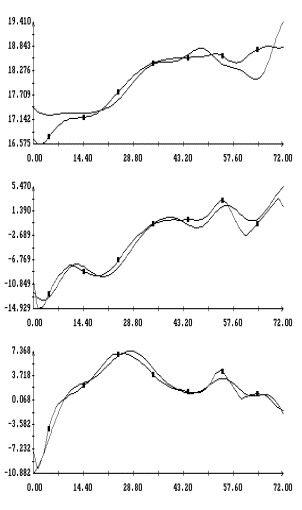
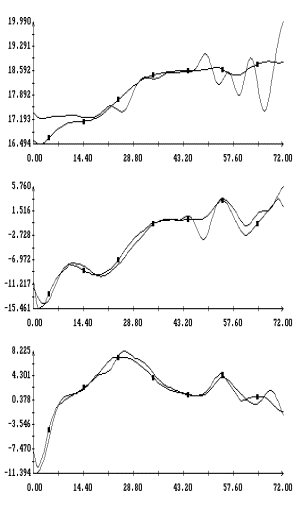
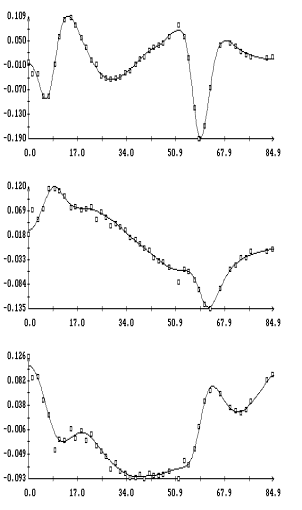
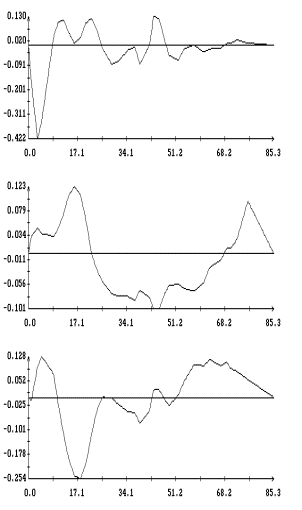
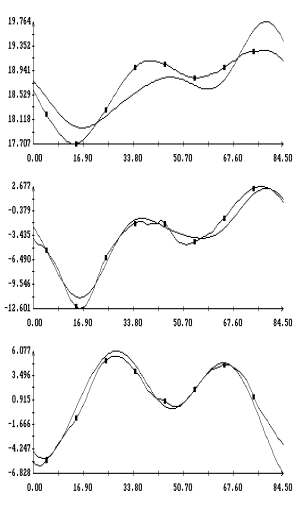
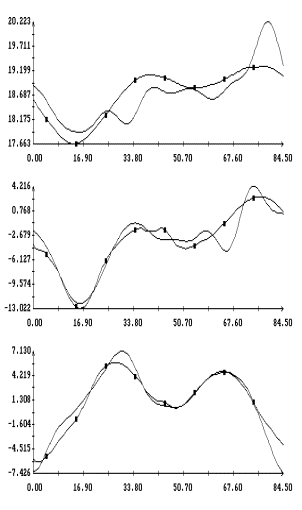
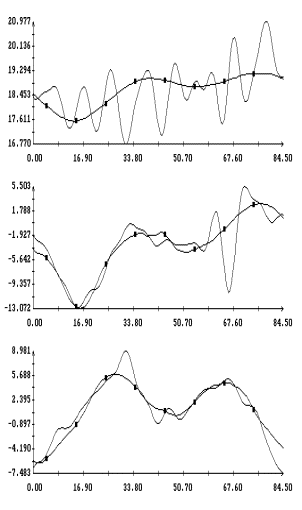
Примеры аппроксимации движения
станции по информации (2) и расчета на основании этой аппроксимации
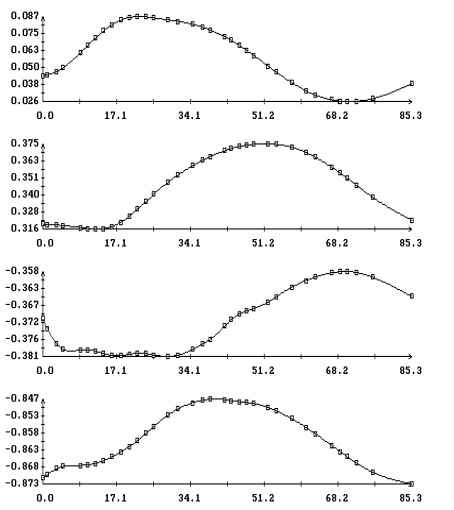
квазистатической компоненты микроускорения приведены на рис. 1а,б – 4а,б. Некоторые характеристики интервалов
времени, которые были выбраны для проводимого анализа, приведены в трех первых
столбцах табл. 1. Правые графики на рис. 1а
– 4а иллюстрируют сглаживание
телеметрических данных (они обозначены маркерами) сплайнами, которые были
построены для 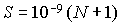 в
(3); левые графики представляют собой квазистатическую компоненту ускорения в
(3); левые графики представляют собой квазистатическую компоненту ускорения 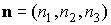 в
точке в
точке 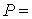 ( (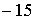 м, м, 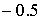 м, 1м). Выбор этой точки будет ясен ниже. м, 1м). Выбор этой точки будет ясен ниже.
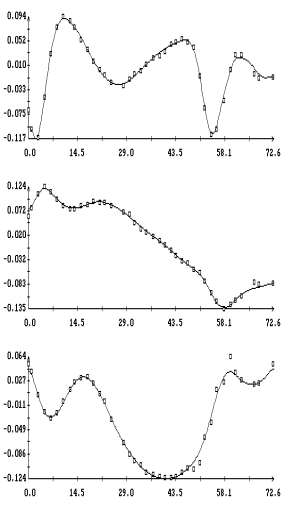
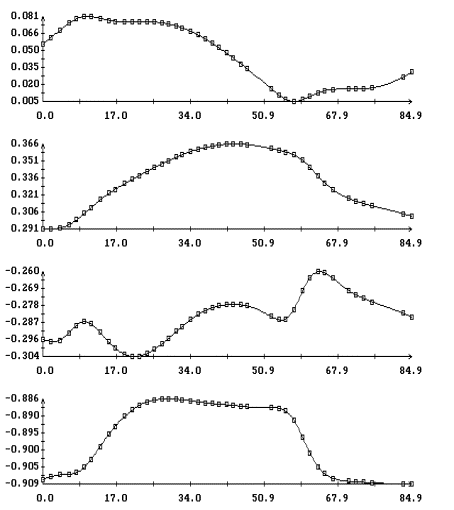
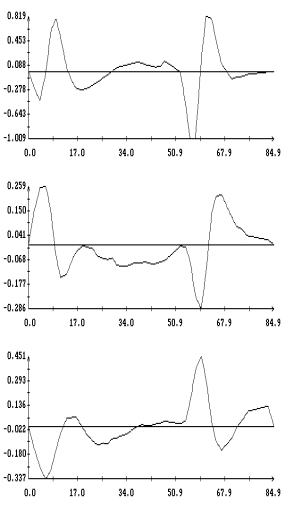
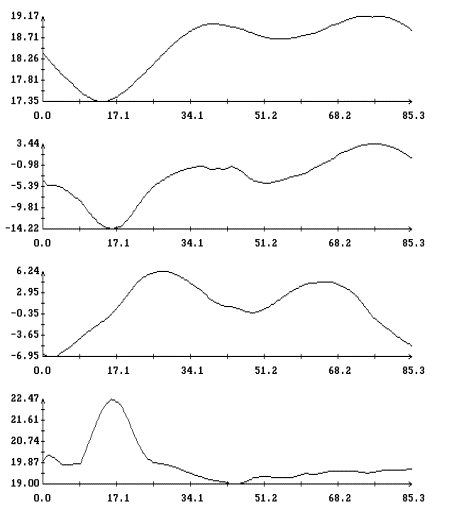
Некоторые
детали реконструированного движения показаны на рис. 1б – 4б. Здесь слева непрерывными кривыми
изображены графики углов, задающих ориентацию системы 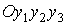 относительно системы относительно системы 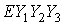 , маркерами
указаны значения тех же углов, рассчитанные по данным (2). Углы введены с помощью
условия: при совпадении точек , маркерами
указаны значения тех же углов, рассчитанные по данным (2). Углы введены с помощью
условия: при совпадении точек 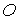 и и 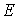 система система 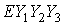 переводится в
систему переводится в
систему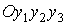 тремя последовательными поворотами: 1) на угол тремя последовательными поворотами: 1) на угол 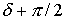 вокруг оси вокруг оси 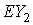 , 2) на угол , 2) на угол 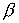 вокруг новой оси вокруг новой оси 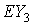 , 3) на угол , 3) на угол 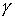 вокруг новой оси вокруг новой оси 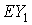 , совпадающей с осью , совпадающей с осью 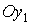 . Однако способ введения углов в данном случае не важен.
Важны только диапазоны их изменения, которые характеризуют точность поддержания
ориентации. В средней части рис. 1б –
4б приведены графики компонент
угловой скорости станции. Непрерывные кривые – результат реконструкции, маркеры
– данные телеметрии. Справа на рисунках 1б
– 4б приведены графики компонент
углового ускорения станции . Однако способ введения углов в данном случае не важен.
Важны только диапазоны их изменения, которые характеризуют точность поддержания
ориентации. В средней части рис. 1б –
4б приведены графики компонент
угловой скорости станции. Непрерывные кривые – результат реконструкции, маркеры
– данные телеметрии. Справа на рисунках 1б
– 4б приведены графики компонент
углового ускорения станции 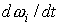 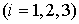 ,
горизонтальные прямые указывают нуль. ,
горизонтальные прямые указывают нуль.
Рисунки иллюстрируют движение
станции во время поддержания гиродинами ее неизменной ориентации в инерциальной
системе координат. Это достаточно мягкое движение – в данных примерах не было
включений реактивных двигателей системы ориентации. Учет работы этих двигателей
потребовал бы включения в формулу (1) дополнительных слагаемых, что значительно
осложнило бы расчет микроускорений описываемым способом.
Сглаживание данных измерений
низкочастотных микроускорений
На Американском сегменте МКС
установлен трехкомпонентный акселерометр MAMS
[6], измеряющий микроускорение с частотами менее несколь-ких сотых долей герца.
В настоящее время этот акселерометр функционирует практически непрерывно, и
полученные с его помощью данные доступны в цифровом виде через Интернет. Файлы
данных содержат целое число четверок действительных чисел формата single. В четверку входят момент времени и три
отвечающие ему компоненты микроускорения. Файлы имеют разную длину и охватывают
от нескольких минут до нескольких десятков ми-нут полетного времени. Как
правило, измерения в файлах даются с шагом 16 с, но иногда имеются пропуски
продолжительностью до нескольких минут.
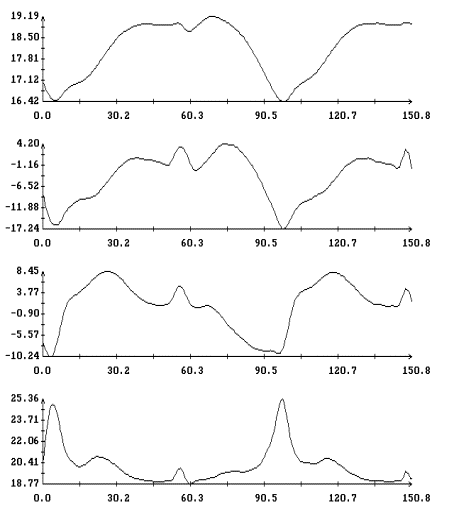
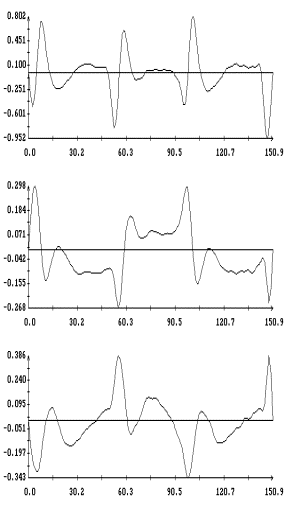
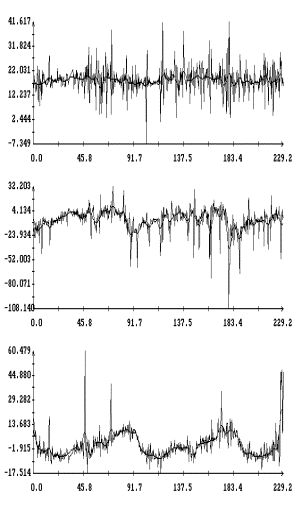
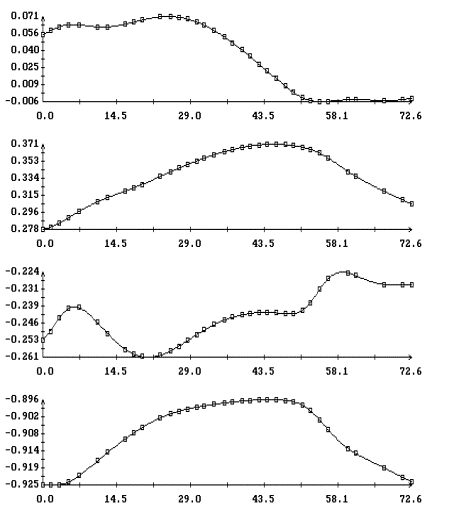
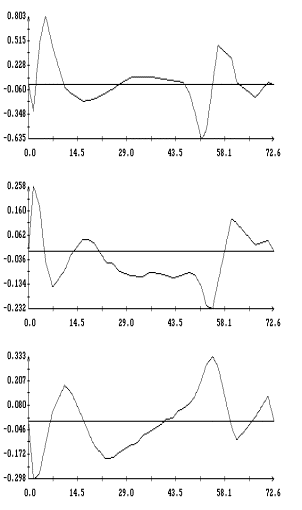
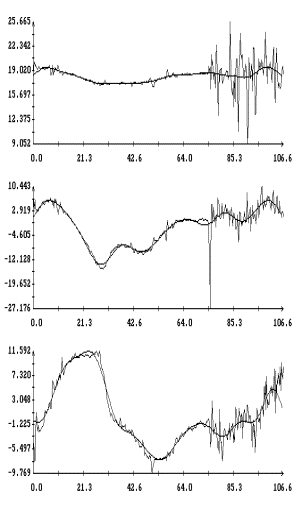
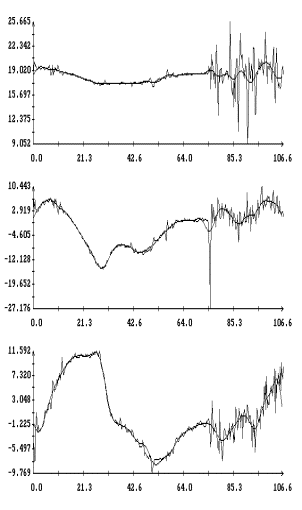
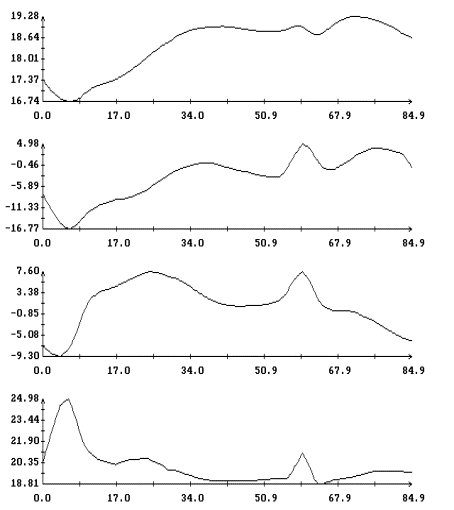
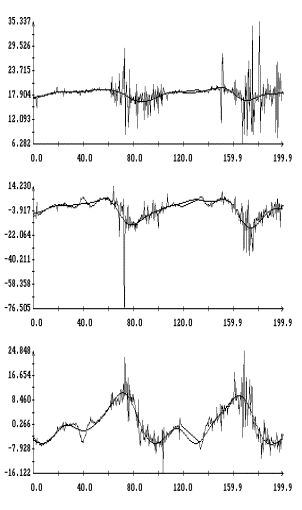
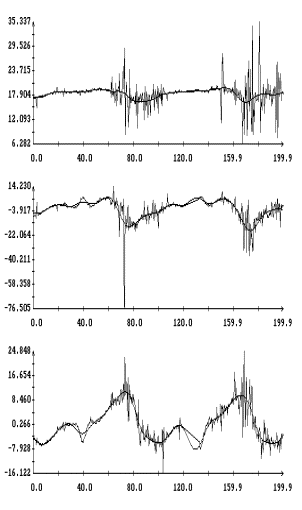
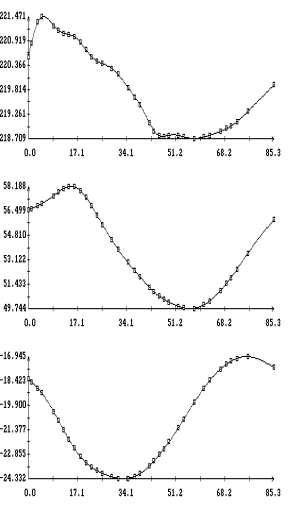
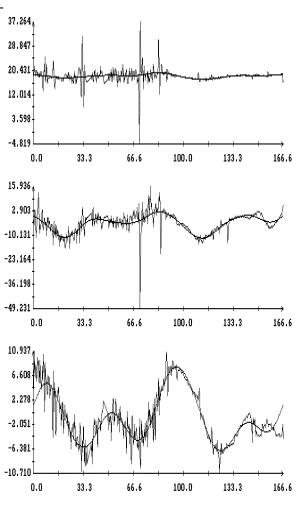
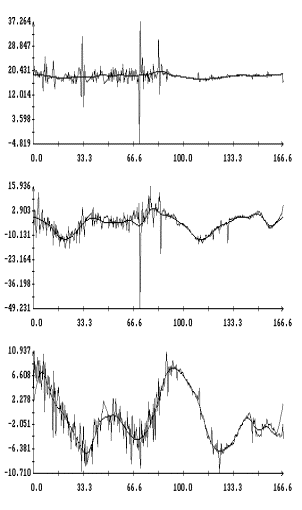
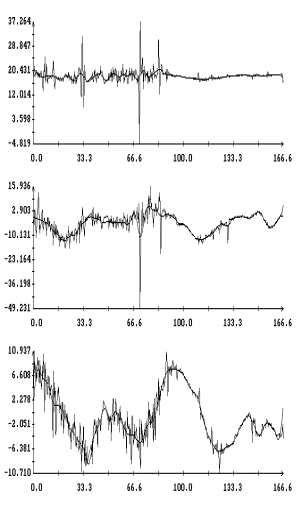
Данные
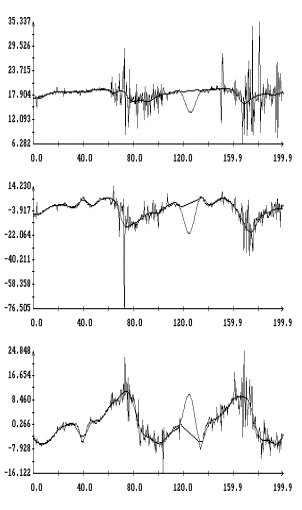
измерений MAMS представлены на рис. 1в
– 4в в виде ломаных с вершинами в точках,
отвечающих этим данным (каждый рисунок содержит три экземпляра одинаковых
ломаных). Отрезки данных, приведенные на этих рисунках, охватывают интервалы
времени, показанные на рис. 1а,б – 4а,б. Ломаные на рис. 1в – 4в
выглядят как пилообразные линии. Функции, имеющие такого рода графики, трудно
принять в качестве выражения квазистатической компоненты микроускорения. Во
всяком случае, эти функции существенно отличаются от функций, графики которых
представлены на рис. 1а – 4а. Чтобы получить более приемлемые с
нашей точки зрения результаты, данные измерений MAMS сглаживались с помощью
дискретных рядов Фурье. Цель сглаживания – исключить из данных колебания с
частотами выше нескольких тысячных долей герца. Сглаживающие ряды строились
независимо для каждой компоненты микроускорения. Ряды, построенные по данным
измерений на отрезке времени 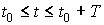 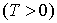 ,
имели вид ,
имели вид
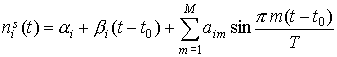 . . 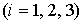 (4) (4)
Коэффициенты
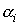 , , 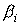 , , 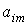 находились
методом наименьших квадратов. Полученные выражения (4) иногда испытывают
заметные сравнительно высокочастотные колебания. Чтобы избавиться от них,
тригонометрические члены в (4) модифицировались с помощью корректирующих
множителей: находились
методом наименьших квадратов. Полученные выражения (4) иногда испытывают
заметные сравнительно высокочастотные колебания. Чтобы избавиться от них,
тригонометрические члены в (4) модифицировались с помощью корректирующих
множителей:
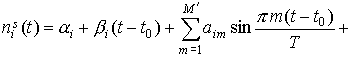 (5)
(5)
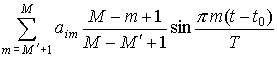 . . 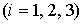 . .
Здесь 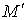 – целая часть числа – целая часть числа 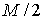 . .
Примеры сглаживания данных
измерений акселерометра MAMS приведены на рис. 1в – 4в. Здесь плавные
кривые – графики сглаживающих выражений (5). Для каждого отрезка данных
построены три набора таких выражений. Они отличаются числом гармоник 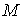 ,
которое указано в подписях к рисункам. Значения ,
которое указано в подписях к рисункам. Значения 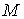 в примерах на рис. 1в, 2в, и 4в выбраны так, чтобы отношение в примерах на рис. 1в, 2в, и 4в выбраны так, чтобы отношение 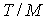 составляло приблизительно 10 мин, 5 мин и 2.5
мин. Это условие нарушено в примере на рис. 3в, поскольку здесь имеется большой пропуск в данных при составляло приблизительно 10 мин, 5 мин и 2.5
мин. Это условие нарушено в примере на рис. 3в, поскольку здесь имеется большой пропуск в данных при 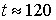 мин. мин.
У третьей компоненты микроускорения
на рис. 1в – 4в изменен знак. Это связано с тем, что рисунки построены
непосредственно по исходным данным измерений, а MAMS измеряет кажущееся
ускорение 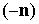 в системе координат в системе координат 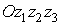 ,
связанной с системой ,
связанной с системой 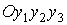 формулами перехода формулами перехода 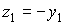 , , 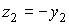 , , 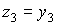 .
Чтобы пересчитать данных измерений MAMS в компоненты микроускорения в системе
координат .
Чтобы пересчитать данных измерений MAMS в компоненты микроускорения в системе
координат 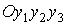 , у третьей компоненты этих данных следует изменить знак. , у третьей компоненты этих данных следует изменить знак.
Сравнение данных измерения с результатами
вычисления
Формулу
микроускорения (1) представим в виде
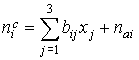 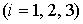 . (6) . (6)
Здесь
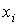 –
координаты точки –
координаты точки 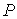 ,
т. е. ,
т. е. 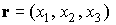 , , 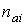 – компоненты аэродинамической составляющей микроускорения – компоненты аэродинамической составляющей микроускорения 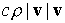 , ,
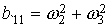 , , 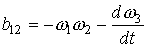 , , 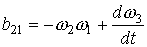 , ,
выражения для остальных коэффициентов 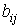 получаются из приведенных циклической перестановкой индексов. Описанная
выше аппроксимация движения станции позволяет найти величины получаются из приведенных циклической перестановкой индексов. Описанная
выше аппроксимация движения станции позволяет найти величины 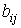 и и 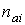 в
функции времени. в
функции времени.
Сравним
микроускорение, рассчитываемое по формуле (6), с данными измерений MAMS, точнее, с результатами сглаживания этих
данных выражениями (5). Для проведения сравнения следует преобразовать
сглаженные данные измерений к системе 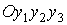 и
использовать реальные координаты акселерометра MAMS
в качестве координат и
использовать реальные координаты акселерометра MAMS
в качестве координат 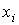 в
(6). Переход к системе в
(6). Переход к системе 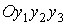 выполняется по
правилу, указанному выше. Что же касается координат выполняется по
правилу, указанному выше. Что же касается координат 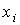 , то эти параметры будем считать параметрами согласования и
выбирать из условия наилучшего совпадения функций , то эти параметры будем считать параметрами согласования и
выбирать из условия наилучшего совпадения функций 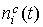 и и 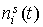 на отрезке,
являющемся пересечением их областей определения. Дело в том, что хотя положение
акселерометра на станции известно точно, положение ее центра масс время от времени
меняется, и нет уверенности, что это изменение достаточно точно отражается в
документации. Кроме того, показания низкочастотных акселерометров обычно
содержат постоянные смещения, которые следует учитывать при сопоставлении
расчетных микроускорений с данными измерений. на отрезке,
являющемся пересечением их областей определения. Дело в том, что хотя положение
акселерометра на станции известно точно, положение ее центра масс время от времени
меняется, и нет уверенности, что это изменение достаточно точно отражается в
документации. Кроме того, показания низкочастотных акселерометров обычно
содержат постоянные смещения, которые следует учитывать при сопоставлении
расчетных микроускорений с данными измерений.
С
учетом сделанных замечаний задачу сравнения функций 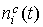 и и 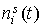 переформулируем как
задачу оценивания координат переформулируем как
задачу оценивания координат  и постоянных смещений
в данных измерений. Новую задачу будем решать методом наименьших квадратов.
Пусть моменты времени и постоянных смещений
в данных измерений. Новую задачу будем решать методом наименьших квадратов.
Пусть моменты времени 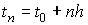 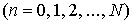 лежат в областях определения функций лежат в областях определения функций 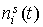 , , 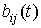 и и 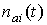 . Составим выражение . Составим выражение
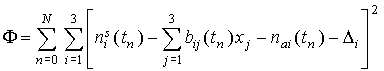 , ,
где 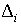 – постоянное смещение в
функции – постоянное смещение в
функции 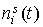 . Согласно методу наименьших квадратов оценками параметров . Согласно методу наименьших квадратов оценками параметров 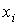 и и 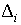 считаются их
значения, минимизирующие считаются их
значения, минимизирующие 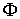 . Поскольку . Поскольку 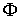 квадратично зависит
от квадратично зависит
от 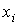 и и 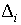 , вычисление оценок сводится к решению
линейной системы так называемых нормальных уравнений с симметрической
неотрицательно определенной матрицей. Эту матрицу, отвечающую вектору
неизвестных , вычисление оценок сводится к решению
линейной системы так называемых нормальных уравнений с симметрической
неотрицательно определенной матрицей. Эту матрицу, отвечающую вектору
неизвестных 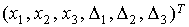 , обозначим , обозначим 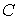 . Почти во всех случаях обработки телеметрической информации
с борта МКС, матрица . Почти во всех случаях обработки телеметрической информации
с борта МКС, матрица 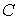 была положительно определенной
и достаточно хорошо обусловленной. была положительно определенной
и достаточно хорошо обусловленной.
Пусть 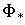 – значение – значение 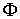 в точке минимума. Точность согласования
функций в точке минимума. Точность согласования
функций 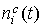 и и 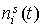 будем характеризовать
средней квадратической ошибкой будем характеризовать
средней квадратической ошибкой
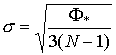 , ,
а
точность найденных оценок величин 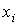 и и 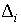 – их стандартными
отклонениями – их стандартными
отклонениями 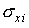 и и 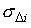 – квадратными корнями
из соответствующих диагональных элементов матрицы – квадратными корнями
из соответствующих диагональных элементов матрицы 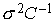 . Такие характеристики точности отвечают обычным
предположениям метода наименьших квадратов. Хотя эти предположения в данном
случае не выполнены, стандартные отклонения являются естественными
характеристиками точности вычисляемых оценок, согласованными со способом их получения. . Такие характеристики точности отвечают обычным
предположениям метода наименьших квадратов. Хотя эти предположения в данном
случае не выполнены, стандартные отклонения являются естественными
характеристиками точности вычисляемых оценок, согласованными со способом их получения.
Табл.
2 содержит оценки параметров 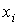 , , 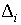 и
стандартные отклонения и
стандартные отклонения 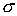 , , 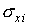 , , 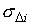 для
интервалов, указанных в табл. 1. Оценки были получены при для
интервалов, указанных в табл. 1. Оценки были получены при  мин для чисел гармоник мин для чисел гармоник 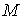 приведенных на рис. 1в –
4в. Соответствующие значения приведенных на рис. 1в –
4в. Соответствующие значения 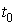 и и 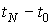 указаны в двух
последних столбцах табл. 1. Нижняя строка табл. 2 содержит значения параметров указаны в двух
последних столбцах табл. 1. Нижняя строка табл. 2 содержит значения параметров 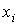 , найденные по данным эксплутационных документов станции.
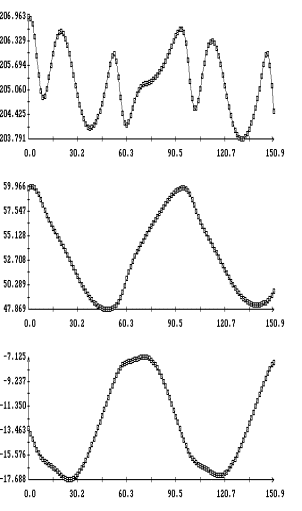
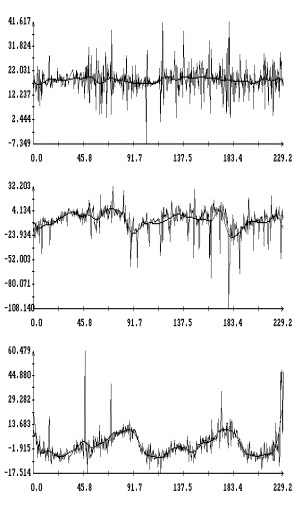
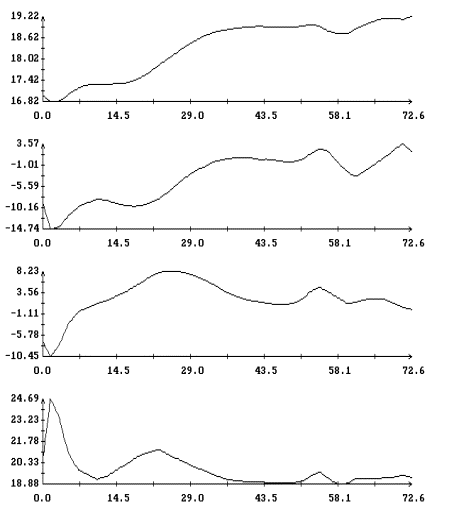
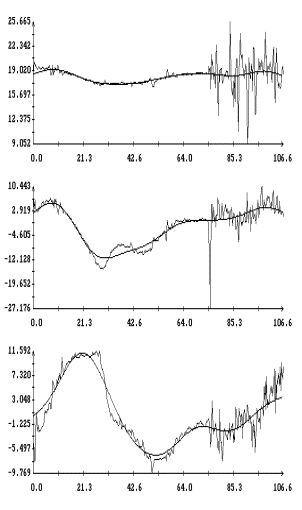
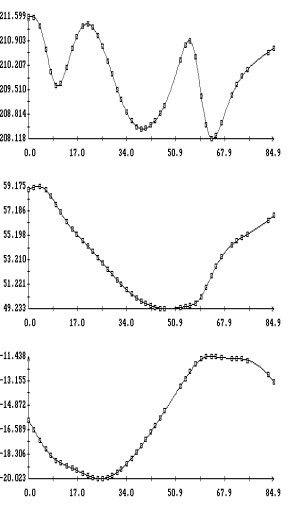
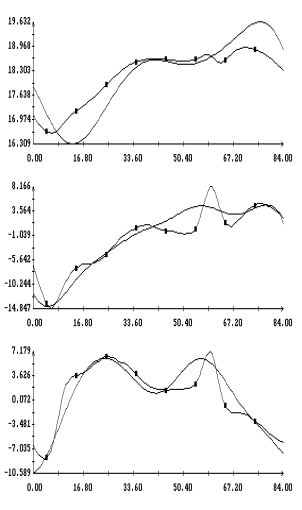
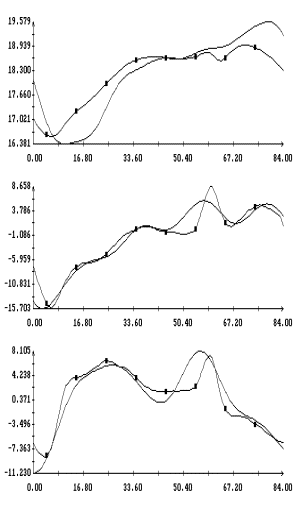
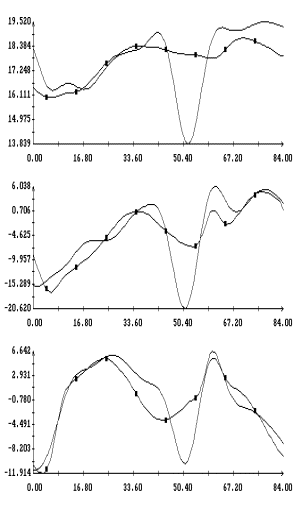
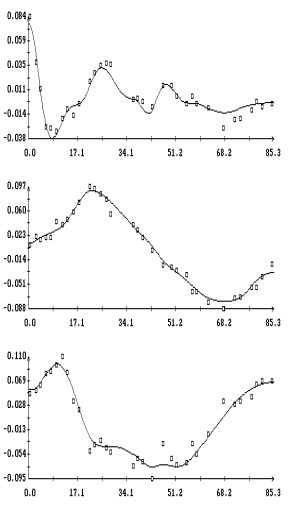
Графики функций , найденные по данным эксплутационных документов станции.
Графики функций 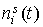 и
наилучшим образом совпадающих с ними функций и
наилучшим образом совпадающих с ними функций 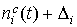 представлены на рис. 1г
– 4г. Здесь графики функций представлены на рис. 1г
– 4г. Здесь графики функций 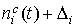 отмечены маркерами. Как видно из рисунков, функции отмечены маркерами. Как видно из рисунков, функции
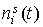 и и 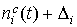 совпадают достаточно хорошо. Оценки координат совпадают достаточно хорошо. Оценки координат 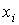 , приведенные в табл. 2, примерно соответствуют официальным
значениям. Официальные значения этих координат поясняют выбор точки , приведенные в табл. 2, примерно соответствуют официальным
значениям. Официальные значения этих координат поясняют выбор точки 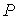 для расчета микроускорений
на рис. 1а – 4а. для расчета микроускорений
на рис. 1а – 4а.
Описанный
способ оценивания параметров 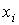 является по существу
способом оценивания положения центра масс станции. Поскольку положение акселерометра
в системе координат станции, связанной с характерными элементами ее конструкции,
известно точно и направления осей этой системы координат совпадают с
направлениями осей системы является по существу
способом оценивания положения центра масс станции. Поскольку положение акселерометра
в системе координат станции, связанной с характерными элементами ее конструкции,
известно точно и направления осей этой системы координат совпадают с
направлениями осей системы 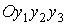 , знание величин , знание величин 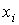 означает знание
фактического положения точки означает знание
фактического положения точки  . Судя по стандартным отклонениям . Судя по стандартным отклонениям 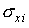 , точность оценивания этого положения составляет несколько
десятков сантиметров, однако разброс оценок координаты , точность оценивания этого положения составляет несколько
десятков сантиметров, однако разброс оценок координаты 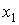 показывает, что
реальная погрешность составляет около 2 м. показывает, что
реальная погрешность составляет около 2 м.
Ввиду
важности задачи оценивания положения центра масс станции, исследуем природу
погрешностей определения величин 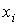 и и 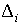 описанным способом. С
этой целью соотнесем стандартные отклонения описанным способом. С
этой целью соотнесем стандартные отклонения 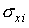 , , 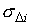 с собственным вектором введенной выше матрицы с собственным вектором введенной выше матрицы 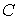 , отвечающим ее минимальному собственному числу. Справедлива
формула , отвечающим ее минимальному собственному числу. Справедлива
формула
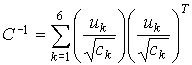 , ,
где 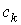 и и 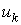 – собственные числа и
ортонормированные собственные векторы матрицы – собственные числа и
ортонормированные собственные векторы матрицы 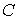 . Если выполнены неравенства . Если выполнены неравенства 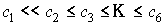 , то согласно этой формуле наибольшие стандартные отклонения
имеют те определяемые параметры, которым отвечают компоненты вектора , то согласно этой формуле наибольшие стандартные отклонения
имеют те определяемые параметры, которым отвечают компоненты вектора 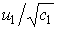 с наибольшими
модулями. с наибольшими
модулями.
В качестве примера
рассмотрим интервал 2 из табл. 1. Матрица 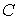 системы нормальных
уравнений не зависит от числа системы нормальных
уравнений не зависит от числа 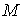 гармоник,
использованных для аппроксимации данных измерений. От этого числа зависит
только правая часть системы нормальных уравнений. Для интервала 2 собственные
числа матрицы гармоник,
использованных для аппроксимации данных измерений. От этого числа зависит
только правая часть системы нормальных уравнений. Для интервала 2 собственные
числа матрицы 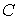 , расположенные в порядке возрастания, составляют , расположенные в порядке возрастания, составляют 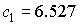 , , 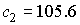 , , 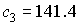 , , 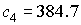 , , 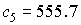 , , 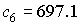 . В данном случае . В данном случае 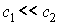 , собственный вектор , собственный вектор 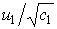 этой матрицы имеет
вид этой матрицы имеет
вид
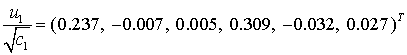 . .
Абсолютные величины компонент остальных векторов 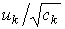 не превосходят 0.08. В
соответствии со сделанным выше замечанием наибольшие стандартные отклонения во
всех трех случаях обработки данных измерений на этом интервале (при разных
значениях не превосходят 0.08. В
соответствии со сделанным выше замечанием наибольшие стандартные отклонения во
всех трех случаях обработки данных измерений на этом интервале (при разных
значениях 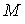 ) имеют параметры ) имеют параметры 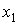 и и 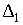 , причем , причем 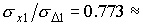 0.237/0.309=0.767. Последнее соотношение справедливо для всех
рассмотренных 0.237/0.309=0.767. Последнее соотношение справедливо для всех
рассмотренных 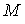 . Аналогичная ситуация наблюдается и при обработке
остальных интервалов. Таким образом, приходится признать, что хотя уточнение
смещений . Аналогичная ситуация наблюдается и при обработке
остальных интервалов. Таким образом, приходится признать, что хотя уточнение
смещений 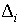 улучшает
согласие измеренных и расчетных значений микроускорений, на точность оценок
координат акселерометра это уточнение влияет плохо. улучшает
согласие измеренных и расчетных значений микроускорений, на точность оценок
координат акселерометра это уточнение влияет плохо.
В
табл. 3 приведены результаты оценивания координат 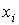 в предположении, что в предположении, что 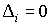 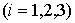 . Оценки находились методом наименьших квадратов. Выражение . Оценки находились методом наименьших квадратов. Выражение 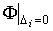 минимизировалось по
трем определяемым параметром. Стандартные отклонения оценок находились по
описанной выше схеме с учетом того обстоятельства, что число определяемых
параметров теперь уменьшилось до 3 (в частности в формуле средней
квадратической ошибки согласования функций минимизировалось по
трем определяемым параметром. Стандартные отклонения оценок находились по
описанной выше схеме с учетом того обстоятельства, что число определяемых
параметров теперь уменьшилось до 3 (в частности в формуле средней
квадратической ошибки согласования функций 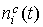 и и 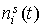 число число 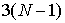 было заменено числом было заменено числом 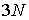 ). Как видно из таблицы, кучность вычисленных оценок
координаты ). Как видно из таблицы, кучность вычисленных оценок
координаты 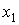 заметно повысилась.
Если отбросить резко выделяющийся большим значением заметно повысилась.
Если отбросить резко выделяющийся большим значением 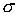 вариант оценивания,
отвечающий интервалу 3 при вариант оценивания,
отвечающий интервалу 3 при 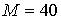 , то разности максимальной и минимальной оценок координат , то разности максимальной и минимальной оценок координат 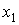 , , 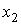 и и 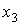 в табл. 3 составят
соответственно 0.5, 0.7 и 0.8 м. Такая кучность говорит о том, что
рассматриваемый метод определения координат центра масс станции может оказаться
перспективным. в табл. 3 составят
соответственно 0.5, 0.7 и 0.8 м. Такая кучность говорит о том, что
рассматриваемый метод определения координат центра масс станции может оказаться
перспективным.
Следует заметить также, что
значения 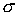 в табл. 3 незначительно
превышают значения этого параметра для соответствующих интервалов из табл. 2.
Следовательно, смещения в данных измерений MAMS малы. в табл. 3 незначительно
превышают значения этого параметра для соответствующих интервалов из табл. 2.
Следовательно, смещения в данных измерений MAMS малы.
Данная работа выполнена
при финансовой поддержке РФФИ (проект 02-01-00323). Авторы благодарны Mr. Kenol Jules за полезные
консультации по использованию данных измерений MAMS.
Литература
1.
Бабкин Е.В., Беляев М.Ю., Ефимов Н.И.,
Обыденников С.С., Сазонов В.В., Стажков В.М. Первые результаты определения
микроускорений на Российском сегменте Международной космической станции.
Препринт ИПМ им. М.В.Келдыша РАН, 2001, № 83.
2.
Сазонов В.В., Беляев М.Ю., Ефимов Н.И.,
Стажков В.М., Бабкин Е.В. Определение квазистатической компоненты
микроускорения на станции Мир. Космические исследования, 2001, т. 39, № 2, с.
126-136.
3. Сазонов В.В.,
Комаров M.М, Полежаев В.И., Никитин С.А., Ермаков M.K., Стажков В.М., Зыков
С.Г., Рябуха С.Б., Асеведо Х., Либерман Е. Микроускорения на орбитальной станции
«Мир» и оперативный анализ гравитационной чувствительности конвективных
процессов тепло-массоперехода. Космические исследования, 1999, т. 37, № 1, с.
80-94.
4. ГОСТ
(Государственный стандарт) 22721-77: Модели верхней атмосферы для
баллистических вычислений, 1977, М., Изд. стандартов, 1978.
5.
Reinsch C.H. Smoothing by spline
functions. Numerische mathematik, 1975, B. 24, H. 5, S. 383-393.
6.
Jules K., Hrovat K., Kelly E.
International Space Station Increment-2. Quick Look Report. NASA, Glenn
Research Center, Cleveland, Ohio, 2001.
Приложение
|
![]()
![]()
![]() (
(![]() )
)![]() (мин)
(мин)
![]() (мин)
(мин)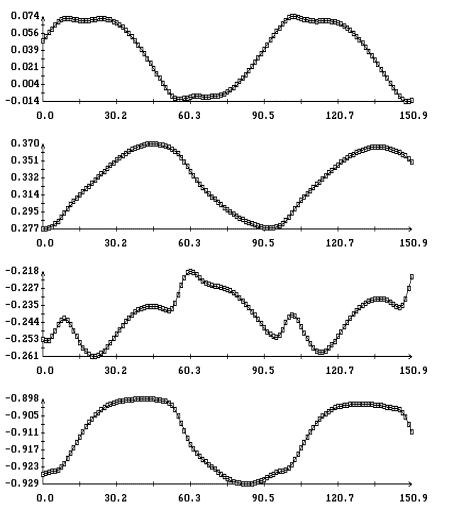
![]() соответствует
соответствует ![]() UTC 2001.11.05.
UTC 2001.11.05.![]() .
.![]() (град.)
(град.) ![]() (
(![]() )
) ![]() (
(![]() )
)
![]() (мин)
(мин) ![]() (мин)
(мин) ![]() (мин)
(мин)![]() соответствует
соответствует ![]() UTC 2001.11.05.
UTC 2001.11.05.![]()
![]() (
(![]() )
)![]() (мин)
(мин)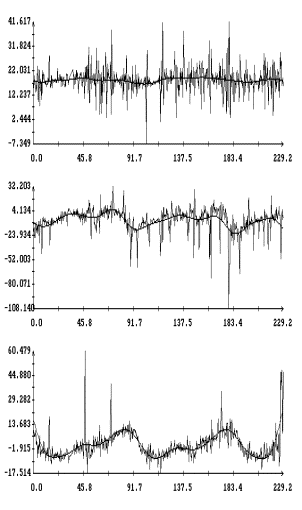
![]() соответствует
соответствует ![]() UTC
2001.11.05.
UTC
2001.11.05.![]()
![]() (
(![]() )
)
![]() (мин)
(мин)![]()
![]()
![]()
![]() соответствует
соответствует ![]() UTC
2001.11.05.
UTC
2001.11.05.![]()
![]()
![]() (
(![]() )
)
![]() (мин)
(мин)
![]() (мин)
(мин)![]() соответствует
соответствует ![]() UTC
2001.11.05.
UTC
2001.11.05.![]() .
.![]() (град.)
(град.) ![]() (
(![]() )
) ![]() (
(![]() )
)
![]() (мин)
(мин) ![]() (мин)
(мин) ![]() (мин)
(мин)![]() соответствует
соответствует ![]() UTC 2001.11.05.
UTC 2001.11.05.![]()
![]() (
(![]() )
)
![]() (мин)
(мин)![]()
![]()
![]()
![]() соответствует
соответствует ![]() UTC
2001.11.05.
UTC
2001.11.05.![]()
![]() (
(![]() )
)
![]() (мин)
(мин)![]()
![]()
![]()
![]() соответствует
соответствует ![]() UTC
2001.11.05.
UTC
2001.11.05.![]()
![]()
![]() (
(![]() )
)
![]() (мин)
(мин)
![]() (мин)
(мин)![]() соответствует
соответствует ![]() UTC
2001.11.04.
UTC
2001.11.04.![]() .
.![]() (град.)
(град.) ![]() (
(![]() )
) ![]() (
(![]() )
)
![]() (мин)
(мин) ![]() (мин)
(мин) ![]() (мин)
(мин)![]() соответствует
соответствует ![]() UTC 2001.11.04.
UTC 2001.11.04.![]()
![]() (
(![]() )
)
![]() (мин)
(мин)![]()
![]()
![]()
![]() соответствует
соответствует ![]() UTC
2001.11.04.
UTC
2001.11.04.![]()
![]() (
(![]() )
)
![]() (мин)
(мин)![]()
![]()
![]()
![]() соответствует
соответствует ![]() UTC
2001.11.04.
UTC
2001.11.04.![]()
![]()
![]() (
(![]() )
)
![]() (мин)
(мин)
![]() (мин)
(мин)![]() соответствует
соответствует ![]() UTC
2001.11.02.
UTC
2001.11.02.![]() .
.![]() (град.)
(град.) ![]() (
(![]() )
) ![]() (
(![]() )
)
![]() (мин)
(мин) ![]() (мин)
(мин) ![]() (мин)
(мин)![]() соответствует
соответствует ![]() UTC 2001.11.02.
UTC 2001.11.02.![]()
![]() (
(![]() )
)
![]() (мин)
(мин)![]()
![]()
![]()
![]() соответствует
соответствует ![]() UTC
2001.11.02.
UTC
2001.11.02.![]()
![]() (
(![]() )
)
![]() (мин)
(мин)![]()
![]()
![]()
![]() соответствует
соответствует ![]() UTC
2001.11.02.
UTC
2001.11.02.