Аннотация
Рассматриваются примеры механических систем с неголономными связями удерживающими и
неудерживающими. Удар диска о шероховатую прямую, односторонний конек, удар двухстороннего
конька о прямую. Показывается, что движение с односторонними однородными связями носит
безударный характер.
Abstract
The examples of mechanical systems with nonholonomic unilateral restrictions are considered.
Impact of a disk about a rough straight line, unilateral skate, impact bilaterial skate about
a straight line. Is shown, that the movement with unilateral homogeneous restrictions carries
nonimpact character.
Содержание
Введение
1. Принцип
Даламбера-Лагранжа для односторонних связей.
2. Основные
законы динамики.
3. Уравнения
Лагранжа 2-го рода.
4. Циклические
интегралы и теорема Рауса.
5. Система
с условными связями.
6. Односторонний
конек.
7. Удар в неголономной
системе.
8. Удар о
неголономную связь.
9. Малые
колебания.
10. Плоское
тело с каналом.
ЛИТЕРАТУРА
При исследовании механических систем с
односторонними связями и импульсными воздействиями с успехом используется
аппарат обобщённых функций и функций с ограниченным изменением [1-5]. Следуя
этому, будем считать траектории движения абсолютно непрерывными функциями,
скорости которых представляет собой функции ограниченного изменения. Это
обуславливается тем, что пространство функций с ограниченным изменением
является простейшим банаховым пространством содержащим функции скачков, которые
характерны для изменения скорости в системах с ударами. Уравнения движения при
этом приобретают форму уравнений с мерами Лебега-Стилтьеса [3, 6], или, иначе
говоря, обыкновенных дифференциальных уравнений с импульсными правыми частями.
Их удобство состоит, в том, что они позволяют описывать движение на всем его
протяжении, включающем как безударные участки, так и точки удара, а также
участки движения по границе односторонних связей.
Для натуральных механических систем c
односторонними связями методом штрафных функций в [7] выведены уравнения
движения с мерами в форме уравнений Лагранжа второго рода. В данной работе
предлагается способ вывода уравнений движения механических систем общего вида
основанный на общепринятом в механике аппарате возможных перемещений и принципе
Даламбера-Лагранжа, сформулированных в интегральной форме подобно тому, как это
делалось в [8]. Это позволяет для систем с идеальными двухсторонними и
односторонними связями получить уравнения движения с мерами в форме уравнений
Лагранжа первого рода. Такие уравнения пригодны как для голономных, так и для
неголономных систем. Из них выводятся основные законы механики таких систем, а
также уравнения движения в форме уравнений Лагранжа второго рода.
Помимо
систем с обычными односторонними связями мы рассмотрим системы с неголономными,
и т.н. условными односторонними связями. Односторонними неголономными связями
мы называем такие ограничения, накладываемые на движение системы, которые не
представлены (и, может быть, не представимы) в виде задания какой-либо области
в конфигурационном пространстве. Пример таких ограничений – это линейные
ограничения, задаваемые неравенствами вида 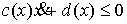 . Они возникают, при описании движения одностороннего конька. . Они возникают, при описании движения одностороннего конька.
Другой вид
подобных ограничений – это т.н. условные связи, возникающие, например, при
соударении абсолютно шероховатых поверхностей, которые прокатываются друг по
другу без проскальзывания. Формально подобные ограничения можно описать
системой: 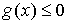 всегда, и всегда, и 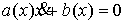 , при , при 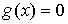 . Первое условие запрещает взаимное проникновение тел, а
второе описывает качение без проскальзывния при их соприкосновении. . Первое условие запрещает взаимное проникновение тел, а
второе описывает качение без проскальзывния при их соприкосновении.
Перейдем
теперь к общему описанию. Рассмотрим систему из 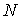 материальных точек,
перемещающихся в пространстве под действием приложенных к ним сил. Координаты
точек объединим в вектор материальных точек,
перемещающихся в пространстве под действием приложенных к ним сил. Координаты
точек объединим в вектор 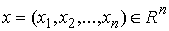 , , 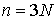 . Введём диагональную . Введём диагональную 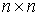 матрицу масс матрицу масс  . На её диагонали располагаются массы точек системы, по три одинаковых
значения для каждой точки. . На её диагонали располагаются массы точек системы, по три одинаковых
значения для каждой точки.
В отсутствии
связей движение системы описывается вторым законом Ньютона
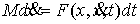
где 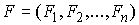 – сводный вектор сил,
действующих на точки системы. – сводный вектор сил,
действующих на точки системы.
Наложим на
систему семейство 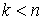 линейных удерживающих
связей: линейных удерживающих
связей:
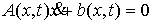
где 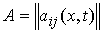 – – 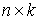 матрица удерживающих
связей, матрица удерживающих
связей, 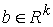 . .
Добавим к
ним семейство 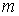 односторонних
голономных связей односторонних
голономных связей
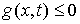
где 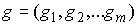  -мерная вектор-функция, -мерная вектор-функция, 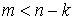 . Здесь и ниже подобные неравенства надо понимать как
покоординатное выполнение неравенств: . Здесь и ниже подобные неравенства надо понимать как
покоординатное выполнение неравенств: 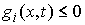 , , 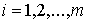 . .
Наложим на
систему также семейство 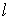 неголономных
односторонних связей: неголономных
односторонних связей:
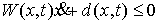
где 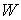 – матрица – матрица 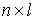 , , 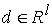 . .
Добавим
также одну группу 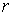 условных связей: условных связей:
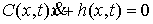
при 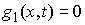 , где , где  – матрица – матрица 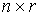 , , 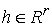 . Мы полагаем, что . Мы полагаем, что 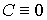 при при  . Рассмотрение систем, где число групп условных связей больше
одной, может быть произведено аналогично. . Рассмотрение систем, где число групп условных связей больше
одной, может быть произведено аналогично.
Введем 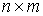 матрицу односторонних
связей матрицу односторонних
связей 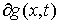 . Строка . Строка 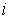 этой матрицы – это
вектор этой матрицы – это
вектор 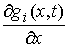 , если , если 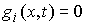 , и нулевой вектор, если , и нулевой вектор, если 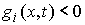 . .
Определим также 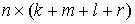 матрицу матрицу 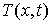 касательного
оператора. Она составлена (сверху – вниз) из строк матрицы удерживающих связей касательного
оператора. Она составлена (сверху – вниз) из строк матрицы удерживающих связей 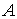 и строк матриц
односторонних и условных связей и строк матриц
односторонних и условных связей 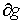 , , 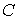 и и 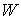 . Мы считаем, что эта матрица имеет максимальный ранг (если
отбросить заведомо нулевые строки). . Мы считаем, что эта матрица имеет максимальный ранг (если
отбросить заведомо нулевые строки).
Пространством возможных перемещений 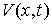 в точке в точке  назовем множество
векторов назовем множество
векторов 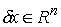 , удовлетворяющих условиям , удовлетворяющих условиям
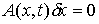 , , 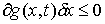 , , 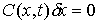 , , 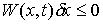
Пространством касательных перемещений 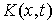 в точке в точке  назовем множество
векторов назовем множество
векторов  , удовлетворяющих условию , удовлетворяющих условию
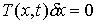
Любое
касательное перемещение является возможным.
Следуя [8] будем формулировать условия
идеальности связей в интегральной форме. Вариацией кривой 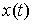 , , 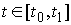 будем называть любую
непрерывную вектор-функцию будем называть любую
непрерывную вектор-функцию  . Вариация . Вариация 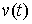 называется возможной,
если называется возможной,
если 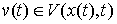 для всех для всех 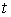 . Вариация . Вариация 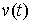 называется касательной,
если называется касательной,
если 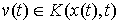 для всех для всех 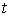 . Поскольку . Поскольку 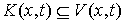 , то любая касательная вариация является возможной. Если
вариация , то любая касательная вариация является возможной. Если
вариация 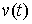 является касательной,
то вариация является касательной,
то вариация 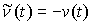 также касательная. также касательная.
Принцип освобождения от связей. Пусть 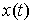 – траектория
движения. Тогда систему можно
освободить от связей и добавить некую силу – реакцию связей – траектория
движения. Тогда систему можно
освободить от связей и добавить некую силу – реакцию связей 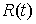 таким образом, что таким образом, что 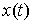 останется траекторией
движения освобожденной системы. При этом компоненты реакции связей представляют
собой меры Лебега-Стилтьеса останется траекторией
движения освобожденной системы. При этом компоненты реакции связей представляют
собой меры Лебега-Стилтьеса 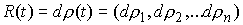 . Они могут иметь особенности, сосредоточенные на множестве
тех моментов времени, в которые траектория . Они могут иметь особенности, сосредоточенные на множестве
тех моментов времени, в которые траектория  выходит на
односторонние ограничения. Траектория системы представляет собой такую
абсолютно непрерывную функцию выходит на
односторонние ограничения. Траектория системы представляет собой такую
абсолютно непрерывную функцию 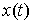 , производная которой, , производная которой, 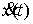 , является функцией с ограниченной вариацией. При этом будут выполнены уравнения движения с мерами. , является функцией с ограниченной вариацией. При этом будут выполнены уравнения движения с мерами.
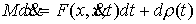 (1.1) (1.1)
Идеальность связей. Связи называются идеальными, если для любой
траектории системы 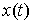 , и для любой её возможной вариации , и для любой её возможной вариации 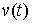 интегральная
элементарная работа сил реакции связей неотрицательна, т.е. интегральная
элементарная работа сил реакции связей неотрицательна, т.е.
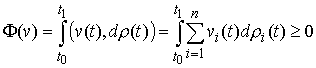 (1.2) (1.2)
Это условие, в частности, означает, что,
при выходе траектории системы на границу удерживающих связей, реакция связей
направлена внутрь области, допустимой этими связями.
Из (1.2) следует, что для любой
касательной вариации 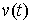 интегральная
элементарная работа сил реакции связей равна нулю интегральная
элементарная работа сил реакции связей равна нулю 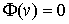 . Если допустить противное,
то найдется касательная вариация . Если допустить противное,
то найдется касательная вариация  такая, что такая, что 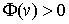 . Взяв касательную и, следовательно, возможную вариацию . Взяв касательную и, следовательно, возможную вариацию 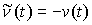 получим получим 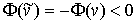 , что противоречит (1.2). , что противоречит (1.2).
Найдя 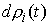 из (1.1) и подставив
в (1.2) получим эквивалентную форму записи условия идеальности связей. На
траекториях системы для любой возможной вариации из (1.1) и подставив
в (1.2) получим эквивалентную форму записи условия идеальности связей. На
траекториях системы для любой возможной вариации 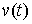 должно выполняться должно выполняться
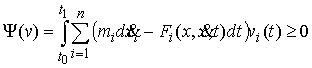 (1.3) (1.3)
Отсюда
следует, что для любой касательной вариации 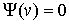 . .
Сформулируем
теперь известное утверждение из функционального анализа, необходимое для вывода
уравнений движения нашей системы.
Для
заданного движения 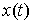 обозначим обозначим 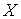 – банахово
пространство вариаций – банахово
пространство вариаций 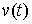 , т.е., пространство непрерывных , т.е., пространство непрерывных 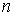 -мерных вектор-функций. Определим на -мерных вектор-функций. Определим на  касательный оператор касательный оператор 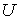 как отображение в
пространство как отображение в
пространство  мерных непрерывных
функций: мерных непрерывных
функций: 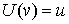 , где , где 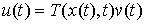 . Обозначим . Обозначим 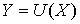 . Это также банахово пространство. Пространство касательных
вариаций . Это также банахово пространство. Пространство касательных
вариаций  является ядром линейного
оператора является ядром линейного
оператора 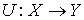 . В соответствии с леммой об аннуляторе ядра регулярного
оператора (см., например, [9]) имеем . В соответствии с леммой об аннуляторе ядра регулярного
оператора (см., например, [9]) имеем 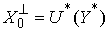 . Здесь символом . Здесь символом 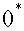 обозначены
сопряженные пространства и сопряженные
операторы, а обозначены
сопряженные пространства и сопряженные
операторы, а   – аннулятор множества – аннулятор множества
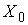 , т.е. множество
линейных функционалов обращающихся на нем в ноль. , т.е. множество
линейных функционалов обращающихся на нем в ноль.
Из теоремы
Рисса о виде линейного функционала в пространстве непрерывных функций вытекает
следующее утверждение: пусть 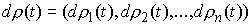 векторная мера Лебега
Стилтьеса на векторная мера Лебега
Стилтьеса на 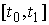 , и , и
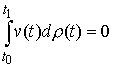
для любой непрерывной вектор-функции 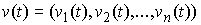 такой, что такой, что 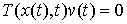 для всех для всех 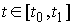 . Тогда найдется мера Лебега-Стилтьеса . Тогда найдется мера Лебега-Стилтьеса 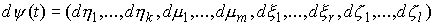 на на 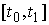 , такая что , такая что
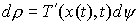
где  – транспонированная
матрица – транспонированная
матрица 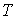 . При этом каждая компонента . При этом каждая компонента 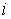 меры меры 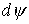 сосредоточена на том
множестве, где не обращается в ноль строка сосредоточена на том
множестве, где не обращается в ноль строка 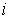 матрицы касательного
оператора матрицы касательного
оператора 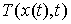 . .
Разделяя
этот оператор на составляющие удерживающих и односторонних связей, получаем
 (1.4) (1.4)
Более
подробно с этими вопросами можно ознакомиться в [14].
Принцип Даламбера-Лагранжа. Пусть абсолютно непрерывная кривая 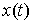 удовлетворяет
идеальным связям, наложенным на систему, а ее производная существует почти
всюду и является функцией ограниченного изменения. Кривая удовлетворяет
идеальным связям, наложенным на систему, а ее производная существует почти
всюду и является функцией ограниченного изменения. Кривая 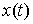 является траекторией
движения тогда и только тогда, когда для любой возможной вариации является траекторией
движения тогда и только тогда, когда для любой возможной вариации 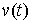 выполнены соотношения
(1.3). выполнены соотношения
(1.3).
Применив (1.4) для касательных вариаций
получаем отсюда уравнения Лагранжа 1-го рода [10, 11]. Кривая 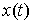 является траекторией
движения системы с идеальными связями
(1.1-2) тогда и только тогда, когда найдутся такие векторные меры
Лебега-Стилтьеса является траекторией
движения системы с идеальными связями
(1.1-2) тогда и только тогда, когда найдутся такие векторные меры
Лебега-Стилтьеса  , ,  , , 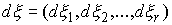 и и 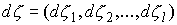 , что , что
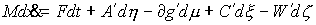 (1.5) (1.5)
где
знак 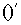 означает
транспонирование матриц. При этом
каждая мера означает
транспонирование матриц. При этом
каждая мера 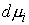 и и 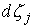 неотрицательна и
сосредоточена на множестве моментов времени, в которые неотрицательна и
сосредоточена на множестве моментов времени, в которые 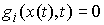 и и 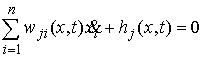 соответственно.
Каждая мера соответственно.
Каждая мера  сосредоточена на
множестве моментов времени, в которые сосредоточена на
множестве моментов времени, в которые 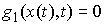 . Неотрицательность мер . Неотрицательность мер 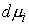 , , 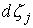 следует из условия
идеальности связей (1.2). следует из условия
идеальности связей (1.2).
Функции 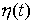 , ,  , , 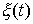 , и , и  , как функции ограниченной вариации, однозначно раскладываются
на сумму трех функций – абсолютно непрерывной, непрерывной сингулярной и
функции скачков. Последняя представляет собой ступенчатую функцию с не более
чем счетным числом ступеней. В точках скачка мер (и только в них) траекторная
скорость , как функции ограниченной вариации, однозначно раскладываются
на сумму трех функций – абсолютно непрерывной, непрерывной сингулярной и
функции скачков. Последняя представляет собой ступенчатую функцию с не более
чем счетным числом ступеней. В точках скачка мер (и только в них) траекторная
скорость 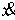 также может иметь
скачок. Обозначим эти скачки соответственно также может иметь
скачок. Обозначим эти скачки соответственно 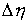 , , 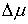 , , 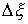 , , 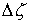 и и 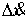 . В силу (1.5) они связаны соотношением . В силу (1.5) они связаны соотношением
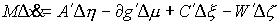
Отсюда,
заметив, что во все время движения
выполнены уравнения удерживающих связей, т.е. 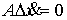 , получаем условие скачка , получаем условие скачка
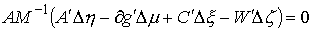
Заметим, что, если функции, описывающие
связи, имеют второй класс гладкости, то скорость движения имеет только две
составляющие – абсолютно непрерывную функцию и функцию скачков [10].
Для систем с идеальными удерживающими и
односторонними голономными связями известны теоремы об изменении количества
движения системы и о движении ее центра
масс в точках мгновенного удара [13].
Эти теоремы верны и в общем случае, когда выход на границу односторонних
связей не является мгновенным [10, 11].
Вывод этих законов почти дословно совпадает с традиционным выводом,
применяющимся для случая только удерживающих связей. Отличие здесь состоит
в использовании формулы Лейбница дифференцирования
по частям. В пространстве функций с ограниченным изменением эта формула
применима в следующем виде. Если  – абсолютно
непрерывная функция, а – абсолютно
непрерывная функция, а 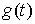 функция ограниченного
изменения, то функция ограниченного
изменения, то
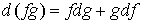 (2.1) (2.1)
Для краткости мы ограничимся
формулировками основных законов. В качестве примера полное доказательство
приводится только для теоремы об изменении импульса системы.
Теорема об изменении количества движения. Если удерживающие, и односторонние связи,
наложенные на систему, идеальны и допускают поступательный сдвиг всех точек
системы как твердого тела вдоль какого-нибудь направления постоянного во времени,
то проекция количества движения системы на это направление является абсолютно непрерывной функцией и
скорость ее изменения равна суммарной проекции на это направление вектора
активных сил.
Доказательство. Эта
теорема непосредственно вытекает из аналогичного утверждения для сводных
векторов системы. Введем сводный вектор импульса системы 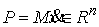 . Если удерживающие, и односторонние, наложенные на систему,
идеальны и допускают поступательный сдвиг всех точек системы как твердого тела
вдоль какого-нибудь направления . Если удерживающие, и односторонние, наложенные на систему,
идеальны и допускают поступательный сдвиг всех точек системы как твердого тела
вдоль какого-нибудь направления 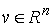 постоянного во
времени, то проекция вектора импульса на это направление постоянного во
времени, то проекция вектора импульса на это направление 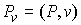 является абсолютно
непрерывной функцией и скорость ее изменения равна является абсолютно
непрерывной функцией и скорость ее изменения равна 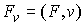 , т.е. равна проекции на это направление сводного вектора
активных сил. , т.е. равна проекции на это направление сводного вектора
активных сил.
Докажем это. Пусть 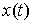 – траектория движения системы. Для нее
выполнены уравнения Лагранжа первого рода (1.5). Условие теоремы означает, что
вектор – траектория движения системы. Для нее
выполнены уравнения Лагранжа первого рода (1.5). Условие теоремы означает, что
вектор 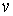 является касательным
перемещением во все время движения, т.е., является касательным
перемещением во все время движения, т.е.,
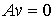
всегда
и
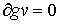 , , 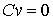 , , 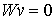
в
точках траектории, расположенных на границе односторонних связей, т.е. в тех
точках, в которых сосредоточены соответствующие меры 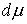 , , 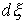 , , 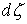 . Отсюда следует, что во все время движения . Отсюда следует, что во все время движения
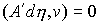 , , 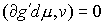 , , 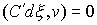 , , 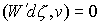
Эти
соотношения, понимаются как равенство мер Лебега-Стилтьеса. Домножив обе части
(1.5) на 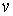 , получаем , получаем
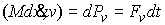
Поскольку
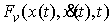 есть функция
ограниченного изменения, то есть функция
ограниченного изменения, то 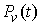 является абсолютно
непрерывной функцией и выполнено является абсолютно
непрерывной функцией и выполнено  . Доказательство закончено. . Доказательство закончено.
Теорема об изменении момента количества движения. Если удерживающие и односторонние связи,
наложенные на систему, идеальны и допускают поворот всех точек системы как
твердого тела вокруг какой-нибудь постоянной оси проходящей через начало
координат, то момент количества движения системы относительно этой оси является
абсолютно непрерывной функцией и скорость его изменения равна суммарной
проекции на эту ось векторов моментов
активных сил.
Пусть удерживающие связи
голономны, 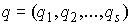 являются обобщенными
координатами, и координатные функции являются обобщенными
координатами, и координатные функции 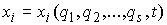 , ,  имеют второй класс
гладкости. Тогда траектория движения имеют второй класс
гладкости. Тогда траектория движения 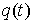 – это абсолютно
непрерывная вектор-функция, производная которой – это абсолютно
непрерывная вектор-функция, производная которой 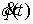 , является функцией ограниченной вариации. , является функцией ограниченной вариации.
Односторонние связи в обобщенных
координатах задаются системой неравенств
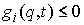 , ,  . .
Группа условных связей задается
системой условий
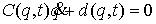 , при , при 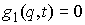
где  – – 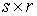 матрица, матрица, 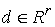 . .
Неголономные односторонние связи
задаются системой неравенств
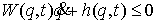
где 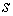 – число связей, – число связей, 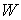 – – 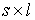 матрица, матрица, 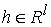 . .
Для краткости записи обозначим 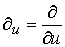 . Пользуясь формулой Лейбница (2.1), получаем . Пользуясь формулой Лейбница (2.1), получаем
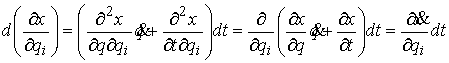
или,
в матричной форме
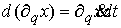 (3.1) (3.1)
Подставив
соотношения
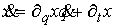 , , 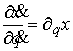 (3.2) (3.2)
в уравнения удерживающих связей 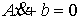 , получим систему , получим систему
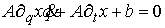
которая
должна тождественно выполняться при всех 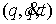 . Отсюда . Отсюда
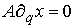
и
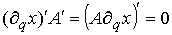
Домножив обе части (1.5) слева на
транспонированную матрицу 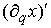 получим получим
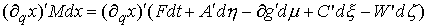
Матрица
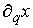 абсолютно непрерывна.
Применив формулу Лейбница (2.1) получаем на действительной траектории абсолютно непрерывна.
Применив формулу Лейбница (2.1) получаем на действительной траектории
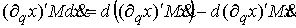
Использовав
(3.1-2), выводим отсюда
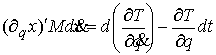
где
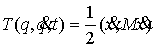
–
кинетическая энергия системы. Введем вектор обобщенных сил
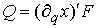
Заметив,
что

и
что это верно и для остальных матриц связей, получаем уравнения Лагранжа
второго рода
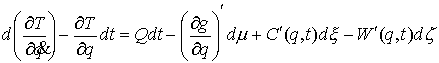 (3.3) (3.3)
Теорема
Аппеля. Пусть в момент  траектория движения
находится на границе односторонних ограничений, и скорость претерпевает скачок.
Тогда вектор обобщенных импульсов траектория движения
находится на границе односторонних ограничений, и скорость претерпевает скачок.
Тогда вектор обобщенных импульсов 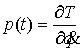 также имеет скачок.
Обозначим также имеет скачок.
Обозначим
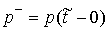 , , 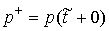
(для функции ограниченной вариации эти
величины всегда существуют). Тогда из (3.3) получим в момент  , что , что
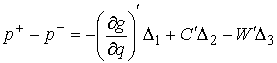
где 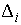 – некие вектора
размерностей – некие вектора
размерностей  , ,  , и , и 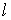 соответственно.
Компоненты соответственно.
Компоненты 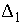 и и 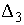 неотрицательны.
Помножив это равенство на любой вектор неотрицательны.
Помножив это равенство на любой вектор 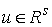 , касающийся границы односторонних ограничений в точке , касающийся границы односторонних ограничений в точке 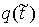 , получим , получим
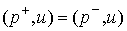
Т.е.
сохраняются проекции вектора обобщенного импульса на плоскость касательную
поверхности удара.
В этом
разделе мы покажем, что теория Рауса игнорирования циклических координат
справедлива и при наличии идеальных односторонних связей. Пусть силы имеют силовую функцию 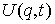 . Введем, как обычно, функцию Лагранжа . Введем, как обычно, функцию Лагранжа  . Уравнения движения (3.3) приобретут форму . Уравнения движения (3.3) приобретут форму
 (4.1) (4.1)
Далее
рассуждаем по обычной схеме. Обобщенная координата  называется
циклической, если она не входит явно в функцию Лагранжа называется
циклической, если она не входит явно в функцию Лагранжа 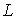 и в условия
односторонних связей, т.е. и в условия
односторонних связей, т.е.
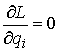 , , 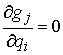 , ,  , , 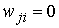
. В
силу уравнений движения (4.1) для циклической координаты  выполнено выполнено

Значит,
величина 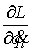 остается постоянной,
т.е. является циклическим первым интегралом уравнений движения. Циклическую
координату остается постоянной,
т.е. является циклическим первым интегралом уравнений движения. Циклическую
координату 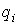 назовём отделяющейся,
если от
нее не зависят матрицы назовём отделяющейся,
если от
нее не зависят матрицы 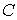 и и 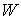 , т.е. для всех , т.е. для всех 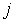 , , 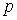 и и  выполняется
условие выполняется
условие
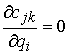 , , 
Пусть
координаты 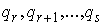 являются
отделяющимися циклическими. Им соответствуют циклические интегралы являются
отделяющимися циклическими. Им соответствуют циклические интегралы
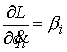 , , 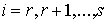 (4.2) (4.2)
где 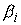 – константы
интегралов. Циклические координаты в эти уравнения не входят. Будем считать,
что уравнения (4.2) функционально независимы и, следовательно, разрешимы
относительно циклических скоростей – константы
интегралов. Циклические координаты в эти уравнения не входят. Будем считать,
что уравнения (4.2) функционально независимы и, следовательно, разрешимы
относительно циклических скоростей 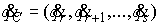 , которые находим как функции позиционных координат , которые находим как функции позиционных координат 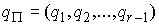 , позиционных скоростей , позиционных скоростей 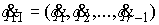 , констант циклических интегралов , констант циклических интегралов 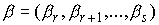 и времени: и времени: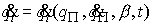 , , 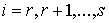 . Эти выражения подставляются в функцию Рауса . Эти выражения подставляются в функцию Рауса
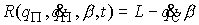 . .
Теорема
Рауса. Пусть  – траектория движения
нашей системы, тогда для позиционных координат выполнены уравнения Лагранжа
второго рода, в которых в качестве функции Лагранжа берется функция Рауса. – траектория движения
нашей системы, тогда для позиционных координат выполнены уравнения Лагранжа
второго рода, в которых в качестве функции Лагранжа берется функция Рауса.
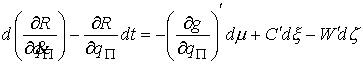 (4.3) (4.3)
Доказательство.
Рассматривая 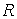 , , 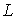 и и  как гладкие функции
от независимых переменных как гладкие функции
от независимых переменных 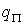 , , 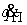 , , 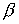 , , 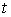 выпишем несколько
соотношений между дифференциальными формами. Дифференцируя левую часть
определения функции Рауса получаем выпишем несколько
соотношений между дифференциальными формами. Дифференцируя левую часть
определения функции Рауса получаем
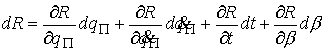 (4.4) (4.4)
Дифференцируя
правую часть получаем
 (4.5) (4.5)
Возьмем
любую точку 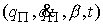 на траектории
движения, тогда выполнены (4.2) и, следовательно, на траектории
движения, тогда выполнены (4.2) и, следовательно,
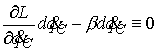
Поэтому
(4.5) в этой точке выглядит следующим образом
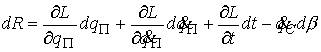 (4.6) (4.6)
Формы (4.4) и (4.6) совпадают во всех
точках траектории движения, поэтому в них
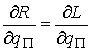 , ,  , , 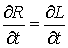 , , 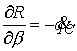
Подставляя эти соотношения в (4.1)
получаем (4.3).
Рассмотрим пример механической системы с условными связями. Пусть по
гладкой плоскости скользит однородный диск единичной массы и радиуса 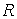 . Введем на плоскости декартову систему координат . Введем на плоскости декартову систему координат 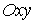 . Положение диска можно описать тремя параметрами . Положение диска можно описать тремя параметрами 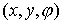 , где , где 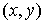 – координаты центра
диска, а – координаты центра
диска, а 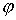 – угол его поворота.
Движение диска ограничено полуплоскостью – угол его поворота.
Движение диска ограничено полуплоскостью  . При выходе на границу, т.е. на прямую . При выходе на границу, т.е. на прямую 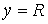 , обод диска касается прямой , обод диска касается прямой 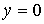 . Предположим, что контакт диска с этой прямой является
абсолютно шероховатым. Это означает, что, как бы ни были слабы силы,
прижимающие диск к граничной прямой, диск катается по ней без проскальзывания.
Такое свойство можно записать в виде двух условий: . Предположим, что контакт диска с этой прямой является
абсолютно шероховатым. Это означает, что, как бы ни были слабы силы,
прижимающие диск к граничной прямой, диск катается по ней без проскальзывания.
Такое свойство можно записать в виде двух условий:
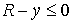
и
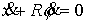 , при , при 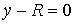
Обозначим 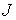 – центральный момент
инерции диска. Для использования теоремы Рауса, перейдем к координатам – центральный момент
инерции диска. Для использования теоремы Рауса, перейдем к координатам 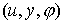 , где , где 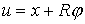 . Тогда связи и лагранжиан системы приобретут следующий вид: . Тогда связи и лагранжиан системы приобретут следующий вид:
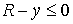 , и , и  , при условии, что , при условии, что 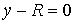 , ,
и
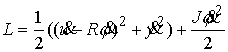
Координата 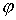 является циклической
и отделяющейся. Циклический интеграл имеет вид является циклической
и отделяющейся. Циклический интеграл имеет вид
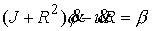
Исключив методом Рауса циклическую переменную получим систему с теми же
связями и Лагранжианом
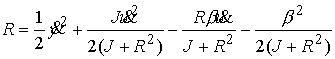
Уравнения
движения
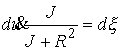 , , 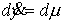
после
нормировки меры  станут следующими: станут следующими:
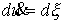 , , 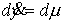
Меры
 и и 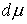 сосредоточены в точках выхода на ограничения. сосредоточены в точках выхода на ограничения.
Рассмотрим абсолютно упругий однократный
удар, т.е. удар, при котором сохраняется энергия системы. Символами 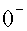 и и 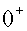 будем обозначать значения
величин до и после удара соответственно. Поскольку у системы две степени
свободы и две неудерживающих связи, то скорости после удара будем обозначать значения
величин до и после удара соответственно. Поскольку у системы две степени
свободы и две неудерживающих связи, то скорости после удара  и и 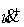 восстанавливаются
неоднозначно. Если обозначить восстанавливаются
неоднозначно. Если обозначить 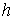 – энергию системы, то – энергию системы, то
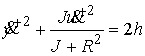
Видно,
что здесь в принципе возможно даже возникновение ситуации, описанной в [2], при которой диск будет отскакивать в
сторону противоположную первоначальному горизонтальному движению.
Для однозначности решения требуется
какая-либо модель удара, из которой можно получить дополнительные условия. Одна
из возможностей – это задание степени “шероховатости” прямой, о которую ударяется диск.
Скорость 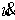 характеризует
величину отклонения значений характеризует
величину отклонения значений 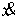 и и  от таких, при которых
диск катится по горизонтальной прямой без проскальзывания (т.е. от от таких, при которых
диск катится по горизонтальной прямой без проскальзывания (т.е. от 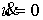 ). Для абсолютно гладкого случая положим ). Для абсолютно гладкого случая положим 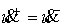 , а для абсолютно шероховатого , а для абсолютно шероховатого 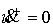 . В линейном приближении этот закон можно задать следующим
образом: . В линейном приближении этот закон можно задать следующим
образом:
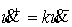
где 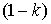 , , 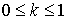 – степень
шероховатости. Тогда – степень
шероховатости. Тогда
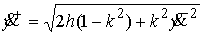
Заметим
в заключение, что в данной системе ситуация принципиально не меняется если
наложить какое-либо вертикальное силовое поле с потенциалом  . .
Рассмотрим теперь пример системы с
неголономными односторонними связями. По гладкой плоскости опять движется диск
радиуса 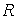 . Он снабжен “односторонним коньком”, который накладывает на движение диска
одностороннюю неголономную связь . Он снабжен “односторонним коньком”, который накладывает на движение диска
одностороннюю неголономную связь
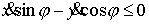
Лагранжиан
этой системы имеет вид
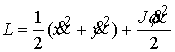
Координата
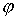 здесь циклическая но
не отделяющаяся. Уравнения движения имеют вид здесь циклическая но
не отделяющаяся. Уравнения движения имеют вид
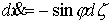 , ,  , , 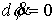
В
моменты, когда 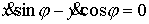 , могут происходить удары о неголономную связь. Посмотрим,
как изменятся скорости после удара. Удар считаем абсолютно упругим. Из
уравнений движения получаем условия скачка , могут происходить удары о неголономную связь. Посмотрим,
как изменятся скорости после удара. Удар считаем абсолютно упругим. Из
уравнений движения получаем условия скачка
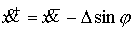 , , 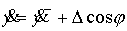
Величину
 находим из равенства
энергий до и после удара находим из равенства
энергий до и после удара
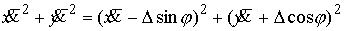
откуда
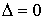 . Значит, составляющая функции скачков в . Значит, составляющая функции скачков в 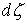 отсутствует и отсутствует и 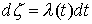 , где , где 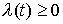 – измеримая функция.
Уравнения движения приобретают вид – измеримая функция.
Уравнения движения приобретают вид
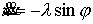 , , 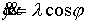 , , 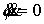 . .
Таким образом, в данной системе удары
отсутствуют. Движение системы описывается следующим образом. Диск все время
вращается с постоянной угловой скоростью. Центр диска движется по прямой до тех
пор, пока конек не повернется в положение, направленное по скорости движения
центра. Затем движение по касательной перейдет к обычной круговой траектории
диска с двухсторонним коньком. Сойти с этой окружности траектория не сможет,
т.к., безударный сход должен происходить по касательной к окружности, но из-за
связи сход возможен только внутрь окружности.
Если
на диске установлен обычный двусторонний конек,
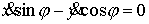
и наложена односторонняя связь  . То такими же простыми рассуждениями получаем, что при
однократном ударе скорость центра диска меняется на противоположную. . То такими же простыми рассуждениями получаем, что при
однократном ударе скорость центра диска меняется на противоположную.
Заметим, что движение будет иметь
безударный характер и в общем случае, когда
на систему наложены только неголономные односторонние связи
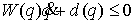
причем все компоненты вектора 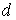 неотрицательны: неотрицательны:
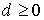 .
Рассмотрим натуральную механическую систему .
Рассмотрим натуральную механическую систему
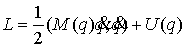
Уравнения Лагранжа 2-го рода дают
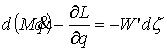
Мера 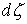 неотрицательна и
сосредоточена в тех точках траектории, где неотрицательна и
сосредоточена в тех точках траектории, где 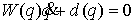 слева или справа.
Допустим, что в момент слева или справа.
Допустим, что в момент 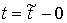 траектория вышла на
ограничение и мера имеет скачок траектория вышла на
ограничение и мера имеет скачок 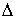 . Тогда все его компоненты неотрицательны: . Тогда все его компоненты неотрицательны: 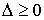 и и 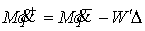 . Считаем, что при ударе полная энергия может рассеиваться. В
точках скачка координаты и, значит, потенциальная энергия остаются
непрерывными. Следовательно, в них может рассеиваться только кинетическая энергия: . Считаем, что при ударе полная энергия может рассеиваться. В
точках скачка координаты и, значит, потенциальная энергия остаются
непрерывными. Следовательно, в них может рассеиваться только кинетическая энергия:
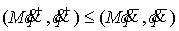
Подставив сюда условие скачка 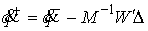 , получим , получим
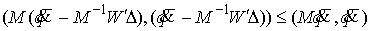
Воспользовавшись условием выхода на
границу связи
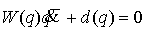
получаем
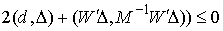
Поскольку все компоненты векторов 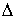 и и 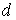 неотрицательны,
то неотрицательно и
первое слагаемое в неравенстве. Значит второе слагаемое неположительно. Однако, неотрицательны,
то неотрицательно и
первое слагаемое в неравенстве. Значит второе слагаемое неположительно. Однако, 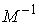 , как и , как и 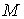 – положительно
определенная матрица, поэтому второе слагаемое обращается в ноль, т.е. – положительно
определенная матрица, поэтому второе слагаемое обращается в ноль, т.е. 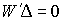 и и 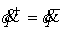 . Это означает, что скачки скорости отсутствуют, скорость
является абсолютно непрерывной функцией. . Это означает, что скачки скорости отсутствуют, скорость
является абсолютно непрерывной функцией.
Рассмотрим малые колебания в системе с
одной степенью свободы. Пусть лагранжиан имеет вид
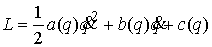
и на систему наложено одно ограничение 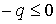 . Обычной калибровкой приведем лагранжиан к виду . Обычной калибровкой приведем лагранжиан к виду
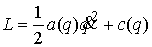
Если удары абсолютно упругие, то в системе
сохраняется энергия: 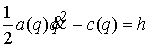 .Уравнения движения с мерами выглядят следующим образом. .Уравнения движения с мерами выглядят следующим образом.
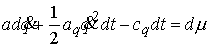 (9.1) (9.1)
Причем мера 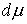 неотрицательна и
сосредоточена в тех точка, где неотрицательна и
сосредоточена в тех точка, где 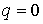 . Условия, при которых точка . Условия, при которых точка  является положением
равновесия, получаются подстановкой в уравнения движения значений является положением
равновесия, получаются подстановкой в уравнения движения значений 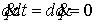 . Они выглядят так: . Они выглядят так:
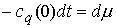
Поскольку мера 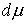 неотрицательна, то
условием равновесия является неотрицательна, то
условием равновесия является  . Если оно выполнено, то, взяв . Если оно выполнено, то, взяв 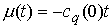 , мы удовлетворим уравнения движения для траектории , мы удовлетворим уравнения движения для траектории 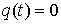 . В соответствии с [4, 15], положение равновесия устойчиво, если
потенциальная энергия . В соответствии с [4, 15], положение равновесия устойчиво, если
потенциальная энергия 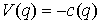 имеет минимум в точке имеет минимум в точке
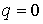 , при ограничениях , при ограничениях 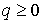 . Достаточным условием этого является выполнение неравенства . Достаточным условием этого является выполнение неравенства 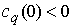 . Таким образом, если . Таким образом, если
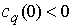 , то точка , то точка 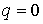 является устойчивым
положением равновесия системы (9.1) при ограничении является устойчивым
положением равновесия системы (9.1) при ограничении 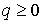 . .
Заметим, что другим достаточным условием
устойчивости является система
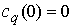 , , 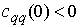
В этом случае точка  является устойчивым
положением равновесия системы без односторонних ограничений. Здесь мы не будем
рассматривать этот случай. является устойчивым
положением равновесия системы без односторонних ограничений. Здесь мы не будем
рассматривать этот случай.
Найдем
частоту малых колебаний в окрестности положения равновесия. Удар считаем
абсолютно упругим. Линеаризовав лагранжиан, получим
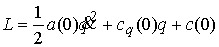
Линеаризованные уравнения движения
приобретет вид
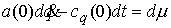
В линеаризованной системе также
сохраняется энергия:
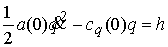 , , 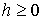
Движение в окрестности точки 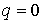 представляет собой
повторяющиеся одинаковые безударные параболические участки, разделенные ударом
о связь представляет собой
повторяющиеся одинаковые безударные параболические участки, разделенные ударом
о связь 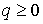 . Будем считать, что очередной удар произошел в момент . Будем считать, что очередной удар произошел в момент  . Найдем момент следующего удара. После удара координата . Найдем момент следующего удара. После удара координата 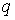 увеличивается до того
момента, когда скорость от значения увеличивается до того
момента, когда скорость от значения
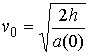
упадет до нуля. Длина этого отрезка времени
составляет
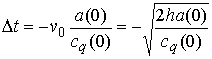
Длина полного безударного участка
составляет 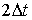 , и частота малых колебаний. Таким образом период малых
колебаний системы падает вместе с энергией системы как ее квадратный корень. , и частота малых колебаний. Таким образом период малых
колебаний системы падает вместе с энергией системы как ее квадратный корень.
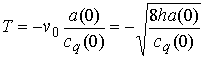 (9.2) (9.2)
Рассмотрим
плоское тело, свободно двигающееся по гладкой плоскости. Внутри тела вырезан
тонкий канал 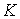 . Пусть в плоскости задана абсолютная система координат . Пусть в плоскости задана абсолютная система координат 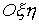 и в точке и в точке 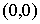 установлен “столбик”. В
начальный момент тело расположено так, что этот столбик попадает в канал установлен “столбик”. В
начальный момент тело расположено так, что этот столбик попадает в канал 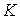 . На движение тела наложена односторонняя связь, состоящая в
том, что “столбик” располагается в канале . На движение тела наложена односторонняя связь, состоящая в
том, что “столбик” располагается в канале 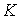 . Толщину “столбика” и
ширину канала считаем нулевыми. . Толщину “столбика” и
ширину канала считаем нулевыми.
Дадим
формальное описание этой системы. Свяжем с телом систему координат 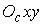 , начало которой , начало которой 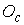 совпадает с центром
тяжести тела. Будем считать, что канал совпадает с центром
тяжести тела. Будем считать, что канал 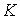 в теле это гладкая
кривая, которая задается параметрически в теле это гладкая
кривая, которая задается параметрически
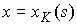 , , 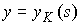 , , 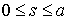 (9.1) (9.1)
где  – натуральный
параметр, длина вдоль кривой – натуральный
параметр, длина вдоль кривой  . Сама кривая имеет длину . Сама кривая имеет длину 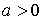 . Положение тела можно было бы описывать тройкой координат . Положение тела можно было бы описывать тройкой координат 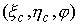 , где , где 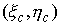 – координаты центра
масс тела – координаты центра
масс тела 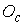 в абсолютной системе,
а в абсолютной системе,
а 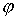 – угол наклона оси – угол наклона оси 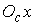 связанной системы
координат по отношению к оси связанной системы
координат по отношению к оси 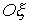 абсолютной системы.
Однако, мы будем использовать тройку абсолютной системы.
Однако, мы будем использовать тройку 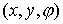 , где , где 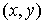 – координаты начала
абсолютной системы координат – координаты начала
абсолютной системы координат 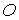 в связанной системе.
Переход от связанной системы координат к абсолютной производится поворотом на
угол в связанной системе.
Переход от связанной системы координат к абсолютной производится поворотом на
угол 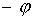 относительно относительно  и сдвигом на вектор и сдвигом на вектор 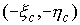 . Поэтому первая и вторая тройки координат связаны соотношениями . Поэтому первая и вторая тройки координат связаны соотношениями
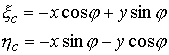 (9.2) (9.2)
а их скорости

Обозначим
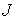 – центральный момент
инерции тела, а его массу – центральный момент
инерции тела, а его массу 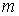 , для краткости записи, будем считать равной единице , для краткости записи, будем считать равной единице 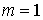 . По теореме Кенига кинетическая энергия тела . По теореме Кенига кинетическая энергия тела 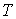 выражается соотношением выражается соотношением
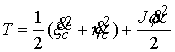 (9.3) (9.3)
или,
в координатах 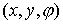 , ,
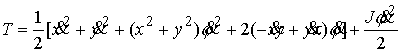
Подставив
сюда (9.1) получим лагранжиан системы
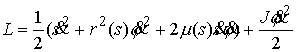
где
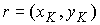 , ,  , , 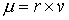 . И использовано то, что . И использовано то, что 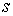 – это натуральный
параметр и, поэтому, – это натуральный
параметр и, поэтому, 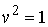 . На систему наложено две односторонних связи: . На систему наложено две односторонних связи:
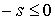 , и , и 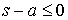 (9.4) (9.4)
Координата 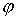 является циклической
и отделяющейся. Циклический интеграл имеет вид является циклической
и отделяющейся. Циклический интеграл имеет вид

Получаем редуцированную систему с функцией
Рауса 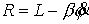 : :
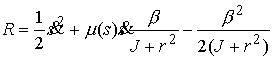
ограничениями (9.4). Это система с одной
степенью свободы. Она интегрируется в квадратурах.
Рассмотрим
случай абсолютно упругого удара. Для краткости введем обозначение
 , , 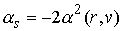
Система допускает интеграл энергии  . Положение . Положение  является положением
равновесия, если является положением
равновесия, если 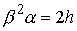 , и реакция связи направлена внутрь допустимой области.
Несложно убедиться, последнее условие эквивалентно следующему , и реакция связи направлена внутрь допустимой области.
Несложно убедиться, последнее условие эквивалентно следующему 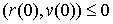 . .
Следуя
[15], заключаем, что, если последнее неравенство –
строгое, то положение равновесия устойчиво. В этом нетрудно убедится прямо. В
самом деле, если 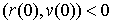 , то при увеличении , то при увеличении  от нуля величина от нуля величина 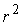 будет уменьшаться, а
потенциальная энергия будет уменьшаться, а
потенциальная энергия 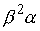 будет увеличиваться.
После удара о связь скорость будет равна будет увеличиваться.
После удара о связь скорость будет равна

В обозначениях предыдущего раздела
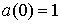 , , 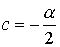 , , 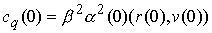
поэтому период малых колебаний равен
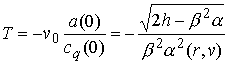
Все значения берутся при 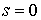 . .
Благодарности. Авторы весьма признательны А.П. Иванову, В.В. Козлову, и Д.В. Трещеву
за советы и полезные обсуждения данной работы.
1.
Панагитопулос
П.Д. Неравенства в механике. М., Мир, 1986.
2.
Козлов В.В.,
Трещев Д.В. Биллиарды. Генетическое введение в динамику систем с ударами. М.,
МГУ, 1991.
3.
Brogliato B. Nonsmooth Impact Mechanics. Springer-Verlag
London Limited, 1996.
4.
Иванов А.П.
Динамика систем с механическими соударениями. М., “Международная
программа образования”, 1997.
5.
Вильке В.Г.
Аналитическая механика систем с бесконечным числом степеней свободы. М., МГУ,
1997.
6.
Schmaedeke
W.W. Optimal control theory for nonlinear vector differential equations
containing measures. SIAM J. Control, 1965, ser. A, vol. 3, N 2, pp. 231 – 280.
7.
Buttazzo G., Percivale D. On the approximation of the
elastic bounce problem on Riemanian manifolds. Journal of Differential
equations, 1983, 47, 227-275.
8.
Козлов В.В.
Принципы динамики и сервосвязи. Вестник
МГУ, сер. 1, математика, механика. 1989, N 5, с.
59-66.
9.
Алексеев
В.М. ,Тихомиров В.М., Фомин С.В. Оптимальное управление. М., Наука, 1979.
10. Сорокина О.В., Кугушев Е.И. Принцип
Даламбера-Лагранжа в механических системах с односторонними связями. Препринт
ИПМ им. М.В. Келдыша РАН, 2002, N 14 .
11. Березинская С.Н., Кугушев Е.И. Об
уравнениях движения механических систем с условными односторонними связями.
Препринт ИПМ им. М.В. Келдыша РАН, 2002 N 16.
12. Сорокина О.В., Кугушев Е.И. Закономерности
движения механических систем с односторонними связями. Препринт ИПМ им. М.В. Келдыша РАН, 2002 N
15.
13. Голубев Ю.Ф. Основы теоретической
механики. М., МГУ, 2000. [14] Гирсанов И.В. Лекции по
математической теории экстремальных задач. М., МГУ, 1970.
14. Иванов А.П. Об устойчивости в системах с
неудерживающими связями. ПММ, 1984, т. 48, вып. 5, с. 725-732.
|