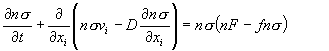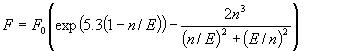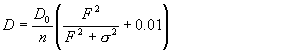Содержание

Введение

§1 Постановка задачи

§2 Общее описание процесса

§3 Основные результаты расчета

§4 Обсуждение результатов

Литература

Введение

Настоящая работа посвящена численному исследованию микро­волнового стримерного раз­ряда в газе и является продолжением наших работ [1], [2], [3]. Сформулирован­ная математическая модель учитывает, кроме рассеяния внешнего электромаг­нитного поля на проводящем объекте, процессы электрон­ного баланса – иониза­цию, диффузию и т.д., а также гидродинамику среды.

§1 Постановка задачи

Взаимодействие высокочастотного электромагнитного поля с прово­дящим плаз­мен­ным облаком описывается системой Максвелла для комплексных амплитуд поля E, H

                                             (1)

                                                      (2)

уравнением непрерывности для концентрации электронной компо­ненты (~ ns)

                 (3)

где

              (4)

                        (5)

и уравнениями гидродинамики для концентрации газа n, его ско­рости v и внутренней энергии ε

                             (6)

                    (7)

                         (8)

где E =|E|, g = 1.4.

      В качестве единиц измерения используются:

[s] = w/4p, w - частота поля,

[x] = c/w,  c – скорость света,

[v] - скорость звука в невозмущенном газе,

[n] - концентрация невозмущенного газа,

[E] = [H] – некоторое критическое значение поля,

и, естественно,  [t]=[x]/[v], [ε]=[v]².

Коэффициент q появился в уравнении (8) из-за несогласованности единиц и равен    где М – масса молекулы газа.

Расчеты проводились для значений ( все в CGS):

w = 2×10¹⁰, [v] = 3×10⁴, [n] = 5×10¹⁸ , [E] = 20, М=5×10^-23,

и, следовательно, [x] = 1.4, [t] = 5×10^-5.

С учетом этих единиц константы в уравнениях имеют значения:

D₀ = 0.16, F₀ = 800,  f = 25, q = 166.   

    Первичное электромагнитное поле E₀ ^­, H₀  является линейно-поляризованной плоской волной, распространяющейся вдоль оси x, с  отличными от нуля компонентами амплитуд .

В двумерном цилиндрически симметрич­ном варианте в качестве первичного поля используется стоячая волна с амплитудами:

E_z = E₀J₀(r) , H_j =-iE₀J₁(r) – функциями Бесселя нулевого и первого порядка.

    Для системы Гельмгольца (1), (2) задача ставится во всем прост­ранстве с асимптотикой Зоммерфельда на бесконечности :

      при |x|®¥

В начальный момент n = ε =1, v=s =0 c локальным возмущением в окрестности начала координат.

§2 Общее описание процесса.

   В рамках сформулированной выше математической модели возникновение и развитие разряда определяются, в основном, процессами ионизации газа и диф­фузии электронной компоненты.   В частности, условием незатухания процесса, вызванного началь­ным возму­ще­нием  ns , является неравенство  D<nFL² , связываю­щее  коэффициент диффузии, частоту ионизации и  L - размер области, где F>0. Математически, это - всего лишь условие неустойчивости решения.

   Поскольку частота ионизации F существенно зависит от соот­ношения  E и n, то основные характеристики процесса определя­ются балансом этих величин. Он  интенсифицируется  при  E > n. Мы рассматриваем подкритический случай, когда в начальный момент E₀ < n₀. Однако, если имеется локальное возмуще­ние, с проводи­мостью отличной от нуля, то оно приводит к джоулеву нагреву, разлету и локальному разрежению газа. В результате может возник­нуть ситуация с выполнением  неравенства  D<nFL²  и иници­ирова­нием незатуха­ющего процесса ионизации.

   Образовавшийся очаг выделения энергии посылает сферическую ударную волну и следующую, как всегда, за ней волну разрежения. Первая из-за увеличения плотнос­ти затрудняет ионизацию, вторая – способствует. Слой, в котором все это проис­­ходит, очень тонок и перемещается  со звуковой скоростью. Но это еще не пробой.

   Шаровой разряд постепенно слегка вытягивается вдоль оси z. И, хотя поле на полю­сах растет,  величина его остается недостаточ­ной для выполнения условия ионизации E > n   из-за сжатия газа в ударной волне.

  В некоторый момент на оси z  возмущение поля обгоняет ударную волну, создавая здесь очаг ионизации с E > n . И когда он достигает достаточных размеров, происходит существенное удлиннение  ионизованного облака – пробой.

  Сжатый удар­ной волной слой газа играет роль оболочки проводя­щего облака. Поэтому все это выглядит как прорыв оболочки .

   Но этот этап длится сравнительно недолго. Снова образуется ударная волна, разрывы плотного слоя затягива­ют­ся и фронт иони­зации замедляется до преж­ней, звуковой скорости. В дальней­шем  возможно многократное повторение описанного эффекта, образо­ва­­ние  стримера

  Упомянутые выше неустойчивость и чрезвычайно тонкая структура фронта порождают причудливые формы области активного процесса – границы сжатого и разреженного слоев. Эти же факторы создают значительные математичес­кие трудности при расчетах используемой модели.

§3  Основные результаты расчета.

   Изложенный выше сценарий процесса газового разряда проиллю­стрируем результатами расчета стандартного варианта, который будем называть основ­ным. На нейтральную среду в стационарном  состоянии, с s = v = 0, n = w = 1, находящуюся во внешнем поле подкритической амплитуды Е₀ =0.5, накладыва­ются  локальные, размером <0.1, возмущения электронной плотности  ( ns~1)  и концен­трации газа ( n <0.1 – для гарантирования инициирования разряда).

   На рис.1 показана эволюция формы ионизованного облака на этапе пробоя. В плоскости  x, z ( в сече­нии y=0 )  для различных моментов времени изображены линии уровня s = 1, которые можно считать границей проводящей полости.

В поперечном сече­нии  x=0, картина аналогична

  Неравномерность распространения ионизации по направлениям и во времени демонстрирует рис. 2, на котором даны положения на осях границ облака Z(t), X(t).

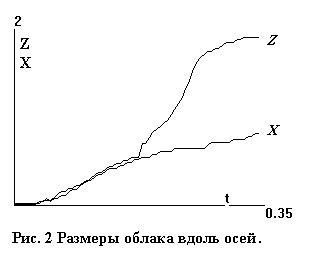
   Отчетливо видно ускорение роста размера по оси  z на интервале 0.17<t<0.25.

  Серия фигур на рис. 3 показывает эволюцию, объемлющего ионизо­ванное облако, сжатого слоя газа. Здесь для тех же моментов и в том же сечении, что и на рис. 1, изображе­ны линии уровня  n = 1.1, обоз­начающие границу плотной оболочки. Они повторяют фигуры рис. 1.

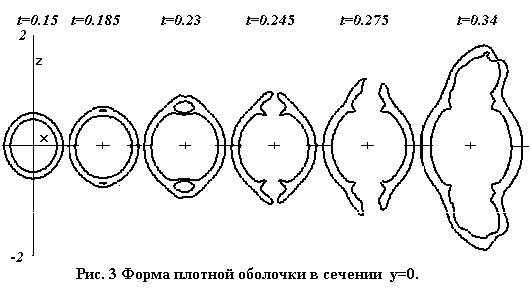
  Рис. 4 демонстрирует распределение s, n, Е вдоль оси z, в крити­чес­кий момент возникновения очага ионизации впереди ударной волны и ускорения фронта.

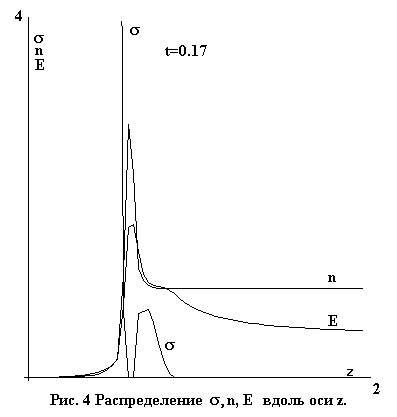
   Рис. 5 аналогичен  рис. 1, 3  и  показывает изменение формы и положения области большого поля. На нем изображены линии уровня E=1 в сечении  y=0  для указанных моментов времени.

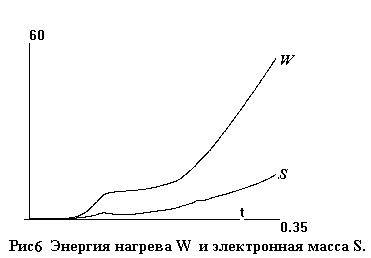
Интегральные величины

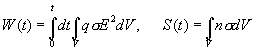
-         энергия, полученная в результате джоулева нагрева, и наработан­ная электрон­ная масса – изображены на рис. 6.

§4  Обсуждение результатов расчетов.

   Естественным и ожидаемым  является  распространение разряда,

в основном, вдоль оси  z  -  по направлению первичного электричес­кого поля. Направление же распространения поля – по оси  x -  ни­чем принципиально не выделяется. Степень возникающей асиммет­рии в основном варианте по направле­ниям x и y демонстрируют рис. 7, 8, на которых изображены (подобно рис. 1 и 3) формы проводя­щей полости и плотной оболочки  в сечениях x=0 и y=0, на один и тот же момент времени  t=0.3.

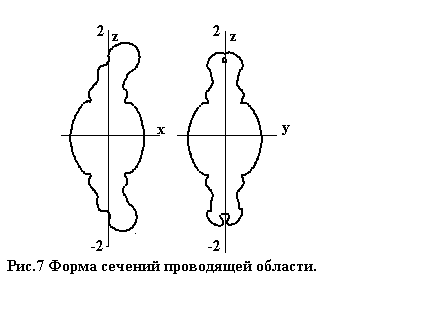
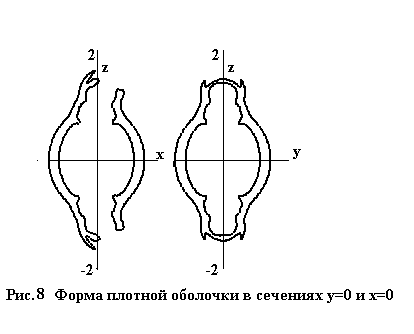
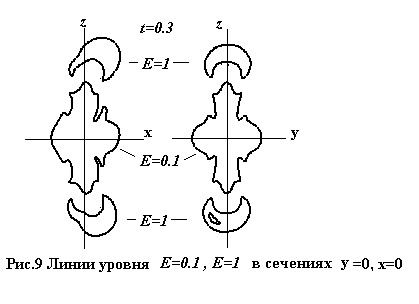
  Рис. 9 аналогичен предыдущим и дает некоторое представление о распределе­нии поля. На нем изображены линии уровня Е=1 и Е=0.1 в тех же двух сечениях на тот же момент времени t=0.3.

    Из качественных результатов стоит отметить значительное разбу­хание проводящей области в радиальном направлении, происходя­щее со звуковой скоростью. Оно свидетельствует о том, что гово­рить о нитеобразном разряде не приходится ( разумеется, в рамках используемой модели). Возможно  по этой же причине в расчетах не наблюдается какое-либо обострение процесса при  достижении стримером «резонансного» размера равного длине полуволны пер­вич­ного поля ( Dz = p ).

    Попытка уточнить модель учетом магнитного давления (см. урав­нение (7) в [3]), в надежде удержать стример от расплывания, не достигает цели.  Из-за высокой частоты поля  ( w[t]»10⁶ ) пинч-эффект не прояв­ляется.

  Упомянутая ранее неустойчивость решения имеет мелкомас­штаб­ный характер и не сказывется существенно на общей картине.

   В вариан­тах с различными по  x и y начальными распределениями асимметрия во време­ни не усиливается.

Литература

[1] О.И.Воскобойникова, С.Л.Гинзбург, В.Ф.Дьяченко, К.В.Ходатаев. Инициация микроволнового стримерного разряда в газе. Препринт ИПМ РАН, 2001г, №13

[2] О.И.Воскобойникова, С.Л.Гинзбург, В.Ф.Дьяченко, К.В.Ходатаев. Численное исследование подкритического микро­вол­нового разряда в газе высокого давления. ЖТФ,2002,т 72, вып 8

[3] О.И.Воскобойникова, С.Л.Гинзбург, В.Ф.Дьяченко, В.В.Палейчик, К.В.Ходатаев. Расчеты микроволнового стример­ного разряда в газе. Препринт ИПМ РАН, 2002г, №35