Аннотация
В работе предложен новый подход к построению экономичных алгоритмов как первого, так и
второго порядка аппроксимации для решения линейных гиперболических систем. Его основные
элементы: независимый друг от друга расчет потоков по каждому пространственному направлению
и локально-неявная разностная схема решения одномерных гиперболических систем, в которой
неявная схема используется там и только там, где соответствующее число Куранта превосходит
единицу.
Abstract
A new approach for the construction of economical algorithms ( of the first and second order
of accuracy ) for the solution of linear hyperbolic systems is presented. Its main
elements are independent calculation of fluxes in each spatial direction and locally
– implicit difference scheme for the solution of one-dimensional hyperbolic systems in
which the implicit scheme is used if and only if the corresponding Courant number is greater
than one.
Введение
Разработка новых разностных методов решения гиперболических систем
направлена, как правило, на преодоление двух основных трудностей. Первая
связана с расчетом обобщенных ( разрывных ) решений и численный алгоритм должен
гарантировать сходимость именно к тому решению, которое диктуется заданными
законами сохранения. В первую очередь, это относится к квазилинейным системам,
среди которых основной является система уравнений Эйлера, описывающая течение
невязкого сжимаевого газа. Впрочем, аналогичная, но существенно более простая
проблема возникает и для линейных систем ( даже с постоянными коэффициентами ),
когда начальные данные разрывны. Среди десятков численных методов расчета
разрывных решений особое место принадлежит методу Годунова, оригинальная версия
которого была опубликована свыше сорока лет назад [1] ( см. также [2] ).
Последующие модификации и усовершенствования, предложенные другими авторами,
уже не обладали четкостью и прозрачностью оригинала и были направлены, в
основном, на повышение порядка аппроксимации и подавление осцилляций, причина
которых также была выяснена С. К. Годуновым [1]. Общий принцип построения
монотонных ( так называемых TVD ) схем был предложен А. Хартеном в 1983 г. [3]. И
хотя в работе А. Хартена речь, по существу, идет об одном, хотя и
квазилинейном, уравнении, сам подход был в дальнейшем распространен  правда, без
доказательных обоснований правда, без
доказательных обоснований  на более широкий
класс задач. Ключевые элементы этого подхода на более широкий
класс задач. Ключевые элементы этого подхода  восполнение сеточных
функций на нижнем слое и решение ( приближенное ) задачи о распаде разрыва ( the Riemann problem ). Но
именно эти же элементы и составляют основу метода Годунова: кусочно-постоянное
восполнение и точное решение задачи о распаде разрыва. Что касается
квазимонотонности, то играющий важную роль в схемах TVD-типа
принцип минимальной производной был, по-видимому, впервые сформулирован В. П.
Колганом [4] применительно к методу
Годунова. В связи с развитием TVD-схем специфический метод приближенного решения
задачи о распаде разрыва был предложен Ф. Роу [5] восполнение сеточных
функций на нижнем слое и решение ( приближенное ) задачи о распаде разрыва ( the Riemann problem ). Но
именно эти же элементы и составляют основу метода Годунова: кусочно-постоянное
восполнение и точное решение задачи о распаде разрыва. Что касается
квазимонотонности, то играющий важную роль в схемах TVD-типа
принцип минимальной производной был, по-видимому, впервые сформулирован В. П.
Колганом [4] применительно к методу
Годунова. В связи с развитием TVD-схем специфический метод приближенного решения
задачи о распаде разрыва был предложен Ф. Роу [5]  т.н.
усреднение по Роу. Этод прием
используется во многих численных алгоритмах. т.н.
усреднение по Роу. Этод прием
используется во многих численных алгоритмах.
Вторая проблема, возникающая при численном решении многомерных
гиперболических систем, связана с минимизацией вычислительной работы 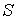 . Поскольку . Поскольку 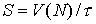 , где , где 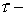 временной шаг, а временной шаг, а 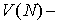 число операций, необходимое для расчета очередного слоя на
разностной сетке объема число операций, необходимое для расчета очередного слоя на
разностной сетке объема 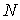 , то речь идет об уменьшении , то речь идет об уменьшении 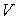 и/или об увеличении и/или об увеличении 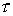 . Явные схемы ( в том числе, классический метод Годунова и
различные модификации TVD – схем ) более приспособлены к расчету
гиперболических задач, поскольку скорость распространения возмущений для соответствующих
разностных решений конечна, а . Явные схемы ( в том числе, классический метод Годунова и
различные модификации TVD – схем ) более приспособлены к расчету
гиперболических задач, поскольку скорость распространения возмущений для соответствующих
разностных решений конечна, а 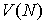 минимально: минимально: 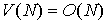 . И, кроме того,
явные схемы обладают лучшей разрешающей способностью. Поэтому, если допустимый
шаг по времени является приемлемым, то предпочтительность явных схем очевидна.
Однако, поскольку выбор шага диктуется самым «опасным» местом, то даже
небольшие по размеру зоны, где либо велики коэффициенты уравнений, либо малы
шаги разностной сетки, могут существенно уменьшить величину временного шага. Именно
вынужденная малость . И, кроме того,
явные схемы обладают лучшей разрешающей способностью. Поэтому, если допустимый
шаг по времени является приемлемым, то предпочтительность явных схем очевидна.
Однако, поскольку выбор шага диктуется самым «опасным» местом, то даже
небольшие по размеру зоны, где либо велики коэффициенты уравнений, либо малы
шаги разностной сетки, могут существенно уменьшить величину временного шага. Именно
вынужденная малость 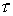 зачастую делает
практически невозможным использование явных схем. зачастую делает
практически невозможным использование явных схем.
Казалось бы, естественный выход из этой ситуации состоит в использовании
безусловно устойчивых неявных схем. Однако, во первых, здесь возникает проблема
минимизации 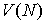 . Для одномерных задач . Для одномерных задач 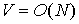 , но при переходе к многомерности трудоемкость алгоритма
существенно возрастает и необходимо применять специальные усилия для ускорения
процесса решения системы разностных уравнений на верхнем слое. Кроме того, по
разрешающей способности неявные схемы уступают явным и, следовательно, их
неоправданно расширенное применение нежелательно. , но при переходе к многомерности трудоемкость алгоритма
существенно возрастает и необходимо применять специальные усилия для ускорения
процесса решения системы разностных уравнений на верхнем слое. Кроме того, по
разрешающей способности неявные схемы уступают явным и, следовательно, их
неоправданно расширенное применение нежелательно.
В данной работе предлагается общий подход, позволяющий преодолеть указанные
выше трудности и противоречия. В его основе лежат две идеи:
(1). Оператор перехода на следующий слой должен сводиться к решению
одномерных задач экономичность и возможность параллелизации. В отличие от
традиционного метода переменных направлений здесь используется иной путь,
который можно назвать методом независимых потоков ( МНП ), поскольку расчет
потоков по каждому пространственному направлению производится независимо друг
от друга. экономичность и возможность параллелизации. В отличие от
традиционного метода переменных направлений здесь используется иной путь,
который можно назвать методом независимых потоков ( МНП ), поскольку расчет
потоков по каждому пространственному направлению производится независимо друг
от друга.
(2). Схема должна быть
неявной там и
только там, где соответствующее число Куранта 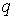 превышает единицу (
по модулю ). превышает единицу (
по модулю ).
Конечно, сформулированный в таком общем виде идея локальной неявности
требует уточнения. Например, как понимать «явность» или «неявность» в случае
системы уравнений, пусть даже одномерной? Как должны состыковываться явная и
неявная компоненты схемы при  ? ?
Важную роль в конструировании разностных схем играет принцип минимального
шаблона, [6]-[7]. Схемы, удовлетворяющие этому принципу, обладают определенными
преимуществами перед схемами, использующими избыточный шаблон. Одна из схем,
предложенных в данной работе,как раз и базируется на минимальном шаблоне.
Поскольку проблемы, связанные с нелинейностью здесь не рассматриваются,
речь пойдет о разностных схемах ( как первого, так и второго порядка
аппроксимации ) для линейных скалярных уравнений и гиперболических систем.
Разумеется, наиболее трудоемкими задачами являются трехмерные системы
уравнений, и именно здесь экономичные алгоритмы дают максимальный эффект.
Однако основные конструкции и идеи
предлагаемого подхода удобнее и проще демонстрировать на двумерных задачах.
Именно двумерным алгоритмам и посвящена данная работа. Что касается трехмерного
случая, то этой проблеме будет посвящена отдельная работа, где основное
внимание уделяется специфическим особенностям трехмерных методов.
Содержание работы:
В п. 1 рассматривается одномерная задача, для которой как раз и
конструируется локально-неявная схема. Именно этот алгоритм является одним из
основных элементов всех многомерных схем. Простейшей скалярной двумерной схеме первого порядка  схеме с усреднением схеме с усреднением  и ее анализу (
аппроксимация и устойчивость ) посвящен п. 2. Реализация той же схемы для
гиперболической системы уравнений дана в п. 3. Следующий класс схем первого
порядка и ее анализу (
аппроксимация и устойчивость ) посвящен п. 2. Реализация той же схемы для
гиперболической системы уравнений дана в п. 3. Следующий класс схем первого
порядка  базовые
локально-неявные схемы базовые
локально-неявные схемы  представлен в п. 4.
Эти алгоритмы представляют собой естественное обобщение базовых явных схем
[6]-[7]. В последующих параграфах речь идет о схемах второго порядка.
Центрально-симметрическая локально-неявная схема представлена в п. 5. Здесь следует отметить, что шаблон этой
схемы ( для явной реализации ) не является
минимальным, что упрощает ее конструкцию, но, возможно, несколько ухудшает
качество. Последняя схема, представленная в работе (п. 6 ) представлен в п. 4.
Эти алгоритмы представляют собой естественное обобщение базовых явных схем
[6]-[7]. В последующих параграфах речь идет о схемах второго порядка.
Центрально-симметрическая локально-неявная схема представлена в п. 5. Здесь следует отметить, что шаблон этой
схемы ( для явной реализации ) не является
минимальным, что упрощает ее конструкцию, но, возможно, несколько ухудшает
качество. Последняя схема, представленная в работе (п. 6 )  базовая
локально-неявная схема второго порядка базовая
локально-неявная схема второго порядка  уже удовлетворяет
принципу минимального шаблона и является более эффективной, хотя, конечно, и
более сложной. Устойчивость всех схем применительно к гиперболическим системам
доказывается в предположении симметричности матричных коэффициентов. уже удовлетворяет
принципу минимального шаблона и является более эффективной, хотя, конечно, и
более сложной. Устойчивость всех схем применительно к гиперболическим системам
доказывается в предположении симметричности матричных коэффициентов.
Представленный в работе широкий набор различных разностных схем ( две схемы
первого и две схемы второго порядка ) позволяет осуществить оптимальный выбор,
исходя из специфики той или иной конкретной задачи и требований, предъявляемых
к ее решению.
1.
Одномерная задача
Поскольку основным элементом
алгоритма является разностная схема решения одномерной задачи, начнем именно с
этого случая. Рассмотрим вначале скалярное уравнение
  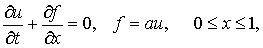 (1.1)
(1.1)
где 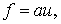 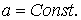
Как уже было сказано во Введении,
искомая локально-неявная схема должна представлять собой комбинацию двух схем –
явной и неявной, каждая из которых работает в своей области. В качестве таковых
возьмем простейшие схемы, реализующие принцип конечных объемов.
Разобъем 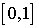 на ячейки на ячейки 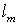 длины длины 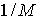 , , 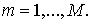 Границы ячеек - Границы ячеек - 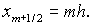 Значения сеточных
функций на нижнем и верхнем слоях будем относить к серединам этих ячеек, т.е. к
точкам Значения сеточных
функций на нижнем и верхнем слоях будем относить к серединам этих ячеек, т.е. к
точкам 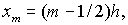 а потоки а потоки 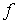 - к границам ячеек,
обозначая их значения через - к границам ячеек,
обозначая их значения через 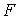 . Тогда . Тогда
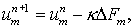 (1.2) (1.2)
где 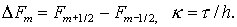
Дивергентное замыкание (1.2) – общее
для обеих схем. Поэтому определяющую роль играет способ вычисления потоков 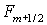 . .
Умножив (1.1) на 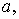 получим получим
 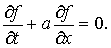 (1.3)
(1.3)
Именно эта форма исходного уравнения используется для конструирования
обеих разностных схем.
Схема 1 (явная):
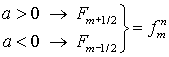 .
(1.4) .
(1.4)
Эта схема расчета потоков, дополненная дивергентным замыканием (1.2),
порождает простейшую противопотоковую (upwind) разностную схему:
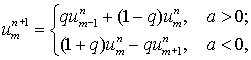 (1.5) (1.5)
где 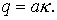 Условие ее
устойчивости (и монотонности) : Условие ее
устойчивости (и монотонности) : 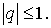
Схема 2 (неявная):
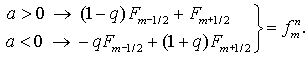 (1.6) (1.6)
Исключив 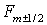 из (1.2) и (1.6),
получим из (1.2) и (1.6),
получим
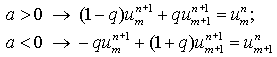 (1.7) (1.7)
(неявный аналог схемы (1.5)).
Легко видеть, что схема 2 устойчива ( и
тоже монотонна ) лишь при  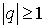 . Подчеркнем, что при . Подчеркнем, что при 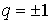 обе схемы совпадают. обе схемы совпадают.
Для нахождения 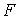 удобно воспользоваться
единой записью в виде формально трехточечного разностного уравнения удобно воспользоваться
единой записью в виде формально трехточечного разностного уравнения
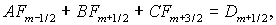 (1.8) (1.8)
где 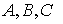 и и 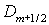 зависят от зависят от 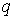 следующим образом: следующим образом:
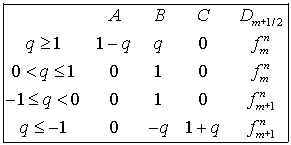 (1.9) (1.9)
Заметим, что при 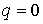 возникает некоторая
неопределенность в возникает некоторая
неопределенность в 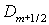 . В этом случае можно просто положить . В этом случае можно просто положить 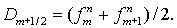
Пусть теперь 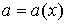 и, соответственно, и, соответственно, 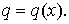 Тогда коэффициенты в
(1.8) должны вычисляться по (1.9) с учетом переменности Тогда коэффициенты в
(1.8) должны вычисляться по (1.9) с учетом переменности 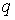 : : 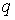 заменяется на заменяется на 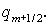 Та же схема пригодна
и для более общего случая Та же схема пригодна
и для более общего случая 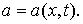 Здесь Здесь 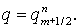
Очевидно, что для любой гладкой 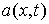 краевая задача для
(1.8) корректо поставлена, если корректна соответствующая смешанная задача для
исходного дифференциального уравнения. Именно схема в форме (1.8) и является
локально-неявной, т.к. ее структура локально зависит от величины и знака числа
Куранта краевая задача для
(1.8) корректо поставлена, если корректна соответствующая смешанная задача для
исходного дифференциального уравнения. Именно схема в форме (1.8) и является
локально-неявной, т.к. ее структура локально зависит от величины и знака числа
Куранта 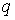 , а переходы с «явного» участка на «неявный» и обратно
происходят гладким образом. , а переходы с «явного» участка на «неявный» и обратно
происходят гладким образом.
Перейдем от скалярного уравнения (1.1) к
соответствующей гиперболической системе. Теперь 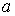 - диагонализируемая
матрица, все собственные значения - диагонализируемая
матрица, все собственные значения 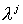 которой веществены.
Приведя (1.3) к диагональному виду, получим которой веществены.
Приведя (1.3) к диагональному виду, получим
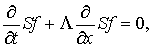 (1.10)
(1.10)
где 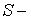 матрица, строками которой являются левые собственные векторы
матрицы матрица, строками которой являются левые собственные векторы
матрицы 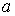 , а , а 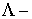 диагональная матрица с элементами диагональная матрица с элементами 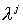 . Из вида (1.10) следует, что для построения схемы расчета
потоков надо просто в (1.4) и (1.6) заменить . Из вида (1.10) следует, что для построения схемы расчета
потоков надо просто в (1.4) и (1.6) заменить 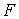 и и 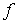 на на 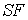 и и 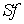 , соответственно. В результате трехточечная система
разностных уравнений будет иметь тот же вид (1.8), но теперь , соответственно. В результате трехточечная система
разностных уравнений будет иметь тот же вид (1.8), но теперь 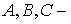 матрицы со строками матрицы со строками 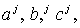 а а 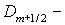 вектор с компонентами вектор с компонентами 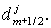 Структура Структура 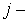 й строки системы (1.8) зависит от й строки системы (1.8) зависит от 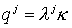 следующим образом: следующим образом:
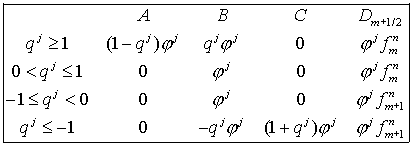 (1 .11)
(1 .11)
(Во второй и третьей строках этой таблицы 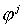 можно заменить на
единицу.) можно заменить на
единицу.)
Обобщение на случай переменной матрицы 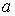 очевидно. очевидно.
2. Двумерная схема с
усреднением
Рассмотрим двумерный аналог скалярного уравнения (1.1):
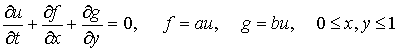 (2.1) (2.1)
с постоянными коэффициентами 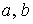 . .
Обобщая одномерную конструкцию, введем пространственные ячейки 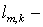 прямоугольники со сторонами прямоугольники со сторонами 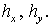 Значения сеточных
функций на обоих временных слоях будем относить к центрам этих ячеек, т.е. к
точкам Значения сеточных
функций на обоих временных слоях будем относить к центрам этих ячеек, т.е. к
точкам 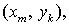 где где  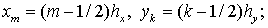 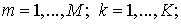 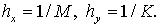 Потоки Потоки 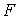 и и 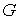 относятся к серединам
границ ячейки и снабжены соответствующими индексами относятся к серединам
границ ячейки и снабжены соответствующими индексами 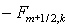 и и 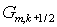 , см. Рис. 1. , см. Рис. 1.
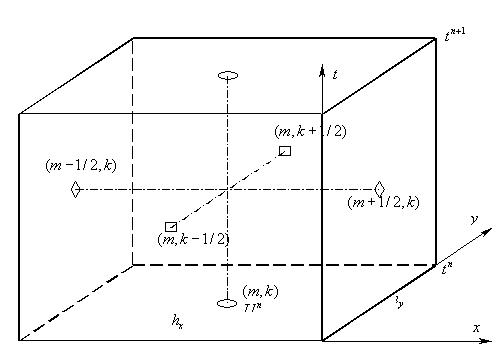
Рис. 1.
Дивергентное замыкание:
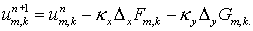 (2.2) (2.2)
Здесь 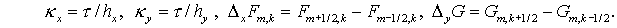 Для чисел Куранта
введем обозначения Для чисел Куранта
введем обозначения 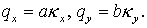
Основная идея метода независимых потоков ( МНП ) состоит в том, что
каждый поток ( в данном случае 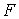 и и 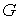 ) определяется как
решение соответствующего уравнения. А именно, ) определяется как
решение соответствующего уравнения. А именно,
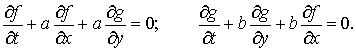
Степень аппроксимации разностных решений этих уравнений задается
порядком аппроксимации результирующей схемы.
Легко видеть, что простое обобщение одномерной схемы не обеспечивает
требуемого свойства совпадения явной и неявной компонент схемы при 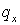 ( или ( или 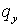 ) = ) = 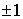 . Действительно, пусть . Действительно, пусть 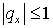 и и 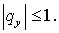 Тогда реализуется
полностью явная схема, условие устойчивости которой : Тогда реализуется
полностью явная схема, условие устойчивости которой :
 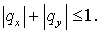 (2.3) (2.3)
Но это и означает, что гладкое переключение этой схемы на любую неявную
невозможно, поскольку на переключении 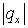 ( или ( или 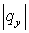 ) =1, что нарушает
(2.3). Очевидно, что для непрерывной стыковки схем необходимо, чтобы явная
схемы оставалась устойчивой при более слабом ограничении: ) =1, что нарушает
(2.3). Очевидно, что для непрерывной стыковки схем необходимо, чтобы явная
схемы оставалась устойчивой при более слабом ограничении:
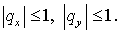 (2.4)
(2.4)
Это требование можно реализовать, например, за счет двухэтапного
перехода на верхний слой. Именно эта идея и лежит в основе схем, представленных
в данной работе. В этом параграфе рассматривается двухэтапная схема,
использующая послойное усреднение. При этом, поскольку речь идет о схеме
первого порядка, вместо полных уравнений для потоков можно ограничиться их
«грубым» приближением:
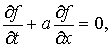 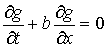 , (2.5) , (2.5)
Этап 1
На этом этапе вычисляются промежуточные значения потоков 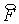 и и 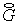 с помощью описанного
выше алгоритма решения одномерных уравнений (2.5). с помощью описанного
выше алгоритма решения одномерных уравнений (2.5).
То есть,
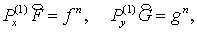 (2.6) (2.6)
где 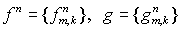 , а операторы , а операторы  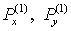 , действующие на сеточные функции , действующие на сеточные функции 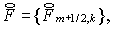 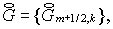 определены следующим
образом: определены следующим
образом:
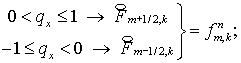
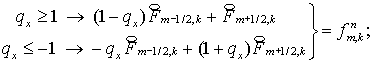
(2.7)
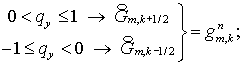
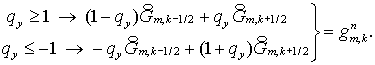
Соответствующие
трехточечные уравнения имеют вид:
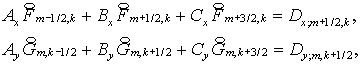
где коэффициенты и правые части вычисляются по (1.9) для каждого
направления в отдельности.
Первый этап завершается дивергентным замыканием, результатом которого
являются промежуточные значения решения на верхнем слое:
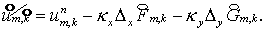 (2.8) (2.8)
Этап 2
Данный этап начинается с процедуры усреднения
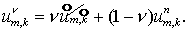 (2.9)
(2.9)
После этого находятся окончательные значения потоков 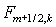 и и 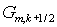 по алгоритму первого
этапа с той лишь разницей, что по алгоритму первого
этапа с той лишь разницей, что 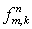 и и 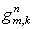 заменяются на заменяются на 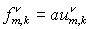 и и 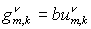 , соответственно. Этап заканчивается стандартным дивергентным
замыканием. , соответственно. Этап заканчивается стандартным дивергентным
замыканием.
Поскольку итоговая схема представляет собой ( в зависимости от знаков и
величин 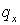 и и 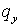 ) ту или иную
комбинацию явной и неявной схем (схем 1 и 2 ), то для ее анализа следует
рассмотреть все возможные комбинации. ) ту или иную
комбинацию явной и неявной схем (схем 1 и 2 ), то для ее анализа следует
рассмотреть все возможные комбинации.
Для удобства перепишем (1.4) и (1.6) в единообразном виде:
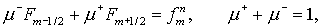 (2.10) (2.10)
где
 (2.11)
(2.11)
Аналогичной формой записи воспользуемся и для системы (2.7), введя
соответствующие индексы 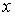 и и 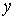 . .
Введем обозначения
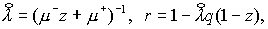 (2.12) (2.12)
где 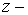 произвольное комплексное число, лежащее на единичной
окружности: произвольное комплексное число, лежащее на единичной
окружности: 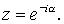 Для анализа
устойчивости понадобится следующая Для анализа
устойчивости понадобится следующая
Лемма 1
Для любых
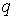 и
и
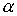
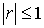
Доказательство сводится к непосредственной
проверке каждого из возможных случаев:
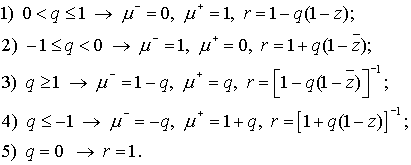 (2.13)
(2.13)
Для нахождения собственного значения 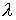 оператора перехода на
верхний слой воспользуемся стандартной техникой. Положим оператора перехода на
верхний слой воспользуемся стандартной техникой. Положим 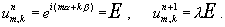 Тогда Тогда
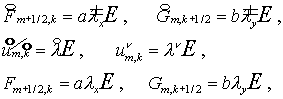 (2.14) (2.14)
Из (2.10) для 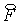 , ,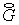 имеем имеем 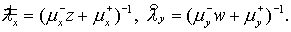 (Здесь и в дальнейшем (Здесь и в дальнейшем
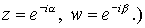
Поскольку 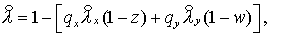 то, с учетом (2.12), то, с учетом (2.12),
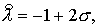 где где 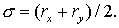 ( (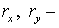 см. (2.12) для см. (2.12) для 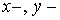 направлений.) направлений.)
Из
(2.11) получаем 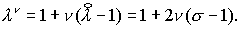
Этап 2 дает 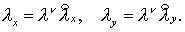
Наконец, дивергентное замыкание
дает: 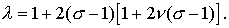
То есть, окончательно
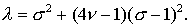 (2.15) (2.15)
Возьмем 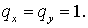 При этих значениях
чисел Куранта обе схемы При этих значениях
чисел Куранта обе схемы 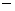 явная и неявная явная и неявная 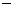 должны совпадать и
быть устойчивыми, т.е. при всех должны совпадать и
быть устойчивыми, т.е. при всех  должно выполняться
неравенство должно выполняться
неравенство 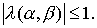 Вычислим Вычислим 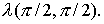 Для этих значений Для этих значений 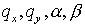 имеем имеем 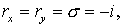 что дает что дает 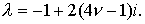 Таким образом, для
любого Таким образом, для
любого 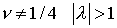 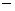 схема неустойчива. схема неустойчива.
Для 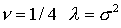 . Поскольку ( см. Лемму 1 ) . Поскольку ( см. Лемму 1 ) 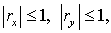 то и то и 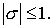 Поэтому Поэтому 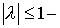 необходимое условие
устойчивости выполнено. необходимое условие
устойчивости выполнено.
Итак, предложенная локально-неявная двумерная схема безусловно
устойчива лишь при усреднении 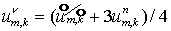 и осталось проверить,
что эта схема действительно является схемой первого порядка. и осталось проверить,
что эта схема действительно является схемой первого порядка.
Порядок аппроксимации определяется сопоставлением 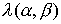 для разностного
оператора перехода со слоя для разностного
оператора перехода со слоя 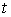 на слой на слой 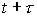 с с 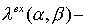 множителем перехода
для точного решения дифференциального уравнения. Взяв начальные данные вида множителем перехода
для точного решения дифференциального уравнения. Взяв начальные данные вида 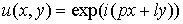 и рассмотрев их на
разностной сетке, получим и рассмотрев их на
разностной сетке, получим 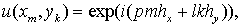 то есть, то есть, 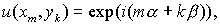 где где 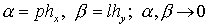 при при 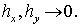 Точный множитель
перехода на верхний слой Точный множитель
перехода на верхний слой
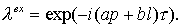 (2.16) (2.16)
Порядок совпадающих членов в разложениях 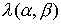 и и 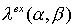 равен порядку
аппроксимации. Легко проверить, что в
линейном приближении для любой реализации схемы равен порядку
аппроксимации. Легко проверить, что в
линейном приближении для любой реализации схемы 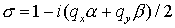 и, следовательно, и, следовательно, 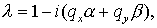 что совпадает с
линейным приближением для точного решения (2.16). что совпадает с
линейным приближением для точного решения (2.16).
Обобщение схемы на переменные коэффициенты осуществляется аналогично одномерному случаю. При решении
неоднородного уравнения
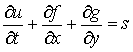
правая часть 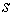 учитывается лишь в
дивергентных замыканиях в виде слагаемого учитывается лишь в
дивергентных замыканиях в виде слагаемого 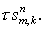
3. Схема с усреднением
для гиперболических систем
Рассмотрим векторную систему вида (2.1), где теперь 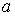 и и 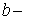 матрицы. Сразу подчеркнем, что конструкция алгоритма не
предполагает симметричность этих матриц, хотя безусловная устойчивость схемы
будет доказана лишь для симметрического случая, то есть в ситуации, когда
существуют интегралы энергии. матрицы. Сразу подчеркнем, что конструкция алгоритма не
предполагает симметричность этих матриц, хотя безусловная устойчивость схемы
будет доказана лишь для симметрического случая, то есть в ситуации, когда
существуют интегралы энергии.
Поскольку на каждом этапе решается одномерные задачи, то фактически
алгоритм остается тем же самым ( см. конец п.1).
Исходя из диагональной формы (1.10), имеем векторный аналог (2.10):
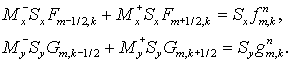 (3.1) (3.1)
Теперь 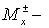 диагональные матрицы с элементами диагональные матрицы с элементами 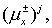 вычисляемыми по
(2.11), где под вычисляемыми по
(2.11), где под 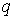 понимается понимается 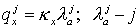 -е собственное значение матрицы -е собственное значение матрицы 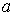 . Аналогичный вид имеет связь между . Аналогичный вид имеет связь между 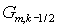 и и 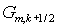 . (Заметим, что на первом этапе искомыми величинами являются . (Заметим, что на первом этапе искомыми величинами являются 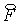 и и 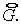 ) )
Прейдем к анализу устойчивости в предположении симметричности матриц 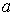 и и 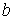 . Возьмем . Возьмем 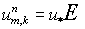 ( (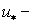 вектор). Тогда вектор). Тогда 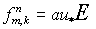 , , 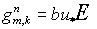 и и
   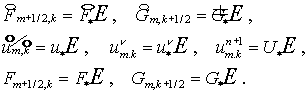 (3.2) (3.2)
Подставив (3.2) в (3.1) как в
систему относительно 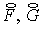 ), получим ), получим
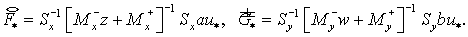 (3.3) (3.3)
Так как 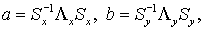 где где 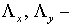 диагональные диагональные матрицы с элементами матрицы с элементами 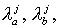 соответственно, то
(3.3) можно переписать в виде соответственно, то
(3.3) можно переписать в виде
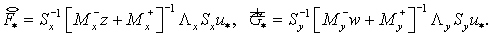 (3.4) (3.4)
По аналогии с (2.12) введем
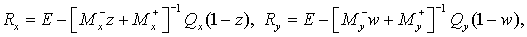 (3.5)
(3.5)
где 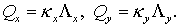 Тогда Тогда
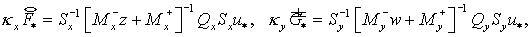 (3.6) (3.6)
после чего дивергентное замыкание дает
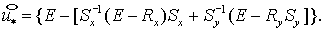 (3.7) (3.7)
Введя 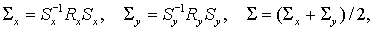 перепишем перепишем 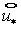 в компактном
виде: в компактном
виде: 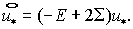 Отсюда для Отсюда для 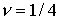 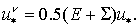
Так как этап 2 отличается от этапа 1 лишь заменой 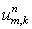 на на 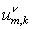 , то, повторяя предыдущие выкладки, получаем: , то, повторяя предыдущие выкладки, получаем: 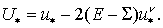 То есть, То есть,
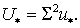 (3.8) (3.8)
Необходимое условие устойчивости: 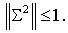 Для доказательства
этого неравенства воспользуемся симметричностью матриц Для доказательства
этого неравенства воспользуемся симметричностью матриц 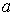 и и 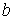 . Следовательно, . Следовательно, 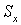 и и  можно выбрать
ортогональными. Матрицы же можно выбрать
ортогональными. Матрицы же 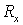 и и 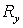 диагональны и по
Лемме 1 их элементы лежат в единичном круге. Поэтому диагональны и по
Лемме 1 их элементы лежат в единичном круге. Поэтому 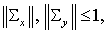 что и доказывает
требуемое неравенство. что и доказывает
требуемое неравенство.
Обобщение схемы на переменные коэффициенты и неоднородность
производится уже знакомым образом.
4. Базовая
локально-неявная схема
Схема с усреднением, представленная в предыдущих параграфах, базируется
на двух ключевых идеях:
(i).
Локально-неявный алгоритм решения одномерной задачи;
(ii).
Расширение области устойчивости явной схемы ( от ограничения типа (2.3) до
условия вида (2.4)) путем введения в схему дополнительного, второго этапа.
Этот алгоритм успешно использовался в расчетах довольно сложных
двумерных нестационарных течений.
Из вычислительной практики известно, что весьма полезным свойством
разностных схем решения гиперболических систем является характеристичность.
Применительно к скалярному уравнению (2.1) это означает перенос точного
значения вдоль характеристики при любой комбинации значений 0, 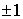 чисел Куранта чисел Куранта 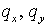 . .
Заметим, что схема с усреднением не является характеристической.
Действительно, при  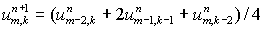 в то время, как для
точного решения в то время, как для
точного решения 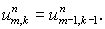 Ясно, что шаблон
характеристической явной схемы обязан содержать «базовый элемент», состоящий из
четырех точек. В зависимости от знаков Ясно, что шаблон
характеристической явной схемы обязан содержать «базовый элемент», состоящий из
четырех точек. В зависимости от знаков  и и  этот элемент имеет
вид: этот элемент имеет
вид:
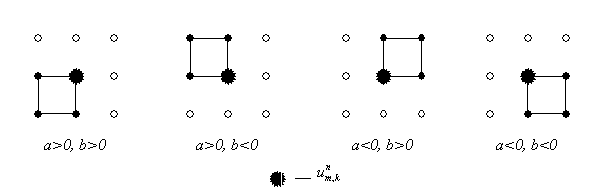
Рис. 2.
Для схемы с усреднением при 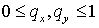
 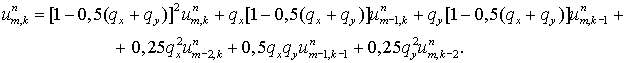
Шаблон схемы состоит из шести точек и содержит базовый элемент. Однако
эта схема не является оптимальной: она не удовлетворяет принципу минимального
шаблона. Ясно, что для характеристической схемы первого порядка минимальным
шаблоном является именно базовый элемент ( четыре точки ), что диктует
единственную реализацию  для явной схемы для явной схемы 
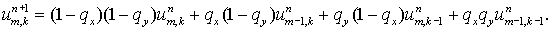
Другие комбинации знаков 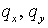 дают аналогичные
выражения для дают аналогичные
выражения для 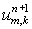 , соответствующие шаблонам, изображенным на Рис. 2. , соответствующие шаблонам, изображенным на Рис. 2.
Потоковый вариант этой явной базовой схемы (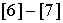 ) для положительных ) для положительных 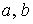 имеет вид: имеет вид:
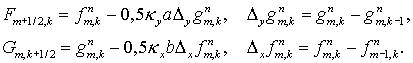 (4.1) (4.1)
Под базовой локально-неявной схемой будем понимать схему первого
порядка, основанную на тех же идеях (i) и (ii), но характеристическую.
Начнем со скалярного уравнения. Согласно (4.1) явная базовая схема
отличается от простейшей (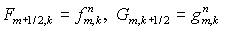 ) дополнительным слагаемым, вычисляемым в той же точке ) дополнительным слагаемым, вычисляемым в той же точке 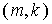 . Однако при произвольном распределении знаков . Однако при произвольном распределении знаков 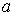 и и 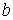 потоки потоки 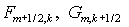 необходимо вычислять,
следуя «противопотоковому» правилу, а именно, необходимо вычислять,
следуя «противопотоковому» правилу, а именно,
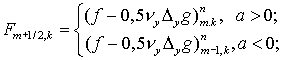 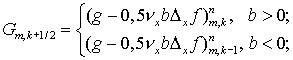 (4.2) (4.2)
При этом 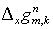 и и 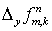 тоже вычисляются
«против потока», т.е. с учетом
знаков тоже вычисляются
«против потока», т.е. с учетом
знаков 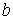 и и 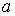 ,соответственно: ,соответственно:

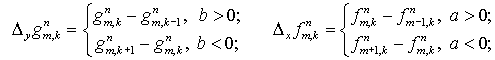
(4.3)

Фактически, эти формулы соответствуют общей операторной записи:
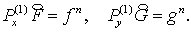 (4.4)
(4.4)
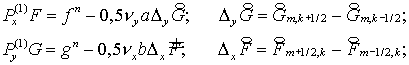 (4.5)
(4.5)
где 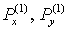 описывают переход по
явной схеме (см. (2.7) при описывают переход по
явной схеме (см. (2.7) при 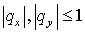 ). А именно, ). А именно,
 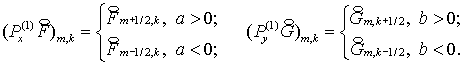 (4.6) (4.6)
Эта форма подсказывает конструкцию локально-неявной базовой схемы. В соответствии с концепцией МНП рассмотрим
соответствующие уравнения для каждого из потоков:
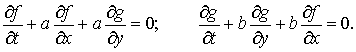 (4.7) (4.7)
Тогда (4.4) можно рассматривать как этап 1 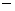 грубое приближение,
полученное путем отбрасывания слагаемых грубое приближение,
полученное путем отбрасывания слагаемых 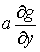 и и 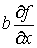 , соответственно. На этапе 2 эти члены уже учитываются , соответственно. На этапе 2 эти члены уже учитываются 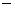 по значениям,
полученным на этапе 1. по значениям,
полученным на этапе 1.
Теперь остается лишь распространить (4.4) 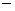 (4.5) на общий случай
произвольного распределения знаков и величин чисел Куранта, то есть заменить
вид операторов (4.5) на общий случай
произвольного распределения знаков и величин чисел Куранта, то есть заменить
вид операторов 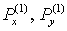 (4.6) (для явной схемы ) на полный набор (2.7),
что и дает искомую схему. Итак, расчетные формулы локально-неявной схемы имеют
вид: (4.6) (для явной схемы ) на полный набор (2.7),
что и дает искомую схему. Итак, расчетные формулы локально-неявной схемы имеют
вид:
Этап 1
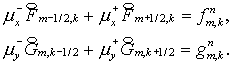 (4.8) (4.8)
Этап 2
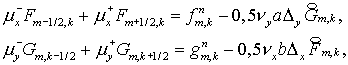 (4.9) (4.9)
где 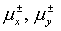 определены для каждого направления по (2.13) или определены для каждого направления по (2.13) или 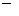 в компактной форме в компактной форме 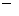 по (2.11). Этап 2 завершается дивергентным замыканием. по (2.11). Этап 2 завершается дивергентным замыканием.
Заметим, что подход, основанный на расчете потоков, каждый из которых
определяется независимо из своего уравнения, то есть на МНП, является
достаточно универсальным ( см.  , где та же идея использована для решения уравнения теплопроводности). , где та же идея использована для решения уравнения теплопроводности).
Устойчивость схемы исследуется аналогично схеме с усреднением. При этом
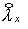 и и 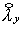 остаются теми же, а остаются теми же, а
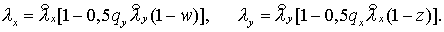 (4.10)
(4.10)
Так как 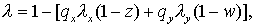 то, введя те же то, введя те же 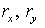 ( по (2.12)), получим ( по (2.12)), получим
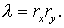
В силу Леммы 1 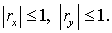 Следовательно, Следовательно, 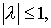 что и является
необходимым условием устойчивости. что и является
необходимым условием устойчивости.
При 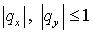 эта базовая схема
положительна. Характеристичность схемы очевидна. эта базовая схема
положительна. Характеристичность схемы очевидна.
Обобщение на случай гиперболической системы осуществляется аналогично
схеме с усреднением. При этом изменяется лишь второй этап:
Этап 2
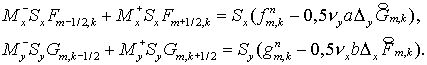 (4.11) (4.11)
То есть,
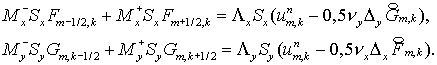 (4.12) (4.12)
Найдя 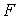 и и 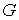 из (4.11) или
(4.12), остается завершить переход на следующий слой дивергентым замыканием. из (4.11) или
(4.12), остается завершить переход на следующий слой дивергентым замыканием.
Исследуем устойчивость схемы в предположении симметричности матриц 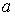 и и 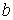 . Сохраняя обозначения схемы с усреднением, получим для . Сохраняя обозначения схемы с усреднением, получим для  , , 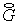 и и 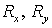 те же выражения (3.4)
и (3.5). Тогда те же выражения (3.4)
и (3.5). Тогда
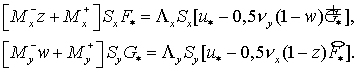 (4.13) (4.13)
Подставив в (4.13) выражения для 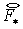 и и 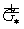 , получим , получим
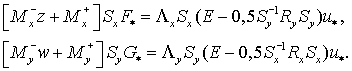 (4.14) (4.14)
Отсюда
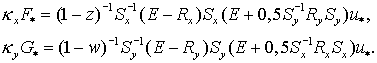 (4.15) (4.15)
Подставив (4.15) в дивергентное замыкание, получим 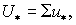 где где
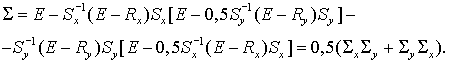
(Здесь, как и прежде, 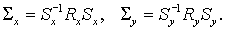 ) )
Требуемая оценка 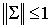 следует, как и для
предыдущей схемы, из Леммы 1 и симметричности матриц следует, как и для
предыдущей схемы, из Леммы 1 и симметричности матриц  и и 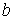 . .
Ясно, что для системы, приводимой к симметрической невырожденным
преобразованием, необходимое условие устойчивости базовой схемы, как, впрочем и
схемы с усреднением, выполняется.
5. Центрально-симметрическая локально-неявная
схема второго порядка
В предыдущих параграфах речь шла о двух разностных схемах первого
порядка. Однако та же идея двухэтапного вычисления потоков позволяет создать и
схемы первого порядка.
Прежде, чем переходить к построению и анализу искомых схем, коснемся
одного общего вопроса о выборе шаблона в явных схемах. Как показывает
вычислительный опыт и теоретические исследования модельных задач, схемы,
базирующиеся на минимальном шаблоне, обладают определенным преимуществом перед
«избыточными», см. 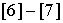 . Применительно к схемам первого порядка для скалярного
уравнения легко показать, что условие устойчивости выделяет среди всех схем
минимального шаблона единственную. Ее шаблон, а, следовательно, и сама схема
зависит от направления «линии тока», т.е. от знаков коэффициентов уравнения.
Такого рода схемы принято называть противопотоковыми ( upwind ). Следует
подчеркнуть, что эти схемы являются линейными, несмотря на переключаемость
шаблона, так как вид схемы зависит лишь от коэффициентов уравнения ( даже
просто от их знаков ), а не от локальной структуры самого решения. Для
гиперболических систем, тем более, многомерных, принцип минимального шаблона
уже не формулируется столь просто. Здесь речь идет о минимизации объема
информации, используемой для вычисления искомого решения на верхнем слое.
Соответствующие схемы тоже можно называть противопотоковыми, хотя явно
выделенные направления могут и отсуствовать. Заметим, что представленная в
предыдущем параграфе схема принадлежит именно к этому классу. . Применительно к схемам первого порядка для скалярного
уравнения легко показать, что условие устойчивости выделяет среди всех схем
минимального шаблона единственную. Ее шаблон, а, следовательно, и сама схема
зависит от направления «линии тока», т.е. от знаков коэффициентов уравнения.
Такого рода схемы принято называть противопотоковыми ( upwind ). Следует
подчеркнуть, что эти схемы являются линейными, несмотря на переключаемость
шаблона, так как вид схемы зависит лишь от коэффициентов уравнения ( даже
просто от их знаков ), а не от локальной структуры самого решения. Для
гиперболических систем, тем более, многомерных, принцип минимального шаблона
уже не формулируется столь просто. Здесь речь идет о минимизации объема
информации, используемой для вычисления искомого решения на верхнем слое.
Соответствующие схемы тоже можно называть противопотоковыми, хотя явно
выделенные направления могут и отсуствовать. Заметим, что представленная в
предыдущем параграфе схема принадлежит именно к этому классу.
При построении схем второго порядка возникает традиционная проблема,
связанная с осцилляциями, обязательно возникающими при работе с линейными
схемами ( ). Для построения квазимонотонных ( т.е. с приемлемым уровнем
осцилляций ) схем можно использовать переменный шаблон, выбор которого
определяется локально в соответствии со структурой разностного решения (см.,
например, ). Для построения квазимонотонных ( т.е. с приемлемым уровнем
осцилляций ) схем можно использовать переменный шаблон, выбор которого
определяется локально в соответствии со структурой разностного решения (см.,
например, 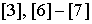 ). Такого рода схемы являются нелинейными и довольно
сложными, если переменность шаблона реализовывать в полной мере. Тем не менее,
во многих ситуациях именно такой подход оказывается весьма эффективным, так как
соответствующие схемы обладают хорошей разрешающей способностью. Подчеркнем,
что, в отличие от схем первого порядка,
здесь выбор шаблона осуществляется из всей ( весьма широкой )
совокупности минимальных шаблонов не только по критерию устойчивости ). Такого рода схемы являются нелинейными и довольно
сложными, если переменность шаблона реализовывать в полной мере. Тем не менее,
во многих ситуациях именно такой подход оказывается весьма эффективным, так как
соответствующие схемы обладают хорошей разрешающей способностью. Подчеркнем,
что, в отличие от схем первого порядка,
здесь выбор шаблона осуществляется из всей ( весьма широкой )
совокупности минимальных шаблонов не только по критерию устойчивости  таких схем несколько
даже для простейшего скалярного уравнения таких схем несколько
даже для простейшего скалярного уравнения  , но и из соображений, связанных с минимизацией осцилляций.
Из всего этого набора шаблонов, а, значит, и схем выделяются схемы, которые
можно назвать центрально-симметрическими. Их место в ряду других схем
объясняется двумя факторами. Во-первых, все остальные устойчивые схемы
минимального шаблона можно получить из них с помощью стандартной модификации. А
во-вторых, эти схемы при расчете гладких решений ( то есть в остуствии
источников осцилляций ) обладают достаточно хорошими свойствами и относительно
просты в реализации. , но и из соображений, связанных с минимизацией осцилляций.
Из всего этого набора шаблонов, а, значит, и схем выделяются схемы, которые
можно назвать центрально-симметрическими. Их место в ряду других схем
объясняется двумя факторами. Во-первых, все остальные устойчивые схемы
минимального шаблона можно получить из них с помощью стандартной модификации. А
во-вторых, эти схемы при расчете гладких решений ( то есть в остуствии
источников осцилляций ) обладают достаточно хорошими свойствами и относительно
просты в реализации.
Начнем с построения схемы, являющейся, в некотором смысле,
локально-неявным обобщением схемы Лакса Вендроффа. Речь, разумеется, идет о построении отдельных
элементов, объединение которых в трехточечную разностную систему осуществляется
уже описанным в п.1 способом. Сразу отметим, что шаблон этой схемы не является
минимальным. Вендроффа. Речь, разумеется, идет о построении отдельных
элементов, объединение которых в трехточечную разностную систему осуществляется
уже описанным в п.1 способом. Сразу отметим, что шаблон этой схемы не является
минимальным.
Конструкция схемы практически совпадает с конструкцией базовой
локально-неявной схемы, рассмотренной в п.4. Единственное, но весьма
существенное отличие заключается в алгоритме решения одномерной задачи.
Начнем, как обычно, со скалярного случая и рассмотрим все то же
двумерное уравнение
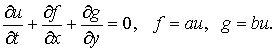 (5.1) (5.1)
Так же, как и для схем первого порядка, основным элементом является
алгоритм расчета потоков при решении одномерного уравнения (1.1)
В зависимости от величины и знака числа Куранта 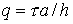 искомые потоки искомые потоки 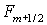 в схеме первого
порядка вычислялись либо по явной схеме (1.4), либо по неявной схеме (1.6). в схеме первого
порядка вычислялись либо по явной схеме (1.4), либо по неявной схеме (1.6).
Для получения схемы второго порядка достаточно лишь более точно вычислять
эти потоки. А именно, для явной схемы
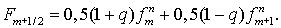 (5.2) (5.2)
Если же 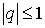 , то соответствующая ( неявная ) схема имеет вид: , то соответствующая ( неявная ) схема имеет вид:
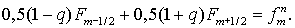 (5.3) (5.3)
Подчеркнем, что эти схемы
совпадают при 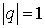 . Легко проверить, что дивергентное замыкание (1.2) порождает для явной реализации схему
типа Лакса . Легко проверить, что дивергентное замыкание (1.2) порождает для явной реализации схему
типа Лакса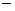 Вендроффа Вендроффа
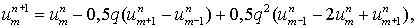 (5.4)
(5.4)
а в неявном случае  схему Бабенко, схему Бабенко, 
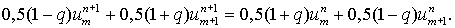 (5.5) (5.5)
Схема (5.4) устойчива при  , а схема (5.5) безусловно устойчива. Таким образом,
комбинированная локально-неявная схема (5.2) , а схема (5.5) безусловно устойчива. Таким образом,
комбинированная локально-неявная схема (5.2) (5.3) решения одномерного уравнения (1.1) безусловно
устойчива. Соответствующая разностная задача корректна при согласованных со
знаком коэффициента (5.3) решения одномерного уравнения (1.1) безусловно
устойчива. Соответствующая разностная задача корректна при согласованных со
знаком коэффициента 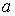 граничных условиях. граничных условиях.
Вернемся к двумерному уравнению. Теперь на первом этапе будем находить
потоки 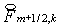 и и 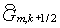 не из «грубых»
уравнений (2.7), а из интерполяционных соотношений для не из «грубых»
уравнений (2.7), а из интерполяционных соотношений для 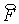 и и 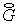 : :
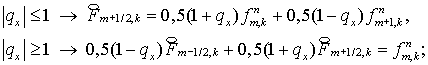
(5.6)
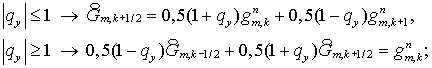
Или же в операторной форме
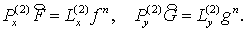 (5.7) (5.7)
Здесь верхний индекс указывает на порядок аппроксимации схемы. Для
упрощения последующих формул перепишем (5.6) в виде
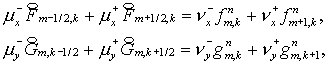 (5.8) (5.8)
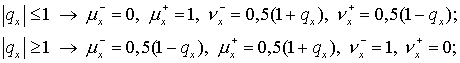
(5.9) 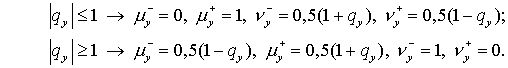
То есть, операторы  и и 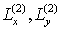 задаются левыми и правыми частями (5.8) . задаются левыми и правыми частями (5.8) .
Второй этап данной схемы аналогичен второму этапу базовой схемы первого
порядка. А именно, 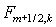 и и 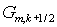 находятся из
разностных уравнений, аппроксимирующих систему (4.7), где «чужие»
производные находятся из
разностных уравнений, аппроксимирующих систему (4.7), где «чужие»
производные 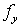 и и 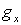 вычисляются по
значениям вычисляются по
значениям 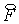 и и 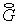 , полученным на первом этапе. Но в базовой схеме, см. (4.9),
второй этап, фактически, является повторением первого с заменой , полученным на первом этапе. Но в базовой схеме, см. (4.9),
второй этап, фактически, является повторением первого с заменой 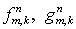 на на
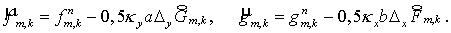 (
5.10) (
5.10)
Теперь же 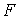 и и 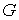 находятся из
уравнений находятся из
уравнений
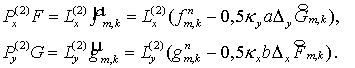 (5.11) (5.11)
Другими словами, вначале вычисляются 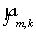 и и 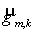 , а затем находятся , а затем находятся и и  из одномерных систем
разностных уравнений: из одномерных систем
разностных уравнений:
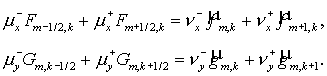 (5.12) (5.12)
Таким образом, речь идет о решении тех же уравнений первого этапа, но с
другими правыми частями. Переход на верхний слой завершается дивергентным
замыканием.
Анализ устойчивости производится
знакомым способом. А именно, последовательно определяются 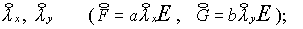 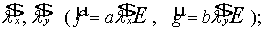 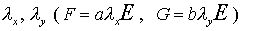 и, наконец, и, наконец, 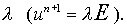 В результате имеем В результате имеем
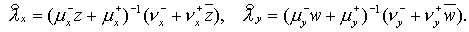
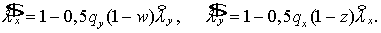

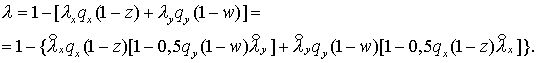
Перейдем от 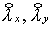 к к 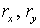 (по (2.12)): (по (2.12)):
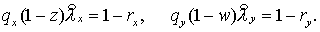
Получим, как и для базовой схемы первого порядка, 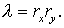 Теперь аналогом Леммы
1 является Теперь аналогом Леммы
1 является
Лемма 2
Пусть 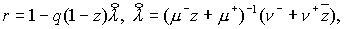 где где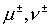 см. (5.9), а см. (5.9), а 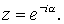 Тогда для всех Тогда для всех 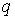 и и 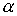 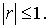
Доказательство 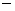 проверка обоих
случаев проверка обоих
случаев 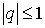 и и 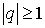 . .
Применив Лемму 2 к 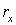 и и 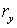 , получим требуемое неравенство , получим требуемое неравенство 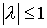  необходимое условие
устойчивости. необходимое условие
устойчивости.
Для проверки второго порядка аппроксимации разложим 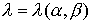 по степеням по степеням 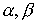 . Начнем с . Начнем с 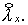
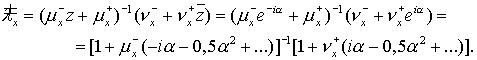 (5.13) (5.13)
(Здесь использованы тождества 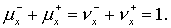 ) )
Так как 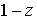 = =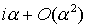 , то для отыскания необходимых членов разложения достаточно
ограничиться в , то для отыскания необходимых членов разложения достаточно
ограничиться в 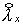 лишь линейным
приближением: лишь линейным
приближением: 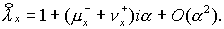 Но Но 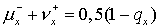 вне зависимости от
величины вне зависимости от
величины 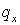 . Поэтому для . Поэтому для 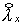 (и аналогично для (и аналогично для 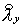 ) имеем ) имеем 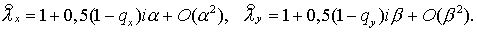 Отсюда Отсюда 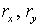 получаем получаем 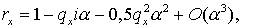 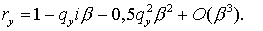
И, наконец, в квадратичном приближении
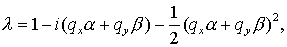 (5.14) (5.14)
что совпадает с соответствующим приближением для точного множителя
перехода 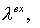 см. (2.16). Это и доказывает второй порядок аппроксимации. см. (2.16). Это и доказывает второй порядок аппроксимации.
Обобщение схемы на случай гиперболической системы очевидно и
использует конструкции и
обозначения схем первого порядка.
Этап 1
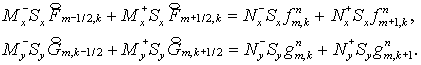 (5.15) (5.15)
Здесь 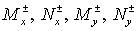 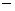 диагональные матрицы
с элементами диагональные матрицы
с элементами 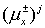 , , 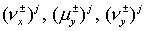 , определенными по (5.9) для каждого , определенными по (5.9) для каждого 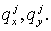
Этап 2 отличается от этапа 1 заменой 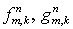 на на 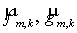 , см. (5.10). , см. (5.10).
Доказательство устойчивости 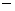 тоже только для
симметрических матриц тоже только для
симметрических матриц 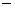 отличается от анализа
соответствующей базовой схемы лишь видом матриц отличается от анализа
соответствующей базовой схемы лишь видом матриц 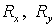 . Теперь . Теперь
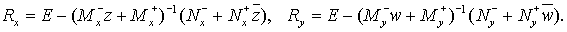
Повторяя знакомые выкладки, получим
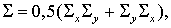 где снова где снова 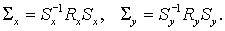 В силу Леммы 2 каждый
диагональный элемент матриц В силу Леммы 2 каждый
диагональный элемент матриц 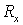 и и 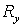 лежит в единичном
круге. Поскольку матрицы лежит в единичном
круге. Поскольку матрицы 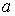 и и 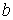 симметрические, то в
качестве симметрические, то в
качестве 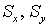 можно выбрать
ортогональные матрицы. Следовательно, можно выбрать
ортогональные матрицы. Следовательно, 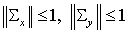 , что и дает необходимое условие устойчивости , что и дает необходимое условие устойчивости 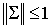 . .
6. Базовая
локально-неявная схема второго порядка
Предыдущий параграф был посвящен центрально-симметрической схеме
второго порядка. Несложно видеть, что ее чисто явная реализация использует
девятиточечный шаблон, не являющийся минимальным. Как уже говорилось, это
обстоятельство создает некоторые проблемы вблизи границ и может порождать, что
более неприятно, нежелательные осцилляции. Как известно, 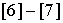 , минимальный шаблон схемы второго порядка для скалярного
двумерного уравнения состоит из шести
точек. В зависимости оз знаков коэффициентов , минимальный шаблон схемы второго порядка для скалярного
двумерного уравнения состоит из шести
точек. В зависимости оз знаков коэффициентов  и и  он должен содержать
один из базовых прямоугольников, показанных на Рис. 2. Другими словами,
соответствующая разностная схема может рассматриваться как надстройка над
базовой схемой первого порядка. он должен содержать
один из базовых прямоугольников, показанных на Рис. 2. Другими словами,
соответствующая разностная схема может рассматриваться как надстройка над
базовой схемой первого порядка.
Для реализации принципа минимального шаблона применительно к схемам
второго порядка, являющимся элементами
локально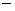 неявной схемы, достаточно лишь несколько видоизменить второй
этап в предыдущей центрально-симметрической схеме. Теперь он будет выглядеть
так: неявной схемы, достаточно лишь несколько видоизменить второй
этап в предыдущей центрально-симметрической схеме. Теперь он будет выглядеть
так:
Этап 2
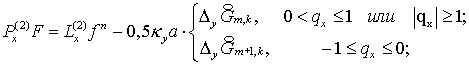
(6.1)
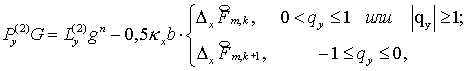
где 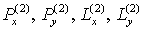  уже известные
операторы, см. (5.7) уже известные
операторы, см. (5.7) (5.9). (5.9).
Другими словами, «ножки» 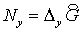 и и 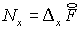 в явной схеме
вычисляются «против потока», см. Рис. 3 для в явной схеме
вычисляются «против потока», см. Рис. 3 для 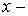 направления направления
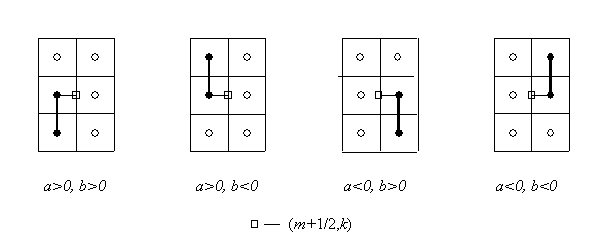
Рис. 3.
Соответствующие уравнения имеют вид
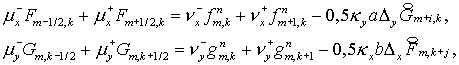 (6.2) (6.2)
где 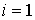 только если только если 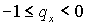 , а , а 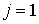 лишь при лишь при 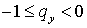 . .
Таким образом, данная схема отличается от предыдущей тем, что в
центрально-симметрической схеме операторы 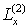 и и 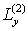 действовали на всю
правую часть действовали на всю
правую часть  и и  , а теперь , а теперь  только на только на 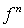 и и 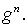
Переход к гиперболических системам выполняется стандартным путем. Для
правильного учета точки вычисления «ножек» необходимо выделить из матриц 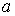 и и 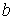 «минус «минус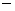 явные» (отвечающие числам Куранта, лежащим на явные» (отвечающие числам Куранта, лежащим на 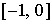 . Имеем . Имеем
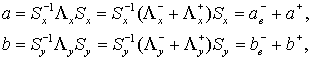 (6.3) (6.3)
где 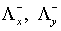 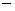 диагональные матрицы,
содержащие лишь те диагональные матрицы,
содержащие лишь те 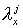 и и 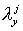 , для которых соответствующие числа Куранта , для которых соответствующие числа Куранта 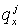 и и 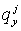 принадлежат принадлежат 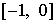 . Для . Для 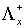 и и 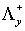 , следовательно, либо , следовательно, либо 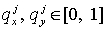 , либо , либо  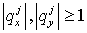 . .
Теперь ясно, что векторный аналог (6.3) должен иметь вид (ср. с (5.15))
 (6.4)
(6.4)
В отличие от всех предыдущих схем, представленных в данной работе, где
оператор перехода на верхний слой разлагался на одномерные, здесь его структура
существенно двумерна. Это обстоятельство осложняет как проверку порядка
аппроксимации, так и исследование устойчивости. Для скалярного уравнения число
различных случаев не слишком велико ( десять вариантов ) и полный анализ можно осуществить путем
перебора, хотя и здесь некоторые варианты технически довольно сложны.
В качестве примера докажем устойчивость полностью явной схемы для
случая положительных коэффициентов 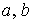 , то есть при , то есть при 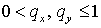 . Имеем . Имеем
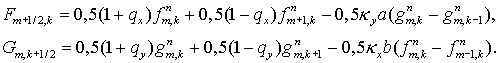
Отсюда получаем, используя стандартные обозначения
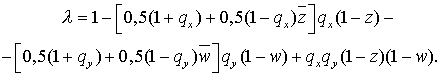 (6.5)
(6.5)
Перепишем (6.5) в виде
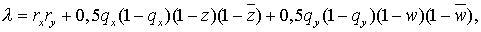
где, как и прежде, 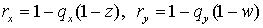 . Легко видеть, что . Легко видеть, что
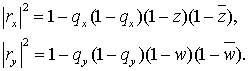
Таким образом, 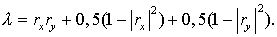 Так как Так как 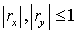 ( по Лемме 1 ),
то ( по Лемме 1 ),
то 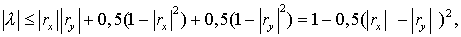 что и дает требуемое
неравенство что и дает требуемое
неравенство 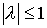 . .
Более просто проверяемым необходимым условием устойчивости является
выполнение неравенства  только для
высокочастотных мод, точнее, для только для
высокочастотных мод, точнее, для 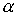 и и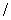 или или 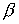 , равных , равных 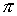 , что эквивалентно , что эквивалентно 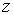 и и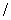 или или 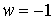 . Для примера рассмотрим полностью неявную схему с положительными . Для примера рассмотрим полностью неявную схему с положительными 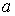 и и 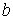 , то есть для случая , то есть для случая 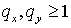 . Для этой схемы этап 1 имеет вид: . Для этой схемы этап 1 имеет вид:
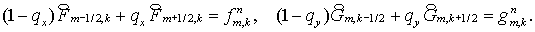
Для 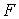 и и 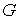 имеем ( этап 2 ): имеем ( этап 2 ):
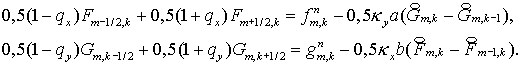
Отсюда ( см. п.2 и п.5 )
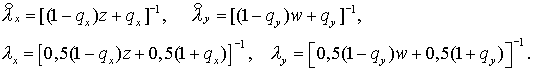
Дивергентное замыкание дает 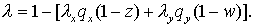 Теперь возьмем Теперь возьмем 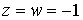 . Тогда . Тогда 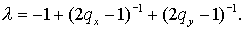 Искомое условие
устойчивости следует из неравенств Искомое условие
устойчивости следует из неравенств 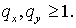
Другие комбинации знаков и величин 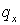 и и 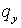 анализируются
аналогичным образом. анализируются
аналогичным образом.
Осталось рассмотреть вопрос об устойчивости схемы применительно к
гиперболическим симметрическим
системам. Начнем с полностью явного случая: все 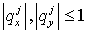 . Тогда система разностных уравнений (6.5) принимает вид: . Тогда система разностных уравнений (6.5) принимает вид:
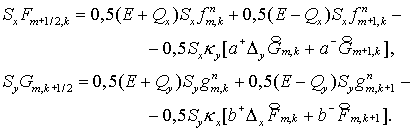 (6.6)
(6.6)
Здесь 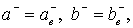 а а
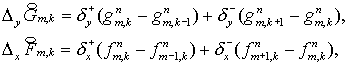
где 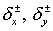 равны равны  , соответственно. Эти формулам можно придать более простой
вид: , соответственно. Эти формулам можно придать более простой
вид:
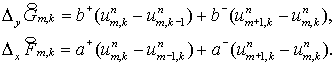
Введем обозачения 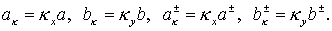 Тогда для Тогда для 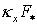 и и 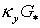 получим (ср. с
базовой схемой, п.4 ) получим (ср. с
базовой схемой, п.4 )
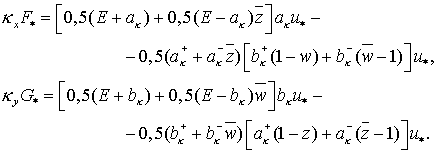 (6.7) (6.7)
Отсюда
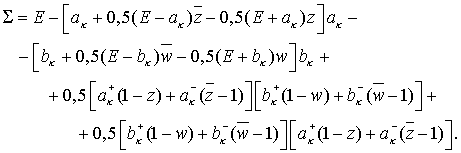 (6.8) (6.8)
Положим 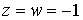 . Тогда . Тогда
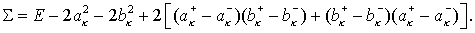
Но 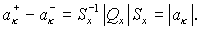 Аналогично, Аналогично, 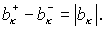 Поэтому Поэтому
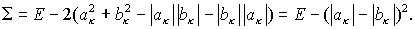 (6.9)
(6.9)
Для дальнейшего понадобится
Лемма 3
Пусть 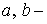 симметрические
матрицы, собственные числа которых положительны и не превосходят единицы.
Тогда симметрические
матрицы, собственные числа которых положительны и не превосходят единицы.
Тогда 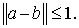
Доказательство:
Для произвольного вектора 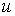 имеем две пары
неравенств имеем две пары
неравенств
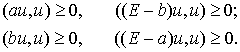
Суммируя неравенства каждой
пары, получаем

Следовательно,
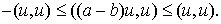
Выбрав в качестве 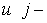 й собственный вектор й собственный вектор 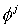 симметрической
матрицы симметрической
матрицы 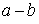 , получим , получим 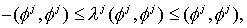 где где 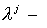 соответствующее
собственное значение. Следовательно, соответствующее
собственное значение. Следовательно, 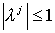 и, значит, и, значит, 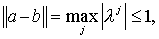 что и завершает
доказательство. что и завершает
доказательство.
Вернемся к анализу устойчивости и обозначим через 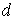 разность разность 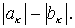 Тогда ( см. (6.9) ) Тогда ( см. (6.9) ) 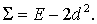 Поскольку Поскольку 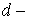 симметрическая
матрица, то оценка симметрическая
матрица, то оценка 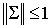 эквивалентна
неравенству эквивалентна
неравенству 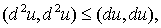 справедливому для
любого справедливому для
любого  . В силу Леммы 3 . В силу Леммы 3 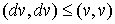 для любого для любого 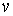 . Полагая . Полагая 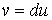 , получим требуемое неравенство , получим требуемое неравенство 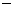 условие устойчивости. условие устойчивости.
В качестве последнего примера рассмотрим полностью неявный
«положительный» случай 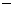 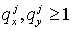 . Тогда . Тогда 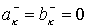 , а , а 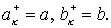 Для Для 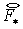 и и 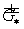 имеем имеем 
Второй этап дает
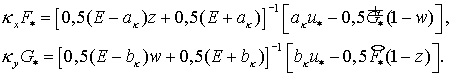
Окончательно, 
Положив 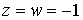 , получим , получим
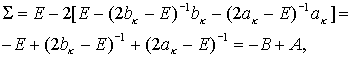
где  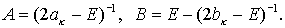
Так как собственные значения симметических матриц 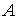 и и 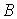 лежат на лежат на 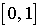 , то по Лемме 3 , то по Лемме 3 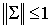 , что и требовалось доказать. , что и требовалось доказать.
Заметим, что хотя необходимые условия устойчивости доказаны лишь в
слабой форме (для высокочастотных мод), численная проверка подтвердила
справедливость неравенства 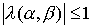 для всех для всех 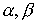 . Что касается систем, то и здесь все преведенные численные
эксперименты продемонстрировали устойчивость базовой схемы второго порядка. . Что касается систем, то и здесь все преведенные численные
эксперименты продемонстрировали устойчивость базовой схемы второго порядка.
Последний вопрос возможная немонотонность разностного решения, присущая любым
линейным схемам второго порядка. Способы ее подавления ( минимизации )
известны. Применительно к данной схеме для этого надлежит возможная немонотонность разностного решения, присущая любым
линейным схемам второго порядка. Способы ее подавления ( минимизации )
известны. Применительно к данной схеме для этого надлежит  в «явной» реализации в «явной» реализации  заменить
интерполяционную процедуру вычисления заменить
интерполяционную процедуру вычисления 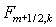 ( или ( или 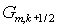 ) на экстраполяцию по
ближайшей паре точек в соответствии, например, с принципом минимальной
производной (оператор minmod ) или другим
родственным ограничителем ( limiter ). ) на экстраполяцию по
ближайшей паре точек в соответствии, например, с принципом минимальной
производной (оператор minmod ) или другим
родственным ограничителем ( limiter ).
В заключение еще раз отметим основные особенности всех схем,
представленных в данной работе:
(1). Переход на верхний слой осуществляется на основе МНП редукцией к
одномерным задачам 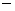 экономичность; экономичность;
(2). Базовая схема второго порядка обладает ( в явной реализации )
минимальным шаблоном;
(3). Каждая одномерная разностная задача имеет локально-неявную
структуру, то есть ее «неявные» элементы включаются (автоматически и гладко )
минимальным образом 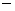 только там, где соответствующее число Куранта начинает
превышать единицу. Причем это включение производится не для всех уравнений, а
лишь для «неявных» инвариантов. Основная формально трехточечная система
одномерных разностных уравнений имеет достаточно простой вид и хорошо
приспособлена для решения с помощью обычной прогонки. только там, где соответствующее число Куранта начинает
превышать единицу. Причем это включение производится не для всех уравнений, а
лишь для «неявных» инвариантов. Основная формально трехточечная система
одномерных разностных уравнений имеет достаточно простой вид и хорошо
приспособлена для решения с помощью обычной прогонки.
И, наконец, последнее замечание. При решении конкретных задач может
возникнуть ситуация, когда из тех или иных соображений по одному фиксированному
направлению желательно использовать полностью явную схему. Реализация такого
требования легко осуществляется  просто за счет
соответствующего ограничения на временной шаг. Это обстоятельство можно учесть
заранее , что приведет к естественному уменьшению объема вычислений и упрощению алгоритма. просто за счет
соответствующего ограничения на временной шаг. Это обстоятельство можно учесть
заранее , что приведет к естественному уменьшению объема вычислений и упрощению алгоритма.
В заключение считаю приятным долгом поблагодарить Н. А. Зайцева за
полезные советы и помощь.
Литература
1. С.
К. Годунов. «Разностный метод численного расчета разрывных решений уравнений
гидродинамики.» //Матем. сборник, 1959, 3, стр. 271-306.
2. С. К.
Годунов, А. В. Забродин, М. Я. Иванов, А. Н. Крайко, Г.П. Прокопов. «Численное
решение многомерных задач газовой динамики.»
// Москва, «Наука», 1976, 400 стр.
3. A. Harten. “High Resolution Schemes for Hyperbolic
Conservation Laws.” // Journal of Comp. Phys., 49 (1983 ), pp. 357 – 393.
4. В. П.
Колган. «Применение принципа минимальных значений производной к построению
конечно-разностных схем для расчета разрывных решений газовой динамики.» //
Ученые записки ЦАГИ, 3, № 6, стр. 68-77.
5. P. L. Roe. «Approximate Riemann solvers,
parameter vectors, and difference schemes.» //J. of Comp. Phys.,43, (1981), pp.
357-372.
6. Ю. Б.
Радвогин. «Квазимонотонные многомерные разностные схемы второго порядка.»
//Препринт Инст. прикл. матем. им. М. В. Келдыша АН СССР, 1991, № 19, стр.
1-30.
7. Yu. B. Radvogin, N. A. Zaitsev.
«Multidimensional minimal stencil
supported second order accurate upwind schemes for solving hyperbolic and Euler
systems.» //Препринт Инст.
прикл. матем. им. М.
В. Келдыша РАН , 1996, № 22, стр. 1-32.
8. Ю. Б.
Радвогин. «Экономичные алгоритмы численного решения многомерного уравнения
теплопроводности.»// ДАН, 2003, т. 388, № 3, стр. 1-3.
9. А.И.Жуков.«Предельная
теорема для разностных операторов.» Успехи мат. наук, 1959, т. 4, № 5, стр.
129-136.
10. К.
И. Бабенко, Г. П. Воскресенский. «Численный метод расчета пространственного
обтекания тел сверхзвуковым потоком газа.»// ЖВМ и МФ, 1961, 1, № 6, стр.
1051-1060.
11. К.
И. Бабенко, Г. П. Воскресенский, А. Н.
Любимов, В.В.Русанов. «Пространственное обтекание гладких тел идеальным газом.» // Москва, «Наука», 1964,
505 стр.
|