ОГЛАВЛЕНИЕ

1.Введение

В современную медицинскую практику все шире входят приборы длительного непрерывного наблюдения за состоянием организма. Они позволяют концентрировать гораздо более точную и адекватную информацию о течении процессов в жизненно важных системах организма, чем обычные методы наблюдения «в отдельные моменты». Систематический характер собранной информации позволяет уменьшить влияние случайных помех за счет знания о возможном характере процессов в организме. С другой стороны, выделение «истинной» части сигнала важно, особенно для автоматических аппаратов, самостоятельно принимающих решения о выработке сигналов опасности.

Предлагаемая работа является частью исследования, имеющего целью разработку алгоритмов автоматического анализа суточных записей артериального давления и частоты пульса больных акушерской клиники. В этой работе сделана попытка моделирования «врачебных» методов отсеивания ошибочных наблюдений.

Первый шаг сделан на основе прямых ответов врача на вопрос «какие измерения он считает ошибочными?». Ответы врача не были ни категорическими, ни исчерпывающими. По этой причине были испытаны различные варианты алгоритмов, не противоречащие требованиям врача.

Отработка алгоритмов производилась на модели постановки диагноза «тяжелый гестоз» у беременных, прошедших обследование в Московском областном научно-исследовательском институте акушерства и гинекологии (МОНИИАГ). Гестозом принято называть патологическое состояние беременных, связанное с определенными клиническими проявлениями, и обычно сопровождаемое повышением артериального давления, наличием белка в моче и отеками. Тяжелый гестоз приводит к гибели плода или заметному отставанию в развитиии. Для женщины гестоз опасен возможной эклампсией (нарушение мозгового кровообращения, приводящее часто к гибели женщины).

Гестоз является одним из часто встречающихся осложнений беременности. В настоящее время он выявляется у 10-25% всех беременных, и этот показатель не имеет тенденции к снижению. В структуре причин материнской смертности в настоящее время гестозы занимают одно из первых мест [1].

В начале прошлого века В. Цангемейстер (1913 г.) описал классическую триаду симптомов, характерных для гестоза (гипертензия, отёки, протеинурия). Артериальной гипертензией называют повышение артериального давления, протеинурией - наличие белка в моче. Возможен неполный комплект признаков гестоза у больной. Наблюдаются формы без протеинурии или без отеков, бывают также односимптомные варианты.

Особенность течения гестоза состоит в том, что он развивается медленно, без ярко выраженных симптомов начала. Обострение его, напротив, скоротечно, ярко выражено, например, эклампсия (осложнение гестоза, судорожный припадок или серия припадков, длится несколько минут с потерей сознания, возможна остановка дыхания), и приводит к тяжёлым последствиям. Осложнения гестоза угрожают жизни женщины и плода.

В подавляющем большинстве случаев летальный исход объясняется недооценкой тяжести состояния беременной, приводящей к несвоевременной госпитализации, недостаточному объёму лечения, неправильному выбору тактики ведения беременности и родоразрешения [7]. Например, в Великобритании 38% случаев эклампсии регистрируются у женщин, которым диагноз гестоза не ставился [8].

Точность и своевременность диагностики гестоза оказывается недостижимой при использовании обычных эпизодических измерений артериального давления. В настоящей работе рассмотрен вопрос об использовании результатов суточной автоматической регистрации артериального давления и частоты пульса для обнаружения ранних признаков начинающегося гестоза.

2. Измерение артериального давления

Кровь в сосудах кровеносной системы человека находится под избыточным давлением относительно атмосферы. Величина этого давления различна в разных сосудах  и непостоянна во времени. По мере продвижения по большому кругу кровообращения от аортального (выходного) клапана сердца по артериям уменьшающегося калибра и далее по венам до впадения в правое предсердие давление систематически понижается от максимального (порядка 100-150 мм.рт.ст.) до практически нулевого. При этом, в соответствии с сокращениями сердца, давление пульсирует от максимального (систолического) до минимального (диастолического). Наибольшие величины этих давлений можно наблюдать в аорте, рядом с сердцем. Практически давление принято измерять на крупных артериях, где оно отличается от аортального лишь незначительно.

Для измерения артериального давления обычно применяется неинвазивный метод, т.е. датчик измерительного прибора не вводится внутрь кровеносного сосуда, а давление оценивается путём определённых манипуляций вне организма.

Традиционный метод измерения АД основан на обнаруженных в 1905 году русским врачом Коротковым звуковых явлениях, возникающих при декомпрессии плечевой артерии. Сначала, повышая давление воздуха в манжетке, пережимают сосуд, прекращая тем самым кровоток. При медленном снижении давления в манжетке возникают шумы (тоны Короткова), которые можно прослушать ниже места сжатия. Считается, что более высокое давление в манжетке, при котором появляются шумы, соответствует систолическому давлению в сосуде, а более низкое, при котором шумы пропадают – диастолическому.

Процедура измерения артериального давления используется в медицине уже около 100 лет и является рутинной. Тем не менее, результат её зависит от очень многих факторов, например, от стрессовой реакции пациентки на саму процедуру измерения. Вообще, артериальное давление чутко реагирует на изменение многих параметров состояния организма. Поэтому при эпизодическом измерении нередко регистрируются показатели, весьма далёкие от характерных для данной больной.

 В последние годы в кардиологической практике используется метод суточного мониторирования, заключающийся в том, что в течение 24-28 ч. у пациента осуществляется периодическое измерение артериального давления и частоты пульса при помощи носимого пациентом портативного аппарата (монитора давления и частоты пульса). В ходе суточного мониторирования артериального давления и частоты пульса эти параметры измеряются многократно (более 60-80 раз за сутки, в том числе и ночью).

В используемом нами методе датчик прибора измеряет давление в манжетке, но вместо акустических шумов он регистрирует осцилляции давления, возникающие в сосуде под действием давления воздуха в манжетке. Кровеносный сосуд представляет собой труднорастяжимую гибкую трубку, т.е. скорее напоминает пожарный рукав, чем резиновый шланг. Когда сосуд пережат, потока крови нет, нет и осцилляций. Начинаем снижать давление в манжетке. С какого-то момента кровь начинает впрыскиваться дискретными порциями в те интервалы, когда давление в сосуде превышает давление в манжетке. Появляются осцилляции. Считается, что в этот момент измеряемое давление соответствует систолическому давлению в сосуде. Снижаем давление в манжетке дальше. Пульсации происходят за счёт дозаполнения, пока стенка сосуда не до конца растянута. Наконец, когда сосуд заполнен, он становится слишком жёстким, чтобы реагировать на пульсовые перепады давления. Осцилляции пропадают. Считается, что в этот момент измеряемое давление соответствует диастолическому. Возвращаясь к тонам Короткова, можно отметить, что звук появляется, когда течение крови в сосуде вихревое, т.е. также при частичном заполнении сосуда кровью.

В исследовании были использованы аппараты фирмы “Meditech” модели ABPM-02 и ABPM-02o. Прибор может делать измерения как в автоматическом режиме, так и в ручном. Он программируется заранее на заданное время мониторирования. Программа может быть достаточно гибкой, например, может содержать задание различной частоты измерений в дневное и ночное время. Обычно выбирают интервал между измерениями, равный 15-ти минутам днём и 30-ти ночью. Всегда остается возможность делать дополнительные измерения в ручном режиме, например, если ситуация волнует врача или пациентку.

Данные, полученные в ходе мониторирования, накапливаются в памяти прибора. По окончании измерений их переносят в базу данных ABPMBASE, обслуживающую аппарат. Для дальнейшей обработки их экспортируют в базу формата dBASE.

На рис.1 представлены два примера диаграммы, получающейся после обработки программой ABPMBASE результатов суточного мониторирования двух пациенток (Num=107 и Num=160). По оси абсцисс – время суток (часы), по оси ординат – систолическое и диастолическое давление (мм. рт. ст.) и частота пульса (уд/мин). Шкалы общие, поскольку диапазоны изменения всех трех величин совпадают. Пунктирная линия – ЧСС (частота сердечных сокращений), вертикальные столбики – артериальное давление (нижний конец столбика представляет нижнее (диастолическое) давление, а верхний – верхнее (систолическое) давление). Кружками отмечены внеплановые измерения. Приподнятая горизонтальная пунктирная линия соответствует дневному времени, сниженная – ночному.

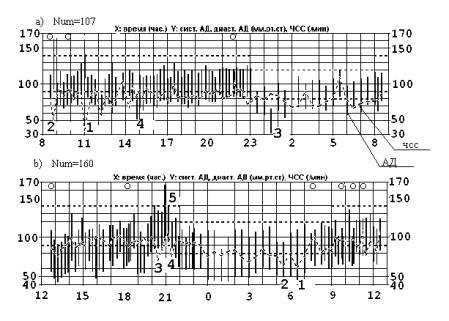
Рис.1. Примеры записей

Ночные и дневные измерения маркировались согласно дневнику самонаблюдения беременной. Интервал между последовательными измерениями ночью больше, чем днем.

 По этим диаграммам можно заметить, что в ночное время величины давлений и частота пульса могут понижаться. Обычно это благоприятный признак. Кроме того, зарегистрированы кратковременные урежения пульса в моменты времени, отмеченные числами «1» и «2», резкие кратковременные падения давления, отмеченные числами «3» и «4» на верхней диаграмме и однократный подъем «5» на нижней диаграмме. С точки зрения врача эти «неправильные» значения не характеризуют состояние организма, и их не следует принимать во внимание при автоматическом анализе. Наша цель состоит в том, чтобы, по возможности исключить «неправильные» точки на предварительном этапе, до начала содержательного анализа наблюдений.

3. Цель работы

Наша задача является частью медицинского исследования, предпринятого с целью найти особенности суточной записи давления и пульса больной, сопутствующие гестозу тяжелой степени. Диагноз гестоза тяжелой степени выбран потому, что его врач ставит достаточно уверенно, даже при воздействии многих искажающих факторов. Найденные признаки можно использовать для выявления ухудшений состояния системы кровообращения, предшествующих этому патологическому состоянию. Тем самым, мы можем пытаться выработать  предупреждение, полезное и врачу.

Наша конечная цель - построить формальное решающее правило, выделяющее признаки ухудшения состояния системы кровообращения на основании анализа одних только данных о суточной динамике артериального давления и пульса.

Воспользуемся традиционным методом [2, 6] построения решающего правила. Возьмем несколько больных (обучающая выборка), отнесенных врачом с достаточной уверенностью к опасному классу, и несколько – к благополучному. Сравнивая между собой значения параметров описания состояния больных этих классов, найдем объективные различия между ними.

В этой работе мы ограничиваемся задачей построения алгоритмов, которые позволят избавиться от неправильных с точки зрения врача измерений. Мы рассмотрим и сравним между собой несколько вариантов таких алгоритмов.

4. Фильтры

Процедуру отделения приемлемых измерений от остальных будем называть фильтром.

Сигнал часто сопровождается разнообразными помехами. Например, апряжение мышцы может исказить результат при измерении артериального давления за счет дополнительной жесткости тканей, окружающих сосуд. Эти ткани принимают на себя часть давления, создаваемого манжеткой, поэтому прибор может зарегистрировать давление, выше истинного. Удары по манжетке имитируют пульсации и также приводят к искажениям, вызывая регистрацию давления вне связи с кровотоком в сосуде.

На рис.1a приведен пример реальной записи. Видно, что давление и пульс в основном изменяются согласованно, т.е. большему значению частоты пульса соответствуют большие значения артериального давления (систолического и диастолического), а меньшим значениям частоты пульса - меньшие. Однако есть измерения, в которых эта согласованность нарушается. Причиной может быть ударная помеха. Например, видно, что точки, отмеченные цифрами ‘1’, ‘2’, ‘3’, выпадают из общей картины. Попробуем сконструировать простейший фильтр, который не пропустит их в дальнейшую обработку. Не будем пока проводить сравнение с соседними точками, от которых выбранная точка может сильно отличаться, тем не менее укладываясь в общую картину (например, точка ‘4’ на рис.1a). Далее мы построим несколько конструкций фильтров, пропускающих на обработку измерения с согласованными значениями переменных.

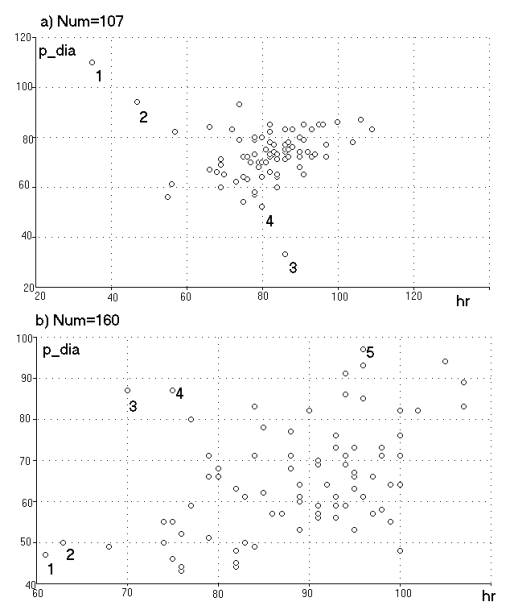
Рис.2. Диаграммы рассеяния для записей рис.1

На рис. 2 приведены диаграммы рассеяния для записей рис.1. По оси абсцисс отложены значения частоты пульса (hr), а по оси ординат – диастолического давления (p_dia). Каждой точке на плоскости hr, p_dia соответствует одно измерение из записи на рис.1 (такую диаграмму мы и будем называть диаграммой рассеяния). Числовые метки для точек те же, что и на рис.1. Точки диаграммы рассеяния образуют сравнительно плотное облако. Несколько точек отстоят от воображаемого центра облака достаточно далеко, и это именно те точки, которые вызвали замечания врача на исходной диаграмме (точки ‘1’, ‘2’, ‘3’ на рис.1a и рис.2a).

Это наблюдение наводит на мысль строить фильтр, как замкнутый непрерывный контур на плоскости hr, p_dia, окружающий плотное облако «хороших» точек и отделяющий далеко отстоящие от него «плохие» точки. Рассмотрим несколько вариантов аппроксимации этого контура.

4.1. «Коридоры»

Проще всего строить разделяющий контур независимо по координатам. Определив отдельно для каждой переменной допустимые интервалы, мы получаем на плоскости hr, p_dia граничные линии для каждой из переменных. Пересечение этих границ даёт прямоугольник со сторонами, параллельными координатным осям.

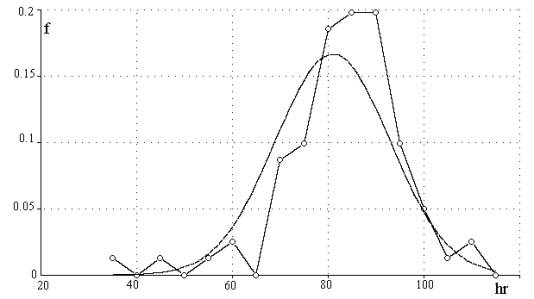
Рис. 3. Гистограмма плотности распределения hr

Для практического применения остаётся решить вопрос о положении границ допустимого интервала по каждой координате. Рассмотрим распределение точек в проекции на соответствующую координату. На рис. 3 представлена гистограмма распределения по частоте пульса, по оси абсцисс – частота пульса, по оси ординат – доля измерений от общего числа измерений.

Максимум кривой занимает небольшую область с высокой плотностью точек, вне которой лежат «хвосты», содержащие малую часть измерений. Для описания произвольного распределения случайной величины удобно использовать границы, отсекающие определенную долю наблюдений. Эти границы называют квантилями [5]. Пусть задана произвольная функция распределения F(x) случайной величины X. Тогда величина m_x есть x-квантиль распределения F(x), если она является решением уравнения

 .                                                   (1)

Тем самым, если выбрать положение границ так, чтобы были отсечены только хвосты распределения с заданными квантильными уровнями x и 1-x, мы получим простейший однокоординатный фильтр.

Техническая трудность этого метода состоит в том, что именно в хвостах реальные эмпирические распределения содержат мало точек, и их локальная структура там оказывается очень грубой. Поэтому будем аппроксимировать эмпирическую функцию распределения подходящей стандартной функцией распределения. Приблизительная симметрия по каждой переменной позволяет взять в качестве аппроксимирующего распределения нормальное:

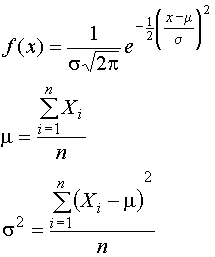                                     (2)

Здесь m - среднее, а s - стандартное отклонение, n – объём выборки. Для оценки среднего и стандартного отклонения будем использовать E и s:

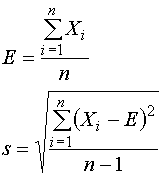                                                (3)

E называется выборочным средним, а s – выборочным стандартным отклонением. Для приведенной кривой (рис.3.) E = 81, s = 12. Аппроксимирующая нормальная кривая дана на рис.3 в виде гладкой сплошной линии.

Выберем квантильный уровень отбрасывания крайних точек равным 0.01, тогда в левом «хвосте» окажется 2 точки, а в правом  0 точек.

Рассмотрим результаты применения двумерного варианта этого фильтра (рис. 4).

На рисунке показаны опять те же диаграммы рассеяния (рис.2) и контур прямоугольника фильтра. По оси абсцисс – частота пульса, по оси ординат – диастолическое давление. Кружочки – оставленные точки, квадратики – отброшенные. Выбранная квантильная доля обозначена буквой p. Параметры аппроксимирующих нормальных распределений: рис. 4a - для hr (E=81, s=12), а для p_dia (E = 73, s = 10); рис. 4b - для hr (E = 89, s = 10), а для p_dia (E = 65, s= 13).

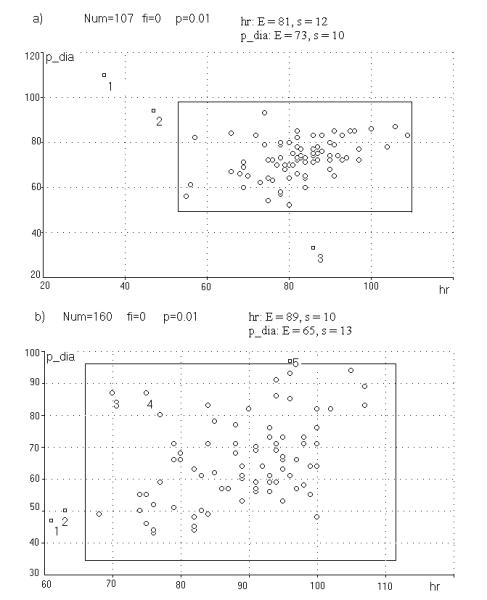
Рис.4. Пример прямоугольного фильтра

Заметим, что на рис. 4b точки ‘3’ и ‘4’, хотя они и удовлетворяют условиям пропускания выбранного фильтра, «на глаз» кажутся более далёкими, чем точки ‘2’ и ‘5’ этим условиям не удовлетворяющие. Это, видимо, связано с тем, что точки облака преимущественно лежат «вдоль» диагонали прямоугольника, т.е. «облако» наклонено, а фильтр этот наклон не учитывает.

Попытаемся учесть этот наклон. Для этого воспользуемся координатными осями, повёрнутыми относительно исходных на некоторый угол j. Дальнейшие операции те же, что и при построении фильтра-«коридора», описанного выше. Угол наклона можно, например, выбрать из условия минимума s для одной из новых координат.

Для этого на плоскости hr, p_dia выберем некоторое направление, заданное осью x₁, на которое будем проектировать распределение. Пусть ось x₁ образует угол j с осью hr. Распределение точек в проекции на это направление аппроксимируем нормальным распределением с параметрами (E_j, s_j).

Повторяем процедуру для углов j от 0⁰ до 180⁰, например, для дискретного набора углов j_i (i=1, … 18) с шагом 10⁰. Выбираем угол j, для которого s_j минимально. Считаем его углом наклона одной из осей «коридора»-прямоугольника. Дополняем это направление перпендикулярным. Отсекая «хвосты» проекций распределений на эти оси с заданными квантильными долями, получим наклонный фильтр-«коридор». В таб.1 приведены последовательные значения угла и ширины распределения. Буквы a) и b) соответствуют результатам суточного мониторинга двух пациенток.

Табл.1

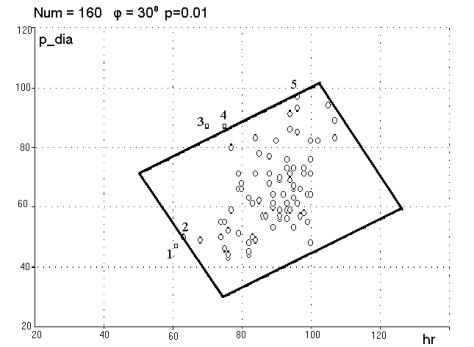
Рис.5. Наклонный «коридор»

Мы видим, что в случае a) минимум s достигается при j=90º, т.е. «коридор» остаётся неповёрнутым, со сторонами, параллельными осям hr и p_dia. А в случае b) s достигает минимума при j=150º, т.е. “коридор» поворачивается на 30º. При этом получаем узкое распределение с параметрами (E = 12.3,  s = 10.3), а широкое с параметрами (E = 109, s = 13). Результат действия такого фильтра приведён на рис.5.

По оси абсцисс – частота пульса, по оси ординат – диастолическое давление. Кружки – оставленные точки, квадратики – отброшенные. Выбранная квантильная доля обозначена буквой p.

Видно, что результаты оказались лучше, чем при использовании «коридора» без учёта наклона, например, точка ‘5’ (и точка ‘2’)   не отброшены, зато оказались отброшенными ‘3’ и ‘4’. Но вспомним случай a), для которого угол наклона «коридора» остался нулевым. Для него  точки, расположенные вблизи углов, по-прежнему попадают в разрешённую область. Т.е. фильтр имеет нежелательные «слепые зоны».

4.2. «Эллиптический» фильтр

Рассмотрим теперь более сложную двумерную модель, в которой контуром является эллипс. Мы видели, что «слепые зоны» располагаются в углах прямоугольника фильтра-«коридора». Эллиптический контур сглаживает углы прямоугольника, и мы ожидаем, что эллиптическая модель поможет решить проблему «слепых зон».

Положение эллипса задаётся координатами его центра и наклоном большой оси. Размеры эллипса определяются длинами большой и малой осей. Поместим центр эллипса в «медианную» точку, т.е. точку, координатами которой являются медианы распределений по соответствующим переменным (med(hr), med(p_dia)). При этом новые координаты точек можно записать в виде:

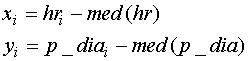                                     (4)

В такой системе координат эллипс задаётся параметрической формулой:

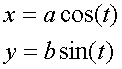                                                               (5)

Теперь перед нами стоит задача определить направление большой оси эллипса.

В полярных координатах эллипс задаётся формулой:

                              (6)

где j₀ – угол наклона большой оси эллипса, r и r₀ – константы, a = r₀ + r – длина большой полуоси эллипса, а b = r₀  - r  – длина малой полуоси эллипса. Рассмотрим модель «вращающегося» сектора. Сопоставим направлению j сектор S_ja, описывающий множество точек:

                                                (7)

с учётом тождественности углов, отличающихся на 360º, a – фиксированный угол, полуширина сектора.

Теперь будем поворачивать этот сектор, плавно меняя значение φ. Очевидно, что в направлении большой оси эллипса должны встретиться точки, более удалённые от центра, чем в перпендикулярном.

Разделим полный полярный угол 360° на ряд последовательных секторов одинаковой угловой ширины. Распределение точек в секторе по радиусу лучше всего задаёт функция распределения F(r). Но восстановление точного вида функции F(r) по ограниченному количеству точек - задача достаточно сложная. Поэтому рассмотрим эмпирические функции распределения точек по радиусу в секторах.

Эмпирической функцией распределения F(r) называется ступенчатая функция, определяемая равенством

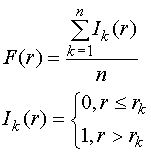                                               (8)

Если посмотреть на эмпирические распределения точек по радиусу в каждом из этих секторов, то становится видно, что в разных секторах они не совпадают. На рис.6 представлены такие распределения для нескольких направлений с угловой полушириной сектора S_ja a=20°. По оси абсцисс – полярная координата r, по оси ординат – значение эмпирической функции распределения.

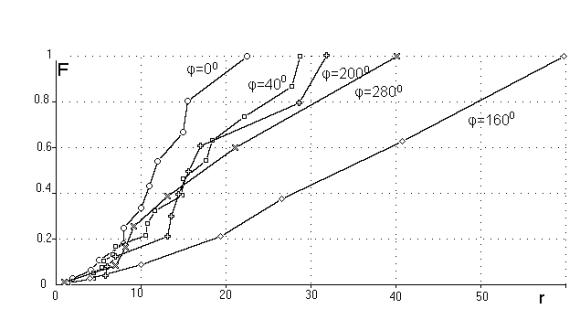
Рис.6. Эмпирические функции распределения точек по радиусу для секторов с разными осевыми направлениями

Если точки принадлежат эллипсу с равномерным заполнением, то линия, соединяющая одинаковые квантильные точки C_m(j) уровня m распределений по

радиусу в разных секторах будет синусоидой с периодом 180° по значениям осевого угла секторов.

                             (9)

Поэтому попытаемся и линию, соединяющую одинаковые квантильные точки эмпирических распределений в разных секторах, аппроксимировать синусоидой с периодом 180˚ по значениям осевого угла секторов. Точность аппроксимации можно увеличить, если взять только «хвосты» распределений в секторах (начиная с некоторого порогового квантильного значения).

Рис.7. Зависимость положения медианной точки от направления φ

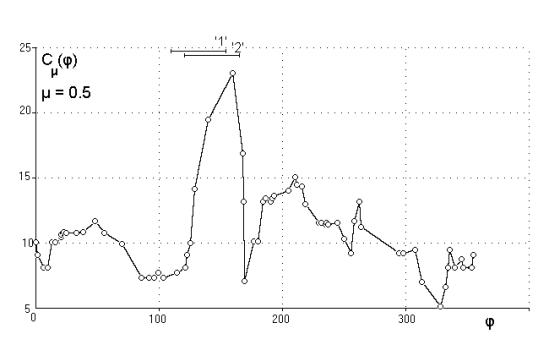
Будем поворачивать сектор S_ja, плавно меняя значение φ, и для каждого такого сектора находить C_m(j). Т.к. сектор имеет постоянную угловую ширину, то значение C_m будет меняться только тогда, когда при повороте сектора в него попадают новые точки диаграммы рассеяния. Получим ломаную функцию C_m(j). На рис.7 приведена такая зависимость для a=20° и m=0.5. По оси абсцисс отложено значение осевого угла сектора j, по оси ординат – C_m(j).

На графике заметен большой пик в диапазоне углов от 130 до 170 градусов. На диаграмме рассеяния (рис. 2a) можно заметить, что в диапазоне углов от 110º до 190º очень низка плотность точек, и именно сюда попадают точки ‘1’ и  ‘2’, отстоящие особенно далеко от центра облака, что и приводит к появлению пика. На рис. 7 отрезками с цифрами указан диапазон секторов в которые попадают точки ‘1’ и ‘2’.

Аппроксимацию функции C_m(j) синусоидой с периодом 180° по значениям осевого угла секторов будем производить выделением второй гармоники ряда Фурье. Напомним, что коэффициенты ряда Фурье вычисляются по формулам:

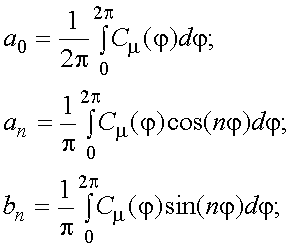                            (10)

где j – угол в радианах.

Для эллипса с равномерным заполнением все гармоники, кроме нулевой и  второй отсутствуют. Для реальных экспериментальных данных это не обязательно. Поскольку в качестве аппроксимирующего контура мы выбрали эллипс, оставим только эти гармоники для эмпирической функции C_m(j). Остальные гармоники будут характеризовать отклонение от эллипса, т.е. погрешность аппроксимации. Тогда для функции C_m(j) получим аппроксимирующее выражение:

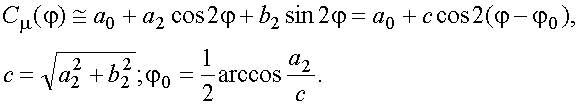(11)

Таким образом, получаем эллипс, поскольку определённый нами вид функции C_m(j) в точности соответствует формуле эллипса в полярных координатах, приведённой выше.

Эксцентриситет эллипса ε определяется из соотношения:

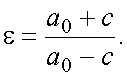                                                (12)

На рис.8 приведена функция C_m(j), та же, что и на рис.7, вместе с аппроксимирующей синусоидой. Аппроксимирующие параметры: a₀ = 11, a₂ = 2.3, b₂ = -0.3, c = 2.3, e = 1.53, j₀ = 4°.

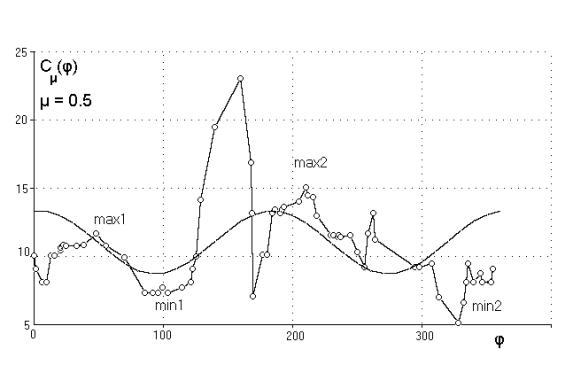
Рис.8. Функция C_m(j), m = 0.5, с аппроксимирующей синусоидой

Хотелось бы, чтобы синусоида проходила через точки max1, min1, max2, min2, ведь именно такая синусоида отражала бы общее поведение функции C_m(j). Однако построенная нами синусоида через указанные точки не проходит. Дело в том, что гармоника смещается из-за присутствия описанного выше пика. Как уже было отмечено, что на формирование пика большое влияние оказывают точки ‘1’и ‘2’ диаграммы рассеяния (рис.2a), соответствующие точкам ‘1’ и ‘2’ исходной записи (рис.1a). Эти точки выпадают из общей картины на этой записи, и именно их мы не хотим пускать в дальнейшую работу. Хотелось бы снизить влияние подобных пиков на формирование аппроксимирующей синусоиды.

Мы видим, что выбор медианных точек в качестве граничного уровня отбора точек не совсем удачен. Испытаем более высокие квантильные уровни. Таким образом, мы исключаем середину облака, где точки лежат плотно, и используем точки вблизи контура, ограничивающего облако. Мы ожидаем ,что результаты окажутся лучше, чем для медианных точек.

На рис.9 приведены результаты аппроксимации для квантильных уровней 0.8 и 0.9. Для m = 0.8 получили: a₀ = 18, a₂ = 4.1, b₂ = -2.5, c = 4.9, e = 1.75, j₀ =15.8°, а для m=0.9 получили: a₀ = 23, a₂ = 5.7, b₂ = -3.4, c= 6.6, e= 1.82, j₀ = 15.3°.

Из рисунка видно, что результаты стали лучше, вклад пика в положение гармоники не так велик, и синусоида намного ближе к точкам max1, min1, max2, min2. Т.е. уровень, действительно, лучше брать выше (точки ближе к «хвосту» распределения). Но мы не можем брать порог очень высоким, поскольку  в «хвостах» содержится мало точек. Это видно и на рис. 9 для m=0.9, где появляется ещё один резкий пик (φ ≈ 290˚), обусловленный точкой ‘3’(рис. 1a).

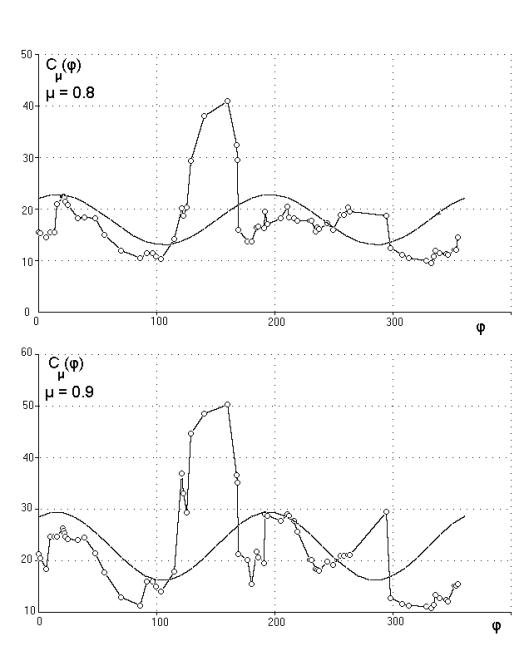
Рис.9. Функции C_m(j), m = 0.8 и m = 0.9, с аппроксимирующими их синусоидами

Отсюда видна трудность подбора подходящего квантильного уровня: при малой величине его аппроксимация хуже, а при большей – мало точек на «хвостах» дискретных распределений.

Если предположить, что распределения точек по радиусу в секторах одинаковы с точностью до масштаба по радиусу, то можно строить аппроксимирующее распределение сразу для всех секторов диаграммы. Для этого сделаем в каждом секторе преобразование масштаба по радиусу. Если получим «хорошее» распределение точек по радиусу, то по его гладкой аппроксимации можем выбрать квантильный уровень. В дальнейшем эти масштабы можно использовать для получения контура фильтра, преобразуя обратно общий граничный радиус в точки границы для секторов.

 Выше мы получили эллипс. Теперь, используя радиусы точек этого эллипса, произведём линейное преобразование фактических радиусов точек диаграммы, уравнивающее размеры секторов:

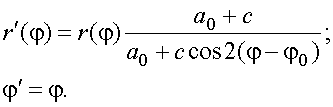                       (13)

Таким образом, мы привели секторы к одинаковому масштабу, поэтому назовём координаты r¢, j¢ приведёнными. Возможен иной способ приведения секторов к общему масштабу, основанный на сопоставлении распределений точек в секторах. В этом случае придется взять один из секторов за образцовый и вычислять масштаб преобразования каждого из секторов к размеру образцового, например, по условию минимизации статистики критерия Смирнова. Но пока вернемся к более простому методу.

В новых координатах точки эллипса окажутся лежащими на окружности, что позволяет построить общее приведённое распределение точек облака по радиусу. Это эмпирическое распределение мы хотим аппроксимировать непрерывным. Если аппроксимация окажется удовлетворительной, то выбором критической квантильной точки непрерывного распределения в приведённой

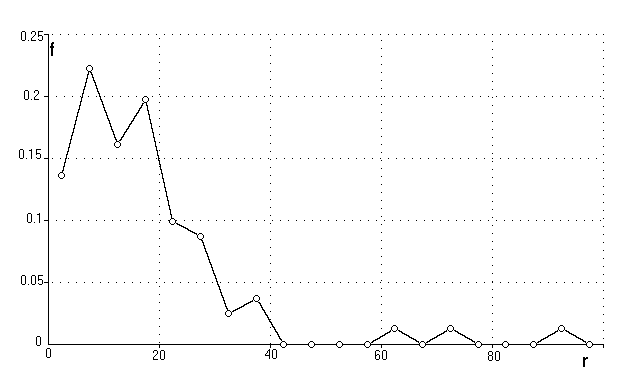
Рис.10. Плотность эмпирического распределения точек диаграммы по радиусу в приведённой системе координат

системе координат определяем масштаб. Используя этот масштаб на плоскости hr, p_dia, получим эллипс. У нас уже были найдены все параметры этого эллипса, кроме масштаба. Полученный критерий будем называть общим квантильным критерием выбора точек облака, пригодных для дальнейшей обработки в задачи классификации записей на «норму/патологию».

Рассмотрим распределения точек диаграммы рассеяния по радиусу в приведённой системе координат. На рис.10 представлено такое эмпирическое распределение, r – полярная координата, f – плотность эмпирического распределения. Распределение оказалось несимметричным, поэтому для аппроксимации была выбрана модель распределения Вейбулла:

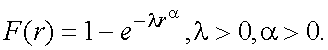                     (14)

Здесь r – полярная координата, F(r) – функция распределения.

Эта модель распределения удобна в прикладных задачах, поскольку позволяет аппроксимировать широкий диапазон эмпирических зависимостей. Квантильная точка r_z уровня z ( 0 ≤ z ≤ 1) распределения задаётся выражением

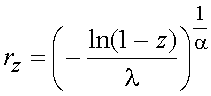                                     (15)

Для аппроксимации эмпирического распределения можно подобрать параметры распределения Вейбулла, используя регрессию (способ 1) вида

                                 (16)

Во многих случаях неплохие результаты даёт подбор коэффициентов a и l по квантильным точкам эмпирического распределения (способ 2). Для вычисления достаточно знать, как минимум, две квантильные точки. Лучшие результаты даёт вычисление по трём точкам (медиана m, нижний q1 и верхний q2 квартили). Подставляя в (16) 3 пары значений (r = q1; F=0.25), (r = m; F = 0.5), (r = q2; F = 0.75), получим 3 уравнения. Из 1-ого и 3-го (для q1 и q2) находим a, из всех трёх, суммируя, определяем ln ( l ):

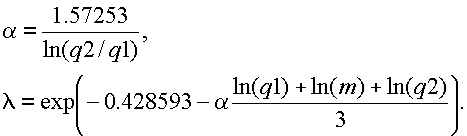           (17)

В нашей задаче мы использовали второй способ, как более простой и, тем не менее, дающий удовлетворительные результаты. На рис.11 приведено распределение точек по радиусу в приведённой системе координат, построенной для m = 0.9.

По оси абсцисс отложено значение расстояния r от точки до начала координат в приведённой системе координат, а по оси ординат – доля измерений со значениями r не меньше заданного. Кружками отмечено эмпирическое распределения, а сплошной линией аппроксимирующее его распределение Вейбулла с параметрами a = 1.40 и l = 0.0183. Далее, мы выбираем критический квантильный уровень (1-b) и возвращаемся к первоначальным координатам, получая эллиптическую границу.

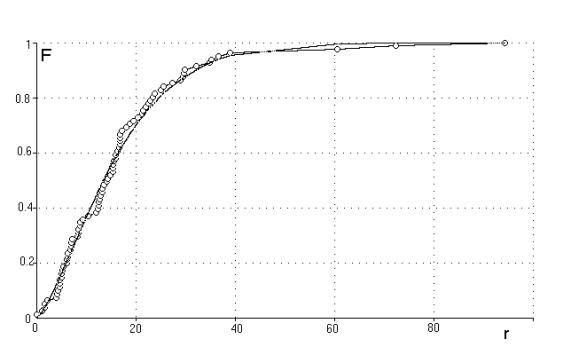
Рис.11. Эмпирическое распределение точек по радиусу в приведённой системе координат с аппроксимирующим его распределением Вейбулла

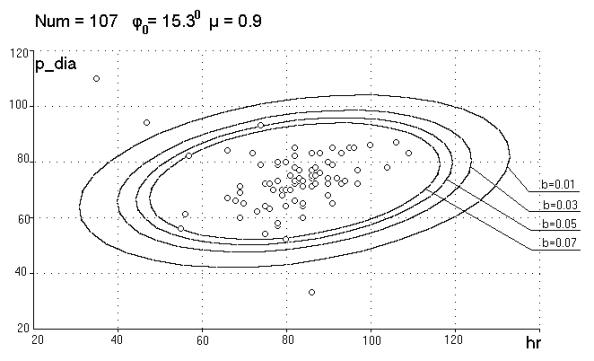
Рис.12. Семейство «эллиптических» фильтров

На рис. 12 представлена диаграмма рассеяния, на которую наложены контуры эллиптических фильтров, соответствующих разным квантильным уровням (1-b), указанным с помощью параметра b. Окончательный выбор уровня будет сделан по результатам фильтрации реальных записей. Отброшенных точек не должно быть много. Если число таких точек окажется большим, то сомнительно приписывать все их случайной помехе.

Рассмотрим другой вариант «эллиптического» фильтра. Напомним, что мы рассмотрели модель, в которой распределения точек по радиусу в каждом направлении одинаковы с точностью до масштаба. И считаем, что зависимость масштаба от угла φ такая же, как и у радиуса эллипса.

 Описанный выше метод выбора направления осей эллипса был основан на разной удалённости точек эллипса от центра в разных направлениях. Но если предположить, что точки внутри эллипса лежат достаточно равномерно, то сектор постоянной ширины должен «захватывать» больше точек в направлении большой оси. Описываемые дальше «эллиптические» фильтры будут это свойство «улавливать», однако, оно не является необходимым для их работы.

Рассмотрим сектор S_ja с осевым направлением j и угловой полушириной a. Введём функцию Chr(j,a), учитывающую и число лежащих в секторе точек диаграммы рассеяния, и удалённость их от центра облака. Припишем каждой точке диаграммы рассеяния (обозначим её A_i) единичную массу m_i. Тогда функцию Chr(j,a) можно ввести разными способами:

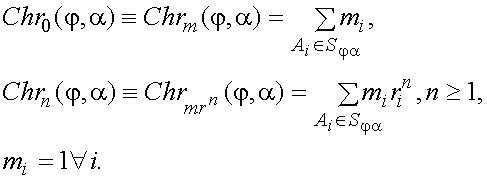     (18)

Chr_n(j,a) (n ³ 1) в разной степени учитывают удалённость точек диаграммы  рассеяния, попавших в сектор, от центра облака. Chr₀(j,a) описывает только число точек диаграммы рассеяния, попавших в сектор S_ja и может рассматриваться как аналог массы сектора. Chr₁(j,a) может рассматриваться как аналог момента сил, Chr₂(j,a) – аналог момента инерции.

Пусть мы построили аппроксимирующий эллипс, задаваемый формулой:

                    (19)

где j₀ – угол наклона большой оси эллипса, a₀ и c – константы, a = a₀ + c – длина большой полуоси эллипса, а b = a₀  - c – длина малой полуоси эллипса. При равномерном распределении точек внутри эллипса Chr_n(j,a) ~ [r(j)]ⁿ⁺², будем считать, что и в нашем случае выполняется именно такая зависимость. Для направления j определим функцию eⁿ⁺²(j, a):

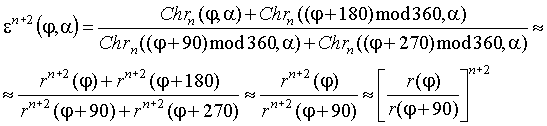    (20)

Как видим, при j = j₀ eⁿ⁺²(j₀, a)=eⁿ⁺², где e = a/b – эксцентриситет эллипса. Покажем, что в точке j = j₀ (j₀ – угол наклона большой оси эллипса) функция eⁿ⁺²(j, a) достигает максимума, действительно:

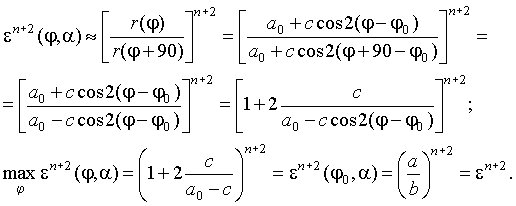     (21)

Поэтому можно искать направление большой полуоси путём максимизации функционала eⁿ⁺²(j,a) по j.

Для каждого сектора фиксированной ширины вычислим значение функционала eⁿ⁺²(j, a). Для этого возвращаемся к модели плавно вращающегося сектора постоянной угловой ширины. Получим ломаную функцию eⁿ⁺²(j, a). Затем находим максимум этой функции, определяя, таким образом, направление большой полуоси j₀ и эксцентриситет e.

На рис.13 представлены графики функции eⁿ⁺²(j, a), построенные для функционалов Chr₀(j,a) (1), Chr₁(j,a) (2) и Chr₂(j,a) (3). Везде a=20°. По оси абсцисс отложено значение угла j в градусах, а по оси ординат значение функционала eⁿ⁺²(j, a). Для Chr₀(j,a) (1) получили j₀ = 23°, e = 1.7, для Chr₁(j,a) (2) j₀ = 31°, e = 2.1, а для Chr₂(j,a) (3) j₀ = 31°, e = 2.7.

Видно, что с увеличением порядка n момента максимумы функции eⁿ⁺²(j, a) становятся более узкими и частыми, в то время как для Chr₀(j,a) было всего два ярко выраженных широких максимума. Это можно объяснить тем, что чем выше степень у r, тем большее влияние оказывают далёкие точки (с большим значением r). При очень больших n влияние сохранят только они, т.е. построение эллипса будет производиться только по точкам с максимальным значением r по каждому направлению. Это равносильно выбору в предыдущем методе значений μ, близких к единице.

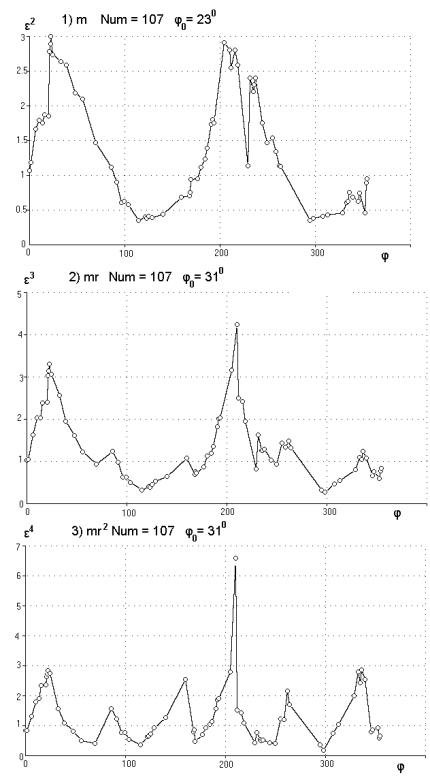
Рис.13. Графики функции eⁿ⁺²(j, a) для разных n

На рис.14 приведён график e¹²(j, a) для момента 10-ой степени. Он даёт следующий результат: j₀ = 153°, e = 2.37. Отметим, что φ = j₀ = 153° почти в точности направление на точки ‘1’ и ‘2’ (рис.2a), что подтверждает вышесказанное. Локальные максимумы ‘1’ и ‘2’ одно и то же, поскольку отличаются на 180º.

Определив направление и эксцентриситет аппроксимирующего эллипса, поступаем так же, как и раньше. Переходим к приведённым координатам, аппроксимируем распределение точек по радиусу в этой системе координат распределением Вейбулла и получаем общий квантильный критерий выбора точек облака, пригодных для дальнейшей обработки.

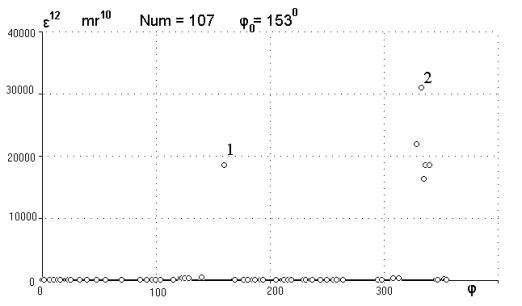
Рис.14. График функции e¹²(j, a)

На рис. 15 представлена диаграмма рассеяния с наложенными на нее контурами семейств «эллиптических» фильтров для случаев (n = 0, 1, 2). В каждом семействе представлены фильтры, отличающихся выбором квантильного уровня (1-b). По оси абсцисс – hr, по оси ординат – p_dia. Обозначения те же, что и на рис. 13.

Видно, что «слепых» зон практически не осталось. И фильтры отсеивают те точки, которые действительно кажутся далёкими.

На рис. 16 представлена диаграмма рассеяния с наложенными на нее контурами семейств «эллиптических» фильтров для случая n = 10. Обозначения те же, что и на рис. 15.

Видно, что в этом случае эллипс действительно строится по самым дальним точкам, не учитывая плотность точек в каждом из направлений. Поэтому в дальнейшем разумно использовать моменты невысоких степеней, например, не выше второй.

Этот метод уже даёт приемлемые результаты. Основной его недостаток в том, что при определении φ₀ и ε используется точечная оценка (для нас не важно поведение функционала eⁿ⁺²(j, a), нам важно лишь положение точки его максимума), которая даёт неплохие результаты при большом количестве данных. Но у нас измерений в одной суточной записи не так много. Поэтому хотелось бы использовать какой-нибудь метод, полнее использующий имеющуюся информацию. Например, выделение гармоник Фурье, как в первом

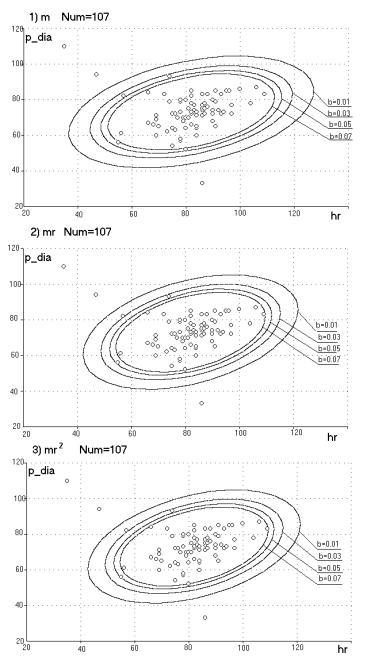
Рис.15. «Эллиптические» фильтры

рассмотренном методе построения «эллиптического» фильтра. Это действительно можно сделать.

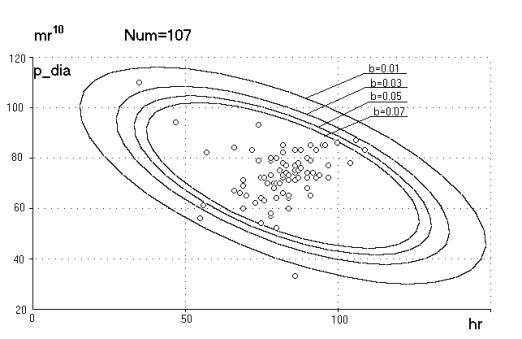
Рис.16. Семейство «эллиптических» фильтров для случая n = 10

Вспомним, что Chr_n(j,a) ~ [r(j)]ⁿ⁺². Тогда

                   (22)

А это уже в точности рассмотренный выше случай, только вместо C_m(j) имеем [Chr_n(φ,α)]^1/(n+2). Будем аппроксимировать функцию [Chr_n(φ,α)]^1/(n+2) синусоидой с периодом 180˚ по значениям осевого угла секторов, оставляя только нулевую и вторую гармоники её ряда Фурье:

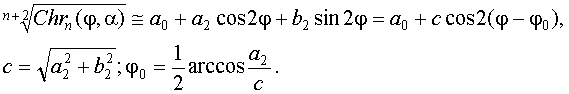 (23)

Здесь a₀, a₂ и b₂ – коэффициенты Фурье:

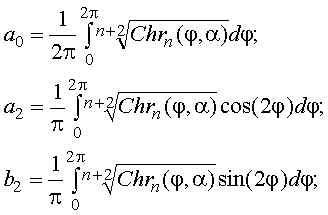                              (24)

φ – угол в радианах.

Эксцентриситет вычисляем по формуле (12).

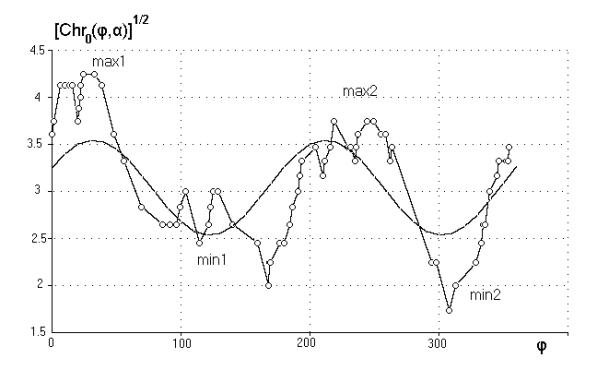
На рис.17 приведена функция [Chr₀(φ,α)]^1/2 вместе с аппроксимирующей синусоидой. Аппроксимирующие параметры: a₀ = 3, a₂ = 0.21, b₂ = -0.46, c = 0.50, e = 1.40, j₀ = 33°.

Рис.17. Функция [Chr₀(φ,α)]^1/2 с аппроксимирующей синусоидой

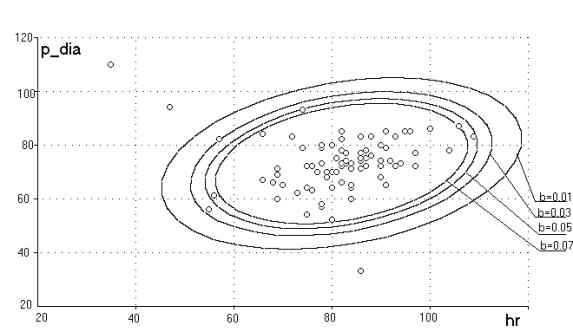
Рис.18. Семейство «эллиптических» фильтров, j₀ = 33°, e = 1.40

Видно, что аппроксимирующая синусоида хорошо отражает положение точек max1, min1, max2, min2. Результаты действия полученного фильтра на поток исходных данных отражены на диаграмме, представленной на рис.18. Обозначения те же, что и на рис.12. Результаты фильтрации не хуже полученных предыдущим методом, однако, отсутствует недостаток точечной оценки, за счёт применения интегральных методов.

5. Заключение

Достижение конечной цели – построения формального решающего правила для классификации суточных записей артериального давления и частоты пульса на относительно благополучные и имеющие признаки ухудшения состояния кровообращения потребовало предварительной фильтрации измерений для устранения помех. Был выбран метод фильтрации из класса «поточечных», рассматривающих каждое измерение вне связи с соседними. Методы этого класса просты в реализации и не требуют привлечения сложных моделей изучаемых процессов.

Построение и оценка фильтров производились от самых простых конструкций (покоординатные коридоры) к более сложным («эллиптические»). Такой подход позволил рассмотреть достоинства и недостатки этих вариантов и наметить их реализацию для практического использования.

Предложены методы оценки вариантов фильтров в рамках поточечного подхода с учетом требований врачей-диагностов.

Чтобы не перегружать читателя большим числом различных записей, все иллюстрации делались всего для двух записей, на наш взгляд, наиболее ярко отражающих особенности каждого из построенных фильтров.

Разработанными в этой работе фильтрами мы предполагаем пользоваться в дальнейшем при решении основной задачи. Однако разработанные фильтры представляют собой не только вспомогательный, но и самостоятельный интерес. Они в большей степени, чем многие использующиеся в настоящее время в практике фильтры, учитывают индивидуальность каждой записи, что особенно актуально в задачах, связанных с медицинскими исследованиями.

Авторы выражают благодарность Малинецкому Г.Г., Гусеву А.В.,  Романову М.Ю. и Анисимовой С.А. за внимание к работе и полезные замечания.

Работа выполнена при поддержке РФФИ (грант №01– 01– 00628).

Литература

1)     Савельева Г.М. Вестник Российской ассоциации акушеров-гинекологов. 1998, 2, 21-26

2)     И.М. Гельфанд, Б.И. Розенфельд, М.А. Шифрин “Очерки о совместной работе математиков и врачей”, Москва, “Наука”, 1989

3)     В.М. Гурьева, Л.С. Логутова, Ю.Б. Котов, В.А. Петрухин “Суточный мониторинг артериального давления и частоты сердечных сокращений при диагностике гестоза”, Российский Вестник акушера-гинеколога,1,2003

4)     Стентон Гланц “Медико-биологическая статистика”, перевод с английского, Москва, Практика, 1999

5)     Холлендер М., Вульф Д.А. Непараметрические методы статистики. – М., Финансы и статистика, 1983. – 518с.

6)     О.И. Ларичев “Теория и методы принятия решений, а также Хроника событий в Волшебных странах”, Москва, “Логос”, 2000

7)     Закирова Н.И. Вестник Российской ассоциации акушеров-гинекологов 1996, 4 53-54

8)     Mushambi M.C., Halhgan A.W., Wilhamson K., Br J Anaesth 1996, 76 133-148