О степенной геометрии

Аннотация

С помощью степенной геометрии, кратко изложенной в § 1, в случае общего положения вычислены все степенные разложения решений второго уравнения Пенлеве вблизи точек z=0, z = Ґ (§ 2) и z = z₀ № 0 (§ 3). Аналогично при a=0 вычислены все степенные разложения решений и логарифма решений (§ 4). Обнаружены новые тонкие свойства некоторых из этих разложений.

Abstract

By means of Power Geometry, shortly presented in § 1, in the generic case we compute all power expansions of solutions to the second Painlevé equation at points z=0, z = _ (§ 2) and z = z₀ № 0 (§ 3). Analogously for a=0 we compute all power expansions of solutions and of logarithm of solutions (§ 4). We have found new fine properties of some of these expansions.

E-mail: bruno@keldysh.ru, zavgorodnyaya@rambler.ru

О степенной геометрии

§ 0. О степенной геометрии

Здесь приводятся те сведения из степенной геометрии [1-7], которые используются в этой работе.

1.1. Постановка задачи. Пусть x - независимая и y - зависимая переменные, x,y О \Bbb C. Положим X=(x,y). Дифференциальным мономом a(x,y) называется произведение обычного монома

cx^r₁y^r₂

def
=

cX^R,

(1)

где c=const О \Bbb C, R=(r₁,r₂) О \Bbb R², и конечного числа производных вида

d^ly/dx^l, l О \Bbb N.

(2)

Сумма дифференциальных мономов

f(X)=

a_i(X)

(3)

называется дифференциальной суммой.

Основная задача. Пусть задано обыкновенное дифференциальное уравнение

f(X)=0,

(4)

где f(X) - дифференциальная сумма, в которую y входит в целых неотрицательных степенях. При x® 0 и при x®Ґ для решений y=j(x) уравнения (4) найти все степенные разложения

y=c_rx^r+

c_s x^s,

(5)

где коэффициенты c_r,c_s=const О \Bbb C, c_r № 0, показатели степени r,s О \Bbb R и не имеют в \Bbb R точек накопления; r < s, если x® 0, и r > s, если x®Ґ.

Положим

w =

м
п
н
п
о

-1,

если

x® 0,

если

x®Ґ.

(6)

Степенная геометрия дает теорию и алгоритмы для решения этой задачи. Процедура вычисления разложений (5) состоит из двух этапов: вычисление первых приближений

y=c_rx^r, c_r № 0

(7)

и вычисление дальнейших членов разложения (5), которые удобно разбить на несколько ветвящихся шагов, описанных ниже.

1.2. Выделение укороченных уравнений. Каждому дифференциальному моному a(X) ставится в соответствие его (векторный) показатель степени Q(a)=(q₁,q₂) О \Bbb R² по следующим правилам. Для монома (1) Q(cx^r₁y^r₂)=(r₁, r₂); для производной (2) Q(d^ly/dx^l)=(-l,1); при умножении дифференциальных мономов их показатели степени складываются как векторы Q(a₁a₂)=Q(a₁)+Q(a₂). Множество S(f) показателей степеней Q(a_i) всех дифференциальных мономов a_i(X), входящих в дифференциальную сумму (3), называется носителем суммы f(X). Очевидно, S(f) О \Bbb R². Через f_Q(X) обозначим сумму тех мономов a_i(X) из (3), у которых Q(a_i)=Q. Тогда дифференциальную сумму (3) можно записать в виде

f(X)=

f_Q(X) по Q О S(f).

(8)

Выпуклая оболочка G(f) носителя S(f) называется многоугольником суммы f(X). Граница ¶G(f) многоугольника G(f) состоит из вершин G_j⁽⁰⁾ и ребер G_j⁽¹⁾. Их называют (обобщенными) гранями G_j^(d), где верхний индекс указывает размерность грани, а нижний - ее номер. Каждой грани G_j^(d) соответствуют граничное подмножество S_j^(d)=S(f)ЗG_j^(d) множества S и укороченная сумма

(d)
j

(X)=

a_i(X) по Q(a_i) О S_j^(d).

(9)

Пусть плоскость \Bbb R_*² сопряжена плоскости \Bbb R² так, что для P=(p₁,p₂) О \Bbb R_*² и Q=(q₁,q₂) О \Bbb R² определено скалярное произведение

бP,Qс

def
=

p₁q₁+p₂q₂.

(10)

Каждой грани G_j^(d) в \Bbb R_*² соответствуют: свое нормальное подпространство

N^(d)_j={P: бP,Qс = бP,Qўс по Q,Qў О S_j^(d)}

и свой нормальный конус

U_j^(d) =

м
п
н
п
о

бP,Qс = бP,Qўс,

Q,Qў О S_j^(d),

бP,Qс > бP,Q"с,

Q" О S(f)\S_j^(d)

ь
п
э
п
ю

Для ребра G_j⁽¹⁾ нормальное подпространство N⁽¹⁾_j это прямая, ортогональная ребру G_j⁽¹⁾ и проходящая через начало координат P=0, а нормальный конус это тот луч прямой N_j⁽¹⁾, который направлен от ребра G_j⁽¹⁾ наружу многоугольника G(f). Для вершины G_j⁽⁰⁾ нормальное подпространство N⁽⁰⁾_j=\Bbb R_*², а нормальный конус U_j⁽⁰⁾ это открытый сектор (угол) на плоскости \Bbb R_*² с вершиной в нуле P=0 и ограниченный лучами, являющимися нормальными конусами ребер, примыкающих к вершине G_j⁽⁰⁾.

Предложение 1.1. Если носитель S(f) состоит из одной вершины G₁⁽⁰⁾, то нормальный конус U₁⁽⁰⁾=\Bbb R_*² т.е. в U₁⁽⁰⁾ лежат оба вектора ±R. В противном случае раствор угла U_j⁽⁰⁾ меньше p, т.е. из двух векторов ±R в нормальный конус U_j⁽⁰⁾ попадает только один. Здесь вектор R № 0, R О \Bbb R_*².

Предложение 1.2. Если многоугольник G(f) состоит из одного ребра G₁⁽¹⁾, то нормальный конус U₁⁽¹⁾ это прямая, т. е. в U₁⁽¹⁾ лежат оба вектора ±R. В противном случае в нормальном конусе U_j⁽¹⁾ лежит только один из векторов ±R. Здесь вектор R № 0 является нормалью к ребру G_j⁽¹⁾.

Итак, каждой грани G_j^(d) соответствуют: нормальное подпространство N_j^(d) и нормальный конус U_j^(d) в плоскости \Bbb R_*² и укороченное уравнение

(d)
j

(X)=0.

(11)

Для разложения решения (5), которое запишем как y-j(x)=0, имеются аналогичные объекты, которые обозначаются малыми буквами: носитель s(y-j), многоугольник g(y-j). Из граней многоугольника g(y-j) нас интересует только ребро g₁⁽¹⁾, которое соответствует укорочению (7) разложения (5), т.е. натянуто на точки Q₁=(0,1) и Q₂=(r,0). Через n и u обозначаются нормальное подпространство и нормальный конус ребра g₁⁽¹⁾. Очевидно, n - это прямая, натянутая на вектор R=(1, r), а u - это ее луч {P=lw(1,r), l > 0}, направленный наружу многоугольника g(y-j) и ортогональный ребру g₁⁽¹⁾

Теорема 1.1 [2, гл. VI, теорема 1.1]. Если разложение (5) удовлетворяет уравнению (4) и u М U_j^(d), то укорочение (7) решения (5) является решением укороченного уравнения (9), (11).

Поэтому для нахождения всех укороченных решений (7) уравнения (4) надо вычислить: носитель S(f), многоугольник G(f), все его грани G_j^(d) и их нормальные конусы U_j^(d). Затем для каждого укороченного уравнения (9), (11) надо найти все его решения (7), у которых вектор R=(1,r) лежит в N_j^(d), и из них отобрать те, у которых один из векторов ±(1, r) лежит в нормальном конусе U_j^(d). Если d=0, то это означает, что один из векторов ±(1,r)=wR лежит в U_j^(d). Если d=1, то это свойство всегда выполнено. При этом согласно предложениям 1.1 и 1.2 определяется также значение w.

1.3. Решение укороченного уравнения. Здесь рассмотрим по отдельности два случая: вершины G_j⁽⁰⁾ и ребра G_j⁽¹⁾.

Вершине G_j⁽⁰⁾={Q} соответствует укороченное уравнение (11) с точечным носителем Q. Положим g(X)=X^-Q[^(f)]_j⁽⁰⁾(X), тогда решение (7) уравнения (11) удовлетворяет уравнению g(X)=0. Подставляя y=cx^r в g(X), получаем, что g(x,cx^r) не зависит от x и c, и является многочленом от r, т.е. g(x,cx^r) є c(r), где c(r) - характеристический многочлен дифференциальной суммы [^(f)]_j⁽⁰⁾(X). Следовательно, для решения (7) уравнения (11) показатель r является корнем характеристического уравнения

c(r)

def
=

g(x, x^r)=0,

(12)

а коэффициент c_r - произвольный. Из корней r_i уравнения (12) надо отобрать только те, для которых один из векторов w(1,r), где w = ±1, лежит в нормальном конусе U_j⁽⁰⁾ вершины G_j⁽⁰⁾. При этом согласно предложению 1.1 значение w определяется однозначно. Соответствующие выражения (7) с произвольной константой c_r являются кандидатами на роль укороченных решений уравнения (4). При этом если w = -1, то x® 0 и в разложении (5) s > r, а если w = 1, то x®Ґ и в (5) s < r.

Укороченное уравнение (11) называется алгебраическим, если оно не содержит производных.

Замечание 1.1 [2]. Если укороченное уравнение (11) с d=0 является алгебраическим, то оно не имеет решений вида (7). Поэтому укорочения, состоящие из одного алгебраического монома, можно не рассматривать.

Ребру G_j⁽¹⁾ соответствует укороченное уравнение (11), нормальный конус U_j⁽¹⁾ которого является лучом { P = lwў(1,rў), l > 0}, где вектор wў(1,rў) является внешней нормалью ребра G_j⁽¹⁾. Нормальный конус u={P=lw(1,r), l > 0} решения (5) пересекается с U_j⁽¹⁾ только если эти лучи совпадают, т.е. w = wў и r=rў. Согласно предложению 1.2 этим однозначно определяется показатель степени r укороченного решения (7) и значение w. Для определения коэффициента c_r надо выражение (7) подставить в укороченное уравнение (11). После сокращения на некоторую степень x получаем алгебраическое уравнение для коэффициента c_r

(c)

def
=

x^-s

(1)
j

(x,c_rx^r)=0.

(13)

Каждому его корню c_r=c_r⁽ⁱ⁾ № 0 соответствует свое выражение (7), которое является кандидатом на роль укороченного решения уравнения (4). При этом если получилось, что w = -1, то x® 0 и в (5) s > r, а если w = 1, то x®Ґ и в (5) s < r.

Итак, каждое укороченное уравнение (11) имеет несколько подходящих решений (7) с u М U_j^(d). Объединим их в непрерывные по w, r, c_r и параметрам уравнения (4) семейства, которые обозначим F_j^(d)k, где k=1, 2,.... Если нас интересуют не все решения (5) уравнения (4), а только те решения (5), у которых нормальный конус u лежит в некотором заданном конусе K, то K называется конусом задачи [2, гл. I, § 6]. Например, для укороченного уравнения (11) нормальный конус U_j^(d) является конусом задачи, если нет других ограничений.

1.4. Критические числа укороченного решения. Если найдено укороченное решение (7), то замена

y=c_rx^r+z,

(14)

приводит уравнение (4) к виду

f(x,cx^r+z)

def
=

(x,z)=0,

(15)

где [(f)\tilde](x,z) - дифференциальная сумма, все точки Q=(q₁,q₂) ее носителя S([(f)\tilde]) имеют целую неотрицательную координату q₂. К уравнению (15) можно применить описанные выше вычисления (т.е. носителя, многоугольника, укорочений и т.д.) и получить следующий член c_s₀x^s₀ разложения (5), у которого s₀ > r, если x® 0, и s₀ < r, если x® Ґ. Следовательно, получилась основная задача для уравнения (15), но теперь с конусом задачи

м
п
н
п
о

P=(p₁, p₂):

p₂/p₁ > r, p₁ < 0,

если

x® 0,

p₂/p₁ < r, p₁ > 0,

если

x®Ґ

ь
п
э
п
ю

Согласно (6) для s=p₂/p₁ этот конус задачи K можно записать в виде

K={s=p₂/p₁: sw < rw}.

(16)

Однако во многих случаях дифференциальная сумма [(f)\tilde](x,z) имеет специальный вид, что позволяет существенно сократить вычисления разложений (5). Предположим, что уравнение (15) имеет вид

(x,z)

def
=

L(x)z+h(x,z)=0,

(17)

где L(x) - линейный дифференциальный оператор и носитель S(Lz) состоит из одной точки (v,1), являющейся вершиной [(G)\tilde]₁⁽⁰⁾ многоугольника G([(f)\tilde]), у всех точек Q=(q₁,q₂) носителя S(h) координата q₂ і 0 и нет точки Q=(v,1), нормальный конус вершины [(G)\tilde]₁⁽⁰⁾ содержит вектор P=(p₁,p₂) с p₁w > 0. Напомним, что дифференциальная сумма f(x,y) имеет первую вариацию [8] df(x,y)/dy, которая обладает следующими свойствами.

d(c x^q₁y^q₂)/dy=cq₂x^q₁y^q₂-1, d(d^l y/d x^l)/dy=d^l/dx^l,

d(f+g)/dy=df/dy+dg/dy, d(fg)/dy=(df/dy)g+f(dg/dy).

Теорема 1.2 [4, 5, 6]. Пусть (7) - решение укороченного уравнения (11) с u О U^(d)_j. Тогда в уравнении (17) оператор

L(x) = d
^

f

(d)
j
(x,y)/dy на y=c_rx^r,
(18)
т.е. равен первой вариации, вычисленной на кривой (7).

Следовательно, после подстановки (15) уравнение (4) принимает вид (17), если L(x)\not є 0. Пусть n(k) - характеристический многочлен дифференциальной суммы L(x)z, т.е.

n(k)=x^-v-kL(x)x^k.

(19)

Корни k₁,...,k_s многочлена n(k) называются собственными значениями укороченного решения (7). Те из вещественных собственных чисел k_i, которые лежат в конусе задачи, т.е. удовлетворяют неравенствам (16), называются критическими числами. Они играют важную роль при нахождении разложения (5), что будет показано в следующем пункте.

Замечание 1.2 [5]. Степенное решение (7) алгебраического укороченного уравнения (11) с d=1 не имеет собственных значений и критических чисел, ибо для него

n(k) є n₀=const=

(1)
j

¶y

(1,c_r).

(20)

Если c_r - простой корень уравнения (13), то n₀ № 0. Если c_r - кратный корень уравнения (13, то n₀=0.

Если L(x)\not є 0, то n(k)\not є 0. Если же L(x) є 0, то для уравнения (15) надо решать основную задачу как описано в пп. 1.2 и 1.3 с учетом конуса задачи (16).

1.5. Носитель разложения решения (5). Рассмотрим уравнение (17) в невырожденном случае, когда n(k)\not є 0. Параллельно сдвинем носитель S([(f)\tilde]) на вектор -(v,1). Тогда вершина (v,1), соответствующая члену L(x)z, сдвинется в начало координат. Пусть Sў₊ - множество конечных сумм векторов Q О Sў[( def) || ( = )] S([(f)\tilde])-(v,1) и пусть

K=Sў₊ З{q₂=-1}.

(21)

Пусть æ - число критических значений k_i укороченного решения (7).
Рассмотрим по отдельности случаи с æ = 0 и æ = 1.

Случай æ = 0.

Теорема 1.3 [7]. В случае æ = 0 имеется разложение (5) решения уравнения (4), в котором все показатели s лежат в множестве K и все коэффициенты c_s определяются однозначно.

Лемма 1.1. Пусть G⁽⁰⁾_j - такая вершина многоугольника G(f) уравнения (4), что укороченное уравнение [^(f)]⁽⁰⁾_j(X)=0 имеет решение (7), вектор w(1, r) О U⁽⁰⁾_j и все точки сдвинутого носителя S(f)-G⁽⁰⁾_j представляются в виде lR^*+mR_*, где целые l,m і 0, R^* и R_* - некоторые вектора. Тогда для множества (21) уравнения (15) справедливо включение

K М {k=r+lr^*+mr_*, целые l,m і 0, l+m > 0 },

где r^*=б(1, r), R^*с, r_*=б(1, r), R_*с.

Точечное множество Z плоскости \Bbb R² называется решеткой, если для любых двух векторов Q, Q^ў О Z их сумма Q+Q^ў и разность Q-Q^ў принадлежат Z. Векторы B₁ и B₂ образуют базис решетки Z, если любая точка Q решетки Z представляется в виде Q=n₁B₁+n₂B₂, где n₁ и n₂ О \Bbb Z, т.е. целые числа. Пусть S - некоторое множество в \Bbb R² и точка Q О S. Множество точек S-Q будем называть сдвинутым множеством S. Для укороченного решения (1.6) носитель s состоит из двух точек Q₁=(0, 1) и Q₂=(r, 0). Поэтому сдвинутый носитель s состоит из точек 0 и Q₂-Q₁=(r, -1).

Замечание 1.3. Если сдвинутые носители S(f) уравнения (4) и s укороченного решения (7) лежат в некоторой решетке Z, то множество

K М ZЗ{q₂ = -1}ЗK.

(22)

Случай æ = 1. Пусть k₁ - единственное критическое значение. Обозначим через Sў₊(k₁) множество конечных сумм векторов Q О Sў[( def) || ( = )] S([(f)\tilde])-(v,1) и вектора (k₁,-1), и положим

K(k₁)=Sў₊(k₁)З{q₂=-1}.

(23)

Теорема 1.4 [7]. Если в случае æ = 1 единственное критическое значение k₁ не лежит в множестве K, то имеется разложение (5) решения уравнения (4), где показатели s лежат в множестве K(k₁), при этом коэффициент c_k₁ произволен, а остальные коэффициенты c_s определяются однозначно.

Лемма 1.2. Если множество (21) имеет вид

K= м
н
о k=r+l
~

r

, целые l > 0 ь
э
ю ,

то множество (23) имеет вид

K(k₁)= м
н
о k=r+l
~

r

+m(k₁-r), целые l,m і 0, l+m > 0 ь
э
ю .

Замечание 1.4. Если множество Sў=S([(f)\tilde])-(v,1) и точка (k₁,-1) лежат в некоторой решетке Z(k₁), то

K(k₁) М Z(k₁)З{q₂=-1}ЗK.

(24)

Теорема 1.5 [7]. Множества (21) и (23) не имеют точек накопления на прямой \Bbb R, если множество S([(f)\tilde]) не имеет точек накопления на плоскости \Bbb R².

Если в ситуации теоремы 1.4 условие на критическое значение k₁ не выполнено (т. е. k₁ О K), то надо вычислить начальный отрезок

y=c_rx^r+

m
е

c_kx^k+u

(25)

разложения (5) до такого значения m, что |m-r| і |k₁-r|. В уравнении для u условие теоремы 1.4 будет выполнено.

1.6. Вычисление коэффициентов разложения. Упорядочим точки s множества K или K(k₁) по росту |s-r|. Двигаясь по точкам s из соответствующего множества в соответствии с этой упорядоченностью, для каждого коэффициента c_s из (5) получаем линейное уравнение L c_s x^s+b_sx^s+v=0, т. е.

n(s)c_s+b_s=0,

(26)

где b_s зависит от предыдущих коэффициентов c_l с индексами l, предшествующими индексу s. Если n(s) № 0, то c_s=-b_s/n(s). Если n(s)=0 и b_s=0, то c_s - произвольно. Если n(s)=0 и b_s № 0, то уравнение (26) не имеет решения.

Замечание 1.5. Если n(s)=0, то получается условие разрешимости (совместности) уравнения (26)

b_s=0.

(27)

Если исходное уравнение (4) зависит от параметров A, то, вообще говоря, коэффициент b_s также зависит от этих параметров, т.е. b_s=b_s(A). При этом возможны три случая: (a) b_s(A) є 0 при любых значениях параметров A; (b) условие (27) является некоторым условием на параметры A; (c) b_s(A) № 0 при любых допустимых значениях параметров A.

Для каждого семейства F_j^(d)k получается некоторое семейство разложений (5) с определенным носителем, в котором для критических коэффициентов c_{k_i} могут существовать условия разрешимости. Если они выполнены, то эти коэффициенты произвольны, а остальные определяются однозначно. Такие семейства разложений будем обозначать G_j^(d)k.

1.7. Вычисление второго приближения. Пусть известны укороченное уравнение (11), его подходящее решение (7) и его критические числа k_i. Покажем, как находится ближайшая к r точка s₀ множества K. Пусть вектор P=w(1, r), где w = ±1 (см. (1.5ў)), направлен наружу многоугольника G(f). Пусть m = бP, Qс и mў=maxбP, Qўс, где Q О S^(d)_j, Qў О S(f)\S^(d)_j.

Теорема 1.6 [4, 5]. Ближайшая к r точка s₀ такова, что |s₀-r|=m-mў.

Если критические значения k_i отсутствуют или таковы, что |k_i-r| > m-mў, то можно вычислить коэффициент c_s₀ следующим образом. Выделим в сумме f(x) второе приближение [^([^(f )])] =еf_Q(X) по Q: бP, Qс = mў, делаем подстановку y=c_rx^r+c_s₀x^s₀ в сумму

(d)
j

(28)

и приведем подобные члены. Приравнивая нулю коэффициент при x^mўw в сумме (28), получаем линейное уравнение (26) для коэффициента c_s₀, где b_s это коэффициент суммы [^([^(f )])](x,c_rx^r) при x^mўw и s=s₀.

Если имеется критическое значения k₁ такое, что |k₁-r| < m-mў, то s₀=k₁ и коэффициент c_s₀ произвольный.

1.8. Вопросы сходимости. Максимум порядков l всех производных (2), входящих в дифференциальный моном a(X), называется его порядком дифференцирования и обозначается p(a). Порядком дифференцирования p(f) суммы (3) называется наибольший из порядков дифференцирования p(a_i) ее мономов a_i(X).

Условие 1.1. В сумме (17) порядок дифференцирования p([(f)\tilde]) Ј p(Lz).

Теорема 1.7 [4, 5]. Пусть в ситуациях теорем 1.3, 1.4 выполнено условие 1.1, тогда разложение (5) абсолютно сходится для достаточно малых |x| № 0, если x® 0, и |x|^-1 № 0, если x® Ґ (т.е. для |x|^-w № 0).

1.9. Нестепенные асимптотики решений. В п.п. 1.1 - 1.4 изложен метод вычисления всех степенных асимптотик, т.е. вида (7). Поэтому здесь сосредоточимся на вычислении всех нестепенных асимптотик решений, т.е. не имеющих вида (7). Порядком функции j(x) называется число r=lim(ln|j(x)|/ln|x|) О [-Ґ,+Ґ], если предел существут. Две функции j(x) и y(x) сильно (асимптотически) эквивалентны, если j(x)=y(x)[1+o(|x|^we|y(x)|^w₂e)] для некоторого e < 0, где

w₂ =

м
п
н
п
о

-1,

если y(x)® 0,

если y(x)®const № 0,

если y(x)®Ґ.

При этом функция j(x) является сильной асимптотикой функции y(x) и наоборот. Пусть y=j(x) - решение уравнения (4), и функция j(x) имеет порядок r. Тогда нормальным конусом u этого решения является луч

u =

м
п
н
п
о

lw(0,-1),

если r=-Ґ;

lw(1,r),

если r О \Bbb R;

lw(0,1),

если r=+Ґ, l > 0.

Понятие конус задачи применимо и к решениям с так определенным нормальным конусом u.

Теорема 1.8 [2, гл. VI, теорема 1.1]. Если решение y=j(x) уравнения (4) имеет нормальный конус u, то укороченное уравнение (11), для которого u М U_j^(d), имеет сильно асимптотически эквивалентное решение y = y(x).

1.10. Случай горизонтального ребра G⁽¹⁾_j. В этом случае у всех точек Q=(q₁,q₂) ребра G_j⁽¹⁾ координата q₂ одинакова. Положим

g(x,y)

def
=

y^-q₂

(1)
j

(x,y)

(29)

и сделаем логарифмическое преобразование

h = dlny/dx.

(30)

Согласно теореме 2.4 из [2, гл. VI] при этом преобразовании дифференциальная сумма g(x,y) перейдет в дифференциальную сумму h(x,h)[( def) || ( = )] g(x,y) и уравнение (11) примет вид

h(x,h)=0.

(31)

Теперь для уравнения (31) получаем основную задачу с конусом задачи p₁+p₂ і 0. Сумму порядков всех производных, входящих в дифференциальный моном a(x,y), назовем суммарным порядком дифференцирования монома a(x,y) и обозначим D(a). Для дифференциальной суммы (3) суммарный порядок дифференцирования D(f)=max_iD(a_i). Пусть ребро G_j⁽¹⁾ соединяет вершины G_j-1⁽⁰⁾=(q₁^ў,q₂^ў) и G_j⁽⁰⁾=(q₁^ўў,q₂^ў) с q₁^ў < q₁^ўў.

Пусть W_j - степень характеристического многочлена c_j(r) укорочения [^(f)]⁽⁰⁾_j, соответствующего вершине G⁽⁰⁾_j.

Теорема 1.9 [7, п. 5.4]. Если W_j-1 = D([^(f)]_j-1⁽⁰⁾)=D([^(f)]_j⁽¹⁾) (или D([^(f)]_j⁽⁰⁾)=D([^(f)]_j⁽¹⁾) = W_j), то уравнение (11) не имеет подходящих решений при x® 0 (или x®Ґ).

Следовательно, если W_j-1 = D([^(f)]_j-1⁽⁰⁾)=D([^(f)]_j⁽¹⁾) = D([^(f)]_j⁽⁰⁾) = W_j, то преобразование (30) и дальнейшее исследование делать не надо.

§ 0. Степенные разложения решений в окрестности нуля и бесконечности при a № 0

Для второго уравнения Пенлеве

f(z,w)

def
=

-w" + 2w³ + zw + a = 0,

(32)

где a - комплексный параметр, при a № 0 найдем все степенные разложения

w = c_rz^r +

c_sz^s

(33)

его решений, где коэффициенты c_r,c_s = const О \Bbb C, c_r № 0, показатели степени r,s О \Bbb R: r < s, если z® 0, и r > s, если z®Ґ.

2.1. Основные объекты степенной геометрии. Пусть параметр a № 0, тогда носитель S(f) уравнения (32) состоит из четырех точек:

Q₁ = (-2,1), Q₂ = (0,3), Q₃ = (1,1), Q₄ = (0,0).

(34)

Их выпуклая оболочка G(f) это четырехугольник с вершинами G⁽⁰⁾_j = Q_j и ребрами G⁽¹⁾_j = {Q_j,Q_j+1}, где j=1,2,3,4, Q₅=Q₁ (см. рис. 1).

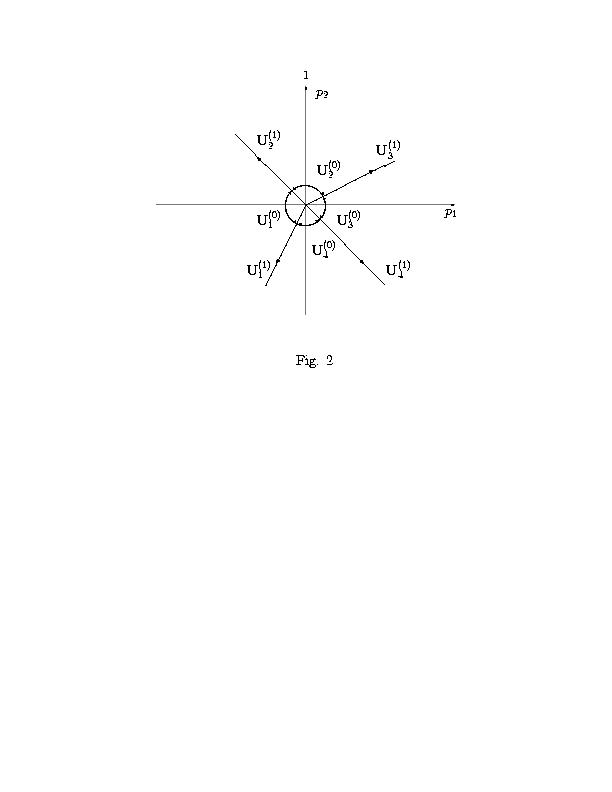
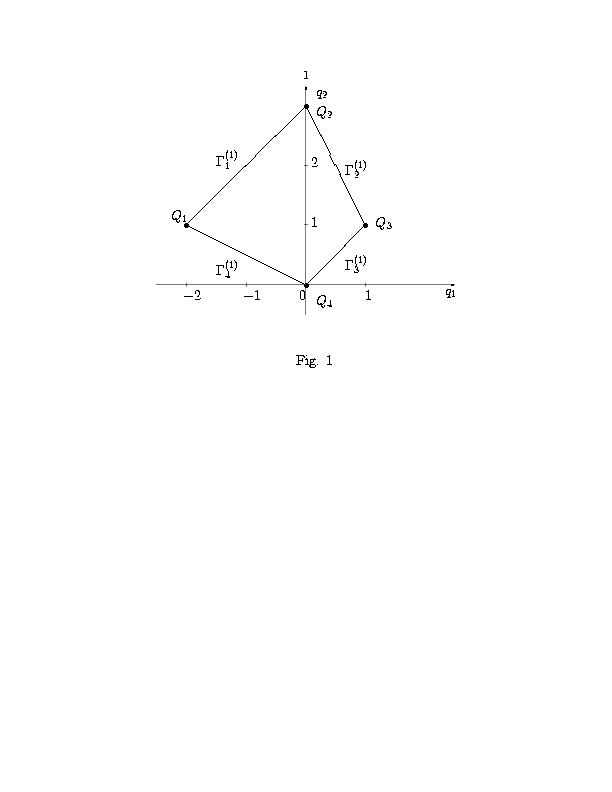Внешние нормали N_j к ребрам G⁽¹⁾_j суть N₁ = (-1,1), N₂ = (1,1/2), N₃ = (1,-1), N₄ = (-1,-2). Нормальные конусы U⁽¹⁾_j ребер G⁽¹⁾_j суть (см. рис. 2):

U⁽¹⁾₁ = {P:p₂ = 2p₁ < 0} = {lN₁},

U⁽¹⁾₂ = {P: p₂ = -p₁ > 0} = {lN₂},

U⁽¹⁾₃ = {P: p₂ = p₁/2 > 0} = {lN₃},

U⁽¹⁾₄ = {P: p₂ = -p₁ < 0} = {lN₄}, l > 0.

(35)

Нормальные конусы U_j⁽⁰⁾ вершин G_j⁽⁰⁾ это углы между нормальными конусами прилегающих к вершине ребер (см. рис. 2):

U⁽⁰⁾₁ = {P: p₂ < -p₁, p₂ > 2p₁ },

U⁽⁰⁾₂ = {P: p₂ > p₁/2, p₂ > -p₁ },

U⁽⁰⁾₃ = {P: p₂ > -p₁, p₂ < p₁/2 },

U⁽⁰⁾₄ = {P: p₂ < -p₁, p₂ < 2p₁ }.

(36)

Теорема 2.1. Носитель S(f) уравнения (32) лежит в решетке Z с базисом B₁ = (1,1), B₂ = (2,-1).

Доказательство. Согласно (34) имеем Q₁ = -B₁, Q₂ = 2B₁ - B₂, Q₃ = B₁, Q₄ = 0, т.е. все точки носителя S(f) имеют вид mB₁ + nB₂ с целыми m и n. При этом точки -Q₁ и Q₃ совпадают с базисными векторами решетки. ^[¯]

2.2. Решения, соответствующие вершинам. Рассмотрим укороченное уравнение, соответствующее вершине G⁽⁰⁾₁:

(0)
1

def
=

- w" = 0

(37)

и найдем все его подходящие укороченные решения

w = c_rz^r, c_r № 0

(38)

с w(1,r) О U⁽⁰⁾₁. Согласно (36) p₁ < 0 в конусе U⁽⁰⁾₁. Следовательно, w = -1, z® 0 и разложения будут по возрастающим степеням z.

Размерность грани d=0, поэтому согласно п. 1.3 положим

g(z,w) = X^-Q₄

(0)
4

= z²w

(0)
4

= z²w^-1(-w").

Для w = z^r получим характеристический многочлен c(r)[( def) || =]g(z,z^r) = r(1 -r), т.е. r₁ = 0 и r₂ = 1 суть корни уравнения c = 0. Рассмотрим их по отдельности.

Корню r=r₁=0 соответствует вектор R=(1,0) и согласно (36), вектор wR О U⁽⁰⁾₁. Итак, получили семейство F⁽⁰⁾₁1 укороченных решений w=c₀ с произвольной постоянной c₀ № 0 и w = -1.

Найдем первую вариацию:

(0)
4

/dw = -d²/dz².

(39)

Согласно теореме 1.2 получаем оператор

L(z) = -d²/dz²\not є 0.

(40)

Его характеристический многочлен n(k) имеет вид

n(k) = z^2-kL(z)z^k = k(1-k).

(41)

Уравнение n(k) = 0 имеет 2 корня: k₁ = 0 и k₂ = 1. В нашем случае w = -1 и r=0, следовательно, конус задачи (16) есть K = {s > 0}. Поэтому имеется одно критическое значение k₂ = 1 > 0 и æ = 1. Согласно п. 1.5. найдем множество K. Сдвинутый носитель решения w=c₀ это вектор (0,1). Вместе с векторами B₁ = (1,1) и B₂ = (2,-1) он порождает целочисленную решетку \Bbb Z². Но множество Sў лежит в секторе, ограниченном лучами, натянутыми на векторы B₁ и B₂. Его целочисленные точки, лежащие на прямой q₂ = -1, образуют множество K. Следовательно,

K = {s = l, целые l > 1}.

(42)

Так как число критических чисел æ = 1 и k₂ П K, то по теореме 1.4 показатели s лежат в множестве K(k₂) = K(1), при этом коэффициент c₁ произволен, а остальные коэффициенты c_s определяются однозначно. Множество K(1) находим, используя лемму 1.2:

K(1) = {s = l, целые l і 1}.

(43)

Таким образом, получаем, что разложение (33) в случае r=0 есть

w = c₀ + c₁z +

Ґ
е
k=2

c_kz^k =

Ґ
е
k=0

c_kz^k,

(44)

где c₀ = const № 0 и c₁ - произвольны, а c_k, k > 1, однозначно определены. Это семейство разложений G⁽⁰⁾₁1.

Рассмотрим теперь случай r=r₂=1. Здесь вектор P=w(1,1) = -(1,1) О U⁽⁰⁾₁. Конус задачи K = {s > 1}. В этом случае первая вариация снова есть (39) и не зависит от укороченного решения (38), тогда по теореме 1.2, учитывая наше решение w=cz, получаем, что оператор L(z) снова есть (40). Характеристический многочлен n(k) имеет вид (41). Опять корни уравнения n(k) = 0 равны k=0 и k=1. Но ни одно из этих собственных значений не лежит в конусе задачи K = {s > 1}. Следовательно, число критических чисел æ = 0. По теореме 1.3 все показатели s разложения (33) лежат в множестве K и все коэффициенты c_s определяются однозначно. Используя замечание 1.3, найдем множество K. Теперь сдвинутый носитель укороченного решения w=cz это вектор (1,-1). Он не лежит в решетке теоремы 2.1. Вместе с векторами B₁, B₂ он порождает целочисленную решетку \Bbb Z². Согласно замечанию 1.3 множество K есть

K = {s = 1+ m, целые m > 0}.

(45)

Следовательно, решение будет выглядеть следующим образом:

w = cz +

Ґ
е
k=2

c_kz^k =

Ґ
е
k=1

c_kz^k,

(46)

где произвольное c = const = c₁ № 0, а остальные c_k определяются однозначно. Вычислим второе приближение. Так как вектор P = w(1,r) = -(1,1), то m = 1, а mў = 0. Поэтому ближайшей точкой s₀ к r=1 будет s₀ = 2. В данном случае критических чисел нет, поэтому можем вычислить коэффициент c₂ по формуле (26). Выделим в сумме f(X) второе приближение [^([^(f )])] = еf_Q(X) по Q:бP,Qс = mў, т.е. [^([^(f )])] = a = b₂. Согласно (26)

c₂ = -

/n(2) = -a/2,

(47)

т.к. по (41) n(2)=2. Таким образом, получили семейство G⁽⁰⁾₁2.

Вершинам G⁽⁰⁾₂, G⁽⁰⁾₃ и G⁽⁰⁾₄ соответствуют алгебраические укороченные уравнения. Согласно замечанию 1.1 они не имеют решений вида (38).

2.3. Решения, соответствующие ребру G⁽¹⁾₁. Ребру G⁽¹⁾₁ соответствует укороченное уравнение

(1)
1

def
=

-w" + 2w³

(48)

с нормальным конусом U⁽¹⁾₁ = {P = l(-1,1) = -l(1,-1), l > 0}. Поэтому здесь r=-1 и w = -1. Для уравнения (48) будем искать решение w=cz^-1, c № 0. Подставляя это выражение в уравнение (48), для постоянной c получаем алгебраическое уравнение 2c³ -2c = 0. Оно имеет два ненулевых решения c = ±1. Итак, получили два укороченных решения w = ±z^-1. Вычислим их критические числа.

Первая вариация по w

(1)
3

/dw = -d²/dz² + 6w²,

(49)

тогда, учитывая наше решение w = cz^-1 и то, что c² = 1, получим:

L(z) = -d²/dz² + 6z^-2.

(50)

Характеристический многочлен n(k) имеет вид

n(k) = z^2-kL(z)z^k = -k(k-1)+6 = -(k+2)(k-3).

(51)

Он имеет два корня k₁ = -2 и k₂ = 3. Конус задачи здесь

K = {s > -1}.

(52)

Следовательно, только k₂ = 3 О K, т.е. имеется только одно критическое число и æ = 1. Согласно п. 1.5 вычислим множество K показателей s в разложении (33). Для укороченного уравнения w = c_-1z^-1 сдвинутый носитель содержит точку (-1,-1) = -B₁, которая лежит в решетке Z, описанной в теореме 2.1. Эта решетка пересекается с прямой q₂=-1 по точкам q₁ = s вида

s = -1+3l,

(53)

где l - целое число. Согласно (52) и замечанию 1.3 получаем, что множество K состоит из точек (53) c l > 0. Критическое число k₂ = 3 не лежит в множестве K, тогда по теореме 1.4 все показатели решения s лежат в множестве K(k₂) = K(3) , причем коэффициент c_k₃ = c₃ - произволен, а остальные c_s однозначно определяются. По лемме 1.2 множество

K(3) = {s = 3l + 4m -1, целые l,m і 0, l+m > 0}.

(54)

Найдем второе приближение решения. Для этого сначала определим значения m и mў. В нашем случае имеем вектор P = w(1,r) = (-1,1), следовательно, получаем, что m = 3, а mў = 0. Тогда получаем, что s₀ = 2. Так как у нас единственное критическое число k₂ = 3 и условие |k₂ -r | > m-mў выполнено, то коэффициент c₂ можем найти по формуле (26). Здесь [^([^(f )])] = zw+a и b₂ = [^([^(f )])](z,cz^-1) = a+c. Согласно (51) n(2)=4, следовательно, согласно (26) c₂ = -(c+a)/4, где c = ±1.

Множество (54) состоит из точек s=2,3,5,6,..., т.е. 2,3 и целые s і 5, поэтому ребру G⁽¹⁾₁ соответствует степенное разложение решений

w = cz^-1 + c₂z² + c₃z³ +

Ґ
е
s=5

c_sz^s,

(55)

где коэффициенты c = ±1, c₂ = -(c+a)/4, c₃ - произвольное, а остальные c_s - однозначно определяются. Они образуют два однопараметрических семейства G⁽¹⁾₁1 и G⁽¹⁾₁2.

Однако, при c₃ = 0 получаем разложения с показателями (53), т.е.

w = cz^-1 + z^-1

Ґ
е
k=1

c_kz^3k.

(56)

2.4. Решения, соответствующие ребру G⁽¹⁾₂. Ребру G⁽¹⁾₂ соответствует укороченное уравнение

(1)
2

def
=

zw + 2w³ = 0

(57)

с нормальным конусом U⁽¹⁾₂ = {P=l(1,1/2)}. Поэтому здесь r=1/2 и w = 1 и ищем решения уравнения (57) в виде w = cz^1/2. Для c получаем алгебраическое уравнение c + 2c³ = 0, которое имеет два ненулевых корня c = ±i/Ц2. Т.к. w = 1, то z®Ґ, поэтому степенные разложения вида (33) являются разложениями по убывающим степеням z^s с s < 1/2. Укороченное уравнение (57) является алгебраическим. По замечанию 1.2 его решения w=cz^1/2 не имеют критических чисел (т.е. æ = 0) и для них

n(k) = n₀ = z^-1

(1)
2

¶w

= z^-1(z+6w²) = -2.

(58)

Найдем множество K значений показателей s в разложении (33). Сдвинутый носитель укороченного решения w = cz^1/2 содержит точку B₃ = (1/2,-1). Вместе с векторами B₁ и B₂ теоремы 2.1 она порождает решетку с базисом B₁, B₃. Она пересекается с прямой q₂=-1 по точкам

q₁ = s =

(59)

где m - целые. Поскольку K = {s < 1/2}, то получаем

K = {

m, целые m > 0}.

(60)

По теореме 1.3 все показатели s лежат в множестве (60) и все коэффициенты c_s определяются однозначно. Найдем коэффициент при втором приближении решения. Здесь [^([^(f )])] = a, согласно (58) n(-1) = -2 и по (26) имеем c_-1 = a/2.

Окончательно получаем, что ребру G⁽¹⁾₂ соответствуют два разложения

w = cz^1/2 + c_-1z^-1 +z^1/2

Ґ
е
s=2

c_sz^-3s/2,

(61)

где c=±i/Ц2, c_-1 = -a/2, а все остальные c_s однозначно определяются. Они образуют семейства G⁽¹⁾₂1 и G⁽¹⁾₂2.

2.5. Решения, соответствующие ребру G₃⁽¹⁾. Ему соответствует укороченное уравнение

(1)
3

= zw + a = 0

(62)

с нормальным конусом U⁽¹⁾₃ = {P=l(1,-1), l > 0}. Следовательно, r=-1 и w = 1. Ищем решение w = c_-1z^-1. Подставляя его в (62), получаем c_-1 = -a и c_-1 № 0, т.к. по преположению a № 0.

Т.к. w = 1, то z ® Ґ и степенные разложения вида (33) являются разложениями по убывающим степеням z^s, s < -1, и конус задачи K выглядит следующим образом

K = {s < -1}.

(63)

Укороченное уравнение (62) является алгебраическим. По замечанию 1.2 его решения w=c_-1z^-1 не имеют критических чисел и для них

n(k) = n₀ = z^-1(

(1)
3

¶w

) = 1.

(64)

По теореме 1.3 все показатели степени s разложения вида (33) лежат в множестве K и все коэффициенты c_s определяются однозначно. Найдем множество K. Для укороченного уравнения w = c_-1z^-1 сдвинутый носитель содержит точку (-1,-1) = -B₁, которая лежит в решетке Z, описанной в теореме 2.1. Эта решетка пересекается с прямой q₂=-1 по точкам q₁ = s вида (53). Согласно (63) и замечанию 1.3 множество

K = {-1-3l, целые l > 0}.

(65)

Таким образом, получили, что разложение

w = c_-1z^-1 +

Ґ
е
k=1

c_k z^-3k-1

(66)

является одним из решений уравнения (32), где c_-1 = -a, а остальные c_s однозначно определяются. Найдем коэффициент во втором приближении. Для этого найдем m и mў. Т.к. P = w(1,r) = (1,-1), то m = 0, а mў = -3. Следовательно, ближайшей точкой к r=-1 является точка s = -4. Т.к. критических чисел нет, то мы можем найти коэффициент c_-4 тем же способом, который использовался при нахождении коэффициента второго приближения в случае ребра G⁽¹⁾₂. Здесь [^([^(f )])] = -w" + 2w³. Поэтому b_-4 = -2a-2a³ и c_-4 = 2a+2a³, согласно (64).

Окончательно получаем, что уравнение (32) имеет одно решение

w = c_-1z^-1 +

Ґ
е
k=1

c_-3k-1z^-3k-1,

(67)

где c_-1 = -a, c_-4 = 2a(a² +1) и все остальные c_s однозначно определяются, образующее семейство G⁽¹⁾₃.

2.6. Решения, соответствующие ребру G⁽¹⁾₄. Ребру G⁽¹⁾₄ соответствует укороченное уравнение

(1)
4

def
=

-w" + a = 0

(68)

с нормальным конусом U⁽¹⁾₄ = {P: p₂ = 2p₁ < 0}, т.е. r=2 и w = -1. Будем искать решение w=cz². Для постоянной c получим следующее значение: c = a/2 и c № 0, т.к. по предположению, a № 0. Т.к. w = -1, то z ® 0, и разложения вида (33) будут по возрастающим степеням z^s с s > 2. Множество

K = {s > 2}

(69)

это конус задачи для ребра G⁽¹⁾₄. Первая вариация d[^(f)] / dw, оператор L(z) и функция n(k) здесь имеют вид (39), (40) и (41) соответственно. Поскольку корни k₁=0 и k₂ = 1 уравнения n(k)=0 не лежат в конусе задачи (69), то критических чисел нет. Найдем множество K показателей s разложения (33). Сдвинутый носитель укороченного решения w=cz² это точка (2,-1) = B₂, которая лежит в решетке Z теоремы 2.1. Эта решетка пересекается с прямой q₂=-1 по точкам q₁=s вида (53). Согласно (69) и замечанию 1.3 имеем

K = {s = 2+3l, целые l > 0}.

(70)

Причем, т.к. нет критических чисел, то по теoреме 1.4 все показатели s лежат в множестве (70). Найдем второе приближение. У нас m = 0, mў = -3, тогда ближайшей точкой к r = 2 будет s₀ = 5. Т.к. æ = 0, то вычислим коэффициент c₅ по формуле (26). Здесь [^([^(f )])] = zw, b₅ = c, по (41) n(5)=-20, откуда по (26) имеем c₅ = c/20 = a/40. Таким образом, ребру G⁽¹⁾₄ соответствует степенное разложение

w = cz² + c₅z⁵ +

Ґ
е
l=2

c_2+3lz^2+3l,

(71)

где c = a/2, c₅ = a/40 и все остальные c_s однозначно определяются. Это семейство обозначим G⁽¹⁾₄.

2.7. Сводка результатов и их обсуждение. Были найдены следующие разложения решений уравнения (32).

Двупараметрическое (по c № 0 и c₁) семейство G⁽⁰⁾₁1 степенных разложений (44).
Однопараметрическое (по c) семейство G⁽⁰⁾₁2 степенных разложений (46), которое включается в предыдущее семейство при c₀ = 0.
Два однопараметрических (по c₃) семейства G⁽¹⁾₁1 и G⁽¹⁾₁2 степенных разложений (55), которые при c₃ = 0 имеют вид (56).
Два степенных разложения G⁽¹⁾₂1 и G⁽¹⁾₂2 (61).
Cемейство G⁽¹⁾₃, состоящее из одного степенного разложения (66).
Cемейство G⁽¹⁾₄ - одно степенное разложение (71).

Существование решений 1, 2 семейств G⁽⁰⁾₁1 и G⁽⁰⁾₁2 следует из теоремы Коши [11, гл. I, § 5, с. 18]. Решения 3 семейств G⁽¹⁾₁1 и G⁽¹⁾₁2 были найдены в [12]. Эти решения также были получены в [13, гл. I, § 4, пример 4.6] с помощью перехода к системе двух уравнений и с использованием специальной сложной программы, проверяющей выполнение условия совместности. Решения 4 и 5 семейств G⁽¹⁾₂1, G⁽¹⁾₂2 найдены в [14]. Решение в семействе G⁽¹⁾₄ и разложения (56) найдены, по-видимому, впервые. В [11, гл. III, § 10, с. 183, 184] утверждается, что второе уравнение Пенлеве не имеет решений, которые вблизи точки z=Ґ разлагаются в ряд вида w = a_kz^k+ a_k+1z^k-1 + ... Но это не верно, ибо разложение 5 (т.е. (66)) является именно таким с k=-1. Отметим еще, что согласно теореме 1.7 разложения 1, 2, 3, 6 сходятся для достаточно малых |z|, а 4, 5 могут расходиться при любых z.

§ 0. Степенные разложения решений в окрестности точки z₀ № 0

Рассмотрим второе уравнение Пенлеве (32) в окрестности точки z₀ № 0, т.е. в исходном уравнении (32) сделаем замену z = [(z)\tilde] + z₀:

,x)

def
=

-w" + 2w³ +

w + z₀w +a,

(72)

где a - комплексный параметр и a № 0. Найдем все степенные разложения вида (33) решений уравнения (72), где z заменено на [(z)\tilde].

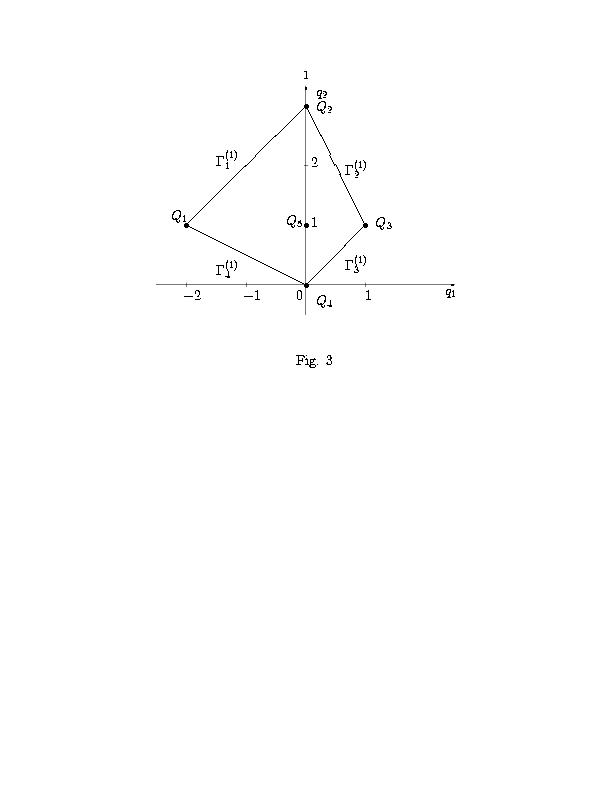
3.1. Основные объекты степенной геометрии. Носитель S(f) уравнения (72) состоит из пяти точек:

Q₁ = (-2,1), Q₂ = (0,3), Q₃ = (1,1), Q₄=(0,0), Q₅ = (0,1)

(73)

и показан на рис. 3. В данном случае ребра, вершины (см. рис. 3) и нормальные конусы (см. рис. 2) для них те же, что были в случае § 2. Носитель S(f) уравнения (72) лежит в целочисленной решетке \Bbb Z² и не лежит в более редкой решетке. Поскольку нас интересуют только решения с [(z)\tilde] ® 0, то конус задачи p₁ < 0. С ним пересекаются только нормальные конусы U⁽⁰⁾₁, U⁽⁰⁾₂, U⁽⁰⁾₄ и U⁽¹⁾₁, U⁽¹⁾₄. Поэтому далее рассматриваем только решения, соответствующие граням G⁽⁰⁾₁, G⁽⁰⁾₂, G⁽⁰⁾₄, и G⁽¹⁾₁, G⁽¹⁾₄.

3.2. Решения, соответствующие вершинам. Случай вершины G⁽⁰⁾₁ аналогичен уже рассмотренному в пункте 2.2. Т.о. получаем, что вершине G⁽⁰⁾₁ соответствуют семейство G⁽⁰⁾₁1 (формула (44)) и семейство G⁽⁰⁾₁2 (формулы (46) и (47)) c заменой z на [(z)\tilde].

Вершинам G⁽⁰⁾₂ и G⁽⁰⁾₄ соответствуют алгебраические укороченные уравнения [^(f)]⁽⁰⁾_j=0. Согласно замечанию 1.1 они не имеют решений вида (38).

3.3. Решения, соответствующие ребру G⁽¹⁾₁. Ему соответствует укороченное уравнение

(1)
1

def
=

-w" + 2w³.

(74)

Этот случай аналогичен уже рассмотренному в п. 2.3. Т.о. ребру G⁽¹⁾₁ соответствует нормальный конус U⁽¹⁾₁ = {P=l(-1,1), l > 0}, поэтому w = -1 и r=-1. Будем рассматривать решение w=c[(z)\tilde]^-1 уравнения (74), где c=±1. Первая вариация d[^(f)]⁽¹⁾₁ /dw, оператор L([(z)\tilde]) и функция n(k) здесь имеют вид (49), (50) и (51) соответственно. Т.к. из корней k₁ = -2 и k₂ = 3 уравнения n(k)=0 в конусе задачи K = {s > -1} лежит только k₂ = 3, то он и является критическим числом и æ = 1. Множество K в данном случае есть

K = {2l-1, целые l > 0},

(75)

где l - целое. Т.к. критическое число k₂ = 3 лежит в множестве (75), то надо вычислить начальный отрезок разложения

w = c

-1

+ c₁

+ c₂

+ c₃

(76)

Найдем значение коэффициента c₁. В этом случае, m = 3, mў=1, тогда ближайшей точкой к r=-1 будет точка s₀ = 1. Тогда по формуле (26), получаем c₁ = -cz₀/6 = -±z₀/6, т.к. c=±1. Чтобы найти коэффициент c₂, в уравнение (72) подставим w = c[(z)\tilde]^-1 + c₁[(z)\tilde] + c₂[(z)\tilde]² и приравняем к нулю коэффициент при [(z)\tilde]⁰. Получаем сумму

-2c₂ + 2(c

-1

+ c₁

+ c₂

)³ + c +c₁

+ c₂

+ z₀c

-1

+ z₀c₁

+ z₀c₂

+a.

(77)

Ее свободный член есть -2c₂ + 6c²c₂ + c. Следовательно, c₂ = -c/4 = -±1/4.

Вычислим в сумме (77) коэффициент при [(z)\tilde]¹. Получаем

b₃ = 6cc₁²+z₀c₁ = c₁(6cc₁+z₀) = c₁(-c²z₀+z₀)=0.

Следовательно, коэффициент c₃ произволен. Это случай (a) замечания 1.5. Итак, ребру G⁽¹⁾₁ соответствуют степенные разложения решений

w = c

-1

+ c₁

+ c₂

+ c₃

Ґ
е
k=4

c_k

(78)

где c = ±1, c₁ = ±z₀/6, c₂ = -±1/4, c₃ - произвольно, а все остальные c_k однозначно определяются. Они образуют два однопараметрических семейства G⁽¹⁾₁1 и G⁽¹⁾₁2.

3.4. Решения, соответствующие ребру G⁽¹⁾₄. Ребру G⁽¹⁾₄ соответствует укороченное уравнение

(1)
4

def
=

-w" + a = 0

(79)

с нормальным конусом U⁽¹⁾₄ = {P: p₂ = 2p₁ < 0}, т.е. r=2 и w = -1. Будем искать решение w=c[(z)\tilde]². Для постоянной c получим следующее значение: c = a/2 и c № 0, т.к. по предположению, a № 0. Т.к. w = -1, то z ®0, и разложения вида (33) у нас будут по возрастающим степеням [(z)\tilde]^s с s > 2. Множество

K = {s > 2}

(80)

это конус задачи для ребра G⁽¹⁾₄. Первая вариация d[^(f)] / dw, оператор L(z) и функция n(k) здесь имеют вид (39), (40) и (41) соответственно. Поскольку корни k₁=0 и k₂ = 1 уравнения n(k)=0 не лежат в конусе задачи (80), то критических чисел нет. Т.к. нет критических чисел, то по теореме 1.4 все показатели s лежат в множестве

K = {4,5,6,7...}.

(81)

Найдем второе приближение. У нас m = 0, mў = -2, тогда ближайшей точкой к r = 2 будет s₀ = 4. Т.к. æ = 0, то вычислим коэффициент c₄ по формуле (26). Здесь [^([^(f )])] = z₀w, b₄ = z₀c, по (41) n(4)=-12, откуда по (26) имеем c₄ = z₀c/12 = az₀/24. Таким образом, ребру G⁽¹⁾₄ соответствует степенное разложение

w = c

+ c₄

Ґ
е
l=5

c_l

(82)

где c = a/2, c₄ = (az₀)/24 и все остальные c_s однозначно определяются. Это семейство обозначим G⁽¹⁾₄.

3.5. Сводка результатов и их обсуждение. Были найдены следующие разложения решений уравнения (72):

Двупараметрическое (по c₀ и c₁) семейство G⁽⁰⁾₁1 степенных разложений вида (44).
Однопараметрическое (по c₁) семейство G⁽⁰⁾₁2 степенных разложений вида (46), которое включается в предыдущее семейство при c₀ = 0.
Два однопараметрических (по c₃) семейства G⁽¹⁾₁1 и G⁽¹⁾₁2 решений (78).
Семейство G⁽¹⁾₄, состоящее из одного решения (82).

По теореме 1.7 все они сходятся при достаточно малых |[(z)\tilde]|. Существование разложений 1 и 2 семейств G⁽⁰⁾₁1 и G⁽⁰⁾₁2 следует из теоремы Коши. Разложения 3 семейств G⁽¹⁾₁1 и G⁽¹⁾₁2 найдены в [12]. Разложение 4, т.е. семейство G⁽¹⁾₄, найдено, по-видимому, впервые.

§ 0. Разложения решений при a=0

При a=0 второе уравнение Пенлеве есть

f(z,w)

def
=

-w" + 2w³ + zw = 0.

(83)

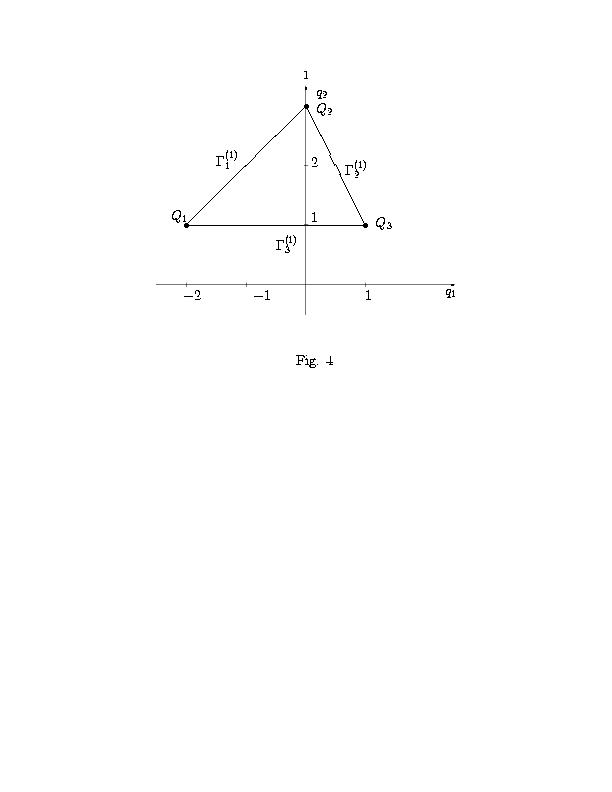
4.1. Объекты степенной геометрии. Носитель S(f) уравнения (83) состоит из трех точек:

Q₁ = (-2,1), Q₂ = (0,3), Q₃ = (1,1).

(84)

Их выпуклая оболочка G это треугольник с вершинами G⁽⁰⁾_j = Q_j и ребрами G⁽¹⁾_j = {Q_j,Q_j+1}, где j=1,2,3,Q₄=Q₁ (см. рис. 4).

Внешние нормали N_j⁽¹⁾ к ребрам G⁽¹⁾_j cуть N₁⁽¹⁾ = (-1,1), N₂⁽¹⁾=(1,1/2), N₃⁽¹⁾ = (0,1). Нормальные конусы ребер суть

U⁽¹⁾₁ = {P: p₁ = 0, p₁ > -p₂} = {lN₁},

U⁽¹⁾₂ = {P: p₁ = -p₂, p₁ < 2p₂ } = {lN₂},

U⁽¹⁾₃ = {P: p₂=p₁/2 > 0} = {lN₃}, l > 0.

(85)

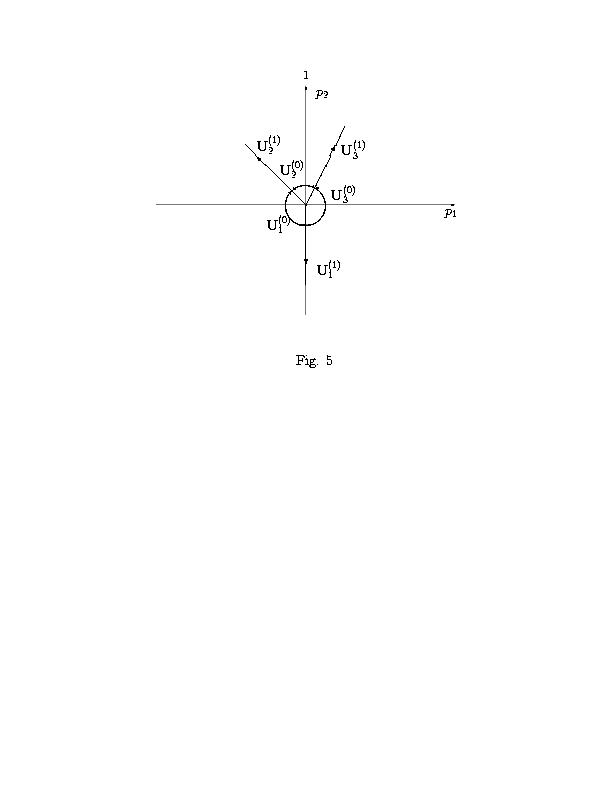
Нормальные конусы U_j⁽⁰⁾ вершин G_j⁽⁰⁾ - это углы между нормальными конусами прилегающих к вершине ребер (см. рис. 5):

U⁽⁰⁾₁ = {P: 2p₂ < p₁, p₁ > 0 },

U⁽⁰⁾₂ = {P: p₁ > -p₂, p₁ < 2p₂ },

U⁽⁰⁾₃ = {P: p₁ < 0, p₁ < -p₂ }.

(86)

Теорема 4.1. Сдвинутый носитель Sў(f) лежит в решетке Z₃ с базисом B₄ = (3,0), B₅ = (-1,2).

4.2. Решения, соответствующие вершинам. Рассмотрим укороченное уравнение, соответствующее вершине G⁽⁰⁾₁:

(0)
1

def
=

- w" = 0.

(87)

Этот случай аналогичен тому, который описан в пункте 2.2.

Следовательно, вершине G⁽⁰⁾₁ соответствуют два семейства решений: семейство G⁽⁰⁾₁1 (формула (44)) и семейство G⁽⁰⁾₁2 (формула (46)).

Укороченные уравнения, соответствующие вершинам G⁽⁰⁾₂ и G⁽⁰⁾₃:

(0)
2

def
=

2w³ = 0,

(0)
3

def
=

zw = 0

(88)

являются алгебраическими. По замечанию 1.1 они не имеют решений вида w = c_r z^r, c_r № 0. Поэтому укорочения, состоящие из одного алгебраического монома, можно не рассматривать.

4.3. Решения, соответствующие ребру G⁽¹⁾₁. Ребру G⁽¹⁾₁ соответствует укороченное уравнение

(1)
1

def
=

-w" + 2w³ = 0.

(89)

Этот случай аналогичен тому, который был описан в п. 2.3. Таким образом, ребру G⁽¹⁾₁ соответствуют степенные разложения (55):

w = cz^-1 + c₂z² + c₃z³ +

Ґ
е
s=5

c_sz^s,

(90)

где коэффициенты c = ±1, c₂ = -c/6, c₃ - произвольное, а остальные c_s однозначно определяются. Они образуют два однопараметрических семействa G⁽¹⁾₁1 и G⁽¹⁾₁2. При c₃ = 0 получается разложение (56).

4.4. Решения, соответствующие ребру G⁽¹⁾₂. Ему соответствует укороченное уравнение

(1)
2

def
=

zw + w³ = 0.

(91)

Уравнение (91) имеет два решения w = cz^1/2, где c² = 1/2, c = ±iЦ{1/2}, которые нам подходят. Этот случай аналогичен тому, который описан в п. 2.4. Исследовав данное ребро по той же схеме, получим, что ребру G⁽¹⁾₂ соответствует степенное разложение

w = cz^1/2+

е
s

c_sz^s,

(92)

где все показатели степени s О K:

K = {-3l-5/2, целые l і 0},

(93)

где l - целое и c = ±i/Ц2, все c_s однозначно определены. Найдем коэффициент второго приближения. Сначала найдем значения m и mў. В нашем случае, т.к. P = w(1,r) = (1, 1/2), m = 3/2, а mў = -3/2. Тогда s₀ = -5/2 и по формуле (26) находим, что c_-5/2 = -c/16. Итак, ребру G⁽¹⁾₂ соответствуют степенные разложения

w = cz^1/2 +

Ґ
е
l

c_lz^-3l-5/2,

(94)

причем c = ±Ц2/2, c_-5/2 = -c/16. Они образуют семейства G⁽¹⁾₂1 и G⁽¹⁾₂2.

4.5. Решения, соответствующие ребру G⁽¹⁾₃. Ему соответствует укороченное уравнение

(1)
3

def
=

-w" + zw = 0.

(95)

Уравнение (95) имеет решение w є 0. Но оно не имеет решений вида w = c_rz^r, c_r № 0. Ребро G⁽¹⁾₃ горизонтально, поэтому для нахождения решений укороченного уравнения (95) воспользуемся методами п.п. 1.9 и 1.10. Согласно п.1.10 сделаем логарифмическое преобразование вида (30), т.е. y = d lnw/dz. Тогда wў = yw, w" = yўw+y²w, и уравнение (95) переходит в уравнение

w(-yў- y² + z) = 0.

(96)

После сокращения на w получаем уравнение

h(z,y)

def
=

-yў- y² + z = 0.

(97)

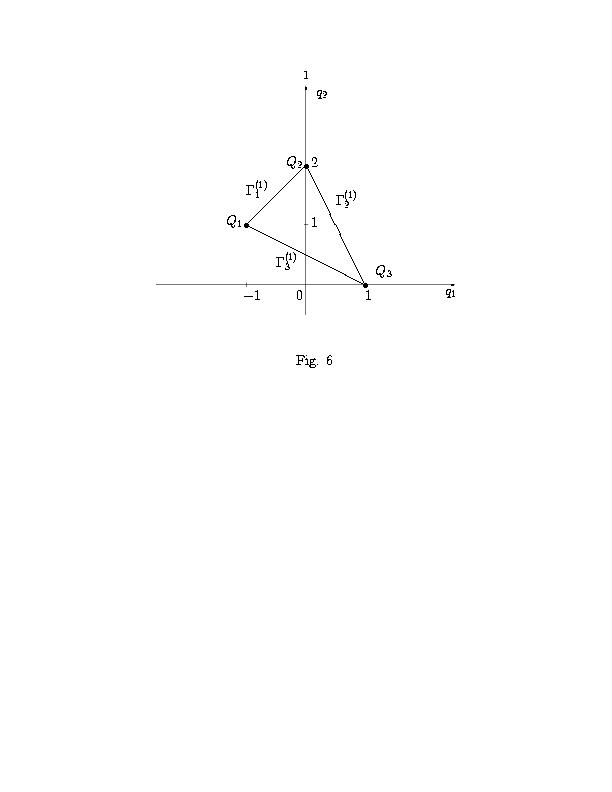
Для уравнения (97) строим его носитель [(S)\tilde] = S(h), многоугольник [(G)\tilde] = G(h), его грани [(G)\tilde]^(d)_j, их нормальные конусы [(U)\tilde]^(d)_j. Носитель [(S)\tilde] (см. рис. 6) состоит из трех точек [(Q)\tilde]₁ = (-1,1), [(Q)\tilde]₂ = (0,2), [(Q)\tilde]₃ = (1,0). Многоугольник [( G)\tilde] = G(h) это треугольник с вершинами [(G)\tilde]⁽⁰⁾_j = [(Q)\tilde]_j (см. рис. 6). Ребра (см. рис. 6) [(G)\tilde]⁽¹⁾₁ = {[(Q)\tilde]₁, [(Q)\tilde]₂}, [(G)\tilde]⁽¹⁾₂ = {[(Q)\tilde]₂,[(Q)\tilde]₃}, [(G)\tilde]⁽¹⁾₃ = {[(Q)\tilde]₃, [(Q)\tilde]₁}.

Внешние нормали [(N)\tilde]_j к ребрам [(G)\tilde]⁽¹⁾_j суть [(N)\tilde]₁ = (-1,1), [(N)\tilde]₂ = (2,1), [(N)\tilde]₃ = (-1,-2).

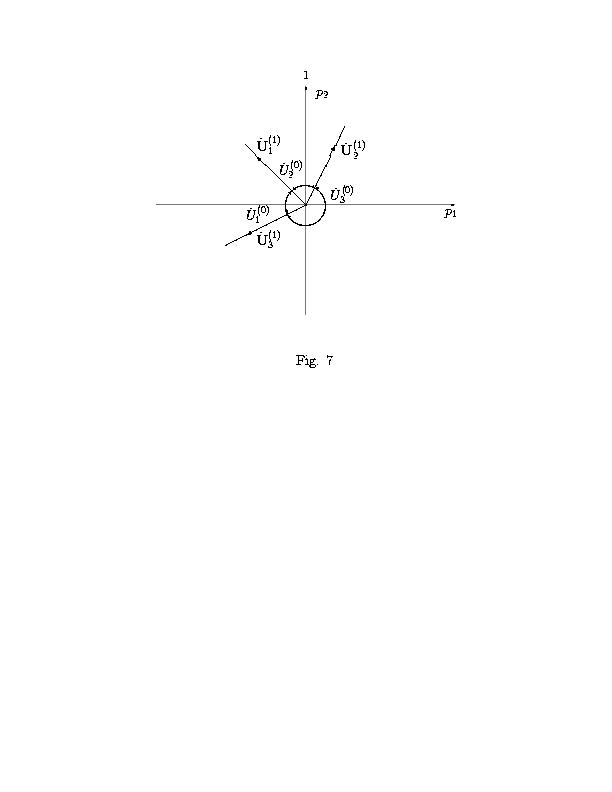Нормальные конусы [(U)\tilde]^(d)_j (см. рис. 7) суть

(1)
1

= {p₁ = -p₂ < 0} = {l

(1)
2

= {p₂ = 2p₁ > 0} = {l

(1)
3

= {p₁ = 2p₂ < 0} = {l

},l > 0.

(98)

(0)
1

= {p₁ < -p₂, p₁ < 2p₂},

(0)
2

= {p₂ > -p₁,p₂ > 2p₁},

(0)
3

= {p₁ > 2p₂, p₂ < 2p₁}.

(99)

Теорема 4.2. Носитель S(h) лежит в решетке с Z₆ базисом B₆ = (3,-1), B₇ = (0,1).

Согласно п. 1.10 для уравнения (97) получаем конус задачи [(p)\tilde]₁ + [(p)\tilde]₂ > 0. На рис.7 показана его граница. С этим конусом задачи пересекаются только нормальные конуса [(U)\tilde]⁽⁰⁾₂, [(U)\tilde]⁽⁰⁾₃ и [(U)\tilde]⁽¹⁾₂. Поэтому в дальнейшем достаточно рассмотреть только решения, соответствующие граням [(G)\tilde]⁽⁰⁾₂, [(G)\tilde]⁽⁰⁾₃ и [(G)\tilde]⁽¹⁾₂. Вершинам [(G)\tilde]⁽⁰⁾₂ и [(G)\tilde]⁽⁰⁾₃ соответствуют алгебраические уравнения -y² = 0 и z=0 соответственно. По замечанию 1.1 они не дают подходящих решений. Ребру [(G)\tilde]⁽¹⁾₂ соответствует алгебраическое укороченное уравнение

-y² + z=0.

(100)

Оно имеет два подходящих решения y = ±z^1/2, т.е. r=1/2 и w = 1. Согласно замечанию 1.2 эти укороченные решения не имеют критических чисел (æ = 0) и для них

n(k) = -±2.

(101)

Здесь вектор сдвинутого носителя укороченного уравнения есть (1/2, -1). Вместе с векторами теоремы 4.2 он порождает решетку Z₆ с базисом (3/2, 0), (1/2, -1). Она пересекается с прямой q₂=-1 по точкам q₁=1/2 + 3l/2, где l - целое. Поскольку конус задачи для искомого разложения есть s < 1/2, то по замечанию 1.3 множество

K = {s = 1/2 - 3l/2, целые l > 0}.

(102)

По теореме 1.3 уравнение (97) имеет решение в виде ряда

y = ±z^1/2 + z^1/2

Ґ
е
l=1

c_lz^-3l/2,

(103)

где все коэффициенты c_l определяются однозначно при фиксированном знаке y корня из z. Вычислим коэффициент c₁ в разложении (103). Здесь [^([^(h )])] = -yў. Поэтому b₁ = -±1/2. Согласно (26) и (101) имеем c₁ = -1/4. Пусть h = lnw, тогда hў = y и согласно (103)

h =

у
х

y dz = ±

z^3/2+c₀ -

lnz+

Ґ
е
l=2

2c_l

3(1-l)

z^3(1-l)/2,

(104)

где c₀ - произвольная постоянная. Для решений w(z) укороченного уравнения (97) это дает разложения

w =

z^1/4

exp[±

z^3/2+

Ґ
е
l=2

2c_l

3(1-l)

z^3(1-l)/2]

(105)

при z® Ґ. Согласно нормальному конусу [(U)\tilde]⁽¹⁾₃ имеем w ® 0 при z® Ґ. Следовательно, в квадратной скобке в (105) знак берется так, чтобы

±Rez^3/2 < 0.

(106)

По теореме 1.8 решение укороченного уравнения (95) является асимптотикой решения исходного уравнения, если w® 0, т.е. при выполнении условия (106) для z. Таким образом, получили два однопараметрических семейства G⁽¹⁾₃1 и G⁽¹⁾₃2 сильных асимптотик.

4.6. Сводка результатов и их обсуждение. Были найдены следующие разложения решений уравнения (83).

Двупараметрическое (по c₀ и c₁) семейство G⁽⁰⁾₁1 степенных разложений (44).
Однопараметрическое (по c) семейство G⁽⁰⁾₁2 степенных разложений (46).
Два однопараметрических (по c₃) семейства G⁽¹⁾₂1 и G⁽¹⁾₂2 степенных разложений (90). При c₃ = 0 получаются разложения (56).
Два семейства G⁽¹⁾₃1 и G⁽¹⁾₃2 степенных разложений (92).
Два однопараметрических (по [(c)\tilde]) семейства G⁽¹⁾₃1 и G⁽¹⁾₃2 асимптотик (105).

По теореме 1.7 разложения 1 - 3 сходятся при достаточно малых |z|. Разложения 4 и 5 могут расходиться при любом z. Интересно, что носители разложений 2 - 4 отличаются от носителей соответствующих разложений в случае a № 0. Это, по-видимому, новый результат. Укороченное уравнение (95) это известное уравнение Эйри [15] и разложения (105) для его решений известны [16].

Литература

Брюно А.Д. Локальный метод нелинейного анализа дифферециальных уравнений. М.: Наука, 1979. 256 c.
Брюно А.Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.: Физматлит, 1998. 288 c.
Брюно А.Д. Автомодельные решения и степенная геометрия // Успехи математических наук, 2000, т. 55, N 1, с. 3-44.
Брюно А.Д. Степенные разложения решений одного алгебраического или дифференциального уравнения // Доклады АН, 2001, т. 380, N 2, с. 155-159.
Брюно А.Д. Степенные разложения решений одного алгебраического или дифференциального уравнения. Препринт N 63. М.: ИПМ им. М.В. Келдыша, 2000. 22 с.
Bruno A.D. Power geometry as a new calculus // Proceeding of ISAAC 2001. Amsterdam: Kluwer, 2003.
Брюно А.Д. Асимптотики и разложения решений обыкновенного дифференциального уравнения. Препринт N 9. М.: ИПМ им. М.В. Келдыша, 2003. 39 с.
Тихомиров В.М. Фреше производная // Математическая Энциклопедия. М.: Советская Энциклопедия, 1985, т. 5, с. 666.
Розов Н.Х. Пенлеве уравнение // Математическая Энциклопедия. М.: Советская энциклопедия, 1984, т. 4, с. 233-234.
Gromak V.I., Laine I., Shimomura S., Painleve Differential Equations in the Complex Plane, Walter de Gruyter. Berlin, New York, 2002. 303 p.
Голубев В.В. Лекции по аналитической теории дифференциальных уравнений. М.-Л.: ГИТТЛ, 1941, 400 с. 2-е изд., М.-Л.: ГИТТЛ, 1950.
Голубев В.В. К теории уравнений Пенлеве. // Матем. сборник, 1912, т. 28, N 2, с. 323-349.
Козлов В.В., Фурта С.Д. Асимптотики решений сильно нелинейных систем дифференциальных уравнений. М.: МГУ, 1996. 244 с.
Яблонский А.И. Асимтотическое разложение правильных решений некоторых классов дифференциальных уравнений // ДАН БССР, 1964, т. 8, N 2, с. 77-80.
Федорюк М.В. Эйри уравнение // Математическая энциклопедия, т. 5, М.: Советская энциклопедия, 1985, с. 939.
Федорюк М.В. Эйри функция // Математическая энциклопедия, т. 5, М.: Советская энциклопедия, 1985, с. 939 - 941.

File translated from T_EX by T_TH, version 3.40.
On 02 Mar 2005, 19:41.

Степенные ряды и нестепенные асимптотики решений второго уравнения Пенлеве

( Power series and nonpower asymptotics of solutions to the second Painlevé equation
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Брюно А.Д., Завгородняя Ю.В.
(A.D.Bruno, Yu.V.Zavgorodnyaya)

ИПМ им. М.В.Келдыша РАН

Москва, 2003
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 02-01-01067)

Аннотация

Abstract

Степенные ряды и нестепенные асимптотики решений второго уравнения Пенлеве ( Power series and nonpower asymptotics of solutions to the second Painlevé equation Preprint, Inst. Appl. Math., the Russian Academy of Science)

Брюно А.Д., Завгородняя Ю.В. (A.D.Bruno, Yu.V.Zavgorodnyaya) ИПМ им. М.В.Келдыша РАН

Москва, 2003 Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 02-01-01067)

Аннотация

Abstract

Степенные ряды и нестепенные асимптотики решений второго уравнения Пенлеве

( Power series and nonpower asymptotics of solutions to the second Painlevé equation
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Брюно А.Д., Завгородняя Ю.В.
(A.D.Bruno, Yu.V.Zavgorodnyaya)

ИПМ им. М.В.Келдыша РАН

Москва, 2003
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 02-01-01067)