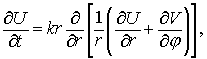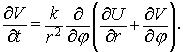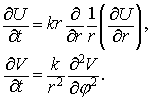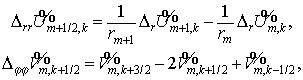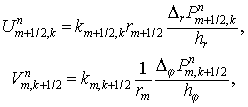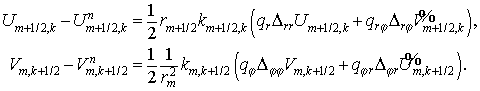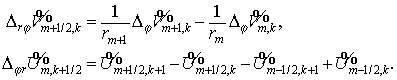Аннотация
В работе предлагается новый подход к построению безусловно устойчивых численных алгоритмов
решения многомерного уравнения теплопроводности в ортогональных системах координат.
Соответствующие методы (как первого, так и второго порядка аппроксимации по времени)
являются абсолютно экономичными и параллелизуемыми, а расчетная область может быть многосвязной.
Основной элемент этих методов — независимый расчет потоков по каждому пространственному
направлению.
Abstract
A new approach for the construction of unconditionally stable numerical algorithms for the
solution of the multidimensional heat equation for orthogonal coordinate systems is presented.
The corresponding methods (both first and second order of accuracy in time) are absolutely
economical and parallelizable. This approach can be applied to multiply connected domains
as well. The key element of the method is the calculation of fluxes along each spatial
direction independently of one another.
Введение
В данной работе предложен новый класс численных алгоритмов решения
смешанной задачи для многомерного уравнения теплопроводности.
Этот класс содержит как схемы первого порядка аппроксимации (остаточный член 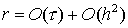 , так и второго — , так и второго — 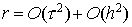 ). Все предлагаемые схемы безусловно устойчивы. Основным
преимуществом данных методов является их абсолютная экономичность: число
операций, необходимых для перехода на следующий временной слой равно ). Все предлагаемые схемы безусловно устойчивы. Основным
преимуществом данных методов является их абсолютная экономичность: число
операций, необходимых для перехода на следующий временной слой равно  , где , где  — объём разностной
сетки, а — объём разностной
сетки, а  — константа, не
зависящая от — константа, не
зависящая от 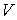 . (Для не слишком сложного вида коэффициентов . (Для не слишком сложного вида коэффициентов  .) .)
Экономичность алгоритмов, как правило, достигается двумя путями. Первый —
наиболее популярный — основан основан на редукции к одномерным разностным
задачам. Именно этот подход лежит в основе метода переменных направлений или, в
более общем плане, методе расщепления [2]. Второй подход состоит в
использовании тех или иных итерационных процедур, самые удачные из которых требуют
 операций [3]. операций [3].
Предлагаемый метод, так же, как и метод расщепления, в своей основе
содержит решение одномерных задач. Однако он принципиально отличен от метода
расщепления. Во-первых, здесь нет никакой факторизации оператора 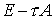 , которая и составляет суть метода расщепления. И, во-вторых,
данные схемы по построению являются консервативными, что автоматически
гарантирует выполнение дискретного аналога соответствующего закона сохранения.
Основная идея алгоритма состоит в способе расчета потоков. Именно неявная
разностная схема расчета потоков допускает редукцию к одномерным задачам, что и
обеспечивает как безусловную устойчивость, так и экономичность. , которая и составляет суть метода расщепления. И, во-вторых,
данные схемы по построению являются консервативными, что автоматически
гарантирует выполнение дискретного аналога соответствующего закона сохранения.
Основная идея алгоритма состоит в способе расчета потоков. Именно неявная
разностная схема расчета потоков допускает редукцию к одномерным задачам, что и
обеспечивает как безусловную устойчивость, так и экономичность.
Следует подчеркнуть, что расчет потоков по каждому из пространственных
направлений выполняется независимо, что позволяет легко распараллеливать
алгоритм. Именно по этой причине метод можно назвать методом независимых
потоков (МНП).
Данный метод предназначен для решения задач в ортогональных координатах. В
качестве таковых в работе рассмотрены две основные координатные системы —
декартова (для 2D и 3D задач) и полярная (для 2D уравнения). Эффективность
алгоритма иллюстрируется численными примерами для различных областей, в том
числе, двухсвязных. Наличие 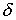 -образных источников не является осложняющим обстоятельством,
что позволяет использовать предлагаемый подход для решения задач с различными
сингулярностями. -образных источников не является осложняющим обстоятельством,
что позволяет использовать предлагаемый подход для решения задач с различными
сингулярностями.
Базовая конструкция алгоритма изложена в §1 на примере уравнения с
постоянными коэффициентами в декартовых координатах. В последующих параграфах
анализируются свойства метода: аппроксимация и устойчивость (§2) и
положительность (§3). Трехмерной версии схемы посвящен §4. Различные обобщения
обсуждаются в §5. Реализация того же подхода применительно к полярным
координатам составляет содержание §6. В последнем параграфе (§7) приведены
некоторые численные результаты, подтверждающие анонсированные свойства.
§1. Двумерное уравнение теплопроводности в декартовых координатах.
Для того, чтобы выделить основные конструкции схемы и исследовать ее
свойства, рассмотрим вначале простейшую двумерную задачу с постоянными
коэффициентами:

в области 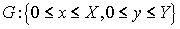 . Граничные условия . Граничные условия
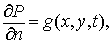
где 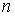 — нормаль к — нормаль к 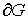 . (Для постоянных . (Для постоянных  эти коэффициенты,
конечно, можно считать равными, но в общем случае это не обязательно.) эти коэффициенты,
конечно, можно считать равными, но в общем случае это не обязательно.)
Разобъём 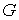 на прямоугольные
ячейки на прямоугольные
ячейки 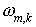 со сторонами со сторонами  и и 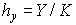 . Обозначим через . Обозначим через 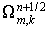 пространственно-временную ячейку пространственно-временную ячейку 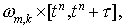 Рис. 1. Рис. 1.
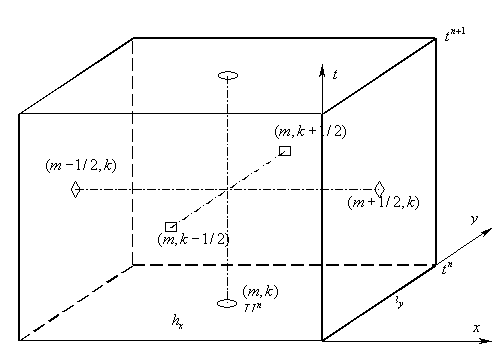
Рисунок 1.
Введем три набора точек и, соответственно, три набора сеточных функций:
а) целые точки — 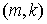 — центры ячеек — центры ячеек 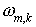 ; к этим точкам будем относить ; к этим точкам будем относить 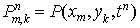 ; ;
б) 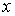 -полуцелые — -полуцелые —  — и — и 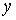 -полуцелые — -полуцелые — 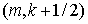 — точки; этим точкам
сопоставляются потоки — точки; этим точкам
сопоставляются потоки 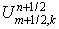 и и 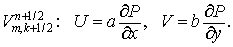
С использованием
потоков уравнение принимает вид
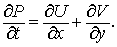
Поскольку имеет дивергентный вид,
воспользуемся стандартной концепцией конечных объемов с тем, чтобы решение
разностного уравнения точно удовлетворяло бы некоторому дискретному аналогу
закона сохранения, соответствующему выбранной форме записи уравнения. Поэтому
заключительным этапом разностной схемы является т.н. дивергентное замыкание
(дивергентный пересчет):

где 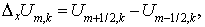 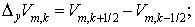   Здесь и далее для
упрощения записи в дальнейшем верхние дробные индексы опущены. Здесь и далее для
упрощения записи в дальнейшем верхние дробные индексы опущены.
Таким образом, любая реализация разностной схемы, базирующаяся на
дивергентном замыкании, полностью определяется способом вычисления потоков.
Напомним об одном важном обстоятельстве. Для получения разностной схемы 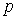 -го порядка аппроксимации ( -го порядка аппроксимации (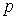 =1 или 2) достаточно вычислять потоки по схеме пониженного, =1 или 2) достаточно вычислять потоки по схеме пониженного,  -го порядка. Повышение порядка до требуемого осуществляется
за счет дивергентного пересчета. Этот факт является общим и не связан с
конкретным типом уравнения (параболические, гиперболические и т.д.). -го порядка. Повышение порядка до требуемого осуществляется
за счет дивергентного пересчета. Этот факт является общим и не связан с
конкретным типом уравнения (параболические, гиперболические и т.д.).
Начнем с простейшей схемы расчета потоков. Заметим, что 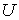 и и  удовлетворяют системе удовлетворяют системе
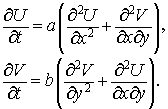
Учитывая сделанное выше замечание о порядке аппроксимации потоков, в
качестве схемы нулевого порядка для расчетов 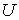 и и 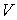 возьмем простейшую
неявную схему для усеченных уравнений возьмем простейшую
неявную схему для усеченных уравнений
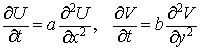 , ,
обозначая искомые потоки через 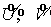 . А именно, . А именно,
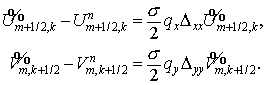
Здесь
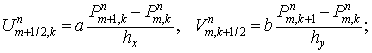
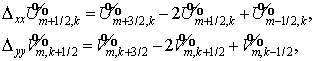
а 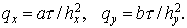
Параметер 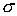 характеризует тот
промежуточный слой характеризует тот
промежуточный слой 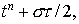 для которого аппроксимирует . Значению для которого аппроксимирует . Значению 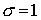 соответствует
срединный слой, значению соответствует
срединный слой, значению 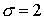 — верхний: — верхний: 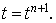
Система состоит из двух независимых подсистем, каждая из которых замыкается
граничным условием, порожденным :
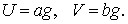
Остается лишь выполнить дивергентный пересчет .
Для построения более точной схемы уточненные значения 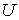 и и  будем находить уже из
полной системы . Таким образом, искомый алгоритм перехода на следующий слой распадается на
три этапа: будем находить уже из
полной системы . Таким образом, искомый алгоритм перехода на следующий слой распадается на
три этапа:
1) Нахождение предварительных, «грубых» значений потоков —  и и 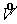 путем решения краевых
задач для разностных систем: путем решения краевых
задач для разностных систем:

Граничные условия — заданные (по ) значения  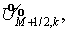 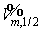 и и 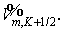
2) Отыскание окончательных (уточненных) значения потоков  и и 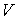 из системы разностных
уравнений, аппроксимирующей : из системы разностных
уравнений, аппроксимирующей :

где 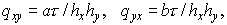 , а , а

Граничные условия — те же, что и на этапе 1.
Подчеркнем, что второй этап характеризуется своим
параметром  , который не обязан совпадать с , который не обязан совпадать с 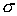 . .
3) Дивергентное замыкание по 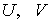 . .
Данный алгоритм решает также и задачу с граничным
условием Дирихле:
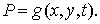
Действительно, пусть нормаль
к рассматриваемому элементу границы направлена вдоль оси 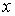 . Дифференцируя по . Дифференцируя по  , получаем , получаем  То есть То есть
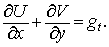
Но 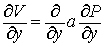 — известная на данном
граничном элементе функция (в силу ). Поэтому эквивалентно заданию — известная на данном
граничном элементе функция (в силу ). Поэтому эквивалентно заданию  , что тривиальным образом формирует граничное условие,
замыкающее разностную краевую задачу. , что тривиальным образом формирует граничное условие,
замыкающее разностную краевую задачу.
Легко видеть, что ни форма
области  , ни даже ее связность не имеют значения. Важно лишь, чобы
любой элемент границы , ни даже ее связность не имеют значения. Важно лишь, чобы
любой элемент границы  являлся стороной
приграничной ячейки являлся стороной
приграничной ячейки 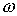 . На Рис. 2 изображен пример достаточно вычурной области,
которая, тем не менее, подвластна обоим (как упрощенному, так и полному)
алгоритмам. Единственным усложнением при обработке таких областей является
переменность длины каждого луча. . На Рис. 2 изображен пример достаточно вычурной области,
которая, тем не менее, подвластна обоим (как упрощенному, так и полному)
алгоритмам. Единственным усложнением при обработке таких областей является
переменность длины каждого луча.
Рисунок 2.
Следует также добавить, что
алгоритм очевидным образом параллелизуем, поскольку потоки на каждом луче обоих
направлений рассчитываются независимо.
§2. Аппроксимация и
устойчивость.
Обычная процедура
определения порядка и аппроксимации с помощью соответствующих тейлоровских
разложений точного решения в узлах шаблона разностной сетки здесь неосуществима
ввиду отсутствия самого конечного шаблона. Специфика алгоритма не позволяет
исключить значения потоков и получить непосредственную связь между 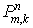 и и 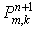 в конечном числе
точек. Поэтому для установления порядка аппроксимации воспользуемся той же
стандартной техникой, с помощью которой исследуется устойчивость схемы. в конечном числе
точек. Поэтому для установления порядка аппроксимации воспользуемся той же
стандартной техникой, с помощью которой исследуется устойчивость схемы.
Положим
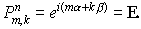 . .
Тогда 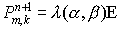 . Для нахождения собственного значения . Для нахождения собственного значения 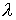 оператора послойного
перехода для полной схемы удобно ввести
промежуточные величины оператора послойного
перехода для полной схемы удобно ввести
промежуточные величины 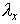 , , 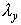 , , 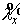 и и 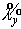 : :

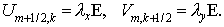
Подставив в , получим
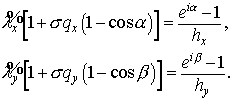
Подставив в , получим

И, наконец, из следует
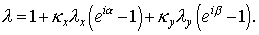
Для укороченной
схемы (без этапа 2) имеем просто
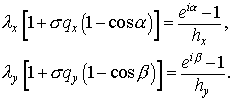
Введем обозначения

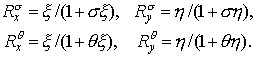
Тогда
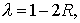
где для укороченной схемы
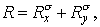
а для полной
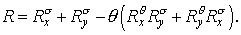
Начнем с порядка
аппроксимации. Сопоставим собственные функции 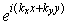 исходного
дифференциального оператора, рассматриваемые в узлах разностной сетки, т.е.
сеточные функции исходного
дифференциального оператора, рассматриваемые в узлах разностной сетки, т.е.
сеточные функции 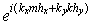 , с собственными функциями разностного оператора перехода , с собственными функциями разностного оператора перехода 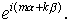 . Ясно, что . Ясно, что 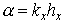 , , 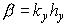 . Обозначим через . Обозначим через  множитель перехода со
слоя множитель перехода со
слоя 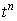 на слой на слой  для точной
собственной функции. Тогда порядок аппроксимации определяется по степени
совпадения тейлоровских разложений по для точной
собственной функции. Тогда порядок аппроксимации определяется по степени
совпадения тейлоровских разложений по 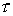 функций функций 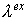 и и 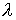 . .
Применительно к для 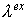 имеем имеем

То есть,
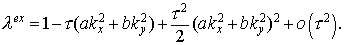
Найдем соответствующие разложения для обеих разностных схем. Имеем

Поскольку речь идет лишь о первом или втором порядке аппроксимации, то
второе слагаемое в разложении  может быть отброшено.
Выполнив аналогичное разложение для может быть отброшено.
Выполнив аналогичное разложение для 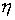 , окончательно получим , окончательно получим
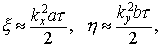
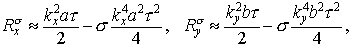
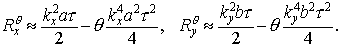
Рассмотрим укороченную схему. Для нее

Сравнение с позволяет заключить, что
(i)
при любом  укороченная схема
является схемой первого порядка аппроксимации; укороченная схема
является схемой первого порядка аппроксимации;
(ii)
ни при каком значении 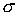 второй порядок не
достигается. второй порядок не
достигается.
Поэтому в дальнейшем будем называть эту схему просто схемой первого
порядка, или схемой 1.
Перейдем к полной схеме. Подставляя и в , найдем, что
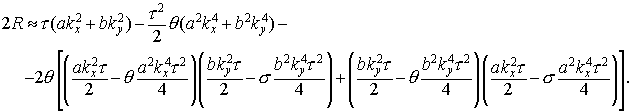
Оставляя лишь члены порядка 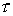 и и 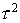 , получим , получим
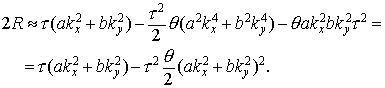
То есть,
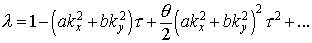
Из сравнения с следует, что
(i)
полная схема реализует второй порядок
аппроксимации лишь при 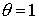 ; ;
(ii)
параметр 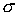 не влияет на порядок
аппроксимации. не влияет на порядок
аппроксимации.
Таким образом, далее эта схема будет рассматриваться лишь при 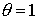 и называться схемой
2. и называться схемой
2.
Перейдем к исследованию устойчивости. Из следует, что необходимым условием устойчивости является выполнение
неравенства
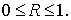
В дальнейшем под устойчивостью будет пониматься безусловная устойчивость,
т.е. устойчивость при всех значениях 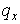 и и  . .
Начнем со схемы первого порядка (схемы 1). Поскольку 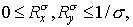 то то 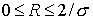 и, следовательно, для
устойчивости этой схемы необходимо, чтобы и, следовательно, для
устойчивости этой схемы необходимо, чтобы
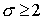
(т.е. «промежуточный» слой должен располагаться не ниже верхнего).
Для схемы 2, с учетом выбора 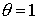 , ,
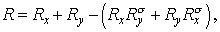
где
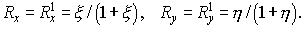
Так как речь идет о безусловной устойчивости, то неравенство должно
выполняться при всех 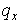 , ,  и, в
частности, при и, в
частности, при 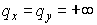 . Для этих предельных значений . Для этих предельных значений  что дает что дает  и и  . Таким образом, . Таким образом, 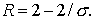 Следовательно, для выполнения
необходимо, чтобы Следовательно, для выполнения
необходимо, чтобы . .
Справедлива следующая
Теорема 1.
Для всех  необходимое условие
устойчивости схемы 2 выполнено. необходимое условие
устойчивости схемы 2 выполнено.
Доказательство.
Очевидно, что
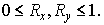
Поэтому
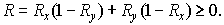
Для доказательства неравенства 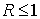 введем введем

Разность 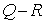 можно представить в
виде можно представить в
виде

Следовательно, при  т.е. при т.е. при 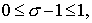 обе дроби в неотрицательны в силу . Поэтому обе дроби в неотрицательны в силу . Поэтому 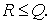 Но Но 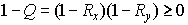 , что дает , что дает 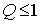 , а, значит и искомую оценку , а, значит и искомую оценку 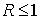 . .
§3. Монотонность (положительность)
Одним из важных свойств разностной схемы является ее монотонность. Впрочем,
это понятие применимо лишь к одномерным задачам. В многомерном случае речь идет
о положительности. Схема называется положительной, если из неотрицательности
всех 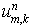 следует
неотрицательность следует
неотрицательность 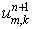 . .
Начнем с анализа схемы 1 и рассмотрим задачу Коши на всей плоскости. Ясно,
что для доказательства положительности схемы достаточно проверить
положительность для начальных данных вида
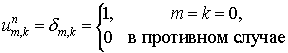
Так как при этих начальных данных
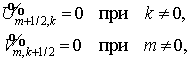
то 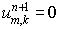 для всех «лучей», не
проходящих через точку для всех «лучей», не
проходящих через точку 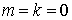 . Поэтому остается проверить положительность лишь величин . Поэтому остается проверить положительность лишь величин 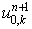 и и 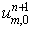 . .
Рассмотрим 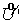 . Поскольку . Поскольку  , то , то 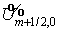 удовлетворяет
разностному уравнению (см. ) удовлетворяет
разностному уравнению (см. )
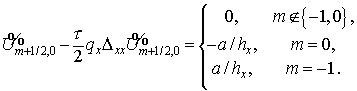
Так как при  и и  это уравнение
является однородным это уравнение
является однородным
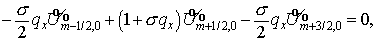
то его ограниченное решение имеет вид
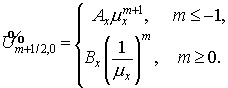
Здесь 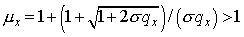 — корень
характеристического уравнения — корень
характеристического уравнения

Константы 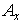 и и 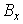 определяются из двух
неоднородных уравнений для определяются из двух
неоднородных уравнений для 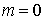 и и 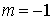 . .
Согласно

Подставив в , получим
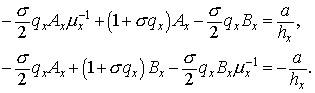
Отсюда следует, что 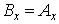 и и

Заметим, что обе ветви последовательности 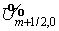 — возрастающие, т.е. — возрастающие, т.е. 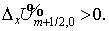 Но поскольку Но поскольку 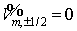 при при 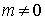 , то вне точки (0,0) , то вне точки (0,0)
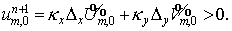
Аналогичные формулы для 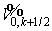 имеют вид: имеют вид:
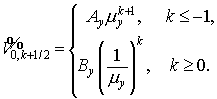
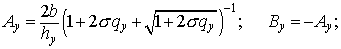

Осталось проверить положительность  Имеем Имеем

Таким образом, условие положительности эквивалентно неравенству
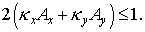
Подставляя явный вид 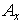  в , получим в , получим

Несложные выкладки дают более удобную форму этого условия:
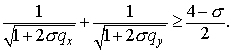
Отсюда следует, что при 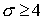 схема положительна при
любых схема положительна при
любых  , , 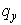 . .
В частном случае 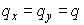 получаем простое
условие положительности (для получаем простое
условие положительности (для 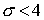 ) )
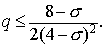
Что касается схемы второго порядка (схема 2), то вопрос об ее монотонности
может быть решен аналогичным образом. Однако интуитивно ответ и так ясен: за
повышение порядка аппроксимации приходится расплачиваться отсутствием
положительности — полная аналогия с теоремой Годунова [5] о монотонности схем
второго порядка для решения уравнения переноса 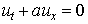 . И действительно, непосредственная проверка схемы 2 (т.е.
вычисление одного шага с . И действительно, непосредственная проверка схемы 2 (т.е.
вычисление одного шага с 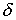 -образными начальными данными) для различных значений -образными начальными данными) для различных значений 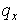 , ,  и и  подтвердила ее
неположительность. подтвердила ее
неположительность.
Этот факт, впрочем, не препятствует использованию схемы. Просто следует
иметь в виду, что расчет сингулярных решений требует особого внимания и все
зависит от того, какой результат более предпочтителен: визуально гладкий или
более точный. Стандартный способ «улучшения» результата состоит в той или иной
процедуре сглаживания — только для визуализации.
§4. Трехмерный случай (декартовы координаты)
Трехмерный аналог имеет вид
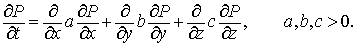
Соответственно теперь  , а , а  . Уравнение переходит в . Уравнение переходит в
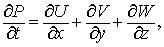
где  . Потоки . Потоки  , , 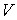 и и 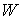 отнесены к отнесены к 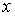 -полуцелым, -полуцелым, 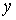 -полуцелым и -полуцелым и  -полуцелым точкам: -полуцелым точкам:  , , 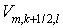 и и 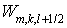 . В соответствии с дивергнтное замыкание имеет вид . В соответствии с дивергнтное замыкание имеет вид

Здесь, как обычно, 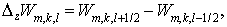 а а 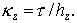
Первый этап схемы 1 — решение независимых краевых задач для разностных
уравнений
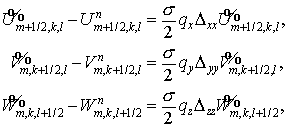
где 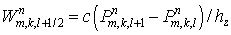 , , 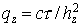 , а , а
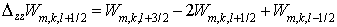 . .
Второй этап — дивергентное замыкание по 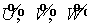 . .
Схема 2 состоит из тех же этапов, что и в двумерном случае. Первый этап —
определение  , , 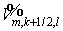 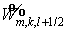 из одномерных
разностных уравнений . из одномерных
разностных уравнений .
На втором этапе уточненные значения  , , 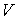 , , 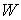 больших величин
отыскиваются путем решения краевых разностных задач, аппроксимирующие смешанные
задачи для системы дифференциальных уравнений вида (ср. с ): больших величин
отыскиваются путем решения краевых разностных задач, аппроксимирующие смешанные
задачи для системы дифференциальных уравнений вида (ср. с ):
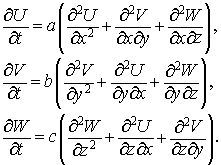
Соответствующим
аналогом теперь является система
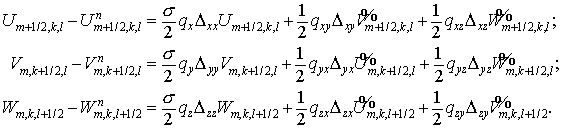
Здесь 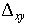 , , 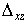 , , 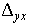 , , 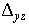 , , 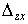 и и 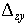 — смешанные разности — смешанные разности
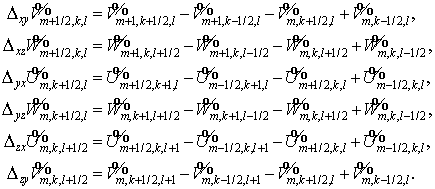
Подчеркнем, что на этом этапе, аналогично двумерному случаю, 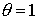 . .
Повторяя все вычисления двумерного случая применительно к 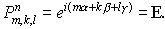 , легко убедиться в том, что снова , легко убедиться в том, что снова  , но теперь для схемы 1 , но теперь для схемы 1
 , ,
Здесь 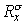 , , 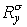 — см. – , а — см. – , а  , где , где  . .
Для схемы 2 выражение для 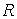 несколько более
сложное, чем . А именно: несколько более
сложное, чем . А именно:
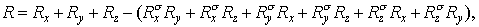
где  . .
Непосредственной проверкой, повторяя все преобразования двумерного случая,
несложно убедиться в том, что и для трехмерного уравнения теплопроводности
схема 1 является схемой первого порядка при любом 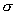 , а схема 2 имеет второй порядок аппроксимации. , а схема 2 имеет второй порядок аппроксимации.
Осталось получить условия устойчивости.
Схема 1:
Поскольку, как и в двумерном случае, здесь  то то  и, следовательно, для
устойчивости этой схемы необходимо, чтобы и, следовательно, для
устойчивости этой схемы необходимо, чтобы
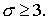
Этот результат выглядит парадоксально, т.к. означает, что «промежуточный»
слой должен располагаться выше верхнего, но это свидетельствует лишь об
условности чисто геометрических интерпретаций.
Перейдём к схеме 2, где ситуация сложнее. Возьмем предельный набор 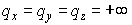 . Тогда . Тогда  , а , а 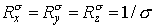 . Поэтому . Поэтому 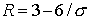 (см. ) и неравенство (см. ) и неравенство  порождает ограничение порождает ограничение
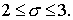
С другой стороны, полагая, например, 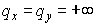 , , 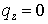 , получим , получим 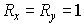 , , 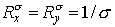 , , 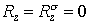 . Тогда . Тогда  , что приводит к неравенству , что приводит к неравенству
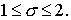
Сопоставляя и , получаем, что единственным значением параметра схемы может быть лишь  . Поэтому в дальнейшем под трёхмерной схемой 2 будет
пониматься только схема с . Поэтому в дальнейшем под трёхмерной схемой 2 будет
пониматься только схема с 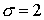 . .
Используя это конкретное значение, представим 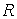 в двух эквивалентных
формах в двух эквивалентных
формах
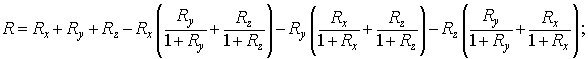
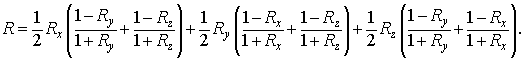
Теорема 2.
Для трёхмерной схемы 2 необходимое условие устойчивости выполнено.
Доказательство.
Из представления  в виде следует, что в виде следует, что 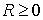 . Что касается неравенства . Что касается неравенства 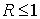 , то его проверка повторяет соответствующее доказательство
для двумерной схемы 2. Введем теперь , то его проверка повторяет соответствующее доказательство
для двумерной схемы 2. Введем теперь
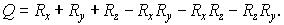
Из очевидного неравенства  , т.е. из неравенства , т.е. из неравенства 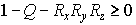 следует, что следует, что  . Осталось доказать, что . Осталось доказать, что 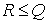 . Взяв . Взяв 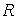 в форме , получим в форме , получим
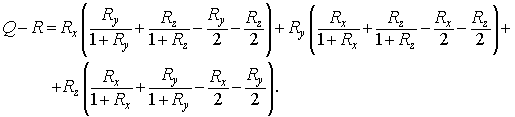
То есть

Таким образом, 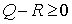 , что и дает , что и дает 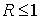 . .
Прежде чем переходить к
уравнению с переменными коэффициентами, рассмотрим — из чистого любопытства —
случай высокой размерности: 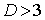 . .
Обе схемы очевидным образом
реализуются для уравнений любой размерности. Однако при 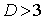 схема 1 безусловно
устойчива лишь при схема 1 безусловно
устойчива лишь при 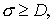
в то время, как
схема 2 ни при каких значениях 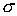 не является
безусловно устойчивой. Этот факт доказывается тем же способом, с помощью
которого была установлена единственность параметра не является
безусловно устойчивой. Этот факт доказывается тем же способом, с помощью
которого была установлена единственность параметра 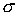 ( (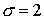 ) для трехмерного случая. ) для трехмерного случая.
Коснемся вопроса
положительности трехмерной схемы 1. Повторяя знакомые выкладки, получим условие
положительности
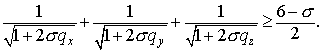
Следовательно, схема 1
является положительной лишь при  . .
Положив, как и в двумерном
случае  получим условие
положительности (для получим условие
положительности (для 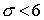 ) в виде ) в виде
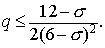
§5. Переменные коэффициенты.
Неоднородность. Система уравнений.
Представленный алгоритм естественным образом обобщается и на более общие
случаи. Для примера рассмотрим двумерную задачу
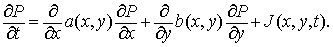
Снова введём  , , 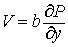 . Тогда . Тогда

Для 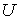 и и 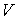 имеем имеем
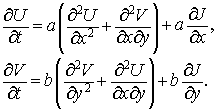
В соответствии со структурой алгоритма, в схеме 1 отыскиваются  и и 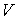 из «укороченной»
системы из «укороченной»
системы

а для схемы 2 используется . Дивергентный пересчет теперь соответствует , т.е. имеет вид
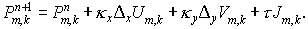
Для схемы 1 слагаемое  можно вычислять при
любом можно вычислять при
любом 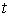 (на нижнем слое, на
верхнем, на промежуточном). Для схемы 2 обязательно (на нижнем слое, на
верхнем, на промежуточном). Для схемы 2 обязательно 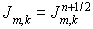 . .
Зависимость коэффициентов 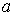 и и 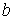 также и от также и от 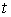 принципиально не
меняет алгоритм. Просто в добавляются слагаемые вида принципиально не
меняет алгоритм. Просто в добавляются слагаемые вида
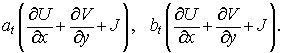
Соответствующим образом модифицируется и разностные уравнения.
Трехмерный случай не вносит принципиальных изменений.
Рассмотрим, наконец, важный случай  -образного источника (стока). Пусть в -образного источника (стока). Пусть в 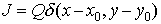 , где , где 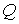 — интенсивность
источника. Для простоты ограничимся случаем — интенсивность
источника. Для простоты ограничимся случаем  . .
Пусть точка  является центром
«источниковой» ячейки, Рис. 3. является центром
«источниковой» ячейки, Рис. 3.
Рисунок 3.
Тогда речь идет о многосвязной области с вырезанным прямоугольником  и остается лишь
задать граничные условия Неймана на всех сторонах этой ячейки. Пренебрегая
угловой зависимостью и остается лишь
задать граничные условия Неймана на всех сторонах этой ячейки. Пренебрегая
угловой зависимостью  в окрестности в окрестности  , т.е. считая , т.е. считая 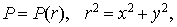 получаем: получаем:
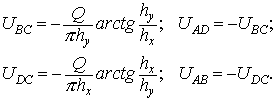
Для квадратной ячейки 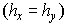 : :
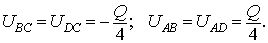
Вернемся к постоянным
коэффициентам и рассмотрим случай системы системы уравнений. Пусть в  — положительные
симметричные матрицы, не обязательно коммутирующие. — положительные
симметричные матрицы, не обязательно коммутирующие.
В силу линейности уравнения и постоянства
коэффициентов векторная сеточная функция на нижнем слое
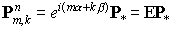
порождает аналогичные
сеточные функции 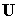 и и 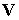 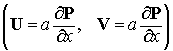 . А именно, . А именно,

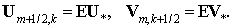
Векторный аналог дает (после сокращения на 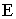 ) )
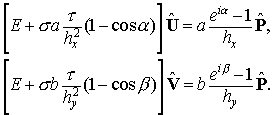
Здесь  — единичная матрица. — единичная матрица.
То есть, введя обозначения

получим (теперь, в отличие
от , 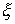 и и 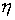 — матрицы): — матрицы):
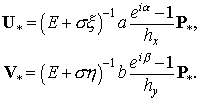
Подстановка в дивергентное замыкание
дает

Выразив  и и 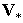 через через 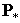 согласно и заменив согласно и заменив 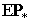 на на 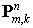 , получим , получим

Используя знакомые обозначения, перепишем в виде

где

Для устойчивости схемы необходимо, чтобы
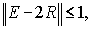
т.е., учитывая
положительность и симметричность матриц 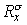 и и 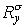
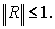
Имеем
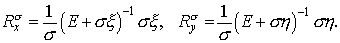
Но для любой положительной симметричной матрицы 

Поэтому 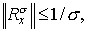 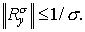 Следовательно, при Следовательно, при 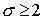 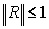 , что и требовалось установить. , что и требовалось установить.
Аналогичный анализ схемы 2 и обеих трехмерных схем
дает те же необходимые условия устойчивости, что и для скалярных схем.
§6. Полярная система
координат.
Уравнение теплопроводности в полярной системе
координат имеет вид (ограничимся случаем изотопной теплопроводности)
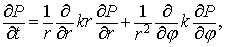
где коэффициент
теплопроводности 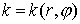 . .
Введем потоки

Тогда аналогом и являются уравнения
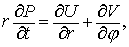
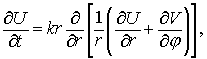
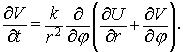
«Усеченные» уравнения – , используемые для расчета
предварительных значений потоков, имеют вид (ср. с ):
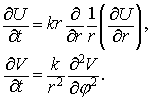
Введя естественным путем разностную сетку 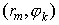 , получим следующую систему уравнений относительно , получим следующую систему уравнений относительно 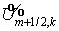 , , 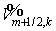 (ср. с ): (ср. с ):
Этап 1
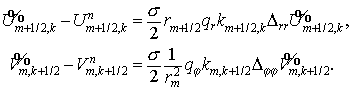
Здесь 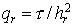 , ,  , ,
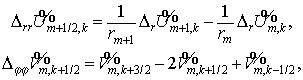

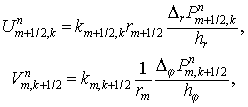
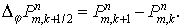
Дивергентное замыкание этого этапа:
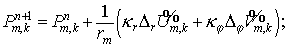
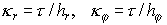
порождает схему первого
порядка.
Для реализации схемы второго порядка следует
выполнить второй этап — пересчет потоков —, соответствующий уравнениям – .
Этап 2
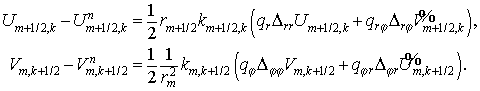
Здесь 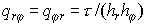 , а , а
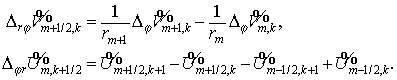
Наконец, дивергентное замыкание этого этапа:
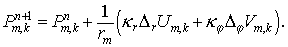
Алгоритм решения соответствующих трехточечных
разностных уравнений — тот же, что для декартовых координат. Для граничных
условий Неймана значения потоков замыкают разностную краевую задачу. В случае
постановки условий Дирихле (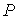 на границе известно) — например, на границе на границе известно) — например, на границе 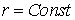 — трансверсальная
производная легко вычисляется ( — трансверсальная
производная легко вычисляется ( ; ;  — известные
величины). Поэтому в качестве замыкающего разностного граничного условия можно
использовать разностную аппроксимацию этой производной. — известные
величины). Поэтому в качестве замыкающего разностного граничного условия можно
использовать разностную аппроксимацию этой производной.
Алгоритм решения задачи с точечным источником
интенсивности  , расположенным в начале координат требует выделения
«нулевой» ячейки , расположенным в начале координат требует выделения
«нулевой» ячейки  радиуса радиуса 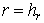 . Таким образом, задача решается во внешней к . Таким образом, задача решается во внешней к  области. На границе области. На границе 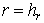 задается поток задается поток 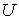 , определяемый интенсивностью источника: , определяемый интенсивностью источника: 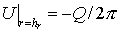 . .
Поскольку данное уравнение — даже при 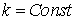 — имеет переменные
коэффициенты, то анализ устойчивости проводится в рамках принципа замороженных
коэффициентов. Для этого просто «заморозим» — имеет переменные
коэффициенты, то анализ устойчивости проводится в рамках принципа замороженных
коэффициентов. Для этого просто «заморозим» 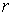 , т.е. заменим все значения , т.е. заменим все значения  и и 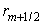 на на 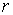 . Повторяя соответствующие преобразования декартового случая,
получим те же выражения для собственного значения оператора перехода: . Повторяя соответствующие преобразования декартового случая,
получим те же выражения для собственного значения оператора перехода:

где снова
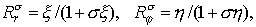
но теперь 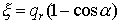 , а , а 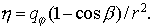
Ясно, что 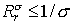 , ,  . Поэтому схема первого порядка безусловно устойчива ( . Поэтому схема первого порядка безусловно устойчива (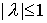 для любых для любых 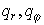 ) лишь при ) лишь при  . .
Анализ схемы второго порядка дает результат,
аналогичный случаю декартовых координат: схема безусловно устойчива при 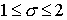 . .
§7. Верификация и численные
эксперименты.
1. Как уже было сказано во Введении, предложенный метод был реализован в
двух координатных системах — декартовой (2D и 3D) и полярной (2D). Для всех этих вариантов была
проверена (экспериментально) аппроксимация обеих схем. Технологически это
осуществлялось стандартным способом: для выбранной в качестве решения неоднородного
уравнения 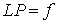 вычислялась
аналитически соответствующая правая часть вычислялась
аналитически соответствующая правая часть  , после чего задача решелась численно. Степень уменьшения
разности , после чего задача решелась численно. Степень уменьшения
разности 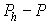 (в различных нормах)
при уменьшении шагов разностной сетки и дает реальный порядок аппроксимации.
При этом для схемы 1 уменьшению временного шага (в различных нормах)
при уменьшении шагов разностной сетки и дает реальный порядок аппроксимации.
При этом для схемы 1 уменьшению временного шага 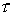 в в 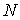 раз соответствовало
уменьшение пространственных шагов раз соответствовало
уменьшение пространственных шагов 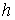 в в 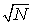 раз, а для схемы 2 раз, а для схемы 2  и и 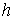 уменьшались
пропорционально. уменьшались
пропорционально.
Анализ численных результатов для различных областей полностью подтвердил
анонсированный порядок аппроксимации как в  -норме, так и в -норме, так и в  -норме. -норме.
2. Для демонстрации эффективности метода применительно к расчету
сингулярных решений были выбраны следующие две задачи:
а) Уравнение теплопроводности (для постоянных 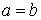 ) в квадратной области ) в квадратной области 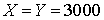 с точечными
источником и стоком одинаковой интенсивности в точках (2685,315) — источник и
(1485,1485) — сток. Начальные данные с точечными
источником и стоком одинаковой интенсивности в точках (2685,315) — источник и
(1485,1485) — сток. Начальные данные  . Граничные условия . Граничные условия  . .
Расчет производился на равномерной сетке 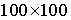 по схеме 2 с по схеме 2 с 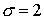 , с постоянным шагом , с постоянным шагом  , соответствующим значению числа Куранта , соответствующим значению числа Куранта 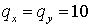 . .
На Рис. 4 представлена картина решения после 1200 шагов по времени.
Несмотря на сингулярный характер  и несоответствие
сетки (квадратная) поведению решения в окрестности особенностей, метод
демонстрирует хорошую разрешающую способность. и несоответствие
сетки (квадратная) поведению решения в окрестности особенностей, метод
демонстрирует хорошую разрешающую способность.
Замечание: поскольку значения 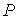 в центрах особых
ячеек не участвуют в алгоритме, для "красоты" рисунка они были
восстановлены с помощью простой экстраполяции. в центрах особых
ячеек не участвуют в алгоритме, для "красоты" рисунка они были
восстановлены с помощью простой экстраполяции.
б) Уравнение теплопроводности (для 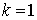 ) в круговой области ) в круговой области 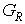 для для  с источником в центре
интенсивности с источником в центре
интенсивности  . Начальные данные: . Начальные данные: 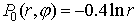 . Граничные условия: . Граничные условия: 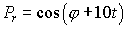 . .
Расчет проводился по схеме 1 с 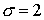 на сетке 60 (по на сетке 60 (по  ) ) 30 (по 30 (по 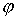 ). Шаг по времени ). Шаг по времени  . .
На Рис. 5 изображено решение на момент 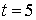 . (Здесь, в отличие от предыдущей задачи, значение . (Здесь, в отличие от предыдущей задачи, значение 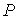 в центре не восстанавливалось
и поэтому поверхность в центре не восстанавливалось
и поэтому поверхность 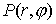 выглядит срезанной.) выглядит срезанной.)
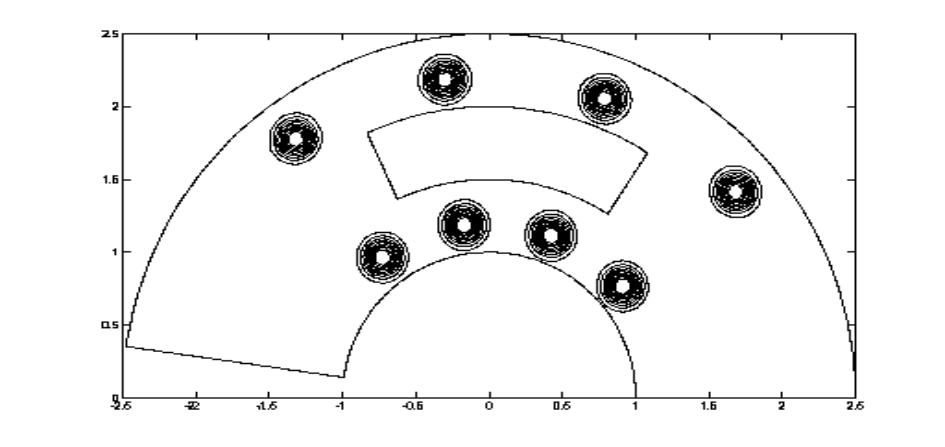
3. Последний пример — решение задачи для в двухсвязной области, представляющей собой сектор с вырезом. Граничные
условия — 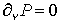 на всех компонентах
границы. Начальные данные моделируют сумму восьми на всех компонентах
границы. Начальные данные моделируют сумму восьми 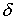 -образных функций (см. Рис. 6, где изображены изолинии
начального распределения -образных функций (см. Рис. 6, где изображены изолинии
начального распределения 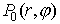 ). ).
Численное интегрирование проводилось по схеме 1 с 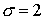 на сетке 120 на сетке 120 120, что соответствует шагам 120, что соответствует шагам 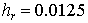 и и 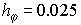 . Шаг по времени . Шаг по времени  . .
Ясно, что с течением времени решение должно выглаживаться, что и
демонстрирует Рис. 7, на котором изображены изолинии 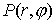 на момент на момент 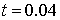 . .
——————————————
Представленный в данной работе метод решения уравнения теплопроводности в
ортогональной системе координат может использоваться как составной элемент при
создании численных алгоритмов решения и более общих задач, таких например, как
система уравнений фильтрации или система Навье-Стокса.
Литература
|
1.
|
Ю. Б. Радвогин. "Экономичные алгоритмы численного решения
многомерного уравнения теплопроводности." — ДАН, 2003, т. 388, №3, 295 –
297.
|
|
2.
|
Г. И. Марчук. "Методы вычислительной математики." — М.,
"Наука", 1988.
|
|
3.
|
А. А. Самарский, Е. С. Николаев. "Методы решения сеточных
уравнений." — М., "Наука", 1978.
|
|
4.
|
Л. М. Дегтярев, А. П. Фаворский. "Потоковый вариант метода
прогонки." — ЖВМиМФ, 1968, том 8, №3.
|
|
5.
|
С. К. Годунов, А. В. Забродин. "Численное решение многомерных задач
газовой динамики." — М., "Наука", 1976.
|
|

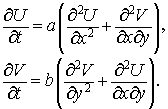
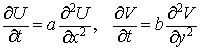 ,
,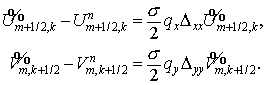
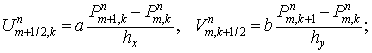
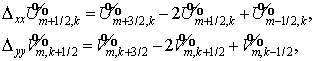




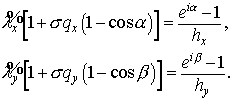

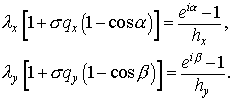
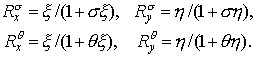

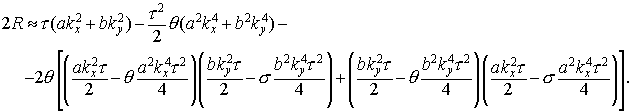
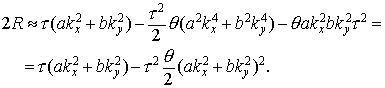

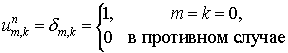
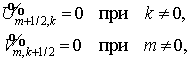
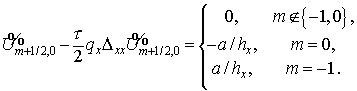
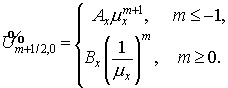

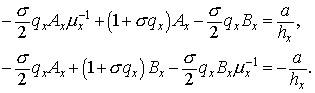
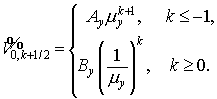


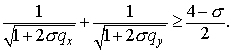
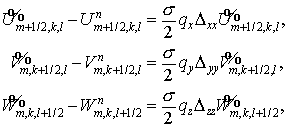
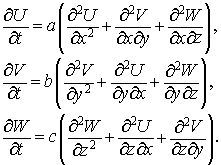
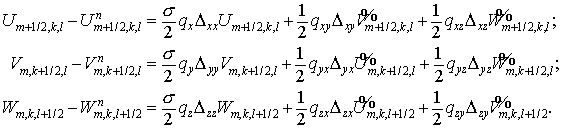
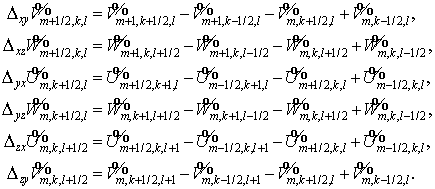
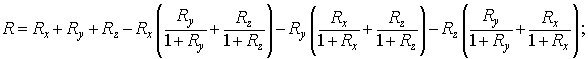
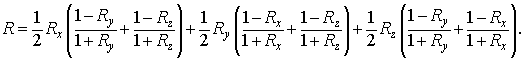
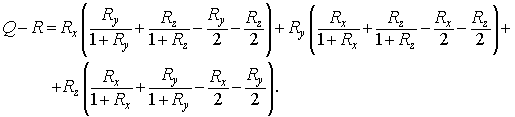

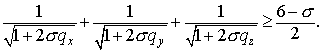
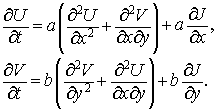

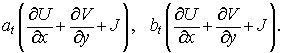

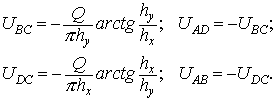
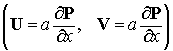 . А именно,
. А именно,