Аннотация
В работе найдено установившееся течение вязкой электропроводной несжимаемой двухкомпонентной
квазинейтральной гидродинамической полностью ионизованной плазмы в плоском бесконечном канале,
обусловленное постоянным градиентом давления плазмы. В МГД-пределе найденное решение переходит
в известное течение Гартмана. Показано, что двухкомпонентность плазмы ответственна
за: (а) двухчастотный характер установившегося течения, (б) своеобразный гидродинамический
эффект Холла, когда плазма течет не вдоль антиградиента давления, а под углом к нему,
(в) пространственный характер профиля скорости. Вычислены частоты пространственных колебаний,
рассмотрены случай электрон – позитронной плазмы и предельные случаи больших и малых
плотностей и поперечного магнитного поля.
Abstract
In this work steady-state flow of hydrodynamic plasma in plane-parallel channel is obtained.
The plasma in channel is taken to be viscous electrically conducting noncompressible
two-component and quasineutral. By MHD-limit, the stationary flow presented converge to
famous Hartmann's flow. The flow obtained , is shown, is superposition of two modulated
oscillations, which amplitudes and frequencies are calculated. In channel, is shown also,
the steady-state plasma flow is directed of such angles to the pressure’s gradient
( it is a peculiar kind of Hall’s effect) and velocity’s profile is not flat. At last,
the cases of electron-positron plasma, large and small density, large and small
cross-magnetic field are considered.
Введение. В работе исследуется установившееся течение гидродинамической плазмы в
плоском бесконечном канале. Плазма предполагается полностью ионизованной
двухкомпонентной электропроводной вязкой несжимаемой и квазинейтральной.
Основная цель работы – изучить влияние взаимодействия электронов и ионов на
установившееся течение плазмы. Хорошо изучены два относящиеся к этой теме
классических результата.
Пуазейль (1840г.) исследовал установившееся течение вязкой
несжимаемой жидкости в плоском канале и вывел параболический закон
распределения скорости жидкости.
Гартман
(1937г.) исследовал влияние поперечного магнитного поля на установившееся течение вязкой
несжимаемой МГД-плазмы в плоском канале. Им было показано, что поперечное
магнитное поле приводит к сплющиванию параболического профиля скорости, профиль
становится более пологим (или, как говорят, заполненным). Результаты этих
исследований кратко приведены в §1. §1.
Что произойдет с установившимся течением, если еще учесть взаимодействие
электронов и ионов, предполагая плазму по-прежнему квазинейтральной вязкой и
несжимаемой? Как установлено в этой работе, во-первых,
направление течения плазмы отклоняется от направления антиградиента давления,
которое изначально это течение и вызывает; иными словами, плазма течет не туда,
куда заставляет ее двигаться гидродинамическое давление, а в сторону от этого
направления (своеобразный гидродинамический эффект Холла – следствие
двухкомпонентности плазмы). Во-вторых,
профиль скорости плазмы в канале становится пространственным, а не плоским, как
это было в течениях Гартмана и Пуазейля. В-третьих,
профиль скорости плазмы является суммой двух гармонических колебаний с
частотами ω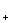 , ω , ω и с промодулированными по некоторому закону амплитудами. Это
указывает на плазму, как на сложную колебательную систему. Заметим, что в
условиях задачи об установившемся течении никаких частот не содержится, и
предоставленная самой себе плазма (сдерживаемая только непериодическими
граничными условиями и постоянным градиентом давления) по собственной
инициативе начинает колебаться подобно двухчастотному маятнику. С другой
стороны, поскольку плазма предполагалась квазинейтральной, указанные колебания
с частотами ω и с промодулированными по некоторому закону амплитудами. Это
указывает на плазму, как на сложную колебательную систему. Заметим, что в
условиях задачи об установившемся течении никаких частот не содержится, и
предоставленная самой себе плазма (сдерживаемая только непериодическими
граничными условиями и постоянным градиентом давления) по собственной
инициативе начинает колебаться подобно двухчастотному маятнику. С другой
стороны, поскольку плазма предполагалась квазинейтральной, указанные колебания
с частотами ω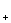 , ω , ω не могут вызываться
разделением зарядов. Частоты ω не могут вызываться
разделением зарядов. Частоты ω , ω , ω , разумеется, не
имеют никакого отношения к известным характерным частотам колебаний плазмы
(циклотронным, плазменным и пр.) и могут быть явно вычислены. , разумеется, не
имеют никакого отношения к известным характерным частотам колебаний плазмы
(циклотронным, плазменным и пр.) и могут быть явно вычислены.
Полученное в работе решение в пределе r ® +¥ (r - плотность плазмы в канале) переходит в течение Гартмана. На языке
колебаний этот процесс выглядит так.
При r ® +¥ одна из частот, ω , стремится к конечному пределу , стремится к конечному пределу 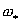 , а отвечающая ей амплитуда при
этом стремится к 0, другая частота, ω , а отвечающая ей амплитуда при
этом стремится к 0, другая частота, ω , напротив, стремится
к 0, а соответствующая ей амплитуда – к
конечному пределу, а именно, к профилю скоростей Гартмана. Практический
вывод из этого анализа для МГД-теории
следующий. Поскольку в действительности реализуется некоторое возмущение
течения Гартмана (ибо плотность r всегда конечна), то это
возмущение получается из течения Гартмана некоторой его деформацией и
наложением ряби с частотой , напротив, стремится
к 0, а соответствующая ей амплитуда – к
конечному пределу, а именно, к профилю скоростей Гартмана. Практический
вывод из этого анализа для МГД-теории
следующий. Поскольку в действительности реализуется некоторое возмущение
течения Гартмана (ибо плотность r всегда конечна), то это
возмущение получается из течения Гартмана некоторой его деформацией и
наложением ряби с частотой  ω ω , что, в
частности, делает профиль
Гартмана пространственным. Частоту ряби
ω , что, в
частности, делает профиль
Гартмана пространственным. Частоту ряби
ω , однако, нельзя вычислить по МГД-теории, еë величина
получена в настоящей работе. Другой полезный результат, недоступный МГД-теории,
- подсчет силы трения электронов и ионов о стенки канала. Кроме того,
установлен факт постоянства продольного электрического поля в канале и получено
выражение этого поля через среднюю скорость потока плазмы в канале. Полученное
соотношение, отличающееся от аналогичного в МГД-теории существенными
поправками, актуально для расчетов плазменных расходометров и насосов
кондукционного типа. Приведенные рассуждения позволяют предположить, что, по
-видимому, МГД-теория описывает асимптотику (в МГД-пределе) амплитуд некоторых
типов колебаний, из которых складывается реальная динамика плазмы. , однако, нельзя вычислить по МГД-теории, еë величина
получена в настоящей работе. Другой полезный результат, недоступный МГД-теории,
- подсчет силы трения электронов и ионов о стенки канала. Кроме того,
установлен факт постоянства продольного электрического поля в канале и получено
выражение этого поля через среднюю скорость потока плазмы в канале. Полученное
соотношение, отличающееся от аналогичного в МГД-теории существенными
поправками, актуально для расчетов плазменных расходометров и насосов
кондукционного типа. Приведенные рассуждения позволяют предположить, что, по
-видимому, МГД-теория описывает асимптотику (в МГД-пределе) амплитуд некоторых
типов колебаний, из которых складывается реальная динамика плазмы.
Стенки канала в работе считались изоляторами
и ставились простейшие (нулевые) граничные условия. Без особого труда все
полученные результаты переносятся на другие случаи: стенки-проводники с
конечной проводимостью (или одна из стенок – проводник, а другая – изолятор),
одна из стенок подвижная, вне стенок вакуумные магнитное поле и поперечное
электрическое поле – произвольные константы и т.д.
§1. Предыстория вопроса.
1.Течение вязкой несжимаемой жидкости в
плоском канале. Рассмотрим бесконечный плоский канал, стенки которого параллельны
плоскости Oyz и отстоят друг от друга на расстояние 2l. Пусть стенки канала задаются уравнениями x = l ( правая стенка ), x= – l (левая
стенка), и мы рассматриваем установившееся (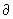 / / t=0) течение вязкой
несжимаемой жидкости в канале под действием градиента давления. Условие
несжимаемости дает для скорости v и плотности
r жидкости: div v = 0, r =const. Предположим, vx=0, vy=0, vz=vz(x), p=p(x,z) (p-давление жидкости).
На стенках канала ставится условие “прилипания”: vz( ±l )=0.
При этих предположениях уравнения вязкой несжимаемой жидкости дают
решение, известное как течение Пуазейля
(J.L.Poiseuille, 1840г.): t=0) течение вязкой
несжимаемой жидкости в канале под действием градиента давления. Условие
несжимаемости дает для скорости v и плотности
r жидкости: div v = 0, r =const. Предположим, vx=0, vy=0, vz=vz(x), p=p(x,z) (p-давление жидкости).
На стенках канала ставится условие “прилипания”: vz( ±l )=0.
При этих предположениях уравнения вязкой несжимаемой жидкости дают
решение, известное как течение Пуазейля
(J.L.Poiseuille, 1840г.):
vz(x)=(2μ)-1.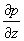 .(x2–l2), |x|≤l, (1) .(x2–l2), |x|≤l, (1)
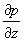 ≡ const, p=p(z), ≡ const, p=p(z),
<vz> = – 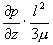 , ,
где μ – коэффициент вязкости, а
< f > =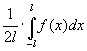
среднее по сечению канала значение функции f. Итак, профиль скорости vz(x) – параболический, а жидкость
двигается, как и положено, в сторону антиградиента давления: v(x), <v> || – grad p.
2. Течение вязкой несжимаемой электропроводной
МГД-плазмы в
плоском канале. Рассмотрим установившееся ( 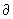 / /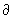 t =0) течение вязкой несжимаемой электропроводной МГД-плазмы в плоском
канале. Теперь к параметрам течения добавляется напряженность магнитного поля H. Основной вопрос: как влияет поперечное магнитное поле на поток
заряженной жидкости? Дополним предположения п.1 соглашением относительно
магнитного поля H: t =0) течение вязкой несжимаемой электропроводной МГД-плазмы в плоском
канале. Теперь к параметрам течения добавляется напряженность магнитного поля H. Основной вопрос: как влияет поперечное магнитное поле на поток
заряженной жидкости? Дополним предположения п.1 соглашением относительно
магнитного поля H:  / /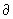 y = 0, y = 0, 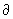 / / z = 0, Hy = 0. Тогда z = 0, Hy = 0. Тогда
Hx ≡ H0 = const – напряженность поперечного магнитного поля.
Будем считать стенки канала изоляторами и положим Hz(±l) = 0 (сохранив для скорости vz(x) граничное условие
“прилипания” vz(±l) = 0 ). При сделанных допущениях уравнения вязкой несжимаемой МГД-
плазмы дают решение, известное как течение
Гартмана (J.Hartmann, 1937г.) :
vz(x) = –  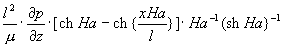 (2) (2)
Hz(х) = 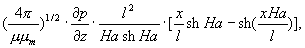
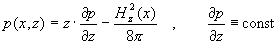 , ,
|x| ≤ l
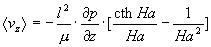 , ,
где μ – коэффициент
гидродинамической вязкости, μm= c2 (4πσ)-1
–
коэффициент магнитной вязкости
(σ – проводимость плазмы),
Ha = lHo(4πμμm)-1/2 – безразмерный параметр (число Гартмана) .
Ответ на поставленный выше вопрос составляет
содержание эффекта Гартмана: с ростом
напряженности поперечного магнитного
поля Ho (или,
что эквивалентно, числа Гартмана Ha )
профиль vz(x) становится все более приплюснутым, при Ha→
+∞ скорость vz(x) становится почти константой, стремящейся к
0, - происходит “запирание” потока плазмы. Заметим, что при Ha → 0 формула (2)
переходит в формулу (1). Эффект
Гартмана легко объясним. На поток
плазмы вдоль оси z действует, помимо градиента
давления, пондеромоторная сила:
Pz = (Div = (Div 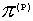 )z = )z = 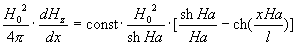 , |x| ≤ l, , |x| ≤ l,
где const не зависит от H0 (здесь  = H2(8π)-1E3 – H∙H∙(4π)-1 –
тензор пондероматорных напряжений). Легко видеть, что Pz обращается в нуль только в двух точках x = ±x(H0), где = H2(8π)-1E3 – H∙H∙(4π)-1 –
тензор пондероматорных напряжений). Легко видеть, что Pz обращается в нуль только в двух точках x = ±x(H0), где
x(H0)= · ·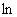 [ [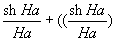 2 –
1)1⁄2] . 2 –
1)1⁄2] .
Причем при |x| ≤ x(H0)
имеем Pz > 0, и
пондеромоторная сила действует
против потока плазмы, тормозя его, а при
x(H0) ≤ |x| ≤ l имеем Pz< 0, и пондеромоторная сила действует вдоль
потока, ускоряя его. При H0 → +∞ имеем x(H0) →l и таким образом почти во всëм канале
поток тормозится. Итак, частицы плазмы с
малыми скоростями (в пристенной области) ускоряются, а с большими
скоростями (в основной части канала) тормозятся – в итоге происходит затупление
профиля скорости.
§2. Уравнения гидродинамики
несжимаемой
квазинейтральной плазмы.
Нас интересует влияние взаимодействия
электронов и ионов на установившееся течение вязкой электропроводной
несжимаемой плазмы в плоском канале. В МГД- теории взаимодействие электронов и
ионов не учитывается. Будем считать гидродинамическую плазму квазинейтральной (e+n+ = e-n-), а каждую плазменную компоненту
- несжимаемой жидкостью: div
v±= 0, 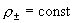 . Для квазинейтральной плазмы условия
несжимаемости эквивалентны двум равенствам: . Для квазинейтральной плазмы условия
несжимаемости эквивалентны двум равенствам:
div U = 0, 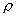 = =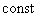  , ,
где
ρ=ρ+ + ρ- , U
= (ρ+v+ +ρ-v-)
/ ρ = (χ+v+ +χ-v-) ⁄ χ
χ± = m± ⁄ e± , χ = χ+ + χ- .
Это следует из очевидных соотношений:
v+ = U+(χ- / ρ)j, v-= U – (χ+ / ρ)j
, ρ± = (χ± / χ)ρ, j = en (v+ –v-)
и условия div j = 0. Последнее вытекает из равенства:
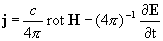
и уравнения div
E = 0, справедливого в силу
условия квазинейтральности. Теперь рассмотрим систему уравнений, получающуюся
объединением трëх систем: двух
систем гидродинамических уравнений вязкой несжимаемой жидкости, написанных
отдельно для электронов и ионов, и системы уравнений Максвелла. Переходя в
полученной объединенной системе от неизвестных
v+, v- к неизвестной U получим систему:
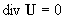 , ,
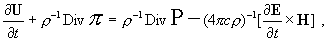
 = (3) = (3)
=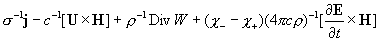 , ,
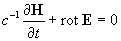 , ,
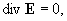
где 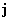 выражается через выражается через  указанным выше способом, указанным выше способом,
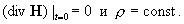 Выражения для тензоров Выражения для тензоров 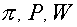 имеют вид: имеют вид:
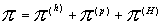 , , 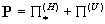
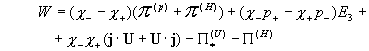 (4) (4)
Тензоры  вычисляются по формулам: вычисляются по формулам:
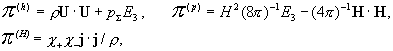 (5) (5)
где 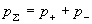 - суммарное
давление. А тензоры - суммарное
давление. А тензоры 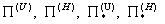 выражаются через
тензоры деформаций выражаются через
тензоры деформаций 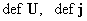 по формулам: по формулам:
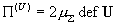 , , 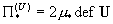 , ,
(6)
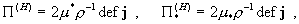 
где
 . .
Система уравнений (3÷6) состоит из 11 скалярных уравнеий и
позволяет в принципе найти 11 скалярных неизвестных функций: компоненты
полей U, H, E и давления p+, p-. После этого
гидродинамические скорости электронов и ионов v+, v- вычисляются по указанным выше формулам.
Заметим, хотя это и не
понадобиться ниже, что температуры Т±
электронов и ионов можно найти из системы:
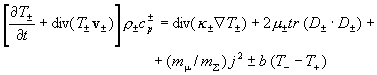 ,
(7) ,
(7)
где mΣ= m+ + m- ,
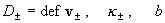 - коэффициенты переноса, - коэффициенты переноса, 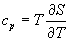 теплопроводность
при постоянном давлении (S – плотность энтропии). Для идеального газа S =km-1(γ –1)-1 теплопроводность
при постоянном давлении (S – плотность энтропии). Для идеального газа S =km-1(γ –1)-1 (k - постоянная Больцмана,
(k - постоянная Больцмана,
γ – показатель адиабаты), откуда
cp = 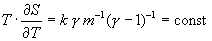 . .
Итак, система (3)÷(7) полностью
описывает изменение скоростей, давлений, температур, электрического и магнитного
полей несжимаемой квазинейтральной вязкой электропроводной плазмы. Она пригодна
для исследования высокочастотных процессов в плазме, равноправным образом
учитывающих динамику компонент, в частости их взаимодействие, и в то же время
является одножидкостной.
§ 3. Постановка
задачи о течении плазмы в плоском канале.
Рассмотрим установившееся
(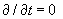 ) течение вязкой электропроводной
квазинейтральной несжимаемой плазмы. Согласно (3), оно подчиняется системе
уравнений: ) течение вязкой электропроводной
квазинейтральной несжимаемой плазмы. Согласно (3), оно подчиняется системе
уравнений:
div
U = 0
Div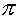 = Div P = Div P
E + c2χ+χ-(4pρ)-1 rot rot E
= s -1 j – c-1
[U 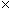 H ] + r -1 Div W H ] + r -1 Div W
rot E = 0
(8)
div E = 0
div H = 0
j = c (4p)-1rot
H ,
где r = const. Пусть теперь плазма
заполняет плоский канал (см.§1). Будем считать, что все параметры плазмы, кроме
давлений, зависят только от x, а p±= p± (x,z). Кроме того,
считаем Ux ≡ 0. Из div
H = 0 следует Hx ≡ H0 = const – постоянное поперечное магнитное поле. Из div E = 0 следует Ex ≡ E0 = const. Итак, подлежат нахождению в области |x| ≤ l, y, z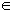 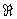 (где (где  -совокупность всех
вещественных чисел) функции: -совокупность всех
вещественных чисел) функции:
Hy(x), Hz(x), Uy(x), Uz(x), p±(x),
Ey(x), Ez (x).
Первые четыре функции пишутся из системы:
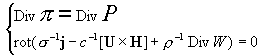 (9) (9)
Давление p± находится из системы:
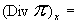 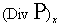
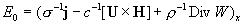 . .
Наконец, 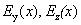 получаются из
равенства: получаются из
равенства:
 .
(10) .
(10)
Систему (9) дополним граничными условиями на стенке. Считая стенку
изолятором и предполагая в вакууме 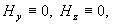 приходим к таким
граничным условиям: приходим к таким
граничным условиям:
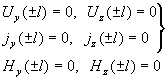 - условия
”прилипания“ (11) - условия
”прилипания“ (11)
Наконец, в нижеследующем решении предполагается μ± = const,
σ
= const .
§ 4. Решение задачи о течении плазмы в плоском
канале.
Подставляя функции Hy(x), Hz(x), Uy(x), Uz(x), p±(x) систему (9), приходим к следующей линейной
системе относительно Hy(x), Hz(x), Uy(x), Uz(x):
 , (12) , (12)
где Lij(D) –
многочлен от D = d/dx степени ≤4,
 l0 ≠ 0 – постоянный вектор. Вот явный
вид матрицы L(D) и вектора l0 : l0 ≠ 0 – постоянный вектор. Вот явный
вид матрицы L(D) и вектора l0 :
 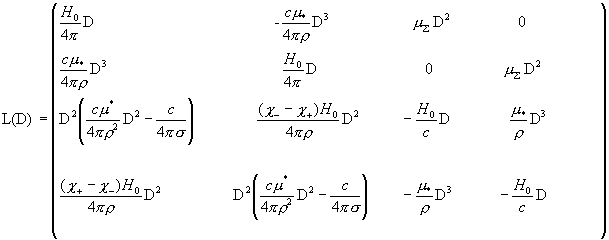
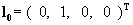 ,
,
где выражения для μΣ, μ* , μ*, χ±
приведены в §2, H0 – магнитное поле, ρ- плотность плазмы в канале. При этом
давления имеют вид:
p±(x,z)
= A±z + φ±(x),
где константы A± должны задаваться, а
функции φ± ищутся. Из системы (12) вытекает важный
эффект (своеобразный гидродинамический эффект Холла ): в плоскости Oyz плазма течет не вдоль антиградиента давления, направленного в сторону
оси Oz, а под углом к нему. Формально
это выражается в том, что система (12) не имеет решений вида Hy = 0, Uy =0 и объясняется наличием y – компоненты
пондеромоторной силы 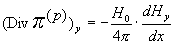 ,
которая и отклоняет движение частиц плазмы от направления антиградиента
давления. Этот эффект проявляется и в том, что, как следует из вычислений ниже,
средние скорости <U>, <v±>
образуют ненулевой угол с направлением антиградиента давления. В
частности, установившееся течение плазмы в плоском канале имеет пространственный профиль скорости. ,
которая и отклоняет движение частиц плазмы от направления антиградиента
давления. Этот эффект проявляется и в том, что, как следует из вычислений ниже,
средние скорости <U>, <v±>
образуют ненулевой угол с направлением антиградиента давления. В
частности, установившееся течение плазмы в плоском канале имеет пространственный профиль скорости.
Нахождение полей Hy ,
Hz , Uy , Uz . Система (12)
состоит из линейных обыкновенных дифференциальных уравнений с постоянными
коэффициентами. Она не приведена к каноническому виду, а ее интеграция делается
возможной использованием комплексификации. Ниже считается
H0 ≠0, μ+ ≠ μ- (невырожденный
случай).
Рассмотрим элементы 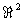 как комплексные числа: a+ib = (a,b). Умножение комплексных чисел и умножение матрицы на вектор связаны
формулой: как комплексные числа: a+ib = (a,b). Умножение комплексных чисел и умножение матрицы на вектор связаны
формулой:
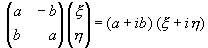 (13) (13)
С другой стороны 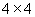 -матрица L(D) может быть разбита на четыре -матрица L(D) может быть разбита на четыре 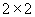 - блока, каждый из
которых имеет такой же тип, что и матрица в (13). Рассматривая поперечную
плоскость OYZ
как комплексную (мнимая ось совпадает с осью OZ) и переходя к переменным w = D(Hy+iHz) , - блока, каждый из
которых имеет такой же тип, что и матрица в (13). Рассматривая поперечную
плоскость OYZ
как комплексную (мнимая ось совпадает с осью OZ) и переходя к переменным w = D(Hy+iHz) ,
u= D(Uy+iUz) , сведем
систему (12) к виду:
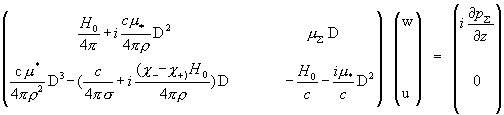 ,
,
или:
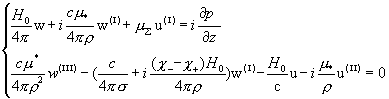 . .
Выражая u(1) из первого равенства и
подставляя во второе, найдем выражение u через w :
 (14) (14)
Подставляя выражение (14) в первое уравнение системы, получим линейное
дифференциальное неоднородное уравнение 4-го порядка с постоянными
коэффициентами для нахожления w :
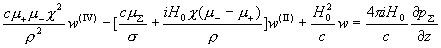 . (15) . (15)
Частное решение неоднородного уравнения (15) имеет вид
wчаст 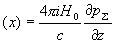
Поскольку характеристический многочлен для уравнения
(15) – биквадратный, то общее решение однородного уравнения (15) есть линейная
комбинация экспонент:
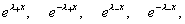
где 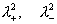 - различные
решения квадратного уравнения: - различные
решения квадратного уравнения:
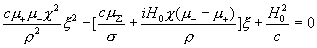
(это уравнение не имеет кратных корней). Поэтому, с
учетом соотношения (14), решение системы (12) имеет вид:

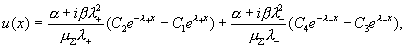
  , ,
где  - произвольные
комплексные константы, - произвольные
комплексные константы, 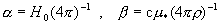 . Шесть констант интегрирования ищутся из шести
граничных условий, являющихся комплексификацией граничных условий (11): . Шесть констант интегрирования ищутся из шести
граничных условий, являющихся комплексификацией граничных условий (11):
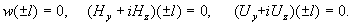
Решая полученную систему шести линейных неоднородных уравнений с шестью
неизвестными, находим константы: 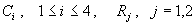 , а вместе с тем и
поля , а вместе с тем и
поля 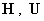 . Эта программа доводится до конца, и мы получаем следующие формулы: . Эта программа доводится до конца, и мы получаем следующие формулы:

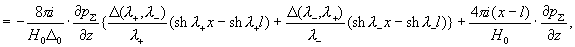
 (16)
(16)
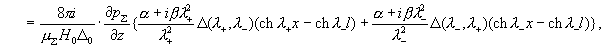
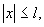
где
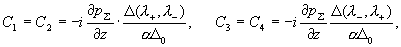
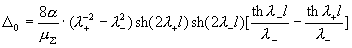 (17) (17)
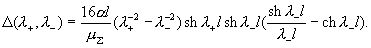
Нахождение давлений. Равенство 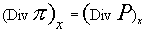 дает: дает:
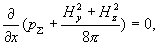
откуда:
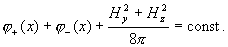 (18) (18)
Далее, x- компонента равенства (10) дает: 
откуда:
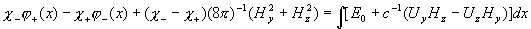 (19)
(19)
Константа  известна: она
равна x -
компоненте вакуумного электрического поля. Поэтому линейная система (18), (19)
позволяет однозначно найти функции известна: она
равна x -
компоненте вакуумного электрического поля. Поэтому линейная система (18), (19)
позволяет однозначно найти функции 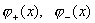 по уже вычисленным
функциям по уже вычисленным
функциям 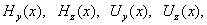 Тем самым и давления Тем самым и давления
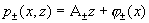 определяются однозначно, с точностью до константы. определяются однозначно, с точностью до константы.
Вычисление функций  Из формулы (10) следуют равенства: Из формулы (10) следуют равенства:
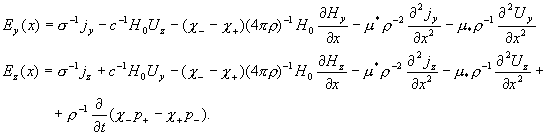
В правых частях
стоят уже вычисленные функции. В комплексном виде эти формулы переписываются
так: 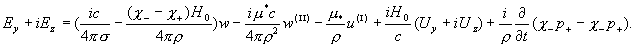 Поскольку Поскольку 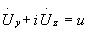 , то, как следует из
второго равенства написанной выше системы дифференциальных уравнений для u и w , , то, как следует из
второго равенства написанной выше системы дифференциальных уравнений для u и w , 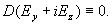 . Поэтому. . Поэтому. 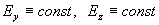 . Итак, электрическое поле в канале
постоянно. Отсюда следует, что среднее по сечению канала от . Итак, электрическое поле в канале
постоянно. Отсюда следует, что среднее по сечению канала от 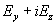 совпадает с совпадает с 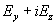 , поэтому имеем: , поэтому имеем:
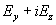 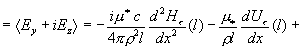
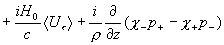 , ,
где 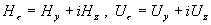 . Используя формулы (16),
(17), находим: . Используя формулы (16),
(17), находим:
 , ,
где величина 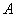 вычисляется по
формуле: вычисляется по
формуле:
 , , 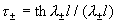 . .
Учитывая выражения
для 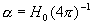 , , 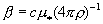 , получим: , получим:
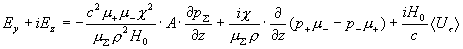 . .
Эта формула отличается от аналогичной в
МГД–теории двумя первыми слагаемыми в правой части, которые при конечных
плотностях дают существенный вклад в электрическое поле в канале.
Тем самым получено решение
задачи об установившемся течении несжимаемой плазмы в плоском канале. Согласно
этому решению (16), скорости 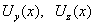 являются суммами синусоидальных колебаний с частотами являются суммами синусоидальных колебаний с частотами  , промодулированных линейными
комбинациями экспонент , промодулированных линейными
комбинациями экспонент 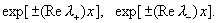 В невырожденном
случае заведомо В невырожденном
случае заведомо 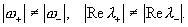
Вычисление других характеристик течения. Вычислим плотность тока,
скорости компонент плазмы, средние по сечению канала скорости и силу трения
плазмы и ее компонент о стенки канала.
Имеем:
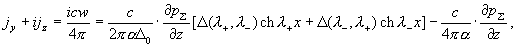 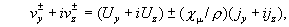
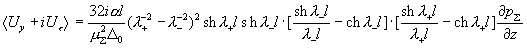
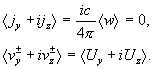
где были использованы соотношения (17) и очевидное равенство:

Силы трения электронов и ионов о правую и левую стенки равны:

Где 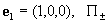 - тензоры вязких
напряжений плазменных компонент: - тензоры вязких
напряжений плазменных компонент:
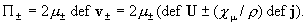
Вычисления в координатах дают:
 
Отсюда следует, что 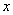 - компоненты всех сил
течения равны нулю. В комплексных обозначениях для - компоненты всех сил
течения равны нулю. В комплексных обозначениях для 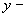 и и 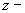 компонент получим: компонент получим:
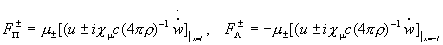 , ,
где точка означает дифференцирование по 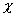 . .
Подсчет с помощью
формул (16), (17) приводит к выражениям: 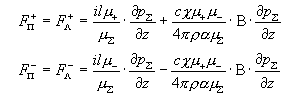 , ,
где

В частности, суммарная сила трения плазмы о стенки равна:
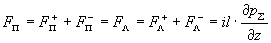 . .
§ 5. Вычисление величин λ+ , λ- .
Ключевую роль в основных
формулах § 4, задававших установившееся течение плазмы в плоском канале, играли
величины λ+ , λ- .
Они могут быть вычислены в
явном, хотя и громоздком виде. Обозначим:
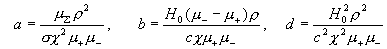 (20) (20)
Тогда (см. § 4) :
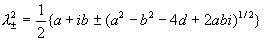 . .
Используем формулу для извлечения квадратного корня:
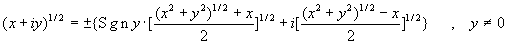
Из этой формулы для невырожденного случая  следует: следует:
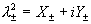 , ,
где
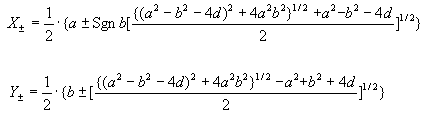 (21) (21)
Отсюда, учитывая, что в невырожденном случае 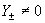 и, более того, и, более того, 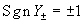 , получаем окончательно: , получаем окончательно:
 (22) (22)
Фомулы (20) ÷ (22) дают явное вычисление величин 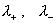 ,
в частности, частот ,
в частности, частот 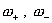 . .
§ 6. МГД-предел.
Покажем, что полученные в §
4 формулы в МГД – пределе дают течение
Гартмана. МГД – предел получается при ρ→ +∞. Тогда ε = 1⁄ρ является малым параметром, и мы
разложим λ+(ε), λ–(ε) в ряд по степеням
в ряд по степеням 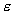 , ограничившись при этом первыми членами разложения. Из § 4
следует, что , ограничившись при этом первыми членами разложения. Из § 4
следует, что 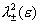 является решением
квадратного уравнения является решением
квадратного уравнения
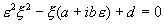 , ,
где
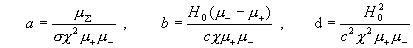 . .
Решая квадратное уравнение, получим :
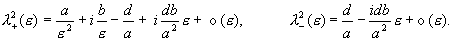
Откуда:
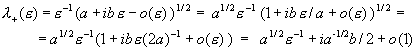
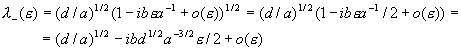
Отсюда следует, что:


В частности, при 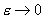 имеем: имеем:
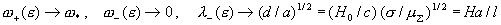 , ,
где  - число Гартмана из § 1, а
предельная частота - число Гартмана из § 1, а
предельная частота 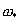 равна: равна:
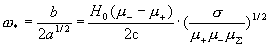 . .
Отсюда следуют предельные при 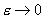 соотношения: соотношения:
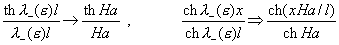 , ,
причем последняя сходимость равномерная по 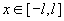 . Наконец, функции . Наконец, функции

локально ограничены в точке  равномерно по равномерно по 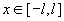 , а , а
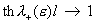 при при 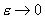 . .
Обозначим 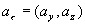 для любого вектора для любого вектора
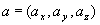 . Тогда из
формулы (16) следует: . Тогда из
формулы (16) следует:
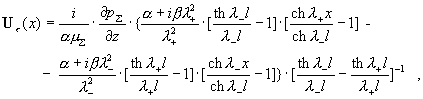
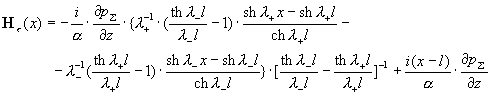
Из предельных соотношений, написанных выше с учетом 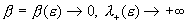 при при  следуют пределы: следуют пределы:
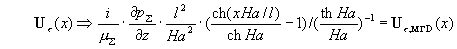

Правые части совпадают с формулами
(2) из § 1, а пределы равномерные по  . Итак, МГД – предел
есть в точности течение Гартмана. . Итак, МГД – предел
есть в точности течение Гартмана.
§ 7. Обзор других результатов
1. Электрон-позитронная плазма.
Более широко, речь идет о случае, когда
χ+= m+ / e+ = χ–= m– / e– , μ+= μ– , но H0 ≠ 0. Тогда
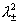 удовлетворяет уравнению относительно ξ : удовлетворяет уравнению относительно ξ :
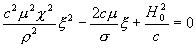 , ,
где μ = μ+ = μ– , откуда:
 . .
Характер установившегося
течения в плоском канале зависит от напряженности поперечного магнитного поля H0 . При
|H0| < Hкр.= ρс(σχ)-1 все корни
характеристического многочлена вещественные и попарно различные, а
установившееся течение является линейной комбинацией экспонент, 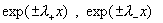 , где , где
 . .
При |H0| > Hкр
корни характеристического многочлена комплексные и попарно сопряженные,
а установившееся течение имеет одночастотный
характер и является гармоническим колебанием с частотой
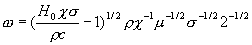 , ,
промодулированным некоторой линейной комбинацией экспонент
 , где , где 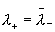 и и
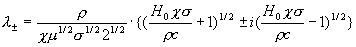 . .
В случае электрон - позитронной плазмы легко разделяются вещественные и
мнимые части в выражениях для 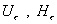 и в явном виде выписываются компоненты полей и в явном виде выписываются компоненты полей 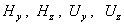 . Имеем . Имеем 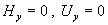
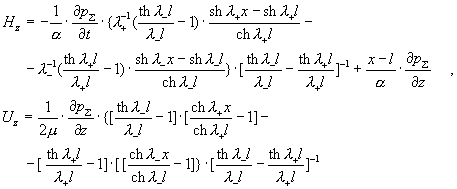
Итак, в рассматриваемом случае, как и для течения Гартмана, поток
плазмы двигается в направлении антиградиента давления.
2. Предел  , эффект “запирания” потока. Величины , эффект “запирания” потока. Величины 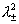 являются корнями уравнения относительно являются корнями уравнения относительно 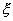 : :
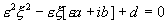 , ,
где  - малый при - малый при  параметр, параметр,
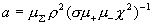 , , 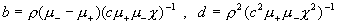 . .
Решая квадратное уравнение и извлекая из полученных выражений корни,
получим:
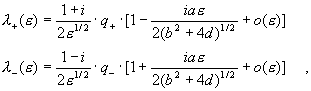
где 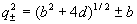 , а в квадратных
скобках стоят аналитические по , а в квадратных
скобках стоят аналитические по 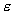 в окрестности в окрестности 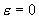 функции. Используя
эти выражения, несложно установить равномерные по функции. Используя
эти выражения, несложно установить равномерные по 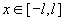  сходимости при сходимости при 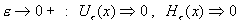 . Таким образом, как и для течения Гартмана, с ростом
поперечного магнитного поля . Таким образом, как и для течения Гартмана, с ростом
поперечного магнитного поля 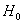 происходит “запирание” потока плазмы в плоском канале: плазма в
канале не течет поперек сильного магнитного поля. Функции происходит “запирание” потока плазмы в плоском канале: плазма в
канале не течет поперек сильного магнитного поля. Функции  являются
аналитическими по являются
аналитическими по  в проколотой
окрестности нуля, а точка 0 – существенно особая точка этих функций. Поэтому
они не разлагаются в степенные ряды по в проколотой
окрестности нуля, а точка 0 – существенно особая точка этих функций. Поэтому
они не разлагаются в степенные ряды по 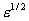 в окрестности нуля, и
стремление к нулю при в окрестности нуля, и
стремление к нулю при 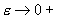 этих функций
происходит достаточно сложным образом: при этих функций
происходит достаточно сложным образом: при
 амплитуды
колебаний, из которых складываются амплитуды
колебаний, из которых складываются 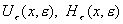 ,
равномерно по ,
равномерно по 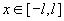 стремятся к 0, а частоты стремятся к 0, а частоты 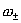 этих колебаний
стремятся к бесконечности. Более того, этих колебаний
стремятся к бесконечности. Более того, 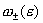 имеют в нуле полюс 1-го порядка по имеют в нуле полюс 1-го порядка по 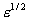 : :

Отсюда следует асимптотика 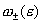 ~ ~ 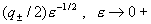 .
Разумеется, в действительности до бесконечности частоты расти не могут,
хотя бы из-за того, что характерные масштабы, равные периодам пространственных
колебаний .
Разумеется, в действительности до бесконечности частоты расти не могут,
хотя бы из-за того, что характерные масштабы, равные периодам пространственных
колебаний 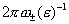 , не могут быть меньше, скажем, длин свободных пробегов электронов
и ионов ( в противном случае плазму нельзя считать гидродинамической), хотя вполне могут быть меньше дебаевского
радиуса. Несложно выделить главный член при стремлении средней скорости , не могут быть меньше, скажем, длин свободных пробегов электронов
и ионов ( в противном случае плазму нельзя считать гидродинамической), хотя вполне могут быть меньше дебаевского
радиуса. Несложно выделить главный член при стремлении средней скорости 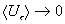 . При . При 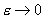 имеем имеем 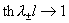 . Используя
разложение . Используя
разложение 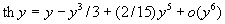 , легко установить: , легко установить:
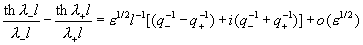
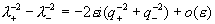
С учетом этого и равенств 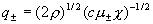 для средней скорости имеем: для средней скорости имеем:
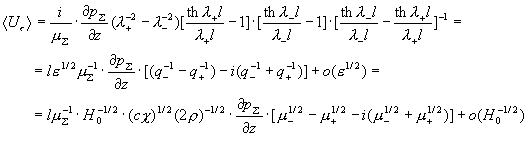
Итак, 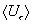 убывает как убывает как 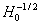 при при 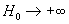 . Для больших . Для больших  средняя
скорость средняя
скорость 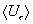 отклоняется от
направления антиградиента (совпадающего с направлением мнимой оси) на угол отклоняется от
направления антиградиента (совпадающего с направлением мнимой оси) на угол 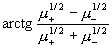 . Для электрон –
ионной плазмы . Для электрон –
ионной плазмы 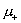 >> >>  , и угол отклонения
равен , и угол отклонения
равен   . .
3. Гидродинамические пределы. При 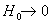 величины величины 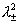 являются корнями
уравнения: являются корнями
уравнения:
 , ,
где  . .
Откуда:
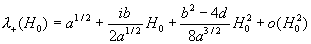
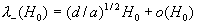
Тогда легко проверить, что при 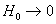 имеют место
равномерные по имеют место
равномерные по 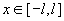 сходимости: сходимости:
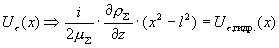
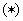
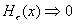
Таким образом, в пределе 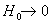 получается течение
Пуазейля (см.§1) вязкой несжимаемой жидкости в плоском канале. Интересно, что
течение Пуазейля получатся и в пределе получается течение
Пуазейля (см.§1) вязкой несжимаемой жидкости в плоском канале. Интересно, что
течение Пуазейля получатся и в пределе 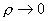 . В этом случае: . В этом случае:
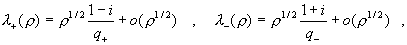
Где 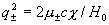 , и, как нетрудно проверить, при , и, как нетрудно проверить, при  имеют место те
же равномерные по имеют место те
же равномерные по 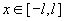 сходимости сходимости 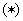 . .
4. Замечания о предельных переходах. Выше считалось, что 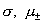 не зависят от не зависят от 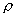 и и  . Для полностью ионизованной электрон – ионной плазмы это
действительно так. Независимость . Для полностью ионизованной электрон – ионной плазмы это
действительно так. Независимость 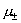 от плотности - важный экспериментальный факт,
подтверждаемый и кинетической теорией [1]. Можно показать [2], что: от плотности - важный экспериментальный факт,
подтверждаемый и кинетической теорией [1]. Можно показать [2], что:
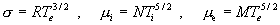 , ,
где выражение для констант  см. в [2]. Как видно, см. в [2]. Как видно, 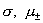 зависят только от
температуры. Поэтому наше решение неявно предполагало изотермичность плазмы.
Безусловно, это не так, поскольку вязкие напряжения и сила трения электронов об
ионы будут постоянно нагревать плазму. Формально, если учесть зависимость зависят только от
температуры. Поэтому наше решение неявно предполагало изотермичность плазмы.
Безусловно, это не так, поскольку вязкие напряжения и сила трения электронов об
ионы будут постоянно нагревать плазму. Формально, если учесть зависимость 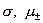 от температур от температур 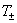 , то система (3) ÷(7) не распадается и скорость,
магнитное и электрическое поля и давления нельзя найти, не вычислив температур.
Предполагая изотермичность плазмы, мы следовали традиции, отход от которой
резко усложняет задачу, и она теряет свой модельный характер. , то система (3) ÷(7) не распадается и скорость,
магнитное и электрическое поля и давления нельзя найти, не вычислив температур.
Предполагая изотермичность плазмы, мы следовали традиции, отход от которой
резко усложняет задачу, и она теряет свой модельный характер.
5. Замечание о граничных
условиях. Примеры постановки других граничных условий
см. в [3].
§ 8. Благодарности.
Авторы выражают благодарность
К.В.Брушлинскому, А.Н.Козлову, В.В.Савельеву, В.С.Рябенькому за участие в
обсуждении различных вопросов, относящихся к двухкомпонентной плазмодинамике.
Мы также признательны Российскому Фонду фундаментальных Исследований за финансовую
поддержку этой работы.
Литература.
1. К.Черчиньяни. Теория и приложения уравнения Больцмана.
М.:”Мир“, 1978, с.214-224.
2. Брагинский С.И. В сб. “
Вопросы теории плазмы“. Под ред. М.А.Леонтовича. Вып.1. М.: Госатомиздат, 1963, с.183.
3. Ватажин А.Б., Любимов Г.А., Регирер С.А. Магнитогидродинамические течения в каналах. М.: Физматгиз,1970.
|