Аннотация
В двумерной геометрии проведены исследования динамики пространственно-временных
диффузионно-дрейфовых распределений объемного отрицательного заряда и напряженности
электрического поля, созданных вследствие эмиссии электронов с поверхности твердого тела.
Определены характерные размеры и инерциальные свойства отрицательно заряженных слоев у
поверхности пластины конечных размеров в неэлектроотрицательном газе.
Abstract
In two-dimensional geometry the researches of dynamics of space-time drift-diffusion
distributions of a bulk negative charge and electric field strength, created due to emission
of electrons from a surface of solid bodies are carried out. The characteristic sizes and
inertial properties of the negatively charged layers at a surface of a plate (of the final
sizes) in no electronegative gas are determined.
Введение
В работе
рассмотрены вопросы, связанные с проблемой получения и поддержания
неравновесных приповерхностных электрических разрядов в быстрых потоках газа, а
также с проблемой экологически чистого получения электрической энергии в
электро-газодинамических [1] (ЭГД) преобразователях.
Рассматриваемые
в данной работе физические явления, лежащие в основе ЭГД преобразования, тесно
связаны с процессом термоэмиссии электронов проводимости твердых тел [2]
в окружающий их газ. Успехи в области разработок современных материалов с
работой выхода электронов £ 1 эв , способных
даже при нормальных условиях создавать в газе у поверхности твердого тела концентрации
заряженных частиц ~ 1010 част/см3 , дают предпосылки для
создания новых технологий, основанных на методе механического разделения
объемного приповерхностного заряда потоками газов [3].
В работе
[3] в случае плоской одномерной геометрии были получены данные о
характерных размерах и инерционных свойствах отрицательно заряженных слоев у
поверхности пластины, эмитирующей электроны в воздушную среду. В [3]
показаны большие потенциальные возможности ЭГД – механизмов преобразования
кинетической энергии газовых потоков в энергию электрических полей большой
напряженности (вплоть до пробойных).
Данная
работа является продолжением изучения диффузионно-дрейфовых распределений
электронов в газах в случае, когда эмиссия электронов осуществляется
металлической пластиной конечной длины и толщины в покоящийся неэлектроотрицательный
газ.
1 Распределение
зарядов в случае неэлектроотрицательных газов
Рассмотрим распределение электрического
поля и концентрации заряженных частиц в газе, вблизи металлической пластины,
способной эмитировать электроны проводимости в окружающую среду. Оценим
характерные размеры и инерциальные свойства отрицательно заряженных слоев у
поверхности пластины.
Задача решается в двухмерной постановке
в плоскости XY. Вдоль оси Z
эмитирующая металлическая пластина не ограничена, а газовая среда считается
однородной. В плоскости XY пластина ограничена
контуром w , изображенным на рис. 1, где L – длина пластины; 2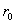 - её толщина; - её толщина; 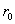 - радиус округления
краев пластины. - радиус округления
краев пластины.
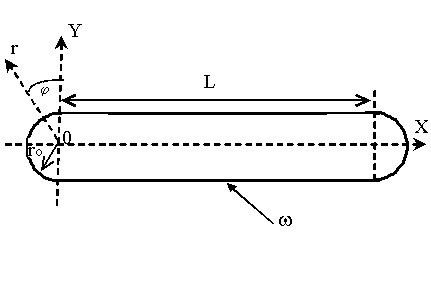
Рис. 1
Рассмотрим
задачу, в которой пространство вне пластины заполнено газом из молекул азота, а
источником эмиссии свободных электронов является поверхность пластины w. Выбранный нами газ
характеризуется тем, что в нем свободные электроны 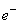 не образуют
устойчивых отрицательно заряженных соединений с молекулами не образуют
устойчивых отрицательно заряженных соединений с молекулами 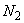 , иначе говоря, в таком газе электроны могут пребывать только
в свободном состоянии. Считаем, что температура пластины , иначе говоря, в таком газе электроны могут пребывать только
в свободном состоянии. Считаем, что температура пластины 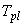 равна температуре
газа равна температуре
газа 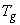 , а в начальный
момент времени в пространстве {r- , а в начальный
момент времени в пространстве {r-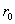 ,y- ,y-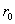 } > d электроны практически
отсутствуют. Здесь d - некоторый
характерный размер начального распределения электронов } > d электроны практически
отсутствуют. Здесь d - некоторый
характерный размер начального распределения электронов 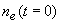 . При условии . При условии 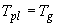 электроны эмиссии в
плотном газе (р ~ 1 атм.) практически всегда
находятся в термолизованном состоянии, т.е. выполняется соотношение: электроны эмиссии в
плотном газе (р ~ 1 атм.) практически всегда
находятся в термолизованном состоянии, т.е. выполняется соотношение: 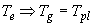 (где (где 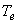 -
температура электронов). -
температура электронов).
Будем считать, что объемный заряд в
газе, представленный свободными электронами, образуется исключительно за счет
термоэлектронной эмиссии. Так, что суммарный объемный заряд электронов в газе и
поверхностный заряд пластины, равен нулю.
По мере протекания эмиссии электроны,
покинувшие проводник создают объемное распределение заряда в газе, приводящее к
возникновению электрических полей в пространстве (иные электрические поля в
рассматриваемой задаче отсутствуют).
В газе отрицательно заряженные частицы
приобретают направленную скорость движения. Это связано с диффузией заряженных
частиц в пространстве, их столкновениями с направленно движущимися молекулами
газового потока, и их дрейфом в самосогласованном электрическом поле. Так
происходит до тех пор пока система не достигнет стационарного состояния, в
котором перечисленные выше компоненты потока электронов компенсируют друг друга
в каждой точке пространства. При этом значение величины объемного эмиссионного
заряда выходит на насыщение.
В силу
пространственной симметрии будем решать задачу в левой верхней четверти
плоскости XY. Система уравнений, описывающая
пространственно-временную эволюцию концентрации электронов и потенциала
электрического поля F в газе, имеет вид[2]:
(1.1) 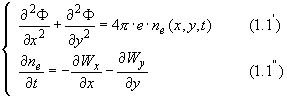
в области плоскости XY : {0 ≤ x ≤ 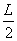 , y ≥ , y ≥ 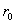 }. Здесь e – заряд электрона; }. Здесь e – заряд электрона;
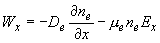 , , 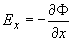
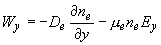 , , 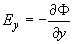 , ,
где 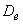 - коэффициент
диффузии электронов в газе, - коэффициент
диффузии электронов в газе, 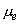 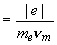 - подвижность электронов в газе [2], - подвижность электронов в газе [2], 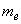 - масса электрона, - масса электрона, 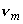 - частота столкновений электронов с частицами газа. - частота столкновений электронов с частицами газа.
(1.2) 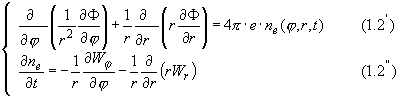
в области плоскости XY : {-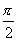 ≤ j ≤ 0, r ≥ ≤ j ≤ 0, r ≥ 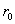 }. Здесь : }. Здесь :
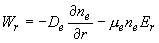 , , 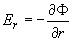
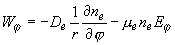 , , 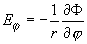 , ,
Задача решается при
следующих начальных и граничных условиях:
(1.1’.1) 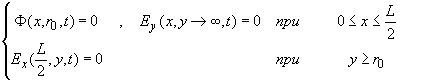
(1.1’’.1) 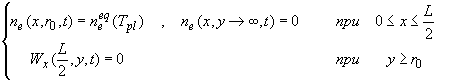
(1.2’.1) 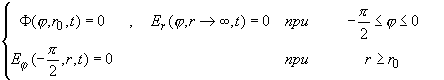
(1.2’’.1) 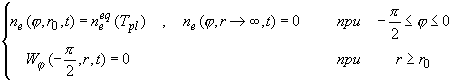
Вдоль прямой {x = 0 (j = 0) , r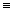 y ≥ y ≥ 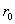 } выполняются равенства, определяющие связь плоской и
полярной областей: } выполняются равенства, определяющие связь плоской и
полярной областей:
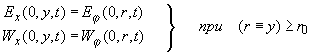
В силу того, что характерное время установления равновесных
значений концентраций заряженных частиц на поверхности пластины (порядка
нескольких десятков наносекунд [3]) существенно меньше характерных
времен диффузии и дрейфа зарядов в газе, начальное распределение 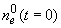 можно представить функциями вида: можно представить функциями вида:
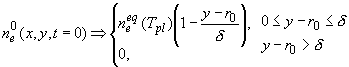 , ,
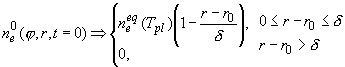 , ,
согласно
[3] выберем 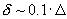 ; где ; где 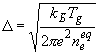 - характерное
дебаевское расстояние. Величина - характерное
дебаевское расстояние. Величина 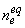 находятся из
граничного условия, отражающего факт равенства прямого и обратного потоков
отрицательного заряда через поверхность пластины: находятся из
граничного условия, отражающего факт равенства прямого и обратного потоков
отрицательного заряда через поверхность пластины:
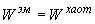 , при {x,y и j,r}Îw . , при {x,y и j,r}Îw .
Здесь 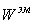 - плотность потока
электронов эмиссии вдоль направления по нормали от поверхности пластины; - плотность потока
электронов эмиссии вдоль направления по нормали от поверхности пластины; 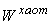 - плотность обратного
потока электронов (поток обусловлен хаотическими столкновениями зарядов с
пластиной). Согласно [2] (гл. 6, п.2) и статистической теории
равновесных газов (см. [4], с.142) имеем: - плотность обратного
потока электронов (поток обусловлен хаотическими столкновениями зарядов с
пластиной). Согласно [2] (гл. 6, п.2) и статистической теории
равновесных газов (см. [4], с.142) имеем:
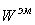 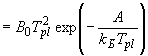 , , 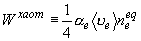
где 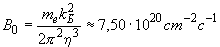 ; ; 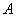 – работа выхода электрона из материала пластины (в проводимых
расчетах – работа выхода электрона из материала пластины (в проводимых
расчетах 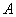 Þ 0,7 эВ); Þ 0,7 эВ); 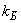 - константа
Больцмана; - константа
Больцмана; 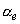 - вероятность «поглощения» электрона стенкой пластины за одно
столкновение (далее мы полагаем, что - вероятность «поглощения» электрона стенкой пластины за одно
столкновение (далее мы полагаем, что 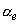 Þ 1); Þ 1); 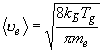 .- средняя хаотическая скорость электрона. .- средняя хаотическая скорость электрона.
В результате
получается: 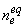 = =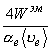 . .
3 Численная модель
При численной реализации сформулированной задачи следует учитывать
характерные пространственные масштабы изменения концентрации электронов и
напряженности электрического поля. Как показывают оценки [3],
основной отрицательный электрический заряд сконцентрирован вблизи поверхности
металлической пластины, испускающей электроны эмиссии. Четырехкратный спад
концентрации электронов в направлении по нормали от поверхности пластины (при 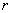 - - 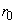 << << 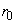 ) происходит на расстояниях D ~ 2.5.10-2
см (для неэлектроотрицательных газов) и D’ ~ .10-3
см (для электроотрицательный газов, в частности, воздушной смеси) при ) происходит на расстояниях D ~ 2.5.10-2
см (для неэлектроотрицательных газов) и D’ ~ .10-3
см (для электроотрицательный газов, в частности, воздушной смеси) при 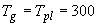 K. При увеличении температуры пластины на 100 К
величины D и D’ уменьшаются более чем на
порядок [3]. Таким образом, численное решение рассматриваемой задачи
в диапазоне температур пластины K. При увеличении температуры пластины на 100 К
величины D и D’ уменьшаются более чем на
порядок [3]. Таким образом, численное решение рассматриваемой задачи
в диапазоне температур пластины 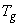 = 300 – 500 K требует введения достаточно мелкого шага по
пространству в = 300 – 500 K требует введения достаточно мелкого шага по
пространству в 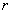 и и 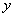 направлениях: направлениях: 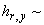 10-5 – 10-6 см . В тоже время, для
корректной реализации граничных условий на внешней границе расчетной области
необходимо учитывать, по крайней мере, ~ 103 дебаевских слоев, т.е. 10-5 – 10-6 см . В тоже время, для
корректной реализации граничных условий на внешней границе расчетной области
необходимо учитывать, по крайней мере, ~ 103 дебаевских слоев, т.е. 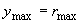 ~ 1м. ~ 1м.
Для численного решения уравнений (1.1)-(1.2) сделаем преобразование
координат, приводящее к решению данной задачи на равномерной сетке. Введем
новые переменные:
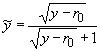 , , 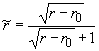 , , 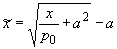 , , 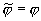
и введем обозначения: 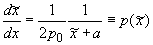 , , 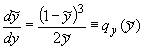 , , 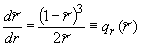 . .
Значения величин 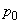 и и 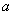 в выражении для в выражении для 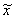 вычисляются из
условия плавного сопряжения сеток в полярной и плоской областях вдоль
поверхности пластины. вычисляются из
условия плавного сопряжения сеток в полярной и плоской областях вдоль
поверхности пластины.
В новой системе координат уравнения (1.1)-(1.2) принимают вид:
(2.1) 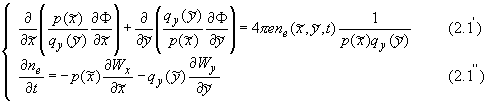
в области : {0 ≤ 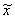 ≤ 1 , 0 ≤ ≤ 1 , 0 ≤ 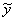 ≤ ≤ 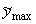 < 1}. < 1}.
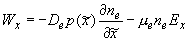 , , 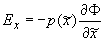
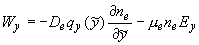 , ,  , ,
(2.2) 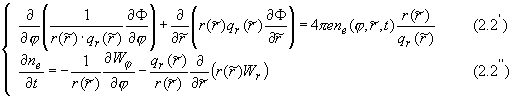
в области: {- ≤ j ≤ 0, 0
≤ ≤ j ≤ 0, 0
≤ 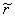 ≤ ≤ 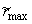 }. }.
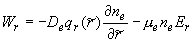 , , 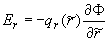
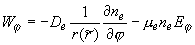 , , 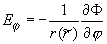 , ,
(2.1’.1) 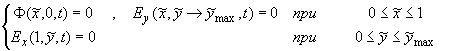
(2.1’’.1) 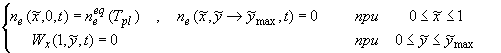
(2.2’.1) 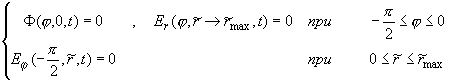
(2.2’’.1) 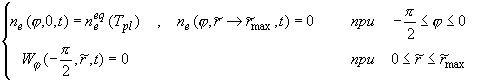
Вдоль прямой линии {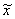 = 0 (j = 0) , = 0 (j = 0) , 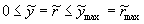 } выполняются
равенства: } выполняются
равенства:
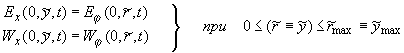
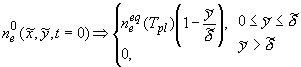 , ,
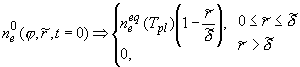 , ,
где 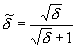 . .
Численное решение уравнений (2.1 – 2.2) будем искать на равномерной
сетке. Построим сетки {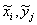 } и { } и {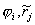 }: }:
{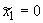 , , 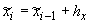 , , 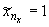 }, },  и и 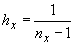 , ,
{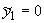 , , 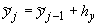 , , 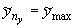 }, }, 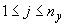 и и 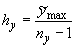 , полагаем , полагаем 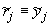 и и 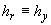 , ,
{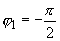 , , 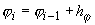 , , 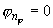 }, }, 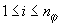 и и 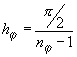 . .
Здесь 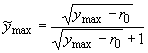 . .
В узлах сеток будем определять потенциал
электрического поля и концентрацию электронов, а на сетках, образованных
сдвигом узлов на пол шага в каждом направлении, напряженность электрического
поля и диффузионно-дрейфовые потоки электронов.
Запишем разностные аналоги уравнений (2.1) и (2.2):
Уравнение Пуассона:
Уравнение Пуассона для плоской и полярной областей решается
модифицированным полинейным методом, предложенным в работе [5].
Разностная форма
эллиптических уравнений (2.1’)-(2.2’) получена с помощью метода контрольного
объема [6] и обеспечивает выполнение интегрального закона
сохранения. Балансовое соотношение для узла разностной сетки выводится путем
интегрирования (2.1’)-(2.2’) по окружающему контрольному объему, в результате
чего получаем разностную пятиточечную аппроксимацию уравнения интегрального
баланса:
(2.3) 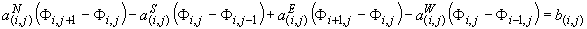 , ,
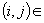 { {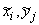 } и { } и {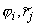 }, },
где 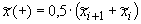 , , 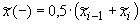 , , 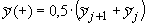 , , 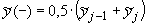 , ,
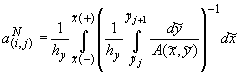 , , 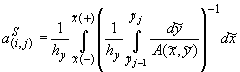 , ,
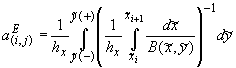 , , 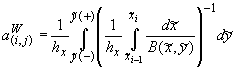 , ,
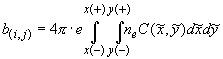 , , 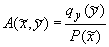 , , 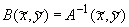 , , 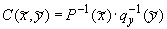
- для плоской
области и: 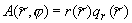 , , 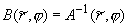 , , 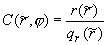 - для полярной области
( - для полярной области
(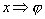 ., ., 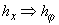 и и 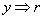 ). ).
Таким образом, разностные
аналоги уравнений (2.1’)-(2.2’) записываются в дивергентной потоковой форме, в
которой сопряжение плоской и полярной областей осуществляется естественным
образом, путем определения потоков через грани контрольного объема, центральная
точка которого лежит на прямой линии {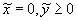 }. }.
Тестовые расчеты показали
высокую эффективность модернизированного полинейного метода, отличительной
особенностью которого является минимальное требование к матрицы коэффициентов 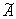 конечной системы
линейных алгебраических уравнений ( конечной системы
линейных алгебраических уравнений (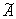 > 0 ). Как в случае плоской двумерной геометрии, так и в
полярных координатах, для получения точного решения разностных уравнений на
сетке размером 250 x 500 при заданных сеточных функциях > 0 ). Как в случае плоской двумерной геометрии, так и в
полярных координатах, для получения точного решения разностных уравнений на
сетке размером 250 x 500 при заданных сеточных функциях 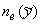 и и 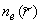 (соответственно) и (соответственно) и 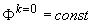 требуется несколько
десятков итераций. В случае если двойной
интеграл от правых частей уравнений, взятый по контрольному объему, вычисляется
аналитически (при линейной интерполяции требуется несколько
десятков итераций. В случае если двойной
интеграл от правых частей уравнений, взятый по контрольному объему, вычисляется
аналитически (при линейной интерполяции 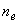 по значениям в
соседних узлах сетки), точное решение разностных уравнений получалось за 1 – 2
итерации. При решении задачи (2.1’)-(2.2’) с по значениям в
соседних узлах сетки), точное решение разностных уравнений получалось за 1 – 2
итерации. При решении задачи (2.1’)-(2.2’) с 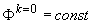 метод [4]
сходится (с относительной невязкой в узле ~ 10-10) в среднем за max( метод [4]
сходится (с относительной невязкой в узле ~ 10-10) в среднем за max(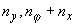 ) итераций. ) итераций.
Уравнение диффузии
Диффузионно-дрейфовые
уравнения (2.1”)-(2.2”) численно решалась методом переменных направлений [7].
(2.4) 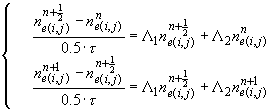
где 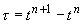 - шаг по времени. - шаг по времени.
Оператор
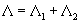 записан в
дивергентной потоковой форме, чем обеспечивается интегральный закон сохранения полного
заряда в пространстве. записан в
дивергентной потоковой форме, чем обеспечивается интегральный закон сохранения полного
заряда в пространстве.
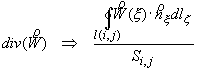 , ,
где 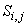 - площадь
контрольного «объема» сеточного узла ( - площадь
контрольного «объема» сеточного узла ( ); ); 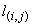 - контур,
ограничивающий - контур,
ограничивающий 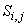 ; ; 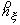 - вектор внешней
нормали к контуру - вектор внешней
нормали к контуру 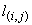 в точке в точке 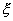 ; ; 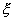 Î Î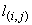 . .
Система уравнений (2.3)-(2.4) является нелинейной. Поэтому,
не усложняя существенно алгоритм решения этой системы, введены промежуточные
итерации на каждом временном шаге по схеме:
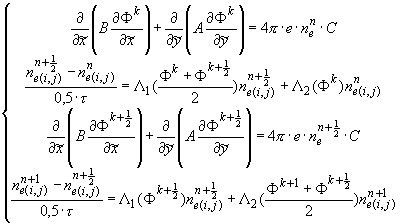 , ,
при этом на первой итерации
выбирается 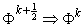 и и 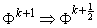 . .
Как
показывают расчеты на каждом временном шаге достаточно выполнить в среднем 4 –
7 итерации (при 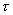 ~ 1 мкс) для достижения значения величин: ~ 1 мкс) для достижения значения величин:
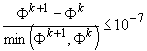 и и 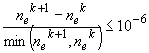 (i,j Î { (i,j Î {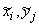 } и { } и {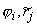 }). }).
4
Результаты расчетов
Рассмотрим диффузию и дрейф электронов в
неэлектроотрицательном газе, состоящем из молекул 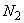 . Считаем, что температура газа и концентрация молекул азота
постоянны по пространству и равны: . Считаем, что температура газа и концентрация молекул азота
постоянны по пространству и равны: 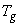 = =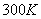 , , 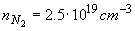 ( (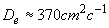 и и 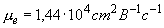 [2]).
Температура пластины полагалась равной температуре газа. [2]).
Температура пластины полагалась равной температуре газа.
В качестве иллюстрации приведем
результаты расчетов, выполненные для пластины длинной 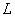 =10 см и толщиной =10 см и толщиной 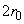 =1 см. Задача
решалась на расчетной сетке { =1 см. Задача
решалась на расчетной сетке {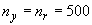 , , 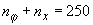 } с шагом интегрирования по времени } с шагом интегрирования по времени 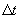 ~ 1 мкс. ~ 1 мкс.
Расчеты показывают, что, как и в
плоском одномерном случае (рассмотренном в [3]) основная доля
отрицательного заряда эмитируется пластиной в газ за 20 – 50 мкс на начальной стадии развития
диффузионных процессов. За это время диффузионно-дрейфовая «волна» успевает
пройти первые 10 дебаевских расстояний 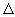 . .
На рис. 2 и 3 для трех моментов
времени 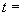 {100 мкс, 1 мс и 15 мс} показаны диффузионно-дрейфовые распределения концентрации
электронов и ( {100 мкс, 1 мс и 15 мс} показаны диффузионно-дрейфовые распределения концентрации
электронов и (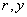 ) – компоненты напряженности электрического поля как функции
расстояния от пластины в трех выбранных направлениях, определяемых нормалью к
поверхности пластины в точках: { ) – компоненты напряженности электрического поля как функции
расстояния от пластины в трех выбранных направлениях, определяемых нормалью к
поверхности пластины в точках: {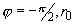 } – сплошные линии; { } – сплошные линии; {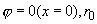 } - пунктирные линии; { } - пунктирные линии; {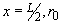 } – линии, образованные точками. Для наглядности на графиках
представлены зависимости } – линии, образованные точками. Для наглядности на графиках
представлены зависимости 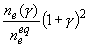 и и 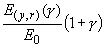 , где , где 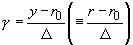 - расстояние от
пластины, выраженное в величинах - расстояние от
пластины, выраженное в величинах 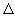 ; ; 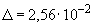 см, см, 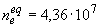 см-3 и см-3 и 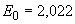 В/см (значения
величин В/см (значения
величин 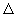 и и 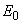 получены в [3]
для условий данной задачи). получены в [3]
для условий данной задачи).
Из приведенных графиков видно, что
на начальной стадии распространения объемного заряда в газ основное влияние на
распределение отрицательного заряда оказывает диффузия и дрейф электронов в
направлении по нормали от поверхности тела. Действительно учитывая симметрию
задачи, следует ожидать, что 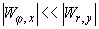 т.к. т.к.  и и  . В этом случае (вблизи пластины) геометрический фактор
играет существенную роль. Так в центре пластины { . В этом случае (вблизи пластины) геометрический фактор
играет существенную роль. Так в центре пластины {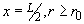 } пространственное распределение заряда близко к распределению
в случае плоской бесконечной пластины, а в полярной области { } пространственное распределение заряда близко к распределению
в случае плоской бесконечной пластины, а в полярной области {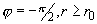 } проявляется дополнительная зависимость величины } проявляется дополнительная зависимость величины 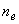 - обратно пропорциональная
радиусу. Характерное время установления стационарного распределения зарядов в
области - обратно пропорциональная
радиусу. Характерное время установления стационарного распределения зарядов в
области  можно оценить по формуле можно оценить по формуле
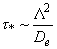 [2] (при [2] (при 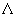 ~ 10 – 20 см ~ 10 – 20 см  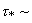 1 с). 1 с).
Анализ расчетных данных
показывает, что распределения концентрации электронов и (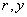 ) – компоненты напряженности электрического поля при ) – компоненты напряженности электрического поля при 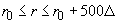 достаточно точно
описываются параметром достаточно точно
описываются параметром 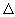 , численное значение которого было получено в [3]
для плоской одномерной задачи. , численное значение которого было получено в [3]
для плоской одномерной задачи.
Работа выполнена при поддержке РФФИ (грант № 01-01-00057).
Л и т е р а т у р а
[1]
Б.М.Смирнов. Введение в физику плазмы. – М., Наука. 1982. 224 с.
[2] Ю.П.Райзер. Физика газового разряда. – М.:
Наука. 1987. 592 с.
[3] В.В.Русанов, В.П.Силаков, А.В.Чеботарев. Диффузионно-дрейфовые распределения зарядов в
газах, обусловленные эмиссией электронов с поверхности твердых тел. – Препринт
ИПМ им. М.В. Келдыша РАН, № 64, 2001, 22 с.
[4] Л.Д. Ландау, Е.М. Лифшиц. Статистическая
физика. – М., Наука. 1964. 568 с.
[5] В.Г.Зверев. Модернизированный
полинейный метод решения разностных эллиптических уравнений. – ЖВМ и МФ, том
38, № 9, 1998, с. 1553-1562.
[6] А.А.Самарский, А.В. Гулин. Численные методы.
– М. , Наука. 1989.
[7] А.А.Самарский. Введение в теорию разностных
схем. – М. , Наука. 1971.
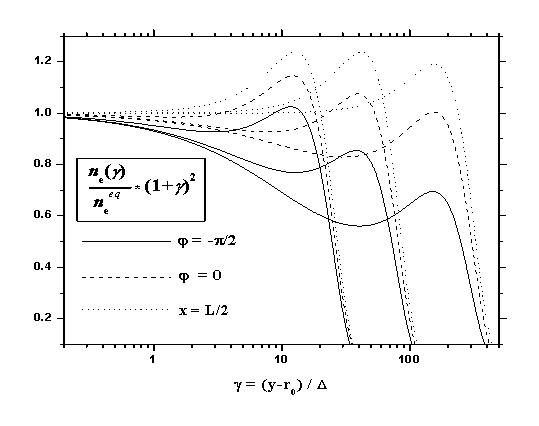
Рис. 2
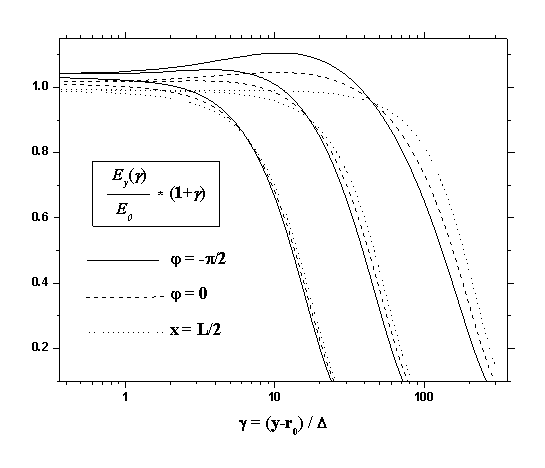
Рис. 3
|