Введение

Уравнение переноса является представителем фундаментальных уравнений математической физики [1], широко используемым для описания движения сплошной среды. Многие задачи газовой динамики, магнитной гидродинамики, астрофизики связаны с решением уравнений такого типа. Учет движения элемента сплошной среды приводит к уравнению переноса квазилинейного типа. Основным следствием нелинейности этих уравнений является “опрокидывание” начального профиля за конечное время и возникновение ударных волн. Изучение закономерностей распространения ударных волн представляет особый интерес в исследовании течений сплошной среды. Наличие разрывов в решении представляет определенные трудности, при этом точность численного решения зависит от качества воспроизведения этих разрывов. На настоящий момент существует большое количество разностных схем для решения задач такого типа. Однако большинство из них дают “расплывчатое” решение, в том числе “размазанный” фронт ударных волн, а схемы повышенного порядка аппроксимации могут приводить к искажениям численного решения, в том числе осцилляциям, т.е. немонотонности решения [2]. Различными способами можно повысить качество численного решения. Один из них связан с использованием неоднородных конечно-разностных схем, в которых реализуется контроль за перемещением разрыва и изменение алгоритма вычислений в его окрестности. Однако основная проблема в использовании таких схем заключается в том, что для нелинейных уравнений гиперболического типа характерно появление разрывных решений даже при гладких начальных условиях, так что положение особых точек заранее неизвестно. К тому же число разрывов может меняться со временем и к каждому из них нужно приспосабливать алгоритм расчета отдельно. Поэтому особый интерес вызывает исследование однородных схем повышенного порядка аппроксимации, а также построение новых квазимонотонных схем на их основе. При этом существуют разнообразные способы монотонизации. В данной работе монотонизация схемы К. И. Бабенко проведена при помощи введения в разностное уравнение искусственной вязкости. Также в данной работе рассмотрена предложенная в [3] схема, монотонизованная с использованием алгоритма, основанного на знании области зависимости точного решения.

В настоящей работе представлен вывод предложенного авторами варианта нелинейной монотонизации схемы К.И. Бабенко для квазилинейного уравнения переноса. Также приведены результаты сравнительного анализа новой и некоторых других известных конечно-разностных схем (явной и неявной схем с левой разностью [2, 4], схемы Lax-Wendroff’a [4] и монотонизованной схемы “Кабаре” [3, 5, 6]). Сравнение численных результатов, полученных по рассмотренным схемам, проведено на системе тестов, аналогичной использованной в работах [4, 5, 7].

Решения получены для финитных начальных условий и различных чисел Куранта на пространственно-временном прямоугольнике достаточно больших размеров. Для определения ошибок численных решений использованы конечномерные анал оги норм пространств C, L₁, L₂. В работе представлены рисунки с точным и численными решениями для некоторых моментов времени, а также таблицы ошибок для тех же моментов времени и для всего временного промежутка. Такой способ представления результатов позволяет качественно и количественно оценивать характеристики схем.

Авторы выражают благодарность Елениной Т.Г. за внимание, советы и полезные обсуждения.

Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований (проект РФФИ № 03-01-00461).

§ 1. Постановка задачи

Будем рассматривать задачу Коши для квазилинейного уравнения переноса

                      , ,                                  (1.1)

с финитными начальными условиями u(x,0)= u₀(x) вида:

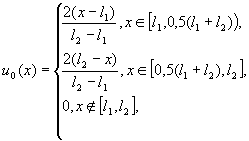
1. “треугольник”

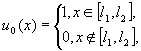
2. “прямоугольник”

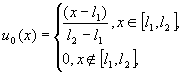
3. “левый треугольник”

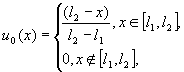
4. “правый треугольник”

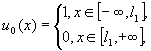
5. “ступенька вниз”

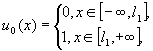
6. “ступенька вверх”

Точное решение уравнения (1.1) имеет вид функционального соотношения

u(x,t)= f(x-ut),

где функция f определяется начальным возмущением при :

Поясним решение (1.1), полученное методом характеристик [8]. Заметим, что выражение  является полной производной функции u(x,t):

вдоль характеристики G, которая задается уравнением

.

Из выражения (1.1) получаем . Это означает, что функция u(x,t) принимает постоянное значение

u(x,t) = u₀(x)

на кривой G, уравнение которой имеет вид

x = x + u₀(x)t.

Приведем точные решения для указанных выше начальных условий:

1. “треугольник”

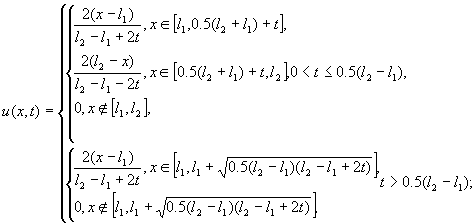
2. “прямоугольник”

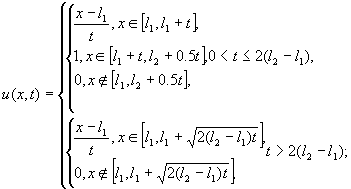
3. “левый треугольник”

4. “правый треугольник”

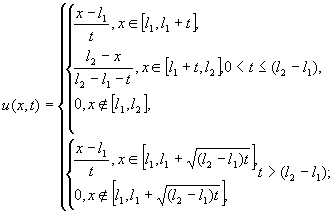
5. “ступенька вниз”

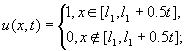
6. “ступенька вверх”

Сравнение численного решения с точным будем проводить с использованием конечномерных аналогов норм в пространствах C, L₁, L₂ на W=(-¥,+¥)´[0,T]:

, , ;

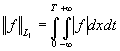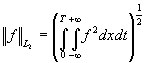и на R=(-¥,+¥) при t=t_i :

, , .

§ 2. Нелинейная монотонизация схемы К. И. Бабенко

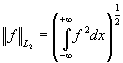Как известно [5], cхема К.И. Бабенко [9] имеет второй порядок аппроксимации по x и t, но является немонотонной. Cхема является неявной, однако это не мешает вычислять искомое решение на новом временном слое “бегущим счетом”. При числе Куранта, равном единице, для линейного уравнения переноса схема дает точное решение.

Для численного решения введем равномерную (для простоты) пространственно-временную сетку

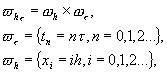
где h,t – шаги разностной сетки по x и t соответственно.

Здесь и далее будем использовать стандартные обозначения для сеточных величин: , где верхний индекс - номер временного слоя, нижний - номер узла по х. Решение на слое n считаем известным.

Перепишем уравнение (1.1) в виде

.

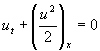Схему Бабенко (“квадрат” [9]) для рассматриваемого уравнения можно записать следующим образом:

                                   (2.1)

где , или

                          (2.2)

Пусть , тогда (2.2) перепишем в виде:

или

                              (2.3)

где через g=at/h обозначено число Куранта.

Заметим, что первые два слагаемых (2.3) дают обычную схему с левой разностью.

Проведем монотонизацию схемы, добавив в (2.3) слагаемые , , где m – искусственная диффузия. Поскольку временные производные ,  на точном решении квазилинейного уравнения переноса аппроксимируют производные

,  

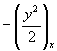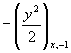
соответственно, то введенные члены дают дополнительные диффузионные слагаемые. Таким образом, модифицированная схема запишется в виде

                   (2.4)

Заметим, что при m ≡ 0 получим исходную схему (2.1), (2.3), а при m ≡ 1 – схему с левой разностью.

Запишем (2.4) в виде

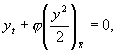
где

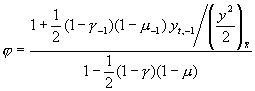
       (2.5)

Предположим, что y ³ 0 во всей пространственно-временной области, тогда схема (2.5) удовлетворяет принципу максимума [10], если выполнены неравенства

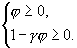
       (2.6)

Отметим, что буквальное условие применимости принципа максимума отличается от второго неравенства (2.6): в нем фигурирует . Однако из второго неравенства (2.6) в предположении  следует нужное условие.

Введем параметр

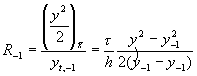
и положим m=m(R,g),

m_-1=m(R_-1,g_-1). Заметим, что

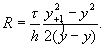
       (2.7)

Неравенства (2.6) выполнены, если функция m=m(R,g) имеет вид [3]:

       (2.8)

Введенная таким образом функция m обеспечивает монотонность рассматриваемой схемы. Отметим, что третьей строке (2.8) соответствует отрезок, на котором схема сохраняет второй порядок аппроксимации для линейных и близким к ним профилей. Четвертая строка обеспечивает переход от нулевого к отрицательным значениям m, что соответствует появлению в схеме антидиффузионных слагаемых, приводящих к уменьшению “размазывания” разрывов решения.

Параметр R^* в данной работе подбирается экспериментально. Для численных расчетов, как и в [5], использовалось R^* =1.2.

Уравнение (2.4) является нелинейным. Из (2.7) следует, что искомую величину  можно вычислить по известному R:

                                          (2.9)

Используя полученную зависимость m=m(R,g), найдем соотношения для R. Распишем уравнение (2.4):

  (2.10)

которое с учетом (2.7) приобретает вид

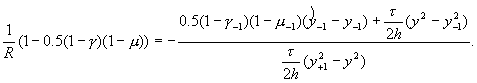
       (2.11)

Обозначим правую часть (2.11) через b:

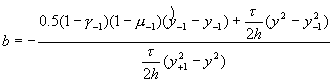
       (2.12)

Отметим, что (2.11) представляет собой нелинейное уравнение относительно R с известной правой частью. При этом левая часть (2.11) – монотонная функция R. Учитывая вид функции m=m(R, g), получим следующие расчетные формулы:

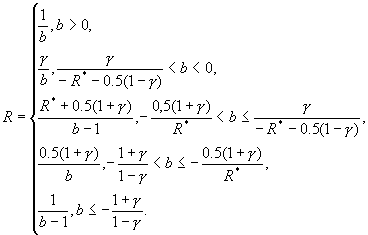
       (2.13)

Замечания:

1.     при  значение b не определено, однако из (2.7) следует, что в этом случае R = 0.

2.     из (2.13) видно, что R не определено при b = 0, но тогда из (2.12) и (2.10) непосредственно вычисляется искомое значение .

Таким образом, используя формулы (2.9), (2.12), (2.13), можно определить искомую величину . Отметим, что g зависит от , поэтому численно величина  определяется итерационным способом. В данной работе в качестве первого приближения  выбирается равной , для которой определяется соответствующее значение γ и по известному b находится значение R. Далее по формуле (2.9) определяется неизвестная величина , тем самым осуществляется переход на следующую итерацию при условии невыполнения критерия окончания итерационного процесса.

§ 3. Другие разностные схемы

Для сравнения предложенной схемы в данной работе были рассмотрены некоторые широко известные конечно-разностные схемы, а именно: явная и неявная схемы с левой разностью, схема Lax-Wendroff’a, а также предложенный в [3] метод прыжкового переноса. В большинстве из них число Куранта g выражается через решение не так, как в § 2. Однако вид его достаточно очевиден, так что мы сохраняем обозначение. Ниже представлена информация об основных свойствах этих схем. Более подробно о них можно узнать в указанной литературе.

1.     Схема с левой разностью [2, 4]

Явная схема, имеющая первый порядок аппроксимации по пространству и по времени. Схема устойчива при числе Куранта g £ 1, при этом в случае линейного уравнения переноса для g = 1 дает точное решение.

2.     Неявная схема с левой разностью [2, 4]

Абсолютно устойчивая схема, также имеющая первый порядок аппроксимации по пространству и по времени.

3.     Схема Lax-Wendroff’a [4]

Явная схема, аппроксимирующая исходное уравнение со вторым порядком  по времени и по пространству. Является устойчивой при g £ 1, при g =1 для линейного уравнения переноса дает точное решение.

4.     Метод прыжкового переноса [3, 5, 6, 11]

В работе [3] предложена схема, построенная с помощью монотонизации схемы “Кабаре” [3], и на ее основе разработан алгоритм метода прыжкового переноса.

Трехслойная схема “Кабаре”, аппроксимирующая уравнение конвективного переноса со вторым порядком точности, является бездиссипативной и обладает улучшенными по сравнению с классическими линейными схемами дисперсионными свойствами [6]. Она устойчива при g £ 1, дает точное решение в случае линейного уравнения переноса для g = 1 и g = 0.5, однако является немонотонной.

Монотонизация проводится при помощи “обрезания” искомого решения из требования выполнения принципа максимума в следующей форме: вычисляемое на новом временном слое значение должно быть ограничено максимальным и минимальным значениями из области зависимости решения. Для контроля возникающего при этом дисбаланса переносимой величины вводится функция “запаса”, что обеспечивает консервативность схемы.

§ 4. Организация вычислительного эксперимента

Аналогично работам [4, 5, 7] численное решение поставленной задачи (1.1) получено для всех указанных форм начальных профилей при следующих значениях параметров: l=520, l₁=0, l₂=20, T=1000, h=1. Число Куранта g () ограничено сверху величиной g_m, которая принимала значения: 0.1, 0.25, 0.5, 0.9. Для неявной схемы с левой разностью также были проведены расчеты при g_m = 3. Таким образом, временной шаг t принимал те же значения, что и число Куранта. Для определения точности полученного при этом решения вычислялись относительные ошибки с использованием норм

, ,

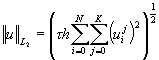
интегрально по временному промежутку 0 £ t £ T, а также

, ,

локально для момента времени t_j.

В рамках данной работы для проведения численного эксперимента была создана программа для персонального компьютера, реализующая алгоритмы поиска решения по указанным разностным схемам. На экран монитора выводится графическое изображение точного и численного решений для каждого временного слоя, а также относительные ошибки вычислений для нескольких промежуточных и конечного моментов времени. Такое представление результатов позволяет визуально и численно оценить качество полученного решения и тем самым сравнить используемые схемы.

§ 5. Результаты численного исследования

Полученные в численном эксперименте результаты представлены следующим образом. Для каждой схемы, используемой для получения численного решения, приведены таблицы интегральных и локальных по времени ошибок для различных чисел Куранта. В каждой таблице указаны относительные ошибки вычислений для всех начальных условий и используемых норм, соответствующее число Куранта приведено в левом верхнем углу таблицы.

С целью иллюстрации всех особенностей поведения решения для каждого из начальных профилей представлены графики решения для нескольких промежуточных моментов времени. При этом каждый рисунок содержит графики точного решения и численных решений для различных чисел Куранта. Такие рисунки приведены для предложенной монотонизованной схемы К. И. Бабенко, неявной схемы с левой разностью и метода прыжкового переноса. Для всех схем ниже представлено описание полученных результатов.

Полученные результаты позволяют проанализировать качественные и количественные свойства предложенной схемы, а также сравнить ее с другими, рассмотренными в данной работе. Выводы, сделанные при сравнительном анализе разностных схем, приведены далее.

1.     Явная схема с левой разностью

Схема передает решение весьма грубо, разрывы решений “размазываются” на несколько шагов (от 4 до 10). Размазывание решения тем сильней, чем меньше g. Решения типа волн разрежения размазываются на большее количество шагов по сравнению с ударными волнами. Этот дефект решения усиливается со временем. Для начальных профилей №№ 1, 2, 4 на тех интервалах времени, на которых происходит эволюция точного решения без изменения амплитуды, амплитуда численного решения непрерывно уменьшается. Поведение решения в эти моменты времени и в последующие, сопровождающиеся образованием и дальнейшим распространением ударных волн, практически ничем не отличается. Моменты образования ударных волн трудно прослеживаются. Скорость распространения ударных волн не зависит от g и совпадает со скоростью распространения ударных волн в точном решении.

Таблицы ошибок для явной схемы с левой разностью (локально при  t = T)

Таблицы ошибок для явной схемы с левой разностью (интегрально по t)

2.     Неявная схема с левой разностью

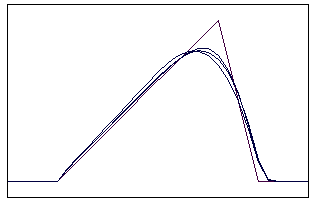
Решение, полученное при помощи этой схемы, повторяет точное еще хуже, чем в случае аналогичной явной схемы. Для этой схемы характерно еще более сильное размазывание разрывов (от 7 до 15 шагов по пространству), которое усиливается с увеличением числа Куранта. Как видно из рисунков 5.2.1-5.2.6, для численного решения характерно "выгибание" заднего фронта на начальных моментах времени, что усиливается при увеличении g. С течением времени зависимость численного решения от числа Куранта ослабевает. Для начальных профилей №№ 1, 2, 3, 4 численное решение, полученное по явной и неявной схемам с левой разностью, эволюционирует в волну треугольного профиля с распространяющейся вправо ударной волной и уменьшающейся амплитудой, что соответствует точному решению. Однако максимум амплитуды численного решения отстает от максимума точного. На рисунках численному решению, наиболее близкому к точному, соответствует g = 0.1.

Таким образом, особенности эволюции решения в виде образования и распространения ударных волн, а также взаимодействие ударных волн и волн разрежения, передаются схемами с левой разностью плохо.

Таблицы ошибок для неявной схемы с левой разностью (локально при  t = T)

Таблицы ошибок для неявной схемы с левой разностью (интегрально по t)

t=6                                                              t=10

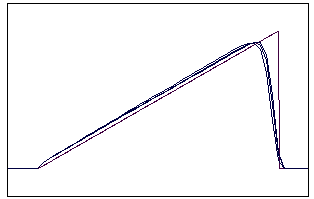
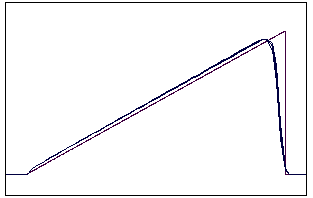
t=70                                                                   t=170

Рис. 5.2.1 Численное решение по неявной схеме с левой разностью для “треугольника” (g = 0,1; 0,5; 0,9)

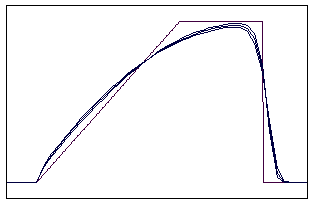
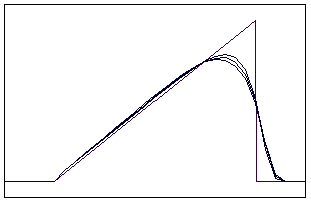
t=18                                                                   t=40

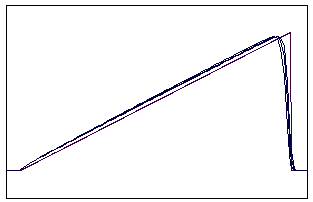
t=90                                                                   t=160

Рис. 5.2.2 Численное решение по неявной схеме с левой разностью для “прямоугольника” (g = 0,1; 0,5; 0,9)

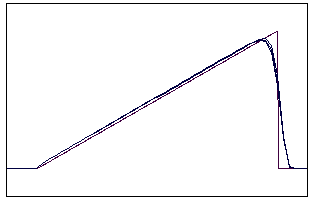
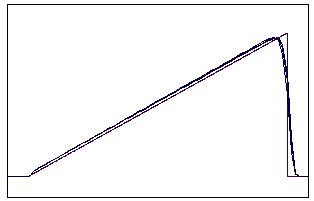
t=60                                                                  t=160

Рис.5.2.3 Численное решение по неявной схеме с левой разностью для “левого треугольника” (g = 0,1; 0,5; 0,9)

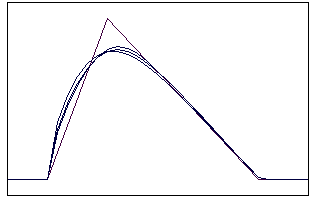
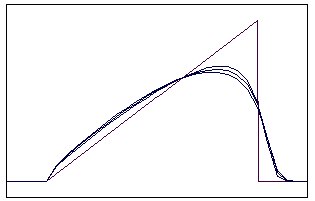
t=5                                                                  t=20

Рис. 5.2.4 Численное решение по неявной схеме с левой разностью для “правого треугольника” (g = 0,1; 0,5; 0,9)

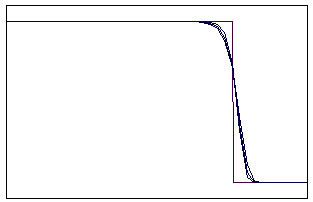
t=20                                                                  t=80

Рис. 5.2.5 Численное решение по неявной схеме с левой разностью для “ступеньки вниз” (g = 0,1; 0,5; 0,9)

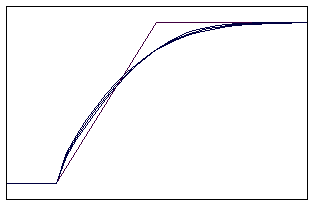
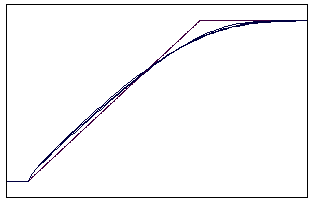
t=10                                                                  t=40

Рис. 5.2.6 Численное решение по неявной схеме с левой разностью для “ступеньки вверх” (g = 0,1; 0,5; 0,9)

3. Схема Lax-Wendroff’a

Для данной схемы характерно явление нормальной дисперсии. Образование ударных волн сопровождается появлением осцилляций за их фронтом. Для начальных профилей №№ 2, 4, 6 характерно возникновение осцилляций на левом фронте образующейся волны разрежения. Эти осцилляции прогрессируют со временем, что приводит к увеличению погрешности вычислений (особенно в норме С). Так, при g = 0.5 для начального профиля № 2 в момент времени t = 10 относительная ошибка вычислений в норме С равнялась 0.17, а в момент t = T – 1.076.

Расплывание решения проявляется в меньшей мере, чем у решений, полученных по явной и неявной схемам с левой разностью. Разрывы решений передаются этой схемой лучше, размазывание разрывов происходит на 3-5 шагах.

Таблицы ошибок для схемы Lax-Wendroff’a (локально при  t = T)

Таблицы ошибок для схемы Lax-Wendroff’a (интегрально по t)

4. Метод прыжкового переноса

По сравнению с указанными выше схемами решение, полученное с использованием метода прыжкового переноса, лучше передает точное. Основным достоинством метода является способность точно передавать разрывы типа ударных волн. Однако в силу специфики данного метода решение меняется скачкообразно, поэтому точное положение ударных волн можно наблюдать только через определенные интервалы времени. Так, для начального профиля № 5 при g = 0.5 решение на каждом 4-ом временном слое скачком смещается вправо на один шаг по x, догоняя тем самым точное решение. Таким образом, ошибка вычислений в эти моменты времени нулевая. Однако увеличение числа Куранта приводит к появлению дефектов численного решения в виде “ступенек” и неверных скоростей движения ударных волн. Из рис. 5.4.3 видно, что для начального условия № 4 на волне сжатия, независимо от числа Куранта, образуются “ступеньки”, а рис. 5.4.2, 5.4.5 показывают, что при g = 0.9 ударные волны в численном решении движутся с меньшими скоростями, чем ударные волны в точном решении. На рис. 5.4.1-5.4.5 численному решению, наиболее близкому к точному, соответствует g = 0.5.

Таблицы ошибок для метода прыжкового переноса (локально при  t = T)

Таблицы ошибок для метода прыжкового переноса (интегрально по t)

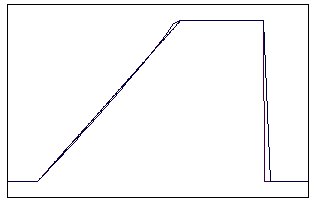
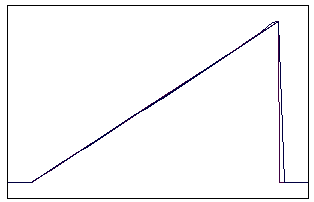
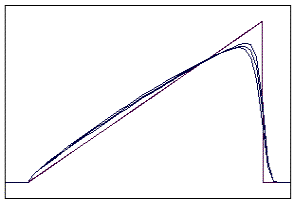
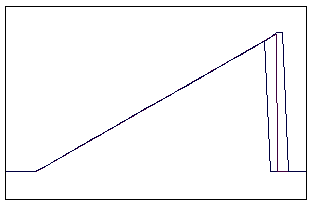
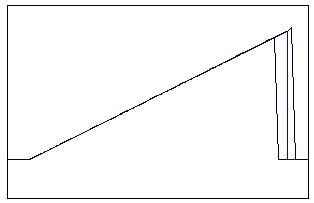
t=18                                                                   t=40

Рис. 5.4.1 Численное решение для метода прыжкового переноса для “прямоугольника” (g=0,5; 0,9)

t=60                                                                  t=160

Рис. 5.4.2 Численное решение для метода прыжкового переноса для

 “левого треугольника” (g=0,5; 0,9)

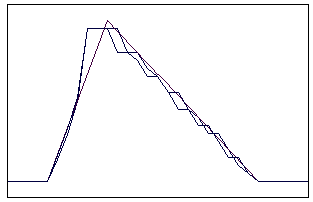
t=5

Рис. 5.4.3 Численное решение для метода прыжкового переноса для

“правого треугольника” (g = 0,5; 0,9)

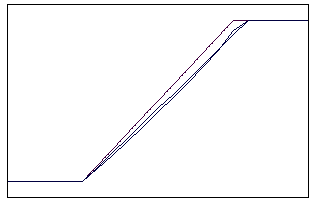
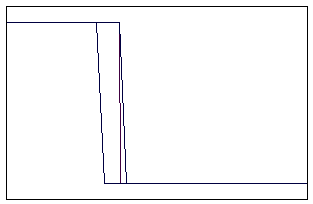
t=10                                                                   t=40

Рис. 5.4.4 Численное решение для метода прыжкового переноса для

“ступеньки вверх” (g = 0,5; 0,9)

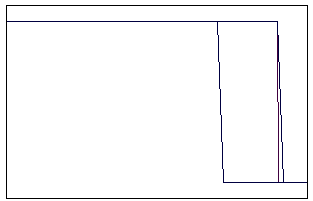
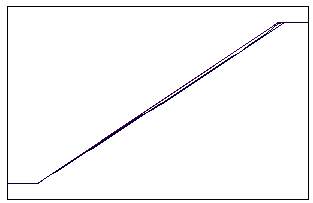
t=20                                                                   t=80

Рис. 5.4.5 Численное решение для метода прыжкового переноса для

“ступеньки вниз” (g = 0,5; 0,9)

5. Монотонизованная схема “Бабенко”

Полученное по данной схеме решение наилучшим по сравнению с рассмотренными выше схемами образом передает точное во всем изученном диапазоне изменения чисел Куранта. У схемы не наблюдается явлений нормальной и аномальной дисперсии, расплывание решения незначительно - размазывание разрывов происходит на меньшее количество шагов по сравнению с другими рассмотренными схемами (1-3 шага). Наблюдается небольшое смещение вправо левого фронта образующейся волны разрежения (для начальных профилей №№ 2, 4, 6). Рисунки 5.5.1-5.5.6 показывают, что численные решения при различных числах Куранта практически не отличаются друг от друга, при этом численному решению, наиболее близкому к точному, соответствует g = 0.1.

Таблицы ошибок для схемы К. И. Бабенко (локально при  t = T)

Таблицы ошибок для схемы К. И. Бабенко (интегрально по t)

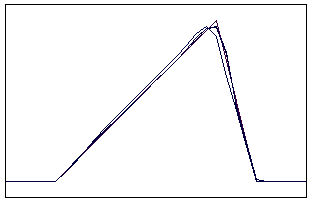
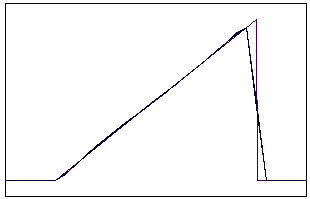
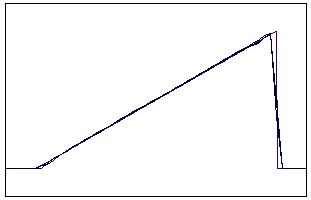
t=6                                                              t=10

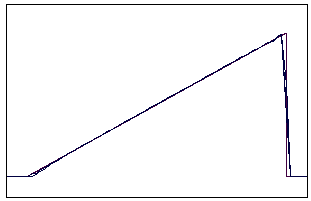
t=70                                                                   t=170

Рис. 5.5.1 Численное решение по схеме К. И. Бабенко для “треугольника” (g = 0,1; 0,5; 0,9)

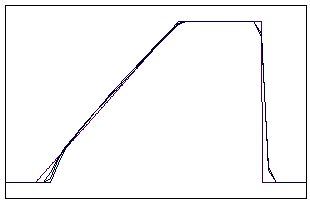
t=18                                                                   t=40

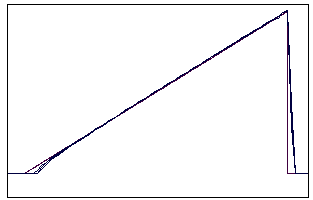
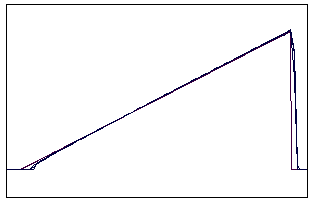
t=90                                                                  t=160

Рис. 5.5.2 Численное решение по схеме К. И. Бабенко для “прямоугольника” (g = 0,1; 0,5; 0,9)

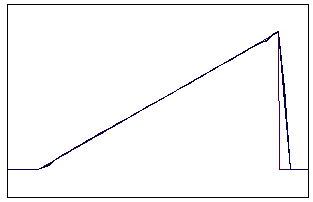
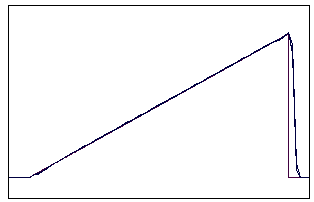
t=60                                                                  t=160

Рис. 5.5.3 Численное решение по схеме К. И. Бабенко для “левого треугольника” (g = 0,1; 0,5; 0,9)

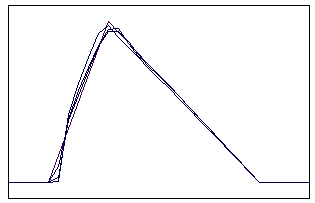
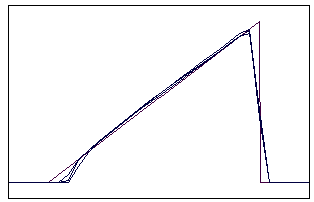
t=5                                                                  t=20

Рис. 5.5.4 Численное решение по схеме К. И. Бабенко для “правого треугольника” (g = 0,1; 0,5; 0,9)

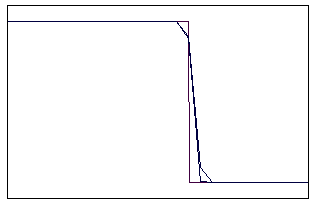
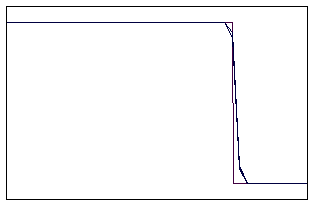
t=20                                                                  t=80

Рис. 5.5.5 Численное решение по схеме К. И. Бабенко для “ступеньки вниз” (g = 0,1; 0,5; 0,9)

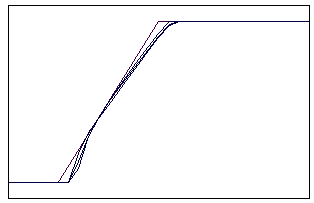
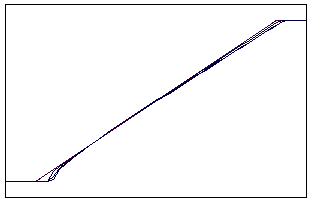
t=10                                                                  t=40

Рис. 5.5.6 Численное решение по схеме К. И. Бабенко для “ступеньки вверх” (g = 0,1; 0,5; 0,9)

§ 6. Сравнение схем

На основе полученных численных результатов были сравнены рассмотренные схемы. Ниже приведены таблицы сравнения, содержащие названия тех схем, которые при данном числе Куранта дали наименьшую относительную ошибку в соответствующей норме. Если в ячейке таблицы указаны несколько схем, то ошибки вычислений, полученные для данных схем, либо совпадают, либо незначительно отличаются друг от друга. При этом используются обозначения: явная схема с левой разностью – ЯЛ, неявная схема с левой разностью – НЛ, схема Lax-Wendroff’a – LW, метод прыжкового переноса – ПП, схема К.И. Бабенко – Б.

1.     Сравнение схем по локальным (при t = T) ошибкам.

1) При γ = 0.1 в нормах С и L₂ для начальных условий №№ 1, 6 лучшие результаты показала предложенная в данной работе схема К.И. Бабенко, для условий №№ 2, 3 – неявная схема с левой разностью и для условия № 5 – метод прыжкового переноса. В норме L₁ лучшей оказалась монотонизованная схема К.И. Бабенко в случае начальных условий №№ 1, 5, 6, метод прыжкового переноса – для начального профиля № 2 и схемы с направленными разностями – для условий №№ 3, 4.

2) При γ = 0.25 в норме С для начального условия № 1 лучшие результаты получены с использованием схемы Lax-Wendroff’a, неявной схемы с левой разностью – для условий №№ 2, 3, метода прыжкового переноса – для условия № 5 и монотонизованной схемы К.И. Бабенко – для условия № 6. В норме L₁ лучшей оказалась схема К.И. Бабенко для начальных условий №№ 1, 5, 6, метод прыжкового переноса – для условий №№ 2, 3 и явная схема с левой разностью – для условия № 4. В норме L₂, как и при γ = 0.1, для начальных условий №№ 1, 6 лучшие результаты показала схема К.И. Бабенко, для условий №№ 2, 3 – неявная схема с левой разностью, для условия № 4 – явная схема с левой разностью и для условия № 5 – метод прыжкового переноса.