Математическое моделирование эрозии металлических контактов в рельсотронном ускорителе
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
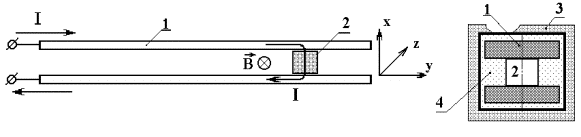
Рис. 0.1. Генерация ускоряющей
силы и принципиальная схема рельсотрона. 1 - направляющий и токоподводящий
рельс, 2 - ускоряемое тело (якорь или иная токовая арматура), 3 - силовой
бандаж канала, 4 – изолятор. |
Основное
преимущество рельсотрона над распространенными пороховыми или легкогазовыми
ускорителями заключается в отсутствии фундаментальных ограничений на величину
скорости метания. Диапазон воспроизводимых результатов, полученных при разгоне
твердых тел в рельсотроне, простирается до 8.5 км/с. Тем не менее, при
ускорении металлического якоря силой Лоренца воспроизводимость результатов
ограничена скоростями 2.5 - 3 км/с. В этом случае при достижении скорости около
1 км/с наблюдается нарушение металлической проводимости в скользящем контакте
между рельсом и якорем. Это приводит к эрозии контакта и ограничению ресурса
работы ускорительного канала. Исследование динамики разрушения контакта
позволило бы разработать соответствующие меры по увеличению скорости снарядов в
таких устройствах, имеющих максимально простую конструкцию.
В экспериментах [3]
и др. показано, что при скоростях разгона металлического якоря, превышающих 1.5
км/с, тепловыделение в зоне контакта якоря и рельса приводит к разогреву и
испарению задней кромки якоря с образованием плазменной перемычки. Этому способствует
эффект скоростного скинирования, приводящий к увеличению плотности тока на
задних кромках контактов. Металлический контакт между якорем и рельсами
разрушается, что сопровождается переходом к дуговой перемычке с характерной
величиной напряженности электрического поля E ~ 300 В/см. Поэтому переход
связан с резким падением КПД преобразования электрической энергии в
кинетическую, а электродинамическая стадия разгона замещается газодинамическим
ускорением, связанным с расширением и нагревом плазмы. В упрощенных моделях
процесса ускорения [4] для различных материалов якоря и рельса получены оценки
критической скорости Vкрит » 0.9 – 1.2 км/с, при
которой происходит нарушение проводимости контакта металлического типа.
Постановка задачи в целом определяется необходимостью исследования ускорителей
типа рельсотрон с более сложной топологией якоря и канала, чем приведена на
рис. 0.1, в которых величина критической скорости могла бы быть увеличена в 2 -
3 раза относительно указанной выше.
В последние годы удалось создать ускорители и
источники питания, обеспечивающие успешный разгон килограммовых масс до
скоростей свыше 2 км/с. Масштаб затрат, вложенных в создание установок, имеющих
импульсные накопители с запасом энергии от 10 до 60 МДж и каналы длиной до 9 м,
вынуждает провести тщательный анализ процессов токопереноса в контактной зоне
канала ускорителя. Проблеме кризиса металлического контакта и поиску возможных
путей его преодоления посвящен обзор [5].
Экспериментальные и теоретические исследования,
выполненные в различных исследовательских центрах, показали, что в начале
разгона, пока скорость меньше нескольких сотен м/с, между якорем и рельсами
существует устойчивый контакт. При скоростях движения 500 - 1000 м/с
практически на всей длине разгона имеет место нестационарный режим протекания
тока через контактную поверхность. Наблюдается возникновение дугового разряда.
Диапазон скоростей, при которых это происходит, зависит в некоторых пределах от
тока, начальной скорости, материалов электрода и якоря, его конфигурации и т.д.
Точка перехода к дуговому разряду идентифицировалась исследователями как
«кризис» металлического контакта. В различных ситуациях диапазон скоростей, в
котором наблюдался «кризис» металлического контакта, достаточно широк: от 0.5
до 1.2 км/с. Попытки кардинального увеличения верхнего предела пока не имели
успеха, за исключением, быть может, работы [6], в которой скоростное скинирование
было подавлено использованием рельсов из плохопроводящего графита.
Многочисленные теоретические и экспериментальные исследования последних лет
направлены на увеличение предельной скорости, при которой сохраняется
металлический контакт с малым переходным импедансом.
Из – за многочисленных
трудностей экспериментального исследования процессов в высокоскоростном
электрическом контакте анализ механизмов эрозии может быть выполнен только с
помощью математического моделирования, учитывающего вклад различных процессов
(трение, распределение токов, нагрев материла и фазовые переходы) в существенно
многомерной перемещающейся области. Для исследования динамики этих процессов в
данной работе выполнено математическое моделирование процесса разгона якоря и
эрозии скользящих токовых поверхностей. Результаты математического
моделирования сопоставлены с экспериментальными данными.
Для верного описания электродинамики ускорения и
тепловых процессов в зоне контакта необходима замкнутая трехмерная нелинейная
модель, объединяющая расчет распределения тока в якоре и локального
тепловыделения с непосредственным расчетом ускоряющей силы. Постановка задачи в
целом определяется необходимостью исследования ускорителей типа рельсотрон со
сложной топологией якоря и канала.
Целью данной работы является представление
экспериментальных данных об эрозии материалов в канале рельсотрона при
электромагнитном ускорении проводящих макротел и проведение математического
моделирования указанного процесса.
Работа выполнена при
частичной финансовой поддержке Российского фонда фундаментальных исследований
(проект РФФИ № 03 – 01 - 00461).
§ 1. Результаты экспериментальных исследований.
В течение последних лет нами
были проведены экспериментальные исследования эрозии скоростного контакта на
ускорителе с калибром 1 см при разгоне Al якоря до 1 км/с, а затем
выполнены ресурсные испытания каналов с рельсами из специальных материалов при
скоростях до 2.5 км/с [6, 7]. При этом общая характерная картина поведения
движущихся контактов восстановлена при анализе полученных результатов по
измерению макрополей вокруг ускоряемого тела.
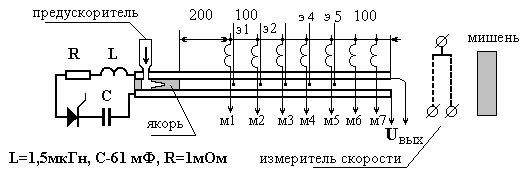
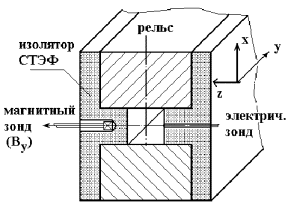
Размещение вдоль рельсотрона
магнитных и электрических зондов и их расположение в поперечном сечении канала
показано на рис. 1.1. Магнитные зонды регистрировали компоненту Вy магнитного поля,
фиксируя момент прохождения якоря с током jx мимо катушки зонда,
размещенной в теле изолятора. Миниатюрные (диаметр медного штырька 0.5 мм)
электрические зонды (э1 - э5 на рис. 1.1), размещенные также в изоляторе,
фиксировали момент соприкосновения иглы зонда с передней кромкой алюминиевого
якоря.
Пороховой предускоритель на длине ~15 см разгонял дуэтное тело с якорем
массой 5 г, показанное на рис. 1.2, до скорости 250 м/с, после чего включался
ток, величина которого за время около 0.5 мс достигала заданной амплитуды 200 –
450 кА в зависимости от величины начального напряжения на батарее
конденсаторов. Время нарастания тока, в основном, определялось источником
питания и не зависело от массы снаряда, состояния контактов, что дало
возможность свободно выбирать режим ускорения при фиксированной длине метрового
канала рельсотрона.
|
|
|
|
Рис. 1.1. Размещение системы диагностических
зондов в рельсотроне и в поперечном сечении канала. |
|
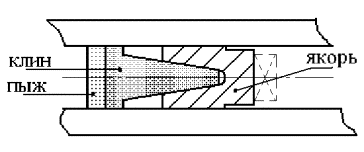
Во всех экспериментах
использовался якорь с продольным разрезом и клиновой вставкой, показанный на
рис. 1.2. Такая конструкция обеспечивала начальное поджатие контактных
поверхностей якоря к токоведущим рельсам на стадии предварительного ускорения
при включении ускоряющего тока. В дальнейшем поджатие поверхностей якоря к
рельсам обеспечивалось магнитным давлением.
|
Рис. 1.2. Сборка якоря с клиновым толкателем
(дуэтное тело) в канале рельсового ускорителя. Пунктиром указано место
установки зонда в одном из экспериментов. |
|
В процессе
экспериментов постоянно контролировались электротехнические параметры: ток
разряда, напряжение на входе в канал, а также выходное напряжение Um на дульном срезе,
по величине которого можно судить о характере механизма проводимости на
контактах рельса и якоря.
А. Начальная стадия
эрозии контактов при ускорении током около 250 кА.
В первой
серии экспериментов исследовалось начало эрозии металлического контакта при
умеренных скоростях разгона якоря. Был выбран режим умеренного ускорения на
всей длине канала до скорости около 1 км/с. Напряжение на конденсаторах при
этом было равно 1.7 кВ, а ток разряда не превышал 230 - 235 кА. Осциллограмма
выходного напряжения, амплитуда которого на всем временном отрезке ускорения не
превышала 45 В, свидетельствует о существовании постоянного металлического
контакта якоря с рельсами. Мягкая мишень из пенопласта позволяла «поймать»
вылетающий якорь без его повреждения.
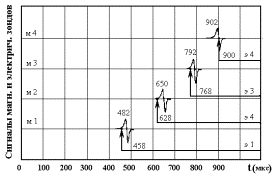
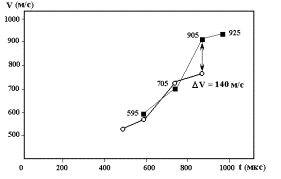
При обработке результатов экспериментов сопоставлялись данные скорости движения якоря, полученные по времени сигналов дифференцирующих магнитных зондов (скорость движения центра токовой перемычки) и физической скорости передней границы якоря, полученной по времени сигналов с контактных электрических зондов. Данные приведены на рис. 1.3.a, а результаты их обработки, представляющие скорости движения, показаны на рис. 1.3.b.
На
основании приведенных результатов можно утверждать, что после достижения якорем
скорости 650 - 700 м/с задний фронт токового распределения начинает
перемещаться по направлению к передней кромке якоря. Очень вероятно, что это
связано с перемещением вдоль якоря задней границы зоны металлического контакта.
Оценка этой скорости, полученной на участке между 3 и 4 парой зондов, дала
величину DVy = 140 м/с. Для
построения графиков использованы усредненные данные по 4 экспериментам. В
результате относительная ошибка в оценке DVz не должна превышать
10 м/с. Однако для использованной нами U - образной конфигурации
якоря говорить об обнаружении этого эффекта только по приведенным выше данным
было бы нельзя.
|
|
|
|
Рис. 1.3.a.
Осциллограммы магнитных зондов и моменты соприкосновения электрических зондов
с якорем (пара зондов в одном сечении по оси y). |
Рис. 1.3.b.
Скорость токовой перемычки (ð) и скорость якоря (о). |
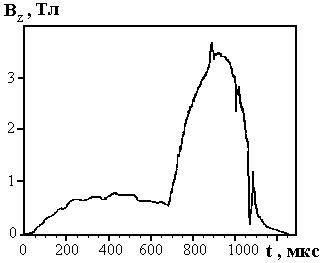
Для корректной оценки времени начала деградации
контактной зоны был дополнительно поставлен специальный эксперимент с магнитным
зондом, установленным на передней поверхности ускоряемого якоря в точке
расположенной на оси канала (см. рис. 1.2). Выводы зонда были подведены мягкими
проводами с надежной изоляцией через канал к осциллографу и не мешали ускорению
якоря. По интегрированной осциллограмме сигнала зонда рассчитана зависимость
величины компоненты индукции магнитного поля Вz перед якорем от
времени, которая показана на рис. 1.4.
|
Рис. 1.4. Компонента магнитной индукции Bz впереди якоря в процессе его ускорения при
амплитудном значении тока 235 кА. |
|
Форма сигнала до момента времени 680 мкс повторяет
форму тока разряда, после чего амплитуда сигнала начинает быстро нарастать. Это
означает, что при уменьшении полного тока разряда распределение плотности тока jx по якорю начинает
интенсивно дрейфовать, перемещаясь вперед к катушке зонда. Совпадение
характерного времени начала дрейфа тока с зондовыми измерениями подтвердило
данные предыдущих экспериментов.
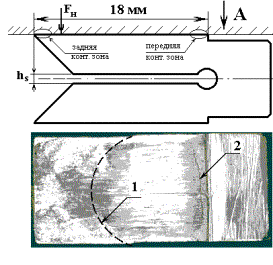
Значительный интерес
представили результаты анализа поверхности якоря в зоне контакта. Характерная
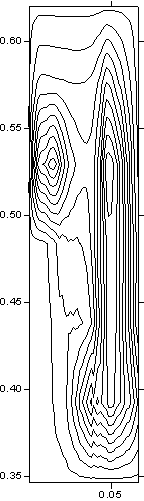
для контактной поверхности якоря картина эрозии показана на фотографии рис.
1.5. Здесь же приведен анализ металлографического исследования ”выноса”
материала с контактной поверхности.
|
|
|
|
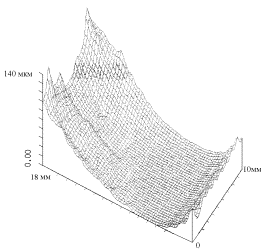
Рис. 1.5. Алюминиевый якорь, фотография контактной
поверхности (по стрелке А) со следами эрозии и результат металлографического
анализа. 1 - условно прорисованная задняя граница эрозионного следа, 2 –
видимая передняя граница зоны эрозии. |
|
По - видимому,
эрозия начинается с угловых точек задней кромки якоря и распространяется по
направлению его движения в виде серпообразной волны. Одновременно распределение
тока смещается вперед к зоне металлического контакта. Однако оценить, какая
доля тока переносится поперек образующейся микрощели в задней части якоря, не
представляется возможным. Можно только предположить, что пока зона
металлического контакта не деградировала до конца (что выполнялось в описанных
экспериментах) доля этого тока невелика. Во всяком случае, после экспериментов
явных следов эрозии на поверхности рельсов, характерных для дуговых разрядов,
не наблюдалось. Интересной особенностью эрозии поверхности якоря на рис. 1.5
было то, что на передней кромке якоря также видны следы эрозии контакта, что
свидетельствует о замыкании части тока по фронтальной поверхности. Ранее это
обсуждалось нами в [8, 9].
Б. Разгон металлического якоря до скорости
более 2 км/с.
В
следующей экспериментальной серии были проведены ресурсные испытания рельсов с
разгоном Al якоря до скорости 2.3 – 2.7 км/с. Для этого в
канале создавалась высокая линейная плотность тока порядка 450 кА/см.
Представляло интерес провести сравнительные испытания ресурса работы рельсотрона
на специально изготовленных рельсах из эрозионностойких материалов. В качестве
таких материалов были выбраны: 1. дисперсноупрочненная Cu с 1 % добавкой
окиси Al; 2. Cu - Mo композит (60 % + 40
%) с добавкой гексаборида La [10]. Оба материала были изготовлены с
использованием технологии порошковой металлургии.
Скорость
предварительного разгона якоря пороховым ускорителем была увеличена до 450 -
500 м/с в соответствии с задачей получения заданных выходных параметров
устройства, а зарядное напряжение батареи задавалось равным 3.7 кВ для
получения ускоряющего тока 430 - 450 кА. В качестве мишени использовалась
алюминиевая пластина, чтобы по величине каверны - углубления иметь
представление о компактности ускоренного тела.
Первый эксперимент проведен на обычных
рельсах из холоднокатаной Cu марки М1, результаты которого служили начальной
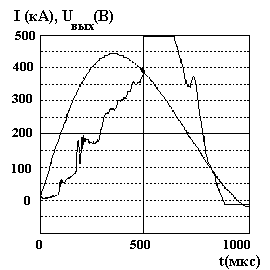
точкой отсчета в сравнительных испытаниях. На рис. 1.6 показана осциллограмма
тока и выходное напряжение Um канала на дульном срезе.
Видно, что надежный металлический контакт (при Um £ 50 В) существовал в
течение 100 - 150 мкс, а к моменту времени 300 мкс напряжение на токовой
перемычке выросло до величины 250 – 300 В. Этот уровень напряжения
соответствовал возникновению дугового разряда в канале, что подтвердили данные
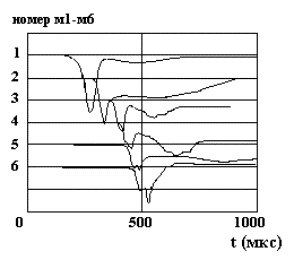
магнитозондовых измерений. Сводная картина интегрированных сигналов с зондов м1
- м6 показана на рис. 1.7, где отчетливо видно образование токопроводящей
плазменной части перемычки, отстающей от металлического якоря.
|
|
|
|
Рис. 1.6. Величина тока и выходного напряжения на канале с медными рельсами при ускорении металлического якоря до 2.7 км/с. Через 500 мкс после старта якорь покидал канал, далее напряжение генерировалось на дуге, загорающейся на дульном срезе. |
Рис. 1.7. Сигналы магнитных зондов в канале с медными рельсами при ускорении металлического якоря до 2.7 км/с. Сигналы зондов проинтегрированы (в отличие от показанных на рис. 1.3). |
Выходная скорость якоря за срезом канала
достигла 2.7 км/с. Повторный пуск на этих же электродах привел к быстрому прорыву
образующейся дуги за переднюю поверхность якоря и срыву ускорения.
Сравнение осциллограмм, полученных в
экспериментах на других рельсах (они не приводятся), показало, что в течение
каждой экспериментальной серии характер поведения контакта рельсов и якоря не
имел резкого отличия от описанного. Дуговая стадия наступала после 350 мкс от
старта разряда. Наилучшее поведение канала (меньшая эрозия поверхности рельса)
обнаружил Cu - Mo композит, позволивший проводить до 5 циклов
ускорения без замены электродов. По - видимому, по мере увеличения числа циклов
наблюдаемый незначительный износ рельсов приводит к ухудшению контактов из-за
нарушения чистоты поверхности рельса и сильному росту эрозии поверхности якоря.
Для якоря этот процесс, в конце концов, оказался значительно более
катастрофичным, чем для рельсов, и привел к разрушению якоря на 6 - м цикле
ускорения. Это было идентифицировано по появлению нескольких каверн на мишени,
соответствующих отдельным частям якоря. Надо отметить, что полная величина
“износа” рельсов в последнем случае не превысила 0.2 мм в наиболее нагруженном
участке. Последний приведенный факт показывает, насколько актуальна исследуемая
проблема сохранения хороших скользящих высокоскоростных контактов для
обеспечения ресурса работы электродов (и канала в целом) рельсотронных
ускорителей.
§ 2. Математическая модель.
Для описания электромагнитных полей использовано
т.н. квазистационарное или МГД – приближение [11] уравнений Максвелла.
Замкнутая пространственно трехмерная нестационарная во времени модель [8, 11 -
13] объединяет расчет распределении тока в проводниках и локального
тепловыделения с непосредственным расчетом ускоряющей силы. При этом модель
однородна по различным подобластям с резко различающейся электропроводностью:
типа проводник или диэлектрик.
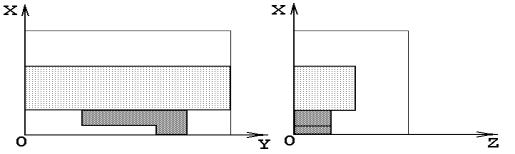
Схема модельной пространственной области
(идеализация схем рис. 1.2, 1.5), использованной в расчетах, представлена на
рис. 2.1. Якорь при этом двигается в положительном направлении оси OY.
|
|
|
Рис.
2.1. Схема сечения рельсотрона плоскостями z = const (слева) и y = const (справа). |
При ускорении тел в рельсотроне наиболее сложные и интересные явления
происходят в окрестности якоря, характерная протяженность которой сравнима с
поперечным размером канала. Поэтому при моделировании целесообразно ограничить
рассматриваемую область и вести описание полей в пространственной области,
жестко связанной со скользящим якорем. Длина этой области (в направлении оси y) составляет
несколько калибров ускорителя в обе стороны от якоря (рис. 2.1). При таком
подходе возникает проблема задания граничных условий на передней и задней
границах исследуемой области. На боковых границах области этой проблемы нет,
так как канал рельсотрона обычно заключен в проводящий силовой бандаж. Поэтому
при расчете будем рассматривать не весь трехмерный ускоритель, а его часть,
приходящуюся на область, жестко связанную с якорем и движущуюся вместе с ним.
При
разработке модели использовано резкое различие длины ускорителя (по y) и его поперечных
размеров. Учтено также, что единственной заданной извне электромагнитной
величиной можно считать полный ток, определяемый источником питания. Поэтому
естественно рассмотреть модель, в которой на торцах расчетной области заданы
тангенциальные компоненты магнитного поля, соответствующие бесконечно длинной
(вдоль оси y) системе проводников, для каждого из которых задан
полный ток. Это поле является решением соответствующей пространственно
двумерной задачи. В результате для постановки граничных условий необходимо
решить две специальные задачи для интегро – дифференциальных уравнений на
торцах [8]. Решение же трехмерной задачи получается путем использования
алгоритма [11] по заданным тангенциальным компонентам магнитного поля.
В работе построены
алгоритмы задания граничных условий, обобщенные для различных конструкций
ускорительного канала, и разработаны новые алгоритмы и программы, позволяющие
получить численные результаты, соответствующие конкретному техническому
объекту. Они позволяют, в частности, исследовать явление деградации
металлической проводимости. В нашем случае получено хорошее качественное и
количественное соответствие результатов расчетов и экспериментов.
В задаче предполагается, что электропроводность
σ материалов зависит от температуры. В проводящей части возможны фазовые
переходы: плавление и кипение.
Подробности
математической модели и вычислительного алгоритма представлены в работах [8, 11
- 13]. Ниже используются обозначения, традиционные для работ по моделированию
электромагнитных явлений. Они совпадают с использованными в [8, 11 - 13].
Для
решения возникающей системы линейных алгебраических уравнений при этом
используется метод сопряженных градиентов совместно с неполным разложением Xолесского [14 - 17].
Далее приведены результаты расчетов
распределений различных полей в ускорителе с U – образным якорем. В данном случае длина
расчетной области, связанной со скользящим якорем (в направлении оси OY), составляет 8.8 см
(четыре калибра позади якоря, три калибра впереди плюс длина самого якоря).
Высота области (по оси OX)
равна 7.0 см (половина высоты якоря, высота рельса плюс высота диэлектрика над
рельсом). Ширина области (по оси OZ)
равна 3.5 см (половина ширины якоря, выступающая часть рельса плюс ширина
диэлектрика за рельсом). Высота канала (калибр) - 1 см. Длина якоря (по y) - 1.8 см. Высота
рельса - 3 см. Расчет будем вести для двух вариантов процесса ускорения: 1.
ускоряется тело массой 5 г с начальной скоростью 250 м/с; 2. тело массой 2.5 г
с начальной скоростью 500 м/с Начальная температура ![]() = 290 град К.
Материал якоря – Al,
направляющих – Cu.
= 290 град К.
Материал якоря – Al,
направляющих – Cu.
В развитие [18]
разработан универсальный для различных конфигураций объекта исследования метод
описания расчетной области. При формировании файла - описателя области в
программу задания характеристик области добавлена система разделения
подобластей, относящихся к якорю и рельсу. В результате трехмерная область
разделяется на параллелепипеды (секции) с гранями, параллельными координатным
плоскостям. Параллелепипеды отличаются друг от друга материалами,
характеристиками сетки или условиями на своих границах. В каждом таком
параллелепипеде определено количество ячеек сетки. Такие характеристики, как
плотность, электропроводность и другие параметры материала, определяются
однозначно номером, сопоставленным данному параллелепипеду, и номером,
определяющим физический смысл объекта (якорь, рельс). Изменение основных
программ, учитывающее новую систему описания области, позволяет применять
программный комплекс для исследования объектов различной конфигурации.
Полученные
параметры пространственной области используются для дальнейшего расчета. По ним
рассчитывается набор логических массивов, полностью определяющих область, ее
границу и, тем самым, матрицу системы линейных алгебраических уравнений (т.е.
разностную схему) для решаемой задачи. Наиболее сложным является задание
значений массивов на границах области. В рамках данной работы разработана новая
система формирования логических массивов в граничных ячейках, позволяющая
независимо от конфигурации (в отличие от старых систем) получать значения
граничных компонент массивов.
Подобласти, различающиеся по материалу, в
проведенных расчетах разбиты на дополнительные разностные ячейки: по x – (4 + 8 + 8 + 4 ),
по y
- (4 + 8 + 8 + 4), по z – (8 + 6 + 4). В результате в пространственной области
находится 35625 ребер сетки, 32544 граней, 10368 ячеек Номера ячеек по
соответствующим осям координат обозначены ix,
iy,
iz.
§ 3. Результаты
математического моделирования.
Приведем некоторые результаты проведенных
расчетов. Ниже в графическом виде представлены распределения H,
j,
силы Лоренца f
= [j, H]
в сечениях области различными плоскостями. Все сечения проходят через якорь или
рельс. Показан и ряд других характеристик ускорения.
А. Ускорение током
250 кА.
На рис.
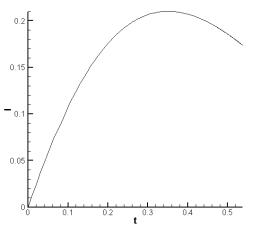
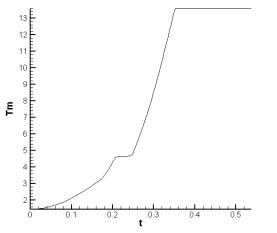
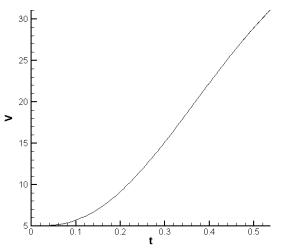
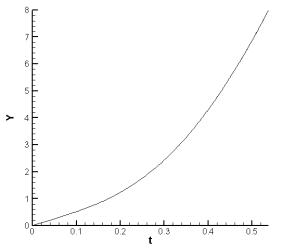
3.1 приведены рассчитанные временные зависимости сосредоточенных характеристик
процесса ускорения: полного тока, максимальной температуры в области, скорости
и координаты якоря.
|
|
|
|
Рис. 3.1.a.
Входной ток (в 2 МА). |
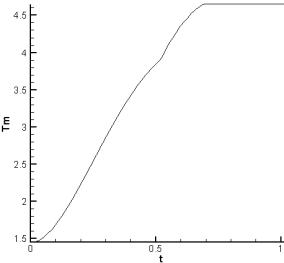
Рис. 3.1.b.
Максимальная температура якоря (в 200 град К). |
|
|
|
|
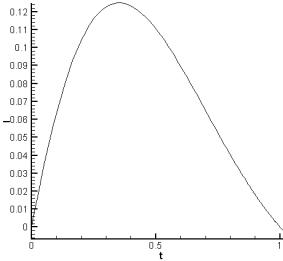
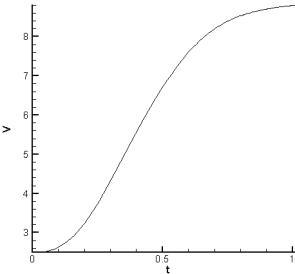
Рис. 3.1.c. Cкорость якоря (в 0.1 км/с). |
Рис. 3.1.d.
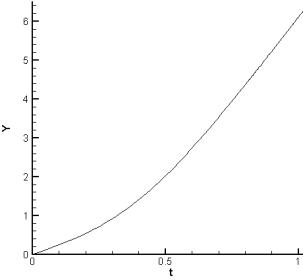
Координата якоря (в 0.1 м). |
|
По оси абсцисс на всех рисунках время в мсек. |
|
Из рис. 3.1.b
и 3.1.c
следует, что при достижении момента времени t
![]() 0.7 мсек, v
0.7 мсек, v ![]() 800 м/c максимум температуры
достигает 920 K,
т.е. начинается плавление якоря. Об этом свидетельствует и своеобразный “излом”
на графике максимальной температуры (рис. 3.1.b). Полный ток (рис. 3.1.a) изменяется по
заданному закону. Якорь покидает ускоритель со скоростью около 900 м/c. В процессе ускорения
температура кипения не достигнута.
800 м/c максимум температуры
достигает 920 K,
т.е. начинается плавление якоря. Об этом свидетельствует и своеобразный “излом”
на графике максимальной температуры (рис. 3.1.b). Полный ток (рис. 3.1.a) изменяется по
заданному закону. Якорь покидает ускоритель со скоростью около 900 м/c. В процессе ускорения
температура кипения не достигнута.
Время и скорость движения якоря в начале
плавления якоря очень хорошо соответствует времени начала смещения токового
распределения (см. § 1. А). Сравнительно невысокая температура указывает на
отсутствие дугового разряда. Выходная скорость тела и время вылета вполне
соответствуют данным, полученным в натурном эксперименте.
Б. Разгон металлического якоря до скорости
более 2 км/с.
На рис.
3.2 приведены рассчитанные временные зависимости сосредоточенных характеристик
процесса ускорения: полного тока, максимальной температуры в области, скорости
и координаты якоря.
|
|
|
|
Рис. 3.2.a.
Входной ток (в 2 МА). |
Рис. 3.2.b.
Максимальная температура якоря (в 200 град К). |
|
|
|
|
Рис. 3.2.c.
Cкорость якоря (в 0.1 км/с). |
Рис. 3.2.d.
Координата якоря (в 0.1 м). |
|
По оси абсцисс на всех рисунках время в мсек. |
|
Из рис. 3.2.b
и 3.2.c
следует, что при достижении момента времени t
![]() 0.21 мсек, v
0.21 мсек, v ![]() 1 км/c максимум температуры
достигает 920 K,
т.е. начинается плавление якоря. Далее при достижении t
1 км/c максимум температуры
достигает 920 K,
т.е. начинается плавление якоря. Далее при достижении t ![]() 0.35 мсек, v
0.35 мсек, v ![]() 1.8 км/c максимум температуры
достигает 2720 K,
т.е. начинается кипение якоря. Об этом свидетельствует и своеобразный “излом”
на графике максимальной температуры (рис. 3.2.b). Полный ток (рис. 3.2.a) изменяется по
заданному закону. Якорь вылетает со скоростью около 3 км/c.
1.8 км/c максимум температуры
достигает 2720 K,
т.е. начинается кипение якоря. Об этом свидетельствует и своеобразный “излом”
на графике максимальной температуры (рис. 3.2.b). Полный ток (рис. 3.2.a) изменяется по
заданному закону. Якорь вылетает со скоростью около 3 км/c.
Время
существования надежного электрического контакта металлического типа,
приведенное в § 1. Б, отлично соответствует времени до начала плавления, начало
кипения – времени окончательного разрушения металлического контакта. Выходная
скорость тела несколько (на 10 %) превышает экспериментальную, что вполне
объяснимо тем, что в используемой математической модели нет учета силы трения.
В данном расчетном варианте картины
распределений физических полей заметно богаче, чем в предыдущем. Поэтому ниже
результаты данного расчета представлены более подробно.
В соответствии с основной целью моделирования –
исследованием эрозии – главный интерес представляет распределение температуры.
Повышению
температуры проводника способствует повышенная в нем плотность электрического
тока j. На рис. 3.3 показаны
картины распределения плотности тока в моменты плавления и кипения материала
якоря. Приведенные картины демонстрируют смещение во времени некоторых
экстремумов компонент j. Соответствующее
движение приводит к движению волн плавления и кипения по поверхности якоря.
|
jx |
|
|
|
jy |
|
|
|
jz |
|
|
|
|
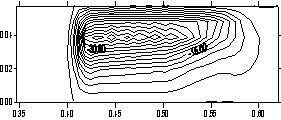
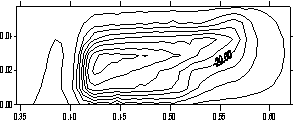
t = 0.216 (плавление). |
t = 0.396 (кипение). |
|
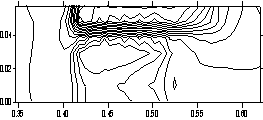
Рис. 3.3. Распределения плотности тока в плоскости
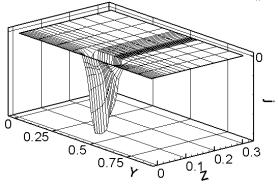
контакта якоря и рельса x = const (ix = 12). Показаны x, y, z - компоненты j
сверху вниз на два момента времени. По оси ординат - z, по оси абсцисс - y. |
||
Сопоставление
распределений j с распределениями T показывает, что
нагрев задней и боковой частей поверхности якоря в плоскости контакта вызван
высокой величиной x и z компонент j. Ток распределяется преимущественно по поверхности якоря. На
поверхности контакта в зонах наибольшего нагрева сила Лоренца также достигает
наибольших значений.
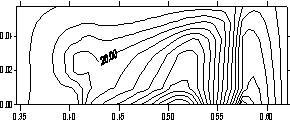
Анализ
распределений T на рис. 3.4 показывает, что максимум достигается в
задней (по направлению движения) части якоря.
|
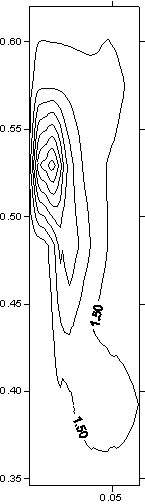
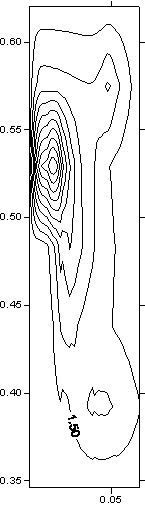
Рис. 3.4. Картины распределения T в якоре в сечениях z
= const (iz =
2, 5, 8 – вблизи плоскости симметрии, в центре области и на краю) при t = 0.216 (плавление). По вертикали - y, по горизонтали - x. |
|
|
|
Картина
изотерм в сечениях плоскостями z = const на рис. 3.4 показывает, что нагрев поверхности
якоря, соприкасающейся с рельсом, возрастает по направлению от центрального к
боковым сечениям. Увеличение температуры можно наблюдать и во внутренних
подобластях якоря (в местах U - образного изгиба). Во всех сечениях z = const рис. 3.4 виден
нагрев в месте изгиба, степень которого возрастает в направлении по z от центра.
Плавление материала (как и кипение) начинается с областей, близких к боковой
(по всем координатам) границе ускоряемого тела.
Т.к.
плавление и кипение якоря начинаются на поверхности контакта с рельсом, то для
исследования эрозии наибольший интерес представляет распределение температуры
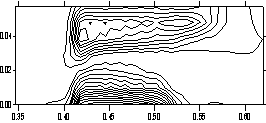
на этой поверхности в различные моменты времени. Ниже на рис. 3.5 приведены
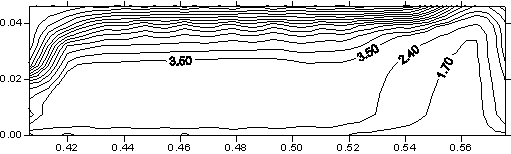
соответствующие изотермы (от минимального до максимального значений).
|
|
t = 0.216 (плавление). |
|
|
t = 0.327 (начало кипения). |
|
|
t = 0.363 (кипение). |
|
|
t = 0.396 (кипение). |
|
|
t = 0.426 (кипение). |
|
|
t = 0.451 (кипение). |
|
|
t = 0.474 (кипение). |
|
|
t = 0.493 (кипение). |
|
Рис. 3.5. Распределение T (в 200 град К) в плоскости контакта якоря и рельса x = const (ix = 12) (y - по
горизонтали, z - по вертикали в 10 см) на различные
моменты времени. |
|
Рис. 3.5
дает картину неравномерного нагрева материала ускоряемого тела с максимальными
значениями на границах области якоря в плоскости контакта с рельсом. Наибольшее
нарушение металлического контакта имеется на участках, где происходит кипение
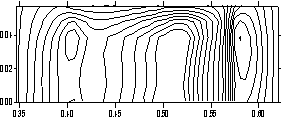
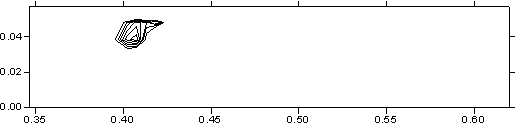
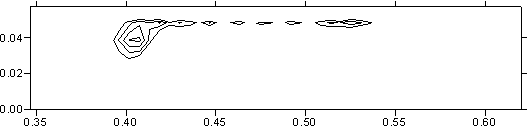
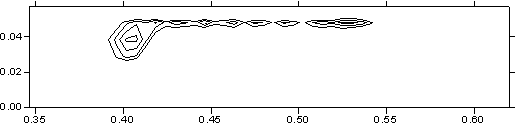
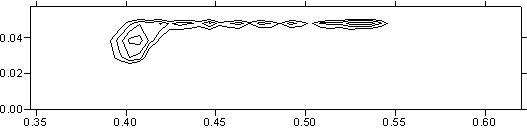
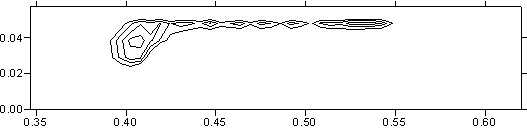
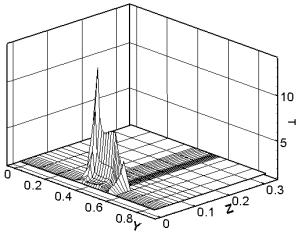
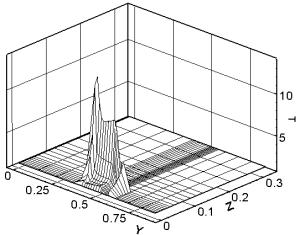
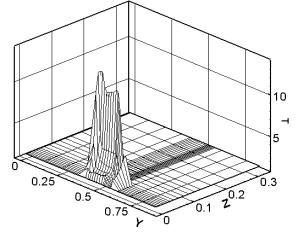
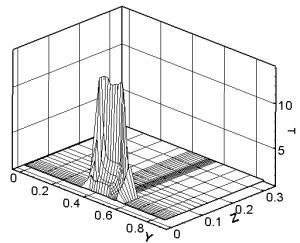
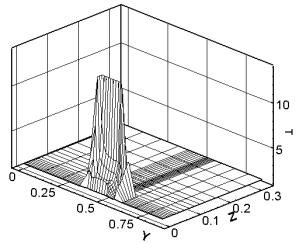
материала. Рис. 3.6 демонстрирует изотермы от уровня температуры в 2000
градусов K до максимального значения в том же сечении
(плоскость контакта якоря и рельса) на различные моменты времени. Тем самым
рис. 3.6 показывает картину распространения по поверхности якоря волны кипения,
которая соответствует максимальной эрозии материала (эрозия возможна и при
плавлении) и деструкции электрического контакта металлического типа.
|
|
t = 0.327 (начало кипения). |
|
|
t = 0.363 (кипение). |
|
|
t = 0.396 (кипение). |
|
|
t = 0.426 (кипение). |
|
|
t = 0.451 (кипение). |
|
|
t = 0.474 (кипение). |
|
|
t = 0.493 (кипение). |
|
Рис. 3.6. Распределение T (от 2000 град К, в 200 град К) в плоскости контакта
якоря и рельса x = const
(ix = 12) (y - по
горизонтали, z - по вертикали, в 10 см) на различные
моменты времени. |
|
Как
видно из построенных изотерм, кипение начинается в задней угловой точке якоря и
распространяется преимущественно по боковой поверхности. По прошествии
некоторого времени кипение начинается и в передней части якоря, после чего с
двух сторон движется к центру области.
Приведенные
изотермы позволяют оценить скорость распространения волны плавления от заднего
края по якорю величиной 50 – 100 м / сек, что несколько меньше данных рис. 1.3.b, но совпадает с
экспериментальными данными по порядку величины.
Ниже на
рис. 3.7, 3.8 построены трехмерные картины распределений некоторых величин в
сечении всей расчетной области (включая рельс и диэлектрик, расположенный над
рельсом) плоскостью контакта якоря и рельса. Начало координат расположено в
левом дальнем углу.
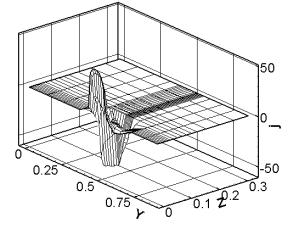
Из
приведенных на рис. 3.7, 3.8 картин видно, что магнитное поле распространяется
по области в основном через диэлектрическую часть, а плотность тока достигает
наибольших значений в области якоря, причем x и y компоненты
плотности тока имеют экстремумы противоположных знаков в различных частях
якоря.
|
|
|
|
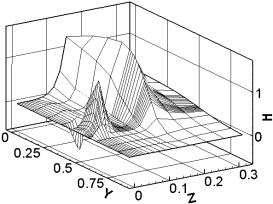
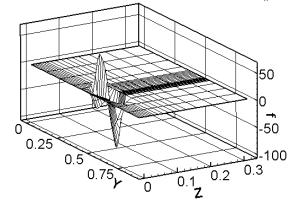
Распределение Нx. |
Распределение fz. |
|
|
|
|
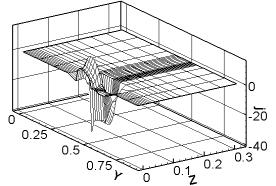
Распределение jx. |
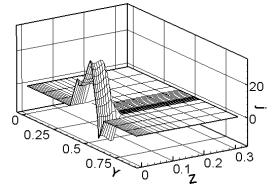
Распределение jy. |
|
Рис. 3.7. Сечение x
= const (ix =
12), плоскость контакта якоря и рельса. Распределение компонент физических
полей при t = 0.233 (плавление). |
|
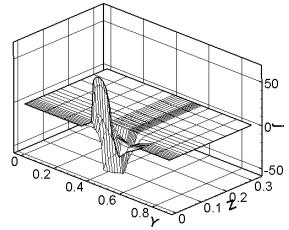
|
Распределение jz. |
|
|
|
|
t = 0.366 (начало кипения). |
t = 0.400 (кипение). |
|
Рис. 3.8. Сечение x
= const (ix =
12), плоскость контакта якоря и рельса. Распределение нормальной компоненты
плотности тока jx на различные моменты времени. |
|
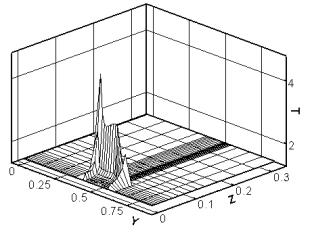
Для
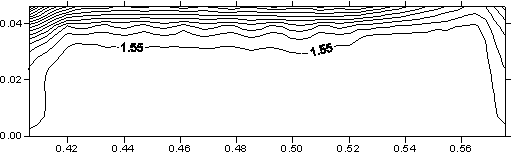
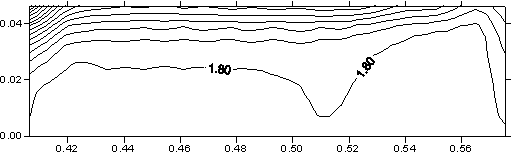
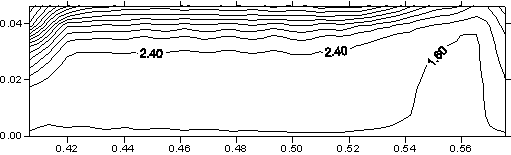
понимания динамики нагрева поверхности якоря на рис. 3.9 построены картины
распределения температуры в плоскости контакта якоря и рельса в различные
моменты времени.
Картины
распределения температуры во всей расчетной области показывают, что самому
сильному нагреву подвержено ускоряемое тело. Температурное поле
распространяется по поверхности якоря с двух сторон, причем наибольшая
температура достигается сначала в задней части якоря, а затем распространяется
по направлению движения якоря.
|
|
|
|
t = 0.233 (плавление). |
t = 0.366 (начало кипения). |
|
|
|
|
t = 0.400 (кипение). |
t = 0.450 (кипение). |
|
|
|
|
t = 0.480 (кипение). |
t = 0.499 (кипение). |
|
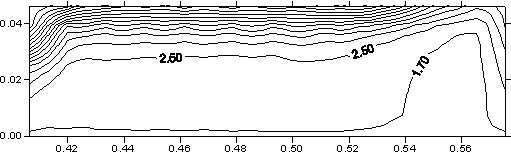
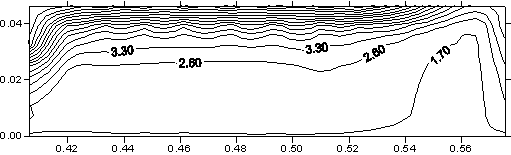
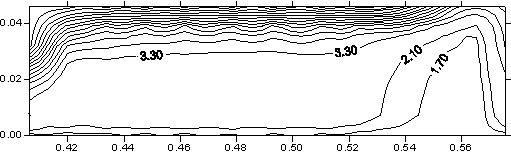
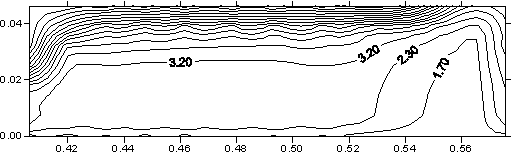
Рис. 3.9. Сечение x
= const (ix =
12), плоскость контакта якоря и рельса. Распределение T. |
|
Заключение.
Проведенные исследования
представляют одну из немногих работ, которые включают измерения на переходной
стадии контакта в рельсотроне от металлической фазы к фазе т. н. “гибридного”
контакта. Получено экспериментальное подтверждение наличия тока на передней
поверхности металлического якоря, определено время начала деградации
металлической проводимости в задней части якоря и соответствующая этому
скорость якоря. Приведенные результаты дают возможность адекватной привязки
результатов численных расчетов к реальной физической ситуации. Сложная картина
электрофизических процессов, происходящих на высокоскоростном контакте,
усугубляется существенной трехмерностью геометрии рельсотронных ускорителей.
Поэтому измерения, проведенные на контактах рельсотрона, позволили пока
получить лишь некоторые оценки для переходных процессов.
Из полученной
картины трехмерного распределения векторных и скалярных полей наибольший
интерес представляют распределения температуры в области контакта якоря и
рельса, где происходит испарение материала и деградация металлического
контакта. Температура испарения материала якоря в первую очередь достигается в
задней части контактной поверхности. В дальнейшем испарение распространяется по
направлению движения якоря в виде серпообразной волны.
Полученные в расчете
данные хорошо качественно и количественно согласуются с экспериментальными
результатами. Время существования надежного электрического контакта
металлического типа, полученное в эксперименте, вполне согласуется с расчетным
временем момента начала плавления. Момент появления кипения материала якоря
соответствует моменту разрушения металлической проводимости. Расчетная скорость
тела на выходе из рельсотрона, как и скорость движения волны разрушения
контакта также хорошо соответствуют экспериментальным величинам. Геометрическая
картина волны испарения материала, полученная численно, также близка к
полученной в экспериментах.
Литература.
1. Материалы I Всесоюзного семинара по
динамике сильноточного дугового разряда в магнитном поле (Новосибирск, 10-13
апреля 1990 г.). // Gод ред. М.Ф. Жукова.
Новосибирск. Изд. Инст. Теплофизики СО АН СССР. 1990. 350 с.
2. Материалы II Всесоюзного семинара по
динамике сильноточного дугового разряда в магнитном поле (Новосибирск, 4-6
декабря 1991г.). // Под ред. В.Е. Накорякова. Новосибирск. Изд. Инст.
Теплофизики СО РАН. 1992. 367 с.
3. В.Б. Железный, А.Д. Лебедев, А.В. Плеханов.
Воздействие на динамику ускорения якоря в РЭУ. // В [2]. С.16 - 32.
4. В.П. Базилевский, Р.М. Заятдинов, Ю.А. Кареев. Кризис электропроводности высокоскоростного металлического контакта. // В [2]. С. 285 - 303.
5. М.П. Галанин, А.Д. Лебедев, А.П. Лотоцкий, К.К.
Миляев. Тепловые и электромагнитные процессы на контактах электродинамического
ускорителя // Препр. ИПМ им. М.В. Келдыша РАН. 2000. № 42. 32 с.
6. А.P. Lototsky,
A.D. Lebedev, Yu.A. Halimullin. The systematic analysis of various electrodes
in a railgun accelerator with linear current density j~500 kA/cm // 6-th Europ.
Symposium on EML Technology. Hague. 25-27 May. 1997. Proceeding. TNO-PLM.
DELFT. Netherlands. P. 306 - 313.
7. Ю.И. Беляков, А.П. Лотоцкий, В.В. Савичев, Ю.А. Халимуллин. Исследование эрозии металлических контактов в
рельсотронном ускорителе. // Вестник МГТУ им. Н.Э. Баумана. Сер.
Фундаментальные науки. 1999. № 2. С. 46 - 60.
8. М.П. Галанин, А.П. Лотоцкий, Ю.П. Попов,
С.С. Храмцовский. Численное моделирование пространственно трехмерных явлений
при электромагнитном ускорении проводящих макротел // Мат. моделирование. 1999.
Т. 11. № 8. С. 3 - 22.
9. M.P. Galanin, Yu.A. Khalimullin, A.P. Lototsky, К.К. Milyayev. 3D
Modelling of Electromagnetic Fields in Application to Electromagnetic Launchers
// IEEE Transactions on Magnetics. January 2003. V. 39. № 1. P. 134 – 138.
10. А.Д. Лебедев, К.В. Малевинский. Влияние структуры
электродного материала на динамику плазменного поршня и эрозионные процессы. //
В [1]. С. 160 - 194.
11.
М.П. Галанин, Ю.П. Попов. Квазистационарные электромагнитные поля в
неоднородных средах: Математическое моделирование. М. Наука, Физматлит. 1995.
320 с.
12. М.П. Галанин. Компьютерное моделирование в задачах конвертирования электромагнитной и кинетической энергии. Задачи и модели. // Информационные технологии и вычислительные системы. 2002. № 4. С. 109 - 123.
13. М.П. Галанин. Компьютерное моделирование в задачах
конвертирования электромагнитной и кинетической энергии. Решение задач. //
Информационные технологии и вычислительные системы. 2003. № 1 – 2. С. 112 -
127.
14.
А.А. Самарский, Е.С. Николаев. Методы решения сеточных уравнений. М. Наука.
1978. 592 с.
15. D.S. Kershaw. The incomplete Cholessky - Conjugate
Gradient Method for the iterative solution of system of a linear equations. //
J. Comput. Phys. 1978. V. 26. P. 43 - 65.
16.
А. Джордж, Дж. Лю. Численное решение больших разреженных систем уравнений. М.
Мир. 1984. 333 с.
17.
В.В. Воеводин, Ю.А. Кузнецов. Матрицы и вычисления. М. Наука. 1984. 320 с.
18. М.П. Галанин, С.С. Храмцовский. Организация
расчета трехмерных квазистационарных электромагнитных полей в областях со
сложной геометрией проводников и диэлектриков. // Препр. ИПМ им. М.В. Келдыша
РАН. 1999. № 42. 18 с.