Содержание

1.  Введение ......................................................................................................... 4

2.  Средства работы с массивами. Общие сведения ................................. 5

3.  Конструктор массива .................................................................................... 6

4.  Секция массива ............................................................................................. 7

5.  Выражения и присваивания с массивами ................................................ 9

6.  Присваивание по маске ............................................................................. 11

7.  Оператор  и конструкция FORALL ........................................................... 14

8.  Механизмы динамического размещения массивов ............................. 16

9.  Встроенные функции для работы с массивами .................................... 17

     9.1. Состав и классификация встроенных функций .............................. 17

     9.2. Поэлементные функции ...................................................................... 18

     9.3. Функции преобразования массивов ................................................. 18

     9.4. Справочные функции для массивов ................................................ 25

10. Заключение ................................................................................................. 25

Литература ......................................................................................................... 26

1. Введение

При разработке больших и сложных программ для решения задач вычислительного характера возникает много разнообразных проблем. Одна из этих проблем связана с тем, что большие программы обычно содержат многочисленные громоздкие вложенные циклы и условные переходы. Это делает программу трудно читаемой, плохо структурированной, что вызывает массу проблем, знакомых каждому программисту. Такие программы трудно отлаживать, модифицировать, распараллеливать, переносить в другое окружение; затруднено и сопровождение таких программ.

Современный Фортран [1-7] (в отличие от Фортрана 77) позволяет во многих случаях обойти эти трудности. Язык предоставляет большой набор средств для работы с массивами и секциями массивов как с целыми объектами на поэлементной основе. Впервые эти средствпа были введены в стандарт языка, неформально называемый Фортран 90 [1], дальнейшее развитие они получили в действующем в настоящее время стандарте – Фортране 95 [2].

Новые средства работы с массивами обеспечивают большие возможности, позволяющие упростить способ организации и написания почти всех программ, использующих массивы, так как позволяют во многих случаях обойтись без вложенных циклов и условных переходов. Mногие алгоритмы, включающие работу с массивами, могут быть записаны более лаконично и наглядно как последовательность вычислений над полными массивами. Такие средства делают программу более структурной и более объектно-ориентированной.

Помимо указанных выше удобств, существенным является тот факт, что операции над массивами фактически специфицируют параллелизм действий над компонентами массивов, поскольку явно специфицируют векторные операции и параллельные циклы. Это позволяет компилятору сгенерировать эффективный код с учетом конкретной архитектуры, особенно для тех современных ЭВМ, которые имеют аппаратные средства векторной обработки. Эти свойства аппаратуры, в свою очередь, формировались на основе требований решаемых задач.

До появления этих средств в стандарте для таких компьютеров создавались векторизующие компиляторы, помогающие эффективно использовать возможности, заложенные в аппаратуре. Однако автоматическая векторизация (т.е. выявление скрытого параллелизма) требует довольно сложного анализа исходной программы, и при этом некоторые конструкции последовательных яэыков могут затруднить или даже сделать невозможной векторизацию. В некоторые системы программирования вводились специальные директивы-комментарии, помогающие компилятору выполнять векторизацию исходной программы, для других систем разработаны языковые расширения, которые не были унифицированы, что усложняло перенос программ.

В данной работе описываются средства явной спецификации векторных операций, имеющиеся в современном стандарте Фортрана, приводятся рекомендации по их использованию. Описание сопровождается большим количеством примеров. Для того, чтобы проиллюстрировать преимущества использования новых средств некоторые примеры приведены и на Фортране 77, и на современном Фортране.

Пути решения других проблем, возникающих при разработке больших вычислительных программ, можно найти, например, в [7-9].

2. Средства работы с массивами. Общие сведения

Современный Фортран, как уже отмечалось, предоставляет большой набор средств для работы с массивами и секциями массивов как с целыми объектами на поэлементной основе. В этом разделе приводится перечень имеющихся средств и вводятся некоторые термины, используемые в дальнейшем описании.

B языке разрешены выражения и присваивания для массивов. Например, если A и B – двумерные массивы, то операция A*B означает не умножение матриц (для этого имеется встроенная функция MATMUL), а поэлементное умножение, выполняемое в произвольном порядке.

Введены секции массива и конструкторы массивов. Секция массива позволяет адресоваться к части массива (см. 4. и 7.). Секция задается с помощью имени массива и списка индексов секции. Конструкторы массивов позволяют задавать последовательность скаляров в качестве одномерного массива без имени (см. 3.).

Имена массивов без индексов (полные массивы), секции массивов и конструкторы массивов могут использоваться в качестве операндов выражений, в левой части оператора присваивания (см. 5.), как фактические аргументы процедур, в списке ввода-вывода. Кроме того, массив может быть также значением выражения и значением функции (как встроенной, так и определяемой пользователем).

Имеется также возможность условного присваивания массиву под управлением логической маски (см. 6.), параллельный цикл (см. 7.), большой набор встроенных процедур для работы с массивами (см. 9.) и средства динамического размещения массивов (см. 8.).

Использование массивов в выражениях и операторах подчиняется определенным ограничениям. Для формулировки этих ограничений используются некоторые термины, приведенные ниже.

Ранг массива (rank) - это число измерений массива, или размерность. Допускаются массивы с рангом от 1 до 7 включительно. Ранг скаляра считается равным 0.

Конфигурация массива (shape) - это одномерный массив целого типа, размер которого равен рангу исходного массива, а элементы равны размерам соответствующих измерений. Например, для массива со спецификацией измерений (2:10, 3, -1:1) конфигурация массива представляет собой одномерный массив длина которого равна трем, элементы -  9, 3, 3.

Массивы, имеющие одинаковую конфигурацию, называются согласованными (conformable). Скаляр считается согласованным с любым массивом. В выражениях могут использоваться только согласованные (по конфигурации) операнды.

Элементы двух массивов считаются соответствующими, если они занимают одинаковое положение относительно первого элемента массива (имеют одинаковый приведенный индекс). Операции выполняются над соответствующими элементами массивов.

3. Конструктор массива

Конструктор массива позволяет задавать одномерный массив без имени. Конструктор массива описывается как последовательность скалярных значений и интерпретируется как одномерный массив. Последовательность значений заключается в скобки “(/” и ”/)”.

Общий вид конструктора можно найти в официальном описании языка [1-2 ]. Приведем несколько примеров для иллюстрации.

Примеры.

(/ 4.0,  2.0,  6.3 /) - одномерный массив, содержащий три элемента.

(/ (2.9,  L=1,10),  9.2 /) - одномерный массив, размер его равен 11, содержит вещественную константу 2.9, повторенную 10 раз, а затем константу 9.2.

(/ (I, I = 1,N) /) - массив содержит целые числа 1, 2, ..., N.

Tаким способом можно сконструировать только одномерные массивы, а массивы большей размерности можно получить из них посредством встроенной функции RESHAPE (см. 9.3.7.).

4. Секция массива

Секция массива обеспечивает возможность адресоваться к части массива. Секция задается именем массива, списком индексов секции и, возможно, списком индексов подстроки (для данных символьного типа). Секция массива может состоять как из расположенных подряд элементов исходного массива, так и из несвязных областей этого массива.

Расположение элементов секции подчиняется тем же правилам, что и расположение элементов обычных массивов.

Bезде, где можно использовать полные массивы, допустимо использование секций массива.

Примеры секций массива.

Z (3, :)    третья  строка матрицы Z;

Z (:, J)    J-й столбец матрицы Z;

Cекция A (:, 1:N, 4, 3:1:-1) содержит целиком первое измерение, позиции с 1 по N второго измерения, позицию 4 третьего измерения и позиции с 1 по 3 из четвертого измерения в обратном порядке. Это искусственный пример, выбранный для иллюстрации разнообразия форм. Конечно, более частым применением может быть выбор строки или столбца из массива, как в первых двух примерах.

В общем виде секция массива схематически может быть представлена следующим образом:

b (i1, i2,..., in) [(j1, j2,..., jm)]

где  b  -  имя  массива или компоненты структуры,

i1, i2,..., in - индексы секции,

j1, j2,..., jm - индексы подстроки (только для массивов символьного типа).

Число индексов секции должно быть равно рангу массива.

Индекс секции – это

·        скалярный_индекс        или

·        индексный_триплет    или

·        векторный_индекс

Скалярный индекс - это скалярное выражение целого типа, т.е. обычное индексное выражение, которое задает значение соответствующего измерения. По крайней мере один элемент списка индексов секции не должен быть скалярным выражением (в противном случае эта конструкция будет просто элементом массива).

Индексный триплет задает последовательность индексных выражений по данному измерению и тем самым выделяет часть массива, состоящую из элементов с соответствующими индексами в данном измерении. Индексный триплет имеет вид:

[e1] : [e2] [:e3]

Последовательность целых значений, определяемая индексным триплетом, формируется по тем же правилам, что и значение управляющей переменной в заголовке цикла, т.е. e1 – нижняя граница индекса, e2 – верхняя граница, e3 – шаг изменения индекса. Если опущено e1, то предполагается, что его значение равно нижней границе соответствующего измерения массива, если опущено e2, оно считается равным верхней границе соответствующего измерения, если опущено e3, оно считается равным 1. Если e1> e2 и e3 > 0 или e1 < e2 и e3 < 0, то размер соответствующего измерения равен нулю. В этом случае размер секции считается равным нулю.

Векторный индекс представляет собой векторное выражение целого типа; значения элементов этого выражения определяют последовательность индексов по соответствующему измерению; эта последовательность определяет элементы массива, принадлежащие секции массива.

Примеры секций массивов с векторным индексом:

INTEGER, DIMENSION :: A(3, 4), U (3), V (4)

U = (/1, 3, 2/);  V = (/2, 1, 1, 3/)

A (3, V)- массив, содержащий элементы A (3, 2)   A (3, 1)   A (3, 1)   A (3, 3)

A (U, V)  - матрица

A (1, 2)    A (1, 1)    A (1, 1)    A (1, 3)

A (3, 2)    A (3, 1)    A (3, 1)    A (3, 3)

A (2, 2)    A (2, 1)    A (2, 1)    A (2, 3)

Как видно из приведенных примеров, секция может содержать по несколько экземпляров одного и того же элемента исходного массива; такие секции называются секциями с дублирующими элементами. Такие секции не должны определяться и переопределяться в программе; например, они не могут использоваться в левой части оператора присваивания. Это ограничение делается для того, чтобы одному и тому же элементу массива не присваивалось более одного значения.

Поскольку секция массива является массивом, для нее определены понятия ранга и конфигурации.

Ранг секции, очевидно, равен числу нескалярных элементов в списке индексов секции.

Конфигурация секции, по аналогии с конфигурацией массива, - вектор, в котором j-ый элемент равен числу значений, определяемых j-ым нескалярным элементом в списке индексов секции.

Например, пусть массив объявлен следующим образом:

REAL, DIMENSION (M, N, 10, 10) :: A

Ранг секции массива A (:, 1:N-1, 2, 5:2:-1) равен 3, конфигурация данной секции - вектор (/ M, N-1, 4/).

Хотя секция массива и является массивом, для нее нельзя указать элемент массива или секцию массива. Так, например, для секции массива в предыдущем примере нельзя задать первый элемент с помощью следующего обозначения:

A ( :, 1:N-1, 2, 5:2:-1) (1, 1, 1)

Секция массива символьного типа может иметь индексы подстроки.

Пример.

CHARACTER (LEN=6) X (10, 10)

X (:, 5) (2: 4) - массив, содержащий подстроки (со 2-го по 4-ый символ) из 5-го столбца матрицы X.

Следует заметить, что для символьного массива X из последнего примера, объект X (:, 2:4) является секцией (содержащей столбцы со 2-го по 4-ый), а не подстрокой. Если нужно для всех элементов массива выделить подстроку, можно написать, например, X (:, :)(2:4).

5. Выражения и присваивания с массивами

Выше уже отмечалось, что семантика операций и встроенных математических функций Фортрана 77 расширена таким образом, что их можно применять не только к скалярам, но и к массивам на поэлементной основе. Операнды, участвующие в одной операции, должны быть согласованы по конфигурации (т.е. должны иметь одинаковую размерность и размер по каждому измерению; скаляр считается согласованным с любым массивом). Значение таких выражений также является массивом.

Например, если A, B, C и D - массивы одинаковой конфигурации, то оператор A = B + C * SIN (D)

является допустимым и интерпретируется поэлементно, т.е. функция синуса берется для каждого элемента D, каждый результат умножается на соответствующий элемент C, добавляется к соответствующему элементу B и присваивается соответствующему элементу A.

Если значение выражения в правой части является массивом, переменная в левой части также должна быть массивом. Если выражение в правой части является скалярным, а переменная в левой части - массив, то всем элементам массива присваивается значение скаляра.

Если переменная и выражение - массивы, то присваивание производится поэлементно для соответствующих элементов массивов левой и правой части. Процессор может выполнить присваивание элементам массива в произвольном порядке, при этом результат выполнения оператора присваивания должен быть такой, как если бы сначала выполнились все операции в правой части и все операции (если они есть) в индексах левой части, а затем выполнилось бы присваивание всем элементам массива левой части в произвольном порядке.

Пример. Изменение порядка элементов массива на обратный

С     Фортран 77                                             ! Фортран 90/95

      DO 1 I = 1, 10                                            W (1:10) = W (10:1:-1)

        TEMP(I) = W(11-I)

        W(I) = TEMP( I )

   1 CONTINUE

Поэлементное выполнение операций и присваиваний могут производится параллельно, однако результат не зависит от того, поддерживает ли компилятор параллельное выполнение.

Если переменная в левой части - секция массива, то присваивание не влияет на статус определенности для тех элементов исходного массива, которые не специфицированы в секции массива (т.е. если эти элементы были определены, их значения не меняются, в противном случае они остаются неопределенными).

Приведем еще несколько примеров.

REAL, DIMENSION (0 : 9) :: A

REAL, DIMENSION (5 : 14) :: C

REAL, DIMENSION (1 : 20, 1 : 20) :: X, Y, Z

! Каждому элементу массива X прибавляется константа

X = X + 5.0

! Последние 5 элементов C присваиваются первым пяти элементам A

A(0:4) = C(10:14)

! Первым 10 элементам первого столбца Y присваиваются значения A

Y(1:10, 1) = A

! Элементы J-й строки матрицы X присваиваются I-му столбцу матрицы Y

Y(1:20, I) = X(J, 1:20)

! Первые M элементов J-й строки матрицы Y

! присваиваются первым M элементам I-й строки матрицы X.

X(1:M, I) = Y(J, 1:M)

! Левая верхняя четверть матрицы X присваивается секции массива Y

Y(11:20, 1:20:2) = X(1:10, 1:10)

! Элементы A, взятые в обратном порядке, присваиваются C

C = A(9:0:-1)

! Элементы с 2-го по 4-й передвигаются и становятся элементами с 3-го по 5-й

A(3:5) = A(2:4)

В Фортране 77 подобные примеры могут быть реализованы только с использованием циклов, для последнего примера требуется еще и временный массив. Очевидно, что запись на современном Фортране более короткая и более наглядная.

В тех случаях, когда часто используется одна и та же секция массива, можно не писать каждый раз секцию, а использовать указатель в качестве псевдонима; в приведенном ниже примере после присваивания указателю WINDOW, его можно использовать везде вместо секции MATR (I-1:I+1, J-1:J+1).

REAL, POINTER :: WINDOW (:, :)

! Указатель WINDOW связывается с секцией массива MATR.

WINDOW => MATR (I-1:I+1, J-1:J+1)

6. Присваивание по маске

Оператор присваивания по маске и конструкция присваивания по маске позволяют, в зависимости от некоторого условия, выполнить вычисление выражения и присваивание значений не для всех элементов массива, т.е. выполнить присваивание под управлением логической маски.

Hапример, чтобы присвоить нуль всему массиву, достаточно написать A=0; чтобы присвоить нуль только отрицательным элементам, потребуется записать условное присваивание:

WHERE (A < 0.0) A = 0.0

Оператор присваивания по маске имеет вид:

WHERE (mask) st

где mask - логическое выражение-массив (маска),

st - оператор присваивания.

Конструкция присваивания по маске в Фортране 90 может иметь одну из двух следующих форм (расширения для Фортрана 95 см. ниже):

WHERE (mask)                            WHERE (mask l)

st                                                     st

END WHERE                                ELSEWHERE

                                            st

   END WHERE

где mask - логическое выражение-массив,

st - последовательности операторов присваивания.

Логическое выражение-массив mask в операторе и конструкции WHERE является маской. Конфигурация массива-маски должна быть такой же, как конфигурации массивов в левых частях операторов присваивания.

Примеры

REAL  X(10, 20),  Z (-9:10),  V (20), W(20)

! Вычисление логарифма для положительных элементов массива V

WHERE (V > 0.0 ) Z = LOG (V)

!  Конструкция WHERE

WHERE (W /= Y )

   X(10, :) = (W + Y)/ (W - Y)

ELSEWHERE

 X(10, :) = 0.0

END WHERE

Выполнение присваивания по маске вызывает вычисление логического выражения-маски. При выполнении оператора присваивания, входящего в оператор WHERE, выражение в правой части вычисляется для тех элементов, для которых значения маски "истина", и результат присваивается соответствующим элементам массива левой части.

Операторы присваивания в конструкции WHERE-END WHERE, следующие за операторами WHERE и ELSEWHERE, выполняются последовательно. При выполнении операторов присваивания, следующих за оператором WHERE, каждое выражение правой части вычисляется для элементов, для которых значение маски есть "истина", а при выполнении операторов присваивания, следующих за оператором ELSEWHERE, - для тех элементов, для которых значение маски есть "ложь"; результат во всех указанных операторах присваивается соответствующим элементам левых частей.

Выражение-маска вычисляется до выполнения операторов присваивания, и их выполнение не влияет на значение маски, даже если будут изменены значения операндов, входящих в логическое выражение mask.

Если в правых частях присваиваний оператора или конструкции WHERE встречается обращение к функции, то действуют следующие правила.

·        Если функция поэлементная (см. 9.2.) и не является фактическим аргументом не поэлементной функции (в приведенном выше примере – LOG), то вычисления и присваивания выполняются под управлением логической маски.

·        Если функция не является поэлементной, то она вычисляется для всех элементов массива, независимо от значения маски.

Так, в приведенном ниже примере

WHERE (V>0.0) Z = SUM(LOG(V))

функция LOG вызывается для всех элементов V, как аргумент функции SUM, которая не является поэлементной.

Передавать управление внутрь конструкции WHERE - END WHERE не разрешается.

В Фортране 95 введены некоторые расширения  конструкции WHERE.

·        Оператор ELSEWHERE может иметь маску.

·        Конструкция WHERE может быть вложенной.

·        Конструкция может иметь имя.

! Пример на Фортране 95

EXAMPLE: WHERE (X>0.0)

                        X = X + 1.0

                    ELSEWHERE (X < 0.0)

                         X = X + 2.0

                     ELSEWHERE

                          X = X + 3.0

                               END WHERE EXAMPLE

Безусловно, что использование оператора и конструкци WHERE позволяют во многих случаях обойтись без циклов и условных операторов. Для иллюстрации приведем простой пример на Фортране 77 и на современном Фортране.

C   На Фортране 77                                            !  На Фортране 90/95

       DO 1 K = 1, N                                                WHERE (A/=0.0) C = B/A

       IF (A(K) .NE. 0.0) C(K) = B(K)/A(K)

   1  CONTINUE

7. Оператор  и конструкция FORALL

Множественное присваивание массиву обеспечивается не только с помощью описанных выше средств, но также с помощью оператора и конструкции FORALL, которые введены в Фортран 95 (в Фортране 90 они отсутствовали).

Пример

! Присваивание диагонали матрицы A

FORALL (I = 1:N) A (I, I) = B(I)

Одно из отличий от WHERE заключается в том, что FORALL использует элементы массивов, а WHERE ориентируется на целый массив. FORALL допускает возможность специфицировать больший класс секций массивов, чем допускалось в Фортране 90. Так, в приведенном выше примере представлена диагональ матрицы; с помощью средств Фортрана 90 можно представить только прямоугольные секции (см. выше 4.).

Хотя FORALL служит той же цели, что и DO-цикл и функционально похож на цикл, но выполняется иначе. Так, оператор

FORALL (I = 2:N) C(I, I) = C(I-1, I-1)

дает результат, отличный от результата приведенной ниже последовательности операторов:

DO I = 2, N

  C(I, I) = C(I-1, I-1)

END DO

Исходная матрица            Результат для FORALL        Результат для цикла

|  1 0 0 0 0 |                          |  1 0 0 0 0 |                              |  1 0 0 0 0 |

|  0 2 0 0 0 |                          |  0 1 0 0 0 |                              |  0 1 0 0 0 |

|  0 0 3 0 0 |                          |  0 0 2 0 0 |                              |  0 0 1 0 0 |

|  0 0 0 4 0 |                          |  0 0 0 3 0 |                              |  0 0 0 1 0 |

|  0 0 0 0 5 |                          |  0 0 0 0 4 |                              |  0 0 0 0 1 |

Разница объясняется тем, что итерации DO-цикла выполняются последовательно так, что каждый следующий элемент диагонали модифицируется до его использования в следующей итерации. В противоположность этому, в FORALL все диагональные элементы выбираются и используются до сохранения модифицированного значения в памяти. Фактически, FORALL специфицирует параллельный цикл, однако результат не зависит от того, поддерживает ли компилятор параллельное выполнение FORALL.

Как  и в предыдущих разделах, для сравнения приведем примеры на Фортране 77 и на современном Фортране.

C   На Фортране 77                                          ! На Фортране 95

       DO 1 I = 1, N                                               FORALL (I = 1, N), A(I, I) = B(I) * 2.0

         A(I, I) = B(I) * 2.0

   1  CONTINUE

Помимо оператора,  имеется  также  конструкция FORALL–END FORALL. Заголовок конструкции может содержать логическую маску.

Пример конструкции FORALL c маской.

FORALL (I = 1:N, Y(I) .NE. 0.0)

     X(I) = 1.0 / Y(I)

END FORALL

Конструкция FORALL допускает вложенность и может быть вложена в конструкцию WHERE и, наоборот, конструкция WHERE может быть вложена в FORALL. Конструкция может иметь имя, которое позволяет идентифицировать конструкцию. Имена особенно полезны для удобства написания и чтения программ, содержащих вложенные конструкции.

Имя конструкции не может использоваться для передачи управления.

Примеры вложенных конструкций.

Пример 1.

INTEGER, DIMENSION (10, 10) :: X, Y

FORALL (I = 1:10)

   WHERE (X(I, :) == 0) X(I, :) = I

   Y(I, :) = I / X(I, :)

END FORALL

Пример 2.

FORALL (I = 1:10)

   WHERE (X(I, :) == 0)

      X( :, I) = I

   ELSEWHERE (X(I, :) >2)

   (X(I, :) = 9

   END WHERE

END FORALL

8. Механизмы динамического размещения массивов

Помимо описанных в предыдущем разделе средств работы с массивами, в языке имеются различные механизмы динамического размещения массивов, которые весьма удобны, а во многих случаях и необходимы для задач, оперирующих с большими массивами.

Заметим, что в предыдущих стандартах языка Фортран не разрешалось использовать массивы, границы которых вычисляются в процессе выполнения программы.

В современном Фортране имеется три механизма динамического размещения массивов:

·        автоматические массивы - массивы, создаваемые при входе в процедуру и уничтожаемые при выходе из нее;

·        размещаемые массивы - массивы, границы которых вычисляются при выполнении программы; размерность их фиксирована, но фактический размер и время жизни полностью управляются программистом с помощью операторов ALLOCATE и DEALLOCATE;

·        массивы, создаваемые в процессе выполнения программы, т.е. массивы, которые не были заранее явно объявлены в программе.

Эти средства позволяют пользователю организовать работу с массивами, размер которых заранее не известен, а также оперативно выделять память под массивы, требующиеся на том или ином этапе выполнения программы и освобождать память по мере необходимости.

При этом для автоматических массивов программист не должен заботиться об отведении или освобождении памяти; это делается процессором автоматически при входе в процедуру и выходе из процедуры.

Примеры

SUB.,RОOUTINE  S (X, M)

COMMON  K

REAL, DIMENSION (M, 2:K) :: A                   ! Автоматический массив A

! Размещаемый одномерный массив Y

REAL, DIMENSION, ALLOCATABLE :: Y(:)

. . .

READ (*, *) N

ALLOCATE  Y (N)                                          ! Размещение массива Y

. . .

DEALLOCATE Y

9. Встроенные функции для работы с массивами

Помимо базовых элементов и конструкций для работы с массивами, о которых говорилось в предыдущих разделах, в языке имеется большой набор встроенных функций, которые также существенно упрощают программирование вычислительных задач. Это объясняется тем, что наиболее часто используемые математические функции входят в состав самого языка, а не программируются каждым пользователем заново. Поскольку такие функции реализуютcя компилятором, они ориентируются на конкретную архитектуру и потому реализуются эффективно. Ниже приводится описание встроенных функций для работы с массивами; более полное описание можно найти в [1-2].

9.1. Состав и классификация встроенных функций

Все встроенные функции Фортрана для работы с массивами можно разделить на три категории:

·        поэлементные функции (9.2.),

·        справочные функции (9.4.),

·        функции преобразования массивов (9.3.).

Встроенная функция, которая допускает обращение как со скалярным аргументом, так и с массивом, является поэлементной. Результат поэлементной функции со скалярным аргументом является скаляром, а с фактическим аргументом-массивом является массивом. Каждая такая функция применяется к каждому элементу массива, вырабатывая массив той же конфигурации.

Функция является справочной, если ее результат зависит от свойств ее основного фактического аргумента, а не от его значения (значение аргумента может быть и неопределенным).

Остальные встроенные функции работы с массивами являются функциями преобразования. Такие функции имеют один или несколько формальных аргументов-массивов и часто имеют результат-массив.

К встроенным функциям (как и к любым процедурам, встроенным или определяемым пользователем) можно обращаться, используя ключевые слова. Для всех встроенных процедур за каждым формальным аргументом в языке закреплено имя - ключевое слово, но использование ключевых слов не является обязательным. Эта возможность полезна тем, что позволяет задавать фактические аргументы в произвольном порядке с использованием мнемоники имен формальных аргументов. Некоторые аргументы ряда встроенных процедур являются необязательными; это также полезно, так как иногда позволяет сделать обращение к встроенным процедурам более лаконичным. В случае, если в списке фактических аргументов какие-либо из предыдущих аргументов опущены, ключевые слова – обязательны.

9.2. Поэлементные функции

Многие встроенные функции традиционные для Фортрана и некоторые новые являются поэлементными. Если поэлементная функция имеет несколько аргументов, все фактические аргументы-массивы должны быть согласованы (по конфигурации). Результат имеет такую же конфигурацию, как и аргументы. Если в обращении к функции все фактические аргументы являются скалярами, результат также будет скаляром. Когда поэлементная функция применяется к массивам, значения элементов результата получаются путем вычисления значений функции для каждого элемента массива-фактического аргумента, т.е. для скаляра.

Примеры.

REAL, DIMENSION (1:20, 1:20) :: X, Y, Z

REAL, DIMENSION (1:40) :: W

Z = EXP(X + Y) – EXP(X – Y)

X = SQRT (W(1:40:2))

Замечание.

В Фортране 95 введены средства, позволяющие использовать не только встроенные поэлементные функции, но также и поэлементные процедуры (функции и подпрограммы), определяемые пользователем. Такие процедуры должны иметь в заголовке префикс ELEMENTAL.

9.3. Функции преобразования

Функции преобразования можно разделить на следующие группы:

·        функции редукции (9.3.1.);

·        функции умножения векторов и матриц (9.3.2.);

·        функция транспонирования матрицы (9.3.3.);

·        функция слияния массивов (9.3.4.);

·        функции упаковки и распаковки массивов (9.3.5.);

·        функция конструирования массива добавлением копий из элементов исходного массива (9.3.6.);

·        функция изменения конфигурации массива 9.3.7.);

·        функции сдвига (9.3.8.);

·        функции определения положения в массиве (9.3.9.).

Во многих функциях преобразования имеется обязательный или необязательный аргумент MASK - логическая маска (логическое выражение). Конфигурация аргумента MASK должна быть согласована с конфигурацией исходного массива (за исключением функций ALL, ANY, COUNT, где MASK - исходный массив). Использование логической маски позволяет ограничить область действия функции любым подмножеством массива (например, подмножеством положительных элементов).

Другим необязательным аргументом в этих функциях является DIM – номер измерения.

В приведенных ниже описаниях необязательные аргументы указываются в квадратных скобках.

9.3.1. Функции редукции

Функции редукции выполняют арифметические, логические, счетные операции над массивами. Они называются так потому, что в качестве исходного аргумента берется массив, а результат является либо скаляром, либо массивом, ранг которого на единицу меньше, чем ранг исходного массива.  

Имеются следующие функции редукции:

SUM (ARRAY [,DIM] [,MASK]) - сумма элементов;

PRODUCT (ARRAY [,DIM] [,MASK]) - произведение элементов;

MAXVAL (ARRAY [,DIM] [,MASK]) - значение  максимального элемента;

MINVAL (ARRAY [,DIM] [,MASK]) - значение минимального элемента;

COUNT (MASK [,DIM]) - число элементов со значением "истина";

ALL (MASK [,DIM]) - результат "истина", если все элементы имеют значение "истина";

ANY (MASK [,DIM]) - результат "истина", если хотя бы один элемент имеет значение  "истина".

Функции редукции могут быть применимы ко всему массиву (см. ниже примеры 1 и 2) или к какому-либо измерению массива (пример 3). Функция редукции, примененная ко всему массиву, дает скалярный результат. Если присутствует аргумент DIM, функция применяется к указанному измерению, при этом результатом функции будет массив, ранг которого на единицу меньше, чем ранг исходного массива.

В качестве одного из необязательных аргументов этих функций может использоваться маска (примеры 4 и 5), позволяющая выполнить различные вычисления над некоторым  подмножеством  исходного массива.

Примеры использования функций редукции.

REAL X (100, 20), B (20), C

INTEGER K, N

   . . .

! Пример 1. Сумма всех элементов X

C = SUM (X)

! Пример 2.  N факториал, т.е. 1*2*...*N

C = PRODUCT ((/K, K = 2, N/))

! Пример 3. Результат - вектор длиной 20, каждый элемент которого равен

! сумме элементов соответствующего столбца матрицы X

B = SUM (X, DIM = 1)

! Пример 4. Сумма положительных элементов массива X

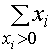
C = SUM (X, MASK = X>0.0)

! Пример 5. Число отрицательных элементов массива X

C = COUNT (X, X < 0.0)

9.3.2. Функции умножения векторов и матриц

Функция MATMUL (MATRIX_A, MATRIX_B) производит операцию умножения двух матриц, матрицы на вектор или вектора на матрицу. Аргументами этой функции должны быть массивы, либо оба числового типа (целого, вещественного, комплексного), либо оба – логического типа. Над логическими матрицами и векторами функция MATMUL производит логическое умножение. Размер первого (или единственного) измерения массива MATRIX_A должен быть равен размеру последнего (или единственного) измерения массива MATRIX_B.

Функция DOTPRODUCT (VECTOR_A, VECTOR_B) производит вычисление скалярного произведения векторов. Правила в отношении типов аргументов те же, что и для функции MATMUL, аргументы должны иметь один и тот же размер.

9.3.3. Функция транспонирования матрицы

Функция TRANSPOSE (MATRIX) – выполняет транспонирование матрицы (массива ранга 2). Аргумент может быть любого типа.

9.3.4. Функция слияния массивов

Функция MERGE (TSOURCE, FSOURCE, MASK) – поэлементная функция, выполняет слияние массивов TSOURCE и FSOURCE путем выбора альтернативного значения в соответствии со значением логической маски MASK. Массивы TSOURCE и FSOURCE должны иметь одинаковый тип и все три исходных массивов должны иметь одинаковую конфигурацию, результат имеет ту же конфигурацию.

Пример.

TSOURCE                      FSOURCE                      MASK                   Результат

   1  6  5                             0  3  2                            t  f  t                       1  3  5

   2  4  6                             7  4  8                            f  f  t                       7  4  8

Здесь и далее t означает true, f – false.

9.3.5. Функции упаковки и распаковки массивов

Функция PACK (ARRAY, MASK [,VECTOR]) - упаковка массива в вектор под управлением логической маски.

Собирается вектор из тех элементов исходного массива (ARRAY), для которых значения маски – “истина”; если присутствует аргумент VECTOR, он доопределяет “хвостовые” элементы результирующего массива.

ARRAY – массив любого типа;

VECTOR – одномерный массив того же типа;

MASK – логический массив той же конфигурации, что и ARRAY.

Пример 1. Собрать ненулевые значения исходного массива AR

I 0  0  0 I

I 0  3  0 I

I 0  0  5 I

PACK(AR, MASK = AR .NE. 0.0) = (/3, 5/)

Пример 2.

PACK (AR, MASK = AR .NE. 0, VECTOR = (/2, 4, 6, 8, 10/)) = (/ 3, 5, 6, 8 10/)

Функция UNPACK (VECTOR, MASK, FIELD) - распаковка вектора VECTOR в массив под управлением логической маски MASK.

VECTOR – одномерный массив любого типа;

MASK – логический массив;

FIELD – скаляр или массив того же типа, что и VECTOR и согласованный по
                          конфигурации с MASK.

Исходный вектор “разбрасывается” в позиции, определяемые маской. Аргумент FIELD определяет конфигурацию и доопределяет результирующий массив. Элемент результата, соответствующий i-му истинному элементу MASK (в порядке следования элементов в памяти) равен i-му элементу VECTOR, а все остальные элементы равны соответствующим элементам FIELD (для массива) или  равны значению FIELD (для скаляра).

MASK                      VECTOR                 FIELD                     Результат

f  t  f                        (/ 1, 2, 3 /)                 1  0  0                     1  2  0

t  f  f                                                          0  1  0                     1  1  0

f  f  t                                                          0  0  1                     0  0  3

9.3.6. Функция конструирования массива путем добавления измерения

Добавляется несколько копий из элементов исходного массива по заданному измерению, т.е. формируется массив с размерностью на единицу большей размерности исходного массива.

SPREAD (SOURCE, DIM, NCOPIES) – расширение массива путем добавления копий

                                                                указанных измерений.

SOURCE –  исходный массив или скаляр любого типа;

NCOPIES – число копий, скаляр целого типа;

DIM –          номер измерения, скаляр целого типа.

Пример.

Если M – массив (/ 1, 2, 3 /), то SPREAD(M, 1, 3) – матрица:   1 2 3

                                                                                                              1 2 3

                                                                                                              1 2 3

9.3.7. Функция изменения конфигурации массива

Функция выполняет конструирование массива заданной конфигурации из элементов исходного массива.

RESHAPE (SOURCE, SHAPE [,PAD] [,ORDER]) - изменение конфигурации массива

SOURCE - исходный массив любого типа;

SHAPE - одномерный массив целого типа специфицирует конфигурацию
        результата;

PAD - массив того же типа, что и исходный массив; используется для
   заполнения результата, если размер результирующего массива
   превышает размер исходного.

ORDER - одномерный массив целого типа специфицирует последовательность, в которой элементы исходного массива помещаются в результирующий массив.

В простейшем случае функция имеет только два аргумента.

Пример 1. Инициализировать двумерный массив последовательными целыми

C       На Фортране 77

      INTEGER ARRAY (2, 4)

       K = 1

      DO 1 J = 1, 4

      DO 2 I = 1, 2

      ARRAY (I, J) = K

       K = K + 1

   2  CONTINUE

   1  CONTINUE

В Фортране 90/95 инициализация может быть выполнена с помощью одного оператора.

ARRAY = RESHAPE (SOURCE = (/1,2,3,4,5,6,7,8/), SHAPE = (/2, 4/))

Результат:

1  3  5  7

2  4  6  8

Результирующий массив заполняется элементами исходного массива в порядке, в котором элементы хранятся в памяти (по столбцам).

Пример 2.

ARRAY = RESHAPE (SOURCE = (/1,2,3/), SHAPE = (/2, 4/) , PAD =(/-1, -2/))

Результат

1    3   -2   -2

2   -1   -1   -1

Первые три элемента берутся из SOURCE, следующие 4 образуются двумя копиями из аргумента PAD,  и последний – частичным копированием аргумента PAD.

9.3.8. Функции сдвигов

Функции сдвигов производят сдвиги позиций элементов массивов. Имеется две функции.

CSHIFT (ARRAY, SHIFT [,DIM]) - циклический сдвиг

EOSHIFT (ARRAY, SHIFT [,BOUNDARY ,DIM]) - нециклический сдвиг

ARRAY – массив, который надо сдвинуть.

SHIFT – скаляр или массив (ранга на 1 меньше ранга исходного массива), целого типа; специфицирует на сколько позиций надо сдвинуть.

BOUNDARY - скаляр или массив (ранга на 1 меньше ранга исходного массива) целого типа; специфицирует значения, которые сдвигаются в результат чтобы заменить элементы выходящие за границы.

DIM – скаляр целого типа специфицирует измерение, которое сдвигается; если аргумент отсутствует, его значение принимается равным 1.

Пример 1.

Инициализировать квадратную матрицу таким образом, чтобы элементы главной диагонали были равными единице, остальные – равными нулю.

C       На Фортране 77                           ! На Фортране 90/95

      INTEGER MATRIX (3, 3)                   MATRIX = 0

      DO 1 I = 1, 3                                       MATRIX (:, 1) = 1

      DO 2 J= 1, 3                                        MATRIX = CSHIFT(ARRAY = MATRIX, &

      IF (I .NE. J) THEN                                      SHIFT = (/0, -1, -2/), DIM = 2)

     MATRIX(J, I) = 1

      ELSE

      MATRIX(J, I) = 0

      ENDIF

   2  CONTINUE

   1  CONTINUE

Пример 2. Установить в нуль все элементы матрицы выше главной диагонали, остальные элементы установить равными 1.

C       На Фортране 77                           ! На Фортране 90/95

      INTEGER MATRIX (3, 3)                 MATRIX = 0

      DO 1 I = 1, 3                                    MATRIX (:, 1) = 1

      DO 2 J= 1, 3                                    MATRIX = EOSHIFT(ARRAY = MATRIX, &

      IF (I .GE. J) THEN                           SHIFT=(/0, -1, -2/), BOUNDARY=1, DIM=2)

     MATRIX(J, I) = 1

      ELSE

     MATRIX(J, I) = 0

      ENDIF

   2  CONTINUE

   1  CONTINUE

Замечание.

Последние два примера – чисто иллюстративные, так как тот же результат можно получить, используя средства, описанные в предыдущих разделах.

9.3.9. Функции определения положения в массиве

Функции определения положения в массиве позволяют определить индексы минимального и максимального элемента массива.

MAXLOC (ARRAY [,DIM] [,MASK]) - положение максимального значения в массиве

MINLOC (ARRAY [,DIM] [,MASK])) - положение минимального значения в массиве

Пример

! Найти строку матрицы A с максимальной суммой элементов

KMAX = MAXLOC (SUM(A, DIM = 2))

Примечание. Аргумент DIM для этих двух функций введен в Фортране 95 (в Фортране 90 он отсутствовал).

9.4. Справочные функции для массивов

Необходимость в справочных функциях для массивов объясняется главным образом тем, что в языке имеются различные механизмы, обеспечивающие динамическое размещение массивов.

Справочные функции для массивов позволяют получить в динамике информацию о свойствах массива любого типа.

По виду выдаваемой информации справочные функции можно разделить на следующие группы:

·        характеристики массива (конфигурация, размер, границы);

·        статус размещенности массива.

Перечень функций

LBOUND (ARRAY [,DIM]) - нижние границы измерений массива

UBOUND (ARRAY [,DIM]) - верхние границы измерений массива

SHAPE (SOURCE) - конфигурация массива или скаляра

SIZE (ARRAY [,DIM]) - общее число элементов массива

ALLOCATED (ARRAY) - статус размещенности массива.

10. Заключение

В работе описаны средства работы с массивами, которые имеются в современном Фортране. Описанные возможности языка и приведенные примеры показывают, что средства явной спецификации векторных операций позволяют программисту описать алгоритмы обработки массивов в более лаконичной и наглядной форме (с элементами непроцедурности), чем при традиционном способе с использованием вложенных циклов и условных переходов. Очевидно, что такую программу легче отлаживать, модифицировать и распараллеливать. Кроме того, операции над массивами неявно специфицируют параллелизм действий над компонентами массивов (массива), что позволяет компилятору сгенерировать эффективный код с учетом особенностей аппаратуры.

Литература

1.      ISO/IEC 1539: 1991(E) Information technology - Programming languages – Fortran

2.      ISO/IEC 1539: 1997 Information technology - Programming languages - Fortran

3.      Фортран 90. Международный стандарт. Перевод с англ. М.: Финансы и статистика, 1998

4.      Горелик А.М. Современные международные стандарты языка Фортран.
// Программирование, 2001, N6

5.      Горелик А.М., Ушкова В.Л. Фортран сегодня и завтра. М.: Наука, 1990

6.      Меткалф М., Рид Дж. Описание языка программирования Фортран 90. Перевод с англ. М.: Мир, 1995

7.      Горелик А.М. Современный Фортран для компьютеров традиционной архитектуры и для параллельных вычислительных систем. - Препринт ИПМ РАН, 2003, N29

8.      Горелик А.М. Объектно-ориентированное программирование на современном Фортране. - Препринт ИПМ РАН, 2002, №70

9.      Горелик А.М. Средства поддержки мобильности и надежности программ в современном Фортране. Препринт ИПМ РАН, 2000, №55