Аннотация
Настоящая работа посвящена топологическим свойствам фрактальных (предфрактальных) графов.
Для фрактальных (предфрактальных) графов, смежность старых ребер которых не нарушается,
получен критерий планарности. Формула Эйлера адаптирована для плоских предфрактальных графов
с учетом их особенностей. Также подсчитано число внутренних вершин плоского предфрактального
графа. Даны оценки нескольких характеристик непланарности (рода и искаженности)
предфрактального графа.
Abstract
This paper is devoted to topological properties of fractal (prefractal) graphs. A simple
criterion for fractal (prefractal) graphs planarity is given. Euler’s formula for plane
prefractal graphs is made more exact. The inner vertex number of prefractal graph is counted up.
Some nonplanarity characteristics (a graph genus and distortion) of prefractal graphs is also
considered in this paper.
Введение. 3
1. Фрактальные и предфрактальные графы.. 4
2. Укладка фрактального графа в различные пространства. 5
3. О критериях планарности фрактальных графов. 6
4. Формула Эйлера для предфрактальных графов. 10
5. Число внутренних вершин плоского предфрактального графа. 11
6. Характеристики непланарности. 15
8. Об алгоритмах визуализации и проверки на планарность. 18
Заключение. 19
Литература. 20
Неоднократно
наглядно изображенное условие задачи в виде схемы или рисунка позволяло быстро
и точно решить саму задачу. Возможно, именно по этой причине теория графов
основательно и небезуспешно “устроилась” в современной науке. Теория графов
является мощным инструментом моделирования и решения большого количества задач
[1, 2, 3]. Кроме того, графы особо популярны и, как показывает практика,
чрезвычайно полезны в представлении и передаче различных видов информации.
Наиболее часто графы используются для изображения различных схем и диаграмм
(диаграммы потоков данных, организационные схемы, диаграммы состояний и
переходов, схемы связей объектов, концептуальные решетки, молекулярные
изображения и т.д.) [3]. От того, насколько удачно изображен граф, зависит то,
насколько хорошо будет воспринята информация, которую он несет. Принципы
“правильного” изображения графа отражаются в критериях визуализации графов [3].
Одной из главных
составляющих визуализации графов является топологическая теория графов [4]. Она
закладывает теоретические основы укладки графов на различные поверхности.
Именно поэтому, топологическая теория графов занимает прочное место в
современной computer science. Если граф с небольшим числом вершин еще
можно нарисовать “от руки”, то визуализация графов большой размерности
производиться автоматизировано [5], и здесь нельзя переоценить значимость
методов топологической теории графов.
Настоящая работа
посвящена изучению топологических свойств “больших” графов, называемых фрактальными
(предфрактальными). Фрактальные (предфрактальные) графы являются моделями
структур, обладающих свойством самоподобия. Отличительной чертой фрактальных
графов является возможность анализа свойств всего фрактального графа, или его
конечного аналога – предфрактального графа, по свойствам его затравки –
наименьшей несамоподобной части. Такой подход особенно актуален и полезен в
наступившей эпохе больших и сложных задач.
Термином затравка
условимся называть какой-либо связный граф 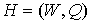 . Для определения фрактального
(предфрактального) графа [6] нам потребуется операция замены вершины затравкой (ЗВЗ). Суть операции ЗВЗ заключается в
следующем. В данном графе . Для определения фрактального
(предфрактального) графа [6] нам потребуется операция замены вершины затравкой (ЗВЗ). Суть операции ЗВЗ заключается в
следующем. В данном графе  у намеченной для замещения
вершины у намеченной для замещения
вершины 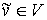 выделяется множество выделяется множество 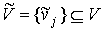 , ,  , смежных ей вершин. Далее из графа , смежных ей вершин. Далее из графа 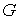 удаляется вершина удаляется вершина 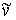 и все инцидентные ей
ребра. Затем каждая вершина и все инцидентные ей
ребра. Затем каждая вершина 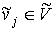 , , 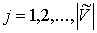 , соединяется ребром с одной из вершин затравки , соединяется ребром с одной из вершин затравки  . Вершины соединяются произвольно (случайным образом) или по
определенному правилу, при необходимости. . Вершины соединяются произвольно (случайным образом) или по
определенному правилу, при необходимости.
Предфрактальный
граф будем обозначать через  , где , где 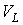 - множество вершин графа, а - множество вершин графа, а  - множество его ребер. Определим его
рекуррентно, поэтапно, заменяя каждый раз в построенном на предыдущем этапе - множество его ребер. Определим его
рекуррентно, поэтапно, заменяя каждый раз в построенном на предыдущем этапе  графе графе 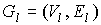 каждую его вершину затравкой каждую его вершину затравкой
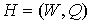 . На этапе . На этапе 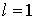 предфрактальному
графу соответствует затравка предфрактальному
графу соответствует затравка 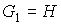 . Об описанном процессе говорят, что предфрактальный граф . Об описанном процессе говорят, что предфрактальный граф  порожден затравкой порожден затравкой  . Процесс порождения предфрактального графа . Процесс порождения предфрактального графа  , по существу, есть процесс построения последовательности
предфрактальных графов , по существу, есть процесс построения последовательности
предфрактальных графов 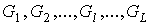 , называемой траекторией. Фрактальный граф , называемой траекторией. Фрактальный граф 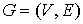 , порожденный затравкой , порожденный затравкой 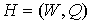 , определяется бесконечной траекторией. , определяется бесконечной траекторией.
Использование операции ЗВЗ в процессе
порождения предфрактального графа 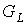 , для элементов , для элементов 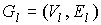 , , 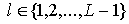 , его траектории позволяет ввести отображение , его траектории позволяет ввести отображение 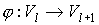 или или 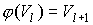 , а в общем виде , а в общем виде
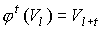 , , 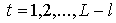 . (1) . (1)
В выражении (1) множество  - образ
множества - образ
множества  , а множество , а множество 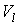 - прообраз
множества - прообраз
множества 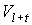 . .
Для предфрактального графа  , ребра, появившиеся на , ребра, появившиеся на  -ом, -ом, 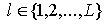 , этапе порождения, будем называть ребрами ранга , этапе порождения, будем называть ребрами ранга 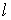 . Новыми ребрами предфрактального графа . Новыми ребрами предфрактального графа  назовем ребра ранга назовем ребра ранга 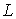 , а все остальные ребра назовем - старыми. , а все остальные ребра назовем - старыми.
Если из предфрактального графа 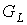 , порожденного , порожденного  -вершинной затравкой -вершинной затравкой  , последовательно удалить все старые ребра (ребра ранга , последовательно удалить все старые ребра (ребра ранга  , ,  ), то исходный
граф распадется на множество связных компонент ), то исходный
граф распадется на множество связных компонент  , каждая из которых изоморфна [7] затравке , каждая из которых изоморфна [7] затравке 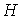 . Множество компонент . Множество компонент 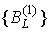 будем называть блоками первого ранга. Аналогично, при
удалении из предфрактального графа будем называть блоками первого ранга. Аналогично, при
удалении из предфрактального графа  всех старых ребер
рангов всех старых ребер
рангов  , получим множество
блоков , получим множество
блоков 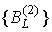 второго ранга. Обобщая, скажем, что при
удалении из предфрактального графа второго ранга. Обобщая, скажем, что при
удалении из предфрактального графа 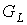 всех ребер рангов всех ребер рангов  , получим множество , получим множество 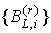 , , 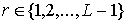 , блоком , блоком 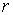 -го ранга, где -го ранга, где  -порядковый номер
блока. Блоки -порядковый номер
блока. Блоки  первого ранга также
будем называть подграф-затравками первого ранга также
будем называть подграф-затравками 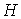 предфрактального
графа предфрактального
графа 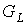 . Очевидно, что всякий блок . Очевидно, что всякий блок 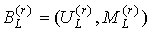 , , 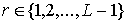 , является предфрактальным графом , является предфрактальным графом  , порожденным затравкой , порожденным затравкой 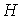 . .
Уточним для отображения  в формуле (1) ряд
подробностей. Для любой вершины в формуле (1) ряд
подробностей. Для любой вершины  , , 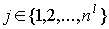 , предфрактального графа , предфрактального графа  , , 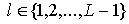 , из траектории графа , из траектории графа 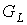 , справедливо , справедливо
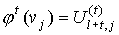 , (2) , (2)
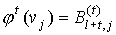 , где , где  , , 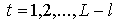 . .
Аналогично,
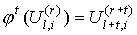 , (3) , (3)
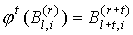 , , 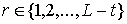 , , 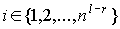 . .
Два блока предфрактального графа назовем смежными, если существует ребро, вершины
которого принадлежат различным блокам. Не требует доказательства тот факт, что
блоки предфрактального графа смежны тогда и только тогда, когда смежны их
прообразы из (2).
Обобщением описанного процесса порождения
предфрактального графа  является такой
случай, когда вместо единственной затравки является такой
случай, когда вместо единственной затравки 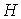 используется
множество затравок используется
множество затравок 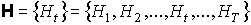 , , 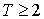 . Суть этого обобщения состоит в том, что при переходе от
графа . Суть этого обобщения состоит в том, что при переходе от
графа 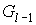 к графу к графу 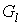 каждая вершина
замещается некоторой затравкой каждая вершина
замещается некоторой затравкой  , которая выбирается случайно или согласно определенному
правилу, отражающему специфику моделируемого процесса или структуры. , которая выбирается случайно или согласно определенному
правилу, отражающему специфику моделируемого процесса или структуры.
Плоским
графом [7] называется граф,
вершины которого являются точками плоскости, а ребра – непрерывными плоскими
линиями без самопересечений, соединяющими соответствующие вершины так, что
никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины.
Любой граф, изоморфный [7] плоскому графу, будем
называть планарным [7].
О планарных графах говорят, что они укладываются на плоскости (имеют плоскую укладку). Вообще говоря,
рассматриваются укладки графов не только на плоскости, но и на других
поверхностях и в пространстве. Поэтому дадим определение укладки графа в
произвольное пространство.
Прежде всего введем понятие жордановой кривой, под которой будем
понимать непрерывную спрямляемую линию, не имеющую самопересечений.
Будем говорить, что граф  , конечный или бесконечный [8], укладывается в пространстве L (часто
говорят о вложении графа в поверхность [9]), если существует такое отображение
вершин и ребер графа , конечный или бесконечный [8], укладывается в пространстве L (часто
говорят о вложении графа в поверхность [9]), если существует такое отображение
вершин и ребер графа 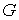 соответственно в
точки и жордановы кривые этого пространства, что различным вершинам соответствуют
различные точки, а кривые, соответствующие различным ребрам, пересекаются
только в инцидентных этим ребрам вершинах. Изображенный таким образом граф
называется укладкой графа соответственно в
точки и жордановы кривые этого пространства, что различным вершинам соответствуют
различные точки, а кривые, соответствующие различным ребрам, пересекаются
только в инцидентных этим ребрам вершинах. Изображенный таким образом граф
называется укладкой графа 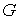 в пространстве L. в пространстве L.
Теорема 1. Всякий предфрактальный граф 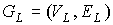 укладывается в трехмерное
пространство E3. укладывается в трехмерное
пространство E3.
Доказательство. Все вершины предфрактального графа 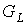 поместим в различные
точки оси ОХ пространства E3. Из пучка плоскостей, проходящих через эту
ось, выберем поместим в различные
точки оси ОХ пространства E3. Из пучка плоскостей, проходящих через эту
ось, выберем  различных плоскостей.
Далее каждое ребро различных плоскостей.
Далее каждое ребро 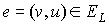 изобразим в
соответствующей плоскости полуокружностью, проходящей через вершины изобразим в
соответствующей плоскости полуокружностью, проходящей через вершины 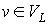 и и 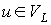 . Как результат получим укладку предфрактального графа . Как результат получим укладку предфрактального графа 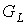 в пространство E3. Действительно все ребра предфрактального
графа лежат в различных плоскостях пространства и поэтому не пересекаются.
◄ в пространство E3. Действительно все ребра предфрактального
графа лежат в различных плоскостях пространства и поэтому не пересекаются.
◄
Теорема 2. Всякий фрактальный граф 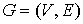 укладывается в
трехмерное пространство E3. укладывается в
трехмерное пространство E3.
Доказательство этой теоремы повторяет доказательство
предыдущей теоремы. С той лишь разницей, что количество фиксируемых плоскостей
из числа проходящих через ось ОХ в
пространстве E3 бесконечно, поскольку множество ребер 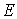 фрактального графа фрактального графа 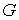 - есть множество счетное. ◄ - есть множество счетное. ◄
Введем операцию подразбиения ребра 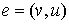 графа. Она
заключается в следующем: из графа удаляется ребро графа. Она
заключается в следующем: из графа удаляется ребро  и добавляются два
новых ребра и добавляются два
новых ребра  и и 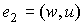 , где , где  - новая вершина. Два графа называются гомеоморфными, если оба они могут быть
получены из одного и того же графа подразбиением его ребер. - новая вершина. Два графа называются гомеоморфными, если оба они могут быть
получены из одного и того же графа подразбиением его ребер.
Теорема Понтрягина – Куратовского (критерий
планарности графа) [10] гласит, что граф планарен тогда и только тогда, когда
он не содержит подграфов, гомеоморфных графам 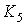 или или 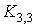 . Ясно, что теорема Понтрягина – Куратовского, как и прочие
критерии планарности графов [10], справедлив и для всех предфрактальных графов.
Графы . Ясно, что теорема Понтрягина – Куратовского, как и прочие
критерии планарности графов [10], справедлив и для всех предфрактальных графов.
Графы  и и 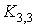 изображены на рис. 1. изображены на рис. 1.
Согласно определению, для предфрактального
графа 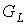 , порожденного затравкой , порожденного затравкой 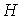 , его блоки первого , его блоки первого 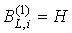 , ,  , изоморфны затравке , изоморфны затравке  . Поэтому из критерия планарности графа совершенно очевидным
образом вытекают следующие утверждения. . Поэтому из критерия планарности графа совершенно очевидным
образом вытекают следующие утверждения.
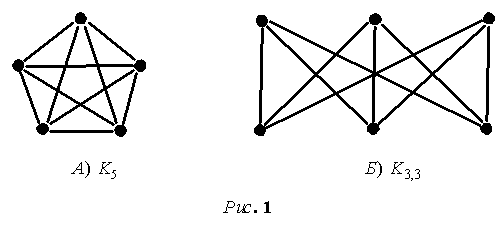
Утверждение 1. Всякий предфрактальный граф, порожденный
затравкой, гомеоморфной 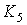 или или 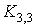 , не является планарным. , не является планарным.
Утверждение 2. Всякий предфрактальный граф, порожденный
затравкой, имеющий подграф гомеоморфный  или или 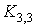 , не является планарным. , не является планарным.
Гранью [7] плоского графа принято называть
максимальное по включению множество точек плоскости, каждая пара которых может
быть соединена жордановой кривой, не пересекающей ребра графа. Тем самым каждая
точка плоскости принадлежит хотя бы одной грани плоского графа. Границей грани [7] будем считать
множество вершин и ребер, принадлежащих этой грани.
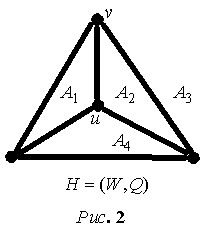 На рис. 2 изображен граф На рис. 2 изображен граф 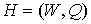 с четырьмя гранями. Отметим, что всякий
плоский граф имеет одну и притом единственную, неограниченную грань. Такая
грань называется внешней, а остальные
грани - внутренними ( на рис. 2 грань с четырьмя гранями. Отметим, что всякий
плоский граф имеет одну и притом единственную, неограниченную грань. Такая
грань называется внешней, а остальные
грани - внутренними ( на рис. 2 грань 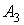 - внешняя). Важно, что всякую внутреннюю грань
плоского графа легко преобразовать во внешнюю [7]. Кроме того, для любого плоского
графа каждая точка плоскости, не лежащая на ребре, входит только в одну грань.
А каждая точка ребра, не являющаяся вершиной, входит только в одну грань, если
это ребро является мостом, и точно в две грани, если оно не мост. Вершина, не
являющаяся висячей, принадлежит не менее чем двум граням. К примеру, вершина - внешняя). Важно, что всякую внутреннюю грань
плоского графа легко преобразовать во внешнюю [7]. Кроме того, для любого плоского
графа каждая точка плоскости, не лежащая на ребре, входит только в одну грань.
А каждая точка ребра, не являющаяся вершиной, входит только в одну грань, если
это ребро является мостом, и точно в две грани, если оно не мост. Вершина, не
являющаяся висячей, принадлежит не менее чем двум граням. К примеру, вершина  , как показано на рис. 2, входит сразу в три грани - , как показано на рис. 2, входит сразу в три грани - 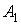 , , 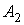 и и 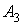 . .
Внутренней
вершиной плоского графа
назовем такую вершину, которую нельзя соединить жордановой кривой с точками
внешней грани графа, так чтобы она не пересекала ни одно из ребер графа,
образующих границу внешней грани. В противном случае, вершина называется внешней. На рис. 2 вершина 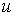 - внутренняя. - внутренняя.
Число
внутренних вершин планарного графа 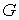 напрямую зависит от вида его плоской укладки.
Поэтому в дальнейшем будем говорить, что фрактальный (предфрактальный) граф
порожден произвольно-плоской затравкой,
если вид плоской укладки затравки в процессе порождения не фиксирован, и что
фрактальный (предфрактальный) граф порожден плоской
затравкой в том случае, когда вид плоской укладки затравки в процессе
порождения строго фиксирован. Вопрос эквивалентности плоских укладок планарного
графа широко освещен в книге [9]. В нашей работе, порождение предфрактального
графа произвольно-плоской затравкой предполагает использование неэквивалентных
плоских укладок затравки. напрямую зависит от вида его плоской укладки.
Поэтому в дальнейшем будем говорить, что фрактальный (предфрактальный) граф
порожден произвольно-плоской затравкой,
если вид плоской укладки затравки в процессе порождения не фиксирован, и что
фрактальный (предфрактальный) граф порожден плоской
затравкой в том случае, когда вид плоской укладки затравки в процессе
порождения строго фиксирован. Вопрос эквивалентности плоских укладок планарного
графа широко освещен в книге [9]. В нашей работе, порождение предфрактального
графа произвольно-плоской затравкой предполагает использование неэквивалентных
плоских укладок затравки.
Теорема 3. Предфрактальный граф  , порожденный произвольно-плоской затравкой , порожденный произвольно-плоской затравкой 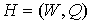 , планарен,
если смежность старых ребер не нарушается. , планарен,
если смежность старых ребер не нарушается.
 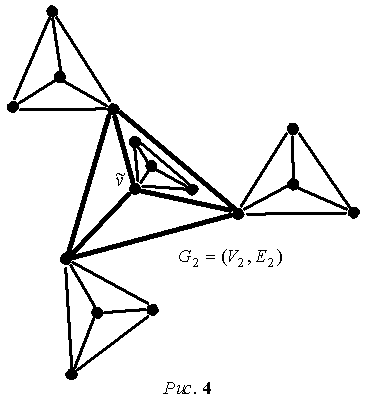
Доказательство. Для доказательства теоремы нам понадобиться операция “склеивания” плоских графов.
Рассмотрим два плоских графа 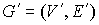 и и  . Произвольным образом выберем две вершины . Произвольным образом выберем две вершины 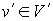 и и 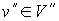 . Тогда, согласно [7], граф . Тогда, согласно [7], граф 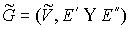 полученный из полученный из 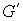 и и  слиянием вершин слиянием вершин  и и 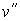 в некоторую вершину в некоторую вершину 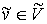 , является планарным, т.е. имеет плоскую укладку. При этом,
очевидно, если все ребра графа , является планарным, т.е. имеет плоскую укладку. При этом,
очевидно, если все ребра графа 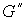 расположатся во
внешней грани графа расположатся во
внешней грани графа 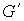 , то полученный при их склеивании граф , то полученный при их склеивании граф 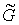 будет плоским. будет плоским.
Доказательство проведем конструктивно. На
этапе 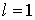 , дан плоский предфрактальный граф , дан плоский предфрактальный граф 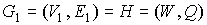 , он изображен
на рис. 2. На этапе , он изображен
на рис. 2. На этапе  на графе на графе 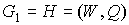 произвольно выделим вершину произвольно выделим вершину  и множество и множество 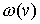 инцидентных ей ребер,
для графа инцидентных ей ребер,
для графа 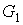 на рис. 3 на рис. 3 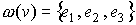 . В соответствии с правилами порождения предфрактального
графа, заместим вершину . В соответствии с правилами порождения предфрактального
графа, заместим вершину  затравкой затравкой  . При этом, удовлетворяя
требованиям теоремы, множество ребер . При этом, удовлетворяя
требованиям теоремы, множество ребер 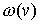 сохраним инцидентными
одной из вершин затравки, что, вообще говоря, будет соответствовать операции
“склеивания” плоских графов сохраним инцидентными
одной из вершин затравки, что, вообще говоря, будет соответствовать операции
“склеивания” плоских графов 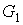 и и  . А поэтому, в
результате, получим планарный граф, см. рис. 3. Который, используя любой из
известных способов [7, 10], преобразуем в плоский граф (граф на рис. 3 уже
преобразован в плоский граф). Далее, описанную последовательность операций
(замена вершины затравкой, преобразование в плоский граф) произведем со всеми
оставшимися вершинами графа . А поэтому, в
результате, получим планарный граф, см. рис. 3. Который, используя любой из
известных способов [7, 10], преобразуем в плоский граф (граф на рис. 3 уже
преобразован в плоский граф). Далее, описанную последовательность операций
(замена вершины затравкой, преобразование в плоский граф) произведем со всеми
оставшимися вершинами графа 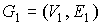 . В итоге, по окончании второго этапа порождения, получим
плоский предфрактальный граф . В итоге, по окончании второго этапа порождения, получим
плоский предфрактальный граф 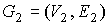 , см. рис. 4. На всех последующих этапах , см. рис. 4. На всех последующих этапах 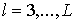 порождения с
предфрактальным графом порождения с
предфрактальным графом 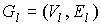 последовательно проделаем
те же операции, что на этапе последовательно проделаем
те же операции, что на этапе  . В результате на этапе . В результате на этапе 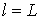 получим планарный
предфрактальный граф получим планарный
предфрактальный граф  . ◄ . ◄
Вообще говоря, процесс “склеивания” затравки 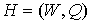 и предфрактального
графа и предфрактального
графа  во всех его вершинах
можно продолжить до бесконечности во всех его вершинах
можно продолжить до бесконечности 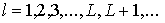 . Для полученного таким путем фрактального графа . Для полученного таким путем фрактального графа 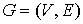 справедливо справедливо
Следствие 3.1. Всякий фрактальный граф  , порожденный произвольно-плоской затравкой , порожденный произвольно-плоской затравкой 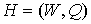 , планарен, если смежность старых ребер не нарушается. , планарен, если смежность старых ребер не нарушается.
Поскольку, операция “склеивания” плоских
графов возможна и для совершенно различных графов, то имеют место и такие
следствия.
Следствие 3.2. Всякий предфрактальный граф 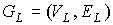 , порожденный множеством произвольно-плоских затравок , порожденный множеством произвольно-плоских затравок  , ,  , планарен, если смежность старых ребер не нарушается. , планарен, если смежность старых ребер не нарушается.
Следствие 3.3. Всякий фрактальный граф  , порожденный множеством произвольно-плоских затравок , порожденный множеством произвольно-плоских затравок 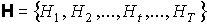 , ,  , планарен, если смежность старых ребер не нарушается. , планарен, если смежность старых ребер не нарушается.
Теорема 4. У сякого плоского предфрактального графа 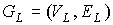 старые ребра
инцидентны внешним вершинам блоков первого ранга. старые ребра
инцидентны внешним вершинам блоков первого ранга.
 Доказательство.
Рассмотрим произвольный плоский предфрактальный граф Доказательство.
Рассмотрим произвольный плоский предфрактальный граф  , порожденный затравкой , порожденный затравкой  . Предфрактальный граф . Предфрактальный граф 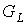 , согласно определению, представляет собой множество
подграфов-затравок , согласно определению, представляет собой множество
подграфов-затравок 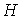 соединенных старыми
ребрами. При чем каждая подграф-затравка соединенных старыми
ребрами. При чем каждая подграф-затравка 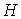 является плоским
графом, в противном случае предфрактальный граф является плоским
графом, в противном случае предфрактальный граф 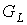 не будет плоским. не будет плоским.
Доказательство теоремы проведем от противного.
Предположим, что у предфрактального графа 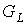 существует старое ребро существует старое ребро
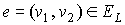 ранга ранга  , ,  , такое что вершина , такое что вершина 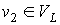 является внутренней
вершиной одного из подграфов-затравок является внутренней
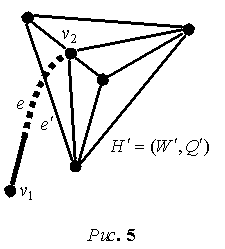
вершиной одного из подграфов-затравок 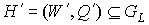 , см. рис. 5. Но тогда, из определения внутренней вершины
следует, что отрезок жордановой кривой, на рис. 5 он изображен пунктиром,
отражающий на плоскости ребро , см. рис. 5. Но тогда, из определения внутренней вершины
следует, что отрезок жордановой кривой, на рис. 5 он изображен пунктиром,
отражающий на плоскости ребро 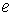 , пересечет хотя бы одно ребро , пересечет хотя бы одно ребро 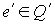 подграф-затравки подграф-затравки 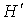 в точке принадлежащей
границе внешней грани. А это противоречит тому, что предфрактальный граф в точке принадлежащей
границе внешней грани. А это противоречит тому, что предфрактальный граф  является плоским
графом. Поэтому, заключаем, что наше предположение не верно, а значит старые
ребра плоского предфрактального графа является плоским
графом. Поэтому, заключаем, что наше предположение не верно, а значит старые
ребра плоского предфрактального графа 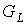 инцидентны внешним
вершинам подграф-затравок инцидентны внешним
вершинам подграф-затравок  , или блоков
первого ранга. ◄ , или блоков
первого ранга. ◄
Граф называется максимально плоским (планарным) [7], если он перестает быть плоским
при добавлении к нему хотя бы одного ребра. На рис. 2 и 5 графы 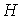 и и  соответственно
являются 4-вершинным и 5-вершинным - максимально плоские графами. Известно [7],
что граф является максимально плоским тогда и только тогда, когда он
представляет собой плоскую триангуляцию, т.е. каждая его грань, в том числе и
внешняя, является треугольником (3-циклом). Поэтому любой максимально плоский
граф имеет ровно три внешние вершины, образующие 3-цикл. Поскольку, как
отмечалось ранее, любая внутренняя грань может быть преобразована во внешнюю,
то из теоремы 4 очевидным образом вытекает следующее соответственно
являются 4-вершинным и 5-вершинным - максимально плоские графами. Известно [7],
что граф является максимально плоским тогда и только тогда, когда он
представляет собой плоскую триангуляцию, т.е. каждая его грань, в том числе и
внешняя, является треугольником (3-циклом). Поэтому любой максимально плоский
граф имеет ровно три внешние вершины, образующие 3-цикл. Поскольку, как
отмечалось ранее, любая внутренняя грань может быть преобразована во внешнюю,
то из теоремы 4 очевидным образом вытекает следующее
Следствие 4.1. У всякого планарного предфрактального графа 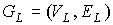 , порожденного максимально планарной затравкой , порожденного максимально планарной затравкой 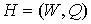 , вершины отдельно взятого блока первого ранга, инцидентные
старым ребрам, образуют 3-цикл. , вершины отдельно взятого блока первого ранга, инцидентные
старым ребрам, образуют 3-цикл.
Многие результаты для планарных графов были
получены благодаря широко известной формуле
Эйлера [7]. Напомним ее. Для всякого связного плоского графа  , у которого , у которого  , ,  , и , и 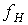 - число граней, справедливо равенство - число граней, справедливо равенство 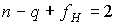 . Вид плоской укладки графа . Вид плоской укладки графа  при этом не имеет
значения. Тогда для плоского предфрактального графа при этом не имеет
значения. Тогда для плоского предфрактального графа  порожденного
затравкой порожденного
затравкой 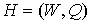 так же справедливо так же справедливо
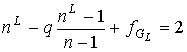 , (4) , (4)
где 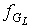 - число граней графа - число граней графа 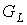 . Из (1) выразим . Из (1) выразим 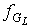 . .
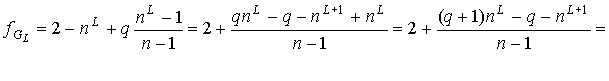
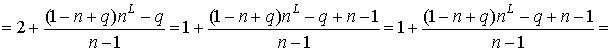
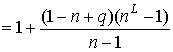 , а т.к. , а т.к.  , то , то
 . (5) . (5)
Проведенные рассуждения являются основанием
для теоремы.
Теорема 5. Для всякого связного плоского
предфрактального графа  , порожденного затравкой , порожденного затравкой 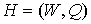 , число граней , число граней 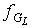 определяется формулой
(5). определяется формулой
(5).
К формуле (5) можно подойти и с другой
стороны. В процессе порождения предфрактального графа 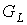 производится ровно производится ровно 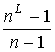 операций ЗВЗ. При
необходимости можно убедиться в том, что каждая операция ЗВЗ приносит графу операций ЗВЗ. При
необходимости можно убедиться в том, что каждая операция ЗВЗ приносит графу 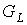 по по  -ой внутренней грани, при этом внешняя грань остается одна и
та же. Поэтому общее число -ой внутренней грани, при этом внешняя грань остается одна и
та же. Поэтому общее число  внутренних граней
предфрактального графа внутренних граней
предфрактального графа 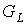 в сумме с одной
внешней гранью дают формулу (5). в сумме с одной
внешней гранью дают формулу (5).
Для предфрактального графа  , порожденного множеством затравок , порожденного множеством затравок  , , 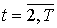 , обозначим через , обозначим через 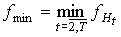 , , 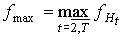 соответственно
минимальное и максимальное число граней среди затравок из множества соответственно
минимальное и максимальное число граней среди затравок из множества  . .
Следствие 5.1. Числа граней 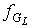 предфрактального
графа предфрактального
графа 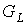 , порожденного множеством затравок , порожденного множеством затравок  ограничено двойным
неравенством ограничено двойным
неравенством
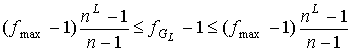 . (6) . (6)
Отметим, что правая часть неравенства (6)
достигается, когда в порождении предфрактального графа 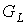 участвует только одна
затравка из участвует только одна
затравка из  с числом граней
равным с числом граней
равным 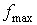 . А левая часть (6) достигается, когда . А левая часть (6) достигается, когда  порожден затравкой из порожден затравкой из
 с минимальным числом с минимальным числом  граней. граней.
Число
внутренних вершин  планарного графа планарного графа  зависит от вида его
плоской укладки. Тогда, в свою очередь, число внутренних вершин зависит от вида его
плоской укладки. Тогда, в свою очередь, число внутренних вершин 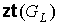 предфрактального
графа предфрактального
графа  зависит от числа
внутренних вершин зависит от числа
внутренних вершин 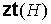 его затравки его затравки 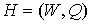 . .
Будем последовательны, и рассмотрим плоский
предфрактальный граф 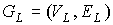 , порожденный плоской затравкой , порожденный плоской затравкой  , ,  , с сохранением смежности старых ребер. Тогда на , с сохранением смежности старых ребер. Тогда на 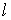 -ом, -ом, 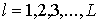 , этапе порождения, замена вершины , этапе порождения, замена вершины 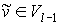 графа графа 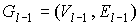 затравкой затравкой 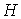 соответствует
операции “склеивания” графа соответствует
операции “склеивания” графа  и затравки и затравки 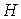 в замещаемой вершине в замещаемой вершине 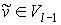 . В операции “склеивания” совмещается по одной вершине графов . В операции “склеивания” совмещается по одной вершине графов
 и и  , поэтому возникает вопрос о взаимном расположении остальных
вершин на плоскости. , поэтому возникает вопрос о взаимном расположении остальных
вершин на плоскости.
 Первое. Если Первое. Если  - внутренняя вершина, то все грани, которым она
принадлежит являются внутренними гранями графа - внутренняя вершина, то все грани, которым она
принадлежит являются внутренними гранями графа 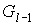 . Поэтому все вершины затравки . Поэтому все вершины затравки 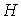 , “склеенной” с графом , “склеенной” с графом 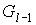 в вершине в вершине  будут принадлежать
только одной из внутренних граней графа будут принадлежать
только одной из внутренних граней графа 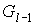 , которой принадлежит и сама вершина , которой принадлежит и сама вершина 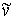 (см. рис. 4). В
противном случае будет нарушаться плоская укладка графа, полученного в
результате проведения “склеивания”. При это все вершины подграфа-затравки (см. рис. 4). В
противном случае будет нарушаться плоская укладка графа, полученного в
результате проведения “склеивания”. При это все вершины подграфа-затравки 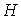 станут внутренними. станут внутренними.
Второе. Если 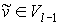 - внешняя невисячая вершина, то она принадлежит
как внутренним так и внешней граням графа - внешняя невисячая вершина, то она принадлежит
как внутренним так и внешней граням графа 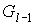 (висячая вершина [7],
в силу свой специфики, может принадлежать либо внешней, либо одной внутренней
грани графа). Поэтому вершины затравки (висячая вершина [7],
в силу свой специфики, может принадлежать либо внешней, либо одной внутренней
грани графа). Поэтому вершины затравки  , кроме вершины совмещенной с , кроме вершины совмещенной с 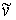 , при “склеивании” с , при “склеивании” с  , не нарушая плоской укладки, могут расположиться либо в
одной из внутренних, либо во внешней грани графа , не нарушая плоской укладки, могут расположиться либо в
одной из внутренних, либо во внешней грани графа  . При расположении затравки . При расположении затравки 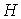 в одной из внутренних
граней графа в одной из внутренних
граней графа 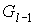 , все ее вершины, кроме совмещенной, станут внутренними (см.
рис. 6), как и в случае с внутренней вершиной , все ее вершины, кроме совмещенной, станут внутренними (см.
рис. 6), как и в случае с внутренней вершиной 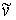 . А при расположении затравки . А при расположении затравки 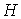 во внешней грани
графа во внешней грани
графа  (см. рис. 3), ее
вершины не поменяют свой тип (внешние вершины останутся внешними). (см. рис. 3), ее
вершины не поменяют свой тип (внешние вершины останутся внешними).
Будем говорить, что плоский предфрактальный
граф имеет внутреннюю укладку, если
границу его внешней грани образуют только старые ребра первого ранга. Также
будем говорить, что плоский предфрактальный граф имеет внешнюю укладку, если смежность его старых ребер не нарушается, а в
процессе порождения этого предфрактального графа, при замещении внешних вершин
затравка располагалась во внешней грани. На рис. 6 изображен предфрактальный
граф  с внутренней
укладкой, порожденный затравкой с внутренней
укладкой, порожденный затравкой 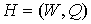 (см. рис. 2). На рис.
4 изображен тот же предфрактальный граф (см. рис. 2). На рис.
4 изображен тот же предфрактальный граф 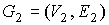 , но с внешней укладкой. , но с внешней укладкой.
Лемма 1. Для числа внутренних вершин 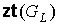 предфрактального
графа предфрактального
графа 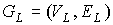 с внутренней укладкой,
порожденного плоской затравкой с внутренней укладкой,
порожденного плоской затравкой  , , 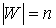 , справедливо равенство , справедливо равенство
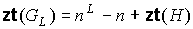 . (7) . (7)
Доказательство. Из определения внутренней вершины следует,
что ребрам плоского графа, образующих границу внешней грани, инцидентны только
внешние вершины этого графа. Ребра, инцидентные внутренним вершинам графа, в
образовании границы внешней грани не участвуют. А поскольку границу внешней
грани предфрактального графа 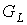 с внутренней укладкой
образуют только лишь старые ребра первого ранга, то число внешних вершин предфрактального
графа с внутренней укладкой
образуют только лишь старые ребра первого ранга, то число внешних вершин предфрактального
графа  будет равно числу будет равно числу 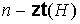 внешних вершин его плоской
затравки внешних вершин его плоской
затравки 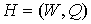 , , 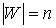 . Но тогда для числа внутренних вершин графа . Но тогда для числа внутренних вершин графа 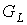 справедливо равенство справедливо равенство
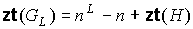 , где , где 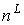 - число всех вершин графа - число всех вершин графа  . ◄ . ◄
Лемма 2. Для числа внутренних вершин 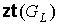 предфрактального
графа предфрактального
графа  с внешней укладкой,
порожденного плоской затравкой с внешней укладкой,
порожденного плоской затравкой 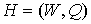 , ,  , справедливо равенство , справедливо равенство
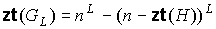 . (8) . (8)
Доказательство проведем по индукции. Пусть дан плоский граф  , ,  , с числом , с числом 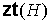 внутренних вершин.
Проследим за процессом порождения предфрактального графа внутренних вершин.
Проследим за процессом порождения предфрактального графа 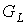 с внешней укладкой и
с затравкой с внешней укладкой и
с затравкой 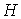 . На этапе . На этапе  предфрактальный граф предфрактальный граф 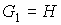 , поэтому число его внутренних вершин , поэтому число его внутренних вершин  , а число внешних вершин, соответственно, равно , а число внешних вершин, соответственно, равно  . На этапе . На этапе 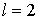 в результате
замещения каждой из в результате
замещения каждой из 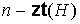 внешних вершин графа внешних вершин графа  затравкой затравкой 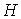 будем получать по будем получать по  внешней вершине для
предфрактального графа внешней вершине для
предфрактального графа  , поскольку, в соответствии с определением внешней укладки,
затравка (все ее ребра и вершины) будут расположены во внешней грани графа , поскольку, в соответствии с определением внешней укладки,
затравка (все ее ребра и вершины) будут расположены во внешней грани графа 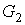 . При замещении внутренних вершин графа . При замещении внутренних вершин графа  затравкой затравкой  мы не будем получать
внешних вершин для предфрактального графа мы не будем получать
внешних вершин для предфрактального графа 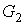 , поэтому число внутренних вершин графа , поэтому число внутренних вершин графа 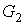 равно равно 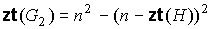 , где , где 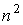 - число всех вершин графа - число всех вершин графа 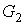 . Продолжая подобным образом, на этапе . Продолжая подобным образом, на этапе 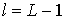 порождения
предфрактального графа порождения
предфрактального графа 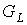 , замещение каждой из , замещение каждой из  внешних вершин графа внешних вершин графа 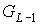 , приведет к появлению числа , приведет к появлению числа  внешних вершин
предфрактального графа внешних вершин
предфрактального графа 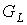 . Но тогда число внутренних вершин предфрактального графа . Но тогда число внутренних вершин предфрактального графа  вычисляется по
формуле вычисляется по
формуле  , где , где 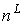 - общее число вершин предфрактального графа - общее число вершин предфрактального графа 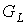 . ◄ . ◄
Вообще говоря, лемма 1 и лемма 2 описывают,
соответственно, условия достижения максимального и минимального числа
внутренних вершин для плоского предфрактального графа, порожденного плоской
затравкой. Действительно, в первом случае число внешних вершин на всей
траектории предфрактального графа не меняется, поэтому число внутренних вершин
для него максимально. Во втором случае, наоборот, максимально число внешних
вершин предфрактального графа, т.к. в процессе его порождения, затравки при
замещении вершин располагаются во внешней грани.
Доказанные леммы позволяют сформулировать теорему
дающую оценку числа внутренних вершин для любого плоского предфрактального графа.
Теорема 6. Для всякого плоского предфрактального графа 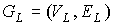 , порожденного произвольно-плоской затравкой , порожденного произвольно-плоской затравкой 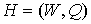 , ,  , число , число 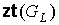 его внутренних вершин
ограничено неравенством его внутренних вершин
ограничено неравенством 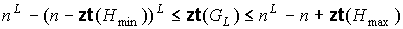 , где , где 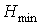 и и  - плоские укладки затравки - плоские укладки затравки 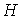 , соответственно, с минимальным и максимальным числом внутренних
вершин. , соответственно, с минимальным и максимальным числом внутренних
вершин.
Доказательство. Рассмотрим плоский предфрактальный граф 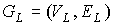 , порожденный произвольно-плоской затравкой , порожденный произвольно-плоской затравкой 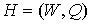 , , 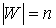 . Как и для любого графа число внутренних вершин . Как и для любого графа число внутренних вершин 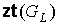 предфрактального
графа предфрактального
графа 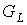 зависит от
конкретного вида его плоской укладки. А вид плоской укладки графа зависит от
конкретного вида его плоской укладки. А вид плоской укладки графа 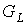 , в свою очередь, зависит от вида укладки его затравки , в свою очередь, зависит от вида укладки его затравки  . Очевидно, что максимальное число внутренних вершин для
предфрактального графа . Очевидно, что максимальное число внутренних вершин для
предфрактального графа  будет достигнуто,
если он порожден плоской затравкой будет достигнуто,
если он порожден плоской затравкой 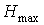 , являющейся укладкой графа , являющейся укладкой графа 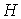 также с максимальным
числом внутренних вершин. Аналогично, минимальное число внутренних вершин для
предфрактального графа также с максимальным
числом внутренних вершин. Аналогично, минимальное число внутренних вершин для
предфрактального графа 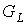 будет достигнуто,
если он порожден плоской затравкой будет достигнуто,
если он порожден плоской затравкой 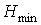 , являющейся укладкой графа , являющейся укладкой графа 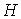 с минимальным числом
внутренних вершин. Далее, следуя сделанным рассуждениям, в формулах (7) и (8)
заменим затравку с минимальным числом
внутренних вершин. Далее, следуя сделанным рассуждениям, в формулах (7) и (8)
заменим затравку  на ее плоские укладки на ее плоские укладки
 и и 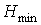 , соответственно, и получим, что число внутренних вершин , соответственно, и получим, что число внутренних вершин  предфрактального
графа предфрактального
графа  ограничивается
двойным неравенством ограничивается
двойным неравенством 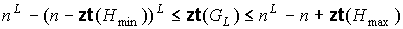 . ◄ . ◄
Для общего случая, когда предфрактальный граф 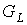 порожден множеством
затравок порожден множеством
затравок  (см. параграф 1)
справедливо (см. параграф 1)
справедливо
Следствие 6.1. Число внутренних вершин  плоского
предфрактального графа плоского
предфрактального графа 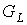 порожденного
множеством порожденного
множеством  произвольно-плоских
затравок ограничено двойным неравенством произвольно-плоских
затравок ограничено двойным неравенством
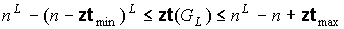 , (9) , (9)
где  и и 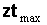 , - соответственно, минимальное и максимальное
числа внутренних вершин среди всех возможных плоских укладок графов из
множества , - соответственно, минимальное и максимальное
числа внутренних вершин среди всех возможных плоских укладок графов из
множества  . .
Левая часть неравенства
(9) достигается, когда плоский предфрактальный граф 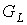 с внутренней укладкой
порождается плоской затравкой с минимальным числом внутренних вершин. Правая
часть (9), в свою очередь, достигается, когда в порождении плоского
предфрактального графа с внешней укладкой участвует только одна плоская
затравка с максимальным числом внутренних вершин из множества с внутренней укладкой
порождается плоской затравкой с минимальным числом внутренних вершин. Правая
часть (9), в свою очередь, достигается, когда в порождении плоского
предфрактального графа с внешней укладкой участвует только одна плоская
затравка с максимальным числом внутренних вершин из множества  . .
В этом параграфе будут приведены оценки для
некоторых характеристик, которые представляют ту или иную меру непланарности
предфрактальных графов.
Одной из самых наглядных характеристик
непланарных графов является искаженность графа [7]. Искаженностью  графа графа 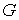 называется наименьшее
число ребер, удаление которых из называется наименьшее
число ребер, удаление которых из 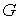 приводит к планарному графу. приводит к планарному графу.
Рассмотрим произвольный граф 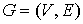 , выделим на нем множество ребер , выделим на нем множество ребер 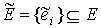 , ,  , удаление которых приводит к планарному графу , удаление которых приводит к планарному графу  . Множество . Множество  будем называть множеством искажения графа будем называть множеством искажения графа 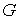 . .
Граф  , без особого труда, можно уложить (вложить [9]) на плоскость
или сферу. Здесь возникает вопрос, на какую поверхность можно уложить сам граф , без особого труда, можно уложить (вложить [9]) на плоскость
или сферу. Здесь возникает вопрос, на какую поверхность можно уложить сам граф 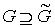 . Утвердительный ответ можно получить сразу, если к сфере, на
которой уложен граф . Утвердительный ответ можно получить сразу, если к сфере, на
которой уложен граф  , добавить , добавить 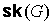 непересекающихся
ручек, и по каждой из которых провести ребро непересекающихся
ручек, и по каждой из которых провести ребро 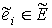 . Таким образом граф . Таким образом граф 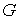 можно уложить на сфере
с можно уложить на сфере
с  ручками. Предположим,
что при укладке графа ручками. Предположим,
что при укладке графа  на сферу с на сферу с 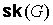 ручками, несколько
ребер из ручками, несколько
ребер из  пройдут по одной
ручке. В этом смысле использование пройдут по одной
ручке. В этом смысле использование  ручек для укладки
на плоскости графа ручек для укладки
на плоскости графа 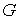 было не оптимальным.
Поэтому целесообразно ввести характеристику, которая качественно иначе отражает
“непланарность” графа было не оптимальным.
Поэтому целесообразно ввести характеристику, которая качественно иначе отражает
“непланарность” графа  . .
Род
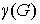 графа графа 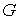 определяется как
наименьшее число ручек, которые необходимо добавить к сфере, чтобы граф определяется как
наименьшее число ручек, которые необходимо добавить к сфере, чтобы граф  можно было бы уложить
на полученной таким образом поверхности. можно было бы уложить
на полученной таким образом поверхности.
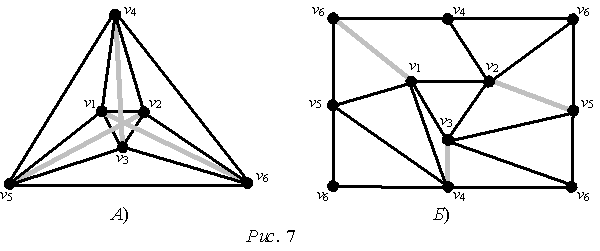
На рис. 7 А
изображен полный шестивершинный граф  . Его искаженность . Его искаженность 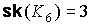 , а род , а род 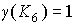 [7]. На рис 7 Б представлена укладка графа [7]. На рис 7 Б представлена укладка графа 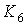 на торе (сфере с
одной ручкой). Укладка изображена в виде прямоугольника с отождествленными
противоположными сторонами. Серым цветом выделено множество искажения. Рис. 7 Б наглядно демонстрирует, как по одной
ручке, добавленной к сфере, проходит несколько ребер из множества искажения графа.
Если быть точным, то по одной ручке на сфере проходят все ребра множества
искажения графа на торе (сфере с
одной ручкой). Укладка изображена в виде прямоугольника с отождествленными
противоположными сторонами. Серым цветом выделено множество искажения. Рис. 7 Б наглядно демонстрирует, как по одной
ручке, добавленной к сфере, проходит несколько ребер из множества искажения графа.
Если быть точным, то по одной ручке на сфере проходят все ребра множества
искажения графа 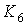 , о чем свидетельствует его род. , о чем свидетельствует его род.
Связь между родом затравки и родом
порожденного ею предфрактального графа устанавливает
Теорема 7. Род  предфрактального
графа предфрактального
графа 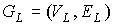 , порожденного затравкой , порожденного затравкой  с сохранением
смежности старых ребер, определяется равенством с сохранением
смежности старых ребер, определяется равенством
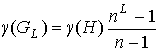 . (10) . (10)
Доказательство. Блоком
[11] графа называется его максимальный не содержащий точек сочленения подграф.
Рассмотрим
предфрактальный граф 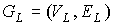 , порожденный затравкой , порожденный затравкой 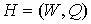 с сохранением
смежности старых ребер. Тогда, как и ранее, предфрактальный граф с сохранением
смежности старых ребер. Тогда, как и ранее, предфрактальный граф 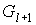 , ,  , из траектории можно получить из графа , из траектории можно получить из графа 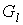 “склеиванием”
(проводя операцию “склеивания”) с затравкой “склеиванием”
(проводя операцию “склеивания”) с затравкой  в каждой его вершине.
Вершины, в которых были проведены склеивания, в соответствии с [12] являются
точками сочленения, поскольку именно в них пересекаются старые ребра
предфрактального графа. Поэтому каждая подграф-затравка в каждой его вершине.
Вершины, в которых были проведены склеивания, в соответствии с [12] являются
точками сочленения, поскольку именно в них пересекаются старые ребра
предфрактального графа. Поэтому каждая подграф-затравка 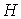 , если она сама не имеет точек сочленения, является блоком
предфрактального графа , если она сама не имеет точек сочленения, является блоком
предфрактального графа 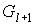 . .
В процессе порождения
предфрактального графа 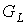 , смежность старых ребер которого не нарушается, было использовано , смежность старых ребер которого не нарушается, было использовано
 затравок затравок 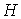 , каждая из которых впоследствии стала блоком графа , каждая из которых впоследствии стала блоком графа 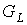 . Это легко подсчитать, если производить переход от . Это легко подсчитать, если производить переход от 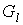 к к 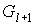 , используя операцию склеивания с затравкой, на всей траектории , используя операцию склеивания с затравкой, на всей траектории
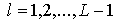 . .
Согласно [11], род графа
равен сумме родов его блоков, поэтому в справедливости формулы (10) можно
убедиться умножив число блоков предфрактального графа 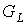 , которое равно , которое равно  , на род , на род 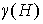 его затравки, не
имеющей точек сочленения. его затравки, не
имеющей точек сочленения.
В случае, когда затравка
 имеет точки
сочленения, а значит и блоки, в процессе порождения предфрактального графа имеет точки
сочленения, а значит и блоки, в процессе порождения предфрактального графа 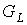 , каждая операция склеивания будет увеличивать род текущего
предфрактального графа в траектории на число , каждая операция склеивания будет увеличивать род текущего
предфрактального графа в траектории на число 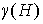 , как и в случае с неразделимой (без точек сочленения)
затравкой. Поэтому (10) верно и для этого случая. ◄ , как и в случае с неразделимой (без точек сочленения)
затравкой. Поэтому (10) верно и для этого случая. ◄
Фактически, род графа
это число ручек, по которым проходит множество искажения, а мощность этого
множества и есть искаженность графа. Для предфрактального графа, смежность
старых ребер которого не нарушается, множество искажения распределено по его
блокам (это показано в доказательстве теоремы 7), поэтому имеет место
Следствие 7.1. Искаженность  предфрактального
графа предфрактального
графа  , порожденного затравкой , порожденного затравкой 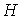 с сохранением
смежности старых ребер, определяется равенством с сохранением
смежности старых ребер, определяется равенством 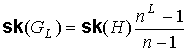 . .
Суть множества искажения непланарного графа - концы каждого ребра из этого множества
являются вершинами, для которых не существует общей грани плоского графа,
полученного из исходного удалением множества искажения. Очевидно, что при
замещении концов любого ребра из множества искажения затравками, их образы
также будут обладать подобным свойством. Т.е ребро, соединяющее образы
замещенных вершин, будет входит в множество искажение полученного графа. А это
значит, что в процессе порождения предфрактального графа (с произвольной
смежностью старых ребер) мощность его множества искажения (или его искаженность)
не убывает. Этот факт отражен в следующих следствиях.
Следствие 7.2. Для рода 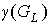 предфрактального графа предфрактального графа
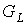 , порожденного затравкой , порожденного затравкой  , справедливо неравенство , справедливо неравенство 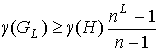 . .
Следствие 7.3. Для искаженности 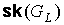 предфрактального
графа предфрактального
графа 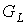 , порожденного затравкой , порожденного затравкой 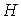 , справедливо неравенство , справедливо неравенство 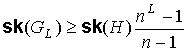 . .
При более широком рассмотрении, когда
предфрактальный граф 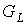 , порожден множеством затравок , порожден множеством затравок  (см. параграф 1), для
характеристик непланарности, исследуемых в настоящем параграфе, очевидны
следующие следствия. (см. параграф 1), для
характеристик непланарности, исследуемых в настоящем параграфе, очевидны
следующие следствия.
Следствие 7.4. Род 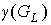 предфрактального
графа предфрактального
графа 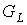 , порожденного множеством затравок , порожденного множеством затравок  ограничивается
неравенством ограничивается
неравенством  , если смежность старых ребер не нарушается и
неравенством , если смежность старых ребер не нарушается и
неравенством 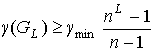 - в противном случае. Где - в противном случае. Где 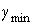 и и 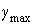 , соответственно наименьший и наибольший род среди всех
графов из множества , соответственно наименьший и наибольший род среди всех
графов из множества  . .
Следствие 7.5. Искаженность 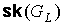 предфрактального
графа предфрактального
графа 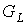 , порожденного множеством затравок , порожденного множеством затравок  ограничивается
неравенством ограничивается
неравенством  , если смежность старых ребер не нарушается и
неравенством , если смежность старых ребер не нарушается и
неравенством  - в противном случае. Где - в противном случае. Где  и и 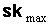 , соответственно наименьшая и наибольшая искаженность среди
всех графов из множества , соответственно наименьшая и наибольшая искаженность среди
всех графов из множества  . .
Для визуализации (изображения на плоскости)
планарных и непланарных графов используются различные методы. Изображение на
плоскости непланарных графов обычно требует оптимизации по ряду критериев [3].
Это связанно с наличием у непланарных графов множества искажения – ребер,
которые обязательно пересекаются с другими ребрами в точках плоскости отличных
от вершин графа. Чрезмерная насыщенность изображения графа такими пересечениями
(их называют скрещиваниями [7]) отрицательно сказывается на восприятии изображения.
Критериев, по которым оптимизируется изображение непланарного графа - много, среди них существуют и чисто
эстетические [3]. В любом случае, произвести автоматизированное изображение
непланарных графов на плоскости существенно сложнее, чем планарных. В такой
ситуации важно знать какой граф нам предстоит визуализировать – планарный или непланарный.
В параграфе 3 предложен критерий планарности
(теорема 3) предфрактального графа. Вообще говоря, не отрицается возможность
существования и других критериев. Основываясь на теореме 3, чтобы убедиться в
планарности предфрактального графа, смежность старых ребер которого не
нарушена, достаточно убедиться в планарности его затравки (затравок). А это
можно сделать любым из известных алгоритмов проверки планарности [3]. Они
позволяют проверять планарность графа за линейное время 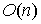 . Важно, что . Важно, что 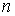 – число вершин
затравки, а не всего предфрактального графа. Число вершин предфрактального
графа – число вершин
затравки, а не всего предфрактального графа. Число вершин предфрактального
графа 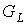 равно равно 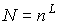 [6]. Поэтому, ввиду
того, что алгоритм обрабатывает всего лишь часть предфрактального графа – его
затравку, а не весь предфрактальный граф, можно говорить об существенном
улучшении эффективности линейного алгоритма проверки планарности предфрактального
графа. [6]. Поэтому, ввиду
того, что алгоритм обрабатывает всего лишь часть предфрактального графа – его
затравку, а не весь предфрактальный граф, можно говорить об существенном
улучшении эффективности линейного алгоритма проверки планарности предфрактального
графа.
После того, как получен утвердительный ответ
на вопрос о планарности предфрактального графа можно переходить непосредственно
к его визуализации, в нашем случае – к изображению предфрактального графа на
плоскости. Изображение графа, в первую очередь, подразумевает разработку
алгоритма укладки графа на плоскости, а потом привязку полученной плоской
укладки к координатной сетке на плоскости.
Фактически, в качестве алгоритма укладки
планарного предфрактального графа на плоскости можно использовать
доказательство теоремы 3 (критерия планарности предфрактального графа). Следуя
доказательству, на первом шаге, необходимо получить плоскую укладку затравки,
для этого можно использовать любой из известных алгоритмов, к примеру алгоритм
предложенный в книге [7]. А на втором шаге, используя операцию склеивания
плоских графов, склеить последовательно требуемое количество затравок.
Количество склеиваемых затравок равно числу проведенных операций ЗВЗ в процессе
порождения предфрактального графа. Во избежание скрещиваний, при склеивании затравки
с текущим графом, надо располагать все вершины и ребра затравки в одной из
граней склеиваемой вершины (см. параграф 3).
Ученые – синергетики часто говорят о “целом” и
его “частях”, иногда только на интуитивном уровне определяя эти важные понятия.
А это с точки зрения математики, не всегда удачный подход, тем более когда
ставится задача исследовать свойства, которые есть у “целого” и не наблюдаются
у его “частей”, или наоборот. К примеру, если моделью какой-либо структуры или
системы является граф, скажем большая периодическая решетка, то нам всегда
удастся выделить на нем “части”, его подграфы, не обладающие свойствами
периодической решетки. Этот пример наглядно подтверждает необходимость
приведения точных определений “целого” и его “частей” касательно конкретно
взятой системы или структуры.
В качестве “частей”фрактального
(предфрактального) графа можно рассматривать его подграф-затравки или, в
зависимости от постановки задачи, блоки различных рангов. Строгое определение
“части” фрактального графа позволило установить связь между свойствами затравки
и всего фрактального графа. Причем установлены правила соединения
подграф-затравок старыми ребрами, при соблюдении которых можно говорить о
наличии (или об отсутствии) у фрактальных (предфрактальных) графов тех или иных
свойств. Анализ состояния всей структуры только по ее отдельным “частям”
существенно снижает трудоемкость решения “больших” задач, и возможно, станет
одним из принципов нелинейной динамики, которые лягут в основу концепции
мягкого моделирования [13].
Подводя итоги, признаем что, проведенное
исследование не претендует на полноту охвата всех топологических свойств
фрактальных (предфрактальных) графов. Поэтому очертим круг исследований по
данной тематике, проводимых в настоящее время и планируемых провести в будущем.
-
Получить
критерий планарности для фрактального (предфрактального) графа, смежность
старых ребер которого не сохраняется.
-
Изучить вопрос
эквивалентности плоских укладок предфрактального графа и подсчитать число
всевозможных неэквивалентных укладок предфрактального графа.
-
Уточнить связь
для искаженности и рода затравки и всего предфрактального графа в случае
произвольной смежности старых ребер.
-
Установить связь
для толщины [11], крупности [11] и числа скрещиваний [11] затравки и всего
предфрактального графа.
-
Разработать
параллельные алгоритмы [3] визуализации фрактальных (предфрактальных) графов.
-
Рассмотреть
вопрос гомеоморфизма предфрактальных графов.
Считаем приятным долгом выразить свою признательность
профессору Малинецкому Г.Г. за неоценимую помощь и поддержку при
выполнении этой и многих других работ.
1.
Басакер Р., Саати Т., Конечные графы и сети. – М.: Наука, 1974.
2.
Райншке К., Ушаков И.А., Оценка надежности систем с использованием графов. –
М.: Радио и связь, 1988.
3.
Евстигнеев В.А., Касьянов В.Н. Графы в программировании: обработка,
визуализация и применение. – СПб.: БХВ-Петербург, 2003.
4.
Archcheacon D., Topological graph theory: a
survey. Congressus Numerantium, 115, 1996, pp. 5 – 54.
5.
Munzler T. Interactive visualization of
large graphs and networks. PhD dissertation, Stanford University, 2000.
6.
Кочкаров А.М. Распознавание фрактальных графов. Алгоритмический
подход. - Нижний Архыз: РАН САО, 1998.
7.
Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич
Р.И. Лекции по теории графов.
- М.: Наука, 1990.
8.
Оре О. Теория
графов. - М.: Наука, 1980.
9.
Дистель Р. Теория графов. – Новосибирск: Изд-во Ин-та математики, 2002.
10.
Асанов М.О., Баранский В.А., Расин В.В. Дискретная математика: графы, матроиды, алгоритмы.
- Ижевск: НИЦ
“РХД”, 2001.
11.
Харари Ф. Теория графов. – М.: Мир, 1973.
12.
Кочкаров А.А., Кочкаров Р.А. Предфрактальные графы в проектировании и анализе
сложных структур. Препринт ИПМ им. М.В. Келдыша РАН, №10, 2003.
13.
Малинецкий Г.Г., Кульба В.В. и др. Управление
риском. – М.: Наука. 2000.
|
![]() . Его искаженность
. Его искаженность ![]() , а род
, а род ![]() [7]. На рис 7 Б представлена укладка графа
[7]. На рис 7 Б представлена укладка графа ![]() на торе (сфере с
одной ручкой). Укладка изображена в виде прямоугольника с отождествленными
противоположными сторонами. Серым цветом выделено множество искажения. Рис. 7 Б наглядно демонстрирует, как по одной
ручке, добавленной к сфере, проходит несколько ребер из множества искажения графа.
Если быть точным, то по одной ручке на сфере проходят все ребра множества
искажения графа
на торе (сфере с
одной ручкой). Укладка изображена в виде прямоугольника с отождествленными
противоположными сторонами. Серым цветом выделено множество искажения. Рис. 7 Б наглядно демонстрирует, как по одной
ручке, добавленной к сфере, проходит несколько ребер из множества искажения графа.
Если быть точным, то по одной ручке на сфере проходят все ребра множества
искажения графа ![]() , о чем свидетельствует его род.
, о чем свидетельствует его род.![]() предфрактального
графа
предфрактального
графа ![]() , порожденного затравкой
, порожденного затравкой ![]() с сохранением
смежности старых ребер, определяется равенством
с сохранением
смежности старых ребер, определяется равенством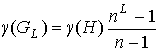 . (10)
. (10)![]() , порожденный затравкой
, порожденный затравкой ![]() с сохранением
смежности старых ребер. Тогда, как и ранее, предфрактальный граф
с сохранением
смежности старых ребер. Тогда, как и ранее, предфрактальный граф ![]() ,
, ![]() , из траектории можно получить из графа
, из траектории можно получить из графа ![]() “склеиванием”
(проводя операцию “склеивания”) с затравкой
“склеиванием”
(проводя операцию “склеивания”) с затравкой ![]() в каждой его вершине.
Вершины, в которых были проведены склеивания, в соответствии с [12] являются
точками сочленения, поскольку именно в них пересекаются старые ребра
предфрактального графа. Поэтому каждая подграф-затравка
в каждой его вершине.
Вершины, в которых были проведены склеивания, в соответствии с [12] являются
точками сочленения, поскольку именно в них пересекаются старые ребра
предфрактального графа. Поэтому каждая подграф-затравка ![]() , если она сама не имеет точек сочленения, является блоком
предфрактального графа
, если она сама не имеет точек сочленения, является блоком
предфрактального графа ![]() .
.![]() , смежность старых ребер которого не нарушается, было использовано
, смежность старых ребер которого не нарушается, было использовано
 затравок
затравок ![]() , каждая из которых впоследствии стала блоком графа
, каждая из которых впоследствии стала блоком графа ![]() . Это легко подсчитать, если производить переход от
. Это легко подсчитать, если производить переход от ![]() к
к ![]() , используя операцию склеивания с затравкой, на всей траектории
, используя операцию склеивания с затравкой, на всей траектории
![]() .
.![]() , которое равно
, которое равно  , на род
, на род ![]() его затравки, не
имеющей точек сочленения.
его затравки, не
имеющей точек сочленения.![]() имеет точки
сочленения, а значит и блоки, в процессе порождения предфрактального графа
имеет точки
сочленения, а значит и блоки, в процессе порождения предфрактального графа ![]() , каждая операция склеивания будет увеличивать род текущего
предфрактального графа в траектории на число
, каждая операция склеивания будет увеличивать род текущего
предфрактального графа в траектории на число ![]() , как и в случае с неразделимой (без точек сочленения)
затравкой. Поэтому (10) верно и для этого случая. ◄
, как и в случае с неразделимой (без точек сочленения)
затравкой. Поэтому (10) верно и для этого случая. ◄![]() предфрактального
графа
предфрактального
графа ![]() , порожденного затравкой
, порожденного затравкой ![]() с сохранением
смежности старых ребер, определяется равенством
с сохранением
смежности старых ребер, определяется равенством 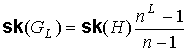 .
.![]() предфрактального графа
предфрактального графа
![]() , порожденного затравкой
, порожденного затравкой ![]() , справедливо неравенство
, справедливо неравенство 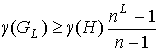 .
.![]() предфрактального
графа
предфрактального
графа ![]() , порожденного затравкой
, порожденного затравкой ![]() , справедливо неравенство
, справедливо неравенство 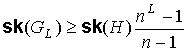 .
.![]() , порожден множеством затравок
, порожден множеством затравок ![]() (см. параграф 1), для
характеристик непланарности, исследуемых в настоящем параграфе, очевидны
следующие следствия.
(см. параграф 1), для
характеристик непланарности, исследуемых в настоящем параграфе, очевидны
следующие следствия.![]() предфрактального
графа
предфрактального
графа ![]() , порожденного множеством затравок
, порожденного множеством затравок ![]() ограничивается
неравенством
ограничивается
неравенством  , если смежность старых ребер не нарушается и
неравенством
, если смежность старых ребер не нарушается и
неравенством 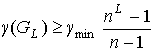 - в противном случае. Где
- в противном случае. Где ![]() и
и ![]() , соответственно наименьший и наибольший род среди всех
графов из множества
, соответственно наименьший и наибольший род среди всех
графов из множества ![]() .
.![]() предфрактального
графа
предфрактального
графа ![]() , порожденного множеством затравок
, порожденного множеством затравок ![]() ограничивается
неравенством
ограничивается
неравенством  , если смежность старых ребер не нарушается и
неравенством
, если смежность старых ребер не нарушается и
неравенством  - в противном случае. Где
- в противном случае. Где ![]() и
и ![]() , соответственно наименьшая и наибольшая искаженность среди
всех графов из множества
, соответственно наименьшая и наибольшая искаженность среди
всех графов из множества ![]() .
.![]() . Важно, что
. Важно, что ![]() – число вершин
затравки, а не всего предфрактального графа. Число вершин предфрактального
графа
– число вершин
затравки, а не всего предфрактального графа. Число вершин предфрактального
графа ![]() равно
равно ![]() [6]. Поэтому, ввиду
того, что алгоритм обрабатывает всего лишь часть предфрактального графа – его
затравку, а не весь предфрактальный граф, можно говорить об существенном
улучшении эффективности линейного алгоритма проверки планарности предфрактального
графа.
[6]. Поэтому, ввиду
того, что алгоритм обрабатывает всего лишь часть предфрактального графа – его
затравку, а не весь предфрактальный граф, можно говорить об существенном
улучшении эффективности линейного алгоритма проверки планарности предфрактального
графа.


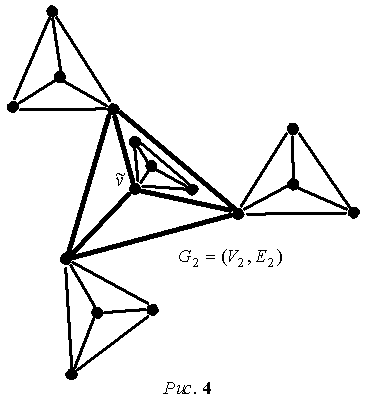

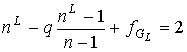 ,
,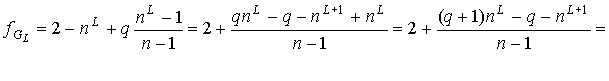
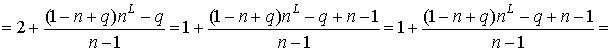
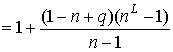 , а т.к.
, а т.к.  .
.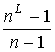

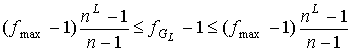 .
.