Параллельные алгоритмы на предфрактальных графах
|
|
Алгоритм |
|
Вход: взвешенный
предфрактальный граф Выход: ОДМВ 1. Назначим каждый из 2.
Одновременно 3.
На выходе шага 2 получаем множество из |
|
Процедура Prim. Вход: взвешенный граф Выход: ОДМВ |
Для
обоснования алгоритма ![]() будем использовать
будем использовать
Утверждение
1. Всякий предфрактальный граф ![]() можно представить в
виде множества подграф-затравок
можно представить в
виде множества подграф-затравок ![]() , соединенных старыми ребрами разных рангов. А именно, старые
ребра
, соединенных старыми ребрами разных рангов. А именно, старые
ребра ![]() -го ранга объединяют множество подграф-затравок в множество
блоков
-го ранга объединяют множество подграф-затравок в множество
блоков ![]() второго ранга, их в
свою очередь, старые ребра
второго ранга, их в
свою очередь, старые ребра ![]() -го ранга объединяют в множество блоков
-го ранга объединяют в множество блоков ![]() третьего ранга и т.д.
Окончательно, старые ребра первого ранга объединяют множество
третьего ранга и т.д.
Окончательно, старые ребра первого ранга объединяют множество ![]() блоков
блоков ![]() -го ранга в связный предфрактальный граф
-го ранга в связный предфрактальный граф ![]() .
.
Теорема
1. Для предфрактального графа ![]() всякий его связный
остовный подграф
всякий его связный
остовный подграф ![]() удовлетворяет двум
условиям:
удовлетворяет двум
условиям:
1. В множество ребер ![]() входит хотя бы одно
ребро каждого ранга.
входит хотя бы одно
ребро каждого ранга.
2. Старые ребра ![]() ранга
ранга ![]() ,
, ![]() , имеющие общую вершину-прообраз, на графе
, имеющие общую вершину-прообраз, на графе ![]() из траектории,
образуют связный подграф.
из траектории,
образуют связный подграф.
Доказательство.
Первая часть теоремы целиком вытекает из утверждения 1.
Действительно, если на подграфе ![]() будут отсутствовать
все ребра какого-либо ранга, то он не будет связным. Вторую часть теоремы докажем
от противного. Предположим, что некоторое множество ребер
будут отсутствовать
все ребра какого-либо ранга, то он не будет связным. Вторую часть теоремы докажем
от противного. Предположим, что некоторое множество ребер ![]() , имеющих общую вершину-прообраз не образует на
предфрактальном графе
, имеющих общую вершину-прообраз не образует на
предфрактальном графе ![]() ,
, ![]() , связный подграф. Это значит, что среди образов концов ребер
, связный подграф. Это значит, что среди образов концов ребер
![]() на графе
на графе ![]() найдутся такие, что
ни одна из цепей их соединяющих не войдет в остовый подграф
найдутся такие, что
ни одна из цепей их соединяющих не войдет в остовый подграф ![]() , что противоречит условию связности этого подграфа. ◄[1]
, что противоречит условию связности этого подграфа. ◄[1]
Теорема
2. Параллельный алгоритм ![]() строит на предфрактальном графе
строит на предфрактальном графе ![]() ОДМВ
ОДМВ ![]() .
.
Доказательство.
Алгоритм ![]() на предфрактальном
графе
на предфрактальном
графе ![]() выделяет
выделяет ![]() ОДМВ
ОДМВ ![]() . Докажем, что множество
. Докажем, что множество ![]() образует ОДМВ предфрактального
графа
образует ОДМВ предфрактального
графа ![]() . ОДМВ
. ОДМВ ![]() ,
, ![]() , выделенные на подграф-затравках
, выделенные на подграф-затравках ![]() , образуют остовный лес, состоящий из
, образуют остовный лес, состоящий из ![]() связных компонент.
Связные компоненты, в данном случае, это ОДМВ выделенные на блоках
связных компонент.
Связные компоненты, в данном случае, это ОДМВ выделенные на блоках ![]() . Согласно правилу взвешивания предфрактального графа, ребра
принадлежащие блокам первого ранга имеют наименьшие веса по сравнению с ребрами
других рангов. Поэтому выделение ОДМВ на подграф-затравках
. Согласно правилу взвешивания предфрактального графа, ребра
принадлежащие блокам первого ранга имеют наименьшие веса по сравнению с ребрами
других рангов. Поэтому выделение ОДМВ на подграф-затравках ![]() необходимо для
получения ОДМВ предфрактального графа
необходимо для
получения ОДМВ предфрактального графа ![]() .
.
Далее ОДМВ ![]() выделенные на
подграф-затравках
выделенные на
подграф-затравках ![]() , в соответствии с утверждением 1, образуют
, в соответствии с утверждением 1, образуют ![]() связных компонент.
Каждая компонента будет представлять собой ОДМВ блоков
связных компонент.
Каждая компонента будет представлять собой ОДМВ блоков ![]() . Продолжая данную линию рассуждений получим, что ОДМВ
выделенные на подграф-затравках
. Продолжая данную линию рассуждений получим, что ОДМВ
выделенные на подграф-затравках ![]() в совокупности с
раннее найденными ОДМВ образуют
в совокупности с
раннее найденными ОДМВ образуют ![]() связных компонент.
Каждая компонента будет представлять ОДМВ блока
связных компонент.
Каждая компонента будет представлять ОДМВ блока ![]() . И, наконец, ОДМВ подграф-затравки
. И, наконец, ОДМВ подграф-затравки ![]() связывает
связывает ![]() компонент в одну
связную компоненту. Полученный связный остовный подграф, в силу добавления
деревьев минимального веса, будет представлять ОДМВ предфрактального графа
компонент в одну
связную компоненту. Полученный связный остовный подграф, в силу добавления
деревьев минимального веса, будет представлять ОДМВ предфрактального графа ![]() . ◄
. ◄
Теорема
3. Время исполнения алгоритма ![]() на предфрактальном графе
на предфрактальном графе
![]() ,
, ![]() при использовании
при использовании 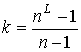 процессоров, равно
процессоров, равно ![]() .
.
Доказательство.
Основой алгоритма является шаг 2, с ним и связано затрата
времени на исполнение. Остальные шаги производят простые операции и
инициализацию переменных. Алгоритм ![]() выполняет шаг 2
параллельно, каждым из
выполняет шаг 2
параллельно, каждым из ![]() процессоров. Для
выполнения шага 2 потребуется
процессоров. Для
выполнения шага 2 потребуется ![]() времени (столько
времени [20] требует процедура Prim для обработки подграф-затравки). Так как это верхняя оценка в
наихудшем случае, тогда будем считать что все
времени (столько
времени [20] требует процедура Prim для обработки подграф-затравки). Так как это верхняя оценка в
наихудшем случае, тогда будем считать что все ![]() процессоров закончат
свою работу – выполнение шага 2 – одновременно, за время
процессоров закончат
свою работу – выполнение шага 2 – одновременно, за время ![]() . Тогда алгоритм
. Тогда алгоритм ![]() исполняется за время
исполняется за время
![]() . ◄
. ◄
Отметим, что ![]() определяет
размерность задачи поиска ОДМВ на подграф-затравке, в то время как размерность
задачи поиска ОДМВ на предфрактальном графе
определяет
размерность задачи поиска ОДМВ на подграф-затравке, в то время как размерность
задачи поиска ОДМВ на предфрактальном графе ![]() равна
равна ![]() ,
, ![]() . Таким образом время исполнения алгоритма
. Таким образом время исполнения алгоритма ![]() равно времени
затрачиваемому на поиск ОДМВ на подграф-затравке.
равно времени
затрачиваемому на поиск ОДМВ на подграф-затравке.
Время исполнения последовательного
алгоритма Прима на предфрактальном графе ![]() ,
, ![]() равно
равно ![]() . Сравнив последовательный алгоритм Прима с параллельным
алгоритмом
. Сравнив последовательный алгоритм Прима с параллельным
алгоритмом ![]() , получаем что время исполнения алгоритма
, получаем что время исполнения алгоритма ![]() меньше на порядок:
меньше на порядок: ![]() .
.
Следствие
3.1. Ускорение параллельного алгоритма ![]() на предфрактальном графе
на предфрактальном графе
![]() ,
, ![]() при использовании
при использовании ![]() процессоров,
процессоров, 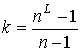 , от последовательного алгоритма Прима равно
, от последовательного алгоритма Прима равно ![]() .
.
Теорема
4. Вычислительная
сложность алгоритма ![]() на предфрактальном графе
на предфрактальном графе
![]() ,
, ![]() равна
равна ![]() .
.
Доказательство.
Алгоритм ![]() представляет собой,
по существу многократное выполнение шага 2. Шаг 2 потребует выполнения
представляет собой,
по существу многократное выполнение шага 2. Шаг 2 потребует выполнения ![]() операций на каждой
подграф-затравке (столько операций требует процедура Прима). В сумме будет
выполнено
операций на каждой
подграф-затравке (столько операций требует процедура Прима). В сумме будет
выполнено ![]() операций,
операций, 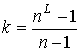 . ◄
. ◄
Тогда, 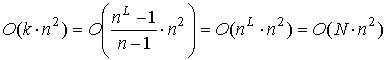 . Отсюда вычислительная сложность алгоритма
. Отсюда вычислительная сложность алгоритма ![]() равна
равна ![]() .
.
Вычислительная сложность алгоритма Прима
равна ![]() . Сравнив ее с вычислительной сложностью алгоритма
. Сравнив ее с вычислительной сложностью алгоритма ![]() , получаем:
, получаем: ![]() .
.
Следствие
4.1. Вычислительная сложность алгоритма ![]() меньше вычислительной
сложности алгоритма Прима в
меньше вычислительной
сложности алгоритма Прима в ![]() раз.
раз.
4. Параллельный алгоритм поиска совершенного паросочетания
Алгоритм ![]() производит поиск
совершенного паросочетания [19] на заданном предфрактальном графе. Рассмотрим
взвешенный предфрактальный граф
производит поиск
совершенного паросочетания [19] на заданном предфрактальном графе. Рассмотрим
взвешенный предфрактальный граф ![]() и траекторию
и траекторию ![]() ,
, ![]() . Алгоритм использует k
процессоров
. Алгоритм использует k
процессоров ![]() . Где
. Где ![]() может варьировать в
промежутке от одного до
может варьировать в
промежутке от одного до ![]() . Назначим каждый процессор одной из подграф-затравок
. Назначим каждый процессор одной из подграф-затравок ![]() ,
, ![]() .
.
Теорема
5. Предфрактальный граф ![]() , порожденный затравкой
, порожденный затравкой ![]() , имеет совершенное паросочетание, если затравка
, имеет совершенное паросочетание, если затравка ![]() имеет совершенное
паросочетание.
имеет совершенное
паросочетание.
Основная идея алгоритма заключается в
том, что каждая подграф-затравка рассматривается как отдельно взятый граф. При
этом каждый из ![]() процессоров
параллельно независимо друг от друга находит совершенные паросочетания на своей
подграф-затравке
процессоров
параллельно независимо друг от друга находит совершенные паросочетания на своей
подграф-затравке ![]() . Поиск совершенного паросочетания подграф-затравки
осуществляется с помощью алгоритма Эдмондса [19]. Алгоритм Эдмондса оформлен в
виде процедуры и используется по мере необходимости. В результате нахождения
совершенных паросочетаний всех подграф-затравок
. Поиск совершенного паросочетания подграф-затравки
осуществляется с помощью алгоритма Эдмондса [19]. Алгоритм Эдмондса оформлен в
виде процедуры и используется по мере необходимости. В результате нахождения
совершенных паросочетаний всех подграф-затравок ![]() , получаем совершенное паросочетание предфрактального графа
, получаем совершенное паросочетание предфрактального графа ![]() . ◄
. ◄
Для
достижения максимальной эффективности алгоритма ![]() предположим, что
число процессоров равно количеству подграф-затравок
предположим, что
число процессоров равно количеству подграф-затравок ![]() , то есть
, то есть ![]() .
.
|
Алгоритм |
|
Вход: предфрактальный граф Выход: совершенное
паросочетание 1. Назначим каждый из 2.
Одновременно 3.
На выходе шага 2 получаем множество |
|
Процедура Edmonds. Вход: граф Выход: совершенное
паросочетание |
Теорема 6. Параллельный алгоритм ![]() строит на
предфрактальном графе
строит на
предфрактальном графе ![]() совершенное
паросочетание
совершенное
паросочетание ![]() .
.
Доказательство.
На последнем шаге ![]() порождения
предфрактального графа
порождения
предфрактального графа ![]() все вершины
замещаются затравкой
все вершины
замещаются затравкой ![]() . Совершенное паросочетание
. Совершенное паросочетание ![]() подграф-затравки
подграф-затравки ![]() ,
, ![]() , покроет все вершины принадлежащие данной подграф-затравке.
Так как множество вершин графа
, покроет все вершины принадлежащие данной подграф-затравке.
Так как множество вершин графа ![]() можно представить в
виде совокупности вершин подграф-затравок
можно представить в
виде совокупности вершин подграф-затравок ![]() , то покрыв совершенными паросочетаниями все
подграф-затравки, получим покрытие всего множества вершин
, то покрыв совершенными паросочетаниями все
подграф-затравки, получим покрытие всего множества вершин ![]() . Совершенные паросочетания подграф-затравок
. Совершенные паросочетания подграф-затравок ![]() , при этом состоят только из новых ребер и в совокупности
образуют совершенное паросочетание предфрактального графа
, при этом состоят только из новых ребер и в совокупности
образуют совершенное паросочетание предфрактального графа ![]() . ◄
. ◄
Теорема
7. Время исполнения алгоритма ![]() на предфрактальном графе
на предфрактальном графе
![]() ,
, ![]() при использовании
при использовании ![]() процессоров, равно
процессоров, равно ![]() .
.
Доказательство.
Основой алгоритма является шаг 2, с ним и связано затрата
времени на исполнение. Остальные шаги производят простые операции и
инициализацию переменных. Алгоритм ![]() выполняет шаг 2
параллельно, каждым из
выполняет шаг 2
параллельно, каждым из ![]() процессоров. Для
выполнения шага 2 потребуется
процессоров. Для
выполнения шага 2 потребуется ![]() времени (столько времени [20] требует процедура Edmonds для обработки
подграф-затравки). Так как это верхняя оценка в наихудшем случае, тогда будем
считать что все
времени (столько времени [20] требует процедура Edmonds для обработки
подграф-затравки). Так как это верхняя оценка в наихудшем случае, тогда будем
считать что все ![]() процессоров закончат
свою работу – выполнение шага 2 – одновременно, за время
процессоров закончат
свою работу – выполнение шага 2 – одновременно, за время ![]() . Тогда алгоритм
. Тогда алгоритм ![]() исполняется за время
исполняется за время
![]() . ◄
. ◄
Время исполнения последовательного
алгоритма Эдмондса на предфрактальном графе ![]() ,
, ![]() равно
равно ![]() . Сравнив последовательный алгоритм Эдмондса с параллельным
алгоритмом
. Сравнив последовательный алгоритм Эдмондса с параллельным
алгоритмом ![]() , получаем что время исполнения алгоритма
, получаем что время исполнения алгоритма ![]() меньше на два
порядка:
меньше на два
порядка: ![]() .
.
Следствие
7.1. Ускорение параллельного алгоритма ![]() на предфрактальном графе
на предфрактальном графе
![]() ,
, ![]() при использовании
при использовании ![]() процессоров,
процессоров, ![]() , от последовательного алгоритма Эдмондса равно
, от последовательного алгоритма Эдмондса равно ![]() .
.
Теорема
8. Вычислительная
сложность алгоритма ![]() на предфрактальном графе
на предфрактальном графе
![]() ,
, ![]() равна
равна ![]() .
.
Доказательство.
Алгоритм ![]() представляет собой,
по существу многократное выполнение шага 2. Шаг 2 потребует выполнения
представляет собой,
по существу многократное выполнение шага 2. Шаг 2 потребует выполнения ![]() операций на каждой подграф-затравке (столько операций требует
процедура Edmonds). В сумме будет выполнено
операций на каждой подграф-затравке (столько операций требует
процедура Edmonds). В сумме будет выполнено ![]() операций,
операций, ![]() . ◄
. ◄
Тогда, ![]() . Отсюда, вычислительная сложность алгоритма
. Отсюда, вычислительная сложность алгоритма ![]() равна
равна ![]() .
.
Вычислительная сложность алгоритма
Эдмондса равна ![]() . Сравнив ее с вычислительной сложностью алгоритма
. Сравнив ее с вычислительной сложностью алгоритма ![]() , получаем:
, получаем: ![]() .
.
Следствие
8.1. Вычислительная сложность алгоритма ![]() меньше вычислительной
сложности алгоритма Эдмондса в
меньше вычислительной
сложности алгоритма Эдмондса в ![]() раз.
раз.
5. Параллельный алгоритм поиска эйлеровой цепи
Для поиска эйлеровой цепи [19]
предфрактального графа предложим алгоритм ![]() . Рассмотрим предфрактальный граф
. Рассмотрим предфрактальный граф ![]() и его траекторию
и его траекторию ![]() ,
, ![]() . Алгоритм использует k
процессоров
. Алгоритм использует k
процессоров ![]() . Число процессоров
не обязано соответствовать количеству входных записей, а может варьировать в
промежутке от одного до
. Число процессоров
не обязано соответствовать количеству входных записей, а может варьировать в
промежутке от одного до 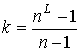 . Назначим каждый процессор одной из подграф-затравок
. Назначим каждый процессор одной из подграф-затравок ![]() ,
, ![]() ,
, ![]() .
.
Утверждение
2. Для того чтобы на предфрактальном графе ![]() существовала эйлерова
цепь, достаточно выполнение следующих условий:
существовала эйлерова
цепь, достаточно выполнение следующих условий:
1. Смежность старых ребер
предфрактального графа ![]() сохраняется.
сохраняется.
2. На затравке ![]() существует эйлерова
цепь.
существует эйлерова
цепь.
Таким образом, будем предполагать, что алгоритм требует выполнения условий утверждения 2.
Основная идея алгоритма заключается в
следующем. Каждая подграф-затравка ![]() рассматривается как
отдельно взятый граф. При этом каждый из
рассматривается как
отдельно взятый граф. При этом каждый из ![]() процессоров
параллельно независимо друг от друга находит эйлерову цепь на своей
подграф-затравке
процессоров
параллельно независимо друг от друга находит эйлерову цепь на своей
подграф-затравке ![]() . Поиск эйлеровой цепи отдельно взятой подграф-затравки
осуществляется алгоритмом Эйлера [20]. Алгоритм Эйлера используется в алгоритме
. Поиск эйлеровой цепи отдельно взятой подграф-затравки
осуществляется алгоритмом Эйлера [20]. Алгоритм Эйлера используется в алгоритме
![]() в виде процедуры по
мере необходимости. В результате нахождения эйлеровых цепей всех
подграф-затравок
в виде процедуры по
мере необходимости. В результате нахождения эйлеровых цепей всех
подграф-затравок ![]() , получаем эйлерову цепь предфрактального графа
, получаем эйлерову цепь предфрактального графа ![]() .
.
Использование
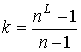 процессоров, равное
числу подграф-затравок позволяет достичь максимальной эффективности алгоритма
процессоров, равное
числу подграф-затравок позволяет достичь максимальной эффективности алгоритма ![]() .
.
|
Алгоритм |
|
Вход: предфрактальный граф Выход: эйлерова цепь
1. Назначим каждый из 2.
Одновременно 3.
На выходе шага 2 получаем множество |
|
Процедура Eiler. Вход: граф Выход: эйлерова цепь
|
Теорема 9. Параллельный алгоритм ![]() строит на
предфрактальном графе
строит на
предфрактальном графе ![]() эйлерову цепь
эйлерову цепь ![]() .
.
Доказательство.
По определению, эйлерова цепь покрывает все ребра графа по
одному разу, при этом любая вершина графа может состоять в цепи сколь угодно
раз. Эйлерова цепь также представляет собой замкнутую цепь. На шаге 2 алгоритма
![]() найдены
найдены ![]() эйлеровых цепей
эйлеровых цепей ![]() . Таким образом на подграф-затравке
. Таким образом на подграф-затравке ![]() найдена эйлерова цепь
найдена эйлерова цепь
![]() . Так как смежность старых ребер предфрактального графа
. Так как смежность старых ребер предфрактального графа ![]() сохраняется, к
эйлеровой цепи
сохраняется, к
эйлеровой цепи ![]() добавляются цепи
добавляются цепи ![]() , выделенные на подграф-затравках
, выделенные на подграф-затравках ![]() . В результате получаем эйлерову цепь
. В результате получаем эйлерову цепь ![]() . Продолжая по данному принципу добавлять эйлеровы цепи
подграф-затравок
. Продолжая по данному принципу добавлять эйлеровы цепи
подграф-затравок ![]() , в итоге получим эйлерову цепь предфрактального графа
, в итоге получим эйлерову цепь предфрактального графа ![]() . ◄
. ◄
Теорема
10. Время исполнения алгоритма ![]() на предфрактальном графе
на предфрактальном графе
![]() ,
, 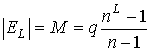 при использовании
при использовании 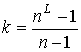 процессоров, равно
процессоров, равно ![]() .
.
Доказательство.
Основой алгоритма является шаг 2, с ним и связано затрата
времени на исполнение. Остальные шаги производят простые операции и
инициализацию переменных. Алгоритм ![]() выполняет шаг 2
параллельно, каждым из
выполняет шаг 2
параллельно, каждым из ![]() процессоров. Для
выполнения шага 2 потребуется
процессоров. Для
выполнения шага 2 потребуется ![]() времени (столько
времени [20] требует процедура Eiler для обработки подграф-затравки). Так как
это верхняя оценка в наихудшем случае, тогда будем считать что все
времени (столько
времени [20] требует процедура Eiler для обработки подграф-затравки). Так как
это верхняя оценка в наихудшем случае, тогда будем считать что все ![]() процессоров закончат
свою работу – выполнение шага 2 – одновременно, за время
процессоров закончат
свою работу – выполнение шага 2 – одновременно, за время ![]() . Тогда алгоритм
. Тогда алгоритм ![]() исполняется за время
исполняется за время
![]() . ◄
. ◄
Отметим, что ![]() определяет
размерность задачи поиска эйлеровой цепи на подграф-затравке, в то время как
размерность задачи поиска эйлеровой цепи на предфрактальном графе
определяет
размерность задачи поиска эйлеровой цепи на подграф-затравке, в то время как
размерность задачи поиска эйлеровой цепи на предфрактальном графе ![]() равна
равна ![]() ,
, ![]() . Таким образом время исполнения алгоритма
. Таким образом время исполнения алгоритма ![]() равно времени
затрачиваемому на поиск эйлеровой цепи на подграф-затравке.
равно времени
затрачиваемому на поиск эйлеровой цепи на подграф-затравке.
Время исполнения последовательного
алгоритма поиска эйлеровой цепи на предфрактальном графе ![]() ,
, ![]() равно
равно ![]() . Сравнив последовательный алгоритм Эйлера с параллельным
алгоритмом
. Сравнив последовательный алгоритм Эйлера с параллельным
алгоритмом ![]() , получаем, что время исполнения алгоритма
, получаем, что время исполнения алгоритма ![]() меньше на порядок:
меньше на порядок: ![]() .
.
Следствие
10.1. Ускорение параллельного алгоритма ![]() на предфрактальном графе
на предфрактальном графе
![]() ,
, ![]() при использовании
при использовании ![]() процессоров,
процессоров, 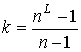 , от последовательного алгоритма Эйлера равно
, от последовательного алгоритма Эйлера равно ![]() .
.
Теорема
11. Вычислительная
сложность алгоритма ![]() на предфрактальном графе
на предфрактальном графе
![]() ,
, ![]() равна
равна ![]() .
.
Доказательство.
Алгоритм ![]() представляет собой,
по существу многократное выполнение шага 2. Шаг 2 потребует выполнения
представляет собой,
по существу многократное выполнение шага 2. Шаг 2 потребует выполнения ![]() операций на каждой
подграф-затравке (столько операций требует процедура Eiler). В сумме будет
выполнено
операций на каждой
подграф-затравке (столько операций требует процедура Eiler). В сумме будет
выполнено ![]() операций,
операций, 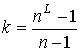 . ◄
. ◄
Тогда, 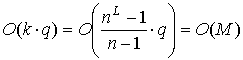 . Вычислительная сложность алгоритма
. Вычислительная сложность алгоритма ![]() равна
равна ![]() .
.
Следствие
11.1. Вычислительная сложность алгоритма ![]() равна вычислительной
сложности алгоритма Эйлера.
равна вычислительной
сложности алгоритма Эйлера.
6. Параллельный алгоритм поиска гамильтонова цикла
Алгоритм ![]() производит поиск
гамильтонова цикла [19] на заданном предфрактальном графе. Опишем принцип
работы алгоритма
производит поиск
гамильтонова цикла [19] на заданном предфрактальном графе. Опишем принцип
работы алгоритма ![]() . Для этого рассмотрим предфрактальный граф
. Для этого рассмотрим предфрактальный граф ![]() и траекторию
и траекторию ![]() ,
, ![]() . Алгоритм использует k
процессоров
. Алгоритм использует k
процессоров ![]() . Где
. Где ![]() может варьировать в
промежутке от одного до
может варьировать в
промежутке от одного до ![]() .
.
Утверждение
3. Для того чтобы на предфрактальном графе ![]() существовал
гамильтонов цикл, достаточно выполнение следующих условий:
существовал
гамильтонов цикл, достаточно выполнение следующих условий:
1. Смежность старых ребер
предфрактального графа ![]() не сохраняется.
не сохраняется.
2. На затравке ![]() существует
гамильтонов цикл.
существует
гамильтонов цикл.
3. Между любой парой вершин затравки ![]() существует
гамильтонова цепь.
существует
гамильтонова цепь.
Таким образом, будем предполагать, что алгоритм требует выполнения условий утверждения 3.
Работа алгоритма начинается с того, что
на подграф-затравке ![]() производится поиск
гамильтонова цикла. Затем на каждой подграф-затравке
производится поиск
гамильтонова цикла. Затем на каждой подграф-затравке ![]() выделяется
гамильтонова цепь между двумя вершинами, которые являются концами ребер,
выделенного на подграф-затравке
выделяется
гамильтонова цепь между двумя вершинами, которые являются концами ребер,
выделенного на подграф-затравке ![]() , гамильтонова цикла. Поиск гамильтоновых цепей на подграф-затравках
, гамильтонова цикла. Поиск гамильтоновых цепей на подграф-затравках
![]() осуществляется
параллельно и независимо
осуществляется
параллельно и независимо ![]() процессорами. На
следующем этапе
процессорами. На
следующем этапе ![]() процессоров также параллельно
и независимо находят гамильтоновы цепи на подграф-затравках
процессоров также параллельно
и независимо находят гамильтоновы цепи на подграф-затравках ![]() . Поиск гамильтоновой цепи на подграф-затравке
. Поиск гамильтоновой цепи на подграф-затравке ![]() осуществляется между
двумя вершинами, которые являются концами гамильтоновой цепи, найденной на
предыдущем этапе. Работа алгоритма продолжается до тех пор, пока на этапе
осуществляется между
двумя вершинами, которые являются концами гамильтоновой цепи, найденной на
предыдущем этапе. Работа алгоритма продолжается до тех пор, пока на этапе ![]() не будут найдены
гамильтоновы цепи подграф-затравок
не будут найдены
гамильтоновы цепи подграф-затравок ![]() . В результате нахождения гамильтоновых цепей всех
подграф-затравок
. В результате нахождения гамильтоновых цепей всех
подграф-затравок ![]() , получаем гамильтонов цикл предфрактального графа
, получаем гамильтонов цикл предфрактального графа ![]() .
.
Основная идея алгоритма заключается в
том, что каждая подграф-затравка рассматривается как отдельно взятый граф. При
этом на ![]() этапах каждый из
этапах каждый из ![]() процессоров
параллельно и независимо друг от друга находит гамильтонову цепь на своей
подграф-затравке
процессоров
параллельно и независимо друг от друга находит гамильтонову цепь на своей
подграф-затравке ![]() . Поиск гамильтоновой цепи подграф-затравки осуществляется с
помощью алгоритма Hamilton [20]. Алгоритм Hamilton оформлен в виде процедуры и используется по мере необходимости.
. Поиск гамильтоновой цепи подграф-затравки осуществляется с
помощью алгоритма Hamilton [20]. Алгоритм Hamilton оформлен в виде процедуры и используется по мере необходимости.
Использование
![]() процессоров, равное
числу подграф-затравок
процессоров, равное
числу подграф-затравок ![]() позволяет достичь
максимальной эффективности алгоритма
позволяет достичь
максимальной эффективности алгоритма ![]() .
.
|
Алгоритм |
|
Вход: предфрактальный граф Выход: гамильтонов
цикл 1. Процессор 2. На данном шаге необходимо выполнить 2.1. Назначим каждый из 2.2. Одновременно 3.
На выходе шага 2 получаем множество гамильтоновых цепей |
|
Процедура Hamilton_Cycle. Вход: граф Выход: гамильтонов
цикл |
|
Процедура Hamilton. Вход: граф Выход: гамильтонова
цепь |
Теорема 12. Параллельный алгоритм ![]() строит на
предфрактальном графе
строит на
предфрактальном графе ![]() гамильтонов цикл
гамильтонов цикл ![]() .
.
Доказательство.
Гамильтонов цикл покрывает все вершины графа строго по
одному разу, а покрытие ребер графа определяется вершинами цикла. На шаге 1
алгоритм ![]() производит поиск
гамильтонова цикла на подграф-затравке
производит поиск
гамильтонова цикла на подграф-затравке ![]() . Затем осуществляется поиск гамильтоновых цепей на
подграф-затравках
. Затем осуществляется поиск гамильтоновых цепей на
подграф-затравках ![]() . Поиск проводится между двумя вершинами подграф-затравки
. Поиск проводится между двумя вершинами подграф-затравки ![]() , которым инцидентны два старых ребра 1-го ранга, входящих в
гамильтонов цикл подграф-затравки
, которым инцидентны два старых ребра 1-го ранга, входящих в
гамильтонов цикл подграф-затравки ![]() . Более простыми словами, на подграф-затравке
. Более простыми словами, на подграф-затравке ![]() находится гамильтонов
цикл, а затем вместо вершин вставляются гамильтоновы цепи соответствующих
подграф-затравок
находится гамильтонов
цикл, а затем вместо вершин вставляются гамильтоновы цепи соответствующих
подграф-затравок ![]() . Таким образом, получаем гамильтонов цикл предфрактального
графа
. Таким образом, получаем гамильтонов цикл предфрактального
графа ![]() . Продолжая по данному принципу добавлять гамильтоновы цепи
подграф-затравок
. Продолжая по данному принципу добавлять гамильтоновы цепи
подграф-затравок ![]() , в итоге получим гамильтонов цикл предфрактального графа
, в итоге получим гамильтонов цикл предфрактального графа ![]() . Так как покрыты все вершины предфрактального графа
. Так как покрыты все вершины предфрактального графа ![]() , тогда найденный гамильтонов цикл является искомым. ◄
, тогда найденный гамильтонов цикл является искомым. ◄
Заключение
В выполненной работе можно выделить несколько важных аспектов.
Во-первых. Вычислительная сложность всех описанных алгоритмов решения теоретико-графовых задач на порядок ниже чем у известных аналогичных алгоритмов.
Во-вторых. Распараллеливание в исследованных задачах является геометрическим. Т.е. входные данные алгоритмов делятся на определенные группы, которые затем обрабатываются на различных процессорах. Входными данными, в нашем случае, являются предфрактальный граф, а группами, соответственно, являются все его подграф-затравки.
В-третьих. Это самый важный аспект. Возможность выделение на предфрактальном графе подграф-затравок, а значит и проведение геометрическое распараллеливания, существует только благодаря свойству самоподобия.
Считаем приятным долгом выразить признательность профессору Малинецкому Г.Г. за неоценимую помощь и поддержку в выполнении работы.
Литература
1. Бандман О.Л. Методы параллельного микропрограммирования. - Новосибирск: Наука, 1981.
2. Горбунова Е.О. Формально-кинетическая модель бесструктурного мелкозернистого параллелизма // Сибирский журнал вычислительной математики. 1999. Т. 2. № 3. С. 239-256.
3. Бандман О.Л. Мелкозернистый параллелизм в вычислительной математике // Программирование. 2001. №4. С. 5-20.
4. Бочаров Н.В. Технологии и техника параллельного программирования // Программирование. 2003. №1. С. 5-23.
5. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002.
6. Кочкаров А.А., Кочкаров Р.А. Предфрактальные графы в проектировании и анализе сложных структур. Препринт ИПМ им. М.В. Келдыша РАН, №10, 2003.
7. Кузюрин Н.Н. Параллельный алгоритм для задачи о балансировке множеств. // Дискретная математика. 1991. Т.3. В.4. С. 153-158.
8. Bader D.A., Illendula A.K., Moret B.M.E., Weisse-Bernstein N.R. Using PRAM algorithms on a uniform-memory-access shared-memory architecture. WAE 2001. LNCS 2141. 2001. P. 129-144.
9. Agbaria A., Ben-Asher Y., Newman I. Communication–processor tradeoffs in a limited resources PRAM. Algorithmica. 2002. № 34. P. 276–297.
10. Макконелл Дж. Анализ алгоритмов. Вводный курс. – М.: Техносфера, 2002.
11.
Metaxas P. Parallel Algorithms for Graph Problems. PhD
dissertation,
Dartmouth College, 1991.
12. Han Y., Pan V.Y., Reif J.H. Efficient parallel algorithms for computing all pair shortest paths in directed graphs. Algorithmica. 1997. № 17. P. 399–415.
13. King V., Poon Ch.K., Ramachandran V., Sinha S. An optimal EREW PRAM algorithm for minimum spanning tree verification. Information Processing Letters. 1997. № 62. P. 153-159.
14. Sajith G., Saxena S. Optimal parallel algorithm for Brook's colouring bounded degree graphs in logarithmic time on EREW PRAM. Discrete Applied Mathimatics. 1996. № 64. P. 249-265.
15. Johnson D.B., Metaxas P. Optimal algorithms for the single and multiple vertex updating problems of a minimum spanning tree. Algorithmica. 1996. № 16. P.633–648.
16. Chen Z.-Z., He X. Parallel algorithms for maximal acyclic sets. Algorithmica. 1997. № 19. P. 354-368.
17. Непомнящая А.Ш. Представление алгоритма Эдмондса для нахождения оптимального ветвления графа на ассоциативном параллельном процессоре // Программирование. 2001. №4. С. 43-52.
18. Кочкаров А.М. Распознавание фрактальных графов. Алгоритмический подход. - Нижний Архыз: РАН САО, 1998.
19. Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. - М.: Наука, 1990.
20. Асанов М.О., Баранский В.А., Расин В.В. Дискретная математика: графы, матроиды, алгоритмы. - Ижевск: НИЦ "РХД", 2001.
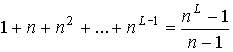 . Тогда мощность множества
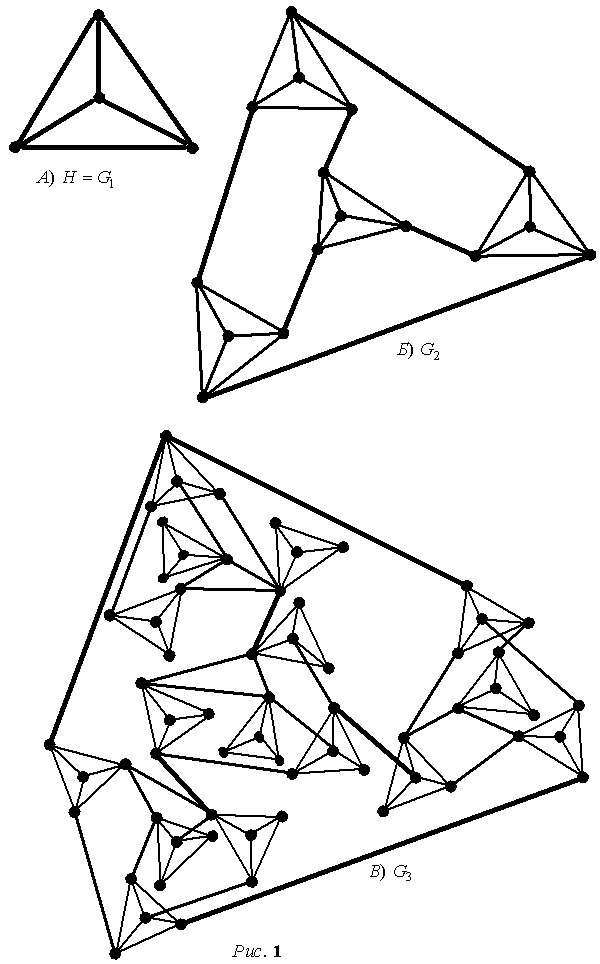
. Тогда мощность множества 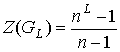 .
.
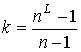 .
.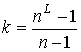
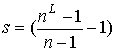 , которое в совокупности с циклом
, которое в совокупности с циклом