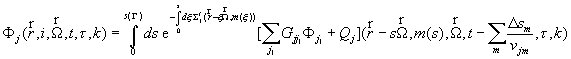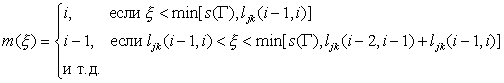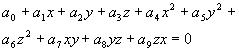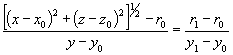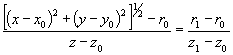PARSE 3.0 – комплекс программ трехмерного расчета переноса нейтральных и заряженных
частиц методом Монте-Карло
|
Вид поверхности
|
Уравнение поверхности |
|
|
Вводимые величины |
|
Поверхность 2го
порядка |
|
j |
0 |
|
|
Плоскость |
|
1 |
1 |
|
|
Плоскость |
|
2 |
2 |
|
|
Плоскость |
|
3 |
3 |
|
|
Плоскость // оси x |
|
3 |
4 |
|
|
Плоскость // оси y |
|
3 |
5 |
|
|
Плоскость // оси z |
|
2 |
6 |
|
|
Конус // оси x |
|
6 |
7 |
|
|
Конус // оси y |
|
6 |
8 |
|
|
Конус // оси z |
|
6 |
9 |
|
|
Цилиндр // оси x |
|
6 |
10 |
|
|
Цилиндр // оси y |
|
6 |
11 |
|
|
Цилиндр // оси z |
|
5 |
12 |
|
|
Эллипсоид |
|
6 |
13 |
|
Напишем основные формулы,
которые используются в комплексе программ при расчетах пересечения линии с
поверхностью. Определим:
![]() - радиус-вектор любой
точки в пространстве,
- радиус-вектор любой
точки в пространстве,
![]() - единичный вектор,
определяющий направление из точки
- единичный вектор,
определяющий направление из точки ![]() ,
,
![]() - направляющие
косинусы относительно осей X, Y, Z соответственно,
- направляющие
косинусы относительно осей X, Y, Z соответственно,
![]() - скалярное
расстояние из точки
- скалярное
расстояние из точки ![]() по направлению
по направлению ![]() ,
, ![]() ,
, ![]() - точка на линии.
- точка на линии.
Значение уравнения (4) в
точке ![]() :
:
![]() , (5)
, (5)
где ![]() задается уравнением
(4), а значения
задается уравнением
(4), а значения ![]() и
и ![]() получаются
подстановкой в это уравнение
получаются
подстановкой в это уравнение ![]() и суммированием коэффициентов
при
и суммированием коэффициентов
при ![]() и
и ![]() . Условие пересечения линии с поверхностью:
. Условие пересечения линии с поверхностью:
![]()
или
![]() (6)
(6)
В результате имеем:
а) одно пересечение, если ![]() ,
, ![]() ,
,
![]() ,
,
б) два пересечения, если ![]() ,
, ![]() ,
,
![]()
 (7)
(7)
Определим соответствующий
знак при многократных пересечениях, для чего найдем производную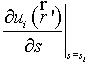 из уравнения (6). Используя затем решение (7), получим:
из уравнения (6). Используя затем решение (7), получим:
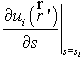 =
= ![]() . (8)
. (8)
Таким
образом, эта производная должна иметь знак (+/-), используемый в уравнении
пересечения. Отметим, что каждая поверхность определяет два разделенных объема,
которые назовем следующим образом: внутренний объем, если ![]() и внешний объем, если
и внешний объем, если
![]() . Следовательно, если
. Следовательно, если ![]() , то начало линии лежит с внутренней стороны поверхности и
первое пересечение с поверхностью получается из уравнения (7), используя
положительный знак. При пересечении с внешней стороны поверхности, т. е. когда
, то начало линии лежит с внутренней стороны поверхности и
первое пересечение с поверхностью получается из уравнения (7), используя
положительный знак. При пересечении с внешней стороны поверхности, т. е. когда ![]() ,
, 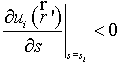 , и в первом пересечении используется отрицательный знак.
, и в первом пересечении используется отрицательный знак.
Рассмотренные
поверхности используются для описания протяженности геометрических зон, имеющих
постоянные физические свойства. Эти свойства определяются для каждой зоны с
помощью номера в композиции ![]() (
(![]() показывает, что зона пустая). Описание геометрии каждой зоны
включает список поверхностей, которые ограничивают зону.
показывает, что зона пустая). Описание геометрии каждой зоны
включает список поверхностей, которые ограничивают зону.
Описание
каждой зоны завершается расчетом "индексов неопределенности" ![]() для каждой граничной
поверхности. Эти индексы показывают расположение зоны относительно каждой из ее
границ, а также дают знак, используемый при расчетах расстояний до квадратичной
поверхности.
для каждой граничной
поверхности. Эти индексы показывают расположение зоны относительно каждой из ее
границ, а также дают знак, используемый при расчетах расстояний до квадратичной
поверхности.
3. Алгоритм геометрического блока комплекса
программ.
Геометрический
блок комплекса программ предназначен для определения принадлежности точки
геометрической зоне и длин частичных отрезков линии, лежащих в геометрических
зонах задачи. Для этого в исходных данных задаются коэффициенты уравнений поверхностей
![]() , номера поверхностей
, номера поверхностей ![]() , которые являются границами зоны, где
, которые являются границами зоны, где ![]() - порядковый номер
зоны,
- порядковый номер
зоны, ![]() - порядковый номер
границы, а также материал, заполняющий зону, и координаты произвольной точки
- порядковый номер
границы, а также материал, заполняющий зону, и координаты произвольной точки ![]() , принадлежащей зоне
, принадлежащей зоне ![]() . После ввода исходных геометрических данных в подпрограмме
GEOMIN номера
. После ввода исходных геометрических данных в подпрограмме
GEOMIN номера ![]() запоминаются в виде:
запоминаются в виде:
![]() =103
=103![]() +106
+106![]() (1+
(1+![]() ), (9)
), (9)
где![]()
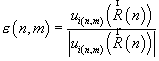 ,
,![]()
![]() - дельта-функция.
- дельта-функция.
Номер зоны N, которой
принадлежит точка ![]() , определяется из условия, что для всех
, определяется из условия, что для всех ![]() выполняется
неравенство
выполняется
неравенство ![]() , где
, где ![]() определяется
процедурой деления
определяется
процедурой деления ![]() на 106:
на 106:
![]()
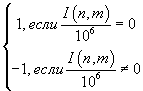 (10)
(10)
Общая
схема определения частичных отрезков между двумя точками ![]() и
и ![]() такова:
такова:
1. Определяется номер зоны
N1, которой принадлежит ![]() .
.
2. Определяется вектор 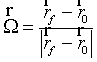 .
.
3. Определяются ![]() - расстояния до точек
пересечения линии с поверхностями
- расстояния до точек
пересечения линии с поверхностями ![]() . Все границы зоны задаются так, что все точки зоны лежат по
одну сторону от каждой границы. Поэтому длина частичного отрезка в зоне N1
равна минимуму
. Все границы зоны задаются так, что все точки зоны лежат по
одну сторону от каждой границы. Поэтому длина частичного отрезка в зоне N1
равна минимуму ![]() , который реализуется при
, который реализуется при ![]() .
.
4. Поочередно проверяются все зоны подряд на условие соседства через
поверхность ![]() . Таким условием является выполнение равенства для одной из
границ
. Таким условием является выполнение равенства для одной из
границ ![]() проверяемой зоны
проверяемой зоны ![]() :
:
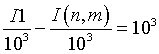 , где
, где ![]() .
.
Для
зоны, удовлетворяющей этому условию (т.е. соседней), с целью дополнительного
контроля проверяется условие принадлежности ей точки ![]() . Второй частичный отрезок лежит в зоне, для которой выполнены
эти два условия. Этой зоне присвоим номер N2.
. Второй частичный отрезок лежит в зоне, для которой выполнены
эти два условия. Этой зоне присвоим номер N2.
5. Выполняется операция:
![]()
Таким
образом, мы запоминаем номер зоны N2, с которой граничит зона N1 через
поверхность i1.
6. Определяется ![]() и выполняются
операции, которые выполнялись при определении
и выполняются
операции, которые выполнялись при определении ![]() и т.д.
и т.д.
, если не определяли расстояние до точки
пересечения прямой с поверхностью i
При
определении частичных отрезков на данном интервале, при нахождении точки
пересечения прямой с поверхностью
![]() в алгоритме используется
следующий прием ускорения. Запоминаются значения переменных массива
в алгоритме используется
следующий прием ускорения. Запоминаются значения переменных массива ![]() :
:
, если прямая линия не пересекается с поверхностью , если рассчитали два расстояния до поверхности , если получили значения коэффициентов квадратного уравнения для
определения расстояний до пересечений
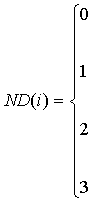
Ускорение при этом
достигается вследствие того, что в сложной геометрии значительное число
поверхностей, как правило, являются границами многих зон, которые пересекает
прямая линия.
Операция
5 позволяет по числу ![]() определить номер
зоны, с которой зона
определить номер
зоны, с которой зона ![]() граничит через
границу
граничит через
границу ![]() , но через некоторое небольшое число итераций, на которых
считаются частичные отрезки. Определив номер этой зоны, определяют
принадлежность ей точки пересечения линии с их общей границей. Если зона
, но через некоторое небольшое число итераций, на которых
считаются частичные отрезки. Определив номер этой зоны, определяют
принадлежность ей точки пересечения линии с их общей границей. Если зона ![]() граничит через
поверхность
граничит через
поверхность ![]() не с одной зоной и
точка не принадлежит зоне, номер которой определили по
не с одной зоной и
точка не принадлежит зоне, номер которой определили по ![]() , то следующую зону определяют, используя пункт 4.
, то следующую зону определяют, используя пункт 4.
4. Построение траекторий.
Взаимодействия
высокоэнергетических заряженных частиц со средой бывают двух видов:
многократные кулоновские - "атомные" и "ядерные", связанные
с возникновением внутриядерного каскада.
Моделируются
следующие физические события, происходящие с частицей: частица ![]() -того типа
-того типа ![]() -той энергетической группы рождается источником, после чего
двигается по траектории в системе, испытывая атомные и ядерные взаимодействия,
при которых могут рождаться различные другие частицы, и, в конце концов,
погибает при вылете из системы или ядерном взаимодействии.
-той энергетической группы рождается источником, после чего
двигается по траектории в системе, испытывая атомные и ядерные взаимодействия,
при которых могут рождаться различные другие частицы, и, в конце концов,
погибает при вылете из системы или ядерном взаимодействии.
Траектории
заряженных частиц строятся следующим образом:
1. Разыгрывается частица источника с параметрами ![]() , рождённая в
, рождённая в ![]() -той материальной зоне или независимым источником, или в
результате ядерного взаимодействия.
-той материальной зоне или независимым источником, или в
результате ядерного взаимодействия.
2. После этого разыгрывается её пробег в оптических толщинах, и она
летит по прямой до ближайшей из следующих трех точек: sk - точки пересечения лучом ![]() границы
границы ![]() -ой материальной зоны, точки
-ой материальной зоны, точки ![]() , где она переходит в следующую энергетическую группу, или
точки
, где она переходит в следующую энергетическую группу, или
точки ![]() , где она распадается.
, где она распадается.
2.1.
Случай ![]() . Частица летит до точки
. Частица летит до точки ![]() пересечения лучом
пересечения лучом ![]() границы
границы ![]() -той материальной зоны, где сечения взаимодействия меняются,
потому что она попадает в другую зону.
-той материальной зоны, где сечения взаимодействия меняются,
потому что она попадает в другую зону.
2.2.
Случай ![]() . Частица летит до точки
. Частица летит до точки ![]() , где сечения взаимодействия также меняются, потому что она
попадает в другую энергетическую группу.
, где сечения взаимодействия также меняются, потому что она
попадает в другую энергетическую группу.
2.3.
Случай t=0, когда частица
нестабильна и расстояние до точки распада ![]() . Частица летит до точки
. Частица летит до точки ![]() , в которой она распадается. В этом случае частица погибает и
следует переход к пункту 1.
, в которой она распадается. В этом случае частица погибает и
следует переход к пункту 1.
3. После
последовательного повторения (если это требуется) этапов пункта 2, частица или
вылетит за границу системы (тогда мы переходим к пункту 1), или распадётся, или
же её разыгранный пробег будет исчерпан, и она попадет в некоторую точку ![]() , принадлежащую зоне
, принадлежащую зоне ![]() *. В этой точке
должно произойти ядерное взаимодействие.
*. В этой точке
должно произойти ядерное взаимодействие.
4. В результате
ядерного взаимодействия в соответствии с сечением ![]() будет рождена другая
частица. После этого следует переход к пункту 1.
будет рождена другая
частица. После этого следует переход к пункту 1.
5. Расчет ядерного взаимодействия.
Считая,
что дифференциальное сечение рассеяния зависит только от косинуса угла
рассеяния ![]() , определим следующие величины:
, определим следующие величины:
-
плотность вероятности для определения типа вторичной частицы;
-
плотность вероятности для определения косинуса угла рассеяния;
-
плотность вероятности для определения энергетической группы вторичной частицы.
С помощью этих плотностей в
блоке взаимодействия определяется состояние частицы после ядерного
взаимодействия. Эти плотности нормированы на полную множественность частиц.
6. Задание исходных данных.
Исходная
информация вводится в виде наборов данных, описывающих параметры, управляющие
признаки, геометрию, групповую структуру и источник задачи. При этом
используются форматы языка программирования FORTRAN-77.
Ввод
исходной информации осуществляется с использованием 72-х позиций в строке в
описанной ниже последовательности.
6.1.
Параметры и управляющие признаки.
1.
NSTORE, NSOD
формат
(2I3)
NSTORE - полное число
историй частиц задачи, 100 историй,
NSOD - число историй частиц
задачи в одном пакете, 100 историй.
2.
NSMAX, NAMAX, NRMAX, NBMAX, NSTMAX, NMMAX
формат (6I3)
NSMAX - число поверхностей,
NAMAX - максимальное
число коэффициентов в уравнениях поверхностей,
NRMAX - число зон,
NBMAX - максимальное число
границ,
NSTMAX - максимальное число
частичных отрезков,
NMMAX - число материалов.
3. NSGMIN, NSGMAX, NSAMIN,
NSAMAX
формат (4I3)
NSGMIN - минимальный номер
энергетической группы источника,
NSGMAX - максимальный номер
энергетической группы источника,
NSAMIN - минимальный номер
временного интервала источника,
NSAMAX - максимальный номер
временного интервала источника.
4.
NXSECT, KALIDE
формат
(2I3)
NXSECT - тип первичной
частицы (источника),
KALIDE - максимальное число
соударений частиц с атомами среды.
5.
NREG1, NREG2
формат
(2I3)
NREG1 - номер зоны первого
детектора (оценка по пробегу),
NREG2 - номер зоны
последнего детектора.
6. VOL(NRMAX)
формат
(9E9.2)
VOL -
массив объемов геометрических зон задачи с номерами от 1 до NRMAX.
6.2.
Геометрия задачи.
7.
I, NTP(I), NEX, AA(1), AA(2), AA(3)
формат (3I3, 7E9.2)
I - индекс
поверхности, которая описывается,
NTP(I)
- индекс последнего ненулевого коэффициента, если поверхность задается в общем
виде; вычисляется внутри программы для всех других поверхностей (в табл.1
обозначение ![]() ),
),
NEX -
вид поверхности; 0 - для поверхности в общем виде, 1 - 13 – для специальных
видов поверхностей (в табл.1 обозначение ![]() ),
),
AA - массив параметров, определяющих поверхность (1 - 7).
8.
A(7,I), A(8,I), A(9,I)
формат (3E9.2)
A(7,I) - коэффициент при XY
в уравнении поверхности,
A(8,I) - коэффициент при YZ
в уравнении поверхности,
A(9,I) - коэффициент при ZX
в уравнении поверхности.
9.
I, ISV(I), MTL(I), NS(1,I), ..., NS(NBMAX,I), RO, XR(1,I),.., XR(3,I)
формат
(12I3,4E9.2)
I - индекс зоны, которая описывается,
ISV(I)
- индекс объемного источника, наложенного на эту зону. 0 - указывает на
отсутствие такого,
MTL(I)
- индекс композиции в зоне,
NS(1,I),
..., NS(NBMAX,I) - индекс граничных поверхностей 1.. NBMAX
RO -
зарезервировано
XR(1,I),
..., XR(3,I) - X, Y и Z координаты произвольной точки в зоне (см)
6.3.
Групповая структура и источники задачи.
10. NUMGR(1), ..., NUMGR(5)
формат
(9E9.2)
NUMGR(*)
- число энергетических групп соответственно протонов (p), нейтронов с энергией
выше 14.5 МэВ (n), пионов (![]() ), гамма-излучения (
), гамма-излучения (![]() ) и нейтронов с энергией ниже 14.5 МэВ (n<14.5)
) и нейтронов с энергией ниже 14.5 МэВ (n<14.5)
11. XMIN(1), ..., XMIN(5)
формат (9E9.2)
XMIN(*)
- минимальные координаты источника по пространственным переменным X,Y,Z и
угловым переменным ![]() соответственно.
соответственно.
12. XLENG(1), ..., XLENG(5)
формат (9E9.2)
XLENG(*)
- протяженность источника по пространственным переменным X,Y,Z и угловым
переменным ![]() =
=![]() соответственно.
соответственно.
13.
WSE(1), ..., WSE(NSGR)
формат (9E9.2)
WSE(*)- веса источников в
группах (сумма весов по группам равна 1).
14.
WST(1), ..., WST(NSAG)
формат (9E9.2)
WST(*)
- веса источников во временных интервалах (сумма весов по интервалам равна 1).
15.
AGEBO(1), ..., AGEBO(NSAG+1)
формат (9E9.2)
AGEBO(*)- границы временных интервалов.
16. E(1,1), ..., E(13,1)
формат (9E9.2)
E(*,1) - границы групп p, ![]() .
.
17. E(1,2), ..., E(13,2)
формат (9E9.2)
E(*,2) - границы групп n.
7. Библиотека констант HELICON.
Библиотека
констант HELICON (High Energy LIbrary CONstant) комплекса программ
PARSE 3.0 содержит данные по ядерно-физическим сечениям взаимодействия нуклонов
с энергиями до 1480 МэВ. Она может быть заполнена сечениями для любых элементов
таблицы Д. Менделеева. Для этого предназначена программа ELEM-G-V.EXE. При
выполнении данной программы создаётся файл ELEM.DAT, который необходимо переименовать
в файл с расширением DAT и названием, соответствующим атомному номеру элемента,
например, для водорода этот файл должен иметь название - 001.DAT, а для
урана-238 - 092-238.DAT.
Для
выполнения программы ELEM-G-V.EXE необходимо задать атомный номер и атомный вес
элемента в файле ELEM.IN
1. KIZ, A
формат свободный, через
пробел
KIZ - атомный номер
элемента,
A - атомный вес элемента.
8. Подготовка сечений взаимодействия нуклонов для
материалов задачи.
Файлы
сечений p, n, ![]() для материалов,
которые рассчитывает программа COMP-G.EXE., создаются в директории INCPU. Для
выполнения программы COMP-G.EXE необходимо задать элементный состав материалов
задачи в файле COMP-IN.DAT в следующем порядке:
для материалов,
которые рассчитывает программа COMP-G.EXE., создаются в директории INCPU. Для
выполнения программы COMP-G.EXE необходимо задать элементный состав материалов
задачи в файле COMP-IN.DAT в следующем порядке:
1. NM
формат свободный
NM - количество материалов.
2. N, FLAGFIS
формат свободный, числа
вводятся через пробел
N - количество элементов в
материале,
FLAGFIS
- указатель делящегося материала (1 - делящийся материал, 0 - иначе)
Далее вводится N операторов
для каждого элемента, входящего в состав материала, в следующем порядке:
3. NK, NZ, AN
формат свободный, числа
вводятся через пробел
NK - плотность ядер элемента
в материале (ядер/см3![]() ),
),
NZ -
атомный номер элемента,
AN - атомная масса элемента.
Далее аналогично задаются
операторы для последующих материалов.
9. Дополнительная информация для проведения
расчетов.
Исходные
данные содержатся в файлах:
1. ISDDAT.DAT
-подготавливается в соответствии с разделом 4.
Вызов в программе :
OPEN(UNIT=5..ISDDAT.DAT)
2. DPDL.DAT - плотности
вероятностей массовой толщины.
Вызов в программе:
OPEN(UNIT=6..DPDL.DAT) Использование данной возможности для расчетов
случайно-неоднородных сред не автоматизировано и требует обращения к
разработчику.
3. INELAS. DAT - неупругие
сечения взаимодействия частиц.
Вызов в программе: OPEN
(UNIT=4... INELAS. DAT)
4. RCHEX. DAT - пробеги
внутри групп частиц
Вызов в программе: OPEN
(UNIT=4... RCHEX. DAT)
5. WNNA, WNPA, WPNA, WPPA, WCNN , WCNP, WCPN.WCPP,WFNN, WFPN - угловые
вероятности образования частиц в нуклон-ядерных реакциях.
Вызов в
программе: OPEN (UNIT=4.………)
Результат
решения записывается в файл SOL.DAT
Вызов в
программе: OPEN (UNIT=3..SOL.DAT))
Процедура
определения коэффициента СОЕ, необходимая для реализации возможности расчетов в
случайно-неоднородных средах, генерируется разработчиком (для гомогенных сред
СОЕ=1 и не требует дополнительных установок). Для случайно-неоднородных сред
СОЕ определяется процедурой случайной выборки:
CALL
RANDOM (R)
PRO=0.
DO
1600 I=1,NSTRG
PRO=PRO+PRD(I)
IF(R.LT.PRO*A17) GO TO 1700
1600
CONTINUE
1700
COE=A17*FLOAT(I)/А1.01
где NSTRG и A17 –
соответственно число узлов и шаг сетки по толщине для здания функции плотностей
вероятностей массовой толщины РRD в файле DPDL.DAT, а А1.01 плотность
гомогенного материала, для которого заданы ядерно-физические сечения
взаимодействий.
10. Тестирование комплекса программ.
Проверка
комплекса программ PARSE 3.0 в части расчета нуклон-ядерных взаимодействий
проведена путем расчета спектров нейтронов и гамма-квантов, генерируемых
протонами в пластинах из углерода, алюминия и урана, толщиной 2.1, 4.03 и 3 см
соответственно [7], [8]. На Рис. 1 приведены результаты расчетов энергетических
спектров нейтронов для алюминия и урана в сравнении с экспериментальными данными,
представленными соответственно в работе.
F(En), нейтр./(МэВ×ср×протон)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
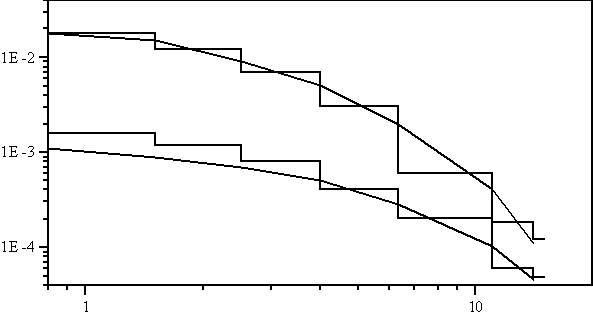
Рис.
1. Энергетические спектры вторичных нейтронов из урана и алюминия при энергии
протонов 113 МэВ.
Мощность источника протонов
принята равной 1 протон/(см2 с). Получено удовлетворительное
согласие результатов расчета по программе PARSE 3.0 с экспериментальными
данными, расхождение между которыми не превысило 35% для нейтронов. Аналогичные
расчеты проводились для гамма-квантов, генерируемых в углеродной пластине. Максимальная
погрешность составила 40%. В расчетах параметров вторичных нейтронов и
гамма-квантов, образующихся под действием протонов, использованы константы,
которые формируются на основе данных, содержащихся в работах авторов Alsmiller
R.G., Барашенкова В.С., Сычева Б.С., в препринтах организаций РТИ, NASA, ИТЭФ и
периодических изданиях. Для расчета прохождения вторичных частиц с энергиями до
14.5 МэВ, как указывалось выше, используется библиотека констант БНАБ-78.
Анализ источников погрешностей показал, что систематическая погрешность
результатов в основном обусловлена погрешностями задания сечений образования
высокоэнергетическими нуклонами вторичных частиц в ядерных реакциях, которые
составляют от 12% до 45%.
Проверка
комплекса программ PARSE 3.0 в части расчета взаимодействий нейтронов с
энергиями ниже 14.5 МэВ проведена путем расчета спектра утечки нейтронов из
критической сборки Godiva. В Tабл. 2 приведены нормированные на единичный флюенс
результаты расчетов в сравнении с экспериментальными данными работы [9]. С
учетом погрешностей эксперимента можно констатировать удовлетворительное согласие
результатов расчета по комплексу программ PARSE 3.0 с экспериментальными
данными, расхождение между которыми составляет 5 - 30% в энергетической группе.
Исключение составляет интервал энергий 6.5 - 10 МэВ, где точность эксперимента
и совпадение результатов несколько ниже.
Таблица 2. Спектры
утечки нейтронов из критической сборки Godiva.
|
Интервал энергий, МэВ |
Эксперим. спектр, |
Погр., % |
Расчетный спектр, |
Погр., % |
|
10.5 -
14 |
- |
- |
2.01-4 |
|
|
6.5 -
10.5 |
1.49-2 |
|
7.21-3 |
|
|
4.0 -
6.5 |
6.81-2 |
|
5.04-2 |
|
|
2.5 -
4.0 |
1.28-1 |
|
1.35-1 |
|
|
1.4 -
2.5 |
2.03-1 |
|
2.11-1 |
|
|
0.8 -
1.4 |
2.15-1 |
|
1.61-1 |
|
|
0.4 -
0.8 |
2.41-1 |
|
1.84-1 |
|
|
0.2 -
0.4 |
1.30-1 |
|
1.31-1 |
|
|
0.1 -
0.2 |
- |
- |
6.91-2 |
|
|
0.0465 -
0.1 |
- |
- |
3.67-2 |
|
|
0.0215 -
0.0465 |
- |
- |
2.19-3 |
|
11. Пример подготовки исходных данных (тест Godiva).
... 100 100 0
... 2 6 2 2
50 9
... 16 16 1 1
... 5 100
... 1 2
... 1 6 13 .0000E+00 .8731E+01 .0000E+00
.8731E+01
.0000E+00 .8731E+01 .0000E+00
... 2 6 13 .0000E+00
.8741E+01 .0000E+00 .8741E+01
.0000E+00 .8741E+01 .0000E+00
... 1
0 1 1 0 0
0 0 0 0 0
0 .0000E+00
.0000E+00 .0000E+00 .0000E+00
... 2
0 1 1 2 0
0 0 0 0 0
0 .0000E+00
.8735E+01 .0000E+00 .0000E+00
... .2790E+04 .9590E+01
... 10 12 15 20
28
... .0000E+00 .0000E+00
.0000E+00 -.1000E+01 -.3140E+01
... .0000E+00 .0000E+00
.0000E+00 .2000E+01 .6280E+01
... .1000E+01
... .1000E+01
... .0000E+00 .1000E-02
... .1480E+04 .9000E+03
.5460E+03 .3310E+03 .2010E+03
.1220E+03 .7390E+02 .4480E+02
... .2720E+02 .1650E+02
.1000E+02 .6070E+01 .3680E+01
... .1480E+04 .9000E+03
.5460E+03 .3310E+03 .2010E+03
.1220E+03 .7390E+02 .4480E+02
... .2720E+02 .1650E+02
.1000E+02 .6070E+01 .3680E+01
.20E+01
12. Пример результатов расчета (тест Godiva).
DATA FOR DETECTOR NUMBER 1
AFTER 1000000 PACKETS
FUL FLUX NEUTRONS LESS 14,5 MEV
.1749E-01
FLUX NEUTRONS LESS 14,5 MEV
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00 .0000E+00 .6613E-05
.1413E-03 .8207E-03
.1883E-02 .4284E-02
.2778E-02 .3194E-02 .2305E-02 .1164E-02
.6433E-03 .2319E-03
.4256E-04 .3987E-06
.1397E-08 .0000E+00 .0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E-00
FLUX NEUTRONS LESS 14,5 MEV DERIVATION
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00 .0000E+00 .1893E+00
.5793E-01 .3157E-01
.4012E-01 .2286E-01
.2308E-01 .3334E-01 .2884E-01 .2119E-01
.8551E-01 .3286E+00
.7553E-01 .2224E+00
.1000E+01 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E-00
DATA FOR DETECTOR NUMBER 2 AFTER
1000000 PACKETS
FUL FLUX NEUTRONS LESS 14,5 MEV
.9771E-02
FLUX NEUTRONS LESS 14,5 MEV
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00 .0000E+00 .2893E-05
.7038E-04 .4918E-03
.1320E-02 .2058E-02
.1573E-02 .1793E-02 .1282E-02 .6761E-03
.3583E-03 .1246E-03
.2134E-04 .3040E-06
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E-00
FLUX NEUTRONS LESS 14,5 MEV DERIVATION
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00 .0000E+00 .1854E+00
.4279E-01 .4951E-01
.1117E+00 .2274E-01
.2692E-01 .3362E-01 .2661E-01 .4072E-01
.9699E-01 .4038E-01
.9870E-01 .9742E-01
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00
.0000E+00 .0000E+00 .0000E+00 .0000E+00
.0000E+00 .0000E+00
Заключение
Разработан
комплекс программ PARSE 3.0, необходимый для моделирования образования пучком
ускоренных протонов нейтронного источника в мишени и полей нейтронов и фотонов
в гибридных системах. Комплекс программ позволяет рассчитывать энерговыделение
и другие характеристики нуклон-ядерного каскада в объектах трехмерной геометрии
методом Монте-Карло. Используется многогрупповое представление уравнения
переноса нуклонов в предположении непрерывного замедления заряженных частиц и
модель катастрофических столкновений. Проведенные тестирование по результатам
экспериментов и апробация комплекса программ показали достаточную его
эффективность при решении задач исследования ядерно-физических процессов в
гибридных системах.
Литература
1. Proc.
of the First International Conference on Accelerator-Driven Transmutation
Technologies and Application, Las Vegas, July 1994.
2. Proc.
of the Second International Conference on Accelerator-Driven Transmutation
Technologies and Application, Kalmar, 3-7 June 1996.
3. Proc.
of the 3rd International Conference on Accelerator-Driven Transmutation
Technologies and Application (ADTT&A), Prague, 7-11 June 1999.
4. Е.В.
Ефремов, Н.А. Иванов, О.Б. Москалев. PARSE-2 – комплекс программ для расчетов
методом Монте-Карло адронного каскада в трехмерной геометрии. Тезисы докладов VI Всероссийской
научной конференции по защите от ИИ ЯТУ, Обнинск, 1998.
5. T.
M. Jordan. FASTER – A Fortran Analytic Solution of the Transport Equation by
Random Sampling. WANL-PR-(LL)-010, 1968.
6. Л.П. Абагян, Н.О. Базазянц, М.Н. Николаев, А.М. Цибуля. Групповые константы
для расчета реакторов и защиты. Энергоиздат, Москва,
1981.
7. Nucl.
Sci. and Eng. -1989. -Vol.102, 3. -P.310-321.
8. Nucl.
Instr. and Methods. -1978. -Vol.151, 3. -P.493-503.
9. Nucl.
Sci. and Eng. -1960. -Vol.12, 8. -P.595