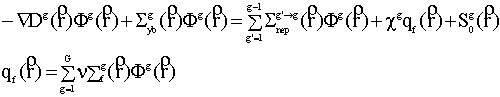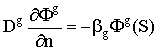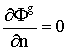Моделирование ядерно-физических процессов в мишенях и бланкетах гибридных систем (ADS - систем) с помощью пакета РЕАКТОР

( Simulation of Nuclear - Physical Processes in Targets and Blankets of Hybrid Systems (ADS - Systems) with the Help of Program Package REACTOR

Preprint, Inst. Appl. Math., the Russian Academy of Science)

Оглавление

Введение                                                                                                           

1.     Организация связи по источнику нейтронов “spallation” программных комплексов LAHET и РЕАКТОР.                                                                    

2.     Использование универсальных алгоритмов ускорения сходимости

при решении многогрупповой системы диффузионных уравнений

с внешним источником                                                                                   

Заключение                                                                                                             

Литература                                              

Введение.

Одной из перспективных концепций в стратегии развития атомной энергии является концепция гибридных ядерных систем ускоритель + мишень + бланкет (Accelerator Driven System-ADS). В настоящее время ведется интенсивная работа по изучению и оптимизации характеристик таких систем. Определяющую роль в этой работе имеет численное моделирование процессов взаимодействия пучка высокоэнергетических протонов с веществом мишени и процессов размножения нейтронов скалывания в активной зоне - бланкете установки.

В сложившейся практике физический расчет гибридной ядерной системы делится на два крупных этапа: вначале определяется по программам нуклон-ядерного каскада однородный по пространству и по энергетическому спектру источник нейтронов скалывания (spallation), который затем используется в реакторных программах в качестве внешнего источника для определения нейтронных потоков и функционалов в бланкете. Очевидно, что такое упрощение вносит определенную погрешность в расчет.

На данный момент в различных научных организациях для расчета этих процессов по отдельности существуют развитые программы. Однако для адекватного моделирования требуются такие программные комплексы, которые производили бы совместный расчет как протонной, так и нейтронной задачи.

В данной работе представлена программная связка двух кодов: LAHET (ЛАНЛ, США) [1] (расчет переноса высокоэнергетических протонов в мишени с учетом процессов внутриядерного каскада при взаимодействии протонов с веществом мишени) и РЕАКТОР (ИПМ, Россия) (нейтронно-физический расчет ядерных реакторов и гибридных ядерных установок) [2]. Для этой цели созданы модули, позволяющий из файлов с результатами расчета по LAHET выходов нейтронов в нуклон-ядерном каскаде сформировать детальный источник нейтронов “скалывания” (spallation) и автоматически его записать во входной файл для дальнейшего расчета по программе РЕАКТОР. На примере расчета теста, сформулированного рабочей группой при МАГАТЭ в рамках программы по ADS  [3] показано, что детальный учет объемного и энергетического распределения этого источника существенно уточняет расчет основных физических величин: нейтронный коэффициент усиления бланкета, коэффициент неравномерности поля энерговыделения и др.

Одной из характерных особенностей, присущих нейтронно-физическому расчету системы мишень + бланкет, является медленная сходимость итерационных алгоритмов для решения системы диффузионных уравнений с внешним источником. Медленная сходимость объясняется тем, что в системах с подкритическим бланкетом максимальное собственное значение l₀=К_эфф близко к единице (~0.95¸0.98), отношение двух соседних максимальных собственных значений также близко к единице. Для ускорения сходимости цикла внешних итераций можно воспользоваться тем обстоятельством, что весь спектр собственных значений заключен в интервале (-1,1). В этих условиях  для ускорения можно выбрать трехчленные универсальные алгоритмы с полиномами Чебышева 2-го рода [4], использующие заданное расположение спектра. Эффективность такой процедуры ускорения продемонстрирована также на расчете теста МАГАТЭ.

1. Организация связи по источнику нейтронов “spallation” программных комплексов LAHET и РЕАКТОР.

Программный комплекс РЕАКТОР, разработанный в ИПМ им. М.В.Келдыша РАН, позволяет детально рассчитывать основные нейтронно-физические характеристики ядерных реакторов, в том числе и бланкетов гибридных ядерных систем: уровень подкритичности, нейтронные потоки, распределение энерговыделения, расчет кампании, трансмутацию актинидов и др. Для моделирования процесса переноса нейтронов в этом пакете решается многогрупповая система диффузионных уравнений, которая имеет вид:

               (1)

где в общепринятых обозначениях:

   - поток нейтронов группы g в точке r;

         - коэффициент диффузии в группе g;

     - макросечение увода нейтронов из группы g;

- макросечение перехода нейтронов из группы g` в группу g;

         - доля спектра деления в группе g;

  - макросечение генерации быстрых нейтронов в группе g за счет деления;

         - внешний источник в группе g.

На внешней границе S задается одно из граничнах условий:

  - нулевое значение потока на границе;

       - альбедное граничное условие;

  - нулевое значение тока на границе.

Для расчета гибридной ядерной системы в пакете РЕАКТОР необходимо задать внешний источник нейтронов , возникающий при взаимодействии высокоэнергетических протонов с веществом мишени.

Как правило, при расчете гибридных систем задается однородный по пространству источник с некоторым заранее рассчитанным спектром (Spallation Spectr). В действительности же в источнике наблюдается “эффект факела”: наибольшее энерговыделение и наиболее интенсивное рождение нейтронов происходит вблизи  от точки проникновения пучка протонов в мишень. Энергетический спектр нейтронов также меняется в зависимости от расстояния от оси пучка протонов.

Задание детального источника нейтронов “spallation” вручную слишком трудоемкая задача. Для ее автоматизации разработаны две программы LahIn и ReakIn, осуществляющие программную связь по источнику нейтронов между пакетом LAHET и пакетом РЕАКТОР.

Модуль LahIn дает возможность пользователю, не имеющему навыков работы с LAHETом, сравнительно легко получить входной файл для пакета РЕАКТОР с заданным объемным источником, который рассчитывается LAHETом на пространственной сетке, согласованной с сеткой пакета РЕАКТОР. Для этого программа LahIn берет из модуля GEOM2D пакета РЕАКТОР информацию о количестве геометрических зон, числе расчетных узлов, границах физических зон. Далее определяется местоположение источника и высчитывается его физический размер и разбиение на расчетные узлы. Из модуля INCON берется информация о нуклидах и ядерных концентрациях для зоны источника. Пользователю необходимо ввести информацию о параметрах пучка протонов: энергия, форма распределения. Энергия пучка задается в МэВ. Типы источников: точечный, эллиптический с равномерным распределением, эллиптический с гаусовским распределением, эллиптическое кольцо с равномерным распределением. В случае эллиптического источника пользователь должен ввести полуоси. По умолчанию выставляется эллиптический тип с гаусовским распределением и полуосями 1.2см. На основании полученных данных формируется исходный файл для программы LAHET. Затем программа LAHET рассчитывает источник. Далее программе ReakIn на вход следует подать выходной файл LAHETa, из которого она извлекает информацию об энерговыделении и о нейтронах “spallation” в расчетных ячейках. После необходимых нормировок во входном файле пакета РЕАКТОР для модуля INFLUX задается групповое представление нейтронов источника по всем физическим зонам.

Ниже представлен сравнительный анализ расчета с однородным и объемным источником, проведенный на примере ADS-Neutronic Benchmark IAEA [3]. Расчетная модель мишени и бланкета в (R,Z)-геометрии представлена на Рис. 1. Температура топливных зон (зоны 6, 2, 3) 1200 К, остальных 900 К. Ядерные концентрации элементов в зонах представлены в Таблице 1.

Рис. 1. Расчетная модель в (R,Z)-геометрии.

Таблица 1. Ядерные концентрации элементов в зонах (в ед. 10²⁴яд/см³)

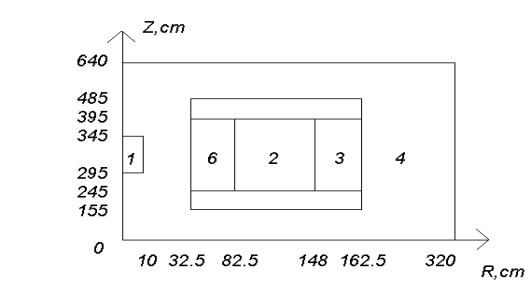
В стандартном реакторном расчете объемный внешний источник задан в цилиндрической области и расположен в центре системы (на Рис. 1 отмечен как зона 1). Он заранее рассчитан для пучка протонов с энергией 1Гэв и приведен к групповому виду (см. Таблицу 2). Считается, что по объему мишени источник постоянный.

Таблица 2. Спектр источника нейтронов.

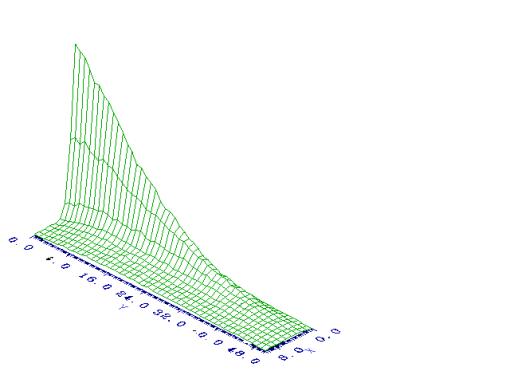
Детальный расчет источника нейтронов “spallation” показал, что он имеет неоднородный вид. На Рис. 2 показана форма распределения наработанных в мишени нейтронов.

Рис. 2. Интегральный по всем группам источник нейтронов в мишени.

Мишень облучается пучком протонов с энергией 1000 МэВ. Пучок имеет гауссово распределение на эллипсе, с полуосями 1.2 и 1.2. Наработка нейтронов рассчитывалась по программе LAHET со 100000 историй на равномерной сетке с 50 шагами по Z (Y) и 10 по R (X). Максимальное значение достигается в узле, расположенном наиболее близко к точке попадания протонного пучка в мишень, и равняется 0.7 нейтрон/см³ на один протон. Всего же на один протон в мишени произведено 25.4 нейтрона.

При использовании в реакторном расчете источника нейтронов “spallation” с детальной пространственной и энергетической формой уточняются и такие интегральные величины, как UKF-умножение бланкета по нейтронам (число нейтронов деления в бланкете на один нейтрон источника) и K_s (аналог К_эфф в подкритической системе). В случае однородного источника UKF=40.44, К_s=0.9758, а объемного UKF=43.10 и К_s=0.9773.

При уточнении формы источника происходит и существенное уточнение в пространственном распределении энерговыделения в бланкете. На Рис. 3- 7 показано относительное энерговыделение в различных частях активной зоны по ее длине и высоте для двух расчетов.

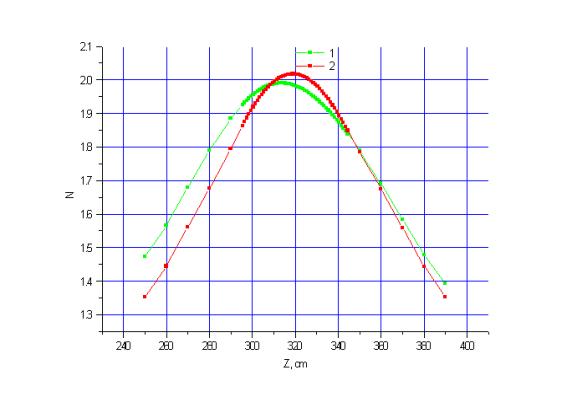
Рис. 3. Распределение энерговыделения по высоте бланкета

 на радиусе 32.5 см.

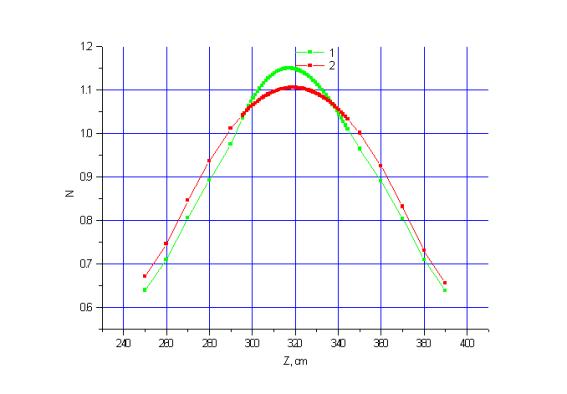
Рис. 4. Распределение энерговыделения по высоте бланкета

 на радиусе 97.5 см.

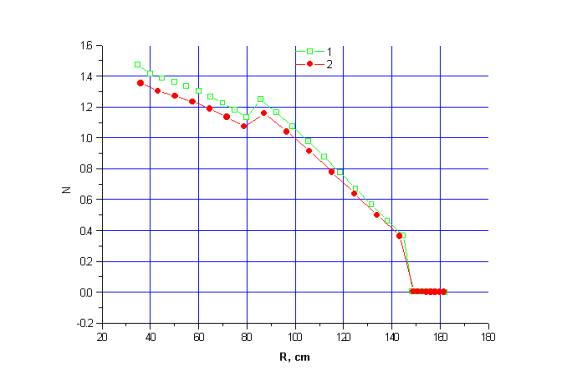
Рис. 5 Распределение энерговыделения по радиусу бланкета

 на высоте 245 см.

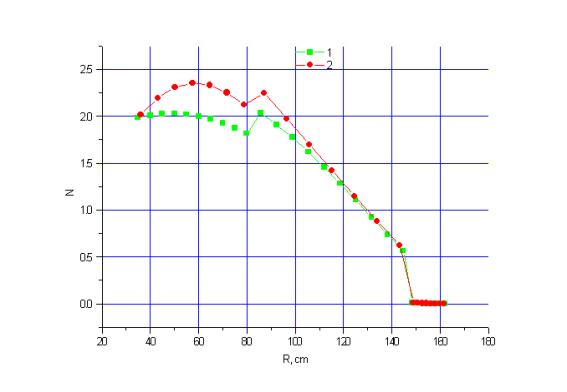
Рис. 6. Распределение энерговыделения по радиусу бланкета

 на высоте 320 см.

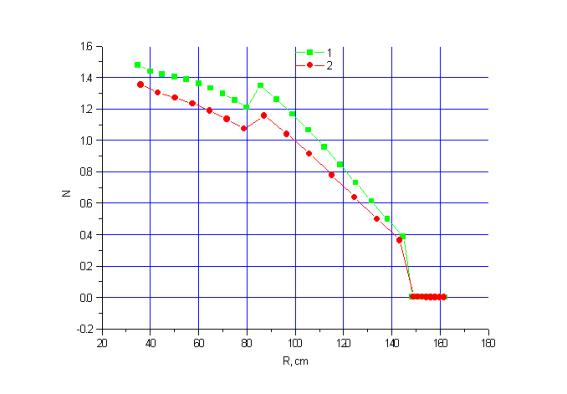
Рис. 7. Распределение энерговыделения по радиусу бланкета

 на высоте 395 см.

Кривая с номером 1 на рисунках 3-7 соответствует энерговыделению, рассчитанному с использованием объемного источника, кривая с номером 2 соответствует энерговыделению с однородным источником. Максимальные расхождения составляют 15% на Рис. 7.

2. Использование универсальных алгоритмов ускорения сходимости при решении многогрупповой системы диффузионных уравнений с внешним источником.

При расчете гибридных ядерных систем рассматриваемый уровень подкритичности соответствует К_эфф=0.95¸0.98. Метод простых итераций для решения системы диффузионных уравнений (1) сходится очень медленно. Покажем, как в этом случае можно реализовать универсальные алгоритмы ускорения сходимости.

После выполнения процедуры пространственной дискретизации системы уравнений (1) получаем систему линейных неоднородных уравнений, которую в матричном виде можно записать следующим образом:

,                                                (2)

где матрицы A, F, S_s - конечно-разностные аналоги операторов утечки+увода, деления и рассеяния, S- вектор аппроксимации пространственного внешнего источника. Техника получения системы (2) детально описана в [5]. Задаче (2) соответствует однородная система уравнений на собственное значение:

,                                                         (3)

Теоретический анализ спектральных свойств системы (3) подробно выполнен в работах [6,7]. Показано, что в случае отсутствия рассеяния нейтронов “вверх” по энергии, задачу (3) можно эквивалентно преобразовать к классической задаче на собственное значение вида

,                                                                                        (4)

которая обладает следующим свойством: единственной положительной собственной функции (вектору с положительными координатами) соответствует наибольшее простое собственное значение l₀, ( для всех l_k¹l₀).

Для нахождения решения как системы (2), так и системы (3), как правило, организуют два итерационных цикла: цикл внешних итераций по источнику нейтронов и цикл внутренних итераций в отдельной энергетической группе. Можно считать, что циклы внутренних итераций по группам заданной длины обращают с определенной точностью матрицу A, тогда цикл внешних итераций играет роль итерационной процедуры для решения системы (3) или системы с внешним источником.

При численном моделировании гибридных ядерных систем с подкритическим бланкетом максимальное собственное значение l₀=К_эфф имеет значение, близкое к единице. Отношение двух соседних максимальных собственных значений также близко к единице. В этих условиях простая итерационная процедура сходится медленно, и возникает задача ускорения внешнего цикла итераций.

Воспользовавшись отмеченными выше свойствами спектра собственных значений и тем обстоятельством, что для подкритического бланкета К_эфф всегда меньше единицы, для ускорения сходимости можно выбрать трехчленные универсальные алгоритмы [4], использующие заданное расположение спектра. Характерными особенностями таких алгоритмов является то, что быстрота их сходимости не зависит от размерности матрицы, она определяется только ее обусловленностью, они просты в реализации и достаточно эффективны. Применительно к системе (2) последовательность приближений строится по формулам:

,                                   (5)

начиная с начального вектора F⁽⁰⁾, выполняя первый шаг при a₀=0. Если выбрать цикл длиной М и определить

, к=1,2,…,М,

тогда вектор ошибки будет подавляться полиномом  Чебышева второго рода:

с условием нормировки  Последовательность этих полиномов равномерно стремится к нулю во всяком сегменте, внутреннем для интервала (-1,1), и тем самым обеспечивается подавление компонент вектора ошибок.

Описанный алгоритм целесообразно использовать, определяя из численных экспериментов оптимальную длину цикла М.

На Рис. 8 и в Табл. 3 приведены результаты использования представленного алгоритма ускорения сходимости при расчете нейтронных потоков по пакету РЕАКТОР во втором тесте, сформулированном в 1996 году рабочей группой при МАГАТЭ в рамках программы по гибридным ядерным системам [8] и подробно рассчитанном в [9]. Все расчеты выполнены с относительной точностью в групповых потоках 10^-7 при различном числе внутренних итераций. От числа последних зависит процедура обращения матрицы А в системе (2), что сказывается на оптимальной длине цикла ускорения.

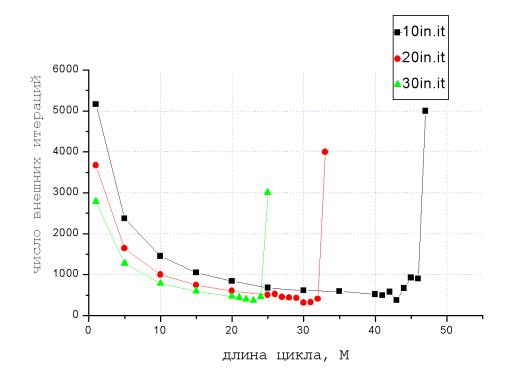
Рис. 9. Зависимость числа внешних итераций от длины цикла ускорения при различном числе внутренних итераций.

Таблица 3. Зависимость числа внешних итераций от длины цикла ускорения при различном числе внутренних итераций, эффективность цикла ускорения: отношение числа простых итераций к числу итераций с ускорением.

Приведенные результаты свидетельствуют о том, что универсальные трехчленные алгоритмы ускорения, несмотря на свою простоту, позволяют существенно ускорить решение задач, связанных с нейтронно-физическим расчетом гибридных ядерных систем. Из результатов расчета следует, что оптимальная длина цикла ускорения зависит от числа внутренних итераций для каждой энергетической группы. По-видимому, при точном обращении матрицы А (бесконечное число внутренних итераций) эта длина будет определяться числом энергетических групп, в которых нейтронные потоки имеют значимые величины. В этом случае спектр собственных значений матрицы Т из (3) располагается в минимальном интервале (-К_эфф,+К_эфф), при неточном обращении матрицы А происходит некоторое уширение интервала, содержащего спектр, что приводит к увеличению оптимальной длины цикла ускорения.

Заключение.

Для расчета физических характеристик гибридных ядерных систем (мишень + бланкет) требуется комплексный подход, позволяющий рассчитывать как взаимодействие пучка высокоэнергетических протонов с веществом мишени, так и нейтронно-физические процессы в бланкете.

В работе представлена программная реализация связи двух комплексов LAHET и РЕАКТОР, по нейтронам, рождающимся за счет внутриядерного каскада в мишени и попадающим затем в бланкет. На примере расчета теста МАГАТЕ показано, что детальное задание источника нейтронов “spallation” приводит к существенному уточнению нейтронно-физических характеристик гибридной ядерной системы.

При расчете гибридных ядерных систем по реакторным программам наблюдается медленная сходимость итерационных алгоритмов. В работе показано, что в этом случае значительного ускорения сходимости можно получить, используя простые в реализации универсальные алгоритмы с полиномами Чебышева 2-го рода.

Литература.

1.     R.E. Prael and H. Lichtenstein. “User Guide to LCS: The LAHET Code System”, LANL report LA-UR-89-3014 (September 1989).

2.     А.V.Voronkov, V.I.Arzhanov. “REACTOR - program system for neutron-physical calculations”, Proc. International topical meeting, Advances in Mathematics, Computational and Reactor Physics, Pittsburg, USA, 1991.

3.     Carminati F., Kadi Y. ADS Neutronic Benchmark (stage 1). A New Approach to the Design of Accelerator Driven Systems. Proc. Of IAEA technical Committee Meeting, Madrid, 17-19 September 1997.

4.     Фаддев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М., Физматгиз, 1960.

5.     Земсков Е.А., Аржанов В.И. Спектральный анализ условий счетной устойчивости некоторых схем решения задач пространственной кинетики ядерного реактора. Препринт ИПМ РАН №92, 1996.

6.     Габетлер Г.И., Мартино М.А. Теоремы существования и теория спектров для многогрупповой диффузионной модели. Сб. Теория ядерных реакторов, под ред. Биркхофа Г. и Вигнера Э. М., Госатомиздат, 1963, стр.145.

7.     Вагра Р. Численные методы решения многомерных многогрупповых диффузионных уравнений, там же, стр.187.

8.     Slessarev, V. Arkhipov. Study of a Neutronic Potential of a Modular Fast Spectrum ADS for Radiotoxic Waste Transmutation. Proc. of ADTTA'99, Mo-O-F2, Praha, June 7 – 11, 1999.

9.     Воронков А.В., Земсков Е.А., Новикова Н.Н., Сычугова Е.П. Расчет по программному комплексу REACTOR-S теста для гибридных ядерных систем IAEA-ADS benchmark. Препринт ИПМ РАН №77, 2000.