����� VI. ������� ��������������� � ������� ������ �������
� ������� ��������� ����������� ������������
� ����������� ������� ������������� � ��������� �� �������� ������� ���� �
�������� �������� ���������, ����������� �����, ��������� ������� � ���������
��������. ����� �� �������� ������ ����� �������� ������ ����������
�������������� ������������ � ������� ������ ����� �������� ������, ������
����������� ������� "���������" ��� ������������ ���� ���. ����������
������� ���� ���������� ����������� ��������� ���������� ������� ���������������
������� � �������� �������.
�������� �� �������� ��������� �� �������
�������� � ����������� � ����������� �� �������� � ����� ���������� � ���������.
�1. ������� �������
�������������
������������� �������� ������ ����������
������� � ������������� ������� ����, ����������� ���������. ������� ��������
������������, ������������ �������� ������ ������� � ���� �����. � ������
�������, ��������� ������� �������� ������� �������������� ����������, � ���
����� ����� ���� �����������. ������ � ���� ������������� ������� �������������
� ��������� �������� �� ������� ������������ � ��������� �� ��� ����. ������������
������� ������� ����� �������� ������ �������������, ������ ��������
������������� ����� ������������� �� ��������� ������� (����� �������������
������������������) �� �������
����������� ��������� �������� �� ��������������� ������������ � ���������,
�������� ������� �������������� ���������.
����������� �� ���������� ����� ��������
�������������, �������� ���� "�� ������" ��� �� ������, ��� �
�������� ������� ���������� �������, ���������� ����� ����������� � �� ��������,
�������������� � ���������������� ��������� ������� (���������� �������), ��
������� ������� �� ����������� ������� (������� �������������). ���
�����������, ������� �� ����������� ������������, �������� ��������� ��������
�������������� ������������ �������:
- ���� ����������� ������������
��� ���� ������� � �����, ��� � �� ��������� �������������� �������;
- ���� �������������� ����
�������, ����������������� � ��������������� ��������� ��������� �������������
����� �������;
- ���� �������������
������������� ����� ������� �������������� (��������, "�����
����������");
- ���������� ����� ����������
����������������� ������������ ������� � ���� ��������� ��������������
����������� �������;
-
��������������
���������� �������� ��� ���������� ���� ����������;
- �������������� ����������
������������� ����� ������� �� �� ������� �� ������������ ��� ������������
������� ������� ������ �������������;
-
������� �������
������� �� ������� �����������;
-
��������������
������� ������� � ���� ���������� ������� �������.
����� ��������� ������� ������� ����������
������ ������������ � �������� ����� ����������� ��������� (������� �������,
�.�. ������� �������������). ����� ��������������� ��������� �������� �������
������� �� ��������������� ������ ������� �� ��������� ������.
�� ���������� ������� ������� ���������
������� ������ D��
����� ������� �� �������. ��� "��������������" ������� �������������
������� ����������� ����������� � ���������� ������� ����� ������� �
����������� ������������ �� ��������. �� ����������� ������� � ���������� "�������" �������
(D) ������ D�d, ������������ �� D�d �� �������. ���������� �� � ������� ���������� ����������� (N).
��� ������� D, ��� � N ������� �� ������ ���������.
����� ������ ������������� ������ �����������
��������� �����, ����������� ��������� �������, ������ �������� ������������
(��������) � ������ ������ ������� �� ���� ���������� (���� ���������� �����
������� ����� �������). ����� �������, � ��� ���� ����� �������� (��������) ��
�������� D, ����������� ������� �
��������������� ���������, � ����� �������� �� �������� N, ����������� ������� � ���������� ���������. �������� ������
������������� ���� ���� ����� ��������, �.�., ���������� ������� �� D � N,
���������� ����� "��������" �������, �� ��������, ���� ������,
����������� ������� � ������������ ������ ������� (����� ��������������
��������), ����� ����������, ����������� �� ���� �������� � ������� D ��� N.
����� �������������� �� ������ �� ���������
������� (�.�. �� ������� �����������) ���������� �������������. ����� � D � N
�������� ������� � ��������. �����
������ ���������� f ������������ � ����������. ���������� ����� ���
�������� ������, ������� ��� �������� �� ��� ������ ������ �������� (��������):
�����, ������� � �������. ����� ����� ��� �������� ������ ���������� ����������
����� ��������� ���������. ����� ������� ���������� ��� � ��������, � �������� ������� ���������� � ���������� ����������.
���� �������������, ��������, �
�������������� ��������� ����, ������� � ������ ��� ���������, ��� �����
����������� � D � ����� � N � (������ I), � ��������, � ������ II
���������� �� ��������, ��� ����� ����������� � �������� N � ����� � � D.
��������, ��� ���������� ������ ������ ���� ������������ � ������ �������
�������� ��������. ������� ������ ����� ���� ������������, ��� ��� ������ ��
������������ ����� ���� ���������. ����� ������ ��������� ���������� �������� �
������������� ������� �����������, �.�. ����� D, �
������� �������� �������� ����������� ������� (���������), ���� n(I)‑n(II) > D, ��� n(I) � n(II)
� ����� ���������� ������������, ��������������, �� ����� I � II.
��� ���������� ���������� ��������
������������ ��������� �������������� ����� � ���������, ����������� �������
�������������, �������� � ������������ ��������. ����������������� ��������
������� �������� �������� ������� ������������� �8 .����� �����, � 1985 �.
���������� ��������� "������". ��������� ���������� ���� ��������
��������� � ����. 1. � ������ �������, ���������� �� ����� ���������,
��������������� ���� ������������� ����������� ���������� "��������
���������" (��, ���������� ����� �������� �������� ������������� � ������������
���� ������� � 5‑20 ���.
������� 1.���������� �������� ���������� ��������
|
�������� |
�������, �� |
�����������
������������� / �� ����� ����� |
������������-����� ������� |
������������� ������� |
|
M8 |
������������� ������[1],
8.0 |
7/7 |
39% |
> 99% |
|
M8+C� |
6/7 |
20% |
> 99% |
|
|
M8 |
������������� ������[2],
7.5 |
20/30 |
42% |
> 99% |
|
M8+�� |
11/30 |
12% |
> 99% |
�������� ��, ��� ����� ��������� �������� � �������
������� ����������� ������� ������������� ������������. �� ���������� � �����
��������������� ������� �� ������. ���� �� ��� ������� � ���, ��� ����������
(������������������) �������������� ������������ ������� ���� ���������� �������������� �����, �.�.
������� ��� �� ��������������� � ����� ��������
������� ����� ������. ����� ����, ���� ������������� ����� �� ��������, �
���������������� �������� (������ �����), � ����� �������, ��� ���� ����
������� ������� ���������� ��� �������� ����� �������������� �����. ����������
���������� ������, ������ ��������� ���������� ���������������� ������� �
������������� ��������.
���������� ������������� ������� ���������
(������) � ���������� ����� 3 � �������� R
(�������� ������� ��� R = 4 ����������� �� ���. 1). ������ �� ��� ��������� ����� ���� � ��������� 0
��� 1. ������� ��������� � ��������� ������� (i+1)‑�� ������, ����� �����
������ (��������) ����� ��������� � ��� 3‑� ��������� i‑�� ������ ��������� ���
�������� ��������� ����� �.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
������� 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���� |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���� |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
������� 1 |
���. 1. �������� ������������� �������
������� ������� ���������� ������ ������� �� ���� ��������� �����������.
����� �(i) � ��������� ��������
(������) �� i‑� ������, ����� �(i+1) = F(�(i)). ����� �������, ���������
������� ������� �� ������� F (������������
�������) � �������� ��������� �������� �(1)
�� ������ ������. ���������� �������, ����� ��� ������������� ������� ��
������ i+1 ��� ��� ���������������
�������� ����������� ������ i
������ ���� ��������, �.�. � = 3.
����� F(�) = �3. ����� � = 0 � � = 1 �������� ������������, ��� ���� ����� � = 1 �����������, � ����� � = 0 ���������. ��� ��� �� ����
�������, ����� �������� ��������� � < 1,
� ����������� ������ ��������� �������� ��������� � 0, �.�. �������� ��������
������� ������ �� ���� �����������. ������� ���� ������ ������������� (S).
����� � = 1, �.�. ��� �������� ������� �� ���������
������� ���������� ���� �� ������ ������� ����� ��������������� ���������
������� ������. ����� F(�) = 1‑(1‑�)3
� ���������� �� �� ��� ����������� �����: � = 0
� � = 1, ������ ��������� ��������
����������, ��� ��� ��� �������� ��������� � > 0
� ����������� ������ ��������� �������� ��������� � 1. ������� �������, �����
������ ������� ������ �������� ���������� ��������������� ��������� �������
�������. ������� ��� ����������� (C).
|
���. 3. ������ ������������ ������� F (����������� �����) � ������ ������������������ ����������� (������ ���������� ��������� � K=1 � K=3) |
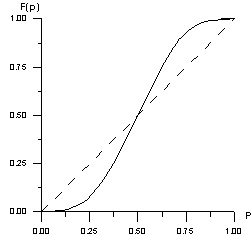
����� � = 2,
����� F(�) = 3�2(1‑�)+�3. � ���� ������ ����������
��� ����������� �����: ���������� � = 0,
� = 1 � ������������ � � = 0,5. ��� ��������
��������� � < 0,5 �
����������� ������ ��������� �������� ��������� � 0, � ��� � > 0,5 � ��������� �������� ��������� � 1 (���. 2). ����� � = 0,5
�������� ����������� �, ���� ��� ������� ������ ��������� �������� ����� 0,5,
�� ��� ��������� ����� �� �� ��������� �������. ���� ������� �� ���������
������� M(i) = i lg 3, �� ����� ��������, ��� ������
������������� � ������ ����������� ��������� ����� �������� �� ���������, �
������� � ���������� ������� �������, �.�. ��� ������� �, ����� ����� ���� ��� � < 0,5,
�.�. � ����������� ����� ������ ������, � ��� � > 0,5 � �����
����� �����. ������� �������, � ����� � = 0,5 ���������� ������� ������� ������� ��
������������ � ����������. ������� ������ ������ ������������ ������������ (UC).
���������� �������, ��������� �� ���������
���� ������ �����: ������ ���������� ����������, ���� � = 3, � ������ � ���� � = 1. �����������, ��� �� �����
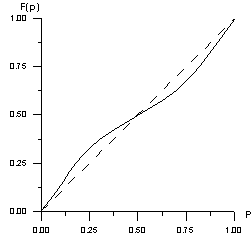
������ ����� ��������� ������� ���� ����� ����� ��������� ������� ����. ����� F(p) = 0,5(1‑(1‑p)3) + 0,5p3. ��� ������� ����� ���
������ �����: � = 0,
� = 0,5 � � = 1
(���. 3). ����� � = 0,5
�������� ����������, � ��� ������ � ���, �.�. ��� ����� ��������� ���������
�������� p ¹ 0;1
� ����������� ������ ��������� �������� ���������������. ��� ���� ������
������������� ������. ������
����� ���� �������� � ��������� ���������. ��
���������� ������ ����� ���� ������������ ����������� ���������������� ����������
� ������������� ���� �� �������� ������������ ������� ���������. ������, �����
������� ����������� ��������, �������� ���������� ������������������
����������, ���� �� ���������� ������������, �� ������� ����� ����������, ��
��������� ���������, �������������� ������ �������.
� ������� ������������ � ����� �����
���������� ������������ ��������������
������, �������� ��������, �� ������ ���������� � �������������
��������������� ���������������� ������� ��������������� � ���������������
������. ������� ����������� ������������� �������� � ��������������
���������������, � �������������� ��������, ���� � ������ ���������� �������
����������������� ������ (� ������� ������� ���������� ������������ �������), ����
���������� ��������. � ������ ����� �� ������ ���� ������������ ���� �������������
������.
������ �������������� ������ �����������,
������������, ���������, ���� ���������� ��������������� ������ ����� ����������
�������� ����� ������. � ������� ��������, ������� ��������� �������
�����������, ���� ����� � ��� �����������, � ��� ������������������. �
��������� ���������� ��������� ����������� �� �������� � ��������� ��������, �
������ ��� ����� ������� ������. � ����� ������� ����� ����� ������� �������
��������������� � ������� �������� ��������, � ������ �����������
�������������� ��������. ��� ��������� ������������ �������, ���������� ������������������
������������. �� ��� �������� ������������� �������� �� �������������� �
����������������-�������������� �������� ������ ������� �������. ��-��������,
������ ��� ��������� ����� �������� � ������ ������ �������������� �������
���������� ������.