Численное моделирование трансформации рентгеновского излучения
в объектах с учетом влияния форм-факторов на угловое распределение фотонов
|
|
|
(1) |
где ![]() ,
, ![]() , а из закона сохранения энергии и импульса следует связь
между углом рассеяния и энергиями фотона до и после рассеяния:
, а из закона сохранения энергии и импульса следует связь
между углом рассеяния и энергиями фотона до и после рассеяния:
|
|
(2) |
где e и e’ – соответственно энергия фотона до и после рассеяния (Рис. 5).
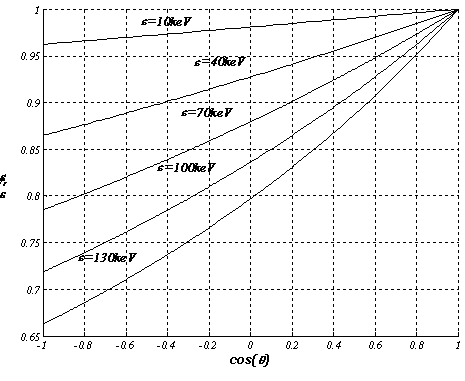
Рис. 5 Зависимость отношения энергии рассеянного фотона к энергии первичного в зависимости от угла рассеяния и энергии первичного фотона.
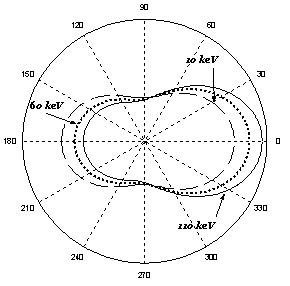
Рис. 6
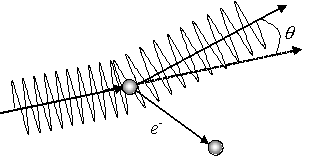
Угловое распределение фотонов при комптоновском рассеянии определяется в соответствии с (1) следующей формулой:
|
|
((3) |
где 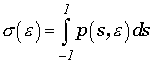 - полное комптоновское сечение. График углового распределения представлен
на Рис. 6.
- полное комптоновское сечение. График углового распределения представлен
на Рис. 6.
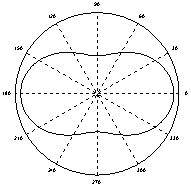
Рис. 7
Если импульс, передаваемый электрону много меньше ![]() (при
(при ![]() для всех направлений
или при
для всех направлений
или при ![]() для всех энергий), то
формула (1) переходит в формулу Томсона
для всех энергий), то
формула (1) переходит в формулу Томсона
|
|
(4) |
Рис. 6.
и угловое распределение будет описываться
следующей формулой (см. Рис.7):
|
|
(5) |
Предположение о свободном и покоящемся электроне
справедливо только при условии, что импульс, передаваемый электрону, намного
превышает импульс его первоначального движения в атоме ![]() , где l и le ‑ первоначальные длины волн соответственно фотона и электрона.
Наличие связей и первоначального движения электронов приводит к уменьшению вероятности
комптоновского рассеяния и исчезновению жёсткого соотношения между
, где l и le ‑ первоначальные длины волн соответственно фотона и электрона.
Наличие связей и первоначального движения электронов приводит к уменьшению вероятности
комптоновского рассеяния и исчезновению жёсткого соотношения между ![]() и q (так называемый «binding»
эффект). В этом случае дифференциальное сечение некогерентного Комптоновского
взаимодействия можно рассчитать, введя поправку к распределению Клейна–Нишины:
и q (так называемый «binding»
эффект). В этом случае дифференциальное сечение некогерентного Комптоновского
взаимодействия можно рассчитать, введя поправку к распределению Клейна–Нишины:
|
|
(6) |
![]() ‑
соответствующая нерелятивистская функция рассеяния Хартри‑Фока [9],
учитывающая эффект связи электронов (приведена на Рис. 10 для алюминия и железа).
‑
соответствующая нерелятивистская функция рассеяния Хартри‑Фока [9],
учитывающая эффект связи электронов (приведена на Рис. 10 для алюминия и железа).
Угловое распределение рассеянных фотонов в этом случае будет определяться следующей формулой:
|
|
(7) |
где 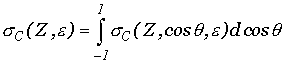 .
.
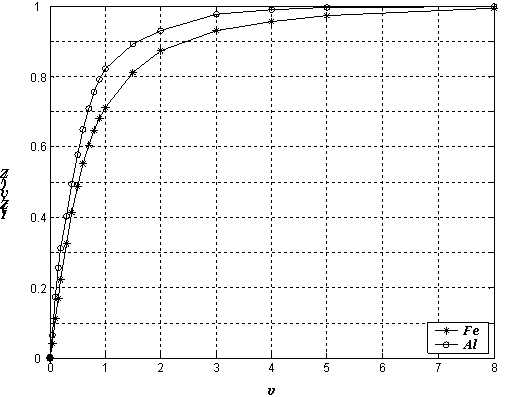
Рис. 8 Нерелятивистская функция рассеяния Хартри – Фока.
Отметим, что в отличие от распределения Клейна ‑ Нишины, в формуле (6) появляется зависимость от материала. Как видно из Рис. 9, эффект учета связи электронов, приводит к уменьшению вероятности рассеяния вперёд (к полному запрету рассеяния по направлению первоначального движения фотона) и к некоторому увеличению вероятности рассеяния назад, относительно первоначального движения g ‑ кванта для небольших энергий и более тяжелых элементов.
Как было сказано выше, рассеяние фотонов на электронах становится когерентным при небольшой величине передаваемого импульса. Если бы все атомные электроны участвовали в когерентном рассеянии независимо друг от друга, то их суммарный эффект при малых значениях передаваемого импульса точно компенсировал бы уменьшение комптоновского рассеяния, однако вследствие эффекта связанности, электроны атома участвуют в рассеянии когерентно. Поэтому вероятность рассеяния возрастает вследствие явлений интерференции.
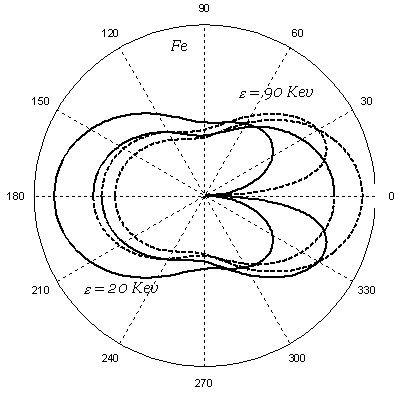
Рис. 9 Угловое распределение фотонов для железа в случае рассеянии на свободном электроне и в случае учета связи между электронами. Пунктирной линией отмечено распределение при 90 кэв, сплошной – при 20 кэв.
Интерференция может охватывать электроны,
принадлежащие разным атомам, и полная интенсивность когерентно рассеянных g ‑ квантов возрастает
ещё больше и концентрируется в узком пучке в направлении первичных фотонов. В
этом случае, дифференциальное сечение когерентного Рэлеевского рассеяния
вычисляется путем введения дополнительного множителя к распределению Томсона по
следующей формуле:
|
|
(8) |
где ![]() - релятивистский атомный форм-фактор Хартри-Фока [10], учитывающий
эффект связанности электронов (приведен на Рис.
10 для алюминия и железа).
- релятивистский атомный форм-фактор Хартри-Фока [10], учитывающий
эффект связанности электронов (приведен на Рис.
10 для алюминия и железа).
В формулах (7) и (8) ![]() ,
, ![]()
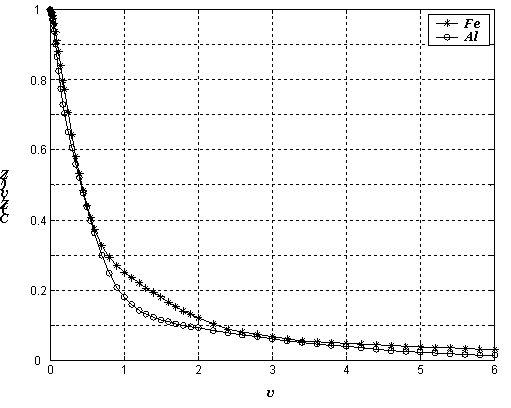
Рис. 10. Форм-фактор Хартри-Фока для когерентного рассеяния.
Угловое распределение рассеянных g ‑ квантов будет аналогично (7) определяться по следующей формуле:
|
|
(9) |
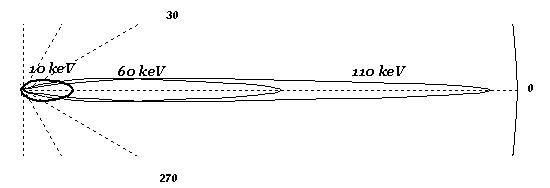
Рис. 11
Основной эффект влияния форм-фактора заключается в
уменьшении вероятности рассеяния фотонов в обратном направлении для высоких
энергий и лёгких элементов, что противоположно действию функции рассеяния ![]() . Этот эффект показан на Рис. 11.
. Этот эффект показан на Рис. 11.
Алгоритм расчета.
В рассматриваемой модели предполагается, что фотоны не взаимодействуют друг с другом и переход из одного состояния в последующее зависит только предыдущего. В этом случае задача сводится к моделированию «цепи Маркова», представляющей собой последовательность случайных событий (актов взаимодействия фотонов с веществом). Поэтому для решения задач моделирования взаимодействия рентгеновского излучения с материалами и трансформации этого излучения при прохождении через многокомпонентные объекты, удобным вследствие высокой гибкости и приспособленности к решению сложных граничных задач является метод статистических испытаний, или метод Монте-Карло. Развитие высокопроизводительных многопроцессорных суперкомпьютеров в сочетании с возможностью эффективного распараллеливания метода Монте-Карло дает в настоящее время мощный и эффективный инструмент для математического моделирования рассматриваемых процессов.
Рассмотрим основные особенности моделирования фотонных траекторий, использованные при построении расчетного алгоритма.
Будем считать, что внешние границы объекта являются абсолютно поглощающими, в том смысле, что фотон, однажды вылетевший из объекта, обратно не возвращается.
Траекторию фотона, испытавшего n‑кратное
рассеяние, можно записать в следующем виде: ![]() , где
, где ![]() ‑ пространственные координаты,
‑ пространственные координаты, ![]() ‑ направление движения,
‑ направление движения, ![]() ‑ длина волны фотона,
‑ длина волны фотона, ![]() ‑ статистический «вес» фотона.
‑ статистический «вес» фотона.
Для каждой фотонной траектории исходными данными являются начало первого звена, направление движения частицы, энергия фотона и его статистический вес (обычно равен единице, когда g ‑ квант «покидает» источник).
Метод расчета траекторий фотонов строится следующим образом:
- в случае, если луч в направлении движения фотона пересекает детекторную плоскость, рассчитывается вклад данного звена фотонной траектории в интенсивность регистрируемого излучения;
- вычисляется конец текущего звена траектории путем розыгрыша случайной величины – оптической длины пути фотона до точки взаимодействия;
- в случае если конец звена лежит вне объекта, траектория считается оконченной;
- в противном случае «вес» фотона уменьшается путем умножения текущего веса на вероятность его непоглощения:
![]() ,
,
i ‑ номер компоненты объекта, в которой находится очередная точка рассеяния фотона;
- определяется тип рассеяния (когерентное или некогерентное);
- вычисляется новое направление движения кванта и его энергия путем розыгрыша случайной величины – косинуса угла рассеяния фотона.
Остановимся на этом более подробно.
Азимутальный угол ![]() (рассматривается неполяризованное первичное
излучение) нового направления движения фотона определяется по формуле
(рассматривается неполяризованное первичное
излучение) нового направления движения фотона определяется по формуле ![]() , где g - случайное число из интервала (0, 1).
, где g - случайное число из интервала (0, 1).
Для определения полярного угла q используется следующий алгоритм. Имея нормированное распределение ![]() , q -
полярный угол отклонения кванта от направления движения до рассеяния, и
равномерно распределенную в интервале (0,1) случайную величину g,
, q -
полярный угол отклонения кванта от направления движения до рассеяния, и
равномерно распределенную в интервале (0,1) случайную величину g, ![]() можно получить из уравнения (см., например,
[5]):
можно получить из уравнения (см., например,
[5]):
|
|
(8) |
Основную трудность при определении полярного угла q представляет решение уравнения (8) ![]() . Вычисление
. Вычисление ![]() на каждом звене
траектории, учитывая, что число таких траекторий может достигать 1010
и более, требует огромных вычислительных затрат. Поэтому в алгоритме
предусмотрено использование заранее подготовленных двумерных таблиц
на каждом звене
траектории, учитывая, что число таких траекторий может достигать 1010
и более, требует огромных вычислительных затрат. Поэтому в алгоритме
предусмотрено использование заранее подготовленных двумерных таблиц ![]() , построенных с заданной точностью на равномерных сетках по
, построенных с заданной точностью на равномерных сетках по ![]() и
и ![]() .
При этом внимание уделяется как точности вычисления интеграла в (8), так и
требованию малости изменения значений
.
При этом внимание уделяется как точности вычисления интеграла в (8), так и
требованию малости изменения значений ![]() в соседних ячейках
таблиц. Методика
построения указанных таблиц основана на численном интегрировании сеточных
функций, построенных путем интерполяции экспериментальных данных [11].
в соседних ячейках
таблиц. Методика
построения указанных таблиц основана на численном интегрировании сеточных
функций, построенных путем интерполяции экспериментальных данных [11].
Применение этих таблиц позволяет свести вычисление
косинуса полярного угла рассеяния фотона к нескольким арифметическим операциям
определения номера элемента двумерного массива ![]() .
.
В случае, когда влияние функции рассеяния для
некогерентного рассеяния не учитывается, в качестве ![]() используется
используется ![]() (решение
(решение ![]() уравнения (8)
изображено на Рис. 12). Если влияние binding-эффектов учитывается, то для Комптоновского
рассеяния используется
уравнения (8)
изображено на Рис. 12). Если влияние binding-эффектов учитывается, то для Комптоновского
рассеяния используется ![]() и, соответственно,
для Рэлеевского -
и, соответственно,
для Рэлеевского - ![]() . В этом случае необходимо для каждого материала создание
таблиц, как для Комптоновского, так и для Рэлеевского рассеяния (решение
. В этом случае необходимо для каждого материала создание
таблиц, как для Комптоновского, так и для Рэлеевского рассеяния (решение ![]() уравнения (8)
показано на Рис.13, 14).
уравнения (8)
показано на Рис.13, 14).
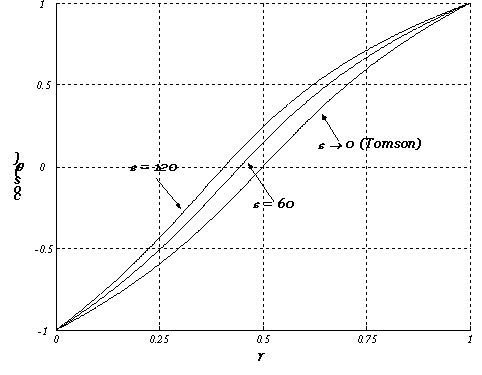
Рис. 12

Рис. 13
Отметим, что для описания трехмерных объектов используется поверхностно ориентированный подход [3,4] в совокупности с триангуляционной моделью дискретизации граничных поверхностей, разделяющих гомогенные части многокомпонентного объекта.
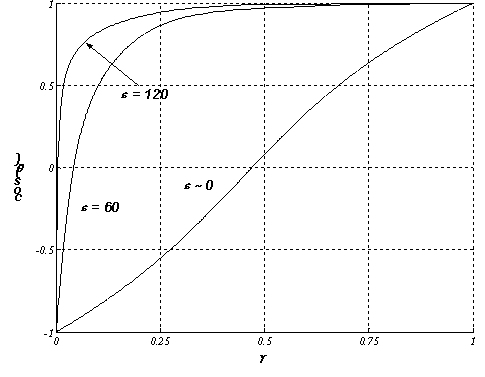
Рис. 14
Результаты расчетов.
В настоящей работе исследовалось влияние «binding»-эффектов на пространственное распределение и интенсивность рассеянного излучения. Рассматривались следующие модели:
- Модель A, не учитывающая эффект связанности электронов, при этом предполагается, что все электроны свободные;
![]() ;
;
- Модель B, учитывающая «binding» эффект:
![]() .
.
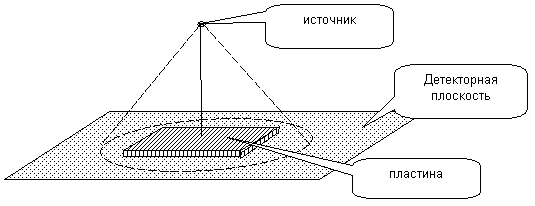

Рис. 15 Схема численного эксперимента.
Расчеты проводились в следующей геометрии (см. рис.15):
пластина размерами 5см х 5см х 1см, высота расположения источника - 100 см. угол «раствора» источника выбирался таким образом, чтобы излучение покрывало всю пластину. Анализ влияния рассматриваемых эффектов проводился как для моноэнергетических источников g‑квантов, так и для источника с распределённым энергетическим спектром (см. Рис. 16).
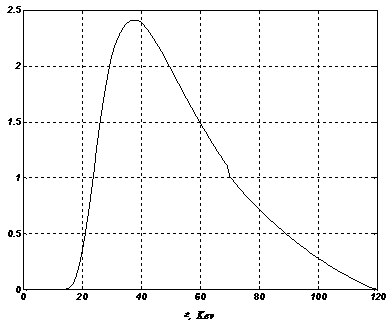
Рис. 16 Спектр использованного полиэнергетического источника.
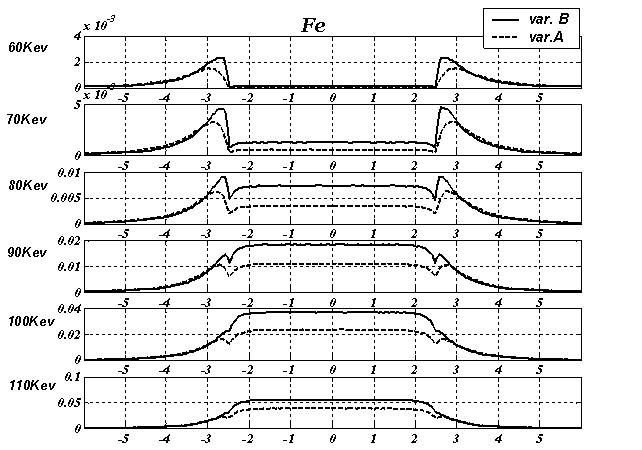
Рис. 17 Интенсивность рассеянного излучения для железной пластины при различных энергиях источника фотонов.
На Рис. 17 приведены результаты расчета для железной пластины, облучаемой моноэнергетическим источником ионизирующего излучения при различных энергиях фотонов. Для источника со спектром, приведенном на Рис. 16, результаты представлены на Рис. 18. На Рис.19 и Рис. 20 соответствующие результаты расчетов для алюминиевой пластины. Результаты приведены по центральному срезу пластины.
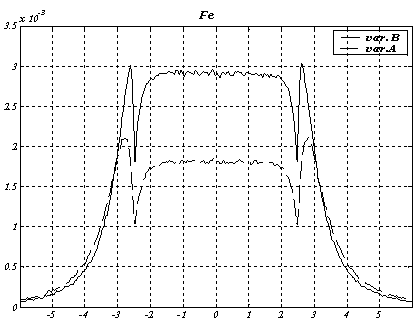
Рис. 18 Интенсивность рассеянного излучения для железной пластины для немоноэнергетического источника g‑квантов.
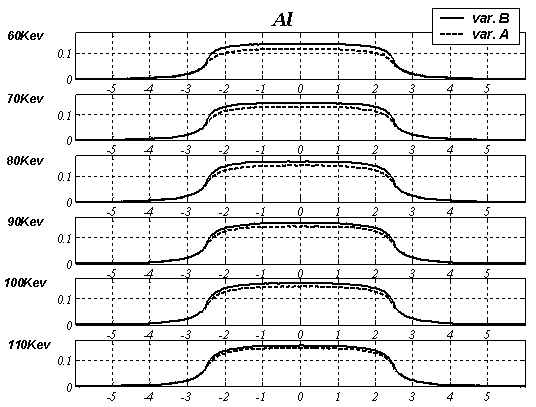
Рис. 19 Интенсивность рассеянного излучения для алюминиевой пластины при различных энергиях источника g ‑ квантов.
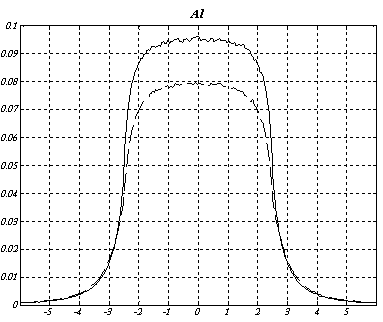
Рис. 20 Интенсивность рассеянного излучения для алюминиевой пластины для немоноэнергетического источника фотонов.
Результаты проведенных расчетов показали, в частности, следующее.
Учет форм-факторов для когерентного рассеяния и для некогерентного (комптоновского) рассеяния (binding-эффектов) приводит к увеличению интенсивности рассеянного излучения по сравнению со случаем, когда эти эффекты не учитываются. Причем соответствующее изменение интенсивности зависит как от просвечиваемого материала, так и от энергии проникающего излучения.
На Рис. 21 приведены графики зависимости отношения интенсивности рассеянного излучения, рассчитанного без учета эффектов связанности электронов (модель A), к интенсивности излучения, рассчитанной с учетом этих эффектов, (модель B) от энергии фотонов рентгеновского излучения. Приведенные графики показывают, во-первых, что, что для более жесткого излучения влияние исследуемых эффектов меньше (величина указанного отношения ближе к единице), и, во-вторых, для тяжелых элементов учет указанных эффектов более важен (соответствующая кривая ниже для железа, чем для алюминия), чем для легких.
Проведенные численные исследования показали также, что степень влияния рассматриваемых факторов на интенсивность рассеянного рентгеновского излучения зависит также от толщины облучаемого материала. А именно, с увеличением толщины влияние учета «binding» ‑ эффектов возрастает, в особенности это относится к более тяжелым материалам.
На рисунке Рис. 22 в качестве примера приведен график зависимости рассмотренной выше величины степени влияния связанности атомных электронов от толщины железной пластины для монохроматического рентгеновского излучения с энергией фотонов 80 кэВ.
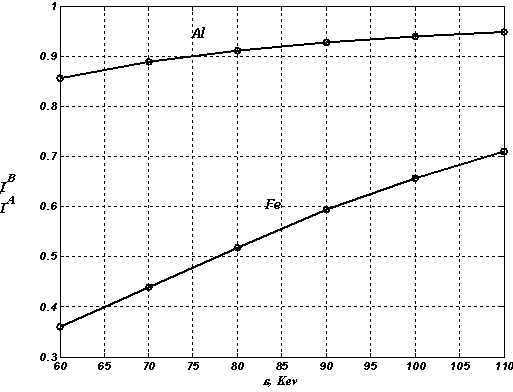
Рис. 21 Зависимость отношения интенсивностей при разных энергиях.

Рис. 22 Зависимость отношения интенсивностей для разной толщины железной пластины.
Заключение.
Анализ результатов расчетов, проведенных с использованием
разработанного алгоритма, реализованного на языке FORTRAN с использованием
параллельного интерфейса MPI, показал, что в ряде ситуаций учет рассмотренных
физических факторов оказывает существенное влияние на интенсивность и
пространственное распределение трансформированного ионизирующего излучения.
Проведено исследование различных типов взаимодействия фотонов ионизирующего излучения с материалами объектов, в частности, комптоновского и рэлеевского рассеяния этих фотонов. Проведен анализ влияния на характеристики рассеянного излучения изменений угловых распределений рассеянных фотонов, обусловленных влиянием связанных атомных электронов, в зависимости от материала объекта и энергетики квантов. Этот анализ показал, что учет форм-факторов для когерентного рассеяния и для некогерентного (комптоновского) рассеяния (binding-эффектов) приводит к увеличению интенсивности рассеянного излучения по сравнению со случаем, когда эти эффекты не учитываются. Причем соответствующее изменение интенсивности зависит как от плотности облучаемого материала, так и от энергии проникающего излучения, в частности, для более жесткого излучения влияние исследуемых эффектов меньше. В тоже время, для тяжелых элементов учет указанных факторов более важен, чем для легких.
Проведенные численные исследования показали также, что степень влияния рассматриваемых факторов на интенсивность рассеянного рентгеновского излучения зависит также от толщины облучаемого материала. А именно, с увеличением толщины влияние учета binding-эффектов возрастает, в особенности это относится к более тяжелым материалам.
Полученные результаты предполагается использовать, в частности, при исследовании процессов образования потоков электронов при прохождении рентгеновского и гамма-излучения через объекты.
1. М.Е.Жуковский. Самосогласованная квазитрехмерная модель радиационного возбуждения электромагнитных полей. Математическое моделирование, том 8, N4, 1996, с.3-20.
2.
Proceedings of
the 2nd International Conference on Computer Methods and Inverse Problems in
Nondestructive Testing and Diagnostics.
Minsk, Belarus, DGZfP Berichtsband
64, 1998.
3.
V.P.Zagonov and
S.V.Podolyako. «On a boundary description approach in NDE problems.» Keldysh
Institute for Applied Mathematics of Russian Academy of Sciences, № 3, 2000.
4. V.P. Zagonov, S. V. Podolyako, G.-R. Tillack, C. Bellon. Fast «3D ray tracer algorithm for cone beam radiography.» 3-я международная конференция «Компьютерные методы и обратные задачи в неразрушающем контроле и диагностике», Москва 2002, с.102
5. У. Фано, Л. Спенсер, М. Бергер. «Перенос гамма-излучения» Госатомиздат, Москва, 1963.
6. А.И.Ахиезер, В.Б.Берестецкий «Квантовая электродинамика», Издательство «Наука», Москва, 1969
8. Н.Г. Гусев, Л.Р. Кимель, В.П. Машкович, Б.Г. Пологих, А.П. Суворов «Защита от ионизирующих излучений», Атомиздат, Москва, 1969
9.
Hubbell, J. H.,
Veigele, W. J., Briggs, E. A., Brown, R. T., Cromer, D. T., and Howerton, R.
J.: «Atomic Form Factors, Incoherent Scattering Functions, and Photon
Scattering Cross Sections.» J. Phys. Chem. Ref. Data 4, 471-538 (1975); erratum
in 6, 615-616 (1977)
10. Hubbell, J. H. and Overbo: «Relativistic Atomic
Form Factors and Photon Coherent Scattering Cross Sections» J. Phys. Chem. Ref.
Data 8, 69-105, (1979)
11. J. F. Briesmeister (ed.): MCNP–A General Monte Carlo
N–Particle Transport Code. LANL Report LA–13709–M, Los Alamos, 2000.
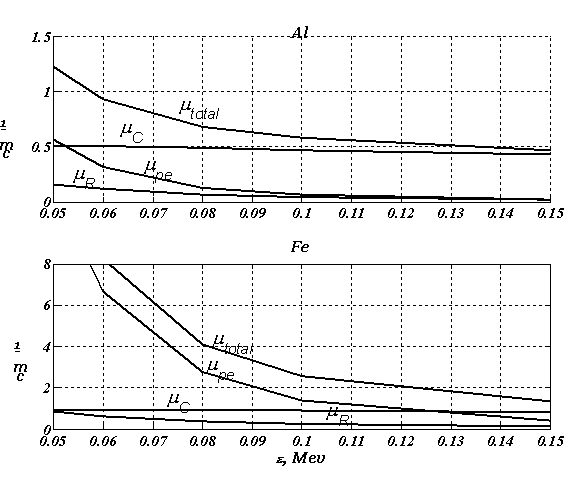
[1] Следует отметить, что при решении обратных задач вычислительной
диагностики обычно используют полный коэффициент ослабления, поскольку в этом
случае можно выписать прямой оператор для «теневой» области объекта:  , что для моноэнергетического источника приводит к линейному
уравнению относительно µ и позволяет использовать известные методы для его
восстановления.
, что для моноэнергетического источника приводит к линейному
уравнению относительно µ и позволяет использовать известные методы для его
восстановления.

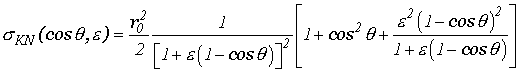 ,
,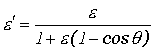 ,
,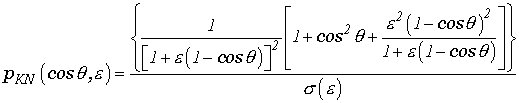
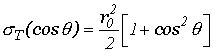 ,
,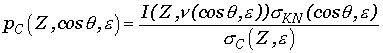

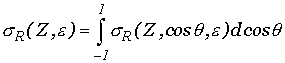
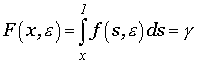 ,
,