СОДЕРЖАНИЕ

Введение

Микроволновая радиометрия приобретает все большее распространение в различных областях науки и техники [1]. Вместе с тем, многие импульсные высокоэнергетические процессы в атмосфере сопровождаются генерацией микроволнового излучения. К таким процессам относятся мощные взрываы., техногенные катастрофы с выбросом радиоактивного излучения, всплески космического рентгеновского и гамма излучений (например, от солнечных вспышек) и др.  Представляется перспективным использование микроволнового метода дистанционного обнаружения и определения параметров таких объектов, поскольку этот метод объединяет достоинства оптического и радиометодов, в частности высокую точность и независимость от погодных условий.

Микроволновый метод регистрации обеспечивает наиболее высокую точность (как и оптический), если излучение регистрируется в пределах прямой видимости, когда сам источник микроволнового излучения находится в пределах «антенного пятна» регистрирующего прибора. Чем выше постоянная времени прибора, тем выше его чувствительность. Однако на практике местоположение и момент возникновения излучающего объекта заранее, как правило, неизвестны. Время существования ионизирующего излучения невелико (до 0,1 – 1,0 с). Поэтому важно иметь возможность регистрировать микроволновое излучение даже в том случае, когда его источник оказывается вне диаграммы направленности регистратора.

В данной работе (для решения задач обнаружения) проводится расчет параметров воздушной плазмы, созданной источником ионизирующих излучений, и радиояркостной температуры микроволнового излучения этой плазмы при произвольных ориентациях диаграммы направленности регистрирующего прибора по отношению к источнику. Отметим, что предлагемый авторами метод расчета после сравнительно несложной модернизации может быть испрользован для расчета параметров воздушной плазмы (и радиояркостной температуры) при наличии нескольких источников (например, при мноржественных взрывах).

Авторами создан пакет программ “BRIGHT”, позволяющий моделировать воздушную плазму, образованную источником ионизирующих излучений, рассчитать в зависимости от координат и времени радиояркостную температуру плазмы как основную характеристику тормозного микроволнового излучения (МКИ).

Разработанный ранее аналогичный пакет “OPTHICK” [2] существенно модернизирован. Главной задачей авторов  было совершенствование пакета и расширение его функций. Если в предыдущем варианте расчет параметров плазмы был возможен только в направлении луча зрения от радиометра на источник, то в предлагаемом варианте направление луча зрения может быть произвольным. Направление оси диаграммы направленности приемника задается углом места, т.е. углом между лучом и горизонтальной плоскостью, и углом j в горизонтальной плоскости между вертикальной плоскостью, в которой находятся приемник и источник и вертикальной плоскостью, в которой расположен луч зрения.

Меняя входные параметры модели (мощность, тип и высоту источника, высоту приемника и направление его луча зрения, временные интервалы и шаг расчета во времени, пространственный шаг расчета параметров вдоль луча зрения, диапазон длин волн регистрируемого МКИ), можем рассчитать временные и пространственные распределения концентраций частиц ионизованной плазмы, вычислить электронную проводимость ее, рассчитать зависимость коэффициента поглощения от координаты вдоль луча зрения. Интегрируя коэффициент поглощения вдоль луча с учетом высотной зависимости воздуха, вычисляем оптическую толщину плазмы, а затем ее радиояркостную температуру.

Структура пакета осталась прежней. Для удобства читателя приведем в этой работе структуру и основные назначения ее узлов, оставляя за рамками более подробные описания. Читатель найдет их в работе [2].

Пакет программ ориентирован в первую очередь на быстрое качественное исследование в диалоговом режиме характеристик плазмы в широком диапазоне изменения параметров задачи. При разумно ограниченных требованиях к точности предпочтение отдано скорее быстроте анализа, чем максимальной точности алгоритмов.     

         Входными параметрами пакета являются:

- энергия источника;

- высота источника над поверхностью Земли;

- характерная длина волны микроволнового диапазона;

- угол места - угол между лучом зрения (т.е. осью диаграммы направленности приемника) и горизонталью;  

- угол в горизонтальной плоскости - угол между вертикальной плоскостью, в которой находятся источник и приемник, и вертикальной плоскостью, проходящей через луч зрения;

- эпицентральное расстояние до приемника;

- высоту приемника;

- величины, характеризующие тип источника, начальный и конечный моменты времени расчета, число расчетных точек по времени и по координате.               

Результатами расчета являются зависящие от времени:

- пространственное распределение концентраций частиц плазмы (концентрация электронов; концентрация положительных ионов  ; концентрация положительных ионов ; концентрация отрицательных ионов кислорода; концентрация отрицательных ионов ; концентрация нейтральных молекул );

- электронная проводимость плазмы;

- коэффициент поглощения микроволнового излучения;

- оптическая толщина плазмы вдоль направления наблюдения;

- яркостная температура плазмы.

По рассчитанным пространственным распределениям концентраций частиц и по распределению яркостной температуры можно оценить размеры и форму плазменного облака и области, «светящейся» в микроволновом диапазоне.

Созданный для решения этой задачи пакет программ “BRIGHT” позволяет вычислить электрофизические параметры воздушной плазмы, решить уравнение переноса микроволнового излучения, диагностировать плазму микроволновым методом, обнаруживать и классифицировать источники ионизирующих излучений. Программы написаны на языке С и предназначены для работы в среде DOS.

ОРГАНИЗАЦИЯ ПАКЕТА

Пакет состоит из программы приема параметров задачи и четырех программ, реализующих основные этапы расчета. В качестве самостоятельной части в него входит программа графической визуализации результатов GRFM [3] (версия GRF). В комплект также следует включать редактор ASCII текста (авторы использовали Lexicon) для корректировки заданий. Вызовы всех программ пакета (и внешних по отношению к пакету программ) производятся из главного меню, управляющего работой всей программы, и из отдельных меню, каждое из которых решает специфические задачи моделирования. Ниже приведена структура управления пакетом:

       ГЛАВНОЕ  МЕНЮ

     МЕНЮ  1: “РАСЧЕТ ПОЛЯ КОНЦЕНТРАЦИЙ”;

     МЕНЮ  2: “АППРОКСИМАЦИЯ КОЭФФИЦИЕНТОВ ПОГЛОЩЕНИЯ”;

     МЕНЮ  3: “РАСЧЕТ ОПТИЧЕСКОЙ ТОЛЩИНЫ”;

     МЕНЮ  4: “ РАСЧЕТ ЯРКОСТНОЙ ТЕМПЕРАТУРЫ”.

Каждое из частных меню (1-4) управляет отдельным этапом расчета. Этап начинается с указания входного файла данных (входной таблицы) и задания имен выходных файлов (выходных таблиц). В ходе расчета будут созданы поименованные выходные таблицы. Ввиду принципиальной важности корректной аппроксимации коэффициентов поглощения в меню второго этапа предусмотрен режим графического контроля качества аппроксимации на каждом шаге этого этапа.

Полное задание содержит расчет и формирование выходных файлов всех параметров воздушной плазмы. В этом случае выходной файл предыдущего шага задания служит входным файлом последующего. Файлы каждого шага имеют уникальное расширение. Возможно выполнение каждого шага как независимого задания с использованием специально заготовленных или ранее рассчитанных входных файлов с соответствующими данными.

Вызов пакета осуществляется командой BRIGHT.EXE . На экране появляется заглавие пакета. Нажатием любой клавиши перейдем в главное меню. Далее во всех заданиях пакета все команды однобуквенные. Сквозные команды, использующиеся во всех заданиях пакета:

G  - запуск счета;

V  - вывод на экран графиков. График, находящийся на экране, можно поместить в  файл формата  PCX   нажатием клавиши “X” или отпечатать на 9-иголочном принтере (EPSON 80 или аналогичном) нажатием клавиши «пробел».

         Q  - возврат к  главному меню, повторно  -  прекращение работы.    

Расчет параметров плазмы происходит в несколько этапов. Поэтапная работа позволяет либо полностью решить задачу (с определением всего набора выходных данных), либо решить любую ее часть, опустив ненужное.

На первом этапе методом Рунге-Кутта интегрируется система кинетических уравнений. Этот этап является центральной частью программного пакета. Входная информация  вводится в виде таблицы энергетических и геометрических параметров задачи. Основное назначение этапа -  расчет поля концентрации электронов и зависящего от нее  поля локальных коэффициентов поглощения микроволнового излучения.  Кроме концентрации электронов вычисляются концентрации остальных частиц, участвующих в процессах рождения и рекомбинации электрон-ионных пар.  На этом же этапе вычисляется электронная электропроводность плазмы. Все расчетные величины определяются как функции времени для фиксированного набора значений радиуса r (расстояния от источника). Используется стандартное распределение [4]  температуры и плотности атмосферы по высоте.

Второй этап необходим для подготовки расчета оптической толщины плазмы. Центральной частью этого этапа является программа - аппроксиматор. Эта программа аппроксимирует двумерную зависимость коэффициента поглощения а(r,t) от времени и расстояния по серии графиков зависимости a от времени при фиксированных r.

Третий этап содержит расчет оптической плотности плазмы (для набора фиксированных моментов времени) интегрированием коэффициентов поглощения вдоль луча наблюдения. При интегрировании используется аппроксимация из предыдущего этапа. Входная информация содержится в файле коэффициентов аппроксимации, на выходе получаем файл с таблицей значений оптической плотности.

Последний, четвертый этап предназначен для вычисления яркостной температуры плазмы в зависимости от времени. Он использует файл с таблицей значений оптической плотности, а создает файл с таблицей значений яркостной температуры.

На каждом этапе рассчитанные десятичные логарифмы параметров воздушной плазмы заносятся в свой файл, который далее может быть использован по усмотрению оператора. Возможен вывод таблиц на экран в виде графиков и печать графиков.

Ниже мы обсудим физическую постановку задач и опишем методику и характер решаемых задач в каждом из меню.

ГЛАВНОЕ  МЕНЮ

Главное меню запускает все принципиальные этапы расчета. Оно состоит из  4-х шагов задания.

Список команд главного меню:

С - расчет поля концентраций, электропроводности и коэффициентов поглощения как функций времени для набора расстояний от источника.

А - аппроксимация двумерной зависимости коэффициента поглощения;

         S -  расчет оптической толщины вдоль луча наблюдения;

         K - расчет яркостной температуры как функции времени.

Кроме того, для удобства пользователя введена команда

                D - вызов команды DOS.

При  решении  задачи  целиком  команды  должны выполняться  в следующем  порядке: C, A, S, K.

РАСЧЕТ ПОЛЯ КОНЦЕНТРАЦИЙ

При вводе команды С в главном меню переходим к расчету концентраций, коэффициентов поглощения и электропроводности воздушной плазмы.

Центральной частью этого раздела является функция RUNGE9, рассчитывающая концентрации частиц в воздухе методом Рунге-Кутта. Решается система кинетических уравнений, приведенных в работе [2]. По вычисленной концентрации электронов рассчитывается проводимость плазмы, эффективная частота столкновений электронов с нейтральными частицами и коэффициент поглощения электромагнитных волн.

Приведем список однобуквенных команд и их значения.

I - выбор входного файла задачи (обязательное расширение .OPI),  в  котором должны быть указаны все необходимые для расчета входные данные. В файле даны  пояснения  ко  всем входным  параметрам. Обязательно вводятся: энергия источника; длина волны; высота источника; высота приемника; эпицентральное расстояние между источником и приемником; начальный момент времени счета; конечный  момент времени, на  котором счет обрывается; число расчетных точек по времени; число расчетных точек по расстоянию; угол места; угол j; а также характеристики источника. Имена заранее приготовленных файлов с расширением .OPI  выводятся в правом верхнем  углу экрана после нажатия клавиши I. Выбор файла осуществляется с помощью курсора - звездочки на левом крае рамки меню. Программа предлагает отредактировать выбранный файл текстовым ASCII редактором (имя редактора должно быть указано в  конфигурационном  файле OPTHICK.CFG).  Можно использовать редакторы: Lexicon, Kedit, WordStar, NE (Norton Еditor), ME(MultiEdit) и др. Непригодны ChiWriter и текстовые процессоры Windows. Программа  вычисляет автоматически  концентрации,  проводимости  и коэффициенты поглощения как функции времени и расстояния от источника. Рассчитан-ные величины выводятся в файлы только по заказу оператора.

Имена файлов можно ввести командами:

C - ввод имени выходного файла концентраций (расширение .OPC);

Е - ввод имени выходного файла проводимости (расширение .OPE);

L - ввод имени выходного файла коэффициентов поглощения (расширение .OPL).      

Команда L обязательна для продолжения работы с пакетом.

Исполнение полностью подготовленного задания запускаем командой G.

В файлы выводятся десятичные логарифмы соответствующих величин. При этом концентрации измеряются в см^-3, проводимости в Ом^-1см^-1, коэффициенты поглощения в см^-1. В каждом файле образуется семейство зависимостей от времени. Параметром семейства служит расстояние до источника. Чтобы перейти потом к расчету оптической толщины, обязательно нужно создать файл коэффициентов поглощения по команде L. Имена заказанных файлов появляются на экране.

Для графического просмотра на экране только что полученных зависимостей из указанных файлов используется программа GRFM [3], вызываемая командой V. Она может вывести на экран до 20 графиков одновременно. Файл концентраций (с расширением .ОРС) в типичном случае содержит 50-100 таблиц. Он состоит из 5-15 блоков, каждый из которых сформирован при определенном значении параметра r (расстояния между источником и точкой, где определяется концентрация). В каждом блоке содержится 7 столбцов (один столбец - значения аргумента, шесть - значения концентраций разных частиц). Такое обилие графиков нельзя просмотреть сразу. Поэтому в программе предусмотрена возможность отсроченного просмотра содержимого файла концентраций с помощью вспомогательной базы данных формата DBF.

Базу данных можно сформировать по заказу оператора после расчета концентраций. Для этого достаточно ответить Y(YES) на запрос программы, нужно ли создать базу. Тогда на основе файла концентраций будет создана база с тем же именем, но расширением .DBF. После завершения работы с программой BRIGHT можно просмотреть любые графики из базы данных, набрав команду GRF  и выбрав в главном меню этой программы работу с базой данных (команда B). Указав аргумент и ту функцию, график которой нужно построить, необходимо ввести параметр “radius = =“, задав в нем после знака двойного равенства расстояние от источника). Подробно работа  программы GRFM c базой данных описана в препринте [3].

АППРОКСИМАЦИЯ КОЭФФИЦИЕНТОВ ПОГЛОЩЕНИЯ

         Процесс распространения электромагнитного излучения в ионизированном воздухе зависит от оптической толщины плазмы. Последняя зависит от коэффициента поглощения электромагнитных волн. Для расчета оптической толщины воздушной плазмы необходимо проинтегрировать коэффициент поглощения вдоль луча зрения. На предыдущем этапе расчета мы получили поле коэффициентов поглощения в виде небольшого числа таблиц для нескольких радиусов r и несколько большего числа моментов времени t. В процессе интегрирования нам потребуется значительно большее количество отсчетов оптической толщины в точках, определяемых требуемой точностью интегрирования по r, и в моменты времени, нужные для выходной таблицы. При повторном многократном решении системы кинетических уравнений методом Рунге-Кутта время счета будет неоправданно велико, поэтому естественно использовать аппроксимацию полученных ранее решений подходящими гладкими функциями.

      Первоначальная постановка задачи требовала исследования качественного поведения искомых зависимостей в широком диапазоне изменения параметров задачи в диалоговом режиме при разумно ограниченных требованиях к точности конкретного решения, т.е. ориентировала скорее на быстрые, нежели максимально точные алгоритмы. Это определило предпочтение кусочно-линейной аппроксимации в основных зависимостях. Была разработана процедура, допускающая полностью автоматическое построение аппроксимирующих отрезков при небольшом количестве хранимых коэффициентов. Подробное описание алгоритма аппроксимации приведено в работе [2].

Напомним команды меню этого раздела.

L - выбор имени входного файла (расширение .OPL) из меню в правом верхнем углу.

В - ввод имени выходного файла (расширение .OPB),  в которое будут заноситься результаты аппроксимации.

V - назначение режима просмотра каждого графика в процессе аппроксимации. Исходно по умолчанию установлен режим без просмотра графиков. После нажатия клавиши V устанавливается вывод точек каждого очередного графика семейства на экран вместе с аппроксимирующей кривой. В строке меню с командой V появляются три звездочки (просмотр включен). Повторное нажатие V отменяет режим просмотра (звездочки исчезают). В режиме просмотра кривых после вывода очередного графика для продолжения счета следует нажать «Ввод». Нажатие клавиши X приведет к фиксации графика в файле формата PCX, а нажатие пробела - к его печати на 9-иголочном принтере EPSON 80.

Шкальные коэффициенты для разбиения области значений аргумента на субсегменты заданы в конфигурационном файле OPTHICK. CFG. Если оператора при просмотре графиков не удовлетворяет качество аппроксимации, число субсегментов можно увеличить, добавив новые шкальные коэффициенты в этот файл, после чего перезапустить программу BRIGHT.

РАСЧЕТ ОПТИЧЕСКОЙ ТОЛЩИНЫ

Расчет оптической толщины плазмы t₀  необходим для вычисления яркостной температуры. Кроме того, знание оптической толщины полезно само по себе.  Если плазма оптически толстая (t₀  >> 1) , микроволновое излучение заперто внутри ионизованной области, и яркостная температура практически равна радиационной температуре плазменного образования. В случае источников ионизирующих излучений, находящихся на большой высоте, оптическая толщина плазмы обычно мала (на временах порядка нескольких десятков мкс и более после возникновения источника). В оптически тонкой плазме (t₀  << 1) радиояркостная температура области генерации микроволнового излучения пропорциональна ее оптической толщине.

Входным файлом программы интегрирования коэффициентов поглощения по лучу зрения является файл с расширением .OPB, содержащий константы кусочно-линейной аппроксимации, проведенной на предыдущем этапе вычислений. В этом файле находится набор констант для каждой из заданных теперь аналитически  кривых семейства зависимостей коэффициента поглощения от времени с заданным параметром r (расстоянием от источника). Проведя сечение кривых при t = const, получаем набор точек, определяющий зависимость коэффициента поглощения от расстояния. По этому набору и производится пространственное интегрирование. Между узлами сетки значений параметра r используется линейная интерполяция. При интегрировании использован метод Симпсона.

Команды этого раздела имеют следующий вид.

В - выбор имени входного файла (расширение .OPB) из меню в правом верхнем углу.

S - ввод имени выходного файла (расширение  .OPS).

МЕТОДИКА РАСЧЕТА

РАДИОЯРКОСТНОЙ ТЕМПЕРАТУРЫ ВОЗДУШНОЙ ПЛАЗМЫ

1. ЯРКОСТНАЯ ТЕМПЕРАТУРА

Рассмотрим луч зрения радиометра (Ra), сканирующего атмосферу в вертикальной и горизонтальной плоскостях (рис.1). Источник S ионизирующих излучений находится на высоте Н над поверхностью Земли. Радиометр расположен на произвольной высоте h. Угол места q  считается положительным, если луч зрения  проходит  выше горизонтали (-p/2 £ q  £ p/2). Угол  j   (0 £

£ j £ 2p), расположенный в гори-зонтальной плоскости (на рисунке он не изображен), отсчитывается от вертикальной плоскости, в которой лежат источник и радиометр (плоскость рис.1). Параметры плазмы вычисляются в произвольной точке луча А на расстоянии r от источника.

Гамма-кванты с энергией порядка 1 МэВ от высотных и космических источников (для которых Н > 40 км) рассеиваются в атмосфере в слое, находящемся на высотах 20-40 км. В слое образуется область частичной ионизации (ОЧИ) со степенью ионизации a << 1. Кроме того вблизи источника создается область повышенной ионизации (ОПИ) (a ³ 1) – плазменное облако, имеющее конечные размеры (на рис.1 это область с радиусом r_фр). Если источник находится в нижней атмосфере (Н < 40 км), то он окружен областью повышенной ионизации, а снаружи ее охватывает область частичной ионизации. При любых положениях источника ОЧИ расположена всегда ниже 40 км.

Задача расчета - определение радиояркостной (далее для краткости просто яркостной) температуры воздушной плазмы в микроволновом диапазоне и установление связи между яркостной температурой и характеристиками источника для интервала времени, когда можно пренебречь изменениями параметров плазмы за время распространения излучения. В нашей работе этому условию удовлетворяет интервал времени t ³ 1 мкс. Яркостная температура Т_я определяется из решения уравнения переноса [5,6]. Если луч пересекает только область частичной ионизации, то

 ,                                     (1)

где T_r - радиационная температура, ; r’ - плотность воздуха на заданной высоте; r₀ - плотность воздуха на уровне моря; t - оптическая толщина (); х - координата вдоль луча зрения; t₀ - полная оптическая толщина плазмы вдоль луча; - коэффициент поглощения среды на частоте w.

Для луча зрения произвольного направления введем переменную (см. рис.1). Тогда полная оптическая толщина примет вид:

.                                (2)

Здесь r - прицельный параметр (рис.1), r₁ и r₂ - координаты границ частично ионизованной плазмы на луче зрения. Если луч проходит  через область повышенной ионизации, локализованной вблизи источника, то яркостная температура имеет вид:

,                      (3)

где Т_f  - радиационная температура  области повышенной ионизации. Радиационная температура рассчитана в работе [6] и представлена на рис.2. Она зависит от времени и энергии источника. Аргумент z на рис.2 имеет вид , где  t – время в секундах, а Е – энергия источника в ТДж. В момент взрыва от места выделения энергии распространяется тепловая волна. По мере уменьшения скорости фронта тепловой волны за ее фронтом вследствие градиента давлений формируется ударная волна, догоняющая фронт тепловой.  При уменьшении прогретого тепловой волной слоя радиационная температура возрастает. Максимальное значение Т_f зависит от длины волны излучения. Выход ударной волны на фронт тепловой и исчезновение прогретого слоя сопровождается резким уменьшением температуры. По мере дальнейшего распространения ударной волны уменьшается температура газа за ее фронтом, падает проводимость, а значение спектральной мощности нагретой области проходит через максимум. В момент достижения максимума излучение фронта ударной волны эквивалентно излучению абсолютно черного тела. Этот момент времени зависит от частоты излучения. При этом плазменная частота электронов становится меньше частоты МКИ.

Радиационная температура в программном пакете представлена кусочно-гладкой аппроксимацией, полученной методом, изложенным в работе [7]:

 U(-z – 4,3)×[3,8 – 0,17(z + 4,3)²] + U(-z – 4,2)×U(z + 4,3)×(-14 – 4z) +

+ U(-z – 2,75)×U(z + 4,2)×[2,62 + 0,5(z + 4,1)²] +

+ U(-z – 2,6)×U(z + 2,75)×(5,9 + 0,87z) + U(z + 2,6)×[3,65 – 0,13(z + 2,4)²]. (4)

Здесь U(z) – симметричная единичная функция:

.

Из (1)-(3) следует, что для решения задачи необходимо определить зависимость коэффициента поглощения от координаты и времени, найти величину прицельного параметра r, определить границы r₁ и r₂ области частичной ионизации на луче зрения, вычислить оптическую толщину (2) и затем яркостную температуру (1) или (3).

Выбор формулы расчета (1) или (3) диктуется величиной прицельного параметра (см. рис.1). Если r < r_фр, где r_фр - радиус фронта ударной волны (считаем, что величина этого радиуса является оценкой радиуса области повышенной ионизации), то яркостная температура должна рассчитываться по формуле (3). Если же r ³ r_фр, будем принимать во внимание только область частичной ионизации. Тогда справедлива формула (1).

Перейдем в формуле (1) к интегралу по переменной r (см. рис.1), используя (2):

.                      (5)

Границы r₁ и r₂ принадлежат поглощающей области, расположенной ниже 40 км. В работе [2] расчет полной оптической толщины проводился с помощью программы, реализующей интегрирование по методу Симпсона. Для сокращения времени интегрирования подынтегральная функция для каждого аргумента r вычислялась с помощью аналитических выражений, полученных путем аппроксимации значений коэффициентов поглощения . Здесь мы используем аналогичную методику. При вычислении полной оптической толщины по формуле (2) сохраним в виде таблицы промежуточные частичные суммы. Тогда интеграл, стоящий в аргументе экспоненты формулы (5), рассчитаем по таблице методом интерполяции. Окончательный интеграл снова берем методом Симпсона.

2. ГЕОМЕТРИЯ ЗАДАЧИ

Положение границ интегрирования вдоль луча зрения существенно зависит от положения источника и наблюдателя. Если источник расположен в нижней атмосфере (ниже 40 км), то область повышенной ионизации находится внутри области частичной ионизации. В этом случае положение границ интегрирования зависит от того пересекает ли луч зрения ОПИ или нет, проходит ли он через область частичной ионизации или нет. Когда источник находится в верхней атмосфере  или в ионосфере (Н > 40 км), пределы интегрирования ограничивают только ту часть луча зрения, которая расположена ниже 40 км. Исключением является случай, при котором луч зрения целиком лежит выше 40 км. Радиометр зарегистрирует источник ионизирующих излучений, только если его антенна направлена прямо на источник (луч зрения пересекает ОПИ). В последнем случае зависимость яркостной температуры от времени определяется только радиационной температурой Т_f  ОПИ в формуле (3), поскольку оптическая толщина t₀ равна нулю.

Во входном файле программного пакета обязательно задаем (см. рис.3): высоту источника Н, высоту наблюдателя h, эпицентральное расстояние  r₀, угол места q  между горизонтом и лучом зрения (на рис.3 угол q  равен нулю), а также угол j - угол между вертикальной плоскостью, в которой лежит луч зрения, и вертикальной плоскостью, проведенной через источник и радиометр.

Вычислим расстояние между источником и радиометром:

.                                                    (6)

Рассмотрим сначала ситуацию, когда луч зрения A-Ra расположен горизонтально. К таким ситуациям отнесем все значения угла места, удовлетворяющие условию q < q  _min=1,7×10^-17. Определим прицельный параметр r луча зрения и угол b между  лучом зрения и направлением r₁ (см. рис.3а и 3б).

Из рис.3а и3б следуют простые формулы для r и b :

                                             (7)

                                (8)

Выделим очевидные ситуации, когда нет микроволнового излучения вдоль луча зрения.

1.     Источник S  расположен выше 40 км над поверхностью Земли, радиометр оказался тоже выше 40 км, а угол места q ³ q  _min . Так как на этих высотах пробег гамма-излучения велик, область частичной ионизации практически не образуется. Только, если прицельный параметр меньше радиуса области повышенной ионизации, следует рассчитывать непосредственно радиационную температуру Т_f в соответствии с формулой (4).

2.      Источник S  расположен ниже 40 км, радиометр оказался выше 40 км, а угол места q ³ q  _min . В этом случае луч зрения не пересекает области ионизации, и яркостная температура источника равна нулю (существует только фоновая).

Все остальные конфигурации требуют отдельного рассмотрения.

2.1.         Источник ионизирующих излучений расположен на высоте,

не превышающей 40 км

2.1.1. Оценка размеров области повышенной ионизации

Рассмотрим сначала источник, расположенный на высоте Н £ 20 км. При энергии источника Е  ³ 4,2 ТДж, согласно  работе  [8], радиус фронта  ударной  волны имеет вид:

r_фр = ,                                                (9)

и область повышенной ионизации можно приближенно считать сферической. Энергия источника Е в формуле (9) измеряется в ТДж, а время t в миллисекундах. Параметр s определен в формуле (1). На рис.4 построены  графики зависимости  r_фр от высоты источника для момента времени t = = 1 мс и высот, превышающих 20 км. В расчете использован параметр s, соответствующий высоте источника. Кривая 1 соответствует  энергии источника Е = 84 ТДж,   кривая  2  -   энергии   Е =  4,2×10³ ТДж.

Из рис.4 видно, что до высоты взрыва 40 км размер области повышенной ионизации гораздо меньше самой высоты взрыва и почти не превышает 300 м на высоте 40 км. Изменение параметра s по высоте на расстоянии удвоенного радиуса r_фр не превышает согласно работе [4] 5% . Поэтому далее будем пренебрегать асимметрией фронта ударной волны, полагая формулу (9) пригодной для оценки среднего радиуса области повышенной ионизации на высотах Н £ 40 км.

2.1.2. О фоновой концентрации электронов

Согласно справочнику [9] в обычных условиях (т.е. при отсутствии искусственных источников ионизирующих излучений) вблизи поверхности Земли рождается за 1 с в 1 см³ от 1 до 10 ионизированных частиц за счет космического излучения и естественной радиоактивности грунта. Будем считать в связи с этим, что фоновая (естественная) концентрация электронов имеет порядок 1 электрон в 1 см³, или 10⁶ электронов в 1 м³. Поэтому при вычислении концентрации электронов вдоль луча между точками с координатами r₁ и  r₂ счет прекращается, если число электронов, созданных источником ионизирующих излучений, меньше фона, то есть n_e < 10⁶ м^-3 . Сохраним это ограничение вплоть до высот 40 км.

2.1.3.  Определение границ интегрирования

Рассмотрим различные взаимные положения источника, радиометра и луча зрения.

1). Радиометр расположен ниже 40 км, а угол  места отрицателен. 

Пусть высота наблюдателя (Ra) h £ 40 км (рис.5). Найдем расстояние r₂ от источника до точки пересечения С луча зрения 1 с поверхностью Земли. Из рис.5 следует:

,

,

  ,            (10)

длина луча 1:

.

С другой стороны расстояние r₂  можно выразить из треугольника CS(Ra):

,

откуда находим угол

     (11)

и прицельный параметр

.                                                      (12)

Расстояние r₁ определяется формулой (6). Если r₁ <  r_фр (радиометр оказался внутри области повышенной ионизации, где очень высока температура), нет смысла проводить расчеты. В этом случае появится сообщение «Радиометр сгорел».

Введем координату х вдоль луча (х = D(Ra)), отсчитываемую от радиометра Ra. Тогда текущее расстояние rr от источника S до произвольной точки луча с координатой х будет иметь вид

,                                         (13)

где координата х с заданным шагом может изменяться от значения х = 0 до значения х_max = С(Ra), где С(Ra) – полная длина луча зрения (см. рис.5).

Высота текущей точки луча над поверхностью Земли равна:

.                                                  (14)

 Это значение высоты hg используется в программе для определения плотности воздуха в каждой точке луча.

Если прицельный параметр r удовлетворяет   условию r ³ r_фр, величины r₁ и r₂ являются искомыми пределами интегрирования в формуле (5) для данной конфигурации. В этом случае расчет проводится вдоль всего луча, пока электронная концентрация не снизится до фоновой, а яркостная температура является температурой (1) только области частичной ионизации.  

Если же r  £  r_фр (см. рис.6), то луч зрения пересекает ОПИ, а яркостная температура (3) складывается из температуры и ОПИ, и ОЧИ. Причем вместо границы r₂ в формуле (5) следует использовать величину   r_фр (r₂ = r_фр).

2). Радиометр расположен ниже 40 км, а угол места положителен

Пусть теперь угол места положителен: q > 0. В этом случае вторая граница r₂  на луче зрения определяется расстоянием от источника до точки пересечения луча зрения с горизонтальной поверхностью на высоте 40 км.  Из рис.7 следует, что расстояние r₁ определяется формулой (6),

,

,

а  для границы r₂  на луче зрения 1 получаем:

.   (15)

Далее из рис.7 находим:

,

.

Величины r, rr и hg находим по формулам (12)-(14) соответственно. Все дальнейшие вычисления  проводим при условии r_фр < r. Если же r_фр > r, вместо границы r₂  берем значение r₂  = r_фр.

3). Радиометр расположен выше 40 км, а угол места отрицателен

Если радиометр расположен выше 40 км (рис.8), то расчет концентраций частиц вдоль луча зрения выше 40 км не проводится. В этом случае граница r₁ не совпадает с расстоянием (6) и рассчитывается по формулам:

,

,

.       (16)

Для расстояний СВ, АС, r₂ и С(Ra) остаются справедливыми формулы пункта 1), а для вычисления угла b из рис.8 получаем:

,

,

.                                                      (17)

Тогда для прицельного параметра r , текущего радиуса-вектора точки на луче rr  и высоты этой точки hg справедливы формулы (12) – (14) соответственно.

2.2.         Источник ионизирующих излучений расположен на высоте

 свыше 40 км

2.2.1. Оценка размеров области повышенной ионизации

Когда луч зрения пересекает область повышенной ионизации вблизи источника, необходимо учитывать яркостную температуру этой области. Следовательно, надо знать размеры ОПИ. Для высотного источника граница ОПИ вообще говоря несимметрична, форма ее зависит от высоты источника и его энергии, а также от геометрии линий магнитного поля Земли вблизи источника. Строгий расчет формы границы может быть сделан только численно, так как форма границы связана со скоростью убывания давления и плотности воздуха в атмосфере. От энергии источника зависит масштаб расстояний, на котором надо учитывать изменение давления и плотности воздуха. От высоты источника и его географических координат зависит природа сил торможения границы: будут ли это противодавление и дополнительная захваченная при разлете облака масса воздуха, или этой силой будет в первую очередь магнитное давление поля Земли (или и то, и другое, вместе взятые). Такого рода расчеты проводились в работе [10].

Будем рассматривать источники с энергией от 10^-3 до  10³ ТДж.  Ограничим  также  область  высот   источника  диапазоном 40 км < Н £ 1200 км. Гамма-кванты, излучаемые источником, находящимся на максимальной высоте этого диапазона Н = 1200 км, достигают поглощающих слоев атмосферы (лежащих ниже 40 км) за время около 40 мс. Начиная с момента их прихода в нижние слои атмосферы, измерения параметров плазмы с помощью радиометра требуют еще десятков миллисекунд. Разумная длительность процесса измерения заканчивается примерно к 100 мс с момента взрыва. Для более низких высот локализации источника полное время наблюдения меньше. Примем время t_к = 0,1 с за максимально возможное время наблюдения. В работе [10] показано, что для выбранных диапазонов энергии и высоты источника разлет плазменного облака на временах t £ t_к происходит инерционно, т.е. на этих временах  механизмы торможения плазмы (противодавление атмосферы, захват массы окружающего воздуха и торможение магнитным полем) еще практически не включены.

Воспользуемся автомодельным решением газодинамической задачи разлета, развитой в [10] в секторном приближении. Поскольку разлет инерционный, облако сферически симметрично и радиус его равен

R = Vt,                                                    (18)

где скорость инерционного разлета имеет вид

.                                             (19)

Здесь R_g – универсальная газовая постоянная, T₀(Е) – температура испаренного вещества в момент взрыва, зависящая от энергии источника Е, М – молярная масса газа, g  - показатель адиабаты.

Температура плазмы в момент взрыва зависит не только от Е, но и от материала изделия, его массы и объема. Возьмем, как принято в работе [9], усредненные значения М » 30 кг/кмоль (алюминий), массу источника » 1 т, а начальный средний радиус » 0,5 м. Тогда рассчитанную в работе [9] зависимость температуры от энергии можно аппроксимировать в рассматриваемом диапазоне Е формулой:

.                        (20)

Здесь Е измеряется в ТДж, а температура в кельвинах.

Используя аппроксимацию (20) и формулы (18) и (19), находим радиус плазменного облака к моменту t = 1 c : R = 2,3 км при Е = 0,42 ТДж и R = 33 км при Е = 4,2×10⁴  ТДж. Максимальный радиус торможения R_m сектора, разлетающегося в направлении к поверхности Земли, равен согласно работе [10] R_m= 340 км на высоте взрыва Н = 1000 км и достигается между 2-й и 3-й секундами разлета. На  высоте около 100 км радиус инерционного разлета R = = 2,3 км сравним с R_m » 4 км. Таким образом, к моменту наблюдения t » 0,1 с разлет можно считать инерционным.

Далее в программе в расчете яркостной температуры будет учитываться радиационная температура области повышенной ионизации, если прицельный параметр луча зрения окажется меньше рассчитанного по формулам (18) – (20) радиуса плазменного облака.

2.2.2. Определение границ интегрирования

1). Радиометр расположен ниже 40 км.

Пусть радиометр Ra находится на высоте h, не превышающей 40 км, как изображено на рис.9. Рассмотрим геометрию задачи для разных положений радиометра и разных направлений луча зрения.

1.1. Пусть угол между лучом зрения и горизонталью не отрицателен: q  ³ 0. Тогда вклад в яркостную температуру области частичной ионизации происходит на расстоянии A(Ra) вдоль луча 1 между радиометром Ra и плоскостью, расположенной на высоте 40 км, ниже которой начинается эффективное поглощение микроволнового излучения. Из рис.9 получаем:

,      (27)

АВ = 40 – h,                                                 (28)

B(Ra) = AB ctgq,                                              (29)

,                                       (30)

,                      (31)

.                          (32)

Выразим теперь расстояние r₂ из треугольника SA(Ra) с углом b  при вершине Ra:

,                            (33)

откуда для угла b получаем выражение:

,                                    (34)

а для прицельного параметра:

.                                                  (35)

Зная прицельный параметр и сравнивая его с соответствующими размерами области повышенной ионизации, можем теперь решить вопрос о необходимости учета яркостной температуры этой области.

Введем снова координату х вдоль луча, отсчитываемую от радиометра Ra. Тогда текущее расстояние rr = SЕ от источника S до произвольной точки луча Е будет иметь вид

,                                       (36)

где координата х с заданным шагом может изменяться от значения х = 0 до значения х_max = A(Ra), где A(Ra) – полная длина луча зрения в области поглощения микроволнового излучения (точка А находится на высоте 40 км).

Высота ЕF текущей точки E луча над поверхностью Земли равна:

.                                                  (37)

Это значение высоты используется в программе для определения плотности воздуха в каждой точке луча.

Рассмотрим отдельно два частных случая, когда угол места q  = p/2 и q = 0. В первом случае (q = p/2) луч зрения направлен вертикально вверх (см. рис.10). Из формул (29)–(31) получаем B(Ra) = 0, A(Ra) = = 40 – h, сторона BC  (на рис.9) равна r₀ и не зависит от азимута j. Расстояние r₂  принимает вид:

,

угол , а высота . Таким образом, при таком луче зрения все формулы (27) – (37) работают автоматически правильно.

Иная ситуация возникает при q  = 0. В этом случае луч зрения лежит в горизонтальной плоскости (рис.11). Расстояния B(Ra), A(Ra), BC и r₂ , введенные на рис.9, обращаются в бесконечность. Из рис.11 следует, что

,

и , а координату х необходимо ограничить сверху каким-либо разум-

ным значением: либо х_max »  » (2-3)r₀, либо х следует оборвать, когда концентрация электронов станет ниже фоновой.

Остается обсудить вариант, когда высота радиометра в точности равна 40 км. В этом случае при q = 0 остаются в силе последние формулы. А если q > 0, то надо исследовать только такие лучи зрения, которые пронизывают область повышенной ионизации.

1.2. Пусть теперь угол места отрицателен (q < 0). В этом случае луч зрения A(Ra) упирается в земную поверхность (см. рис.12). Выражение для расстояния r₁ сохраняет вид (27). Остальные формулы в соответствии с рис.12 принимают следующий вид:

,                                           (38)

,                                              (39)

,                            (40)

.  (41)

Для остальных параметров справедливы соотношения (33) – (37). Причем высота hg текущей точки на луче A(Ra) в формуле (37) будет теперь меньше h, поскольку угол места q < 0.

2) Радиометр расположен выше 40 км

Рассмотрим теперь ситуацию, когда радиометр размещен над уровнем 40 км от поверхности Земли (h > 40 км).

2.1. Пусть сначала угол места положителен:q > 0. Тогда следует принимать во внимание только такие лучи зрения, которые пронизывают область повышенной ионизации. На рис.13 изображена область по-вышенной ионизации (ОПИ) источника S, лучи 1 и 2, проведенные под углами q₁ и q ₂ к горизонту в плоскости j = 0 так, чтобы они касались границ ОПИ. Из рис.13 видно, что ОПИ будет пронизываться только такими лучами, для которых азимутальные углы удовлетворяют условию:

.   (42) Будем считать, что это условие выполнено.                                      

Тогда из геометрии следующего рисунка (рис.13 а)  получаем формулы:

;

;

;

;

.

Мы получили систему из шести алгебраических уравнений с шестью неизвестными. Решая ее относительно r, находим прицельный параметр луча зрения:

.

При q  = p/2 получаем r = r₀, а при  q  = 0

r­² =   =  (H – h)² +  =  (H –  h)² + ,

то есть формула работает правильно. Легко показать, что выражение для прицельного параметра справедливо и для случая, когда радиометр находится выше источника.

Ограничения на углы места зависят от формы границ ОПИ. Найдем эти ограничения.

Выше мы показали, что для типичного времени регистрации излучения (порядка нескольких десятков и даже сотен микросекунд) плазменное облако взрыва  не может еще приобрести заметной асимметрии. Будем считать облако сферически симметричным, имеющим радиус r_фр.

Если менять угол места при неизменном угле j, то при q = q’ луч коснется поверхности облака в точке Е. Угол q’ при данном азимуте и будет максимально возможным углом места. На рис.14 изображен луч зрения DRa, ориентированный под углом q  к горизонту. Угол j этого луча меньше предельного, определяемого 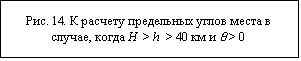формулой (42).

2.2. Для отрицательных углов места геометрия задачи изображена на рис.15.

Расчетные формулы принимают вид:

,                                         (43)        

,                                          (44)

,                                  (45)

,                                        (46)

,                                                (47)

,                                   (48)

.                                             (49)

Выразим теперь расстояние r₁ из треугольника S(Ra)D:

,                    (50)

тогда                            ,                           (51)

,                                               (52)

.                                            (53)

Здесь координата х отсчитывается от точки D, лежащей на пересечении луча зрения C(Ra) и горизонтальной плоскости, проведенной на высоте 40 км, в направлении к точке С.

2.3. Рассмотрим теперь геометрию задачи, когда радиометр расположен выше источника. Очевидно, в этом случае при углах места q  ³ 0 радиометр либо вообще не зарегистрирует микроволновое излучение (если прицельный параметр окажется больше размеров ОПИ), либо для тех лучей зрения, которые проходят через ОПИ, можно сразу считать яркостную температуру ОПИ. Аналогично для отрицательных углов места: если луч зрения пересекает ОПИ, уже не важно, как он пойдет дальше - яркостная температура определяется только областью повышенной ионизации. Поэтому рассмотрим далее только отрицательные  углы места (q < 0) и такие лучи зрения, прицельный параметр которых превышает размеры ОПИ. Пример такого луча представлен на рис.16. Сравнивая рис.16 и рис.15, видим, что все формулы (43)–(53) остаются справедливыми и в этом случае.

Команды этого меню имеют вид:

S - выбор имени входного файла (расширение .OPS) из меню в правом верхнем углу;

К - ввод имени выходного файла (расширением .OPK).

ПРИМЕР РАСЧЕТА ЯРКОСТНОЙ ТЕМПЕРАТУРЫ

ДЛЯ ВОЗДУШНОГО ВЗРЫВА

Рассмотрим микроволновое излучение взрыва S с энергией 4,2 ГДж и полным выходом гамма-квантов 10²⁰, произведенного на высоте H = 1 км над поверхностью Земли. Пусть радиометр Ra, сканирующий пространство, размещен на самолете, летящем на высоте h = 10 км на расстоянии r₀ = 100 км по горизонтали от взрыва (рис.17). Направление наблюдения А(Ra) задается углом q в вертикальной плоскости и углом j между вертикальной плоскостью, проходящей через источник S и радиометр Ra, и вертикальной плоскостью, в которой лежит луч зрения (на рис.17 угол j не изображен). В заданной геометрии лучу зрения S(Ra), проходящему через  источник, соответствует  угол q = -5,4⁰. Расчет произведен для окна прозрачности воздуха вблизи длины волны 8,6 мм.

На рис.18 представлена зависимость логарифма коэффициента по-глощения МКИ от времени, рассчитанная вдоль луча зрения, проходящего через источник при j = 0. Координата х отсчитывается вдоль луча от радиометра. Кривая 5 на рис.18 соответствует точке луча вблизи источника S. На очень малых временах коэффициент поглощения на кривой 5 становится равным единице, т.е. происходит полное поглощение микроволнового излучения. Так как начальные участки кривых рис.18 в выбранном масштабе не разрешены, мы рассчитали электронные концентрации и коэффициенты поглощения на малых временах после взрыва для нескольких точек пространства вблизи источника S. Результаты расчета электронных концентраций приведены на рис. 19. Расстояния r от источника до точки наблюдения на соответствующих лучах зрения указаны прямо на поле рисунка. Уровень 5 на рисунке соответствует предельной электронной концентрации, при которой плазменная частота превышает частоту микроволнового излучения. При концентрациях, превышающий этот уровень, плазма становится непрозрачной для МКИ, и коэффициент поглощения становится равным единице. Из рис. 19 видно, что в рассматриваемом примере это происходит на очень ранних временах после взрыва. Задавая углы q и j и рассчитывая концентрацию электронов в окрестности источника, с помощью простой геометрии можно оценить размеры непрозрачной области в сечении а-а (см. рис.17), перпендикулярном лучу S(Ra). Примерные границы этой области  к  моменту времени t = 0,04 мкс изображены на рис.20. На интересующих нас достаточно больших временах (t ³ 1 мкс) при заданной энергии источника плазма становится прозрачной для МКИ во всей области пространства. Поэтому далее, в расчетах яркостной температуры воздушной плазмы будет учитываться только температура (5) области частичной ионизации.

На рис.21 представлены зависимости яркостной температуры от времени для разных углов места и угла j = 0. Кривые получены интегрированием коэффициентов поглощения вдоль лучей зрения по формуле (5). Кривая 3 рис.21 соответствует углу q = -5,4⁰, при котором луч зрения проходит через источник. Яркостная температура в этом направлении максимальна. Асимметрия температуры по углам q связана с изменением по высоте плотности воздуха и длины свободного пробега гамма-квантов. Чем меньше по модулю угол места, тем выше проходит луч зрения над источником. При этом убывает плотность воздуха и возрастает пробег гамма-квантов.

На рис.22 построены кривые зависимости яркостной температуры от угла j  для фиксированных моментов  времени и  угла  места q  = -2⁰. Они иллюстрируют симметрию яркостной температуры по углу j: в горизонтальной плоскости средняя длина пробега постоянна, так как плотность воздуха не меняется.

Современные импульсные радиометры [1] имеют чувствительность в сотни и даже десятки кельвин. Однако шумовая температура в микроволновом диапазоне вблизи поверхности земли может достигать 300 К. В рассматриваемом примере диаграмма направленности радиометра ориентирована в сторону земли. Оценим, используя представленные на рис.21 и 22 яркостные температуры для разных лучей зрения, размеры плазменного облака, «светящегося» в микроволновом  диапазоне, задав его границу на уровне 1000 К (троекратно превышающем шумовой). Границы этой области в сечении а-а (см. рис.17) приведены на рис.23 к моменту времени t = 100 мкс.

В заключение сделаем одно замечание. Мы ограничились расчетом радиояркостной температуры, не вычисляя антенную температуру. Это возможно, если размеры «антенного пятна» гораздо меньше размеров светящейся плазменной области. Для радиометра  с углом раскрытия диаграммы направленности 1,4⁰ [10] диаметр антенного пятна на расстоянии 100 км составляет примерно 2,5 км, что заметно меньше размеров плазменного облака.

Работа частично поддержана РФФИ, грант 02-01-00844

СПИСОК ЛИТЕРАТУРЫ

1. Горелик А.Г. и др. Радиометрическое исследование импульсного микроволнового излучения // Инж. Физика. № 1. 2002. С. 2 – 10.

2. Котов Ю.Б., Семенова Т.А., Федоров В.Ф. Пакет программ “OPTHICK”

для расчета параметров воздушной плазмы, образованной источником ионизирующих излучений. М.: Препринт ИПМ РАН, № 73. – 1999.-24 с.

3. Филипович Б.И., Котов Ю.Б. Программа графической поддержки исследовательских работ (GRFM). Препринт. М. Институт проблем управления. – 1997.-28 с.

4. Атмосфера стандартная. Параметры. ГОСТ 4401-81.-М.: Изд. Стандартов. 1981. 180 с.

5. Федоров В.Ф. Микроволновое излучение воздушной плазмы, образованной источником длиннопробежного излучения. -М.: Препринт МИФИ, 038-90, 1990.-20 с.

6. Федоров В.Ф., Семенова Т.А. Генерация микроволнового излучения ударным фронтом мощного атмосферного взрыва // Инж. Физика. № 4. 2003. С. 36-38.

7. Котов Ю.Б. Программа получения скользящих нормативов по набору реализаций процесса. М.: Препринт ИПМ. № 27. 1993. 23 с.

8. Федоров В.Ф., Соколов В.Б. Микроволновое излучение высотных взрывов.-М.: Препринт МИФИ, 004-96, 1996.-28 с.

9. Физические величины: Справочник / А.П. Бабичев, Н.А. Бабушкина, А.М. Братковский и др.; под ред. И.С. Григорьева, Е.З. Мейлихова.-М.; Энергоатомиздат, 1991. - С.1196.

10. Безус В.А., Белобрагина Е.В., Взоров Н.Н. и др. Изучение нестационарных высокоэнергетических процессов, протекающих в атмосфере и океане Земли // Итоговый отчет. М.: МИФИ, 1985. - № гос. регистр. 80056465 0286.0 045402. С. 9–29.