Аннотация
Компьютерная модель была применена для численного расчета разряда в высокочастотном поле.
Модель учитывает гидродинамику газа, ионизацию, диссоциацию, диффузию электронов и т.д.
Abstract
A computer code has been developed for numerical calculation of the discharge in UHF fields.
The model takes into account plasma-gas dynamics, ionization, dissociation, electron diffusion
etc.
Содержание
Введение............................................................................................. 3
§1 Постановка задачи......................................................................... 5
§2 Инициализация разряда................................................................. 6
§3 Бесконечный разряд……………………………………………… 9
Литература......................................................................... … ….….12
Введение
Микроволновый разряд в газе высокой
плотности – сравнительно новый объект исследования, имеющий много возможных
весьма перспективных приложений в различных технологиях. Среди огромного
многообразия видов стримерных микроволновых разрядов [1,2,3,4] особый интерес
представляет возможность получения плазмы с очень высокой температурой в
разряде, возникающем в поле микроволнового резонатора при высоком давлении
заполняющего его газа. Опыты показывают, что в фокусе квазиоптического
открытого резонатора, образованного двумя сферическими зеркалами [5], в момент
пробоя формируется безэлектродный разряд стримерного типа, вытянутый вдоль
электрического поля с линейной поляризацией [6,7,8,9]. С ростом давления газа диаметр
образующегося ионизованного канала уменьшается при сохранении длины, которая в
процессе развития разряда обычно достигает половины длины волны
электромагнитного поля. Разряд потребляет почти всю энергию, накопленную в
резонаторе к моменту пробоя. Величина накопленной энергии пропорциональна
квадрату давления газа в резонаторе, поскольку пробойное значение амплитуды
поля пропорционально давлению (при высоком давлении). Поэтому энергия,
приходящаяся в среднем на единицу массы в пределах объема разрядного канала,
растет с увеличением давления по кубическому закону. При давлении выше одной
атмосферы степень ионизации в канале близка к единице. Более того, в момент
электродинамического резонанса, как показывают оценки, ток, наведенный в канале
электромагнитным полем, достигает значений, при которых среднее за период
колебаний давление магнитного поля на поверхности тонкого разрядного канала
достигает газокинетического давления в нем [10]. Наблюдение ярко выраженных
гидродинамических неустойчивостей типа шеек и змеек в опытах с водородом при
давлении несколько атмосфер
подтверждает это обстоятельство [11,12,13,14]. Весь процесс формирования
разряда занимает около ста наносекунд, а резонансная стадия поглощения энергии
резонатора – единицы наносекунд. Чрезвычайно малые габариты объекта и
длительность во времени, близкое соседство горячего и холодного газа,
случайность места развития, присутствие рассеянного мощного электромагнитного
излучения создают условия, при которых применение традиционных методов диагностики
практически невозможно. Поэтому сопровождение экспериментов со стримерным
микроволновым разрядом численным моделированием особенно востребовано.
В общем случае модель
разряда должна базироваться на уравнениях газодинамики и физико-химической кинетики
и уравнениях Максвелла, чтобы описывать взаимодействие электропроводного
объекта с волновым электромагнитным полем. Решение электродинамической части
серьезно осложняется тем обстоятельством, что соотношение продольного и
поперечного размеров разрядного канала достигает нескольких порядков. Модель
среды должна описывать события в широком спектре температур от холодного
неионизованного газа на периферии канала до горячей полностью ионизованной
плазмы в средней части. Вообще развитие стримерного разряда, как правило, не
обладает симметрией и чутко реагирует на направление вектора потока
распространения электромагнитной энергии. Однако, в стоячей волне
электромагнитного поля, в частности в резонаторе, нарушение симметрии, как
показывает эксперимент, несущественно. Поэтому при моделировании разряда в
резонаторе возможно ограничиваться двумерным приближением.
Моделирование стримерного разряда в
микроволновых полях прошло определенный путь. Довольно успешно использовалась
для интерпретации наблюдений и прогноза модель развития разряда, основанная на
описании взаимодействия стримера с электромагнитным полем с помощью
интегрального уравнения типа Поклингтона, используемого в теории тонких антенн,
модифицированного для канала с произвольным продольным распределением
проводимости [15].
В более поздних работах [16,17,18,19] для
описания плазмы использовалась минимально необходимая модель ионизованного
молекулярного газа и исследовалась возможность полного газодинамического и
электромагнитного (в волновом приближении) описания процесса в одно- , дву- и
трехмерной постановке.
В настоящей работе применяется модель
среды, разработанная в [20, 21, 22]. В этой модели водородная плазма
представляется как двухтемпературная четырехкомпонентная смесь двухатомных
молекул, атомов и их ионов и электронов. Из элементарных процессов учтены
ионизация электронным ударом, диссоциация, рекомбинация (диссоциативная, фото-,
радиационно-ударная тройная, ударная тройная), диффузия с модельным учетом
амбиполярности [23], радиационные потери (рекомбинационные, тормозные).
Газоразрядная плазма является неравновесной, то-есть температура газа не равна температуре электронов. Столь
сложный набор обусловлен тем, что одновременно в зоне расчета присутствуют
области с холодным неиони-зованным молекулярным газом и с горячей почти
полностью ионизованной плазмой. Газодинамические уравнения учитывают силу
усредненного магнитного давления.
Основные использованные упрощения:
1. Температура тяжелых
компонент (молекулы, атомы и их ионы) одинакова.
2. Коэффициент
диссоциации считается равновесным и определяется температурой тяжелой
компоненты по Саха.
3. Фотоионизацией
пренебрегается.
4. Скорость ионизации
для всех тяжелых компонент принята одинаковой.
5. Ионы считаются
однозарядными.
6. Плазма столкновительная
7. При расчете
скоростей реакций по дифференциальным сечениям функции распределения
принимались равновесными.
Освоение описанной модели плазмы целесообразно начать с расчетов в
одномерном приближении.
§1
Постановка задачи

Взаимодействие электромагнитного поля
заданной частоты с проводящим частично
ионизованным газом описывается
системой Максвелла для ком-плексных амплитуд поля E, H
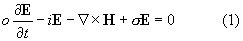
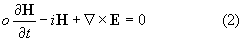
совместно с уравнениями двухтемпературной
плазмодинамики

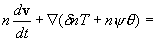 oQ oQ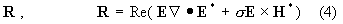
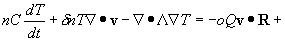 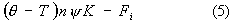
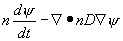 
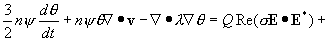 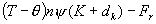 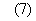
Здесь n, v, T - это плотность числа
частиц, скорость и температура газа, соответственно, ψ – относительная концентрация электронов, θ – их темпе-ратура.
Выражения для всех коэффициентов, проводимости σ, диссоциации
δ, теплоемкости C, теплопроводности λ, диффузии D, ионизации
νi, рекомби-нации νr, теплообмена K и т.д.
даны ниже.
Параметрами задачи являются : частота
ω и амплитуда [E] внешнего поля, а
также начальная концентрация [n], температура [T] и масса
молекулы M газа. Используем их для выбора
единиц измерения [*] и положим: расстояние [x]=c/ω,
проводимость [σ]=ω/4π, скорость [v]2=[T]/M и, разумеется, [θ]=[T], [H]=[E], [t]=[x]/[v].
За основной
примем вариант с параметрами (все в СГС): частота ω=2.2×1010
, амплитуда [E]=36, концентрация [n]=2.4×1019,
температура [T]=4.1×10-14, масса
молекулы M=3.3×10-24 и, следовательно, [x]=1.36, [v]=1.11×105,
[t]=1.22×10-5.
При этом константы и функции, входящие в систему
уравнений (1)-(7), принимают следующий вид:
o=3.7·10-6
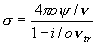 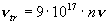 a=0.026 a=0.026 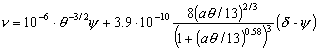
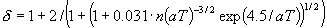
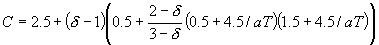
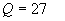 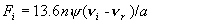 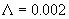 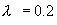
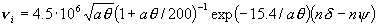
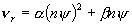 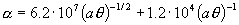
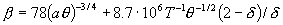
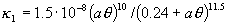 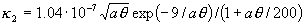
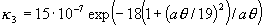 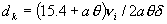
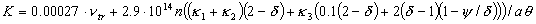
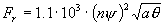 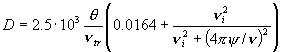
Заметим, что величина  зависит от [E] квадратично. зависит от [E] квадратично.
Ввиду малости коэффициента (o~10-6) при производных по
времени в уравнениях (1), (2), пренебрежем этими членами и будем решать
полученную систему Гельмгольца как стационарную, при каждом t , с условиями Зоммерфельда на бесконечности для возмущения поля. Внешнее, первичное, поле является
решением этой системы при σ =0.
Систему (3)-(7) решаем в ограниченной части пространства, целиком
содержащей ионизованную область.
Начальные данные:
n =T =1, v = ψ = 0, последняя имеет малое локальное возмущение ψ0, развитие которого и является предметом
расчета. Требуется задать еще начальное значение температуры электронов θ0 , которых нет. Чтобы
обеспечить спокойный старт определим это значение из условия равенства нулю
правой части (7), т.е. зависящей от [E].
Хотя процесс развития разряда является,
очевидно, многомерным, уже простейшие одномерные варианты могут дать ответы на
некоторые вопросы. Два таких варианта мы и
рассматриваем в данной работе. Они описывают два, в некотором смысле, крайних случая, один соответствует начальной
стадии разряда, другой – конечной.
§2
Инициализация разряда.
Пренебрегая изменением поля, вызванного
малым локальным возмущением – появлением электронной компоненты и
проводимости, рассмотрим систему
(3)-(7) в одномерном сферически
симметричном варианте и исследуем вопрос
об эволюции этого
возмущения.
Некоторые оценки можно сделать и не решая
уравнений. Как нетрудно проверить, условием неустойчивости нулевого решения
уравнения (6) является неравенство L2 < D/νi , где L – размер области возмущения. Величина D/νi при n = T = 1 и ψ = 0, является функцией θ. Диапазон изменения ее таков: 1019
при θ=1, 10-6
при θ=70 и 10-8
при θ=1000. Поскольку величина θ определяется, в основном, полем, то отсюда можно получить
“критическое” значение поля, достаточное для инициализации разряда.
Представленный выше, как основной, набор параметров и соответствует этому значению.
Итак, в начальный момент n = T = 1, v = ψ = 0, θ = 70.
Возмущение
ψ0 <10-6
внутри сферы радиуса L=0.001. Величина ψ0 сколько-нибудь существенной
роли не играет, влияя лишь на масштаб времени
t~ln1/ψ0 из-за экспоненциальности
нарастания ψ.
Основной результат расчета
представлен на рис.1, где даны графики поло-жения фронта ионизации R(t) и общая масса
электронной компоненты S(t)=∫nψr2dr .
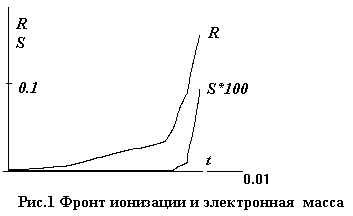
Начальное значение S(0) =10-15. До t=0.006 наблюдается плавный рост S(t) и
распространение возмущения со (звуковой) скоростью порядка единицы. На
интервале 0.006 <t<0.007 происходит существенное изменение характера
процесса. Скорость dR/dt возрастает сразу на
два порядка. Резко увеличивается темп ионизации dS/dt.
На первой, медленной, стадии расширение ионизованного
шара сопро-вождается падением плотности, увеличением доли электронов и ростом
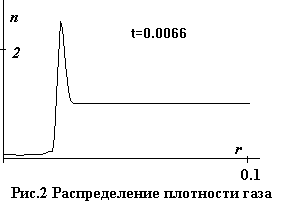
температур до нескольких сотен. К моменту
t=0.0066 шар
оказывается полностью ионизованным и довольно горячим, но почти пустым.
Интенсивная ионизация начинается на его поверхности, где значительные
концентрации и температуры. Распределения величин в этот момент показаны на
рис. 2 - 6.
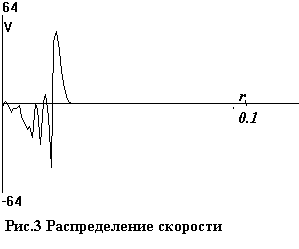
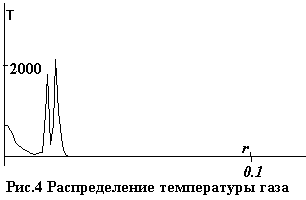
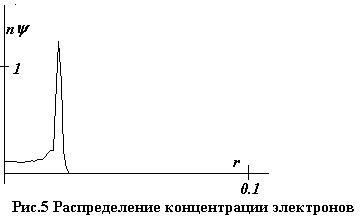

К этому моменту проводимость оказывается
значительной, и допущение о слабом влиянии изменений поля на процесс –
малообоснованным. Тем не менее, оценка скорости перемещения фронта ионизации и
представление о взрывном характере процесса
могут быть справедливы и в общем случае.
Наконец, отметим, что определенное выше
условие критичности поля подтверждается прямым расчетом. Уменьшив в описанном
основном варианте величину поля в три
раза ( что означает θ0=20 и Lкр =1), при неизменности всех остальных
параметров, получаем в результате полное отсутствие малейших признаков
возбуждения каких-либо процессов.
§3
Бесконечный разряд
Другой возможный одномерный вариант
задачи – цилиндрически симметричный ( ∂/∂φ = ∂/∂z =0), бесконечно
протяженный по z разряд. В этом
случае рассматриваем полную систему
(1)-(7) с полем, имеющим отличные от нуля компоненты Ez, Hφ в виде стоячей волны. При этом первичное,
внешнее поле Ez=J0(r), Hφ=-iJ1(r) - функции Бесселя.
В отличие от рассмотренного сферически
симметричного случая, здесь нас
интересует не развитие малого возмущения среды, а наоборот, свойства уже существующего
бесконечного разряда. Поскольку условие критичности размера – следствие
математических свойств уравнения, то оно справедливо и здесь, но используется с
противоположной целью. А именно, если радиус ионизованного цилиндра достаточно
мал, то неустойчивости ( по отношению к одномерным возмущениям) нет и разряд
стационарен.
По-прежнему будем ориентироваться на
основной набор параметров и рассмотрим вариант с теми же начальными данными,
что и выше. Изменим лишь ψ0,
поскольку малость возмущения не требуется, и положим ψ0= 0.5.
Результаты расчета изображены на
рисунках. Рис.7 аналогичен рис.1, на нем даны радиус ионизованного цилиндра R(t) и погонная масса
электронной компоненты S(t) = ∫nψrdr как функции времени. Начальное значение S(0) =10-7.

Поле внутри проводящего цилиндра и в его окрестности падает. На рис.8
показано его распределение на момент t=0.01. Как видим, его значение на оси в несколько раз
меньше по сравнению с первичным, внешним Е=1.
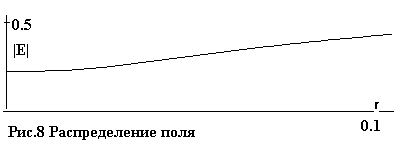
На рис.9-13 даны распределения плотности n, скорости v, температуры газа T, а также доли ψ и температуры θ электронов на тот
же момент t=0.01.
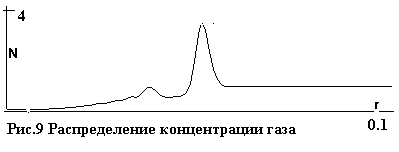
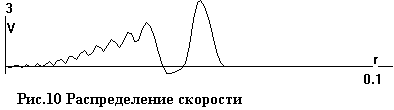
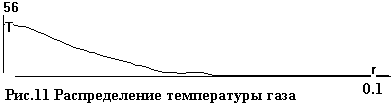

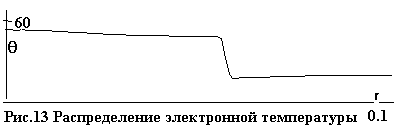
Основное отличие от сферически симметричного случая – малая ионизация. Одна из причин этого –
существенное падение величины поля. В предыдущем случае уменьшение поля в три
раза прекращало процесс иници-ализации. А при малой ионизации ослабевают и все
другие процессы.
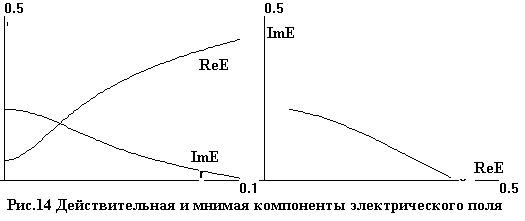
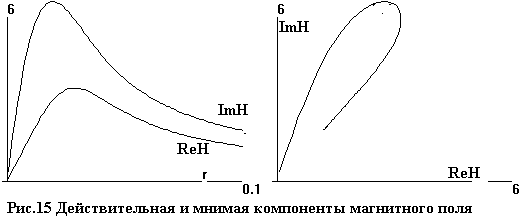
На рис.14, 15 показаны распределения
действительных и мнимых компонент
амплитуд электрического и магнитного полей,
соответственно, как функций радиуса и их изображения в комплексной плоскости.
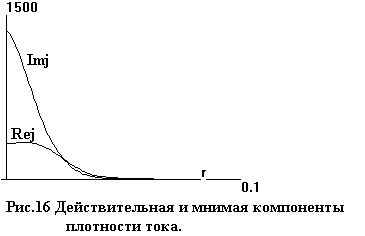
На рис.16 дано распределение
действительной и мнимой компонент плотности тока j=σE.
Изменение ψ0 в данном варианте на результатах практически не
сказывается, в других оно может быть
заметным. Например, в вариантах с
уменьшенным в три раза внешним полем, при малых ψ0 процесс по радиусу вообще не
развивается, стационарен. При значительных же значениях ψ0
, за счет начального запаса
ионизованной массы, процесс получает радиальный гидродинамический импульс, как
и в данном варианте.
Отмеченное (рис. 8) падение значений поля на оси, в варианте с
увеличен-ным внешним полем, только
усиливается.
Хотя
возникновение и развитие разряда – процесс многомерный, результаты
одномерных расчетов позволяют описать
некоторые детали его и сделать правильные оценки.
Литература
[1] Л.П. Грачев, И.И. Есаков, К.В. Ходатаев.
Особенности развития импульсных СВЧ разрядов в квазиоптическом пучке в различных
газах. // ЖТФ, 1998, Т. 68, Вып. 4, С. 33-36.
[2] Л.П. Грачев, И.И. Есаков, Г.И. Мишин, К.В. Ходатаев. Стадии развития
безэлектродного СВЧ разряда. // ЖТФ, 1996, Т. 66, Вып. 7, С. 32-45.
[3] Л.П. Грачев, И.И. Есаков, К.В. Ходатаев.
Диапазон существования самостоятельно развивающегося подкритического
стримерного разряда. // ЖТФ, 1999, Т. 69, Вып. 11, С. 19-24.
[4] Л.П. Грачев, И.И. Есаков, Г.И. Мишин,
К.В. Ходатаев, В.В. Цыпленков. Фоторазвертка разряда высокого давления в
волновом пучке. // Письма в ЖТФ, 26 ноября 1992, Т. 18, Вып. 22, С. 34-38.
[5] Л.П. Грачев, И.И. Есаков, С.Г. Малык,
К.В. Ходатаев. Двухзеркальный резонатор для исследования СВЧ
безэлектродного разряда в газах высокого давления. // ЖТФ, 2001, Т. 71,
Вып. 6, С. 66-74.
[6] А.П. Вихарев, Б.Г. Еремин. СВЧ разряд в квазиоптическом
резонаторе. // ЖЭТФ. 1975. Т. 68.
Вып. 2. С. 452-455.
[7] L.P. Grachev, I.I.
Esakov, G.I. Mishin, K.V. Khodataev. Tech. Phys.
39(2), February 1994, P. 130-136.
Л.П. Грачев, И.И. Есаков, Г.И. Мишин, К.В.
Ходатаев. Разряд в воздухе в квазиоптическом микроволновом резонаторе. // ЖТФ,
1994, Т. 64, Вып.2, С. 26-37
[8] К.В. Александров, Л.П. Грачев, И.И.
Есаков, С.М. Покрас, К.В. Ходатаев. Импульсный СВЧ разряд в атмосферном воздухе
в фокусе двухзеркального резонатора. // ЖТФ, 2003, Т. 73, Вып. 1, С. 46-50.
[9] Л.П. Грачев, И.И. Есаков, К.В. Ходатаев.
Особенности развития импульсных СВЧ разрядов в квазиоптическом пучке в
различных газах. // ЖТФ, 1998,
Т. 68, Вып. 4, С. 33-36.
[10] Л.П. Грачев, И.И. Есаков, Г.И. Мишин,
К.В. Ходатаев. Возможность осуществления термоядерного синтеза в резонансном
стримерном СВЧ разряде высокого давления. // Препринт ЛФТИ им. А.Ф. Иоффе,
1992, № 1577.
[11] В.С. Барашенков, Л.П. Грачев, И.И.
Есаков, Б.Ф. Костенко, К.В. Ходатаев, М.З. Юрьев. Порог кумулятивного
резонансного стримерного СВЧ разряда в газах высокого давления. // ЖТФ, 2000,
Т. 70, Вып. 11, С. 31-35.
[12] Л.П. Грачев, И.И. Есаков, К.В.
Ходатаев. Магнитогидродинамические неустойчивости самосжатого резонансного
стримерного СВЧ разряда. // ЖТФ, 2003, Т. 73, Вып. 5, С. 35-40.
[13] I.I. Esakov, L.P. Grachev, K.V. Khodataev. The pinch effect in microwave resonant streamer
discharge. // Problems of Atomic Science and Technology. 2000, #3. Series: Plasma
Physics (5). P. 138-140.
[14]
I.I. Esakov, L.P. Grachev, K.V. Khodataev. The pinch-effect in microwave
discharge at gas of high pressure. 4th Symposium “Current Trends in International Fusion Research” March
12-16, 2001, Washington, DC, U.S.A. Book of abstracts, P. 64-66.
[15] K.V. Khodataev. Physics of super undercritical
streamer discharge in UHF electromagnetic wave. Proc. XXIII ICPIG, 17-22 July
1997, Toulouse-France, Contributed papers, IV-24.
[16] О.И. Воскобойникова, С.Л. Гинзбург,
В.Ф. Дьяченко, К.В. Ходатаев. Инициация микроволнового стримерного разряда в
газе. // Препринт ИПМ им. М.В.
Келдыша РАН, 2001, № 13.
[17] О.И. Воскобойникова, С.Л. Гинзбург, В.Ф.
Дьяченко, К.В. Ходатаев. Численное исследование подкритического микроволнового
разряда в газе высокого давления. // ЖТФ, 2002, Т. 72, Вып. 8, С. 21-26.
[[1]8]
О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик, К.В. Ходатаев. Расчеты микроволнового
стримерного разряда в газе. // Препринт ИПМ им. М.В.
Келдыша РАН, 2002, № 35.
[[1]9]
О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик. Расчеты
микроволнового разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2003, №
30.
[20] K.V. Khodataev. Theory of the microwave
high-pressure discharge. //Proc. of IV International workshop “Microwave
discharges: fundamentals and applications”, September 18-22, 2000. Zvenigorod,
Russia, P. 35-44. (Yanus-K, Moscow 2001)
[2[1]]
I.I. Esakov, L.P. Grachev, K.V. Khodataev. Parameters of plasma in the resonant
channel microwave streamer discharge of high pressure. // Proc. of The 2nd Workshop on Magnetoplasma
Aerodynamics in Aerospace Applications. 5-7 April 2000, Moscow, Russia, P.
154-162.
[22] I.I. Esakov, L.P.
Grachev, K.V. Khodataev. The pinch effect in microwave resonant streamer
discharge and its possible applications. // Proc. of the international workshop
“Strong microwaves in plasmas” (2-9 August 1999, Nizhny Novgorod), 2000, v.1 P.
291-305.
[23] К.В. Ходатаев, Б.Р.
Горелик. Диффузионный и дрейфовый режимы распространения плоской волны
ионизации в СВЧ - поле. // Физика Плазмы. 1997, Т.23, № 3, С. 236-245
|