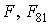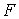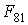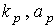Влияние учета вариаций плотности атмосферы, вызванных солнечной активностью, на точность
определения движения МКС
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Интервал |
время (ч:мин) |
время (ч:мин) |
|
|
|
1 |
26.III 12:15 |
30.III 02:24 |
310.1 |
12 |
|
2 |
30.III 20:51 |
3.IV 12:31 |
315.6 |
18 |
|
3 |
4.IV 03:54 |
7.IV 18:01 |
310.0 |
12 |
|
4 |
8.IV 03:15 |
11.IV 15:49 |
304.5 |
17 |
|
5 |
12.IV 04:08 |
14.IV 11:29 |
199.3 |
8 |
|
1Ú2 |
26.III 12:15 |
3.IV 12:31 |
692.2 |
30 |
|
2Ú3 |
30.III 20:51 |
7.IV 18:01 |
681.0 |
30 |
|
3Ú4 |
4.IV 03:54 |
11.IV 15:49 |
647.7 |
29 |
|
4Ú5 |
8.IV 03:15 |
14.IV 11:29 |
548.0 |
25 |
|
1Ú2Ú3 |
26.III 12:15 |
7.IV 18:01 |
1057.6 |
42 |
|
2Ú3Ú4 |
30.III 20:51 |
11.IV 15:49 |
1018.7 |
47 |
|
3Ú4Ú5 |
4.IV 03:54 |
14.IV 11:29 |
891.3 |
37 |
Опишем сначала результаты сглаживания, полученные с использованием
системы (I).
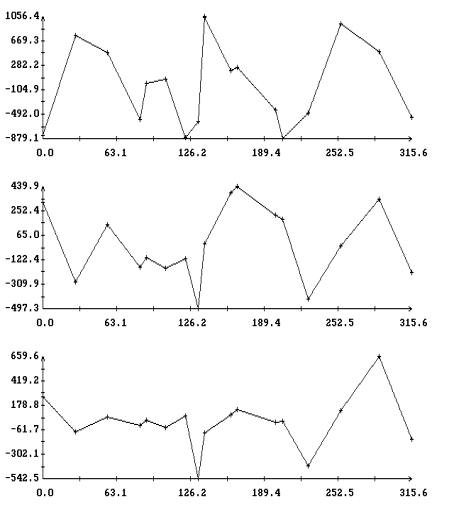
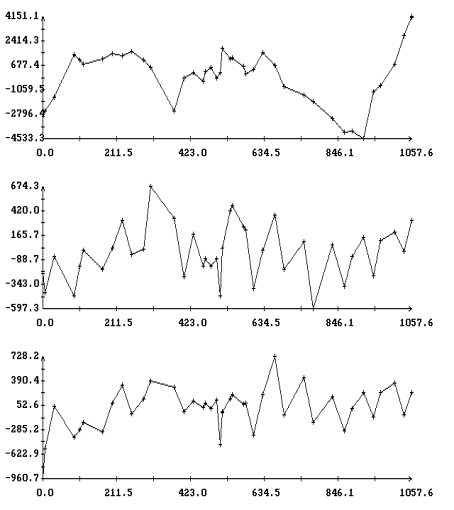
Эти результаты приведены в табл. 2 – 4 и на рис. 3, 4. Табл. 2 содержит
значения параметра ![]() , стандартные отклонения ошибок задания исходных данных и
стандартные отклонения определяемых параметров сглаживающих решений – начальных
условий и
, стандартные отклонения ошибок задания исходных данных и
стандартные отклонения определяемых параметров сглаживающих решений – начальных
условий и ![]() . В табл. 3, 4 приведены характеристики рядов остатков
. В табл. 3, 4 приведены характеристики рядов остатков ![]() для
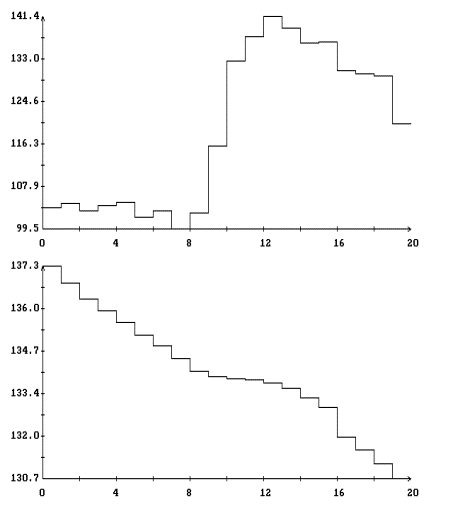
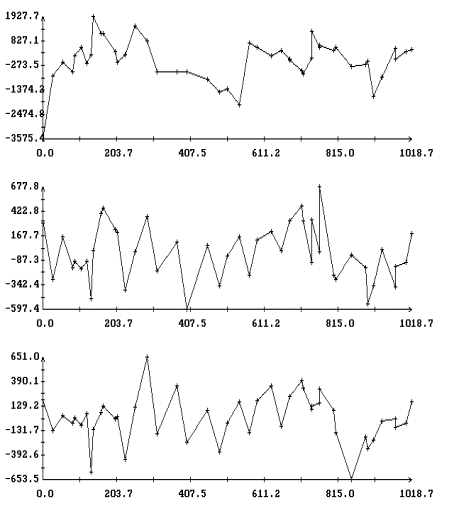
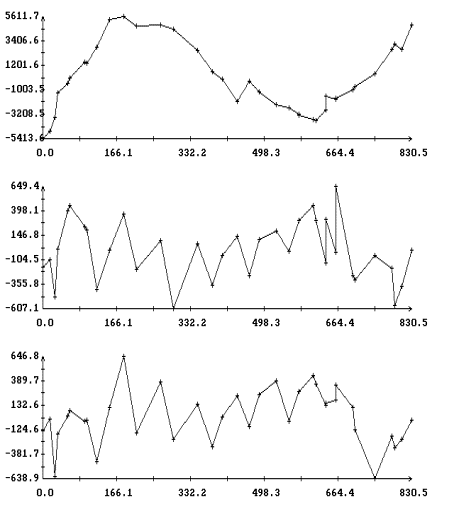
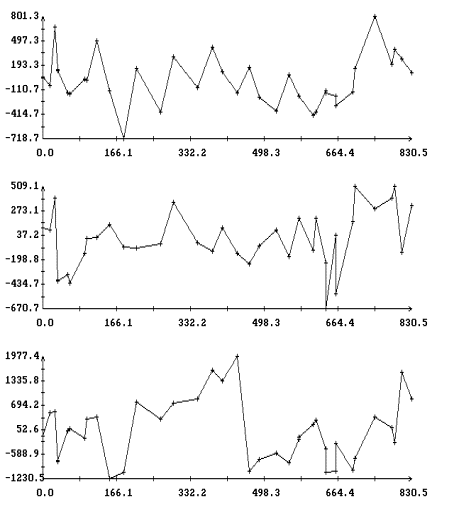
для ![]() . На рис. 3, 4 изображены диаграммы этих рядов, полученных
при аппроксимации интервалов 2 и 1Ú2Ú3 из табл. 1. Диаграммы представляют собой ломаные с вершинами в точках
. На рис. 3, 4 изображены диаграммы этих рядов, полученных
при аппроксимации интервалов 2 и 1Ú2Ú3 из табл. 1. Диаграммы представляют собой ломаные с вершинами в точках
![]() . Для большей наглядности вершины указаны маркерами.
. Для большей наглядности вершины указаны маркерами.
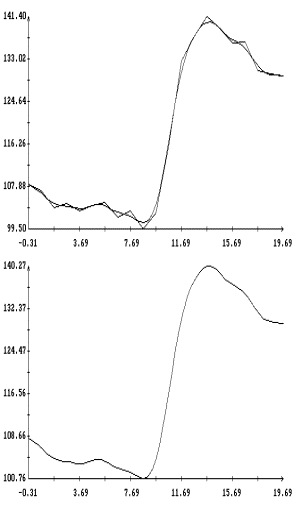
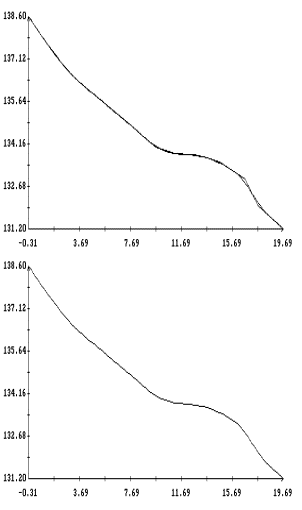
Сопоставление табл. 2 с графиком функции ![]() на рис. 1 показывает,
что изменение параметра
на рис. 1 показывает,
что изменение параметра ![]() отслеживает изменение
индекса
отслеживает изменение
индекса ![]() . Этот факт легко объясним. Поскольку в системе (I) индексы
. Этот факт легко объясним. Поскольку в системе (I) индексы ![]() и
и ![]() приняты постоянными,
фактическое увеличение индекса
приняты постоянными,
фактическое увеличение индекса ![]() приводит к увеличению
приводит к увеличению
![]() . Однако изменением
. Однако изменением ![]() не удается полностью
скомпенсировать резкое изменение
не удается полностью
скомпенсировать резкое изменение ![]() внутри интервала
сглаживания. Например, интервалы 2Ú3 и 2Ú3Ú4, содержащие примерно посередине
участок резкого возрастания индекса
внутри интервала
сглаживания. Например, интервалы 2Ú3 и 2Ú3Ú4, содержащие примерно посередине
участок резкого возрастания индекса ![]() (см. рис. 1),
сглажены заметно менее точно, чем имеющие примерно одинаковую с ними длину
соседние интервалы табл. 1. Заметим, что соседние интервалы 3Ú4, 1Ú2Ú3, 3Ú4Ú5 содержат тот же самый участок, но с краю.
(см. рис. 1),
сглажены заметно менее точно, чем имеющие примерно одинаковую с ними длину
соседние интервалы табл. 1. Заметим, что соседние интервалы 3Ú4, 1Ú2Ú3, 3Ú4Ú5 содержат тот же самый участок, но с краю.
Таблица
2. Параметр ![]() , стандартные отклонения ошибок данных измерений
, стандартные отклонения ошибок данных измерений
и параметров сглаживающих решений системы (I).
|
Интервал |
|
|
|
|
|
|
|
|
|
|
м |
мм/с |
||||||||
|
1 |
1.027 |
381 |
133 |
90 |
159 |
122 |
182 |
96 |
0.0097 |
|
2 |
1.063 |
440 |
163 |
68 |
189 |
96 |
243 |
90 |
0.0097 |
|
3 |
1.393 |
417 |
131 |
140 |
199 |
203 |
184 |
105 |
0.0102 |
|
4 |
1.524 |
448 |
125 |
99 |
158 |
138 |
169 |
94 |
0.0113 |
|
5 |
1.252 |
436 |
181 |
100 |
195 |
141 |
227 |
133 |
0.0361 |
|
1Ú2 |
1.138 |
723 |
182 |
123 |
226 |
165 |
265 |
119 |
0.0029 |
|
2Ú3 |
1.178 |
1209 |
329 |
154 |
375 |
205 |
478 |
195 |
0.0050 |
|
3Ú4 |
1.467 |
576 |
133 |
140 |
206 |
212 |
191 |
96 |
0.0026 |
|
4Ú5 |
1.577 |
606 |
142 |
110 |
178 |
153 |
191 |
106 |
0.0040 |
|
1Ú2Ú3 |
1.152 |
1228 |
268 |
185 |
331 |
242 |
391 |
175 |
0.0018 |
|
2Ú3Ú4 |
1.327 |
3014 |
660 |
334 |
744 |
415 |
949 |
403 |
0.0051 |
|
3Ú4Ú5 |
1.515 |
1089 |
226 |
237 |
348 |
358 |
324 |
163 |
0.0027 |
Таблица 3. Средние
квадратические значения рядов остатков
сглаживающих решений
системы (I).
|
Интервал |
|
|
|
|
|
|
|
м |
мм/с |
|||||
|
1 |
401 |
298 |
349 |
423 |
166 |
461 |
|
2 |
660 |
271 |
245 |
276 |
230 |
646 |
|
3 |
596 |
266 |
224 |
244 |
172 |
639 |
|
4 |
624 |
314 |
256 |
296 |
331 |
638 |
|
5 |
587 |
205 |
183 |
217 |
332 |
652 |
|
1Ú2 |
1136 |
284 |
310 |
359 |
209 |
1218 |
|
2Ú3 |
1959 |
269 |
238 |
265 |
211 |
2166 |
|
3Ú4 |
871 |
298 |
248 |
218 |
278 |
957 |
|
4Ú5 |
957 |
296 |
236 |
274 |
332 |
973 |
|
1Ú2Ú3 |
1982 |
279 |
297 |
339 |
202 |
2213 |
|
2Ú3Ú4 |
4902 |
289 |
268 |
299 |
269 |
5592 |
|
3Ú4Ú5 |
1787 |
292 |
236 |
266 |
291 |
1923 |
Таблица 4. Медианы рядов модулей остатков сглаживающих
решений системы (I).
|
Интервал |
|
|
|
|
|
|
|
м |
мм/с |
|||||
|
1 |
198 |
131 |
220 |
294 |
156 |
189 |
|
2 |
560 |
204 |
86 |
107 |
144 |
570 |
|
3 |
330 |
177 |
181 |
157 |
127 |
385 |
|
4 |
396 |
227 |
168 |
176 |
226 |
485 |
|
5 |
523 |
180 |
155 |
154 |
243 |
510 |
|
1Ú2 |
918 |
190 |
142 |
220 |
142 |
751 |
|
2Ú3 |
1330 |
193 |
124 |
147 |
130 |
1319 |
|
3Ú4 |
561 |
217 |
164 |
180 |
185 |
598 |
|
4Ú5 |
840 |
168 |
155 |
155 |
228 |
853 |
|
1Ú2Ú3 |
1222 |
191 |
178 |
208 |
135 |
1305 |
|
2Ú3Ú4 |
3945 |
195 |
151 |
164 |
158 |
4491 |
|
3Ú4Ú5 |
1204 |
199 |
168 |
182 |
201 |
1306 |
Отметим еще, что с
возрастанием длины интервала сглаживания величины ![]() и
и ![]() возрастают
существенно заметнее величин
возрастают
существенно заметнее величин ![]() при
при ![]() . Последние, вообще, практически не меняются. Именно за счет
увеличения
. Последние, вообще, практически не меняются. Именно за счет
увеличения ![]() ,
, ![]() происходит увеличение
происходит увеличение
![]() и ухудшение точности
аппроксимации данных измерений. Напомним, что величины
и ухудшение точности
аппроксимации данных измерений. Напомним, что величины ![]() характеризуют невязки
аппроксимации положения станции вдоль орбиты, величины
характеризуют невязки
аппроксимации положения станции вдоль орбиты, величины ![]() характеризуют невязки
аппроксимации ее абсолютной скорости в направлении радиуса-вектора.
характеризуют невязки
аппроксимации ее абсолютной скорости в направлении радиуса-вектора.
Возрастание величин ![]() и
и ![]() при возрастании длины
интервала сглаживания обусловлено потерей точности модели. В случае
сравнительно коротких интервалов все диаграммы остатков выглядят примерно
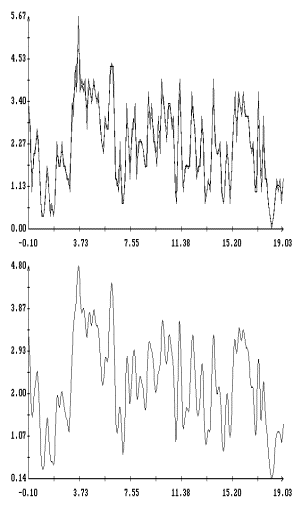
одинаково и ведут себя хаотически (рис. 3). В случае длинных
интервалов в остатках
при возрастании длины
интервала сглаживания обусловлено потерей точности модели. В случае
сравнительно коротких интервалов все диаграммы остатков выглядят примерно
одинаково и ведут себя хаотически (рис. 3). В случае длинных
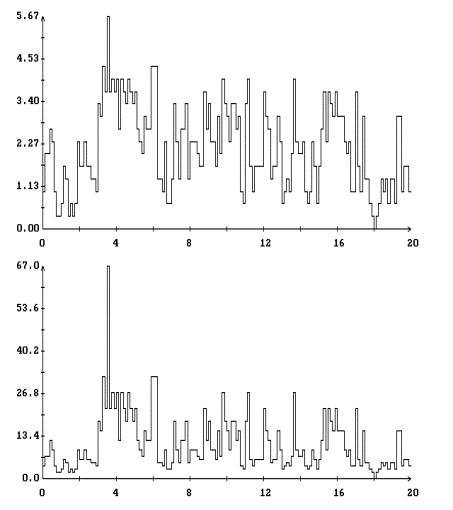
интервалов в остатках ![]() и
и ![]() заметны систематические
составляющие (рис. 4).
заметны систематические
составляющие (рис. 4).
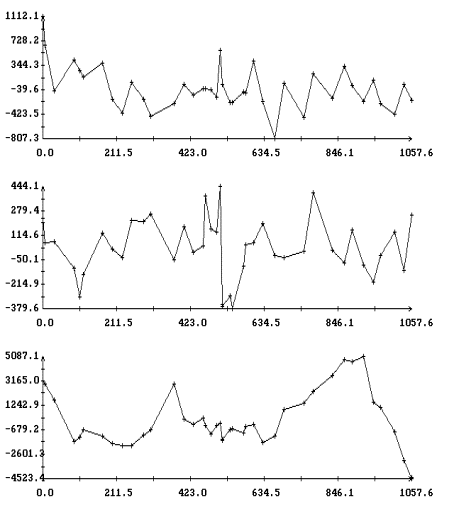
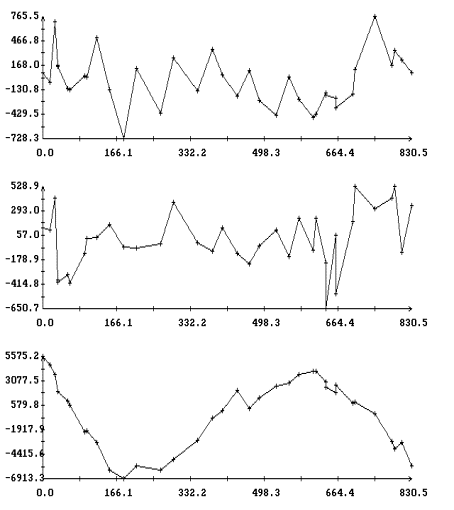
Результаты сглаживания,
полученные с использованием системы (II), приведены в табл. 5 – 7 и на рис. 5, 6. Эти таблицы и
рисунки аналогичны описанным выше табл. 2 – 4 и рис. 3, 4. Попарное сравнение
табл. 2 и 5, 3 и 6, 4 и 7 показывает, что при переходе от системы (I) к системе (II) точность аппроксимации
измерений на сравнительно коротких интервалах времени 1 – 5 не улучшилась. В
большинстве случаев (3 из 5) она даже незначительно ухудшилась. Точность
аппроксимации на более длинных интервалах повысилась. Особенно значительно это
повышение в случае интервалов 2Ú3 и
2Ú3Ú4. Такое повышение обусловлено,
прежде всего, учетом изменения параметров ![]() и
и ![]() в системе (II). Именно учет
изменения этих параметров позволил устранить влияние резкого скачка функции
в системе (II). Именно учет
изменения этих параметров позволил устранить влияние резкого скачка функции ![]() внутри интервалов 2Ú3 и
2Ú3Ú4. Сравнение рис. 5, 6 с рис. 3 и 4 и аналогичных
рисунков, не вошедших в препринт, показывает уменьшение систематической
составляющей в остатках
внутри интервалов 2Ú3 и
2Ú3Ú4. Сравнение рис. 5, 6 с рис. 3 и 4 и аналогичных
рисунков, не вошедших в препринт, показывает уменьшение систематической
составляющей в остатках ![]() и
и ![]() в случае
аппроксимации решениями системы (II) данных измерений на продолжительных
интервалах времени.
в случае
аппроксимации решениями системы (II) данных измерений на продолжительных
интервалах времени.
Таблица
5. Параметр ![]() , стандартные отклонения ошибок данных измерений
, стандартные отклонения ошибок данных измерений
и параметров сглаживающих решений системы (II).
|
Интервал |
|
|
|
|
|
|
|
|
|
|
М |
мм/с |
||||||||
|
1 |
1.250 |
381 |
133 |
90 |
159 |
122 |
182 |
96 |
0.0118 |
|
2 |
1.219 |
473 |
176 |
73 |
204 |
103 |
262 |
97 |
0.0120 |
|
3 |
1.371 |
478 |
150 |
159 |
226 |
231 |
210 |
120 |
0.0115 |
|
4 |
1.361 |
462 |
129 |
102 |
163 |
142 |
174 |
97 |
0.0104 |
|
5 |
1.251 |
426 |
177 |
98 |
191 |
138 |
222 |
130 |
0.0353 |
|
1Ú2 |
1.268 |
513 |
128 |
87 |
159 |
117 |
187 |
84 |
0.0023 |
|
2Ú3 |
1.332 |
685 |
186 |
87 |
211 |
116 |
269 |
111 |
0.0032 |
|
3Ú4 |
1.335 |
484 |
111 |
117 |
172 |
176 |
159 |
81 |
0.0020 |
|
4Ú5 |
1.419 |
532 |
124 |
97 |
156 |
135 |
168 |
93 |
0.0032 |
|
1Ú2Ú3 |
1.299 |
898 |
196 |
136 |
242 |
177 |
285 |
128 |
0.0015 |
|
2Ú3Ú4 |
1.340 |
620 |
133 |
67 |
150 |
85 |
191 |
83 |
0.0011 |
|
3Ú4Ú5 |
1.367 |
877 |
181 |
190 |
278 |
286 |
260 |
132 |
0.0019 |
Таблица 6. Средние
квадратические значения рядов остатков
сглаживающих решений
системы (II).
|
Интервал |
|
|
|
|
|
|
|
м |
мм/с |
|||||
|
1 |
394 |
298 |
352 |
425 |
166 |
462 |
|
2 |
715 |
271 |
244 |
276 |
230 |
719 |
|
3 |
686 |
266 |
227 |
246 |
172 |
773 |
|
4 |
649 |
314 |
256 |
296 |
330 |
671 |
|
5 |
571 |
205 |
182 |
217 |
332 |
630 |
|
1Ú2 |
784 |
284 |
306 |
356 |
209 |
792 |
|
2Ú3 |
1103 |
268 |
240 |
266 |
211 |
1159 |
|
3Ú4 |
706 |
298 |
247 |
277 |
278 |
766 |
|
4Ú5 |
808 |
296 |
234 |
273 |
332 |
839 |
|
1Ú2Ú3 |
1430 |
279 |
297 |
388 |
201 |
1583 |
|
2Ú3Ú4 |
984 |
288 |
247 |
278 |
265 |
1036 |
|
3Ú4Ú5 |
1426 |
292 |
234 |
265 |
291 |
1525 |
Таблица 7. Медианы рядов модулей остатков сглаживающих
решений системы (II).
|
Интервал |
|
|
|
|
|
|
|
м |
мм/с |
|||||
|
1 |
216 |
130 |
218 |
295 |
156 |
252 |
|
2 |
637 |
204 |
88 |
107 |
144 |
656 |
|
3 |
413 |
177 |
191 |
159 |
127 |
578 |
|
4 |
479 |
227 |
168 |
181 |
226 |
588 |
|
5 |
528 |
180 |
154 |
153 |
243 |
506 |
|
1Ú2 |
438 |
190 |
146 |
215 |
140 |
548 |
|
2Ú3 |
733 |
195 |
125 |
149 |
126 |
630 |
|
3Ú4 |
463 |
217 |
171 |
174 |
187 |
589 |
|
4Ú5 |
707 |
168 |
153 |
151 |
228 |
710 |
|
1Ú2Ú3 |
1084 |
191 |
184 |
211 |
132 |
1301 |
|
2Ú3Ú4 |
537 |
206 |
151 |
151 |
152 |
599 |
|
3Ú4Ú5 |
1161 |
198 |
169 |
181 |
204 |
1240 |
Результаты сглаживания, полученные с использованием системы (III), приведены в табл. 8 – 10. Эти таблицы аналогичны таблицам, рассматривавшимся выше. Анализ таблиц показывает, что переход от системы (I) к системе (III) также заметно повышает точность аппроксимации данных измерений на продолжительных интервалах, но в целом точность системы (III) ниже точности системы (II).
Таблица
8. Параметр ![]() , стандартные отклонения ошибок данных измерений
, стандартные отклонения ошибок данных измерений
и параметров сглаживающих решений системы (III).
|
Интервал |
|
|
|
|
|
|
|
|
|
|
м |
мм/с |
||||||||
|
1 |
1.220 |
406 |
142 |
96 |
170 |
130 |
194 |
102 |
0.0123 |
|
2 |
1.213 |
471 |
175 |
73 |
203 |
102 |
262 |
97 |
0.0188 |
|
3 |
1.450 |
468 |
147 |
156 |
222 |
227 |
206 |
118 |
0.0120 |
|
4 |
1.360 |
451 |
126 |
99 |
159 |
139 |
170 |
95 |
0.0102 |
|
5 |
1.234 |
423 |
176 |
97 |
190 |
137 |
221 |
129 |
0.0345 |
|
1Ú2 |
1.265 |
539 |
135 |
91 |
168 |
123 |
197 |
89 |
0.0024 |
|
2Ú3 |
1.354 |
877 |
238 |
112 |
272 |
148 |
346 |
142 |
0.0042 |
|
3Ú4 |
1.370 |
537 |
123 |
129 |
190 |
195 |
177 |
90 |
0.0022 |
|
4Ú5 |
1.410 |
512 |
120 |
93 |
150 |
130 |
161 |
90 |
0.0030 |
|
1Ú2Ú3 |
1.304 |
1187 |
260 |
179 |
320 |
234 |
378 |
169 |
0.0020 |
|
2Ú3Ú4 |
1.375 |
813 |
175 |
90 |
197 |
112 |
251 |
109 |
0.0014 |
|
3Ú4Ú5 |
1.385 |
626 |
129 |
135 |
197 |
203 |
184 |
94 |
0.0014 |
Таблица 9. Средние
квадратические значения рядов остатков
сглаживающих решений
системы (III).
|
Интервал |
|
|
|
|
|
|
|
м |
мм/с |
|||||
|
1 |
455 |
298 |
351 |
424 |
166 |
523 |
|
2 |
714 |
271 |
244 |
275 |
230 |
714 |
|
3 |
671 |
266 |
227 |
246 |
172 |
753 |
|
4 |
628 |
314 |
256 |
296 |
330 |
647 |
|
5 |
566 |
205 |
182 |
217 |
332 |
625 |
|
1Ú2 |
814 |
284 |
307 |
357 |
209 |
846 |
|
2Ú3 |
1422 |
269 |
240 |
266 |
211 |
1531 |
|
3Ú4 |
805 |
298 |
246 |
277 |
278 |
878 |
|
4Ú5 |
776 |
296 |
234 |
273 |
332 |
796 |
|
1Ú2Ú3 |
1913 |
279 |
300 |
341 |
202 |
2137 |
|
2Ú3Ú4 |
1311 |
288 |
247 |
278 |
265 |
1419 |
|
3Ú4Ú5 |
991 |
292 |
233 |
265 |
291 |
1041 |
Таблица 10. Медианы рядов модулей остатков сглаживающих
решений системы (III).
|
Интервал |
|
|
|
|
|
|
|
м |
мм/с |
|||||
|
1 |
245 |
130 |
217 |
294 |
156 |
275 |
|
2 |
633 |
204 |
88 |
107 |
145 |
653 |
|
3 |
407 |
177 |
192 |
158 |
127 |
565 |
|
4 |
434 |
227 |
168 |
180 |
226 |
547 |
|
5 |
526 |
180 |
154 |
152 |
243 |
502 |
|
1Ú2 |
475 |
190 |
145 |
215 |
141 |
522 |
|
2Ú3 |
923 |
194 |
127 |
149 |
128 |
1000 |
|
3Ú4 |
412 |
216 |
171 |
170 |
188 |
421 |
|
4Ú5 |
670 |
168 |
155 |
153 |
228 |
736 |
|
1Ú2Ú3 |
1249 |
193 |
180 |
216 |
138 |
1591 |
|
2Ú3Ú4 |
571 |
208 |
149 |
153 |
152 |
627 |
|
3Ú4Ú5 |
675 |
197 |
164 |
173 |
209 |
763 |
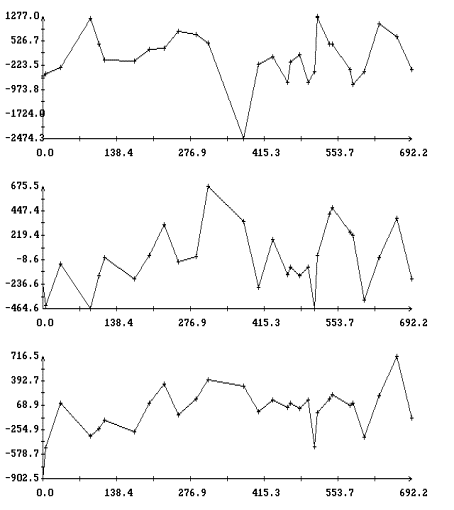
Проведенное исследование показало, что на интервалах времени более 5 сут
учет изменения индекса ![]() позволяет заметно
увеличить точность аппроксимации данных измерений. Специфическое поведение
индекса солнечной активности в период с 26.III по 14.IV.1999 г. дает возможность проиллюстрировать
это и ряд других сделанных утверждений следующим более ярким примером, чем
приведенные в табл. 1 – 10. Возьмем часть рассматривавшегося выше исходного
отрезка данных измерений, у которой
позволяет заметно
увеличить точность аппроксимации данных измерений. Специфическое поведение
индекса солнечной активности в период с 26.III по 14.IV.1999 г. дает возможность проиллюстрировать
это и ряд других сделанных утверждений следующим более ярким примером, чем
приведенные в табл. 1 – 10. Возьмем часть рассматривавшегося выше исходного
отрезка данных измерений, у которой ![]() ,
, ![]() 01.IV,
01.IV, ![]() 10.IV (использована
шкала времени UTC),
10.IV (использована
шкала времени UTC), ![]() . Новый отрезок данных назовем интервалом 6. Характеристики точности
аппроксимации этого интервала решениями систем (I), (II) и (III) указаны в табл. 11 – 13. Как видно из таблиц, учет изменения индекса
. Новый отрезок данных назовем интервалом 6. Характеристики точности
аппроксимации этого интервала решениями систем (I), (II) и (III) указаны в табл. 11 – 13. Как видно из таблиц, учет изменения индекса ![]() позволил повысить точность
аппроксимации более чем в три раза.
позволил повысить точность
аппроксимации более чем в три раза.
Таблица
11. Параметр ![]() , стандартные отклонения ошибок данных
, стандартные отклонения ошибок данных
измерений и параметров сглаживающих решений для интервала 6.
|
Система |
|
|
|
|
|
|
|
|
|
|
М |
мм/с |
||||||||
|
(I) |
1.331 |
1879 |
221 |
416 |
460 |
567 |
286 |
275 |
0.0047 |
|
(II) |
1.344 |
529 |
62 |
116 |
127 |
157 |
81 |
77 |
0.0013 |
|
(III) |
1.385 |
611 |
72 |
134 |
147 |
182 |
93 |
89 |
0.0016 |
Таблица 12. Средние
квадратические значения рядов остатков
сглаживающих решений
для интервала 6.
|
Система |
|
|
|
|
|
|
|
м |
мм/с |
|||||
|
(I) |
3015 |
300 |
282 |
314 |
279 |
3471 |
|
(II) |
822 |
301 |
270 |
305 |
278 |
815 |
|
(III) |
960 |
301 |
269 |
305 |
278 |
991 |
Таблица 13. Медианы рядов
модулей остатков сглаживающих
решений для интервала 6.
|
Система |
|
|
|
|
|
|
|
м |
мм/с |
|||||
|
(I) |
2555 |
218 |
182 |
190 |
176 |
2928 |
|
(II) |
614 |
219 |
164 |
162 |
169 |
639 |
|
(III) |
602 |
219 |
164 |
161 |
169 |
531 |
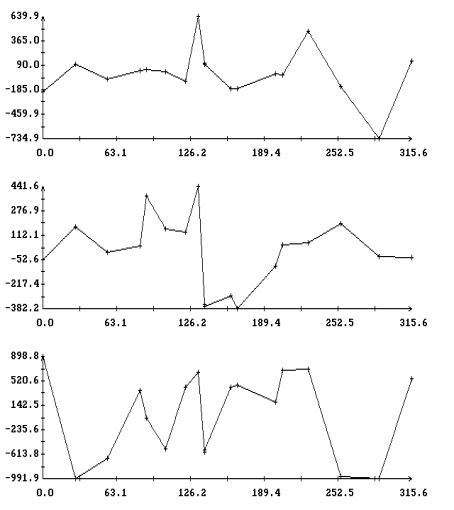
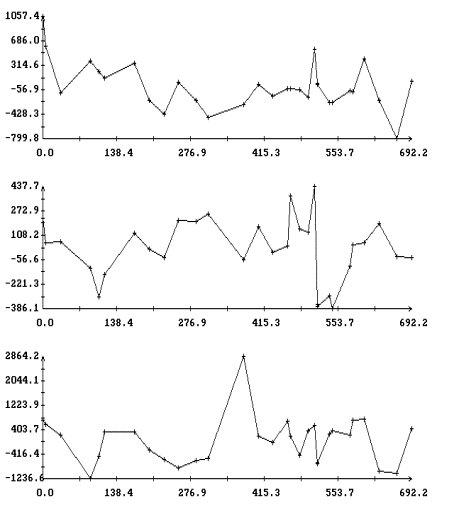
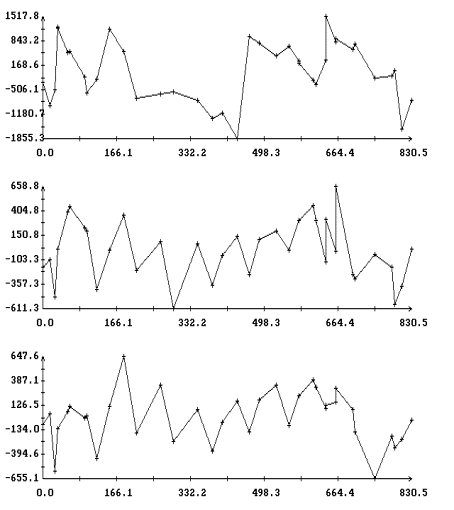
На рис. 7, 8 изображены диаграммы рядов остатков ![]() для решений систем (I) и (II). Сравнение рисунков
показывает значительное уменьшение систематической составляющей в остатках
для решений систем (I) и (II). Сравнение рисунков
показывает значительное уменьшение систематической составляющей в остатках ![]() и
и ![]() в случае аппроксимации
данных измерений решением системы (II).
в случае аппроксимации
данных измерений решением системы (II).
4. Заключение. Проведенное исследование показало, что учет изменения параметра ![]() позволяет в несколько
раз увеличить точность аппроксимации данных измерений на интервалах времени
более 5 сут. При аппроксимации данных измерений на интервалах времени менее 3
сут выигрыш в точности практически отсутствует.
позволяет в несколько
раз увеличить точность аппроксимации данных измерений на интервалах времени
более 5 сут. При аппроксимации данных измерений на интервалах времени менее 3
сут выигрыш в точности практически отсутствует.
Литература
1. Ветлов В.И., Новичкова С.М., Сазонов В.В., Матвеев Н.В., Бабкин Е.В. Режим гравитационной ориентации Международной космической станции. Космические исследования, 2001, т. 39, № 4, с. 436-448.
2. Ланцош К. Практические методы прикладного анализа. М., Физматгиз, 1961.
Приложение
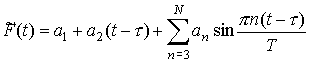 ,
,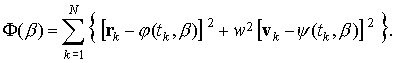
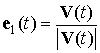 ,
,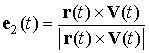 ,
,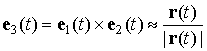 .
.