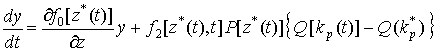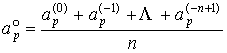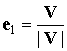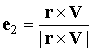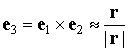Влияние вариаций плотности атмосферы, вызываемых геомагнитной активностью, на точность
прогноза движения МКС
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
14604 |
0.01 |
260.6 |
0.00 |
0.26 |
0.00 |
5.49 |
|
2 |
14603 |
-8.30 |
263.3 |
0.01 |
0.26 |
0.16 |
5.46 |
|
4 |
14601 |
-19.5 |
276.3 |
0.02 |
0.27 |
0.37 |
5.60 |
|
8 |
14597 |
-33.5 |
299.0 |
0.03 |
0.29 |
0.64 |
5.91 |
|
|
|
|
|
|
|
|
|
|
1 |
0.103 |
0.00 |
2.79 |
0.00 |
0.08 |
-0.01 |
294.6 |
|
2 |
0.103 |
-0.08 |
2.78 |
0.00 |
0.08 |
9.39 |
297.6 |
|
4 |
0.115 |
-0.19 |
2.85 |
0.01 |
0.09 |
22.0 |
312.3 |
|
8 |
0.139 |
-0.32 |
3.01 |
0.01 |
0.10 |
37.9 |
338.0 |
Таблица
2. Прогноз 1 при ![]() и
и ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч |
|
м |
мм/с |
||||||||||
|
2.5 |
0 |
-0.9 |
8.3 |
0.0 |
0.0 |
0.1 |
1.2 |
-0.1 |
0.7 |
0.0 |
0.0 |
1.0 |
9.3 |
|
4.5 |
0 |
-2.9 |
26.4 |
0.0 |
0.0 |
0.2 |
1.6 |
-0.1 |
0.7 |
0.0 |
0.1 |
3.3 |
30.1 |
|
6.0 |
0 |
-5.2 |
47.2 |
0.0 |
0.0 |
0.2 |
2.1 |
-0.1 |
0.9 |
0.0 |
0.1 |
5.9 |
53.6 |
|
7.5 |
0.001 |
-8.2 |
74.0 |
0.0 |
0.0 |
0.3 |
2.6 |
-0.1 |
1.1 |
0.0 |
0.1 |
9.3 |
83.9 |
|
9.0 |
0.008 |
-11.9 |
107 |
0.0 |
0.1 |
0.4 |
3.2 |
-0.2 |
1.4 |
0.0 |
0.2 |
13.5 |
121 |
|
10.5 |
0.022 |
-16.3 |
145 |
0.0 |
0.1 |
0.4 |
3.8 |
-0.2 |
1.7 |
0.0 |
0.2 |
18.4 |
165 |
|
12.0 |
0.047 |
-21.3 |
190 |
0.0 |
0.2 |
0.5 |
4.5 |
-0.2 |
2.1 |
0.0 |
0.1 |
24.1 |
215 |
|
13.5 |
0.086 |
-27.1 |
242 |
0.0 |
0.2 |
0.6 |
5.1 |
-0.3 |
2.5 |
0.0 |
0.0 |
30.6 |
273 |
|
15.0 |
0.139 |
-33.5 |
299 |
0.0 |
0.3 |
0.6 |
5.9 |
-0.3 |
3.0 |
0.0 |
0.1 |
37.9 |
338 |
Из табл. 1 видно, что точность прогноза довольно слабо зависит от числа
![]() измерений индекса
измерений индекса ![]() , по которым вычисляется используемое в прогнозе значение
, по которым вычисляется используемое в прогнозе значение ![]() . Хотя, как и следовало ожидать, с уменьшением
. Хотя, как и следовало ожидать, с уменьшением ![]() точность прогноза несколько повышается. Согласно табл. 2 ошибка
прогноза быстро уменьшается с уменьшением
точность прогноза несколько повышается. Согласно табл. 2 ошибка
прогноза быстро уменьшается с уменьшением ![]() . Согласно обеим таблицам основная ошибка в прогнозе
положения станции совершается вдоль орта
. Согласно обеим таблицам основная ошибка в прогнозе
положения станции совершается вдоль орта ![]() – по направлению вектора
абсолютной скорости в точке
– по направлению вектора
абсолютной скорости в точке ![]() . Ошибка в направлении орта
. Ошибка в направлении орта ![]() (по радиусу-вектору)
примерно в 50 раз меньше, ошибка в направлении орта
(по радиусу-вектору)
примерно в 50 раз меньше, ошибка в направлении орта ![]() (по нормали к
плоскости орбиты) пренебрежимо мала. Ошибки прогноза абсолютной геоцентрической
скорости станции наиболее велики в направлении орта
(по нормали к
плоскости орбиты) пренебрежимо мала. Ошибки прогноза абсолютной геоцентрической
скорости станции наиболее велики в направлении орта ![]() и пренебрежимо малы в
направлении
и пренебрежимо малы в
направлении ![]() . Эти факты находятся в полном согласии с теорией
возмущенного движения ИСЗ в атмосфере [2, 3].
. Эти факты находятся в полном согласии с теорией
возмущенного движения ИСЗ в атмосфере [2, 3].
Распределение ошибок в пространстве ![]() можно пояснить,
рассмотрев собственные числа и собственные векторы ковариационной матрицы
можно пояснить,
рассмотрев собственные числа и собственные векторы ковариационной матрицы ![]() . Эти величины слабо зависят от
. Эти величины слабо зависят от ![]() , поэтому ограничимся анализом
случая
, поэтому ограничимся анализом
случая ![]() . Собственные числа матрицы
. Собственные числа матрицы ![]() при
при ![]() составляют (при
расчете
составляют (при
расчете ![]() единицей измерения
длины служили метры, скорости – мм/с)
единицей измерения
длины служили метры, скорости – мм/с)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Нормированные собственные векторы, отвечающие максимальному и второму по величине собственным числам, соответственно имеют вид
![]() ,
,
![]() .
.
Модули компонент вектора
![]() ,
,
достаточно точно
совпадают с соответствующими стандартными отклонениями ![]() ,
, ![]() , …,
, …, ![]() . Указанный факт обусловлен
доминированием
. Указанный факт обусловлен
доминированием ![]() над остальными
собственными числами матрицы
над остальными
собственными числами матрицы ![]() – в этом случае
– в этом случае ![]() . Некоторое несовпадение модулей третьей и четвертой
компонент с
. Некоторое несовпадение модулей третьей и четвертой
компонент с ![]() и
и ![]() обусловлено влиянием одноименных компонент вектора
обусловлено влиянием одноименных компонент вектора ![]() . Последнее утверждение следует из более точной формулы
. Последнее утверждение следует из более точной формулы ![]() .
.
Из приведенного анализа собственных чисел и векторов матрицы ![]() следует, что ошибки
прогноза в пространстве
следует, что ошибки
прогноза в пространстве ![]() распределены в
основном вдоль направления
распределены в
основном вдоль направления ![]() . Модули коэффициентов корреляции лишь в случае пар
. Модули коэффициентов корреляции лишь в случае пар ![]() ,
, ![]() составляют 0.88.
Модули коэффициентов корреляции остальных пар переменных превосходят 0.96.
Проекции вектора
составляют 0.88.
Модули коэффициентов корреляции остальных пар переменных превосходят 0.96.
Проекции вектора ![]() на подпространства
на подпространства ![]() и
и ![]() характеризуют
распределение ошибок прогноза положения и скорости станции в базисе
характеризуют
распределение ошибок прогноза положения и скорости станции в базисе ![]() .
.
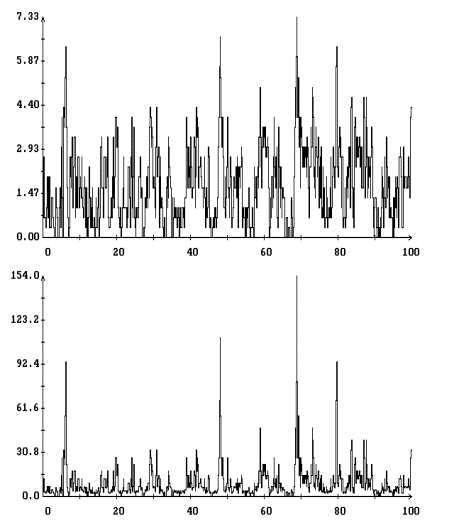
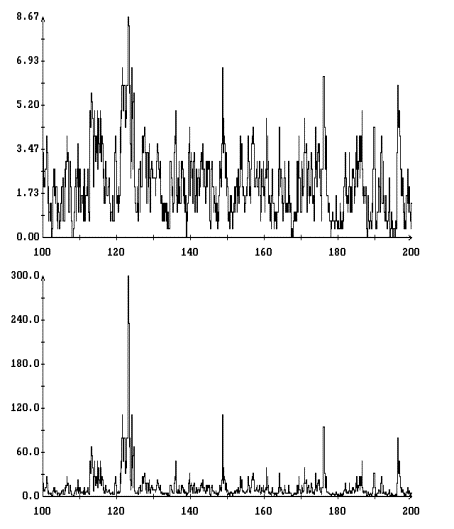
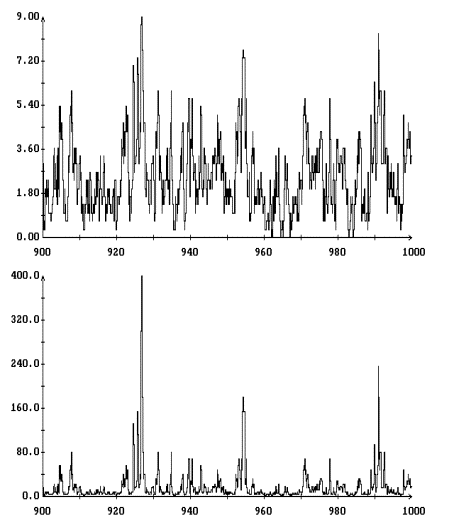
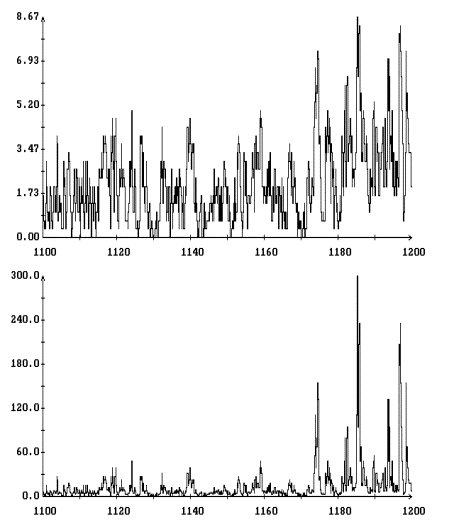
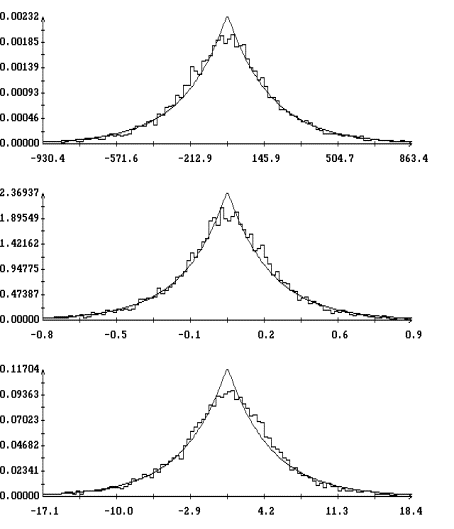
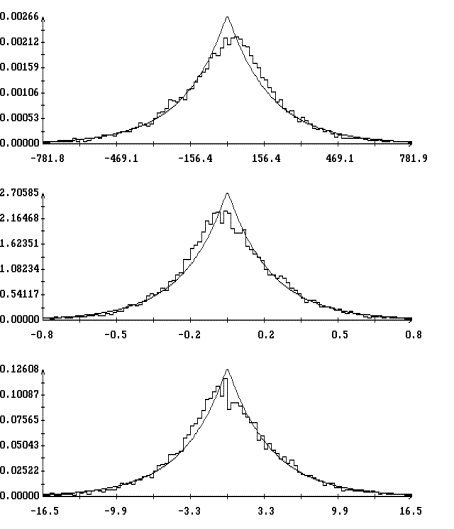
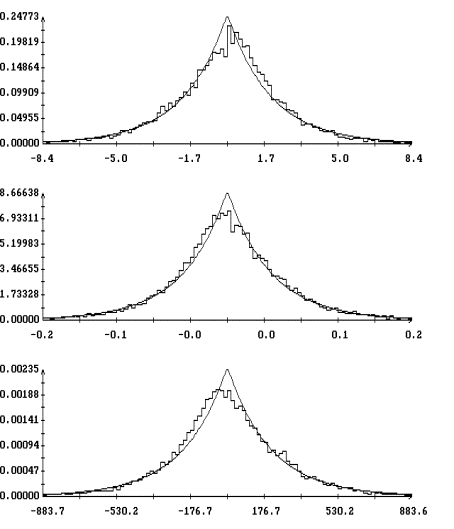
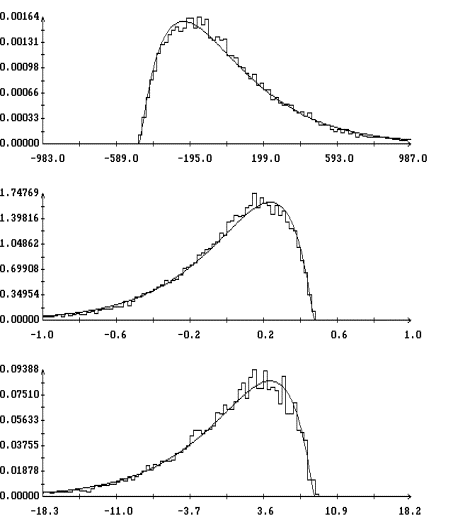
Детальное представление о полученном
при статистическом моделировании распределении ошибок прогноза по величине дают
гистограммы [1] переменных ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() . Гистограммы строились единообразно, поэтому ограничимся
описанием построения гистограммы координаты
. Гистограммы строились единообразно, поэтому ограничимся
описанием построения гистограммы координаты ![]() . Пусть
. Пусть ![]() – натуральное число.
Отрезок
– натуральное число.
Отрезок ![]() разбивался на
разбивался на ![]() отрезков равной
длины, и для каждого отрезка разбиения подсчитывалось число оказавшихся в нем
полученных при моделировании значений
отрезков равной
длины, и для каждого отрезка разбиения подсчитывалось число оказавшихся в нем
полученных при моделировании значений ![]() . Пусть в отрезок с номером
. Пусть в отрезок с номером ![]() попало
попало ![]() точек. Гистограммой
называется кусочно-постоянная функция
точек. Гистограммой
называется кусочно-постоянная функция ![]() , которая на отрезке с номером
, которая на отрезке с номером ![]() принимает значение
принимает значение ![]() . Напомним,
. Напомним, ![]() – общее число
испытаний в данном варианте моделирования (при данном
– общее число
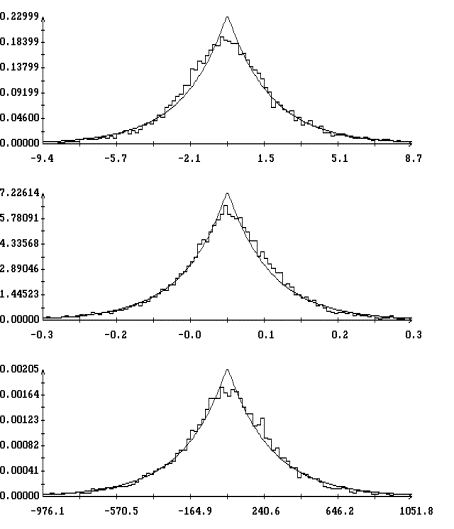
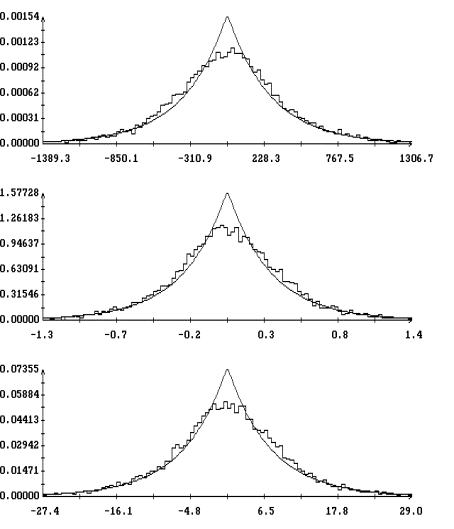
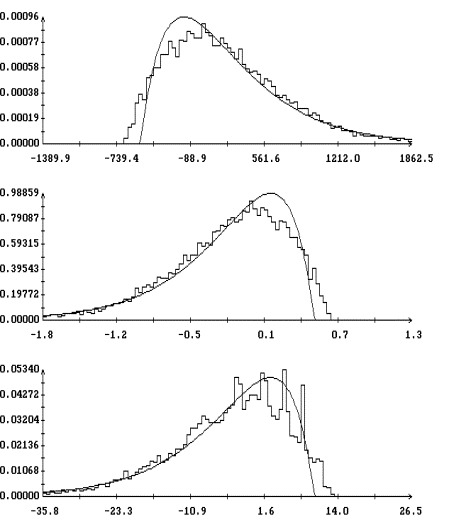
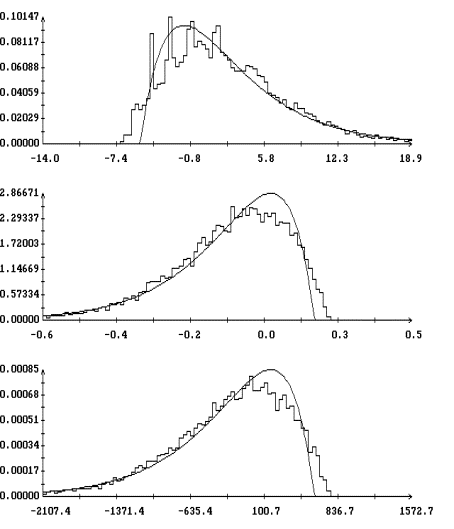
испытаний в данном варианте моделирования (при данном ![]() ). Графики гистограмм
). Графики гистограмм ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() , построенные для варианта с
, построенные для варианта с ![]() при
при ![]() , изображены на рис. 3. Эти графики выглядят как ступенчатые
линии, поскольку для наглядности на рисунках указаны вертикальные отрезки,
соединяющие предельные значения гистограмм в точках разрыва.
, изображены на рис. 3. Эти графики выглядят как ступенчатые
линии, поскольку для наглядности на рисунках указаны вертикальные отрезки,
соединяющие предельные значения гистограмм в точках разрыва.
Полученные гистограммы достаточно точно аппроксимируются плотностью вероятности двухстороннего показательного распределения
![]()
при надлежащем
выборе ![]() и
и ![]() . Для определения этих параметров надо приравнять первый и
второй моменты выписанной плотности соответствующим выборочным моментам. В
частности, для аппроксимации
. Для определения этих параметров надо приравнять первый и
второй моменты выписанной плотности соответствующим выборочным моментам. В
частности, для аппроксимации ![]() надо взять
надо взять ![]() ,
, ![]() . Графики построенных таким образом аппроксимирующих функций
также приведены на рис. 3. Эти графики выглядят как плавные линии с изломом
посередине. Аппроксимации гистограмм всех переменных выглядят весьма похоже,
что объясняется указанной выше сильной корреляцией этих переменных.
. Графики построенных таким образом аппроксимирующих функций
также приведены на рис. 3. Эти графики выглядят как плавные линии с изломом
посередине. Аппроксимации гистограмм всех переменных выглядят весьма похоже,
что объясняется указанной выше сильной корреляцией этих переменных.
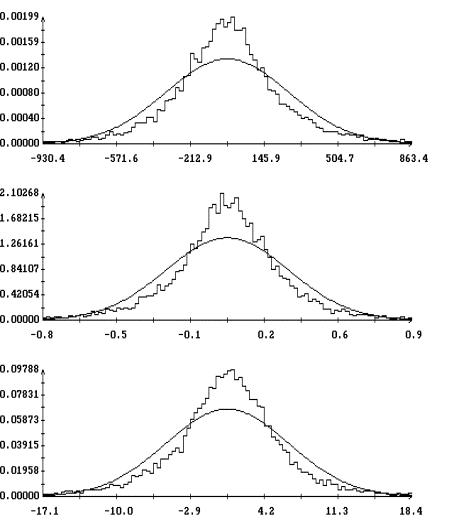
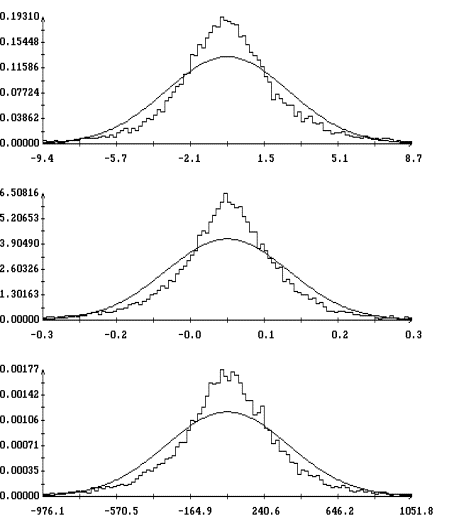
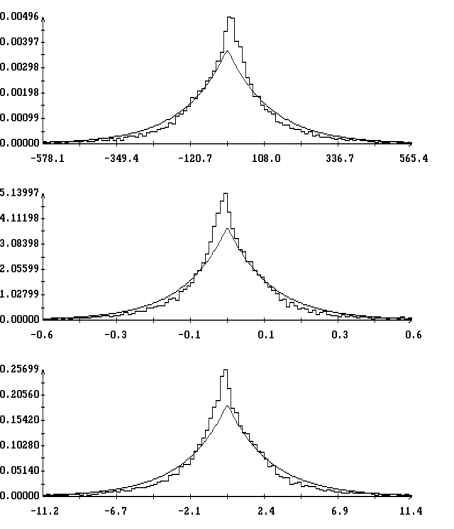
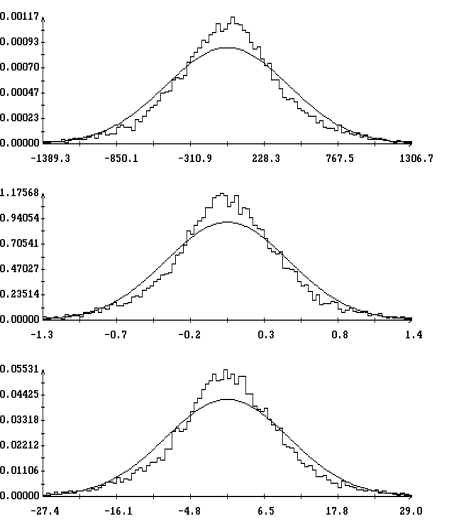
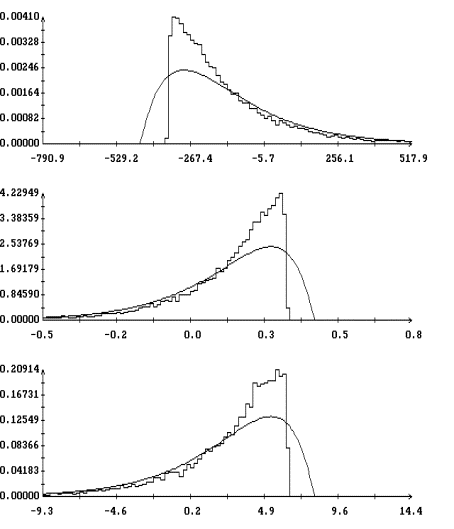
Для сравнения на рис. 4 приведены результаты аппроксимации полученных гистограмм плотностью вероятности нормального распределения
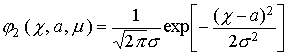 .
.
В этом случае при
аппроксимации ![]() принималось
принималось ![]() ,
, ![]() и т. д. Как
показывает рисунок, такая аппроксимация является существенно менее точной.
и т. д. Как
показывает рисунок, такая аппроксимация является существенно менее точной.
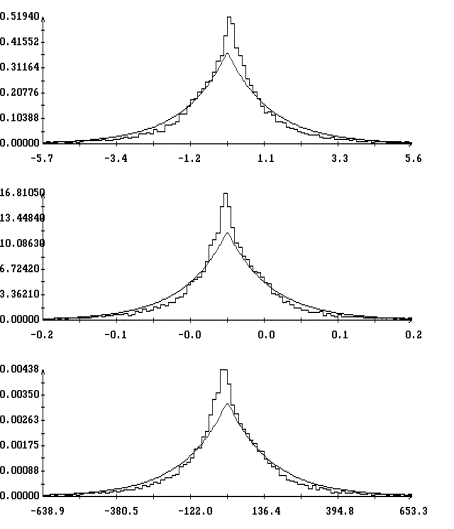
Рис. 3, 4 построены для варианта ![]() в случае
в случае ![]() . Визуально примерно такое же качество аппроксимации
достигается во всех вариантах из табл. 1 при
. Визуально примерно такое же качество аппроксимации
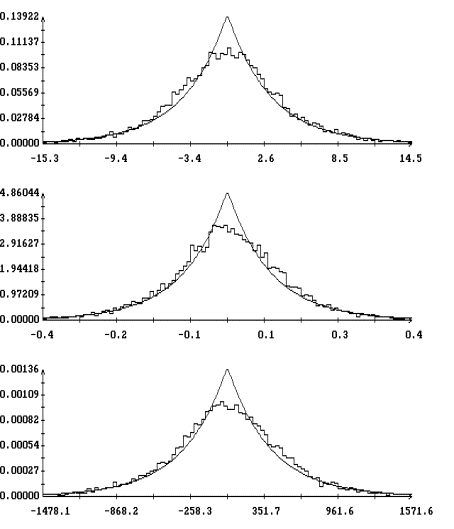
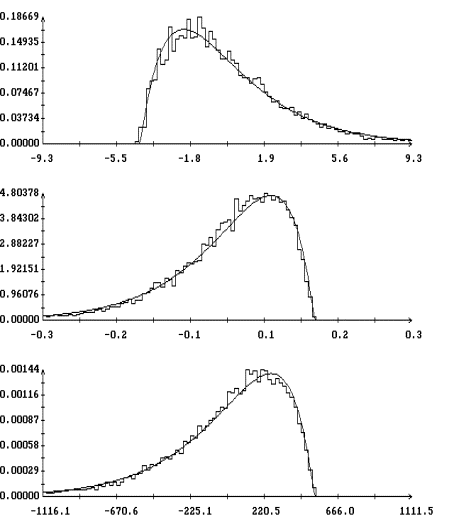
достигается во всех вариантах из табл. 1 при ![]() . На рис. 5 приведены гистограммы и их аппроксимации
плотностью вероятности
. На рис. 5 приведены гистограммы и их аппроксимации
плотностью вероятности ![]() для варианта
для варианта ![]() в случае
в случае ![]() .
.
Чтобы оценить влияние параметров ![]() и
и ![]() на точность прогноза,
описанные расчеты были повторены для опорных решений, рассчитанных при прежних
начальных условиях и
на точность прогноза,
описанные расчеты были повторены для опорных решений, рассчитанных при прежних
начальных условиях и ![]() , но при
, но при ![]() и
и ![]() . Результаты расчетов в случае
. Результаты расчетов в случае ![]() приведены в табл. 3,
4 и на рис. 6. Новые таблицы в точности аналогичны табл. 1, 2. Из них видно,
что погрешность прогноза заметно уменьшилась. На рис. 6 изображены гистограммы
приведены в табл. 3,
4 и на рис. 6. Новые таблицы в точности аналогичны табл. 1, 2. Из них видно,
что погрешность прогноза заметно уменьшилась. На рис. 6 изображены гистограммы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() (ступенчатые линии),
построенные при
(ступенчатые линии),
построенные при ![]() для варианта
для варианта ![]() , и аппроксимации этих гистограмм плотностью вероятности
, и аппроксимации этих гистограмм плотностью вероятности ![]() (плавные линии с
изломом посередине) при описанном выше способе выбора значений
(плавные линии с
изломом посередине) при описанном выше способе выбора значений ![]() и
и ![]() . Из рисунка видно, что в данном случае аппроксимация не так
точна, как в случае
. Из рисунка видно, что в данном случае аппроксимация не так
точна, как в случае ![]() . Распределение ошибок прогноза стало более кучным и уже не
может адекватно описываться двухсторонним показательным распределением.
Аппроксимация гистограмм плотностью
. Распределение ошибок прогноза стало более кучным и уже не
может адекватно описываться двухсторонним показательным распределением.
Аппроксимация гистограмм плотностью ![]() выглядит еще менее
точной.
выглядит еще менее
точной.
Таблица
3. Прогноз 1 при ![]() и
и ![]() ч.
ч.
|
|
|
|
|
|
|
|
|
|
1 |
14604 |
0.00 |
178.7 |
0.00 |
0.18 |
0.00 |
3.69 |
|
2 |
14603 |
-2.47 |
181.2 |
0.00 |
0.18 |
0.05 |
3.69 |
|
4 |
14601 |
-6.35 |
190.6 |
0.01 |
0.19 |
0.12 |
3.78 |
|
8 |
14597 |
-11.3 |
205.0 |
0.01 |
0.20 |
0.21 |
3.96 |
|
|
|
|
|
|
|
|
|
|
1 |
0.042 |
0.00 |
1.83 |
0.00 |
0.05 |
0.00 |
201.8 |
|
2 |
0.042 |
-0.02 |
1.83 |
0.00 |
0.06 |
2.79 |
204.7 |
|
4 |
0.048 |
-0.06 |
1.87 |
0.00 |
0.06 |
7.17 |
215.4 |
|
8 |
0.058 |
-0.10 |
1.97 |
0.00 |
0.07 |
12.8 |
231.7 |
Таблица
4. Прогноз при ![]() и
и ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч |
|
м |
мм/с |
||||||||||
|
2.5 |
0 |
-0.3 |
5.7 |
0.0 |
0.0 |
0.0 |
0.8 |
0.0 |
0.5 |
0.0 |
0.0 |
0.3 |
6.4 |
|
4.5 |
0 |
-1.0 |
18.1 |
0.0 |
0.0 |
0.1 |
1.1 |
0.0 |
0.4 |
0.0 |
0.1 |
1.1 |
20.6 |
|
6.0 |
0 |
-1.8 |
32.3 |
0.0 |
0.0 |
0.1 |
1.4 |
0.0 |
0.6 |
0.0 |
0.1 |
2.0 |
36.8 |
|
7.5 |
0.000 |
-2.8 |
50.7 |
0.0 |
0.0 |
0.1 |
1.7 |
0.0 |
0.7 |
0.0 |
0.1 |
3.2 |
57.5 |
|
9.0 |
0.003 |
-4.0 |
73.2 |
0.0 |
0.1 |
0.1 |
2.1 |
0.0 |
0.9 |
0.0 |
0.1 |
4.6 |
82.9 |
|
10.5 |
0.010 |
-5.5 |
99.9 |
0.0 |
0.1 |
0.1 |
2.5 |
-0.1 |
1.2 |
0.0 |
0.1 |
6.2 |
113 |
|
12.0 |
0.020 |
-7.2 |
131 |
0.0 |
0.1 |
0.2 |
3.0 |
-0.1 |
1.3 |
0.0 |
0.1 |
8.2 |
148 |
|
13.5 |
0.036 |
-9.2 |
166 |
0.0 |
0.2 |
0.2 |
3.4 |
-0.1 |
1.6 |
0.0 |
0.0 |
10.4 |
187 |
|
15.0 |
0.058 |
-11.3 |
205 |
0.0 |
0.2 |
0.2 |
4.0 |
-0.1 |
2.0 |
0.0 |
0.1 |
12.8 |
232 |
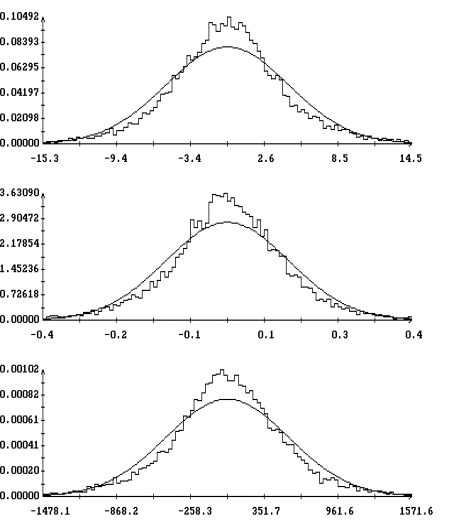
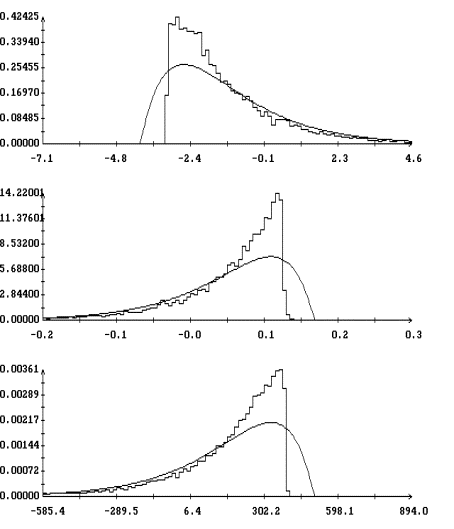
Результаты расчетов в случае ![]() приведены в табл. 5,
6 и на рис. 7, 8. Таблицы аналогичны предыдущим. Они показывают, что погрешность
прогноза заметно возросла по сравнению со случаем
приведены в табл. 5,
6 и на рис. 7, 8. Таблицы аналогичны предыдущим. Они показывают, что погрешность
прогноза заметно возросла по сравнению со случаем ![]() . На рис. 7, 8 изображены гистограммы
. На рис. 7, 8 изображены гистограммы ![]() , …,
, …, ![]() , построенные при
, построенные при ![]() для варианта
для варианта ![]() , и аппроксимации этих гистограмм плотностями вероятностей
, и аппроксимации этих гистограмм плотностями вероятностей ![]() (рис. 7) и
(рис. 7) и ![]() (рис. 8). Параметры
(рис. 8). Параметры ![]() ,
, ![]() и
и ![]() аппроксимирующих
функций определялись выборочными средними значениями и дисперсиями найденных
ошибок прогноза. По сравнению со случаем
аппроксимирующих
функций определялись выборочными средними значениями и дисперсиями найденных
ошибок прогноза. По сравнению со случаем ![]() аппроксимация
гистограмм плотностью
аппроксимация
гистограмм плотностью ![]() стала точнее.
Точность аппроксимации плотностью
стала точнее.
Точность аппроксимации плотностью ![]() уменьшилась, но в
отличие от случая
уменьшилась, но в
отличие от случая ![]() это уменьшение
точности вызвано увеличением разброса переменных
это уменьшение
точности вызвано увеличением разброса переменных ![]() , …,
, …, ![]() . Распределение ошибок прогноза приблизилось к нормальному.
. Распределение ошибок прогноза приблизилось к нормальному.
Таблица 5. Прогноз 1 при ![]() и
и ![]() ч.
ч.
|
|
|
|
|
|
|
|
|
|
1 |
14604 |
0.02 |
426.3 |
0.00 |
0.42 |
0.00 |
9.26 |
|
2 |
14603 |
-18.0 |
429.4 |
0.02 |
0.42 |
0.35 |
9.20 |
|
4 |
14601 |
-41.3 |
449.3 |
0.04 |
0.44 |
0.81 |
9.41 |
|
8 |
14597 |
-70.4 |
486.8 |
0.07 |
0.47 |
1.39 |
9.97 |
|
|
|
|
|
|
|
|
|
|
1 |
0.291 |
0.00 |
4.89 |
0.00 |
0.13 |
-0.02 |
482.2 |
|
2 |
0.291 |
-0.19 |
4.86 |
0.01 |
0.13 |
20.3 |
485.7 |
|
4 |
0.310 |
-0.43 |
4.97 |
0.01 |
0.14 |
46.7 |
508.3 |
|
8 |
0.347 |
-0.73 |
5.27 |
0.02 |
0.16 |
79.7 |
550.8 |
Таблица
6. Прогноз при ![]() и
и ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч |
|
м |
мм/с |
||||||||||
|
2.5 |
0 |
-1.9 |
13.5 |
0.0 |
0.0 |
0.3 |
1.9 |
-0.2 |
1.2 |
0.0 |
0.0 |
2.1 |
15.3 |
|
4.5 |
0 |
-6.1 |
43.5 |
0.0 |
0.0 |
0.4 |
2.7 |
-0.2 |
1.3 |
0.0 |
0.1 |
7.0 |
49.5 |
|
6.0 |
0.000 |
-11.0 |
77.3 |
0.0 |
0.0 |
0.5 |
3.6 |
-0.2 |
1.7 |
0.0 |
0.2 |
12.5 |
87.8 |
|
7.5 |
0.009 |
-17.3 |
121 |
0.0 |
0.1 |
0.6 |
4.5 |
-0.3 |
2.1 |
0.0 |
0.2 |
19.7 |
137 |
|
9.0 |
0.035 |
-25.1 |
174 |
0.0 |
0.1 |
0.8 |
5.5 |
-0.4 |
2.6 |
0.0 |
0.3 |
28.4 |
197 |
|
10.5 |
0.089 |
-34.3 |
237 |
0.0 |
0.2 |
0.9 |
6.5 |
-0.4 |
3.1 |
0.0 |
0.2 |
38.8 |
269 |
|
12.0 |
0.168 |
-44.9 |
310 |
0.0 |
0.3 |
1.1 |
7.6 |
-0.5 |
3.7 |
0.0 |
0.2 |
50.8 |
351 |
|
13.5 |
0.257 |
-56.9 |
393 |
0.1 |
0.4 |
1.2 |
8.7 |
-0.6 |
4.4 |
0.0 |
0.1 |
64.4 |
445 |
|
15.0 |
0.347 |
-70.4 |
487 |
0.1 |
0.5 |
1.4 |
10.0 |
-0.7 |
5.3 |
0.0 |
0.2 |
70.7 |
551 |
Поведение матрицы ![]() , ее собственных чисел и векторов в случаях
, ее собственных чисел и векторов в случаях ![]() и
и ![]() в точности такое же,
как в случае
в точности такое же,
как в случае ![]() .
.
4. Прогноз при неизменном ![]() . Для более полной оценки полученных
результатов сравним прогноз движения станции, выполняемый при выборе
. Для более полной оценки полученных
результатов сравним прогноз движения станции, выполняемый при выборе ![]() по схеме раздела 3, с более простым прогнозом, который всякий раз
рассчитывается при одном и том же значении этого индекса. Статистическое
моделирование такого прогноза проводилось следующим образом. Все варианты рассчитывались
при
по схеме раздела 3, с более простым прогнозом, который всякий раз
рассчитывается при одном и том же значении этого индекса. Статистическое
моделирование такого прогноза проводилось следующим образом. Все варианты рассчитывались
при ![]() ч
ч ![]() . Задавалось значение
. Задавалось значение ![]() . На первом шаге из имеющегося
упорядоченного массива данных измерений трехчасового индекса
. На первом шаге из имеющегося
упорядоченного массива данных измерений трехчасового индекса ![]() (см. раздел 2) выбирались первые пять элементов. Эта упорядоченная
пятерка принимались в качестве параметров
(см. раздел 2) выбирались первые пять элементов. Эта упорядоченная
пятерка принимались в качестве параметров ![]()
![]() . Для таких значений
. Для таких значений ![]() и
и ![]() способом, описанным выше, рассчитывался вектор
способом, описанным выше, рассчитывался вектор ![]() . На втором шаге в качестве параметров
. На втором шаге в качестве параметров ![]() использовались взятые подряд 5 элементов этого массива начиная со
второго. Для прежнего значения
использовались взятые подряд 5 элементов этого массива начиная со
второго. Для прежнего значения ![]() и новых
и новых ![]() снова рассчитывался вектор
снова рассчитывался вектор ![]() . На третьем шаге из массива значений
. На третьем шаге из массива значений ![]() выбирались 5 элементов начиная с третьего и т. д. Всего таких
шагов выполнялось 14605. Использовались прежние опорные решения. Обработка
результатов вычислений выполнялась по описанной выше схеме. В качестве значений
выбирались 5 элементов начиная с третьего и т. д. Всего таких
шагов выполнялось 14605. Использовались прежние опорные решения. Обработка
результатов вычислений выполнялась по описанной выше схеме. В качестве значений
![]() для определенности использовались значения 1,1+ (1.3333),
для определенности использовались значения 1,1+ (1.3333), ![]() (1.6667) и т.д. Результаты приведены лишь для некоторых
значений
(1.6667) и т.д. Результаты приведены лишь для некоторых
значений ![]() и обязательно содержат вариант с минимальным значением
и обязательно содержат вариант с минимальным значением ![]() . В заголовках таблиц и подписях к рисункам новый прогноз
обозначен как прогноз 2.
. В заголовках таблиц и подписях к рисункам новый прогноз
обозначен как прогноз 2.
Результаты, полученные для опорного решения в случае ![]() , представлены в табл. 7 и на рис. 9. Таблица аналогична
табл. 1, 3 и 5, только в ней вместо значений
, представлены в табл. 7 и на рис. 9. Таблица аналогична
табл. 1, 3 и 5, только в ней вместо значений ![]() указаны значения
указаны значения ![]() , и отсутствует столбец со значениями
, и отсутствует столбец со значениями
![]() – во всех вариантах моделирования теперь
– во всех вариантах моделирования теперь ![]() . Из таблицы видно, что изменение
. Из таблицы видно, что изменение ![]() приводит только к смещению среднего значения прогноза, а его
стандартные отклонения остаются неизменными. Указанное смещение приводит к
значительному увеличению
приводит только к смещению среднего значения прогноза, а его
стандартные отклонения остаются неизменными. Указанное смещение приводит к
значительному увеличению ![]() . При
. При ![]() смещение весьма мало, и описанный простейший способ прогноза
практически не уступает по точности, способу рассмотренному выше.
смещение весьма мало, и описанный простейший способ прогноза
практически не уступает по точности, способу рассмотренному выше.
Матрица ![]() во втором способе
прогноза практически не зависит от
во втором способе
прогноза практически не зависит от ![]() . При
. При ![]() ее собственные числа составляют
ее собственные числа составляют
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
нормированные
собственные векторы, отвечающие максимальному и второму по величине собственным
числам, совпадают (если указывать две цифры после запятой в каждой компоненте)
с векторами ![]() и
и ![]() , приведенными выше.
, приведенными выше.
Модули компонент вектора
![]() ,
,
достаточно точно
совпадают с соответствующими стандартными отклонениями ![]() ,
, ![]() , …,
, …, ![]() . Ситуация здесь в точности та же,
что и в случае, рассмотренном в предыдущем разделе. Анализ средних значений
. Ситуация здесь в точности та же,
что и в случае, рассмотренном в предыдущем разделе. Анализ средних значений ![]() ,
, ![]() , …,
, …, ![]() в табл. 7 показывает,
что при изменении
в табл. 7 показывает,
что при изменении ![]() эти средние значения смещаются вдоль вектора
эти средние значения смещаются вдоль вектора ![]() .
.
Таблица 7. Прогноз 2 при ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
0.138 |
2.03 |
328.3 |
0.00 |
0.32 |
-0.04 |
6.08 |
|
|
0.203 |
-81.8 |
328.3 |
0.08 |
0.32 |
1.56 |
6.08 |
|
3 |
0.312 |
-170.2 |
328.3 |
0.17 |
0.32 |
3.24 |
6.08 |
|
5 |
0.902 |
-795.7 |
328.4 |
0.78 |
0.32 |
15.2 |
6.08 |
|
|
|
|
|
|
|
|
|
|
0.02 |
3.09 |
0.00 |
0.11 |
-2.30 |
371.3 |
|
|
-0.79 |
3.09 |
0.03 |
0.11 |
92.5 |
371.3 |
|
3 |
-1.65 |
3.09 |
0.05 |
0.11 |
192.4 |
371.3 |
|
5 |
-7.71 |
3.09 |
0.25 |
0.11 |
899.5 |
371.3 |
На рис. 9 приведены гистограммы значений переменных ![]() ,
, ![]() , …,
, …, ![]() , полученных в варианте статистического моделирования с
, полученных в варианте статистического моделирования с ![]() (ступенчатые линии). Способ построения этих гистограмм описан в
предыдущем разделе. В данном случае
(ступенчатые линии). Способ построения этих гистограмм описан в
предыдущем разделе. В данном случае ![]() . Эти гистограммы достаточно точно аппроксимируются
плотностью вероятности гамма распределения с показателем формы 2:
. Эти гистограммы достаточно точно аппроксимируются
плотностью вероятности гамма распределения с показателем формы 2:
![]() .
.
На рис. 9 графики
аппроксимирующих функций изображены плавными кривыми. Для определения
параметров ![]() и
и ![]() использовались
первый, второй и третий выборочные моменты. Например, при аппроксимации
использовались
первый, второй и третий выборочные моменты. Например, при аппроксимации ![]() принималось
принималось ![]() ,
, ![]() , где
, где ![]() – третий центральный
выборочный момент полученных при моделировании значений
– третий центральный
выборочный момент полученных при моделировании значений ![]() . Выписанные соотношения означают, что первый и второй
моменты плотности вероятности
. Выписанные соотношения означают, что первый и второй
моменты плотности вероятности ![]() равны соответствующим
выборочным моментам. Третий центральный момент
равны соответствующим
выборочным моментам. Третий центральный момент ![]() использован для
определения знака
использован для
определения знака ![]() . В принципе должно выполняться соотношение
. В принципе должно выполняться соотношение ![]() , которое также можно использовать для определения
, которое также можно использовать для определения ![]() . Найденные разными способами значения этого параметра
отличаются на несколько процентов, однако визуально более точна аппроксимация с
параметром
. Найденные разными способами значения этого параметра
отличаются на несколько процентов, однако визуально более точна аппроксимация с
параметром ![]() , найденным по выборочной дисперсии. Гистограммы и их
аппроксимации функциями
, найденным по выборочной дисперсии. Гистограммы и их
аппроксимации функциями ![]() при других значениях
при других значениях ![]() выглядят также.
выглядят также.
Результаты, полученные при ![]() , представлены в табл. 8 и на рис. 10. Эта таблица в точности
аналогична табл. 7. Из нее видно, что погрешность прогноза заметно уменьшилась.
На рис. 10 изображены гистограммы
, представлены в табл. 8 и на рис. 10. Эта таблица в точности
аналогична табл. 7. Из нее видно, что погрешность прогноза заметно уменьшилась.
На рис. 10 изображены гистограммы ![]() , …,
, …, ![]() (ступенчатые линии),
построенные при
(ступенчатые линии),
построенные при ![]() для варианта
для варианта ![]() , и аппроксимации этих гистограмм плотностью вероятности
, и аппроксимации этих гистограмм плотностью вероятности ![]() (плавные линии) при
описанном выше выборе параметров
(плавные линии) при
описанном выше выборе параметров ![]() и
и ![]() . Из рисунка видно, что в данном случае аппроксимация не так
точна, как в случае
. Из рисунка видно, что в данном случае аппроксимация не так
точна, как в случае ![]() . Распределение ошибок прогноза стало похоже на одностороннее
показательное распределение. Используя термины гамма распределения можно
сказать, что коэффициент формы заметно уменьшился.
. Распределение ошибок прогноза стало похоже на одностороннее
показательное распределение. Используя термины гамма распределения можно
сказать, что коэффициент формы заметно уменьшился.
Таблица 8. Прогноз 2 при ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
0.059 |
34.0 |
218.1 |
-0.03 |
0.21 |
-0.63 |
3.94 |
|
|
0.031 |
-136.5 |
218.1 |
0.13 |
0.21 |
2.56 |
3.95 |
|
4 |
0.360 |
-281.8 |
218.1 |
0.28 |
0.21 |
5.25 |
3.95 |
|
5 |
0.837 |
-547.2 |
218.2 |
0.54 |
0.21 |
10.2 |
3.95 |
|
|
|
|
|
|
|
|
|
|
0.31 |
1.96 |
-0.01 |
0.07 |
-38.5 |
246.6 |
|
|
-1.26 |
1.96 |
0.04 |
0.07 |
154.3 |
246.6 |
|
4 |
-2.61 |
1.96 |
0.09 |
0.07 |
318.5 |
246.6 |
|
5 |
-5.06 |
1.96 |
0.17 |
0.07 |
618.3 |
246.6 |
Результаты расчетов в случае ![]() приведены в табл. 9 и на рис. 11. Таблица
аналогична табл. 4, 5. Из нее видно, что погрешность прогноза заметно возросла
по сравнению со случаем
приведены в табл. 9 и на рис. 11. Таблица
аналогична табл. 4, 5. Из нее видно, что погрешность прогноза заметно возросла
по сравнению со случаем ![]() .
.
На рис. 11 изображены гистограммы ![]() , …,
, …, ![]() , построенные при
, построенные при ![]() для варианта
для варианта ![]() , и аппроксимации этих гистограмм плотностью вероятности
, и аппроксимации этих гистограмм плотностью вероятности ![]() . Из рисунка видно, что и в данном случае аппроксимация не
так точна, как в случае
. Из рисунка видно, что и в данном случае аппроксимация не
так точна, как в случае ![]() . Распределение ошибок прогноза стало похоже на
гамма-распределение с коэффициентом формы, заметно превышающем 2.
. Распределение ошибок прогноза стало похоже на
гамма-распределение с коэффициентом формы, заметно превышающем 2.
Для второго и третьего опорных решений также имеет место независимость
стандартных отклонений прогноза от ![]() . При высоком уровне солнечной
активности прогноз 2 заметно уступает по точности прогнозу 1. При низком и
среднем уровне солнечной активности оба прогноза обеспечивают в среднем
примерно одинаковую точность.
. При высоком уровне солнечной
активности прогноз 2 заметно уступает по точности прогнозу 1. При низком и
среднем уровне солнечной активности оба прогноза обеспечивают в среднем
примерно одинаковую точность.
Таблица 9. Прогноз 2 при ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
0.406 |
236.3 |
542.1 |
-0.23 |
0.53 |
-4.65 |
10.4 |
|
|
0.463 |
-44.3 |
542.1 |
0.04 |
0.53 |
0.87 |
10.4 |
|
3 |
0.642 |
-335.2 |
542.1 |
0.33 |
0.53 |
6.60 |
10.4 |
|
5 |
0.946 |
-1270 |
542.2 |
1.23 |
0.53 |
25.0 |
10.4 |
|
|
|
|
|
|
|
|
|
|
2.46 |
5.49 |
-0.07 |
0.18 |
-267.4 |
613.4 |
|
|
-0.46 |
5.49 |
0.01 |
0.18 |
50.1 |
613.4 |
|
3 |
-3.49 |
5.49 |
0.10 |
0.18 |
379.2 |
613.4 |
|
5 |
-13.2 |
5.49 |
0.40 |
0.18 |
1436 |
613.5 |
5. Заключение. Статистическое моделирование показало, что влияние геомагнитной
активности на точность предсказания положения станции существенно зависит от
уровня солнечной активности. В случае
длинных интервалов эта зависимость может оказаться критической. Например,
в конце 15-часового интервала прогнозирования при малой солнечной активности
вероятность неудачного прогноза составляет несколько процентов (4% при ![]() . В случае средней солнечной активности (при
. В случае средней солнечной активности (при ![]() . эта вероятность возрастает до 14%. При высокой солнечной
активности (при
. эта вероятность возрастает до 14%. При высокой солнечной
активности (при ![]() вероятность неудачного
прогноза превосходит 35%. С уменьшением длины интервала вероятность неудачного
прогноза снижается. На интервалах с длиной менее 7.5 ч эта вероятность не
превосходит 1%. На интервалах менее 4.5 ч неудачных прогнозов не оказалось.
вероятность неудачного
прогноза превосходит 35%. С уменьшением длины интервала вероятность неудачного
прогноза снижается. На интервалах с длиной менее 7.5 ч эта вероятность не
превосходит 1%. На интервалах менее 4.5 ч неудачных прогнозов не оказалось.
Литература
1.
Ивченко Г.И.,
Медведев Ю.И. Математическая статистика. М., Высшая шклола, 1984.
2.
Охоцимский Д.Е.,
Сихарулидзе Ю.Г. Основы механики космического полета. М., Наука, 1990.
3. Эльясберг П.Е. Введение в теорию полета искусственных спутников Земли. М., Наука, 1965.
Приложение