Аннотация
Рассмотрены теоретические основы и аспекты практического применения метода полиномиальной
регрессии в задачах распознавания образов печатных и рукопечатных символов. Приводятся
характеристики качества программной реализации метода полиномиальной регрессии, определенные
на базах графических образов символов с известными границами.
Abstract
Recognition processes for printed and hand-printed letters are discussed. Theoretical
and practical aspects of Polynomial Regression are considered. The results of the program
realization are presented.
Введение
Задача распознавания печатных и
рукопечатных (написанных от руки печатными буквами) символов весьма актуальна
для различных видов современных наукоемких технологий, использующих процесс
оптического ввода (распознавания) документов: автоматическая обработка
платежных ведомостей в банках, результатов анкетирования или голосования,
пенсионных форм и т.д. Область применения распознавания символов постоянно
расширяется. Существенный прогресс в решении этой задачи наблюдается в
последние годы благодаря развитию современных точных методов. Одним из них
являются нейронные сети [4,7,10]. Другой,
применению которого посвящена настоящая работа, - это линейный регрессионный
анализ [11]. Мы приводим частные, но как показал опыт,
весьма эффективные приложения полиномиальной регрессии к задаче распознавания.
Основные результаты данной работы были получены
авторами еще осенью 1999г. Весь процесс от «абсолютного нуля» до получения
«высоких процентов» в распознавании печатных и рукопечатных символов занял
менее четырех месяцев, и к юбилейному 2000 году «объект был сдан»! Постановка
задачи делалась с привлечением книги Шурмана [4].
Она вызывает несомненный интерес, но содержит лишь общие сведения (формулы,
рассуждения и т.д.) и никак не является практическим руководством по
распознаванию на основе полиномиальной регрессии из-за отсутствия каких-либо
конкретных сведений о структуре используемых многочленов, а также ввиду
рассмотрения растров 2х2, весьма далеких от реальных жизненных ситуаций.
За прошедшее время метод был проверен на различных
базах символов. Практика показала, что он удовлетворяет высоким требованиям по
качеству распознавания, быстродействию, монотонности оценок. Разработанный алгоритм распознавания печатных и рукопечатных
символов на базах графических символов с известными границами оформлен в виде
библиотеки программ, состоящей из двух частей: обучение (с возможным
дообучением) и распознавание для платформ Windows9x / WindowsME / WindowsNT / Windows2000 / WindowsXP. Библиотека готова к практическому использованию.
Работы выполнялись в ИПМ им. М.В.Келдыша РАН и ИСА РАН
при финансовой поддержке ЗАО «Интеллектуальные Технологии».
1. О методе полиномиальной регрессии
Историческая
справка. Первые известные нам
работы по использованию метода
полиномиальной регрессии в задаче распознавания образов были опубликованы в середине 20 века [1,2].
Более подробную информацию по данному вопросу можно получить, в частности, в
трудах Шурмана (Jürgen Schürmann) [3,4]. В [5]
излагается рекурсивный метод вычисления матрицы распознавания на этапе
обучения. В [6] рассматривается проблема отделения от всего обучающего
множества изображений некоторого подмножества трудных для распознавания
изображений. Расширению структуры вектора, который строится по растру изображения,
т.е. переходу от полиномиальной к структурной регрессии, посвящены работы
[7,8].
Дальнейшее изложение метода полиномиальной регрессии
соответствует материалу, содержащемуся в [4], но является более компактным и
представляет самостоятельный интерес.
Постановка
задачи. Задача распознавания символов состоит в разработке
алгоритма, позволяющего по данному растру изображения (рис.1) определить,
какому символу из некоторого конечного множества с K элементами он
соответствует. Представлением символа
является растр, состоящий из N=N1´N2 серых или черных пикселей. Перенумеровав все пиксели
растра, запоминаем в i-ой компоненте (1£i£N) вектора vÎRN состояние i-го
пикселя, а именно, 0 или 1 в случае черно-белого растра и значение на отрезке
[0,1] для серого растра. Пусть V={v} – совокупность всевозможных растров. Очевидно, VÍRN, причем если пиксели черно-белые, то V={0,1}N – конечное
множество, элементами которого являются последовательности из нулей и единиц
длины N. Если пиксели серые, то V=[0,1]N –
N-мерный единичный куб в RN.
Математическая
постановка задачи распознавания состоит в следующем. Пусть для некоторого
растра vÎV можно
найти pk(v) – вероятность того, что растр изображает символ с
порядковым номером k, 1£k£K.
Тогда распознанным считается символ с порядковым номером ko, где
pko(v)=max pk(v),
1£k£K
Для решения задачи следует вычислить вектор вероятностей (p1(v), p2(v),…, pK(v)). Он может быть найден на основе метода наименьших
квадратов.
Метод
наименьших квадратов. Отождествим k-й
символ с базисным вектором ek=(0…1…0) (1 на
k-м месте, 1£k£K)
из RK,
причем Y={e1,…,eK}. Пусть p(v,y) – вероятность
наступления события (v,y), vÎV, yÎY (если V континуально, то плотность вероятности).
Наступление события (v,y) означает, что выпадает растр v, и этот растр изображает
символ y. Тогда вероятность pk(v) – это условная
вероятность pk(v)=p(ek|v)=p(v,ek)/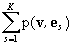 . С другой
стороны, имеет место следующий результат [4,12]: . С другой
стороны, имеет место следующий результат [4,12]:
Теорема 1. Экстремальная
задача
E{||d(v)-y||2}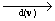 min min (1)
(1)
достигает минимума на векторе d(v)=(p1(v),…,pK(v)),
причем min берется по всем непрерывным d: V® RK.
В Теореме 1 ||×|| - евклидова норма в RK и для любой функции f:
V´Y® R через E{f(v,y)} обозначено
математическое ожидание случайной величины f:
E{f(v,y)}
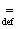
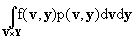
(в случае конечного V или Y интегрирование по соответствующей переменной
заменяется на сумму). Итак, требуемый вектор вероятностей (p1(v),…,pK(v)) ищется как решение экстремальной задачи (1).
Приближенное решение задачи (1) может быть найдено методом полиномиальной
регрессии.
Метод полиномиальной
регрессии. Приближенные значения компонент вектора
(p1(v),…,pK(v)) будем искать в виде многочленов от координат v=(v1,…,vN):
p1(v)
@ c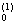 + +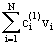 + +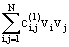 +… +…
p2(v)
@ c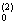 + +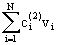 + +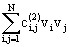 +… (2) +… (2)
………………………………………….
pK(v)
@ c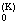 + +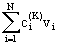 + +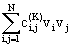 +… +…
Суммы в правых частях равенств (2) конечные и
определяются выбором базисных мономов. А именно, если
x(v)=(1,v1, … ,vN, … )T
конечный вектор размерности L из
выбранных и приведенных в (2) базисных мономов, упорядоченных определенным
образом, то в векторном виде соотношения (2) можно записать так:
p(v) = (p1(v),…,pK(v)) @ ATx(v)
(2’)
где A – матрица размера L´K, столбцами которой являются векторы а(1),…, а(K).
Каждый такой вектор составлен из коэффициентов при мономах
соответствующей строки (2) (с совпадающим верхним индексом), упорядоченных так
же, как в векторе x(v).
Следовательно, приближенный поиск вектора вероятностей p(v) сводится к
нахождению матрицы A. Учитывая результат Теоремы 1, следует
понимать, что матрица А является
решением следующей экстремальной задачи:
E{||АТx(v)-y||2}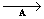 min min (3)
(3)
где min берется по всевозможным матрицам А размера L´K.
Имеет место следующий
результат [4].
Теорема 2. Матрица
А размера L´K
доставляет решение экстремальной задаче (3) тогда и только тогда, когда А является решением матричного
уравнения
E{x(v) x(v)Т}А = E{x(v) yТ} (4)
Итак, согласно методу
полиномиальной регрессии
p(v) @ АТx(v), А = E{x(v) x(v)Т}-1 E{x(v) yТ}
Заметим, что если x(v)=(1,v1,
… ,vN)T,
то метод полиномиальной регрессии называется методом линейной регрессии.
Вычисление
матриц E{x(v) x(v)Т}, E{x(v) yТ} основано на следующем результате математической статистики. Пусть
имеется датчик случайных векторов, распределенных по неизвестному нам закону p(v,y):
[v(1),y (1)], [v(2),y (2)],…
Тогда математическое ожидание любой случайной величины f(v,y) может быть вычислено из предельного равенства:
E{ f(v,y) } = 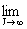 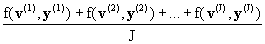
Если J достаточно большое, то верно приближенное
равенство:
E{ f(v,y) } @ 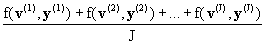 (5) (5)
Практически набор [v(1),y (1)],…, [v(J),y (J)] реализуется некоторой базой данных, а вычисления по формуле (5)
называются обучением. В данном случае f(v,y) = xi(v)xj(v) или f(v,y) = xi(v)yk и по определению
E{x(v)
x(v)Т} = [E{xi(v)xj(v)}]1£i,j£L = [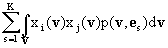 ]1£i,j£L ]1£i,j£L
E{x(v) yТ} = [E{xi(v)yk}]1£i£L, 1£k£K = [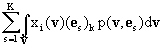 ]1£i£L, 1£k£K= ]1£i£L, 1£k£K=
= [ 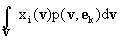 ]1£i£L, 1£k£K ]1£i£L, 1£k£K
А согласно формуле (5), получим выражение для практического вычисления:
E{x(v) x(v)Т}@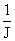 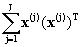 , E{x(v) yТ}@ , E{x(v) yТ}@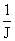 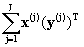 (6) (6)
где x(j)
= x(v(j)), 1£j£J
Практическое нахождение матрицы
А. Согласно (4) и (6), имеем следующее
приближенное значение для А:
А
@ (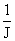 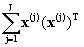 )-1( )-1(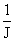 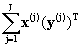 ) (7) ) (7)
В [4] показано, что правую часть (7) можно вычислить
по следующей рекуррентной процедуре:
Aj = Aj-1-ajGjx(j)[A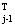 x(j)-y(j)]T , aj = 1/J x(j)-y(j)]T , aj = 1/J
Gj
= 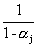 [Gj-1-aj [Gj-1-aj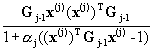 ] 1£j£J (8) ] 1£j£J (8)
где А0 и G0 заданы.
Введение вспомогательной матрицы Gj размера L´L помогает избежать процедуры обращения матрицы
в (7). Реально выбор параметров aj производится экспериментально. Вообще на
практике используются следующие две упрощенные модификации процедуры (8).
Модификация А. Gj º Е
Aj
= Aj-1- x(j)[A x(j)[A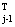 x(j)-y(j)]T (9) x(j)-y(j)]T (9)
Модификация Б. GjºD-1, D=diag( E{x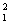 },E{x },E{x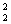 },…,E{x },…,E{x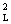 })
(10) })
(10)

Рис. 1. Образы 16х16 печатных и рукопечатных
образов
2. Развитие и практическая реализация метода полиномиальной
регрессии
Следует сразу отметить, что ниже
рассматривается только Модификация Б, так как, в отличие от Модификации А, именно в этом случае
получены приемлемые практические результаты. Поэтому не исследовалась
постановка задачи c уравнениями, записанными в общем виде, и вследствие этого с
существенно более медленными алгоритмами обучения и распознавания. Мы будем
использовать серые растры размера N=256=16´16. Масштабирование
образов до размера 16х16 сохраняет особенности геометрии исходных
символов (рис.1).
Построение вектора x. Используются два варианта
вектора x: короткий и длинный.
Для более длинного вектора больше размеры таблицы (матрицы) распознавания,
медленнее осуществляется обучение и распознавание, но при этом качество распознавания выше. Длинный вектор строится
следующим образом:
x =(1, {vi}, {vi2}, {(dvi)r},
{(dvi)r2}, {(dvi)y}, {(dvi)y2},
{(dvi)r4}, {(dvi)y4}, {(dvi)r(dvi)y},
{(dvi)r2(dvi)y2}, {(dvi)r4(dvi)y4},
{(dvi)r((dvi)r)L}, {(dvi)y((dvi)y)L},
{(dvi)r((dvi)y)L},
(11)
{(dvi)y((dvi)r)L}, {(dvi)r((dvi)r)D},
{(dvi)y((dvi)y)D},
{(dvi)r((dvi)y)D}, {(dvi)y((dvi)r)D})
Короткий вектор составлен
из элементов длинного вектора, записанных в первой строке (11):
х=(1,
{vi}, {vi2},
{(dvi)r},
{(dvi)r2}, {(dvi)y}, {(dvi)y2})
(12)
В (11) и (12) выражения в фигурных скобках соответствуют цепочкам
элементов вектора, вычисляемым по всем пикселям растра (за исключением
указанных ниже случаев). Через (dvi)r и (dvi)y обозначены конечные центральные разности
величин vi по
ортогональным направлениям ориентации растра – нижние индексы r и y соответственно. Если имеется нижний индекс L (left) или D (down), то это
означает, что соответствующие величины относятся к пикселю слева или
снизу от рассматриваемого. Компоненты вектора x, не имеющие индекса L или D, вычисляются для всех
пикселей растра; с индексом L – кроме левых граничных,
с индексом D – кроме нижних граничных пикселей. Вне растра
считаем, что vi=0 (используется при вычислении конечных
разностей на границе растра). Для длинного вектора x к перечисленному
в (11) добавляются компоненты, являющиеся средним арифметическим значений vi (по
восьми пикселям, окружающим данный), а также квадраты этих компонент. Отметим,
что набор компонентов вектора х подобран в процессе численных экспериментов. А
именно, среди множества рассмотренных вариантов оставлены те, которые делают
заметный вклад в улучшение распознавания.
Модификация
Б. При обучении элементы
матрицы D (10) вычисляются следующим образом. Для каждого j-го элемента базы символов, последовательно, начиная с
первого и заканчивая J-м (последним), строится
вектор x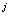 согласно
(11) или (12). Попутно рассчитываются значения компонент вспомогательного
вектора m согласно
(11) или (12). Попутно рассчитываются значения компонент вспомогательного
вектора m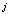 по
рекуррентной формуле: по
рекуррентной формуле:
m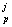 = (1-β = (1-β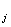 ) m ) m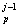 + β + β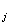 (x (x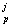 ) ) , j=1,…,J , p=1,…,L (13) , j=1,…,J , p=1,…,L (13)
β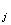 =1/j =1/j
По окончании этой процедуры для последнего
элемента имеем согласно (10):
GJ
º D-1 = diag (1/m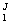 ,1/m ,1/m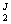 ,…,1/m ,…,1/m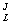 ) (14) ) (14)
После того, как завершено вычисление GJ, элементы матрицы Aj (8) рассчитываются следующим образом. Выполняется
еще один проход по базе и для каждого j-го элемента базы символов, начиная с первого и
заканчивая J-м, строится вектор xj согласно (11) или (12). Попутно вычисляется Aj:
a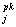 = a = a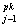 - aj x - aj x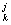 ( (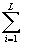 a a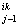 x x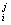 - y - y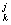 )/m )/m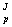 ,
aj = 1/J (15) ,
aj = 1/J (15)
A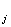 = [a = [a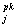 ], j = 1,…,J j=1,…,J, p = 1,…,L , k = 1,…,K ], j = 1,…,J j=1,…,J, p = 1,…,L , k = 1,…,K
На этом этап обучения закончен: матрица A=AJ получена.
Распознавание осуществляется следующим образом. Для
серого изображения размером 16х16 пикселей строится вектор x согласно
(11) или (12). После этого по формуле (2’), используя A=AJ (15), вычисляются оценки, соответствующие
каждому из возможных символов. Затем выбирается символ с максимальной оценкой.
Получаемые оценки могут выходить за рамки отрезка [0,1] из-за того, что
используемый метод является приближенным. Мы искусственно обнуляли
отрицательные значения и делали равными 1 те, которые были больше этой
величины. Практика распознавания показала приемлемость такого довольно грубого
способа коррекции оценок.
3.
Характеристики метода полиномиальной регрессии
Приведем
результаты количественного и качественного анализа программной реализации метода полиномиальной регрессии, обучающейся
с помощью образов из графической базы данных и распознающей образы из той же
базы, содержащей как изображения, так и коды символов. Использование одной и
той же базы при обучении и распознавании служит своего рода гарантом «чистоты
эксперимента», поскольку результат распознавания на символьных
последовательностях, «посторонних» для обучающей базы, может сильно отличаться
для разных последовательностей. Причиной этого, видимо, является большая или
меньшая степень схожести базы обучения и распознавания. Эта заслуживающая
особого внимания проблема в данной работе рассматриваться не будет. Также вне
нашего поля зрения остается вопрос о качестве базы обучения, поскольку использовались
лишь те, которые хорошо себя зарекомендовали для других методов.
Результатом
распознавания образа является код символа и его целочисленная оценка, лежащая в
диапазоне [1,16] (оценка 16 является наилучшей). Эта новая оценка получается
следующим образом. В результате умножения оценки на 16 старый диапазон оценок [0,1] переходит в
новый [0,16], после чего проводится дискретизация, а именно, [0,1]→1,
(1,2]→2,…, (15,16]→16.
Используются следующие характеристики качества методов распознавания
символов: точность, монотонность оценок и быстродействие, подробно описанные в
[9].
Точностью
распознавания по базе B называется разность числа образов
в базе В и числа неправильно распознанных образов, отнесенная к числу образов в
базе В. Заметим, что коды прописных и строчных символов, обладающих одинаковым
начертанием, не различаются, например, группы букв кириллицы и цифр оО0 зЗ3 нН.
Монотонность
оценок –
это свойство оценок характеризовать надежность
распознавания символа. Интуитивно понятно, что особое значение имеет надежность
оценок, близких к максимальным. Пусть для каждой оценки распознавания определяется частота ее ошибочного распознавания, равная отношению количества символов,
распознанных с этой оценкой неверно, к общему числу тестовых символов,
распознанных с такой оценкой. Если количество
символов, распознанных с некоторой оценкой, равно 0, то такие оценки не
рассматриваем. Очевидно, что нас интересуют
методы с монотонным убыванием графика частот в области высоких оценок.
Быстродействием назовем количество распознанных в единицу
времени образов в процессе обработки
тестовой последовательности. Быстродействие учитывает только время работы
реализации метода распознавания и не учитывает накладные расхода на чтение из
хранилища образов. Эта характеристика зависит как от особенностей реализации
метода, так и от платформы.
Печатные
прямые буквы и цифры.
Обучение и распознавание проводилось как на длинном векторе х (11), так и на коротком (12). Ниже
для удобства изложения короткий вектор будем обозначать
х1. Получено, что
повторное обучение на одной и той же базе (в 1 млн. символов) приводит к
улучшению распознавания. Этот итерационный процесс имеет характер затухания по
мере увеличения числа проходов по базе. Так, на одной и той же базе после
первоначального обучения распознавание давало точность 0,9855, а после третьей
итерации – 0,9905. Время однократного обучения для длинного вектора х составило около 9 часов, включая
чтение из базы графических образов и другие затраты времени, не входящие в алгоритм
обучения. Время обучения пропорционально длине базы символов, количеству распознаваемых
символов и числу компонент вектора х (11,12).
Во всех рассмотренных вариантах распознавание проводилось на платформе Pentium IV – 1500МГц – SDRAM, Windows2000 с помощью разработанной
в среде Microsoft Developer Studio 6.0 библиотеки, скомпилированной в режиме
максимальной скорости исполнения
использующей возможности SSE
процессора Pentium IV и оптимизированной с помощью Intel VTune 5.0 .
Отметим, что
для обоих типов векторов ошибки с максимальной оценкой 16 отсутствуют. В
области более низких оценок ошибки имеются, следовательно, метод порождает
оценки, отвечающие критериям монотонности в области высоких оценок. Аналогичные
результаты получены для всех рассмотренных баз символов.
Представляет
интерес тот факт, что длинный вектор не увеличивает количество распознанных
символов с высокими оценками. Он увеличивает точность распознавания за счет
низких оценок. Этим объясняется
сходство в монотонности в области высоких оценок для обоих типов векторов.
Закономерность верна для всех нижеследующих случаев.
Использование
короткого вектора позволяет повысить быстродействие примерно в 2 раза, при этом
почти в 2 раза увеличивается количество ошибок распознавания.
Печатные прямые и курсивные цифры. Обратим
внимание, что алфавит обучения и распознавания содержал 20 символов (10 прямых
и 10 курсивных цифр). Обучение проводилось
на базе в 95 тыс. элементов с коротким вектором х1. При
обучении и распознавании между прямыми и курсивными символами не делалось
различий. Точность на обучающей последовательности составляет 0,9946 при
однократном обучении, а после третьего прохода по базе – 0,9966.
Для этого класса образов отметим,
что распознавание полиномами дало
сходную точность по отношению к распознаванию прямых печатных букв и цифр и
очень высокое быстродействие.
Рукопечатные цифры. После
обучения по базе в 175 тыс.
элементов для длинного вектора х полученная матрица на той же базе
обеспечивает распознавание 98.33% элементов, а после четвертой итерации
качество распознавания возрастает до 98.81%. Также производилось обучение на
коротком векторе х1 (12).
Для него полученная точность равняется 0,9703.
Распознавание методом полиномов (с длинным и коротким
векторами) класса образов рукопечатных цифр дало сходные характеристики
точности и быстродействия по отношению к распознаванию прямых печатных букв и
цифр. Для высоких оценок наблюдается монотонность, что также аналогично случаю прямых печатных букв и цифр.
На основании
приведенных результатов численных экспериментов можно сделать вывод о том, что
реализация метода полиномиальной регрессии показала высокие характеристики
точности, быстродействия и, в особенности, монотонности оценок.
4.
Заключение
Авторы
благодарят А.В.Мисюрева, который в 1999г. стал инициатором привлечения авторов
к проблеме распознавания символов и принимал активное участие в обсуждении
результатов. На основе разработанного авторами программного продукта,
используемого при получении первых высоких результатов по распознаванию
печатных и рукопечатных символов, он в 2000г. создал библиотеку, которая нашла применение в реальных
системах распознавания. Авторы также благодарят О.А.Славина, в 2001г.
участвовавшего в выработке стратегии при создании Н.В.Пестряковой новой версии
библиотеки обучения и распознавания также для действующих распознающих
систем.
5. Литература
[1] Sebestyen G.S. Decision Making Processes in
Pattern Recognition, MacMillan, New York, 1962.
[2] Nilson
N.
J. Learning Machines, McGraw-Hill, New York, 1965.
[3] Schürmann
J. Polynomklassifikatoren,
Oldenbourg, München, 1977.
[4] Schürmann
J. Pattern Сlassification, John Wiley&Sons, Inc., 1996.
[5] Albert A.E. and Gardner
L.A. Stochastic Approximation and
Nonlinear Regression // Research Monograph 42. MIT Press, Cambridge, MA, 1966.
[6] Becker D. and
Schürmann J. Zur
verstärkten Berucksichtigung schlecht erkennbarer Zeichen in der
Lernstichprobe // Wissenschaftliche Berichte AEG-Telefunken 45, 1972, pp. 97 – 105.
[7] Pao Y.-H. The Functional Link Net: Basis for an
Integrated Neural-Net Computing Environment // in Yoh-Han Pao (ed.) Adaptive
Pattern Recognition and Neural Networks, Addisson-Wesley, Reading, MA, 1989,
pp. 197-222.
[8] Franke J. On the Functional Classifier, in
Association Francaise pour la Cybernetique Economique et Technique (AFCET),
Paris // Proceedings of the First International Conference on Document Analysis
and Recognition, St. Malo, 1991, pp.481-489.
[9] Арлазаров В.Л., Логинов А.С., Славин О.А.
Характеристики программ оптического распознавания текста // Программирование №
3, 2002, с. 45-63
[10] Мисюрев
А.В. Использование искусственных
нейронных сетей
для распознавания рукопечатных символов // Сборник трудов ИСА РАН
«Интеллектуальные технологии ввода и обработки информации», 1998, с. 122-127
[11] Дж.Себер. Линейный регрессионный анализ. М.:”Мир”, 1980.
[12] Ю.В.Линник. Метод наименьших квадратов и основы математико-
статистической теории обработки наблюдений. М.:”Физматлит”, 1958.
|