Аннотация
Исследован режим закрутки в плоскости орбиты низколетящего
искусственного спутника Земли. В этом режиме спутник вращается вокруг
своей продольной оси (главной центральной оси минимального момента
инерции), совершающей малые колебания относительно нормали к плоскости
орбиты; угловая скорость вращения вокруг продольной оси составляет
несколько десятых долей градуса в секунду. В уравнениях движения
спутника учитывались гравитационный и восстанавливающий аэродинамический
моменты, а также диссипативный момент от вихревых токов, наведенных
в оболочке спутника магнитным полем Земли. В уравнения введен малый
параметр, характеризующий отклонение спутника от динамически
симметричного и негравитационные внешние моменты. Методом малого
параметра и численно исследована двумерная интегральная поверхность
уравнений движения, описывающая квазистационарные вращения спутника,
близкие цилиндрической прецессии соответствующего симметричного спутника
в гравитационном поле. Такие квазистационарные вращения предлагается
считать номинальными невозмущенными движениями спутника в режиме
закрутки.
Abstract
A spinning mode was analyzed for orientation of an Earth low orbit
artificial satellite. In this mode, a satellite rotated around its
longitudinal axis (the principal central axis of the minimal moment
of inertia) swinging near the normal to the orbital plane. The satellite
angular rate was equal a few tenth of degree per second in this mode.
The equations of satellite attitude motion were written taking into
account a gravitational and restoring aerodynamic torques as well as
a dissipative torque of eddy currents produced by the Earth magnetic
field. The equations contained a small parameter which characterized
asymmetry of the satellite tensor of inertia and non-gravitational
torques. Using small parameter method and numerically, the two-dimensial
integral manifold of the equations was constructed which described
quasi steady satellite rotations closed to the cylindrical precession
of appropriate asymmetrical satellite in the gravitational field. Such
quasi steady rotations could be considered to be nominal motions in
spinning mode.
1. Введение. Необходимость полета орбитальных комплексов в
течение продолжительного времени без экипажа при минимальных
затратах топлива и достаточно большом средневитковом энергосъеме с
солнечных батарей неоднократно возникала в отечественной
космической технике. На орбитальных комплексах Салют-6 -
Космос-1267, Салют-7 - Космос-1443 и Салют-7 -
Космос-1686 для этой цели использовался специальный режим
неуправляемого движения комплекса относительно центра масс,
называемый режимом гравитационной ориентации вращающегося спутника
[1-4] или режимом обобщенной гравитационной ориентации [5]. В
этом режиме орбитальный комплекс вращается вокруг своей продольной
оси, совершающей малые колебания относительно местной вертикали. В
1999 - 2000 гг. этот режим применялся на Международной
космической станции [6,7].
Применение указанного режима возможно при выполнении трех условий.
Во-первых, спутник должен иметь специфический центральный
эллипсоид инерции: малая и средняя полуоси этого эллипсоида должны
мало отличаться друг от друга и быть существенно меньше (примерно
в три раза) большой полуоси. Во-вторых, приложенный к спутнику
гравитационный момент должен существенно превышать другие
действующие на спутник механические моменты. В-третьих, орбита
спутника должна быть близка к круговой. Перечисленные условия
позволяют реализовать движения спутника, близкие так называемой
конической прецессии осесимметричного твердого тела на круговой
орбите с малым отклонением оси симметрии тела от местной
вертикали.
Коническая прецессия - одно из трех точных стационарных движений
осесимметричного твердого тела под действием гравитационного момента
на круговой орбите. Эта прецессия идеально подходит для применения на
вытянутых спутниках, но практически бесполезна, если у эллипсоида
инерции спутника большая и малая полуоси не очень значительно отличаются
друг от друга. Именно к этому последнему типу спутников относилась
орбитальная станция Мир в последние годы своего полета. У нее
отношение малой и большой полуосей центрального эллипсоида инерции
составляло примерно 0.81. Указанное обстоятельство и тот факт, что
большая и средняя полуоси эллипсоида инерции станции были близки между
собой, позволил использовать для ее хранения на орбите неуправляемое
движение относительно центра масс, близкое так называемой цилиндрической
прецессии осесимметричного твердого тела на круговой орбите. Это
движение представляет собой вращение станции вокруг своей продольной
оси, совершающей малые колебания относительно нормали к плоскости орбиты.
Цилиндрическая прецессия - второе из трех упомянутых выше стационарных
движений осесимметричного твердого тела. В этой прецессии ось симметрии
твердого тела направлена по нормали к плоскости орбиты. Недостатком
цилиндрической прецессии является то обстоятельство, что в отличие от
конической прецессии она неустойчива при достаточно малой абсолютной
величине угловой скорости вращения тела вокруг оси симметрии.
Граничные по устойчивости значения угловой скорости (они разные для
вращений в противоположных направлениях) тем выше, чем более вытянуто
тело вдоль оси симметрии. Указанное обстоятельство делает движения,
близкие цилиндрической прецессии практически непригодными для вытянутых
спутников из-за необходимости закрутки с большой угловой скоростью, но
для станции Мир указанные граничные значения угловой скорости
оказались не критичными [8].
Цилиндрическая прецессия уже использовалась в качестве режима
ориентированного движения на некоторых спутниках, стабилизируемых
вращением (SynCom, TIROS-9,-10 и др.), но эти спутники имели весьма
большую угловую скорость и вращались вокруг оси максимального главного
центрального момента инерции. Гравитационный момент действовал на эти
спутники как малое возмущение. При использовании цилиндрической
прецессии на станции Мир вращение происходило вокруг оси минимального
момента инерции и с малой угловой скоростью. Роль гравитационного
момента в этом случае была определяющей, поэтому такое движение можно
считать специфическим видом гравитационной ориентации.
Ниже рассматривается модельная задача о возможности применения
режима закрутки в плоскости орбиты в случае искусственного
спутника Земли типа орбитальной станции Мир. Предполагается,
что на спутник помимо гравитационного момента действуют еще
восстанавливающий аэродинамический момент и диссипативный момент
от вихревых токов, наведенных в оболочке спутника магнитным полем
Земли. Оба этих момента задаются упрощенными выражениями,
обеспечивающими специальный вид уравнений движения спутника. В
уравнения движения введен малый параметр, характеризующий
отклонение спутника от динамически симметричного и
негравитационные внешние моменты. Методом Н.Н.Боголюбова -
Ю.А.Митропольского в виде рядов по степеням малого параметра
построена интегральная поверхность уравнений движения, описывающая
квазистационарные вращения спутника, близкие цилиндрической
прецессии соответствующего симметричного спутника в гравитационном
поле. Получено уравнение, описывающее эволюцию угловой скорости
спутника под действием диссипативного магнитного момента.
Показано, что при учете действия на спутник только гравитационного
и аэродинамического моментов указанная интегральная поверхность
состоит из периодических решений. Проведено исследование таких
решений методом малого параметра Пуанкаре.
2. Уравнения движения.
Спутник будем считать твердым телом, центр масс которого - точка
O - движется по неизменной круговой орбите вокруг Земли. Для
записи уравнений движения спутника относительно центра масс введем
две правые декартовы системы координат: орбитальную OX1X2X3 и
образованную главными центральными осями инерции спутника
Ox1x2x3. Оси OX3 и OX1 направлены соответственно вдоль
геоцентрических радиуса-вектора и скорости точки O, оси Ox1 и
Ox2 отвечают минимальному и максимальному моментам инерции
спутника.
Ориентацию системы координат Ox1x2x3 относительно орбитальной
системы зададим с помощью углов y, q и j,
которые определяются следующим образом. Система OX1X2X3 может
быть переведена в систему Ox1x2x3 тремя последовательными
поворотами: 1) на угол y вокруг оси OX3, 2) на угол
q вокруг новой оси OX2, 3) на угол j вокруг
новой оси OX1, совпадающей с осью Ox1. Введенные углы имеют
следующий смысл: q - угол между осью Ox1 и плоскостью
орбиты (плоскостью OX1X3), y - угол между осью OX1 и
проекцией оси Ox1 на плоскость орбиты, j - угол
поворота спутника вокруг оси Ox1. Матрицу перехода от системы
Ox1x2x3 к системе OX1X2X3 обозначим ||aij|| 3i,j=1 , где aij
- косинус угла между осями OXi и Oxj. Элементы этой матрицы
выражаются через углы y, q и j с помощью формул
|
|
|
|
a12=-sinycosj+cosysinqsinj , |
|
|
a13 = sinysinj+cosysinqcosj , |
|
|
|
|
|
|
|
|
a22=cosycosj+sinysinqsinj , |
|
|
a23=-cosysinj+sinysinqcosj , |
|
|
|
|
|
|
В уравнениях движения спутника относительно центра масс будем
учитывать гравитационный и восстанавливающий аэродинамический
моменты, а также момент от вихревых токов, наведенных в оболочке
спутника магнитным полем Земли. Компоненты гравитационного момента
в системе Ox1x2x3 имеют вид [9]
|
Mg1=3w02(I3-I2)a32a33 , Mg2=3w02(I1-I3)a33a31 , |
|
Здесь w0 - среднее движение спутника (орбитальная
частота), Ij - моменты инерции спутника относительно осей
Oxj.
При выводе выражений для аэродинамического момента внешнюю
оболочку спутника считаем эллипсоидом, задаваемым в системе
координат Ox1x2x3 уравнением
|
|
(x1-d)2
a2
|
+ |
x22
b2
|
+ |
x32
c2
|
= 1 . |
|
Полагаем, что атмосфера неподвижна в абсолютном пространстве, ее
плотность вдоль орбиты спутника постоянна, молекулы воздуха при
столкновении со спутником испытывают абсолютно неупругий удар. При
сделанных предположениях компоненты аэродинамического момента в
системе Ox1x2x3 имеют вид
|
Ma1=0 , Ma2=rv2dSa13 , Ma3=-rv2dSa12 , |
|
|
S=pabc |
ц
╓
|
a112
a2
|
+ |
a122
b2
|
+ |
a132
c2
|
|
. |
|
Здесь r - плотность атмосферы на орбите спутника, v -
геоцентрическая скорость точки O. Выписанные формулы получены в
предположении, что спутник неподвижен относительно набегающего
аэродинамического потока, но если максимальный размер спутника не
превышает нескольких метров, то ими можно пользоваться и в случае,
когда угловая скорость спутника не слишком велика по сравнению с
угловой скоростью орбитального движения.
Компоненты диссипативного момента от вихревых токов вычисляются по
формулам [9]
|
Mdi=K |
ц
ш
|
Hxi |
3
х
j=1
|
HxjWj-Wi |
3
х
j=1
|
Hxj2 |
Ў
°
|
, |
|
|
Hxi= |
3
х
j=1
|
HXjaji (i=1,2,3) , |
|
Эти компоненты относятся к системе Ox1x2x3. Здесь K -
положительный коэффициент, HXi - компоненты вектора напряженности
магнитного поля Земли в точке O в орбитальной системе координат. Это
поле аппроксимируем полем диполя, магнитный момент которого направлена
по оси вращения Земли. Пусть mE - абсолютная величина этого
магнитного момента, u - аргумент широты точки O, r - радиус
орбиты спутника, I - ее наклонение. Тогда в системе единиц СГСМ
|
HXi= |
mE
r3
|
Hi (i=1,2,3) , |
|
|
H1=sinIcosu , H2=cosI , H3=-2sinIsinu . |
|
Исходные уравнения движения спутника относительно центра масс возьмем
в виде динамических уравнений Эйлера для компонент Wi угловой
скорости спутника в системе координат Ox1x2x3 и кинематических
уравнений для углов y, q и j. В этих уравнениях
сделаем замену переменных W2,W3о w2,w3:
|
W2=w2cosj+w3sinj , W3=-w2sinj+w3cosj . |
|
Кроме того, компоненты угловой скорости будем измерять в единицах
w0, в качестве независимой переменной примем u. На
круговой орбите du/dt=w0=const. В результате получим
уравнения
|
|
╫
j
|
=W1+w3tg q- |
siny
cosq
|
, |
╫
W
|
1
|
=Q1 , |
|
|
|
╫
q
|
=w2-cosy , |
╫
y
|
= |
w3
cosq
|
-tg qsiny , |
| (1) |
|
|
╫
w
|
2
|
=- |
ц
ш
|
lW1+w3tg q- |
siny
cosq
|
Ў
°
|
w3+3(1-l)sinqcosq+Qq , |
|
|
|
╫
w
|
3
|
= |
ц
ш
|
lW1+w3tg q- |
siny
cosq
|
Ў
°
|
w2+Qy , |
|
|
Qq=Q2cosj-Q3sinj , Qy=Q2sinj+Q3cosj , |
|
|
Q1=mq1+em1 , Q2= |
l
1+lm
|
[-m(1-l)q2+em2+dsa13] , |
|
|
Q3=l(-mq3+em3-dsa12) , qi=WjWk-3a3ja3k , |
|
|
mi=[hi(hjWj+hkWk)-Wi(hj2+hk2)] , hi= |
3
х
j=1
|
Hjaji , |
|
|
s = |
╓
|
a112+ka122+kвa132
|
, k = |
a2
b2
|
, kв= |
a2
c2
|
, |
|
|
l = |
I1
I3
|
, m = |
I2-I3
I1
|
, e = |
KmE2
I1w0r6
|
, d = |
pbcdrr2
I1
|
. |
|
Здесь точкой обозначено дифференцирование по u, в выражениях для qi
и mi индексы i, j и k образуют четные перестановки чисел 1, 2 и
3, переменные W2 и W3 должны быть выражены через w2,
w3. По своему физическому смыслу параметр e
неотрицателен, параметр d может принимать любые значения,
параметры l и m должны удовлетворять неравенствам |m| < 1,
0 < l < 2/(1-m). Неравенства для l и m следуют из
"неравенств треугольника" Ii+Ij > Ik для моментов инерции спутника.
Ниже полагаем 0 < l < 1, параметры m, e и d
считаем малыми. Для станции Мир l ╗ 0.65,
m ╗ 0.10.
Правые части уравнений (1) являются p-периодическими функциями
j и 2p-периодическими функциями u.
3. Режим закрутки осесимметричного спутника в плоскости орбиты.
Если ось Ox1 является осью материальной симметрией спутника и
на спутник действует только гравитационный момент, т. е.
m = e = d = 0, то уравнения (1) принимают вид
|
|
╫
j
|
=W1+w3tg q- |
siny
cosq
|
, |
╫
W
|
1
|
=0 ; |
| (2) |
|
|
╫
q
|
=w2-cosy , |
╫
y
|
= |
w3
cosq
|
-tg qsiny , |
|
|
|
╫
w
|
2
|
=- |
ц
ш
|
lW1+w3tg q- |
siny
cosq
|
Ў
°
|
w3+3(1-l)sinqcosq , |
| (3) |
|
|
╫
w
|
3
|
= |
ц
ш
|
lW1+w3tg q- |
siny
cosq
|
Ў
°
|
w2 . |
|
В отличие от системы (1) эта система автономна, поэтому
независимую переменную u будем считать здесь не аргументом
широты спутника, а безразмерным временем.
В силу второго уравнения (2) W1=const, и не зависящие от
j уравнения (3) образуют замкнутую систему, в которую
W1 входит в качестве параметра. Система (3) описывает
движение оси материальной симметрии спутника (оси Ox1)
относительно орбитальной системы координат, уравнения (2)
описывают движение спутника вокруг этой оси.
В стационарных решениях системы (3) w2=cosy,
w3=sinysinq, а углы y и q определяются
уравнениями
|
(lW1-sinycosq)sinysinq-3(1-l)sinqcosq = 0 , |
|
Последние уравнения имеют три пары физически различных решений [9,10]
|
y = |
p
2
|
, cosq = |
lW1
4-3l
|
( |lW1| < |4-3l| ) ; |
| (5) |
|
lW1=siny , q = 0 ( |lW1| < 1 ) . |
| (6) |
Здесь в скобках указаны интервалы изменения угловой скорости W1,
в которых существуют решения (5), (6). Эти решения для станции Мир в
конфигурации 1999 г. не представляют интереса (решения (5) описывают
упомянутый выше режим гравитационной ориентации вращающегося спутника),
а решения (4) соответствуют номинальным невозмущенным движениям спутника
в режиме закрутки в плоскости орбиты.
Для практического использования стационарных решений (4) необходимо,
чтобы они были устойчивы. Поскольку уравнения (3) инвариантны
относительно замены переменных yо-y,
W1о-W1, w3о-w3, ограничимся описанием свойств
устойчивости решения (4), в котором y = p/2.
Уравнения (3) допускают обобщенный интеграл энергии
|
|
W22+W32+3(1-l)sin2q
2
|
-W2cosy-W3sinysinq-lW1sinycosq . |
|
Используя этот интеграл в качестве функции Ляпунова, можно найти
[9,10] достаточные условия устойчивости решения (4) при
y = p/2:
|
lW1-1 > 0 , lW1-(4-3l) > 0 . |
| (7) |
Необходимые условия устойчивости такого решения получаются из анализа
соответствующей линеаризованной системы
|
|
╫
q
|
=w2+Dy , D |
╫
y
|
=w3-q , |
| (8) |
|
|
╫
w
|
2
|
=-(lW1-1) w3+3(1-l) q , |
╫
w
|
3
|
=(lW1-1) w2 . |
|
Здесь Dy = y-p/2. Характеристическое уравнение выписанной
линейной системы имеет вид
|
d1=l2W12-2lW1+3l-1 , d2=(lW1-1)(lW1+3l-4) . |
|
Оно биквадратное, поэтому решения линеаризованной системы ограниченны
только в том случае, когда все корни уравнения (9) - чисто мнимые и
простые, т. е. в случае d1 > 0, d2 > 0, d12-4d2 > 0. Последние
неравенства выражают необходимые условия устойчивости решения (4),
в котором y = p/2. Эти условия удовлетворяются при выполнении
неравенств (7) или неравенств [9]
|
lW1-1 < 0 , lW1+3l-4 < 0 , d12-4d2 > 0 . |
| (10) |
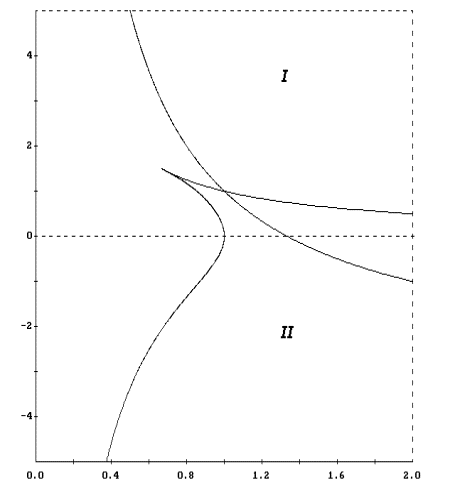
Области выполнения неравенств (7) и (10) в плоскости
(l,W1) показаны на рис. 1. Неравенства (7) выполнены
в области I, неравенства (10) - в области II.
Решению (4) в случае y = p/2 отвечает двухпараметрическое семейство
решений полной системы уравнений (2), (3)
|
j = j0+(W1-1)t , j0=const , W1=const , |
| (11) |
с параметрами j0 и W1. Если W1 удовлетворяет
неравенствам (7) (неравенствам (10)), то решения (11) устойчивы
(устойчивы в первом приближении) по переменным W1, q,
y, w2 и w3. В этом случае решения (11) можно использовать в
качестве номинального невозмущенного движения для хранения спутника на
орбите в течение длительного времени.
Как видно из рис. 1, обеспечивающее устойчивость значение |W1|
должно быть достаточно большим. На интервале 0 < l < 1 определяемые
неравенствами (7), (10) нижние границы |W1| убывают при
увеличении l, поэтому с ростом этого параметра возможности
использования семейства (11) расширяются. При l = 0.65 (в случае
станции Мир) неравенства (7) выполнены при W1 > 3.2, неравенства
(10) выполнены при W1 < -2.2. Эти граничные значения оказались
приемлемыми.
Вследствие погрешности системы управления привести спутник точно
в стационарное вращение (11) не удается, и он совершает вблизи него
некоторое возмущенное движение. Интерес представляют только колебания
оси Ox1 относительно оси OX2, описываемые уравнениями (8).
В областях I и II общее решение этих уравнений имеет вид
|
q = a(c1sinn1u-c2cosn1u)+c3cosn2u+c4sinn2u , |
|
|
Dy = c1cosn1u+c2sinn1u+b(c3sinn2u-c4cosn2u) , |
|
|
a= |
(lW-2)n1
lW-4+3l-n12
|
, b=- |
(lW-2)n2
lW-1 -n22
|
. |
|
Здесь c1, c2, c3, c4 - произвольные постоянные. Для
решения с начальным условиями
|
q(0)=q0 , Dy(0)=Dy0 , w2(0)=w20 , w3(0)=w30 |
|
постоянные c1, c2, c3, c4 вычисляются по формулам
|
c1= |
bw20+(n2+b)Dy0
abn1+n2
|
, c2= |
w30-(1+bn2)q0
n1+abn2
|
, |
| (13) |
|
c3= |
aw30+(n1-a)q0
n1+abn2
|
, c4= |
w20+(1-an1)Dy0
abn1+n2
|
. |
|
В областях I и II (рис. 1) знаменатели этих формул отличны от нуля.
Пусть (случай станции Мир ) l = 0.65,
q0=Dy0=0, W1=-3 и w20=w30=0.15
( ╗ -0.2 и 0.01 град./с), т. е. в начальный момент u=0 ось
Ox1 спутника совпадает с осью OX2, но в угловых скоростях
имеются ошибки. Тогда для соответствующего возмущенного движения
по формулам (12), (13) находим |q|max=18░,
|Dy|max=19░. Такие ошибки ориентации можно
считать допустимыми.
4. Режим закрутки спутника, близкого к осесимметричному, в
плоскости орбиты.
Предположим, что спутник близок к осесимметричному с осью
материальной симметрии Ox1 и что влияние на него
негравитационных внешних моментов мало. Иными словами, |m| << 1, |e| << 1, |d| << 1. Для упрощения формул
оставим только один малый параметр m, приняв
e = e1m, d = d1m,
e1 ~ 1, d1 ~ 1. Тогда в системе (1)
Q1 ~ m, Qq ~ m, Qy ~ m, причем правые части
ее уравнений аналитически зависят от m в окрестности точки m = 0.
При m = 0 такая система (1) имеет семейство решений (11), которое
при m ╣ 0 порождает формальную двумерную интегральную
поверхность. Эта интегральная поверхность может быть построена
методом Н.Н.Боголюбова - Ю.А.Митропольского [11] в виде
формальных рядов по степеням m
|
j = x+ |
е
х
k=1
|
mkjk(x,h,u) , W1=h+ |
е
х
k=1
|
mk W1k(x,h,u) , |
|
|
q = |
е
х
k=1
|
mk qk(x,h,u) , y = |
p
2
|
+ |
е
х
k=1
|
mk yk(x,h,u) , |
| (14) |
|
w2= |
е
х
k=1
|
mk w2k(x,h,u) , w3= |
е
х
k=1
|
mk w3k(x,h,u) , |
|
в которых переменные x и h определяются уравнениями
|
|
╫
x
|
=h-1+ |
е
х
k=1
|
mk Ak(h) , |
╫
h
|
= |
е
х
k=1
|
mk Bk(h) . |
| (15) |
Коэффициенты рядов (14), (15) должны быть p-периодическими
функциями x и 2p-периодическими функциями u. Потребовав,
чтобы эти ряды задавали решения системы (1), получим для
определения коэффициентов рядов цепочку рекуррентных соотношений
|
|
╢jk
╢m
|
+(h-1) |
╢jk
╢x
|
=W1k+g1k-Ak , |
|
|
|
╢W1k
╢m
|
+(h-1) |
╢W1k
╢x
|
=g2k-Bk , |
|
|
|
╢qk
╢m
|
+(h-1) |
╢qk
╢x
|
=w2k+yk+g3k , |
| (16) |
|
|
╢yk
╢m
|
+(h-1) |
╢yk
╢x
|
=w3k-qk+g4k , |
|
|
|
╢w2k
╢m
|
+(h-1) |
╢w2k
╢x
|
=-(lh-1) w3k+3(1-l)qk+g5k , |
|
|
|
╢w3k
╢m
|
+(h-1) |
╢w3k
╢x
|
=(lh-1) w2k+g6k . |
|
Здесь gkj (j=1, ... ,6) - некоторые функции x, h,
u, а также коэффициентов рядов (14), (15) с индексами меньше, чем k,
и производных этих коэффициентов. Функции gkj зависят от x и
u периодически с периодами p и 2p соответственно.
Уравнения (16) и условия периодичности не определяют коэффициентов рядов
(14), (15) единственным образом. Чтобы достичь единственности, потребуем
еще выполнения условий
|
< jk > =0 , < W1k > =0 (k=1,2, ...) . |
| (17) |
Используемый для записи этих условий оператор < ... > и применяемый
ниже оператор {...} определены на p-периодических по x и
2p-периодических по u функциях
|
f(x,u)=f0+ |
х
|l|+|m| > 0
|
[flmcos(2lx+mu)+flmвsin(2lx+mu)] |
| (18) |
с помощью формул
|
< f > =f0 , {f}= |
х
|l|+|m| > 0
|
|
flmsin(2lx+mu)-flmвcos(2lx+mu)
2l(h-1)+m
|
. |
|
Цепочка уравнений (16) решается следующим образом. Пусть найдены
коэффициенты рядов (14), (15) с индексами k=1, ..., N-1,
причем коэффициенты рядов (14) p-периодически зависят от x
и 2p-периодически - от u. Рассмотрим уравнения (16) при
k=N. После подстановки найденных коэффициентов в выражения
gjN эти выражения будут известными p(2p)-периодическими
функциями x(u). Переменная h будет входить в уравнения
(16) как параметр. Решение полученной системы уравнений начнем с
уравнения относительно W1N и BN. При выполнении
условия
|
2l(h-1)+m ╣ 0 (l,m=0,▒1,▒2, ... ; |l|+|m| > 0) |
| (19) |
это уравнение и второе соотношение (17) при k=N единственным
образом определяют искомые функции в виде: BN= < g2n > ,
W1N={g2n} . Аналогичным образом решается первое
уравнение (16). При выполнении условия (19) это уравнение и первое
соотношение (17) однозначно определяют AN= < g1n > ,
jN={g1n} . Последние четыре уравнения (16) образуют
замкнутую систему линейных уравнений с периодическими свободными
членами. Решение этой системы будем искать в виде рядов вида (18).
При выполнении условия
|
[2l(h-1)+m]4-(l2h2-2lh+3l-1)[2l(h-1)+m]2+ |
| (20) |
|
+(lh-1)(lh+3l-4) ╣ 0 (l,m=0,▒1,▒2, ... ) |
|
такое решение существует и единственно. В итоге доказано, что при
выполнении условий (19), (20) цепочка уравнений (16) имеет
единственное p(2p)-периодическое по x(u) решение,
удовлетворяющее соотношениям (17).
Движения спутника, описываемые решениями вида (14), (15), будем
считать невозмущенными движениями в режиме закрутки вокруг нормали
к плоскости орбиты. Наибольший интерес при исследовании таких
движений представляет второе уравнение (15), описывающее вековое
изменение угловой скорости вращения спутника вокруг оси Ox1.
Чтобы получить представление о таком изменении достаточно найти
первую отличную от тождественного нуля функцию Bk(h).
Простые вычисления показывают, что
B1(h)=-[ 5/2] e1hsin2I. В первом
приближении влияние аэродинамического момента не проявляется.
Уравнение
с точностью O(|m|) на интервале 0 <= u <= |m|-1
описывает эволюцию угловой скорости спутника в квазистационарном
вращении. В процессе эволюции при некоторых значениях h могут
нарушаться условия (19), (20). Однако поскольку эти нарушения не
влияют на выражение для B1(h), точность уравнения (21) в
области B1(h) != 0 практически не ухудшается.
5. Периодические движения спутника в режиме закрутки в
плоскости орбиты.
Согласно уравнению (21) угловая скорость закрутки спутника должна
уменьшаться. При использовании описанного режима на станции Мир такое
уменьшение наблюдалось в действительности [8], но наблюдалось и
возрастание этой угловой скорости, причем на том же самом движении
станции. Следовательно, диссипативный момент от вихревых токов не
доминировал среди негравитационных моментов, действующих на станцию. По
этой причине интересно исследовать движение станции в рассматриваемом
режиме под влиянием только гравитационного и восстанавливающего
аэродинамического моментов. Поставленная задача весьма сложна, и ниже в
качестве первого этапа ее решения ограничимся изучением интегральной
поверхности (14), (15) модельной системы (1) в случае e1=0.
Для сокращения записи воспользуемся векторными обозначениями. Введем
вектор z=(j, W1, q, y, w2, w3)T и определим
функцию F(z,m,d) ╬ R6 так, чтобы система (1) при
e = 0 могла быть записана в виде
Эта система автономна, поэтому независимую переменную u будем
считать безразмерным временем. Указанное выше свойство
периодичности системы (1) по углу j в данном случае можно
выразить соотношением
|
F(z+pe1,m,d)=F(z,m,d) , e1=(1,0,0,0,0,0)T . |
|
Кроме того, система (22) обладает свойством
(Е)1 по отношению к матрице S=diag(-1,1,-1,1,1,-1),
т. е. правая часть этой системы удовлетворяет соотношению
Справедливо также соотношение
|
SвF(Sвz,m,-d)=-F(z,m,d) , |
| (24) |
где Sв=diag(-1,1,1,-1,-1,1).
Запишем для удобства интегральную поверхность (14) в векторном
виде
|
z=g(x,h,m) ║ g0(x,h,m)+mg1(x,h,m)+... |
| (25) |
Правые части уравнений (15) обозначим соответственно A(h,m) и
B(h,m). Тогда тот факт, что система (22) при d = md1
имеет интегральную поверхность (25), движение по которой описывается
уравнениями (ср. (15))
|
|
╫
x
|
=A(h,m) , |
╫
h
|
=B(h,m) , |
| (26) |
выражается тождеством
|
|
╢g
╢x
|
A+ |
╢g
╢h
|
B=F(g,m,md1) . |
| (27) |
По построению (см. выше)
Кроме того, в силу свойств симметрии (23) имеем
|
Sg(-x,h,m)=g(x,h,m), B(h,m)=0 . |
| (29) |
Докажем это. Рассмотрим функции
gв(x,h,m)=Sg(-x,h,m),
Aв(h,m)=A(h,m), Bв(h,m)=-B(h,m). Нетрудно
проверить, что новые функции представляются формальными рядами вида
(25), (15) и удовлетворяют соотношениям (28), (27), (17). Кроме того
Sg0(-x,h)=g0(x,h). Отсюда в силу единственности
решения цепочки уравнений (16), удовлетворяющего соотношениям (17) и
(28), получаем равенства gв(x,h,m)=g(x,h,m),
Bв(h,m)=B(h,m), из которых следует (29).
Аналогичным образом можно использовать и соотношение (24), но его
следствия в дальнейшем использоваться не будут.
Рассмотрим уравнения (26). В силу (29) h = const и
решение системы (22), принадлежащее интегральной поверхности (25),
представляет собой периодическое вращение2 с периодом T=p/A(h, m). Это решение содержит
два параметра: h и x(0). Значение h должно
удовлетворять неравенствам (19) при m=0, значение x(0)
произвольно. Без ограничения общности возьмем x(0)=0. В силу
соотношений (28), (29) решение
удовлетворяет соотношениям
|
Sz(-u)=z(u) , z(u+T)=z(u)+pe1 . |
| (31) |
Из (31) следует, что
|
Sz |
ц
ш
|
-u+ |
T
2
|
Ў
°
|
=z |
ц
ш
|
u+ |
T
2
|
Ў
°
|
-pe1 . |
|
Положив здесь и в первом соотношении (31) u=0, находим краевые
условия
|
Sz(0)=z(0) , Sz |
ц
ш
|
T
2
|
Ў
°
|
= z |
ц
ш
|
T
2
|
Ў
°
|
-pe1, |
| (32) |
которым удовлетворяет решение (30). Скалярная форма этих условий
|
j(0)=q(0)=w3(0)=j |
ц
ш
|
T
2
|
Ў
°
|
- |
p
2
|
=q |
ц
ш
|
T
2
|
Ў
°
|
= w3 |
ц
ш
|
T
2
|
Ў
°
|
=0 |
|
Можно доказать, что всякое решение z(u) краевой задачи (22), (32)
удовлетворяет соотношениям (31) и, следовательно, является
T-периодическим вращением.
Докажем существование решений задачи (22), (32) методом Пуанкаре. Пусть
a=(a1,a2,a3)T, z*(u,a,m) - решение системы (22) с начальным
условием z*(0,a,m)=(0,a1,a2,0,0,a3)T. Тогда краевые условия (32)
в точке u=0 выполняются автоматически. Условия в точке u=T/2 запишем
в виде
где левая часть - трехмерный вектор-столбец, образованный первой,
третьей и шестой компонентами вектора z*(T/2,a,m). Будем
рассматривать соотношение (33) как уравнение относительно a. Если
m = 0, то уравнение имеет решение a░(T)=(p/T+1,0,0)T. Как
нетрудно видеть, z*[u,a░(T),0] - векторная запись
стационарного вращения (11) в случае j0=0, W1=p/T+1.
Вследствие аналитичности правой части системы (22) при
d = md1 по m и z в области достаточно малых
|m| и ||z - z*[u,a░(T),0]|| (-е < u < +е)
функция f(a,T,m) аналитически зависит от m и a в
окрестности точки m = 0, a=a░(T). Если
|
J = |
det
| |
╢f[a░(T), T, 0]
╢a
|
╣ 0 , |
| (34) |
то согласно теореме о неявной функции при достаточно малых |m|
уравнение (33) имеет единственное решение a=a*(T,m), аналитически
зависящее от m и удовлетворяющее условию a*(T,0)=a░(T). В
этом случае краевая задача (22), (32) имеет единственное решение
аналитически зависящие от m в окрестности точки m = 0
и совпадающее в этой точке со стационарным вращением (11) при
j0=0, W1=p/T+1.
Исследуем условие (34). Согласно теории Пуанкаре равенство J=0
выполнено в том и только в том случае, когда краевая задача
|
Dj(0)=q(0)=w3(0) = Dj |
ц
ш
|
T
2
|
Ў
°
|
=q |
ц
ш
|
T
2
|
Ў
°
|
=w3 |
ц
ш
|
T
2
|
Ў
°
|
=0 . |
|
для системы (8) и уравнений D[(j)\dot]=DW1,
D[(W)\dot]1=0 имеет нетривиальное решение. Последние два
уравнения получены линеаризацией уравнений (2) на решениях (11).
Поставленная задача содержит два параметра: T (или W1) и
l. Условия существования ее нетривиальных решений
формулируются в виде соотношений, которым должны удовлетворять эти
параметры. Задача разбивается на две независимые подзадачи.
Подзадача для Dj и DW1 всегда имеет
только тривиальное решение, подзадача для остальных переменных
имеет нетривиальное решение лишь в том случае, когда уравнение (9)
имеет корень p=2pk╓{-1}/T=2k(W1-1)╓{-1} при
целом k. Следовательно, условие (34) нарушается при выполнении
одного из соотношений
|
16k2(W1-1)4- 4d1k2(W1-1)2+d2=0 (k=1,2,...) . |
| (37) |
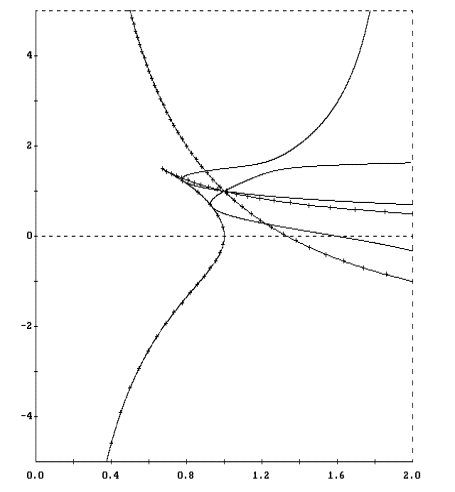
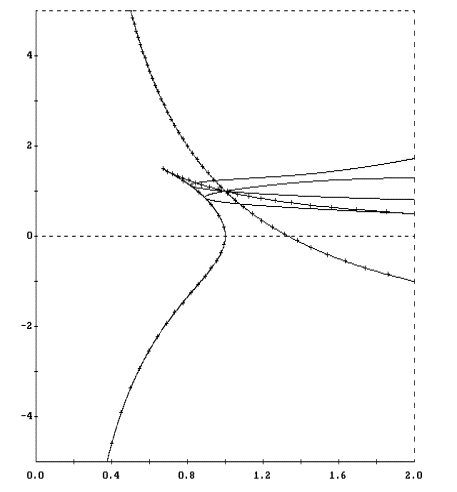
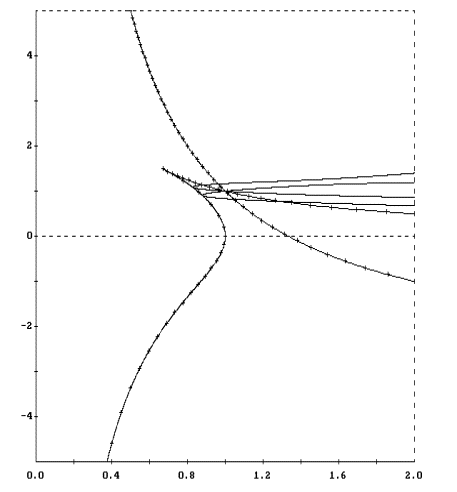
В плоскости (l,W1) каждое соотношение (37) задает кривую.
Кривые, отвечающие значениям k=1, 2, 3, приведены на рис. 2 - 4.
Здесь же указаны границы областей устойчивости цилиндрической прецессии
(ср. рис. 1). Эти границы отмечены маркерами.
Решая численно уравнение (33), можно построить решение (36) в
явном виде и исследовать его зависимость от параметров задачи.
Основным параметром, в функции которого изучались вычисляемые
решения, служил период T. Его значения менялись на равномерной
сетке. В каждой точке этой сетки уравнение (33) решалось
относительно a. Использовался метод Ньютона, для вычисления
вектора f(a,T,m) и матрицы ╢f(a,T,m)/╢a на
отрезке 0 <= u <= T/2 (здесь для определенности полагаем T > 0)
интегрировалась система (1) и соответствующая система уравнений в
вариациях. При решении уравнения (33) в первых трех точках сетки
периода T начальным приближением неизвестного a служил вектор
a░(T). В последующих точках сетки начальное приближение
вычислялось по формуле квадратичного прогноза
|
aprog(T+DT,m)=3a*(T,m)-3a*(T-DT,m)+a*(T-2DT,m) . |
|
Здесь DT - шаг сетки, и предполагается, что в ее точках T,
T-DT и T-2DT решение уравнения (33) уже найдено.
Расчеты проводились для значений параметров l = 0.65, m = 0.1,
a=16 м, b=14 м, c=12 м, d=-1 м, rr2/I1=10-4
м-3, при которых рассматриваемый спутник может служить грубой
моделью станции Мир. Найденные решения уравнения (33) представлены
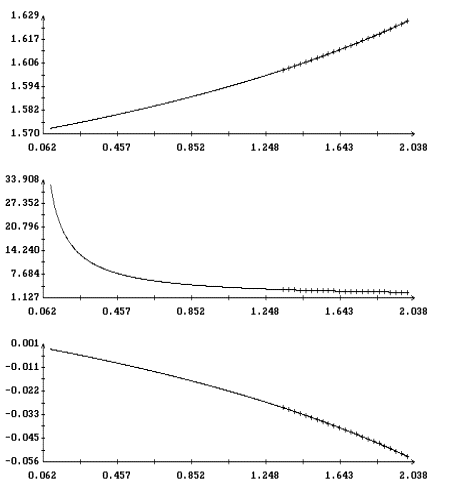
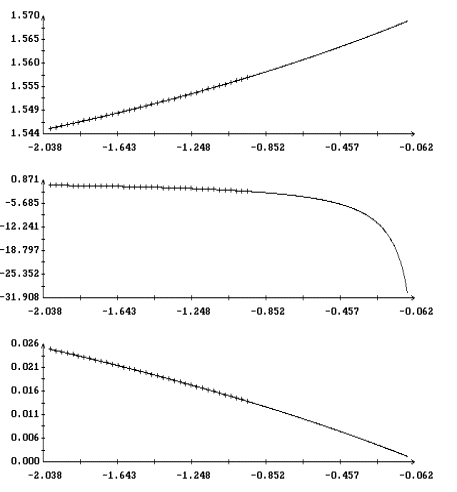
левыми графиками на рис. 5, 6. Эти графики выражают зависимость
компонент вектора a, которые обозначены здесь y(0), W1(0)
и w2(0), от периода T. Правые графики на тех же рисунках
характеризуют свойства устойчивости соответствующих вращательных
периодических решений системы (22).
Устойчивость исследовалась следующим образом. Пусть z(u) - решение
краевой задачи (22), (32), продолженное с помощью соотношений (31) на
всю действительную ось. Для определенности примем T > 0. Рассмотрим
систему уравнений в вариациях
где A(u)=Fz[z(u),m,d], y ╬ R6. В силу соотношений (31)
для матрицы A(u) справедливы равенства
|
-SA(-u)=A(u)S , A(u+T)=A(u) . |
| (39) |
Система (38) является системой с T-периодическими коэффициентами. Ее
характеристическое уравнение запишем в виде
где E6 - единичная матрица шестого порядка, X(t) - решение
начальной задачи [(X)\dot]=A(u)X, X(0)=E6. При любом u имеет место
соотношение X(u+T)=X(u)X(T). Взяв здесь u=T/2, получим
X(T)=X-1(-T/2)X(T/2). Из первого соотношения (39) следует
SX(-u)=X(u)S, поэтому X(-T/2)=SX(/2)S и
Полученная формула дает экономный способ вычисления X(T). Кроме того,
в силу нее X-1(T)=SX(T)S. Используя этот факт можно доказать, что
уравнение (40) - возвратное [12]. Система (38) имеет периодическое
решение y=[(z)\dot](u), следовательно, уравнение (40) имеет корень
r = 1 кратности не ниже 2. С учетом сказанного
|
|X(T)-rE6|=(r-1)2(r2-A1r+1)(r2-A2r+1) , |
| (42) |
где A1 и A2 - коэффициенты. Если A1, A2 действительны
и |A1| <= 2, |A2| <= 2, то все корни уравнения (40) лежат на
окружности |r|=1 и выполнены необходимые условия орбитальной
устойчивости решения z(u). В противном случае это решение
орбитально неустойчиво. Поскольку система (22) автономна, а
исследуемые периодические решения образуют однопараметрические
семейства с периодом в качестве параметра, эти решения всегда
неустойчивы по Ляпунову.
Для определенности будем считать, что если A1 и A2 вещественны,
то A1 <= A2. Если же эти коэффициенты принимают комплексные значения
(в этом случае A2=[`(A)]1), то Im A2 >= 0.
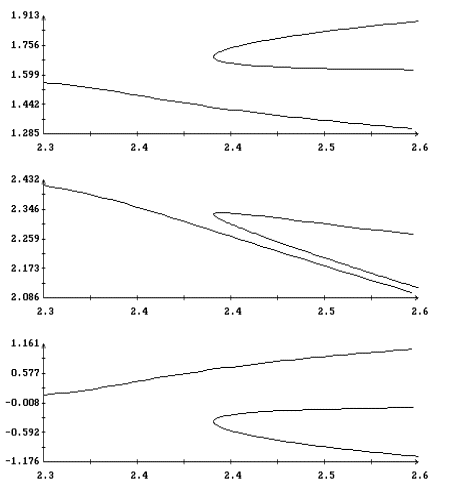
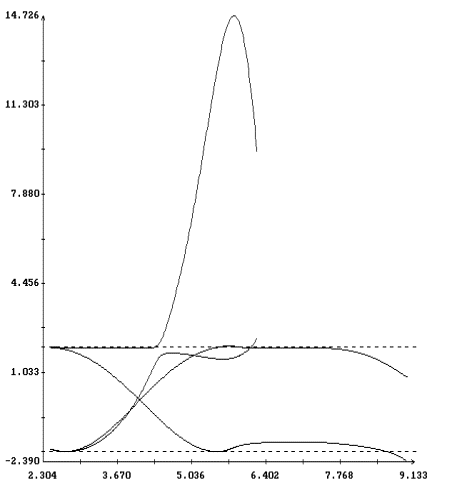
Вернемся к рис. 5, 6. Правые графики на этих рисунках выражают
зависимость от периода коэффициентов A1, A2 в формуле (42).
Штриховые горизонтальные линии - прямые A1,2=▒2. Если
A1, A2 принимают комплексные значения, то на графиках
представлены величины Re A1,2 и Im A2. Такие
участки графиков отмечены маркерами (ср. рис. 6). Участки
неустойчивости на графиках начальных условий также отмечены
маркерами. Как видно из рисунков, отрезки устойчивости на оси T
вычисленных периодических решений примерно совпадают с отрезками
устойчивости стационарного решения (4) (если использовать связь
между параметрами T и W1 по формуле W1=p/T+1).
Характер потери устойчивости также одинаков. В случае T > 0 (рис.
5) график коэффициента A2 пересекает прямую A2=2. В точке
пересечения уравнение (40) имеет дополнительную пару корней
r = 1, что соответствует паре нулевых корней уравнения (9) на
границе области I при l = 0.65. В случае T < 0 (рис. 6) в
точке потери устойчивости A1=A2, что соответствует двум парам
кратных корней уравнения (9). Из этой точки слияния графиков
коэффициентов A1 и A2 начинается расположенный правее нее
график величины Re A1,2. В точке потери устойчивости
Im A2=0.
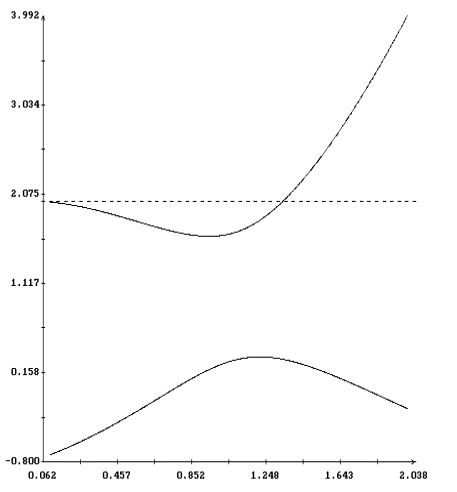
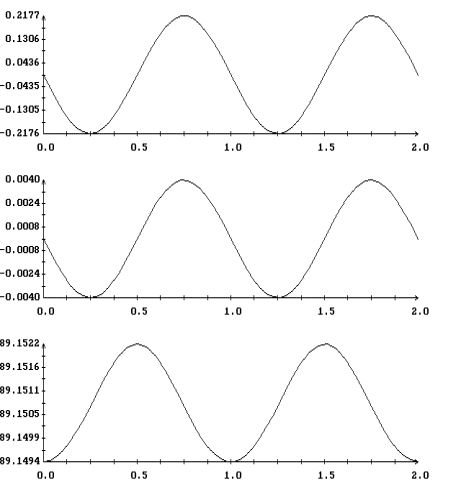
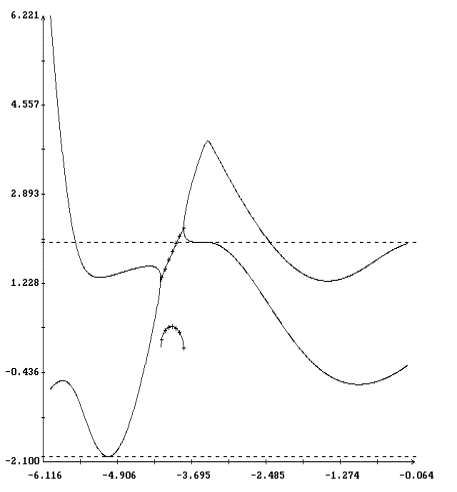
Примеры двух найденных периодических решений системы (22) приведены на
рис. 7, 8. Здесь изображены графики функций
dj(u)=j(u)-pu/T, q(u), y(u).
Начальные условия решения, представленного на рис. 7, лежат на кривых,
приведенных на рис. 5. Начальные условия решения на рис. 8 лежат на
кривых на рис. 6. Как видно из графиков, отклонение каждого из этих
решений от решения (11), имеющего тот же период, весьма мало.
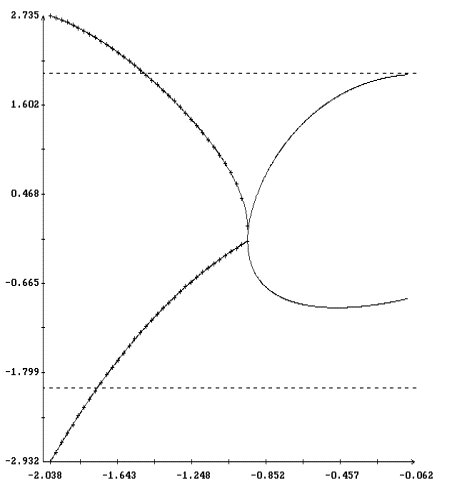
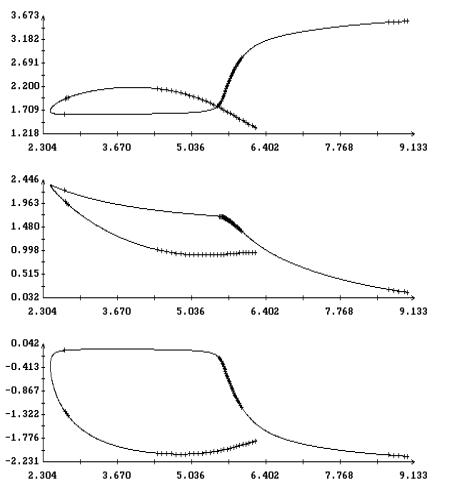
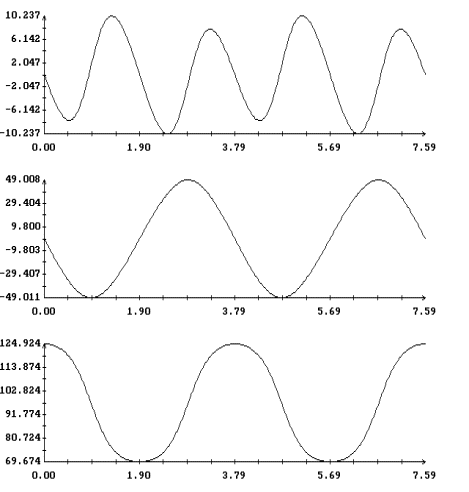
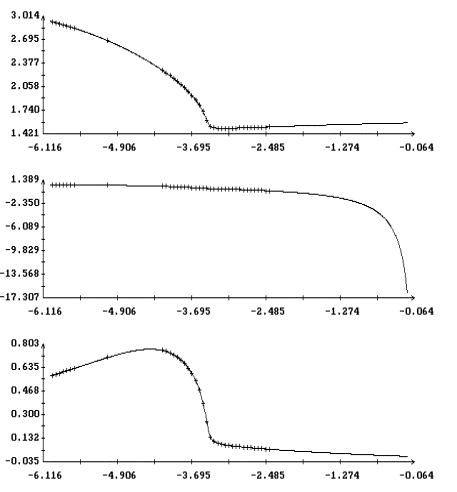
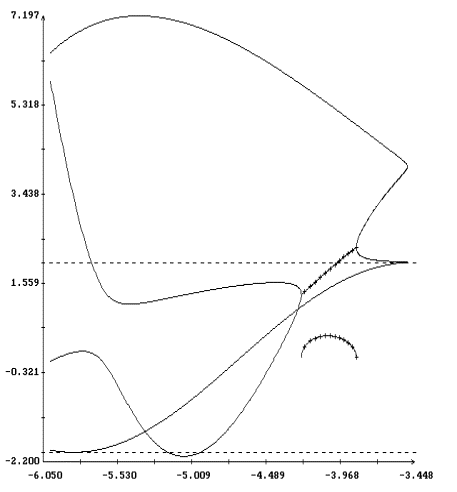
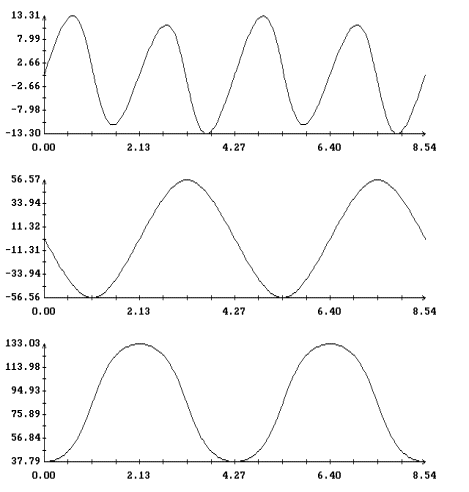
Анализ рис. 2 - 4 показывает, что при l > 1 и достаточно
больших значениях периода T поведение этих решений в зависимости
от периода может оказаться более сложным. На рис. 9 - 16
представлены решения краевой задачи (22), (32) при l = 1.6 и
прежних значениях остальных параметров. На рис. 9, 10 и 13, 14
приведены кривые, задаваемые уравнением (33). Некоторые из этих
кривых получены методом, описанным выше, а для вычисления отрезков
кривых, содержащих точки с вертикальными касательными, применялся
метод продолжения по параметру [13]. В этом методе уравнение (33)
рассматривается как уравнение кривой в пространстве R4(a,T),
причем каждая скалярная компонента вектора (a,T) используется
инвариантным образом. Обнаруженное ветвление решений уравнение
(33) связано с нарушением условия (34), т. е. с резонансами между
колебаниями оси Ox1 и вращением спутника вокруг этой оси (ср.
[1]). Примеры нерезонансных (лежащих на интегральной поверхности
(14)) и резонансных решения краевой задачи (22), (32) приведены
соответственно на рис. 11, 15 и 12, 16.
6. Замечание об обратимых системах. Результаты предыдущего
раздела интересны в следующем отношении. В окрестности
стационарного решения (5) также можно построить интегральную
поверхность уравнений (1). Такое построение при e = 0,
d = md1, т. е. в случае системы (22), было выполнено
в [3]. В этой работе однако использовался другой способ введения
углов, задающих взаимное положение систем координат Ox1x2x3 и
OX1X2X3. Найденная в [3] интегральная поверхность содержала
решения, испытывающие эволюцию подобно решениям, найденным в
предыдущем разделе). Указанное отличие объясняется так.
Система (22) является обратимой. Этот факт выражается соотношением
(23), которое сыграло ключевую роль в доказательстве существования
периодических решений. Преобразование zо Sz переводит
окрестность решения (4) в окрестность этого же решения. Именно это
обстоятельство позволяет использовать свойство обратимости нужным
образом. То же преобразование переводит окрестность одного из
решений (5) в окрестность другого такого же решения, отличающегося
от первого знаком q. В такой ситуации свойство обратимости
ничего не дает.
Данная работа выполнена при поддержке РФФИ (проект 02-01-00323).
Литература
- [1]
- Сарычев В.А., Сазонов В.В. Гравитационная ориентация вращающегося
спутника. Космические исследования, 1981, т. 19, вып. 4, с. 499-512.
- [2]
-
Сарычев В.А., Сазонов В.В. Влияние диссипативного магнитного момента
на гравитационную ориентацию вращающегося спутника. Космические
исследования, 1982, т. 20, вып. 2, с. 177-183.
- [3]
-
Сазонов В.В., Петров А.Л. Эволюция режима гравитационной ориентации
вращающегося спутника под действием непотенциального аэродинамического
момента. Космические исследования, 1987, т. 25, вып. 4, с. 508-522.
- [4]
-
Ветлов В.И., Сазонов В.В., Сарычев В.А. Влияние демпфирования на режим
гравитационной ориентации вращающегося спутника. Известия АН СССР.
Механика твердого тела, 1990, вып. 1, с. 3-12.
- [5]
-
Костенко И.К., Ветлов В.И., Нырков А.Г., Сарычев В.А., Сазонов В.В. Режим
обобщенной гравитационной ориентации на орбитальных комплексах
Салют-6 - Космос-1267 и Салют-7 - "Космос-1443. Космические
исследования, 1986, т. 24, вып. 1, с. 46-50.
- [6]
-
Ветлов В.И., Новичкова С.М., Сазонов В.В. Исследование режима
гравитационной ориентации вращающегося спутника. Препринт Института
прикладной математики РАН, 1995, N 24.
- [7]
-
Ветлов В.И., Новичкова С.М., Сазонов В.В., Матвеев Н.В., Бабкин Е.В.
Режим гравитационной ориентации Международной космической станции.
Космические исследования, 2001, т. 39, вып. 4, с. 436-448.
- [8]
-
Бабкин Е.В., Беляев М.Ю., Ефимов Н.И., Сазонов В.В., Стажков В.М.
Неуправляемое вращательное движение орбитальной станции Мир.
Космические исследования, 2001, т. 39, вып. 1, с. 27-42.
- [9]
-
Белецкий В.В. Движение искусственного спутника относительно центра масс.
М., Наука, 1965.
- [10]
-
Черноусько Ф.Л. Об устойчивости регулярной прецессии спутника. Прикладная
математика и механика, 1964, т. 28, вып. 1, с. 155-157.
- [11]
-
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории
нелинейных колебаний. М., Физматгиз, 1963.
- [12]
-
Hale J.K. Ordinary differential equations. Wiley - Interscience,
New York, 1969.
- [13]
-
Сарычев В.А., Сазонов В.В., Мельник Н.В. Пространственные периодические
колебания спутника относительно центра масс. Космические исследования,
1980, т. 18, вып. 5, с. 659-677.
Footnotes:
1 Система dx/dt=g(x,t), где x,g ╬ Rn, обладает свойством (E), по отношению к S, если
существует постоянная n×n матрица S, удовлетворяющая
соотношениям S=ST=S-1 и Sg(Sx,-t)=-g(x,t) при любых x и
t [12].
2
Решение z(u) системы (22) будем называть вращательным
периодическим решением или, короче, периодическим вращением, если
существует такое число T != 0 (период), что z(u+T)=z(u)+pe1. Значения T разных знаков отвечают вращениям в разные
стороны.
File translated from
TEX
by
TTH,
version 3.40.
On 28 Jun 2004, 18:52.
Приложение
|
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() . Рис. 4. Кривые (37) при
. Рис. 4. Кривые (37) при ![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (град.)
(град.)
![]() (град.)
(град.) 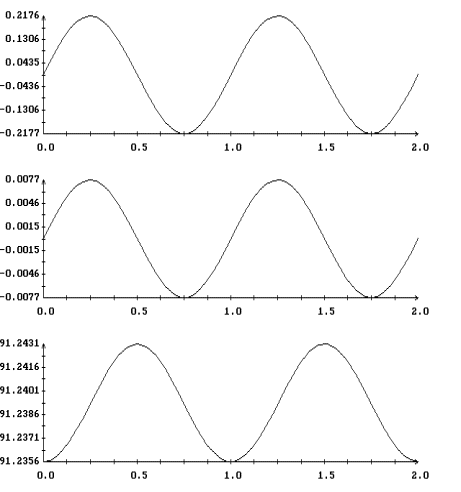
![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.![]()
![]()

![]()
![]()
![]() . Правые графики
. Правые графики![]()
![]()
![]()
![]()
![]() . Правые
графики
в увеличенном виде
воспроизводят фрагменты левых графиков на рис. 9.
. Правые
графики
в увеличенном виде
воспроизводят фрагменты левых графиков на рис. 9.![]() (град.)
(град.)
![]() (град.)
(град.) 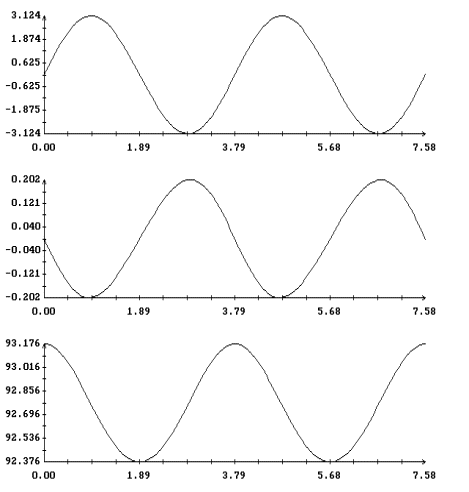
![]()
![]()
![]() , Рис. 12.
Устойчивое решение задачи (22), (32);
, Рис. 12.
Устойчивое решение задачи (22), (32); ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()

![]()
![]()
![]() .
.![]() (град.)
(град.)
![]() (град.)
(град.) 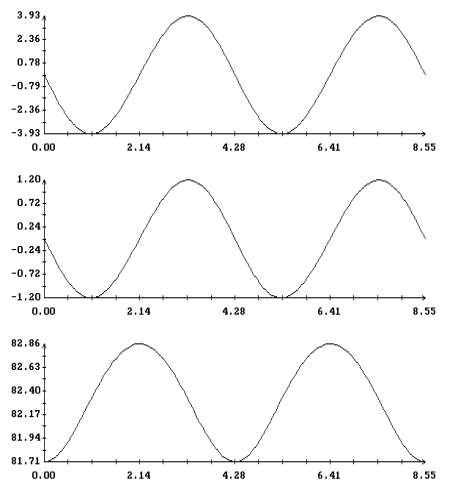
![]()
![]()
![]() , Рис. 16. Устойчивое решение задачи (22), (32);
, Рис. 16. Устойчивое решение задачи (22), (32); ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.