Аналитические оценки оптимизации энерговыделения в гибридной микромишени DT-U238
( Analytical Estimations of Energy Release Optimization for Hybrid DT-U238 Target
Preprint, Inst. Appl. Math., the Russian Academy of Science)

1. Введение.

В данной работе исследуется оптимизация энерговыделения в термоядерной микромишени на DT-топливе в рамках концепции ИТЭФ тяжелоионного синтеза на цилиндрических мишениях, сформулированной в [1]-[3], когда в качестве пушера берется делящееся вещество. Идея такой гибридной мишени была предложена в [14]. Первые расчетные результаты для конкретной структуры мишени, параметры которой приведены ниже в таблице 1, были представлены в [15].

Гибридная мишень в концепции тяжелоионного термоядерного синтеза в идеальной конфигурации представляет собой прямой круговой многослойный цилиндр длиной 1см. Структура цилиндра приведена в таблице 1. Верхний индекс у радиусов отвечает начальному моменту времени (перед сжатием).

Таблица 1. Характерные начальные параметры гибридной мишени.

Зона 3 является абсорбером, куда вкладывается энергия драйвера (тяжелоионного ускорителя), обеспечивающая параметры зажигания термоядерного топлива в зоне 1. Одновременно с этим достигаются большие значения плотности пушера (зона 2), в котором возможно значительное усиление термоядерного энерговыделения за счет деления U238 на быстрых нейтронах. Детальный численный расчет гидродинамики сжатия при заданном профиле энерговложения (например, при безударном сжатии), последующего загорания мишени и энерговыделения в ней с учетом переноса нейтронов является чрезвычайно сложной вычислительной задачей. Поэтому представляется важным сделать предварительные аналитические оценки относительных величин энерговыделения для ядерной и термоядерной составляющих, максимально возможного коэффициента выгорания урана в зависимости от степени сжатия, общего коэффициента усиления мишени. Это исследование позволит понять, насколько близко «базовые» параметры мишени, представленные в таблице 1, находятся к некоторым идеальным, каков относительный (по энерговыделению) эффект увеличения энерговложения в абсорбер в предположении, что гидро-кпд абсорбер-пушер оптимальный. Эти вопросы важны для последующей оптимизации рассматриваемой гибридной мишени и проведении численных экспериментов.

Центральными управляющими параметрами являются: отношение масс DT и U в мишени, а также степень ее радиального сжатия. Обозначим массу DT-топлива через , уранового пушера – через , начальные плотности считаются фиксированными и равными значениям из таблицы 1. Отношение масс термоядерного и ядерного топлив однозначно связано с отношением радиусов кольца пушера:

.                                                                    (1.1)

(Коэффициент 400 в этой формуле есть просто приближенное отношение начальных плотностей урана и дейтерий-тритиевой смеси). Введем факторы радиального сжатия DT-топлива и уранового пушера

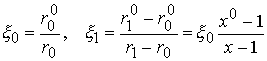.                                                                (1.2)

Они определяют плотность среды, в которой происходит горение DT и формируется спектр нейтронов, воздействующих затем на вещество пушера и вызывающих его деление.

Таким образом, требуется определить функциональные зависимости , , при которых достигается:

а) максимальное выгорание U238;

б) максимальное усиление мишени в целом;

в) максимальное усиление только ядерной и только термоядерной составляющих мишени по отдельности;

г) максимальное энерговыделение в мишени в абсолютных единицах.

Ответы на эти вопросы позволят получить оценки эффективности рассматриваемой системы как для целей энергетики, так и для различных нейтронно-физических задач.

Физическое содержание концепции состоит в следующем. Внешнее энерговложение в абсорбер (свинец) осуществляется с торца (или с двух торцов) мишени пучками тяжелых ионов (положительные и отрицательные изотопы платины) в направлении оси симметрии мишени. Профилирование энерговложения по времени позволяет реализовать т.н. безударное сжатие центральной зоны мишени и достичь параметров зажигания. Безударным сжатием некоторой области газа называется такое коллапсирующее течение, которое приводит в фиксированный момент к схождению всей или части первоначальной области в образование меньшей размерности при сохранении энтропии вещества на протяжении всего процесса. В работах [4]-[6] было показано, что безударное сжатие позволяет получать высокие параметры плотности при оптимальных затратах энергии. Если пушер изготовлен из делящегося материала, то в процессе сжатия он может достигнуть таких значений плотностей, которые позволят развиться цепной реакции деления. Использование высокоэнергетичных термоядерных нейтронов в качестве инициирующей подсветки может в этом случае значительно повысить усиление энергии в мишени.

Первые опубликованные результаты, касающиеся исследований микрокритических масс в сверхсжатом состоянии, относятся к 1975г (Ф. Винтерберг [7] и Г. Аскарьян и В. Намиот [8]). В книге А. Кострицы [9] качественно исследуется поведение нейтронного импульса в изотропно сжимаемой  среде U235 или U238. Однако о развитии цепной реакции в этих случаях говорить не приходится по причине очень малой продолжительности пребывания вещества в состоянии, когда его плотность в сотни раз превышает естественную. Рассматриваемая в данной работе гибридная мишень, обеспечивающая подсветку быстрыми нейтронами внешнего (по отношению к зоне термоядерного горения) слоя из делящегося вещества, существенно меняет точку зрения на использование таких микрокритических масс (порядка 1-100 мг). Даже короткая (в несколько поколений) цепная реакция в течение времени термоядерного горения мишени способна дать энерговыделение, сопоставимое с энергией синтеза, т.е. коэффициент усиления мишени может быть значительно повышен. Кроме того, рассматривая мишень как возможный источник полезной энергии, можно предположить, что относительно безопасная утилизация такого ядерного топлива как U238 расширит временной горизонт энергетической безопасности.

Поскольку спонтанное деление не играет роли в рассматриваемых процессах, то учитывать движение среды для расчета достижения критических плотностей вещества не нужно. Под критическим в данной работе понимается такое состояние вещества, когда коэффициент размножения нейтронов становится больше единицы (хотя сама цепная реакция может быть и затухающей, т.е. количество вторичных нейтронов в последующих поколениях уменьшается). Это возможно из-за того, что начальные нейтроны получаются от термоядерной реакции и почти все они моноэнергетические с энергией 14,1МэВ, а не имеют распределения, характерного для спектра деления. Указанные особенности важны при проведении качественного анализа процессов ядерно-термоядерного микровзрыва, чем по существу и является «горение» гибридной микромишени.

2. Качественная оценка параметров DT-плазмы.

Существуют три характерных безразмерных величины, которыми определяется качественное поведение плазмы:

а) параметр идеальности классической плазмы 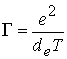, показывающий отношение энергии кулоновского взаимодействия зарядов, находящихся на среднем расстоянии  друг от друга, где  есть длина Вигнера-Зейтца 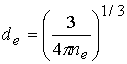  (в сантиметрах), и тепловой энергии движения;

б) параметр, характеризующий влияние релятивистских эффектов ;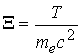

в) квантовый параметр 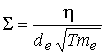, показывающий отношение длины волны Де-Бройля частицы плазмы к длине Вигнера – Зейтца. Для проведения качественных оценок необходимо сначала определить область изменения вышеуказанных параметров.

2.1. Оценка значимости квантовых эффектов. При адиабатическом сжатии DT-газа его температура меняется по закону 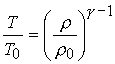, что для идеального газа с показателем адиабаты  дает . Поскольку же , то величина  в квантовом параметре  не зависит от , т.е. роль квантовых эффектов в процессе сжатия будет постоянной. Для начальной температуры DT-газа 1K имеем для электронов (для ионов значение  на два порядка меньше) . Таким образом, электронный газ является существенно квантовым. Ионная DT-плазма при 1K имеет значение параметра , т.е. квантовые эффекты, вообще говоря, надо учитывать, но в первом приближении можно использовать классические формулы.

2.2. Оценка значимости релятивистских эффектов. Поскольку , то энергия движения электронов плазмы будет сравнима с энергией покоя при температурах, существенно превосходящих 100keV. В этом случае величина поправок на релятивизм не превышает 20%. В первом приближении можно ограничиться нерелятивистским рассмотрением, а в следующих приближениях использовать, например, слаборелятивистское уравнение Власова [13]. Характерное время протекания процессов в плазме определяется плазменной частотой

                                             [с^-1].

Поэтому, если характерные времена изучаемых процессов для электронов меньше либо по порядку величины совпадает с  нс (а для ионов на два порядка меньше), то можно использовать для описания плазмы на малых временах линеаризованное уравнение Власова, для которого, как показано в [13], слаборелятивистские поправки отсутствуют. Таким образом, классическое рассмотрение в первом приближении можно считать достаточным.

2.3. Оценка идеальности плазмы. Поскольку , то с ростом плотности параметр  уменьшается, т.е. плазма становится все более идеальной. Следовательно, в первом приближении можно считать ее идеальным газом.

         Основные предположения, упрощающие последующие оценки: U, DT считаются идеальным газом с показателем адиабаты ; цилиндр остается идеально круглым во все моменты времени; разные вещества в процессе сжатия не перемешиваются; нейтроны рассматриваются в одногрупповом приближении (быстрая часть спектра).

3. Оценка энерговыделения в зависимости от степени сжатия мишени.

         3.1. Критическая плотность.

Рассматривается U238, для которого, в отличие от U235, критический размер отсутствует (т.е. в бесконечной среде нейтронный импульс затухает). Критическим размером для U238 в задаче о горении гибридной микромишени будем называть толщину цилиндрического слоя уранового пушера, при которой средняя хорда объема слоя равна длине пробега деления для быстрого нейтрона. Более точно: условие критичности в нашем случае означает, что среднее расстояние, проходимое нейтроном с энергией выше порога деления 1,4МэВ от произвольной точки внутренней границы рассматриваемой области до ее внешней поверхности, равно длине пробега, на которой после деления, поглощения с испусканием фотона, (n, 2n)- реакции и неупругого рассеяния остается ровно один нейтрон в том же энергетическом диапазоне. Другие нейтронно-ядерные реакции в работе не рассматриваются в силу их относительной малости.

Приведем значения сечений взаимодействия нейтронов для U238 (и для сравнения U235) [10]:

Таблица 2. Значения сечений для нейтронных процессов (барн):

Здесь  - сечение упругого рассеяния, - сечение неупругого рассеяния, - сечение захвата с испусканием -кванта, - сечение деления,  - сечение реакции захвата нейтрона с последующим испусканием двух нейтронов. Для конечного полого цилиндра высотой  и радиусами  и  среднюю хорду приближенно оценим как

.                                                             (3.1)

Будем считать, что за одно упругое столкновение энергия нейтрона изменяется незначительно, а при неупругом столкновении нейтрон выходит из быстрой группы и не участвует в дальнейшем рассмотрении, т.к. сечение деления для U238 падает на три порядка при приближении энергии нейтрона к порогу деления (1,4МэВ). Поскольку порог реакции (n,2n) для U238 равен 6,7 МэВ, то в среднем один из двух новых (n, 2n)-нейтронов может участвовать в последующем делении. Далее, для 14-мэвных нейтронов, производящих деление, средняя энергия нейтронов деления в первом поколении равна 7,1 MэВ, поэтому приблизительно 0,8124 из родившихся нейтронов деления пригодны для дальнейшего деления (имеют энергию выше 1,4МэВ). Тогда качественное условие на критическую концентрацию урана  есть

.                                                              (3.2)

Концентрация вещества в пушере на единицу длины есть

.

Число нейтронов, рождаемых от деления урана 14-мэвным нейтроном, оценивается по формуле [10]

,                                                                                               (3.3)

где энергия  выражена в [МэВ], т.е. в нашем случае 4,515. Подставляя в (3.2) данные таблицы 2, получаем условие критичности на быстрых нейтронах для полого цилиндра:

,                                                                               (3.4)

где  выражена в граммах, а радиус – в сантиметрах. Т.к. толщина пушера много меньше радиуса , то приближенно можно считать, что , и тогда . Это условие означает, что, например, для массы пушера в 1 мг при заданном начальном значении радиуса  критический радиус внешней оболочки равен приблизительно 0,25 микрон, т.е. сжатие по радиусу должно быть порядка 4000. Мы не будем обсуждать здесь достижимость таких величин сжатия, т.к. нас интересуют теоретические оценки максимально возможного энерговыделения для рассматриваемой конструкции мишени. Если такой «условно-критический» размер не достигнут, энерговыделение в уране существенно снижается. Соответствующие оценки сделаны ниже.

3.2. Время развития цепной реакции.

Время развития цепной реакции в уране определяется временем «пробега деления» быстрого нейтрона, имеющего скорость порядка см/с:

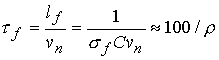   [нс].                                                                (3.5)

Например, если плотность среды порядка 50 000 г/см³, то время пробега нейтрона деления до инициирования им следующего деления порядка 2 пс.

Оценим длину цепи реакции деления U238 на быстрых нейтронах, основываясь на данных о спектре деления с учетом сдвига его в быструю область. От одного первичного нейтрона с энергией 14 МэВ получается в среднем 2,4 быстрых нейтрона с энергией около 7 МэВ. Каждый  из них порождает в среднем еще 1,5 быстрых нейтрона с энергией около 4,5 МэВ. В свою очередь, эти нейтроны дают еще 1,1 нейтронов с энергией в окрестности пика спектра деления, после чего (в четвертом поколении) количество вторичных нейтронов, способных вызвать деление U238, становится меньше 1 и цепная реакция затухает. С учетом уменьшения сечения деления вблизи порога получается приблизительно 3 поколения нейтронов деления с энерговыделением 170 МэВ на деление. Таким образом, если достигнута критическая плотность, то энерговыделение в пушере примерно в три раза больше, чем просто в сжатом состоянии. Отметим, что уже само цилиндрическое сжатие повышает эффективность деления по сравнению с плоской геометрией, где сжатие в этом смысле роли не играет. Здесь концентрация ядер растет обратно пропорционально квадрату радиуса, поэтому с ростом сжатия длина пробега деления убывает быстрее, чем характерный размер. Однако небольшие сжатия все-таки мало эффективны, т.к. при этом энерговыделение увеличивается на проценты, а не в разы, как при достижении критической плотности.

Покажем, что наличие нейтронов от спонтанного деления U238 не влияет на рассматриваемый процесс. Действительно, поскольку U238 имеет период полураспада  лет, то постоянная полураспада равна  с^-1. Таким образом, за 1 секунду в 1 грамме U238 произойдет всего  распадов. Это означает, что вклад спонтанного деления на временах порядка нескольких долей наносекунд отсутствует.

3.3. Время разлета пушера.

Время удержания вещества в сверхсжатом состоянии есть величина порядка , где  – характерный размер, а  –  скорость звука. В приближении идеального газа

 , 2,3·10⁵ см/с, г/см³.                                            

Тогда имеем

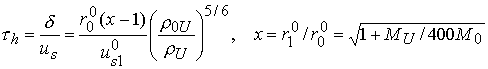.                (3.6)

Таким образом, время эффективного удержания уранового пушера в критическом состоянии убывает в зависимости от степени сжатия как .  Поскольку  характерное время развития цепной реакции  в (3.5) убывает с ростом плотности как , т.е. быстрее, чем , то увеличение сжатия пушера всегда способствует увеличению образования следующих поколений нейтронов:

.

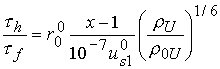Для значений параметров, приведенных в таблице 1, и при степени сжатия по плотности порядка 10⁴ численная оценка дает 1. Следовательно, при большем сжатии вторичные нейтроны деления могут успеть провзаимодействовать с веществом пушера, а при меньшем успевает произойти только первичная реакция деления на собственно термоядерных нейтронах.

3.4. Время горения DT-топлива.

Оценим величину источника термоядерных нейтронов. В эквимолярном приближении (- концентрация DT) , так что уравнение горения DT-топлива без учета изменения концентрации вследствие разлета мишени есть [11]

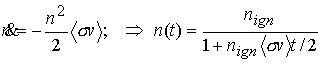,                                                    (3.7)

где - концентрация DT в момент загорания. Это уравнение качественно верно отражает процесс выгорания на временах, меньших характерного гидродинамического времени прохождения поперечного возмущения через мишень, а при больших временах реакция уже практически не идет (мишень разлетелась). Поэтому такое приближение вполне адекватно для качественного анализа. Скорость звука в DT до начала сжатия оценим величиной см/с. Тогда время горения  можно определить как характерное время удержания плазмы, которое по порядку величины равно отношению радиуса цилиндра к скорости звука в плазме:

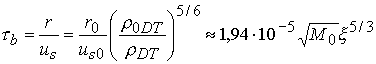     [с].                               (3.8)        

Для получения численной оценки количества выгоревшего DT-топлива положим в (3.7) среднюю скорость реакции синтеза равной см³/с. Тогда коэффициент эффективности выгорания DT-топлива равен

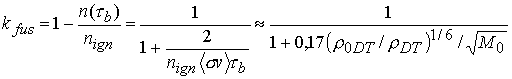.           (3.9)

В частности, при  и  получаем .

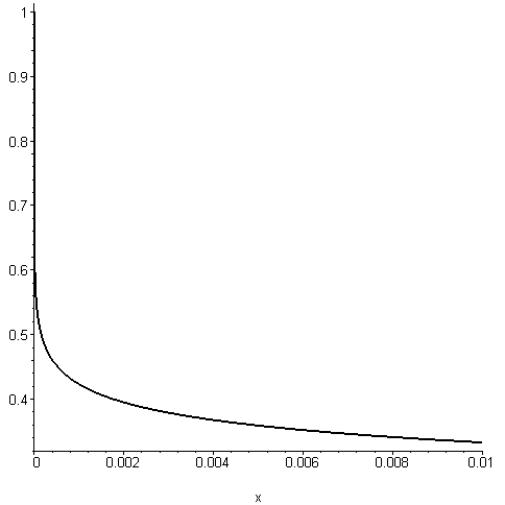
Рис. 1. Зависимость коэффициента выгорания DT-топлива от степени сжатия .

Энерговыделение в результате синтеза составляет

   [МДж].                                                                  (3.10)

Так, для примера выше получаем  [МДж]. Из (3.10) следует, что чем больше , тем, естественно, больше и энергия, выделившаяся в DT при одном и том же сжатии. Однако надо учесть, что с возрастанием массы топлива возрастает и энергия, необходимая для его сжатия. Будем предполагать, что массы пушера и абсорбера оптимизированы по гидро-кпд [12] преобразования энергии драйвера в кинетическую энергию коллапсирующей оболочки (приблизительно 20%). Если считать, что вещество пушера и DT-топлива движется с одной скоростью, то кинетическая энергия делится между ними  пропорционально отношению масс. В частности, для данных таблицы 1 следует, что в сжатие DT предается не более 1% энергии драйвера.

Пусть  – первоначальная энергия драйвера, вкладываемая в мишень. Тогда непосредственно на сжатие DT идет приблизительно  первоначальной энергии. Предположим, что сжатие адиабатическое. Т.к. температура при этом растет не очень сильно (как ), то электроны в процессе сжатия считаем связанными и давление электронного газа не учитываем. Тогда уравнение состояния DT есть , где 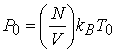. Численное значение постоянной в уравнении адиабаты  равно . Отсюда получаем связь между энерговложением и степенью сжатия  в выражении (3.9) для эффективности выгорания:

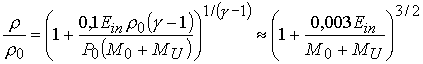.                            (3.11)

Поскольку выражение в скобках в (3.11) много больше единицы, то приближенно можно считать, что

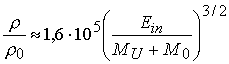,                                                                      (3.12)

где  – в МДж, а масса – в граммах. Подставляя (3.12) в (3.9)-(3.10), получаем коэффициент усиления в термоядерной реакции:

.                         

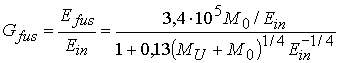Через степень сжатия  коэффициент усиления выражается так:

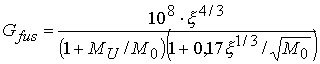.                                                  (3.13)  

Заметим, что  должна быть достаточна для достижения критерия Лоусона зажигания DT [10] (см. также [14]):  [г/см²]. Поскольку при цилиндрическом сжатии , то из (3.12) получаем, что

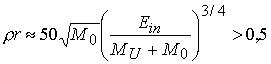.                                                             (3.14)

Это означает, что степень сжатия ограничена сверху:

.                                                                                        (3.15)

В частности, минимальное сжатие для базовой мишени . При этом температура также должна быть достаточной для начала реакции синтеза (приблизительно 10 кЭв или 10 млн. градусов). Непосредственно в адиабатическом сжатии такая температура может быть достигнута только при , поэтому для зажигания DT требуется дополнительная энергия (например, в виде ударной волны, генерируемой в конечной фазе сжатия отходом энерговложения от безударного профиля). Необходимую энергию можно оценить по теплоемкости идеального газа , так что получается приблизительно 0,1 МДж. Эта энергия того же порядка, что и работа на сжатие DT.

Для  МДж из (3.13) получаем . Улучшение этого показателя может быть получено за счет энерговыделения в зоне пушера.

3.5. Поток нейтронов, входящих в пушер.

Как уже говорилось, для эффективного деления урана в пушере требуются только достаточно быстрые нейтроны. Оценку соответствующей доли нейтронов можно получить из численного решения стационарного решения уравнения переноса в многогрупповом приближении по коду MCNP: эффективное сечение выхода нейтронов из быстрой группы оказывается равным (барн). Тогда доля быстрых нейтронов, выходящих из области горения DT и входящих в урановый пушер, равна

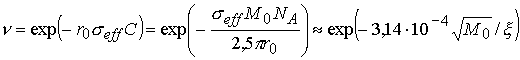.       (3.16)

Поток нейтронов, входящих в пушер, определяется скоростью горения DT. Поскольку в модели (3.7) изменение объема эффективно учтено через время горения , то уменьшение концентрации отвечает уменьшению фактическому числа ядер . Поток рождающихся нейтронов есть

,

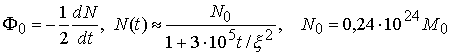 – степень радиального сжатия. С учетом ослабления потока нейтронов (3.16) получаем поток нейтронов, входящих в пушер:

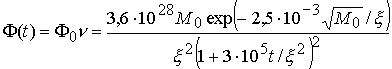       [н/с].                 

Для качественных оценок удобнее исходить из среднего числа нейтронов, рожденных за время реакции :

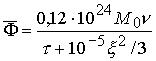.                                                                                     (3.17)

В частности, средний поток нейтронов за время горения  есть

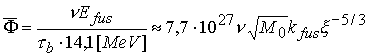    [н/с].                            (3.18)

Таким образом, сжатие DT в определенном смысле конкурирует с последующим энерговыделением в уране: чем сильнее сжато DT-топливо, тем больше в нем энерговыделение, и, соответственно, число рождающихся быстрых нейтронов, но с ростом плотности число нейтронов, выходящих из зоны DT, уменьшается. Следовательно, существует некоторая оптимальная степень сжатия для получения как максимального энерговыделения в зоне пушера, так и максимального суммарного энерговыделения в мишени в целом, а также максимального коэффициента усиления мишени и ее отдельных слоев.

3.6. Энерговыделение в пушере. 

Сравнивая времена протекания процессов горения DT и разлета U (3.6) и (3.8) видим, что если , то определяющим для выделения энергии в уране является время протекания DT-реакции, поскольку тогда все термоядерные нейтроны пройдут через сжатый пушер. Напротив, если , то энерговыделение в уране определяется в основном временем разлета пушера. Имеем

.                                             

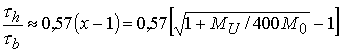Отсюда следует, что длительность горения DT становится определяющим фактором для деления урана в пушере при , т.е. . В противном случае энерговыделение в уране определяется временем разлета пушера. Пусть  - концентрация урана. Тогда

МэВ.                                   (3.19)

Здесь  – некоторое эффективное время деления урана с учетом возможной цепной реакции,  – соответствующее среднее значение потока нейтронов за это время, согласно (3.17). Сечение деления берется для быстрой области (таблица 2). Из (3.4) следует, что для достижения критического размера пушера требуется сжатие

.                                                (3.20)

Таким образом, если , то . Если же критический размер пройден, то в течение времени разлета пушера  реализуется, как было оценено выше, короткая цепь в три поколения нейтронов. Далее надо учесть, что при  14-мэвные нейтроны продолжают взаимодействовать с расширяющимся пушером, но уже без развития цепной реакции. Будем считать, что концентрация меняется по закону изэнтропического разлета идеального цилиндра: . Тогда среднее значение концентрации на интервале времени  равно , а среднее значение толщины пушера . Предположим далее для простоты качественной оценки, что U и DT сжимаются в одинаковой степени. Тогда отношение плотностей (до и после сжатия) в мишени есть  (см. формулу (1.2)). Используя (3.8), (3.12) и (3.17), а также учитывая, что , получаем из (3.19) для энерговыделения в уране:

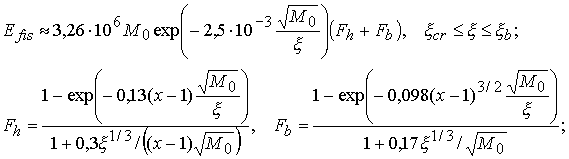
                                                                                                                        (3.21)

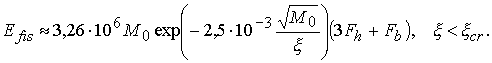
Энерговыделение в (3.21) выражено в МДж. Для базовых параметров рассматриваемой мишени , . Из (3.21) следует, что энерговыделение в пушере определяется тремя параметрами: массой DT-топлива, аспектным отношением пушера и степенью сжатия мишени. Относительный вклад составляющих  и  в (3.21) различен для разных степеней сжатия. При  для базовой мишени отношение  равно . Однако оно монотонно растет с убыванием  (т.е. с увеличением степени сжатия), асимптотически стремясь к 1, поэтому пренебрегать  нельзя, если мы хотим рассматривать асимптотику предельных сжатий. При относительно слабом сжатии  монотонно растет с уменьшением  и ее значения для первого равенства в (3.22) заключены между 10 и 40 [МДж]. Интерес представляет случай больших сжатий (). В этой области имеется максимум энерговыделения (приблизительно 1280 МДж) при сжатии до  по радиусу.

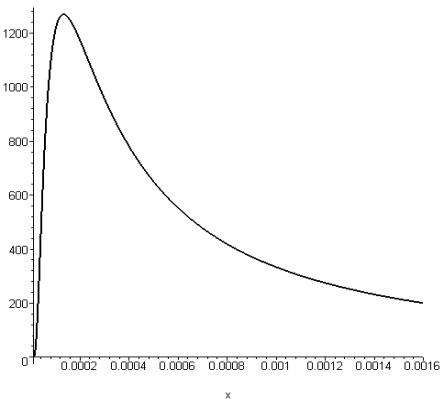
Рис.2. Зависимость энерговыделения в пушере [МДж] от степени сжатия мишени для параметров из таблицы 1.

Оценим степень сжатия  в зависимости от толщины пушера, при которой достигается наибольшее энерговыделение в уране. Поскольку слагаемые  и  в (3.21)  содержат медленно меняющиеся множител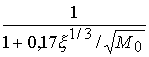и – и 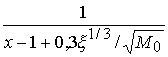, то их можно считать постоянными с характерным отношением первого ко второму порядка 0,3. Далее, т.к. рассматриваем сильные сжатия, то после вычисления производной  учтем, что  при . Тогда для функции , дающей максимум энерговыделения, получаем приближенное аналитическое выражение:

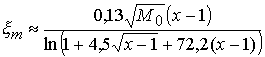.                                                              (3.22)

Подстановка в (3.22) параметров мишени из таблицы 1 дает значение , т.е. величину, достаточно близкую к максимуму на Рис.2.

Из (3.10), (3.21) получаем, что коэффициент усиления энергии синтеза в пушере при малых сжатиях есть

.                          

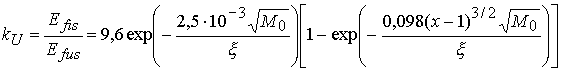В области изменения параметра  с уменьшением  он монотонно растет от 0,05 до 0,25. Следовательно, при малых сжатиях эффект от деления урана незначителен. При больших сжатиях  ведет себя почти так же, как и  на Рис.2:

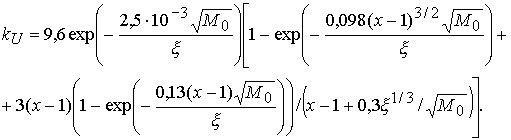          (3.23)

Максимум коэффициента усиления пушера определяется выражением (3.22). Значение  при максимальном энерговыделении в уране зависит только от отношения массы DT-топлива к массе урана (т.е. от аспектного отношения пушера) и растет почти линейно с увеличением доли урана в мишени. Для значения  имеем .

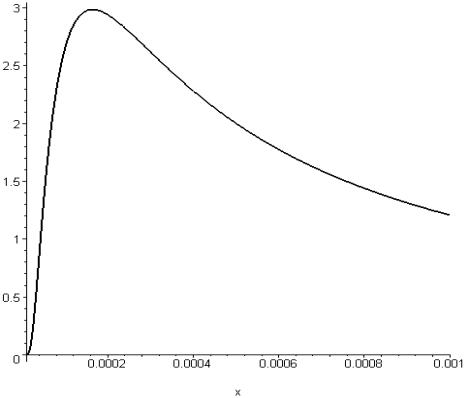
Рис.3. Зависимость усиления энергии синтеза в пушере от степени сжатия мишени для параметров из таблицы 1.

         3.7. Эффективность выгорания пушера.

Для оценки эффективности выгорания пушера надо разделить число актов деления  на число ядер урана . При малых сжатиях имеем

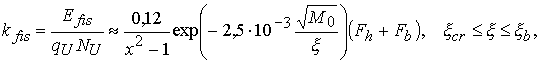    (3.24)

где  и  определены в (3.21). Эта функция монотонно убывает до нуля при  (пушер становится все более тонким) и монотонно растет при фиксированном   с увеличением сжатия. Для базовой мишени  изменяется от 0 до 0,02 с увеличением сжатия до величины . Следовательно, сжатия без достижения критичности неэффективны.

При больших сжатиях имеем

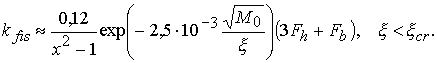                          (3.25)

Максимум  по , как и для  , определяется выражением (3.22). Подставляя (3.22) в (3.25), получаем довольно громоздкую, но все же явную функцию . Ее график приведен на Рис.4. Она имеет максимум, равный примерно 0,18 при толщине пушера, определяемой значением :

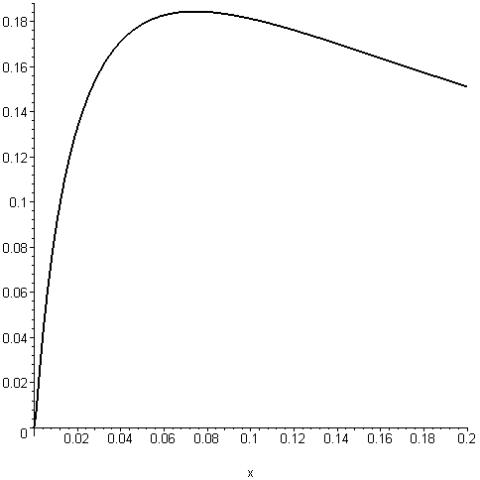
Рис. 4. Зависимость доли выгорания пушера от аспектного отношения.

Таким образом, максимальная утилизация U238 в рассматриваемой схеме составляет 18%. Соответствующее сжатие составляет . Заметим, что для базовой мишени толщине  отвечает оптимальное сжатие   и почти тот же самый коэффициент . Это означает, что в этом смысле мишень хорошо оптимизирована. Поэтому увеличение энерговыделения в уране для мишени из таблицы 1 означает фактически увеличение степени сжатия, т.е. увеличение энергии драйвера до максимально возможных величин. Однако увеличение энергии драйвера приводит к снижению суммарного усиления мишени. Оптимизация этого основного показателя эффективности оценивается ниже.

3.8. Оптимизация суммарного усиления мишени.

Суммарное энерговыделение в мишени есть

.                                                                (3.26)

Коэффициент усиления мишени в целом равен

.                                                                                       (3.27)

Он зависит от трех параметров: исходной вложенной энергии , массы DT  и массы U . Коэффициент термоядерного усиления  монотонно убывает с ростом степени сжатия согласно (3.13), а  имеет максимум, определяемый приближенно выражением (3.22). Для анализа удобно использовать вместо  отношение  из (1.2), а вместо  степень сжатия , т.к из (3.12) следует

  [МДж].                                       (3.28)

Тогда для малых сжатий получаем

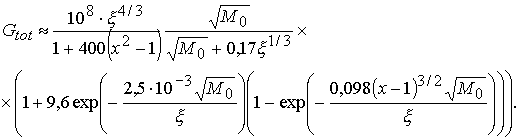         (3.29)

Видно, что при , т.е. при , усиление мишени, как и должно быть, стремится к нулю. Справа предел изменения степени сжатия  ограничен минимально возможной энергией, при которой выполняется критерий зажигания (3.21): . При больших сжатиях  в формуле (3.27) для коэффициента усиления определяется более сложным выражением (3.23). Вид функции  для базовой мишени показан на Рис.5. В силу наличия множителя  полный коэффициент усиления уменьшается с ростом сжатия, т.е. с увеличением энерговложения эффективность мишени в целом падает. Это естественно, т.к. вклад от цепной реакции в пушере для U238 ограничен длиной цепи (3 поколения) и не растет с ростом сжатия.

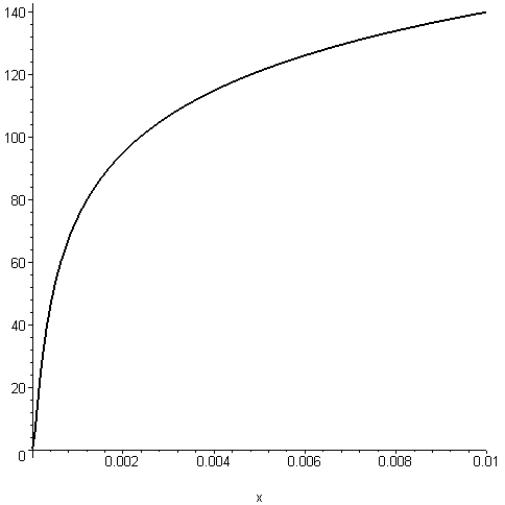
Рис. 5. Зависимость полного усиления базовой мишени от степени сжатия.

4. Учет эффекта дожатия DT.

В предыдущем рассмотрении не был учтен эффект дожатия DT-топлива при энерговыделении в уране. Этот эффект может быть весьма существенным и представляет важную особенность данной мишени: ядерная и термоядерная реакции взаимно усиливают друг друга. Строгое рассмотрение, как уже говорилось выше, требует совместного решения уравнений гидродинамики и уравнения переноса нейтронов в движущейся среде, что является сложной вычислительной задачей. Для качественного анализа этого эффекта будем, как и в п.3, исходить из уравнения выгорания в виде (3.7), но введем поправочный член на увеличившуюся степень сжатия DT. Такой подход оправдан тем, что фактически энерговыделение в пушере представляет собой дополнительную энергию, препятствующую слишком быстрому разлету DT, т.е. идущую на увеличение времени термоядерного горения. Поскольку же степень выгорания  растет с ростом сжатия, то увеличение времени термоядерного горения можно интерпретировать как соответствующее эффективное увеличение плотности DT. Заметим здесь, что для рассматриваемой мишени нет эффекта дожатия уранового пушера при разлете DT-плазмы, т.к. время ее горения превышает время разлета пушера, а время горения в данной модели и есть время, за которое ударная волна разлета достигает границы DT-топлива. Одновременно это означает, что обратного воздействия изменившегося потока нейтронов на урановый пушер нет, т.к. время, в течение которого дополнительное энерговыделение приведет к сжатию DT, и есть фактически время разлета пушера, после чего доля ядерной составляющей резко снижается. Тогда действие на DT энерговыделения в уране приближенно может считаться увеличением исходного энерговложения  на величину, пропорциональную :

.                                                                                 (4.1)

Здесь  и  по-прежнему определяются формулами (3.23), (3.13). Имеем

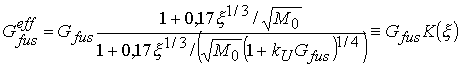.                      (4.2)

Этим выражением определяется теперь вклад от термоядерной реакции. В частности, для примера, приведенного в п.3 , получаем  при дополнительном энерговыделении в пушере . Доля ядерной составляющей остается прежней (3.24)-(3.25). С ростом сжатия эффект ядерного усиления растет, приводя к фактору порядка 2 для коэффициента термоядерного усиления.

         Таким образом, проведенный анализ позволил получить некоторые теоретические оценки эффективности рассматриваемой мишени для инерциального термоядерного синтеза, из которых следует, что урановый пушер может иметь существенное значение для повышения суммарного выхода энергии.

Литература

1. Koshkarev D.G. Charge-Symmetric Driver for Heavy-Ion Fusion. // IL Nuovo Chimento, Vol.106 A, No.11, p.1567-1573. 1993.

2. Koshkarev D.G., Korenev I.L., Yudin L.A. Conceptual Design of Linac for Power HIF Driver. /  CERN 96-05, VI, p.423-426. 1996.

3. Чуразов M.Д., Аксенов A.Г., Забродина E.A. Зажигание термоядерных мишеней пучком тяжелых ионов. // ВАНТ, Сер. Математические модели физических процессов, Вып. 1, №.20. 2001.

4. Сидоров А.Ф. Некоторые оценки  степени кумуляции энергии при плоском и пространственном безударном сжатии. // ДАН. Т.318, №3, 1991.

5. Долголева Г.В., Забродин А.В. Построение решения в задаче движения слоистых оболочек // ВАНТ, Сер. Математическое моделирование физических процессов.1996. Вып. 3. С.27-34.

6. Долголева Г.В., Забродин А.В. Воспроизведение безударного сжатия в оболочечных конструкциях микромишеней. / Препринт ИПМ, № 53, 1999г.

7. Winterberg F. Critical High Density Fission. // Beitr. Plasmaphys., 1975, v.15, No2, p.71-82.

8. Аскарьян Г.А., Намиот В.А., Рабинович М.С. Использование сверхсжатия вещества реактивным давлением для получения микрокритических масс делящегося вещества. // Письма в ЖЭТФ, 1973, т.17, вып. 10, с. 569-572.

9. Кострица А.А. Теория переноса нейтронов в движущейся среде. М.: Энергоиздат, 1981.

10. Физические величины. Справочник. Энергоатомиздат, 1991.

11. Дюдерштадт Дж., Мозес Г. Инерциальный термоядерный синтез. М.: Энергоатомиздат, 1984.

12. Баско М.М. О гидродинамической эффективности облучения ионными пучками. Препринт ИТЭФ №14, 1988.

13. Ю.Н. Орлов, А.В. Тимашева. Решение линеаризованного уравнения Власова в постгалилеевом приближении. Препринт ИПМ РАН, №25, 1990.

14. Д.Г. Кошкарев, Б.Ю. Шарков. Ядерное деление с инерционным удержанием. // Письма в ЖЭТФ. Т.75. Вып. 7. 2002. С. 371-373.

15. А.В. Забродин, Д.Г. Кошкарев и др. Разработка  энергетической установки, сочетающей  процессы  синтеза и деления  на основе микромишеней прямого  действия и мощного тяжелоионного драйвера. / Сб. трудов ЗНЧ, Снежинск, сентябрь 8-12, 2003.