1. Физическая постановка задачи

В работе моделируется взаимодействие продуктов реакции DT-синтеза с первой стенкой камеры и бланкетом термоядерного реактора в рамках концепции FIHIF тяжелоионного синтеза на цилиндрических мишенях. Эта концепция была сформулирована в работах [1-4] и развивалась далее в [5-7]. Специально для нее была предложена конструктивная схема реакторной камеры, в которой происходит микровзрыв, а также общая структура бланкета, поглощающего нейтронное излучение. Описание камеры и первые качественные оценки ее отклика на тепловое и динамическое воздействие термоядерного микровзрыва содержатся в [4-6]. Приведем здесь краткое изложение концепции.

1.1. Тяжелоионный ускоритель. Драйвер формирует и доставляет в точку нахождения термоядерной мишени пучок однозарядных ионов платины с энергией 100 ГэВ. Средняя мощность пучка 0,1 ПВт, длительность профилированного энерговложения 75 нс, полное энерговложение 7,1 МДж. Метод формирования профилированного по времени пучка с необходимыми энергетическими характеристиками был предложен Д.Г. Кошкаревым в работах [1, 2]. Пучок представляет собой тонкостенную трубку внутренним диаметром 0,4 см, получаемую вращением выходящего пучка с частотой  10⁹Гц [1]. Толщина «стенки» трубки (т.е. диаметр пятна пучка) 250 мкм. Этот пучок осуществляет обжатие термоядерного топлива. Для поджига сжатого топлива используется второй пучок мощностью 2 ПВт и длительностью 0,2 нс, поставляющий энергию 0,4 МДж в центральную зону мишени.

Кпд драйвера оценивается величиной 0,25.

1.2. Термоядерная мишень. С тяжелоионным драйвером естественно сочетается мишень с цилиндрической симметрией. Центр радиальной части мишени заполнен эквимолярной DT-смесью, которую окружает свинцовая оболочка. Длина цилиндра (0,71 см) выбирается так, чтобы на этом пути ионы полностью затормозились в материале оболочки. В результате последующего расширения оболочки происходит кумулятивное сжатие центральной зоны (топлива) до достижения параметра  , достаточного для инициирования волны горения путем быстрого поджига топлива. Этот сценарий сжатия был предложен М.Д. Чуразовым, А.Г. Аксеновым и Е.А. Забродиной в [3].

Начальные параметры DT-топлива: плотность г/см³,  радиус цилиндра см, масса мг.

Начальные параметры оболочки: масса однородной свинцовой оболочки г, ее внешний радиус см, плотность  г/см³. Торцы цилиндра закрыты свинцовыми заглушками толщиной 0,45 мм.

1.3. Энерговложение. Драйвер вносит энергию в кольцевой промежуток от 0,19 см до 0,31 см. Из-за эффекта просветления, описанного М.М. Баско в [7], в мишени «полезным образом» поглощается 5,3 MДж. В результате расширения центральной зоны топливо сжимается до значения  г/см², при этом в оболочке достигается  г/см².

1.4. Энерговыделение. Согласно расчетам [7], полное энерговыделение в рассматриваемой мишени составляет 750 MДж, т.е. коэффициент усиления мишени приблизительно равен . Распределение энергии между продуктами синтеза следующее:

- Рентгеновское излучение – 17 MДж.

- Осколки мишени (ионы) – 153 MДж.

- Нейтроны – 580 MДж.

Поскольку «теплосодержание» DT-топлива равно 340 МДж/мг, то выгорание мишени в этом варианте составило 39%. Изменение энерговыделения во времени представлено на Рис. 1.

Рис.1. Временной профиль энерговыделения в мишени. Данные [7].

         Эти данные являются исходными для постановки задачи о тепловом и динамическом отклике первой стенки камеры и бланкета реактора на микровзрыв. Требуется описать следующие процессы: испарение жидкой пленки, защищающей первую стенку, под действием поглощенного в ней рентгеновского излучения; импульс отдачи, идущий внутрь бланкета; дополнительный нагрев образовавшегося «пара» в камере при торможении в нем осколков мишени; последующую конденсацию и остывание пара; поглощение нейтронов в бланкете; термомеханические напряжения в конструкционных материалах. Качественные оценки по порядку величин характерных значений вышеперечисленных параметров были получены авторами ранее в работах [4-5]. Предположения, в рамках которых оценивался отклик камеры, состояли в этих работах в следующем:

- микровзрыв «мгновенный», т.е. взаимодействие продуктов реакции с материалом камеры описывалось на уровне интегральных характеристик, без описания развития процесса во времени в течение самого взрыва;

- спектр нейтронов рассчитывался по стационарному коду MCNP [8] для некоторого среднего профиля плотности материалов мишени в сжатом состоянии, излучение предполагалось изотропным;

- глубина поглощения рентгеновского излучения определялась для средней энергии излучения, падающего нормально к поверхности;

- разлет осколков (ионов) мишени описывался решением задачи о сферическом разлете в вакууме [9];

- поглощение осколков происходило в модели в «парах» защитной пленки, испаренной поглотившимся в ней рентгеновским импульсом; оценка массы испаренного теплоносителя проводилась по модели, предложенной в проекте HIBALL-II [10];

- конденсация испаренного защитного слоя описывалась в однородном и изотропном приближении т.н. кинетической конденсации [11] без учета процессов теплопроводности в защитной пленке и поглощении излучения внутри камеры.

В настоящей работе мы проведем более детальное исследование отклика камеры. Движение вещества в пленке теплоносителя рассчитывается теперь численно на основе уравнений одномерной гидродинамики с учетом реального широкодиапазонного уравнения состояния свинца [12, 13]. Таким образом, при моделировании испарения защитной пленки под действием рентгеновского излучения в данной работе учтены временной профиль и спектр импульса, а также процессы ионизации и теплопроводности в пленке. Остальные из вышеперечисленных модельных приближений относительно конденсации в камере и воздействия нейтронного потока на бланкет остались без изменений.

         Важнейшим пунктом в оценке работоспособности реактора как энергетической установки является описание взаимодействия рентгеновского излучения с защитной пленкой первой стенки. Этим взаимодействием определяется первоначальная масса испаренного материала защиты, его температура, механический импульс, идущий внутрь стенки. Сложность задачи состоит в том, что в литературе в настоящее время достаточно подробно описано влияние короткодействующего импульса длительностью порядка нескольких наносекунд [14]. У нас, как следует из данных Рис.1, другой случай: интервал действия импульса приближается к микросекунде. За такое время не происходит течение испаряемого вещества, и сам временной профиль импульса влияет на формирование теплового и динамического откликов, что существенно отличается от «мгновенных» воздействий. Разработка физической модели для этого случая, насколько известно авторам, является новой задачей, а создание соответствующего расчетного кода для реального вещества имеет и практическую ценность. Описание расчетного кода и примеры численных расчетов для модели испарения жидкой пленки будут представлены авторами в отдельной работе.

         Развитием оценок [4-6] является также численное определение динамического отклика конструкции бланкета на нейтронный импульс. В данной работе сформулирована  математическая модель, описывающая эволюцию волн напряжений в конструкционных материалах и  давления в теплоносителе, а также распространение тепла в системе «бланкет – стенка корпуса реактора – бетонная защита». В численных расчетах учтены прочность материалов и сжимаемость теплоносителя. Развитие этой модели для описания частотного режима работы реактора и конвективного теплопереноса будет осуществлено в следующей работе.

2. Камера

Опишем кратко общую конструкцию камеры термоядерного реактора. Рассматривается цилиндрический дизайн камеры с тонкой жидкой защитной пленкой, продавливающейся через пористую первую стенку. Этот выбор мотивирован тем, что пленочная защита хорошо отработана в современных высокотемпературных технологиях, а канальная схема аккумуляции нейтронного энерговыделения подробно прорабатывается в установках и проектах УТС с магнитным удержанием [15, 16]. Толщина защитной пленки выбрана равной 2 мм.

В нижней части камеры располагается конденсационная полость, которая обеспечивает достижимость необходимых релаксационных параметров камеры, к которым в первую очередь относятся времена релаксации температуры и концентрации. Такая конструкция является дальнейшим развитием более ранних концепций ИТС, представленных в зарубежных проектах LIBRA [17] и HYLIFE-II [18]. Структура бланкета камеры с канальным многоповоротным движением теплоносителя в основном повторяет вариант, описанный авторами в [4-5]. В данной работе мы добавили две секции с теплоносителем (т.к. мощность микровзрыва по ср. с [5] принята большей в 1,5 раза) и увеличили толщину ванадиевых переборок и корпусной стальной стенки, что было вызвано близостью оценочных величин напряжений к предельным значениям.

Геометрическая конфигурация камеры реактора должна обеспечить компромисс между двумя противоположными требованиями к проведению микровзрыва: минимизации пути транспортировки пучка от фокусирующих магнитов к мишени, и уменьшения поверхностной плотности потока энергии взрыва на стенку камеры. Второе из этих требований, как показывает дальнейший анализ, может быть несколько ослаблено. Критерий минимально допустимого радиуса камеры состоит в том, чтобы под действием рентгеновского излучения испарялась бы, во-первых, не вся защитная пленка; во-вторых, нагружение первой стенки импульсом отдачи при испарении пленки не должно превышать предела упругости конструкционных материалов; в-третьих, время релаксации теплофизических параметров камеры должно быть на порядок меньше интервала вбрасывания мишеней внутрь камеры. Частота микровзрывов в рассматриваемой концепции принята равной 2 Гц.

С целью обеспечения достаточно быстрой конденсации паров область камеры разделена на две части: первая – относительно небольшая, в которой происходит собственно микровзрыв, и объемный поддон, в котором пар конденсируется на распыляемых струях теплоносителя. Радиус камеры принят равным м, высота – 8 м, радиус конденсационной полости – 12 м, ее высота – 8 м. Каналы, по которым течет теплоноситель, выполнены из ванадиевого сплава V-4Cr-4Ti. Стенки корпуса реактора выполнены из стали HT-9. Эти материалы выбраны из-за их высоких прочностных и антикоррозийных свойств [19].

3. Теплоноситель

В качестве теплоносителя берется эвтектика Li₁₇Pb₈₃ при температуре 823K. Этому значению отвечает равновесная концентрация его паров в камере 10¹⁸м^-3 (данные [20]). Температура плавления эвтектики – 507 К. Теплофизические параметры теплоносителя приведены в таблице 1.

Таблица 1. Теплофизические параметры теплоносителя Li₁₇Pb₈₃ [20, 21].

При описании теплопроводности в жидкой пленке учитывается также электронная теплопроводность в ионизованной среде, согласно [22]:

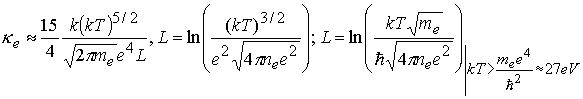(3.1) 

Теплопроводность пара в камере, помимо электронной, имеет также лучистую  и «собственно газовую» составляющие. Последнюю мы возьмем согласно модели газа твердых сфер [22]:

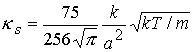                                        ,                                           (3.2)

где  – постоянная Больцмана,  м.

Скорость звука в жидкой пленке оценивается величиной 2000 м/с. Это важный параметр, т.к. он позволяет оценить характерное время, в течение которого отклик пленки можно считать в приближении бесконечного слоя, пренебрегая воздействием собственно первой стенки:

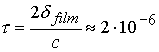                                   с.                                            (3.3)

Поскольку длительность импульса рентгеновского излучения примерно в 3 раза меньше , то в этих условиях допустима упрощенная (как сказано выше) постановка задачи об испарении защитной пленки.

4. Испарение жидкой пленки

         Построим расчетную модель испарения жидкой пленки под действием рентгеновского излучения заданной мощности и температуры. Исходные данные возьмем из расчетов М.М. Баско [7], согласно которым длительность рентгеновского импульса составляет около 700 нс, средняя температура 30 эВ. Тогда средняя поверхностная плотность излучения равна 88 кДж/м². Спектр рентгеновского излучения определяется тепловым излучением горячей плазмы, образующейся в результате термоядерной реакции, поэтому частотное распределение аппроксимируется планковским с некоторой эффективной температурой , которая меняется с течением времени (см. Рис. 2). Пусть  – энергия излучения [эВ]. Тогда

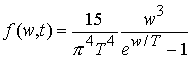                                 .                                                   (4.1)

Максимум распределения приходится на значение энергии , а среднее значение равно . Для первоначальной оценки глубины проникновения излучения в защитную пленку положим, что основная доля имеет энергию  = 115 эВ. Массовый коэффициент поглощения в свинце для такого излучения равен  см²/г [23]. Тогда характерная глубина проникновения излучения равна  [1/м], так что м. Толщина испаренного слоя оценивается в модели [10] как

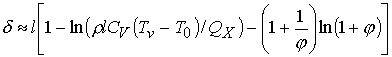                ,                         (4.2)

где  – плотность потока излучения,  – температура кипения теплоносителя,  – его начальная температура, . Для нашего случая получаем м. Температура испаренного слоя оценивается в [4, 5] величиной порядка 8 эВ. Масса первоначально испаренного вещества составляет 1 кг. Для получения более точных результатов следует использовать реальное уравнение состояния вещества и учесть спектр излучения (4.1) при определении характерной глубины проникновения излучения в пленку.

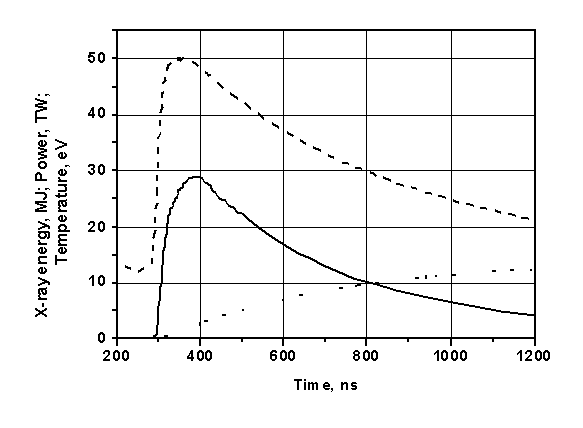
Рис.2. Временной профиль импульса рентгеновского излучения в результате микровзрыва. Пунктирная линия – температура, сплошная линия – мощность излучения, точечная линия – выделившаяся энергия. Данные [7].

Оценим глубину распространения теплового фронта от воздействия горячей плазмы испаренного вещества защитной пленки на оставшуюся часть «холодного» теплоносителя. По данным табл.1 можно определить коэффициент температуропроводности теплоносителя  м²/с. Тогда за время  = 700 нс тепло пройдет внутрь на характерное расстояние м, много меньшее толщины пленки. Волна сжатия пройдет за это время расстояние 1,4 мм, т.е. также не повлияет на поглощение излучения.

Приведем спектральные данные лаборатории NIST о поглощении рентгеновского излучения в среде Li₁₇Pb₈₃ (Рис. 3).

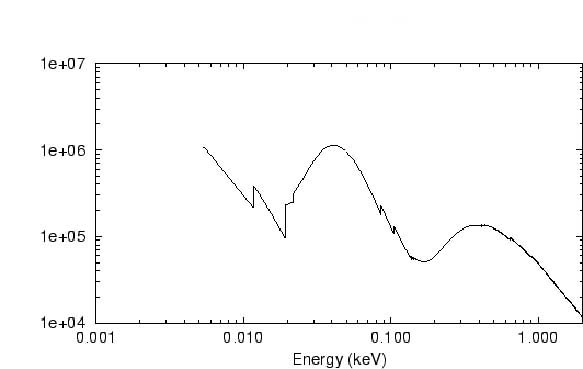
Рис. 3. Обр. длина поглощения [см^-1] нормально падающего рентгеновского излучения в среде Li₁₇Pb₈₃ с плотностью 9,0 г/см³. Данные [24].

         Введем спектральную плотность мощности излучения  на глубине  проникновения в жидкую пленку:

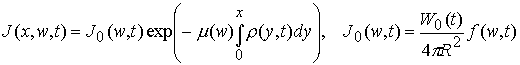.             (4.3)

Первоначальная мощность источника  задана на Рис. 2, функция распределения Планка определяется выражением (4.1). Тогда объемная плотность энерговыделения на глубине  равна

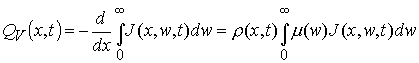.                                   (4.4)

Формулы (4.3), (4.4) описывают поглощение излучения посредством ионизации нейтральных атомов. Характерное время ионизации составляет 5∙10^-17 с, что много меньше длительности импульса . Поэтому можно считать, что коэффициент поглощения  не зависит от времени.

         Ниже на Рис. 4 приведен график объемной плотности поглощенной энергии рентгеновского излучения в защитной пленке. Поглощение излучения внутри камеры на 4 порядка ниже, чем в пленке, в связи с малой плотностью насыщенного пара, но учет этого поглощения важен для правильной постановки граничной задачи об испарении жидкой пленки: температура пара в камере становится тогда того же порядка, что и в слоях пленки, поглотивших излучение, поскольку рост температуры определяется только поглощенной энергией, которая пропорциональна плотности среды. Поэтому естественным граничным условием для проведения детального расчета является отсутствие потока тепла на границе «камера/пленка».

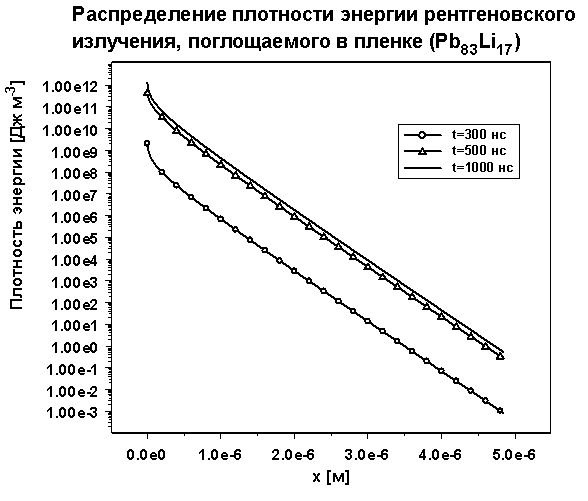
Рис. 4. Зависимость объемной плотности поглощенного излучения в пленке от глубины проникновения в пленку.

Расчетные данные, приведенные на Рис. 4, определяют источниковый член в уравнениях гидродинамики в пленке. Считая излучение сферически симметричным, а пленку – тонкой, ограничимся при описании пленки одномерным плоским случаем. Запишем постановку задачи сначала в эйлеровой форме (см. [25]). Обозначения:  – плотность,  – скорость,  – плотность внутренней энергии,  – давление,  – плотность энтальпии. Коэффициенты вязкости  и теплопроводности  берем из таблицы 1. Коэффициент  определен в (3.1), так что суммарная теплопроводность в пленке определяется коэффициентом .

Записываем уравнения законов сохранения массы, импульса и энергии в виде:

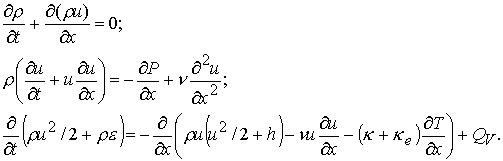                  (4.5)

Начальные условия:

           (4.6)

Здесь 10^-2 Па – давление насыщенного пара в камере,  определяется по соответствующей концентрации 10¹⁸ м^-3. На границе «камера/пленка» приняты условия:

.                                                                                           (4.7)

На «бесконечности», т.е. на границе «пленка/стенка», приняты условия

,                                                                                             (4.8)

а плотность и давление связаны между собой по уравнению состояния, которое мы возьмем из широкодиапазонной модели Медведева [12, 13] для свинца, пренебрегая относительно малым вкладом лития:

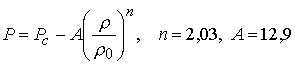ГПа,  г/см³.                         (4.9)

Параметр  (т.н. давление отталкивания) определяется из трансцендентного уравнения как функция температуры и плотности:

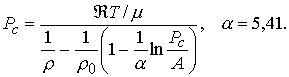                                                              (4.10)

Здесь  – газовая постоянная, а – молярная масса свинца. Ниже на Рис. 5, 6 приведены расчетные изотермы для свинца и кривая насыщения «пар-жидкость» по этой модели.

Учтем в (4.9), (4.10) K-кратную ионизацию согласно [12]. Получаем:

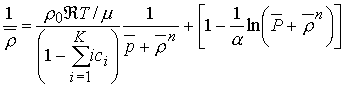,                                                 (4.11)

где ,  – концентрации ионов i-кратной ионизации, которые можно найти (в предположении равновесия) из системы уравнений 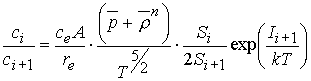,                                                        (4.12)

где  – соответствующий потенциал ионизации, ,  – внутренняя статистическая сумма, .

Давление, Па

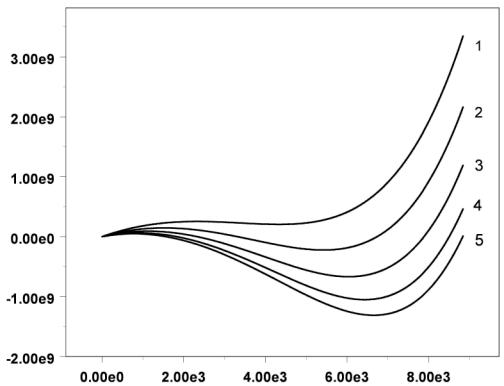Плотн., кг/м³

Рис. 5. Изотермы модели (4.8)-(4.9). Температуры: 1- 6000К, 2- 5000К, 3- 4000К, 4- 3500К, 5- 3000К.

Барическому уравнению состояния соответствует следующее калорическое уравнение состояния:

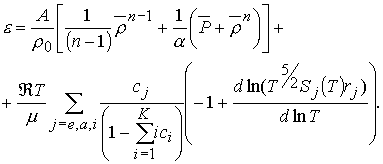                                          (4.13)

Как и выше в (4.11), здесь , только теперь .

В предварительных расчетах мы ограничились однократной ионизацией, первый потенциал ионизации для свинца  эВ.

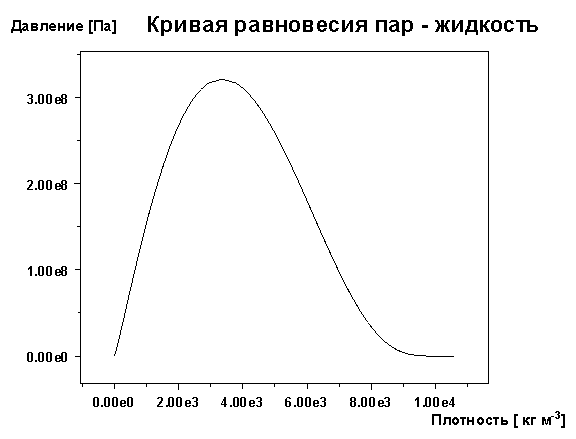
Рис. 6. Расчетная кривая равновесия фаз для модели (4.9), (4.10).

Поставленная задача (4.3)-(4.13) решалась численно в лагранжевых координатах. Обсуждению построенного кода и особенностям решения данной конкретной задачи будет посвящена отдельная работа. Здесь мы приведем только общую постановку задачи и некоторые важные для дальнейшего результаты. Следуя [25, 26], вводится лагранжева координата

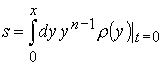                                               ,                                        (4.14)

где n – размерность пространства. Скорость определяется как . Системе (4.5) тогда отвечают уравнения

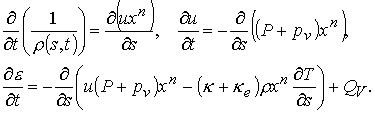                                           (4.15)

Здесь  – диссипативные члены с вязкостью. Начальные и граничные условия модифицируются аналогично.

         Согласно проведенным расчетам, за время действия рентгеновского импульса (700 нс) испарится 1,42 кг жидкой пленки. Средняя температура «пара» 15 эВ, плотность 7∙10^-5 г/см³. Подчеркнем, что эта температура завышена, т.к. не учитывалась многократная ионизация. Испаренный слой имеет внешнюю разреженную корону, нагретую до нескольких миллионов градусов, и внутреннюю часть (вблизи пленки), имеющую температуру около 6000 K. Динамика испарения приведена ниже на Рис. 7.

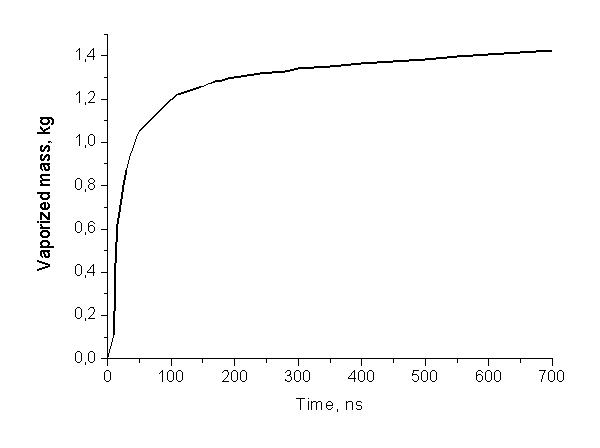
Рис. 7. Зависимость испаренной массы теплоносителя от времени.

Испарение пленки сопровождается также импульсом давления, идущим внутрь камеры со скоростью звука. Расчетное распределение давления в пленке на момент окончания рентгеновского излучения приведено на Рис. 8.

Сделаем также качественную оценку, считая импульс излучения «ступенькой». На нагрев и испарение 1,42 кг теплоносителя требуется, согласно данным табл. 1, около 1,7 МДж. На однократную ионизацию этого количества пара потребуется еще 4,8 МДж, итого – 6,5 МДж. Тогда полная кинетическая энергия пара  будет не больше, чем 17 – 6,5 = 10,5 МДж. Тогда импульс отдачи при испарении будет иметь величину порядка

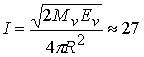                             Па×с.                                            (4.15)

Для оценки соответствующего давления надо взять характерный интервал воздействия. Из Рис. 2 оцениваем его величиной порядка 250-300 нс. Тогда

                                              MПа.                                             (4.16)

Эта оценка, как показывают детальные расчеты (Рис. 8), занижена, т.к. импульс имеет достаточно высокий пик. После воздействия в пленке формируется ударная волна, давление на фронте которой понижается по мере продвижения вглубь. На момент окончания импульса оно равно 250 МПа. Ударная волна прошла к этому времени путь около 1,3 мм, что совпадает с оценкой, приведенной в начале этого пункта.

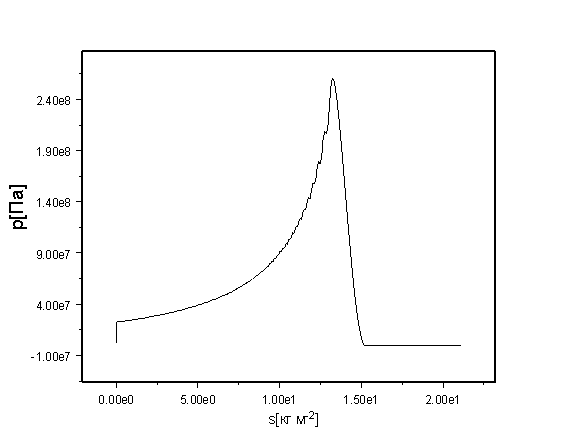
Рис. 8. Распределение давления по толщине защитной пленки на момент окончания рентгеновского импульса. Для перехода от массовой координаты  к физической толщине надо разделить ее на плотность (порядка 10⁴ кг/м³).

         Воздействие ударной волны на стенку SiC оценивается далее в п.7. Эта ударная волна, отразившись от стенки, может привести к разрыву пленки и образованию капель теплоносителя. Количественная оценка этого эффекта выходит за рамки данной работы. Однако можно предположить, что эти капли сыграют положительную роль в ускорении процесса конденсации, т.к. поверхность конденсации в результате этого увеличится. Возможно также, что капли полностью испарятся после того, как температура образованного на первом этапе испаренного слоя теплоносителя еще более возрастет после поглощения в нем осколков мишени.

5. Осколки

Физическая концепция учета влияния осколков термоядерной мишени на первую стенку состоит в нашей работе в том, что за время их прихода перед стенкой успевает сформироваться слой испаренного теплоносителя, в котором и происходит поглощение быстрых ионов мишени. Таким образом, осколки не создают дополнительного механического нагружения первой стенки, а приводят только к увеличению температуры ионизованного пара в камере. Сделаем соответствующие оценки.

Равновесная плотность паров теплоносителя в камере при температуре 823K равна 3,4×10^-10 г/см³, и можно считать, что среда не оказывает влияния на разлет мишени. Тогда время подлета осколков к первой стенке можно оценить по асимптотике (на расстояниях, много больших размера мишени) решения Седова [9] о точечном взрыве в вакууме: скорость фронта осколков м/с, где в данном случае 153 МДж – энергия осколков, а г – масса мишени. Время подлета осколков к первой стенке равно с. Энергия отдельного налетающего иона мишени приближенно равна 75 кэВ. Взаимодействие между потоком ионов и достаточно плотным слоем пара определяется длиной торможения ионов. Оценка тормозного пути по формуле Бете-Блоха [23] дает для этого случая величину

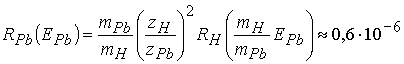г/см².                              (5.1)

Тогда длина торможения равна = 0,05мм. Следовательно, все ионы осколков поглощаются в тонком слое испаренного теплоносителя, передавая ему свою энергию, и не оказывают воздействия непосредственно на жидкую пленку и первую стенку реактора. Поглощение осколков происходит в течение времени около 10^-14с, т.е. практически мгновенно. Считая, что при разлете пар равномерно перемешивается, получаем, что его температура поднимается до  230 эВ = 2,5×10⁶K. Этот горячий ионизованный пар, распространяясь по камере реактора, вызывает дополнительное испарение теплоносителя (как защитной пленки, так и капель, «висящих» в конденсационной полости камеры в распыленных струях и, возможно, в самой камере). Время, в течение которого пар заполняет камеру, оценивается величиной 3∙10^-6с.

6. Конденсация

При описании процессов испарения-конденсации в камере реактора будем считать, что температура пара и его плотность однородны по всему объему камеры, а параметры пара изменяются скачком вблизи жидкой стенки. Ион пара, попавший на стенку или на поверхность жидкой капли, прилипает к ней с некоторой вероятностью . В этом приближении процессы поверхностного испарения и конденсации описываются кинетическим уравнением [11], представляющим собой балансные соотношения для массы и энергии пара. В условиях нашей задачи запишем законы сохранения массы и энергии, учитывая радиационный тепловой поток от горячего пара на стенку реактора (метод повторяет оценки работ [4, 5]):

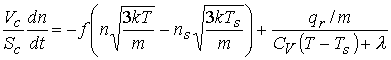,                                         (6.1)

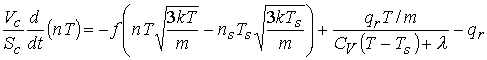,                    (6.2)

                                                                                  (6.3)

Здесь  – плотность потока теплового излучения в полости камеры,  и  – соответственно концентрация и температура пара в камере,  – масса иона пара,  – температура поверхностной жидкой пленки теплоносителя (т.е. 823 К),  – постоянная Стефана – Больцмана,  – поверхность конденсации,  – объем, в котором происходит конденсация, равный объему верхней секции камеры на начальном этапе процесса, и полному объему, включая нижнюю секцию, когда пар распространится по всей камере. Массу теплоносителя, инжектируемого в струях, примем равной 7 тонн на один микровзрыв. Радиус капель в струях положим равным 50 мкм, так что дополнительная поверхность конденсации составит м².

Функция  моделируется эмпирической зависимостью [11]:

         Па;     Па,          (6.4)

 – атмосферное давление. Уравнения (6.1)-(6.3) интегрировались численно при начальных условиях, описанных выше: 2,5∙10⁶ K, 1,5∙10²²м^-3. Результаты расчетов приведены на Рис. 9, 10. Характерное время релаксации температуры составило 0,1 мс, а концентрация достигла значения на линии насыщения через 5 мс, что много меньше периода микровзрывов (0,5 с).

         Обсудим приближения, принятые в данной модели конденсации. Во-первых, в действительности температура пленки в процессе конденсации не остается постоянной, т.к. иначе это означало бы мгновенную передачу тепла внутрь бланкета. На первой стадии разлета горячего пара это приближение оправданно, т.к. система уравнений (6.1)-(6.3) описывает в этом случае не конденсацию, а доиспарение. Однако после снижения температуры в камере до 6000 К (критическая температура свинца) эта модель, очевидно, становится неадекватной. Температуру на поверхности конденсации следует определять из решения сопряженной задачи теплопроводности в жидкой пленке, т.е. считать

.         (6.5)

Такой расчет предполагается сделать в отдельной работе.

Во-вторых, однородное распределение плотности и температуры пара в камере также является весьма грубым приближением. Пока концентрация мала, это приближение можно считать достаточным. Однако в процессе доиспарения масса пара в камере достигает почти 100 кг, и становится существенным влияние лучистой теплопроводности. Расчеты росселандовых пробегов в плазме свинца, выполненные В.Г. Новиковым по программе THERMOS [27] для характерных плотностей и температур нашей задачи, показали, что при плотностях выше 10^-5 г/см³ (а это фактически начальная плотность пара в задаче о конденсации) пробеги становятся меньше размера камеры.

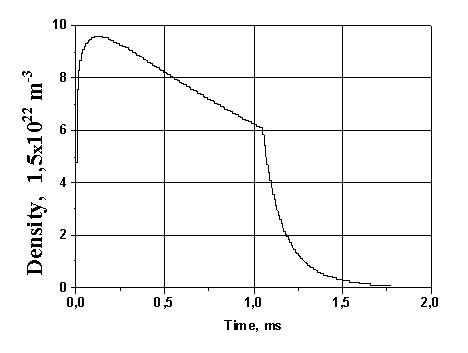
Рис. 9. Зависимость концентрации пара в камере от времени.

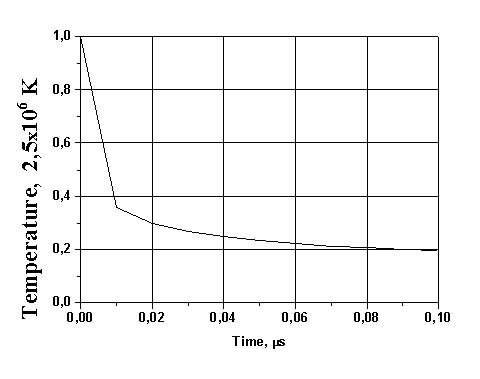
Рис. 10. Зависимость температуры пара в камере от времени.

Следовательно, начальная фаза остывания пара также требует применения более точной модели. Находясь в рамках приближения [11], это можно сделать следующим образом. В правых частях уравнений (6.1)-(6.3) вместо температуры  следует брать температуру , при которой, собственно, и происходит конденсация вещества. В левой части уравнения (6.2) следует использовать среднюю температуру по камере, а радиальное распределение температуры в камере находить из решения уравнения теплопроводности в камере с учетом коэффициента лучистой температуропроводности  [27], который определяется по текущим значениям плотности и локальной температуры.

Таким образом, оптимистические времена релаксации, представленные на Рис. 9-10, являются только первой качественной оценкой процесса и требуют уточнений.

7. Нагружение первой стенки импульсом отдачи

Оценим величину нагружения первой стенки камеры реактора импульсом отдачи паров защитной пленки. Рассмотрим симметричную деформацию тонкой сферической оболочки радиуса м и толщиной см из упругого материала под действием приложенной изнутри поверхностной силы, следуя [28]. Приложенная сила, отнесенная к единице внутренней поверхности оболочки, есть давление  (см. Рис. 8). Снаружи к оболочке прилегает слой жидкости. При смещении  оболочки в радиальном направлении со стороны жидкости на внешнюю поверхность будет действовать давление , где  – плотность жидкости,  – скорость звука в ней. Давление в невозмущенной жидкости считаем равным нулю. Упругая радиальная сила, действующая на единицу внутренней поверхности камеры, равна [28]

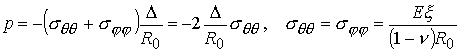.                          (7.1)

Тогда, рассматривая радиальное смещение оболочки, запишем уравнение движения (закон сохранения импульса для единицы поверхности) в виде:

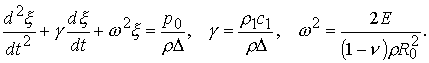                                  (7.2)

Для рассматриваемой пористой стенки из SiC плотностью  кг/м³ модуль Юнга равен [19] ГПа, а коэффициент Пуассона . Тогда оценка частоты собственных колебаний оболочки есть  = 5,7×10³ с^-1, а показатель затухания  с^-1, т.е.  и возмущение апериодически затухает, т.к. все корни характеристического уравнения действительные. Поскольку длительность импульса рентгеновского излучения много меньше, чем 1/, то для определения отклика оболочки на одиночный микровзрыв уравнение движения (7.2) можно приближенно решать с нулевой правой частью, учитывая импульсную нагрузку в виде удельного импульса  в соответствующем начальном условии:

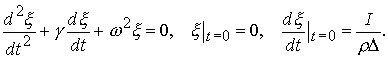                                          (7.3)

Решение уравнения (7.3) имеет вид

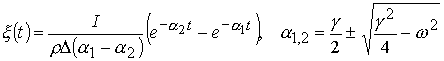.                             (7.4)

Время нарастания смещения до максимального значения  равно

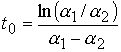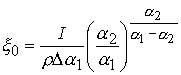,   .                                                        (7.5)

Если , то 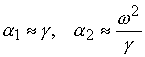, и решение (7.4) примет вид

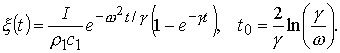                                                     (7.6)

Для рассчитанного в п.4 давления в пленке 250 МПа (Рис. 8) и оценки длительности основного импульса в 300 нс получаем 75 Па∙с.  Тогда:

- время нарастания смещения стенки: 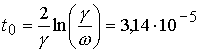        с;

- время затухания смещения стенки: 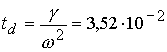          с;

- период собственных колебаний стенки:    с;

- амплитуда смещения первой стенки: 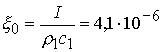        м.

         Эти оценки показывают, что время затухания возмущения в первой стенке на порядок меньше периода проведения микровзрывов. Прилегающий к тыльной стороне стенки слой теплоносителя вызывает сильное демпфирование упругих деформаций. Время нарастания смещения стенки  на порядок больше акустического пробега в стенке и не превышает времени акустического пробега в слое теплоносителя. Поэтому решение (7.11) можно использовать для оценки максимальной деформации сферической оболочки. Время затухания смещения стенки  много больше времени акустического пробега в слое теплоносителя. Отражение акустических возмущений от второй стенки, ограничивающей слой теплоносителя, должно несколько изменить время затухания возмущения первой стенки.

         Максимальные тангенциальные напряжения (7.1) равны

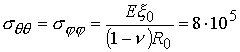Па.                                                                    (7.7)

         Максимальное давление на внешней поверхности первой стенки, контактирующей с теплоносителем, определяется скоростью смещения оболочки в начальный момент времени:

Па.                                                                                       (7.8)

         Предел текучести материала первой стенки из SiC равен Па [19]. Таким образом, напряжения, возникающие при нагружении первой стенки одиночным импульсом отдачи, в 4 раза ниже допустимых значений.

8. Поток нейтронов

         Отклик бланкета реактора ИТС определяется формой и величиной нейтронного импульса от микровзрыва. Расчет потока нейтронов для рассматриваемой мишени был сделан М.М. Баско по программе DEIRA [29].

Средняя мощность нейтронного потока, воспринимаемого первой стенкой, равна 5,7 MВт/м². Из ширины пика нейтронного потока, приведенного на Рис. 11, видно, что эффективное горение мишени длится приблизительно 5 нс. Максимальная плотность нейтронного потока равна 3×10³⁰ н/с.

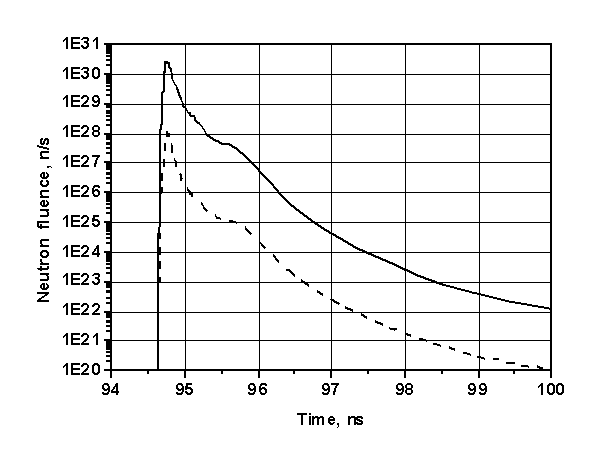
Рис.11. Временной профиль потока нейтронов от микровзрыва. Сплошная линия – 14,1 МэВ, пунктир – 2,45 МэВ.

Детальный расчет нейтронного спектра, выходящего из мишени и воспринимаемого первой стенкой камеры и бланкетом, был проведен по программе MCNP [8] для мишени в сжатом состоянии. Доля 14-мэвных нейтронов в выходящем импульсе 73%, средняя энергия нейтрона – 12,25 MэВ. На основе этого расчета определялось тепловыделение в бланкете.

9. Термомеханический отклик бланкета

Бланкет реактора ИТС упрощенно представляет собой систему нескольких вертикальных коаксиальных круговых цилиндров высотой 8м. Радиус внутреннего цилиндра (собственно камеры) составляет 4м, внешний радиус бланкета – 4,5м. Первая стенка представляет собой пористую керамическую структуру SiC, через которую просачивается теплоноситель, образуя жидкую защитную пленку камеры. Каналы, по которым течет теплоноситель, выполнены из ванадиевого сплава V-4Cr-4Ti. Верхняя и нижняя стенки, как и задняя стенка реактора, выполнены из стали HT-9.

Таблица 2. Структура бланкета и плотность энерговыделения по зонам.

При расчете энерговыделения в бланкете мы исходили из сферически-симметричной модели нейтронного излучения с полной энергией в импульсе 580 МДж (см. п.1). Расчетная область была разбита на три основных слоя (центральный, верхний и нижний, по 17 ячеек в каждом), содержащих всего 51 ячейку, в каждом из которых определялось тепловыделение от фотонов и нейтронов. В таблице 2 приведены значения плотности энергии, усредненной по слоям. Двумерный расчет процесса переноса нейтронов в бланкете по коду MCNP [8] показал, что коэффициент воспроизводства трития (КВТ) для бланкета вышеприведенной структуры равен КВТ = 1,112, а коэффициент усиления M = 1,117. Таким образом, полное энерговыделение за один микровзрыв составляет в данной концепции 818 МДж.

Оценочный расчет напряжений в конструкционных материалах бланкета, возникающих при импульсном тепловыделении, проведен нами в одномерной осесимметричной постановке. Считаем, что в экваториальной плоскости (т.е. в горизонтальной плоскости, проходящей через точку микровзрыва) бланкет представляет собой систему полых цилиндров, промежутки между которыми заполнены теплоносителем (см. Рис. 12). Влиянием концевых зон бланкета, в которых происходит поворот теплоносителя, в одномерном расчёте пренебрегаем. Пренебрегается также изменением энерговыделения по высоте цилиндрической конструкции и принимаются значения плотности энергии по таблице 2.

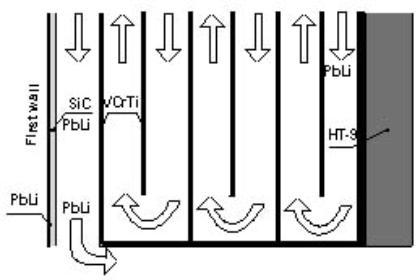
Рис.12. Структура бланкета и схема движения теплоносителя.

Справа от стенки корпуса реактора расположена защита из бетона. Расчётная область включает в себя бланкет со стенкой корпуса (4,0 м ≤ r ≤ 5,2 м) и защиту  (5,2м ≤ r ≤ 7,7м). Свойства первой стенки, представляющей собой пористый карбид кремния, пропитанный теплоносителем Li₁₇Pb₈₇ в весовом отношении 1:1, определялись по смесевым формулам

,     ,     ,

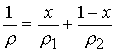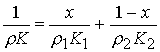,                                                                                             (9.1)

где обозначено:  – объёмная доля 1-го компонента, ,  – плотность, K – модуль объёмного сжатия,  – теплоёмкость,  –теплопроводность. Необходимые для расчетов теплофизические параметры материалов приведены в таблице 3. Модуль сдвига  и коэффициент Грюнайзена  были назначены авторами, опираясь на данные [19].

Таблица 3. Механические и теплофизические свойства теплоносителя и конструкционных материалов камеры. Сводные данные [19, 20, 21, 30].

Для расчетов выбрана лагранжева форма уравнений сплошной среды, описывающих распространение одномерных волн в экваториальной плоскости:

,                      

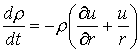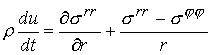 ,                                                                              (9.2)

.                                     

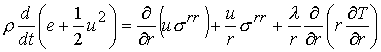Составляющие тензора напряжений представляем в виде , причем  Для компонент девиатора имеем закон Гука:

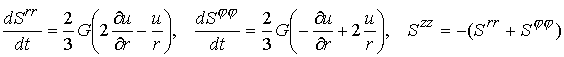.    (9.3)

Давление р определяем по уравнению состояния Ми-Грюнайзена:

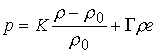,   .                                                              (9.4)

Таким образом, задача о распространении волн напряжений и диффузии тепла замыкается.

При постановке начальных условий учтём, что нейтронное энерговыделение является практически мгновенным (около 5 нс, см. Рис. 11). За это время акустический сигнал проходит расстояние порядка 10мкм,  тогда как характерная глубина энерговыделения составляет 16см (по данным табл. 2). Поэтому нагрев материала бланкета можно считать изохорическим. В начальный момент задается внутренняя энергия  по данным табл. 2, после чего начальное давление определяется из (9.4).

Граничные условия для свободных адиабатических левой и правой стенок имеют вид:

,   при   r = 400 см;  770 см.                                                     (9.5)

Расчет проводился по явной полностью консервативной разностной схеме второго порядка точности. Результаты расчета представлены ниже.

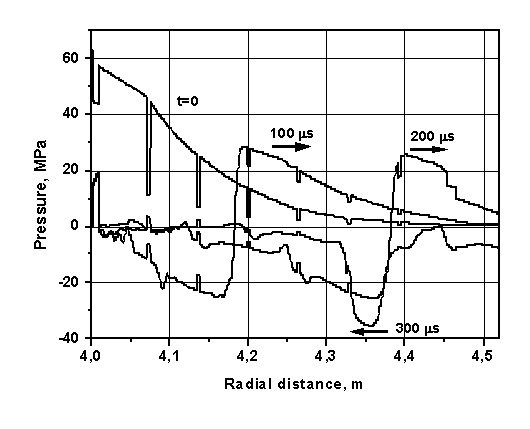
Рис. 13. Профили давления в бланкете и стенке корпуса для различных моментов времени.

Мгновенное энерговыделение приводит к образованию начального профиля давления, показанного на Рис. 13 для момента времени t=0. Общий профиль давления в конструкции отличается большой немонотонностью на участках, где расположены стенки. Положительный профиль давления приводит к формированию волны сжатия, распространяющейся вправо, а разгрузка свободной поверхности порождает волну разрежения, распространяющуюся вслед за формирующейся волной сжатия. Немонотонность профиля давления вызывает генерацию волн более высокой частоты и меньшей амплитуды. Эти волны преломляются на  границах раздела, и волновая картина становится очень сложной. На Рис. 13 профили показаны только для области, включающей бланкет и стенку корпуса (400 см ≤ r  ≤ 452 см).

При использовании лагранжевой схемы представляется естественным следить за напряжённо-деформированным состоянием в выделенных точках, связанных с материалом. Изменение давления в частице материала теплоносителя PbLi, которая в момент времени t=0 располагалась посередине зазора между пористой стенкой SiC и стенкой VCrTi (r = 404 см), показано на Рис. 14. Хорошо прослеживаются волнообмены с частотой примерно 2 кГц и амплитудой до 40 МРа. Эти колебания обусловлены отражениями волны от первой стенки (r = 400 см) и от границы раздела сталь/бетон (r = 452 см). Форма волны хорошо видна на Рис. 13. При отражении от границы раздела сталь/бетон волна, как и следует ожидать, меняет направление и знак амплитуды на противоположные. Именно в этой волне реализуются максимальные (по модулю) значения амплитуд. Эти значения по порядку величины сопоставимы с выбранным пределом текучести для пористого SiC (см. табл.3), хотя и не превышают его. На Рис. 15 видны низкочастотные пульсации, которые соответствуют волнообменам, происходящим в целом в бланкете и стенке корпуса. Видны также высокочастотные пульсации, обусловленные преломлением волн на стенках. Они показывают нагружение и разгрузку первой стенки под действием давления со стороны теплоносителя. Это особенно хорошо наблюдается в течение первых десяти низкочастотных периодов. Видно также, что при мс на основную частоту накладываются промежуточные частоты.

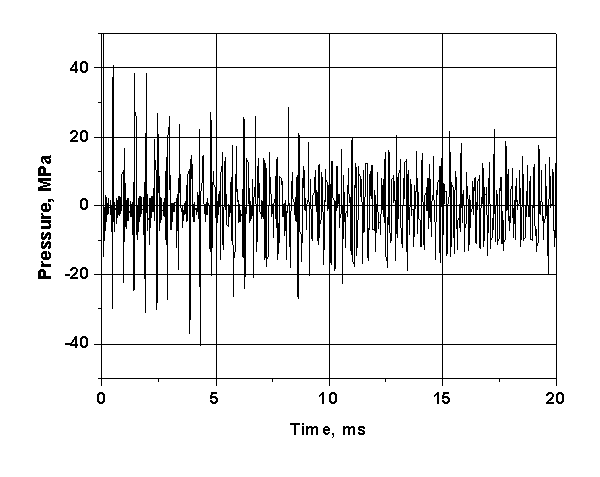
Рис. 14. Давление в теплоносителе между стенками SiC и VCrTi  (r = 404 см).

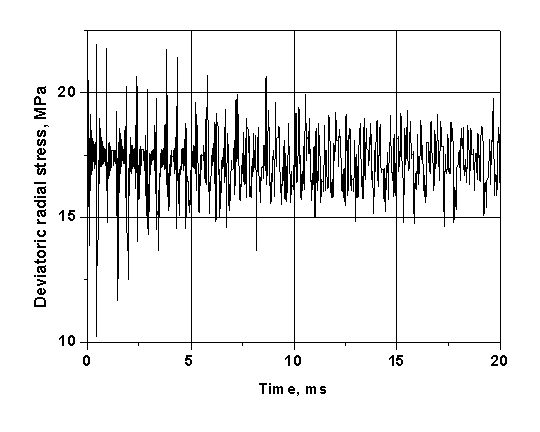
Рис. 15. Радиальное напряжение  в пористой стенке SiC  (r = 400,6 см).

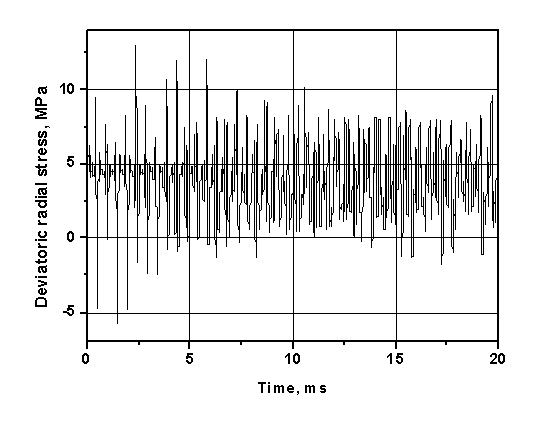
Рис. 16. Радиальное напряжение  в стенке VCrTi (r = 407,2 см).

Во всех рассмотренных точках напряжённое состояние частицы среды в бланкете быстро изменяется с приходом к ней фронта волны и в дальнейшем совершает затухающие колебания до момента повторного нагружения отражённой волной. Частота такого нагружения, как уже говорилось, составляет примерно 2 кГц, колебания же меньшей амплитуды, обусловленные преломлением волны на пластинах конструкции, имеют на порядок большую частоту и на порядок меньшую амплитуду. Но даже самое интенсивное напряжённое состояние находится в упругой зоне, достаточно далеко от предела текучести материала. Говорить об упругопластических (т.е. необратимых) деформациях конструкции бланкета при данном уровне нагружения не приходится: значения  пределов текучести для VCrTi и стали НТ9 равны 223МРа и 422МРа соответственно. Рис. 17 представляет собой визуализацию критерия текучести Мизеса для пористой стенки  SiC и стенки VCrTi, в соответствии с которым определяется переход материала в пластичное состояние при , где   есть второй инвариант девиатора напряжений. На этом графике построено изменение величины , т.е. отношение интенсивности напряжений к пределу текучести. Эта величина показывает, насколько напряженное состояние материала отстоит от границы перехода в текучее состояние. Материалы обеих стенок находятся в упругом состоянии. 

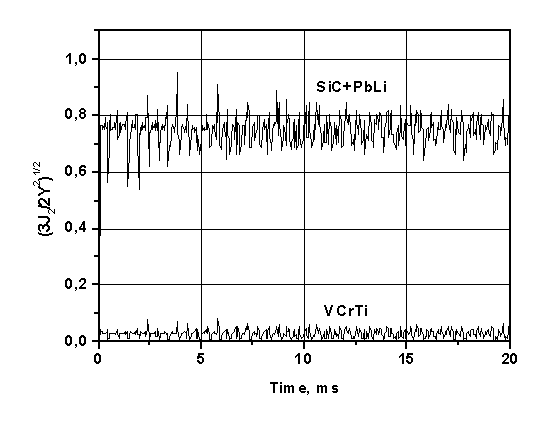
Рис. 17. Отношение интенсивности напряжений к пределу текучести в первой стенке (SiC+PbLi) и ванадиевой стенке (VCrTi).

Времена, при которых рассмотрены динамические процессы в бланкете реактора, слишком малы для того, чтобы начальное распределение температуры могло существенно измениться за счет теплопроводности и повлиять на уровень генерируемых напряжений и давления. Тепловая часть этой задачи при нагружении бланкета в многочастотном режиме будет проанализирована в следующей публикации.

Из расчетов следует, что на короткое время в теплоносителе возникают большие отрицательные давления, которые могут вызвать кавитацию (гомогенное вскипание). Анализ влияния этого эффекта на надежность работы бланкета авторы также предполагают сделать в отдельной работе. В настоящей работе остались не рассмотренными и важные вопросы радиационной стойкости материалов, что является темой специального исследования.

10. Тепловая схема термоядерной электростанции

В заключительном пункте мы кратко опишем тепловую схему термоядерной электростанции (см. [5]), параметры которой приведены ниже в табл. 4. Схема состоит из трех контуров. Теплоноситель: в первом контуре – Li₁₇Pb₈₃, во втором – Na, в третьем – водяной пар. Верхняя и нижняя температуры первого контура приняты равными 823К и 623К. Температуры второго контура определяются автоматически через температурный перепад 773К и 573К. Температура острого пара в третьем контуре 743К, температура промежуточного перегрева также 743К. Давление острого пара примем 18МПа, давление промежуточного перегрева 3 МПа согласно рекомендуемому в литературе оптимуму. Давление в конденсаторе 0,009МПа,  это стандартное значение для энергетики. Число регенеративных отборов пара 8, как в лучших турбинах. Температура питательной воды (после регенераторов) 450К.

Таблица 4. Параметры тепловой схемы термоядерной электростанции.

Заключение

Целью данной публикации было проведение аналитических и расчетных исследований в рамках концепции FIHIF энергетической установки на базе тяжелоионного синтеза. Важность этих расчетов в том, что они увязывают в одно целое ключевые параметры установки, придавая концепции обоснованность и замкнутость.

Аналитическое исследование и численный расчет процессов отклика камеры и бланкета на микровзрыв показали, что для предлагаемой нами конструкции камеры необходимая частота повторений микровзрывов, диктуемая требованиями, предъявляемыми к энергетической установке, согласуется с временами релаксации системы.

         В заключение авторы выражают глубокую признательность всем своим коллегам – членам Совета РАН по физико-техническому анализу энергетических систем, инициировавшим эту работу, в особенности его председателю академику РАН В.И. Субботину, а также академику РАН В.П. Смирнову, чл.-корр. РАН А.В. Забродину, докторам Б.Ю. Шаркову, М.В. Масленникову и С.Л. Недосееву, многократные обсуждения с которыми различных аспектов разрабатываемой концепции принесли авторам неоценимую помощь.

         Мы благодарим также Фонд «Human Capital Foundation», чья спонсорская поддержка позволила выполнить эти исследования.

Литература.

1. Koshkarev D.G. Charge-Symmetric Driver for Heavy-Ion Fusion. // IL Nuovo Chimento, Vol.106 A, No.11, p.1567-1573. 1993.

2. Koshkarev D.G., Korenev I.L., Yudin L.A. Conceptual Design of Linac for Power HIF Driver. /  CERN 96-05, VI, p.423-426. 1996.

3. Чуразов M.Д., Аксенов A.Г., Забродина E.A. Зажигание термоядерных мишеней пучком тяжелых ионов. // ВАНТ, Сер. Математические модели физических процессов, Вып. 1, №.20. 2001.

4. Medin S.A. et al. Evaluation of a power plant concept for fast ignition heavy ion fusion // Laser and Particle Beams, 2002. V.20. P.419-423.

5. Medin S.A. et al. Reactor Chamber and Balance-of-Plant Characteristics for Fast-Ignition Heavy-Ion Fusion Power Plant // Fusion Science and Technology, 2003. V.43. No.3. P.437-446.

6. Medin S.A., et al. Conceptual Analysis of Energy Conversion in Power Plant for Fast Ignition Heavy Ion Fusion / 30-th EPS Conference on Controlled Fusion and Plasma Physics. Russia, S-Petersburg, July 7-11, 2003.

7. Basko M. M., Churazov M. D. and  Aksenov A. G. Prospects of heavy ion fusion in cylindrical geometry. // Laser and Particle Beams, 2002. V.20.P.411-414.

8. Group-6. (1981, April). MCNP-A General Monte Carlo Code for Neutron and Photon Transport. LA-7396-m Revised, LANL.

9. Седов Л.И. Методы подобия и размерностей в механике. М.: ГИТТЛ, 1954.

10. Badger B. et al. HIBALL-II – An improved conceptual heavy beam driven fusion reactor. Report KfK 3840. Karlsruhe, Germany: Kernforschungszentrum. 1984.

11. Исаченко, В.П. Теплоперенос в конденсационных процессах. М.: Энергия, 1972.

12. Копышев В.П., Медведев А.Б. Термодинамическая модель сжимаемого коволюма. Саров: РФЯЦ-ВНИИЭФ, 1995.

13. Медведев А.Б. Модификация модели Ван-дер-Ваальса для плотных состояний. / В сб.: Ударные волны и экстремальные состояния вещества. Под ред. В.Е. Фортова, Л.В. Альтшулера, Р.Ф. Трунина и А.И. Фунтикова. М.: Наука, 2000.

14. Peterson R.R.   et al. Chamber dynamic research with pulsed power. // Nuclear Instr. and Meth. in Phys. Res. A, 2001. V.464. P. 172-179.

15. Основы концепции демонстрационного термоядерного реактора ДЕМО-С. / РНЦ «Курчатовский институт» ИЯС, М., 2000.

16. Moir, R.W. (1996). Liquid inertial fusion energy power plants. Fusion Eng. and Des., Vol. 32-33, p. 93-104.

17. Badger, B. et al. (1980). LIBRA – A Light Ion Beam Fusion Conceptual Reactor Design. / Report KfK 4710. Karlsruhe Kernforschungszentrum.

18. Moir, R. W., et al. (1994).  HYLIFE-II: A Molten Salt Inertial Fusion Power Plant Design – Final Report. // Fusion Technology, vol. 25, p. 5.

19. Zinkle, S.J. (1998, Yuly). Status of  recent activities by the APEX material group. APEX Study Meeting, SNL, p. 18.

20. Hogan, W. J. (ed). (1995). Energy From Inertial Fusion. IAEA, Vienna.

21. dai Kai Sze, Ralph Moir, Steve Zinkle. Data Base for Liquid Breeders and Coolants. / APEX Interim Report, November, 1999.

22. Силин В.П. Введение в кинетическую теорию газов. М.: Наука, 1971.

23. Физические величины. Справочник. М.: Энергоатомиздат, 1991.

24. Hubbell J.H., Seltzer S.M. Tables of X-Ray Mass Attenuation Coefficients. NIST, 1996.

25. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика, Т.VI. Гидродинамика. М.: Наука, 1988.

26. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М.: Наука, 1980.

27. Никифоров А.Ф., Новиков В.Г., Уваров В.Б. Квантово-статистические модели высокотемпературной плазмы и методы расчета росселандовых пробегов и уравнений состояния. М.: Физматлит, 2000.

28. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т.VIII. Теория упругости. М.: Наука, 1987.

29. Баско М.М. Уравнения одномерной радиационной гидродинамики с теплопереносом и кинетикой термоядерного горения. / Препринт ИТЭФ, №145. 1985.

30. Михайлов В.Н. и др. Литий в термоядерной и космической энергетике в XXI веке. М.: Наука, 1999.