Аннотация
Исследуется динамика спутника-гиростата, движущегося в центральном ньютоновом силовом поле
на круговой орбите. В частном случае, когда вектор гиростатического момента параллелен одной
из главных центральных осей инерции спутника, определены все положения равновесия. Для каждой
равновесной ориентации получены достаточные условия устойчивости в результате анализа
обобщенного интеграла энергии и необходимые условия устойчивости в результате анализа
линеаризованных уравнений движения. Подробно исследована эволюция областей выполнения
условий устойчивости положений равновесия в зависимости от параметров задачи. Определены все
бифуркационные значения параметров, при которых происходит качественная смена областей
устойчивости.
Abstract
Dynamics of a gyrostat-satellite moving in a central Newtonian force field in a circular orbit
is investigated. In specific case, when the vector of the gyrostatic moment is parallel to one
of the principal central axes of inertia of the satellite, all equilibrium orientations are
determined. For each equilibrium orientation sufficient conditions of stability are obtained
as a result of generalized energy integral analysis. Necessary conditions of stability are
derived from analysis of linearized equations of motion. Evolution of domains where stability
conditions take place is investigated in detail depending on parameters of a problem. All
bifurcational values of parameters corresponding to qualitative change of stability domains
are found .
1. Введение
Одним из важных направлений
развития космической техники является создание систем ориентации искусственных
спутников Земли. В зависимости от поставленных задач ориентация спутника может
быть осуществлена с использованием активных или пассивных методов. При
разработке пассивных систем ориентации можно использовать свойства
гравитационного и магнитного полей, эффект сопротивления атмосферы и давление
солнечного излучения, гироскопические свойства вращающихся тел и др. Важное
свойство пассивных систем ориентации заключается в том, что эти системы могут
функционировать продолжительное время без расходования энергии или рабочего
тела.
Из систем, использующих
свойства внешней среды, наибольшее распространение получили гравитационные
системы ориентации, принцип работы которых основан на том, что в центральном
ньютоновом поле сил спутник с неравными главными центральными моментами инерции
имеет на круговой орбите четыре устойчивых положения равновесия,
соответствующие совпадению наибольшей оси эллипсоида инерции спутника с
радиусом вектором и наименьшей оси с нормалью к плоскости орбиты. Введение в
конструкцию вращающихся с постоянной угловой скоростью относительно корпуса
спутника маховиков (роторов) позволяет получить новые, более сложные, положения
равновесия спутника-гиростата, интересные для практических приложений.
Основная масса работ по
исследованию динамики спутника-гиростата посвящена определению стационарных
решений (положений равновесия) в орбитальной системе координат и исследованию
их устойчивости. Ниже будет рассмотрена прямая задача, когда ориентация
спутника определяется в зависимости от его инерционных характеристик и
компонент вектора гиростатического момента маховиков. Если в число определяемых
параметров входят компоненты гиростатического момента, говорят об обратной
задаче.
В настоящем препринте
рассмотрена задача о движении спутника-гиростата на круговой орбите под
действием гравитационного момента. В случае, когда вектор гиростатического
момента параллелен одной из главных центральных осей инерции
спутника-гиростата, аналитически определены все положения равновесия, получены
в виде простых неравенств достаточные условия устойчивости этих положений
равновесия. Численно-аналитическим методом проведен детальный анализ эволюции областей
выполнения необходимых условий устойчивости положений равновесия гиростата в зависимости от трех
безразмерных параметров задачи. Определены бифуркационные значения параметров.
Работа
выполнена при финансовой поддержке РФФИ (проект № 03-01-00652) и Португальского
Фонда по науке и технике.
2.
Уравнения движения
Рассмотрим задачу о
вращательном движении спутника-гиростата (далее иногда спутник или гиростат),
представляющего собой твердое тело с расположенными внутри него статически и
динамически уравновешенными роторами. Считаем, что угловая скорость вращения
роторов относительно корпуса спутника постоянна и центр масс спутника движется
по круговой орбите.
Введем две правые декартовы системы координат с началом в
центре масс О спутника-гиростата.
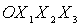 – орбитальная система
координат. Ось – орбитальная система
координат. Ось 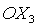 направлена вдоль радиуса-вектора, соединяющего центры масс Земли и
спутника-гиростата; ось направлена вдоль радиуса-вектора, соединяющего центры масс Земли и
спутника-гиростата; ось 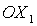 направлена вдоль вектора линейной скорости центра масс O. направлена вдоль вектора линейной скорости центра масс O.
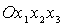 – связанная со спутником-гиростатом система координат; – связанная со спутником-гиростатом система координат; 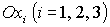 суть главные центральные оси
инерции спутника-гиростата. суть главные центральные оси
инерции спутника-гиростата.
Определим
ориентацию системы координат 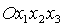 относительно орбитальной
системы углами α, β, γ с последовательностью поворотов 2-3-1 [1]. Первый поворот системы
координат относительно орбитальной
системы углами α, β, γ с последовательностью поворотов 2-3-1 [1]. Первый поворот системы
координат 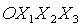 осуществляется на угол α в плоскости осуществляется на угол α в плоскости  (вокруг оси (вокруг оси 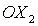 ), второй поворот – на угол β в плоскости ), второй поворот – на угол β в плоскости 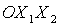 (вокруг оси (вокруг оси 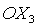 ), третий поворот – на угол γ в плоскости ), третий поворот – на угол γ в плоскости 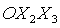 (вокруг оси (вокруг оси 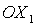 ). Тогда направляющие косинусы осей ). Тогда направляющие косинусы осей 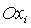 в орбитальной системе координат в орбитальной системе координат
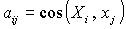 задаются выражениями задаются выражениями
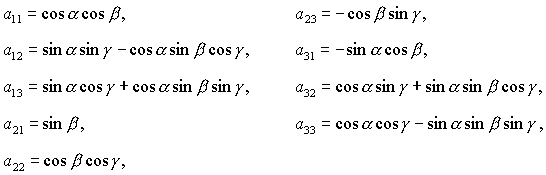 (1) (1)
а уравнения движения спутника-гиростата
относительно его центра масс записываются в виде [2]
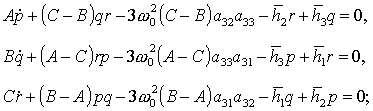 (2) (2)
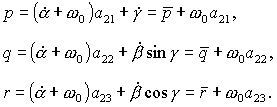 (3) (3)
В уравнениях (2), (3) A, B, C – главные центральные моменты инерции
гиростата; p, q, r, 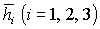 - проекции абсолютной угловой
скорости гиростата и проекции вектора гиростатического момента на оси - проекции абсолютной угловой
скорости гиростата и проекции вектора гиростатического момента на оси 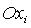 ; ; 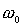 - угловая скорость
движения центра масс гиростата по круговой орбите. Точкой обозначено
дифференцирование по времени t. - угловая скорость
движения центра масс гиростата по круговой орбите. Точкой обозначено
дифференцирование по времени t.
Для системы уравнений (2), (3) справедлив обобщенный
интеграл энергии
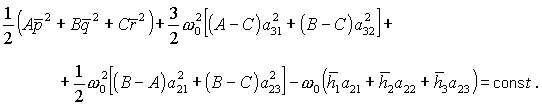 (4) (4)
3.
Положения равновесия спутника-гиростата
Положив в (2) и (3) 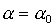 , , 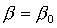 , , 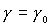 ( (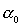 , ,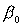 , ,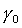 - постоянные величины) и обозначив - постоянные величины) и обозначив 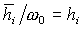 , получим уравнения , получим уравнения
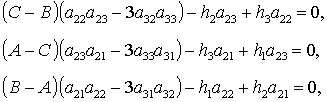 (5) (5)
позволяющие определить положения равновесия
гиростата в орбитальной системе координат. Вместо системы (5) удобнее
использовать эквивалентную ей систему
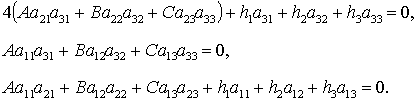 (6) (6)
C учетом (1) систему
(6) можно трактовать как систему трех уравнений с неизвестными 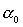 , ,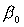 , ,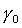 . Другой способ замыкания уравнений (6) заключается в
добавлении условий ортогональности направляющих косинусов . Другой способ замыкания уравнений (6) заключается в
добавлении условий ортогональности направляющих косинусов
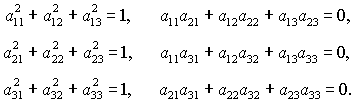 (7) (7)
Далее будем исследовать положения равновесия
гиростата, используя системы (6) и (7).
Как
показано в [3], при 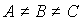 систему уравнений (6), (7)
можно разрешить относительно систему уравнений (6), (7)
можно разрешить относительно  , , 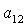 , , 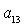 , , 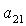 , , 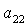 , , 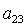 . В результате получим . В результате получим
 (8) (8)
Здесь 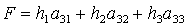 , , 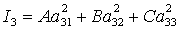 , а направляющие косинусы , а направляющие косинусы 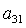 , , 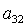 , , 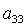 определяются из трех
уравнений определяются из трех
уравнений
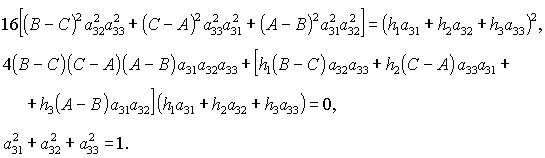 (9) (9)
После решения системы (9)
формулы (8) позволяют определить оставшиеся шесть направляющих косинусов.
Отметим, что решения (8) существуют лишь в том случае, когда из трех
направляющих косинусов 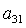 , , 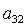 , , 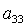 никакие два
одновременно не обращаются в нуль. Случаи никакие два
одновременно не обращаются в нуль. Случаи 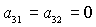 , , 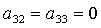 , , 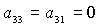 для предлагаемого
метода решения задачи являются особыми и их следует рассматривать непосредственно
обращаясь к системам (6) и (7). для предлагаемого
метода решения задачи являются особыми и их следует рассматривать непосредственно
обращаясь к системам (6) и (7).
В [3] показано, что после перехода к новым неизвестным 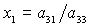 и и 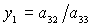 первые два уравнения
системы (9) с использованием понятия результанта сводятся к одному
алгебраическому уравнению 12-го порядка (например, относительно первые два уравнения
системы (9) с использованием понятия результанта сводятся к одному
алгебраическому уравнению 12-го порядка (например, относительно 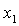 ) с действительными коэффициентами. Число его действительных
корней четно и не превышает 12. Подставляя значение действительного корня
алгебраического уравнения в первые два уравнения системы (9), найдем
совпадающий корень ) с действительными коэффициентами. Число его действительных
корней четно и не превышает 12. Подставляя значение действительного корня
алгебраического уравнения в первые два уравнения системы (9), найдем
совпадающий корень 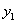 этих уравнений. Для
каждого решения этих уравнений. Для
каждого решения 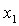 , , 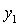 из последнего
уравнения системы (9) можно определить два значения из последнего
уравнения системы (9) можно определить два значения 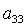 , а затем и соответствующие им величины , а затем и соответствующие им величины 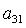 и и 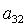 . Таким образом, каждому действительному корню
алгебраического уравнения соответствуют два набора значений . Таким образом, каждому действительному корню
алгебраического уравнения соответствуют два набора значений 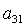 , , 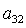 , , 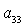 , которые в силу (8) однозначно определяют остальные
направляющие косинусы , которые в силу (8) однозначно определяют остальные
направляющие косинусы 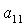 , , 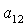 , , 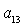 , , 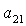 , , 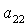 , , 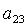 . Из приведенных соображений следует, что спутник-гиростат на
круговой орбите может иметь не более 24 положений равновесия. . Из приведенных соображений следует, что спутник-гиростат на
круговой орбите может иметь не более 24 положений равновесия.
Далее будем рассматривать частный случай, когда вектор
гиростатического момента коллинеарен одной из главных осей инерции спутника.
Пусть для определенности 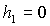 , , 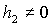 , , 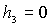 . Тогда система (9) после перехода к безразмерным параметрам . Тогда система (9) после перехода к безразмерным параметрам 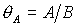 , , 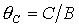 , , 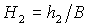 принимает вид принимает вид
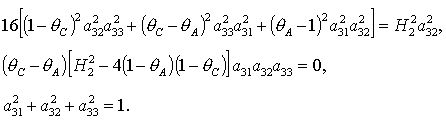 (10) (10)
Заметим,
что достаточно ограничиться рассмотрением положительных 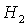 , поскольку случай , поскольку случай  сводится к случаю сводится к случаю 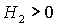 заменой направления
осей заменой направления
осей 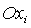 связанной системы
координат на противоположные. связанной системы
координат на противоположные.
Из второго уравнения системы (10) следует
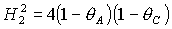 (11)
(11)
или
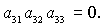 (12) (12)
Пусть выполнено условие (11). Умножив
правую часть первого уравнения (10) на 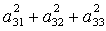 и исключив и исключив 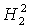 с помощью (11), получим
однородное относительно с помощью (11), получим
однородное относительно 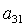 , , 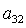 , , 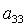 уравнение,
определяющее однопарамет-рические семейства решений. Пусть, например, уравнение,
определяющее однопарамет-рические семейства решений. Пусть, например, 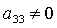 . Тогда первое уравнение (10) можно представить в виде . Тогда первое уравнение (10) можно представить в виде
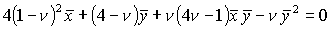 , (13) , (13)
где
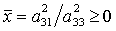 , , 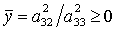 , , 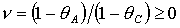 . (14) . (14)
При 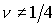 уравнение (13) определяет ветвь
гиперболы, лежащую в первом квадранте плоскости уравнение (13) определяет ветвь
гиперболы, лежащую в первом квадранте плоскости 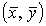 , а при , а при 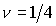 - параболу. Используя
соотношения (14) и третье уравнение системы (10), можно для каждой точки - параболу. Используя
соотношения (14) и третье уравнение системы (10), можно для каждой точки 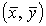 этой кривой получить выражения этой кривой получить выражения
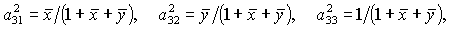 (15) (15)
откуда следует существование
8 однопараметрических семейств решений при любом 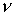 . .
Пусть теперь 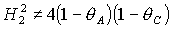 . Тогда второе уравнение (10) примет вид (12). В результате
поочередного рассмотрения случаев . Тогда второе уравнение (10) примет вид (12). В результате
поочередного рассмотрения случаев 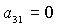 , , 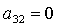 , , 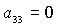 получаем следующие
группы изолированных решений (приведены лишь отличные от нуля направляющие
косинусы): получаем следующие
группы изолированных решений (приведены лишь отличные от нуля направляющие
косинусы):
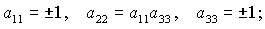 (16)
(16)
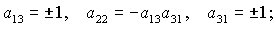 (17) (17)
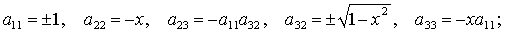 (18) (18)
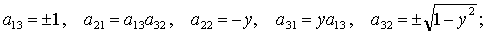 (19) (19)
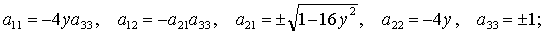 (20) (20)
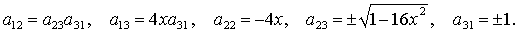 (21) (21)
При этом каждая
группа (16)-(21) состоит из четырех решений, соответствующих одному из четырех
вариантов выбора знаков + и – . Здесь 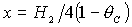 , , 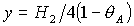 . .
Заметим, что анализ системы (6), (7) в особых случаях 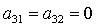 , , 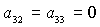 , , 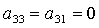 не приводит к новым
решениям. Так, в первом случае не приводит к новым
решениям. Так, в первом случае 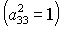 получаются решения
(16) и (20), во втором случае получаются решения
(16) и (20), во втором случае 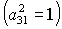 решения (17) и (21),
в третьем случае решения (17) и (21),
в третьем случае 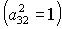 системе (6), (7)
удовлетворяют только решения (18) и (19) при системе (6), (7)
удовлетворяют только решения (18) и (19) при 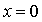 и и 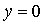 соответственно. соответственно.
Решения
(16) и (17) существуют при любых значениях параметров рассматриваемой задачи,
решения (18) - при 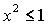 , решения (19) – при , решения (19) – при 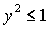 , решения (20) – при , решения (20) – при 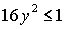 , решения (21) – при , решения (21) – при 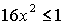 . Условия существования решений (16)-(21) выделяют в
плоскости . Условия существования решений (16)-(21) выделяют в
плоскости 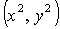 9 областей с фиксированным
числом стационарных решений в каждой области (рис. 1). Разумеется, при 9 областей с фиксированным
числом стационарных решений в каждой области (рис. 1). Разумеется, при 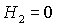 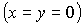 решения (16)-(21) совпадают с
известными 24 равновесными ориентациями твердого тела в орбитальной системе
координат на круговой орбите. решения (16)-(21) совпадают с
известными 24 равновесными ориентациями твердого тела в орбитальной системе
координат на круговой орбите.
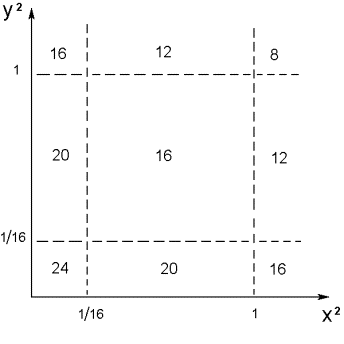
Рис. 1
Следует
обратить внимание на то, что решения (16), (18) и (20) переходят соответственно
в решения (17), (19) и (21), если другим способом определить связанную систему
координат. А именно, введем вместо 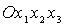 систему координат систему координат 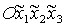 , получающуюся из , получающуюся из 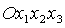 поворотом вокруг оси поворотом вокруг оси 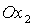 на угол на угол 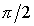 . Ясно, что оси . Ясно, что оси 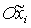 по-прежнему являются
главными центральными осями инерции спутника-гиростата, но их порядок и направления
отличаются от по-прежнему являются
главными центральными осями инерции спутника-гиростата, но их порядок и направления
отличаются от 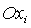 . Фактически переход от осей . Фактически переход от осей 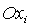 к осям к осям 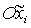 эквивалентен замене эквивалентен замене 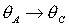 , , 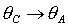 (при этом, как
следствие, (при этом, как
следствие, 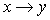 , , 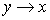 ). ).
Рассмотрим, например, решение (18). В системе координат 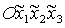 оно принимает вид оно принимает вид
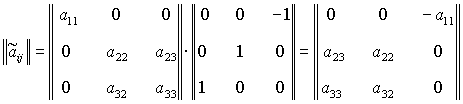 , ,
откуда
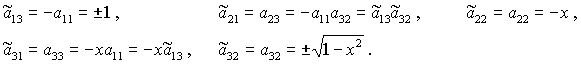
Полученные
выражения с учетом того, что 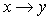 , действительно совпадают с (19). , действительно совпадают с (19).
Таким
образом, можно ограничиться анализом устойчивости решений (16), (18) и (20), а
соответствующие области для решений (17), (19) и (21) будут симметричны им
относительно прямой 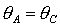 . .
Что касается геометрического смысла полученных решений, то
для четырех решений (16) одноименные оси орбитальной и связанной систем
координат параллельны или антипараллельны друг другу. При этом вектор
внутреннего гиростатического момента (т.е. ось 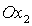 ) параллелен вектору внешней нормали к плоскости орбиты (оси ) параллелен вектору внешней нормали к плоскости орбиты (оси 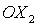 ), если ), если 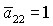 , и противоположно направлен, если , и противоположно направлен, если 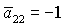 . .
Решения (18) и (20) могут быть получены из (16) путем
поворота вокруг оси 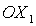 и и 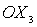 на углы на углы 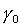 или или 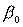 соответственно,
причем значения углов поворота определяются соотношениями соответственно,
причем значения углов поворота определяются соотношениями
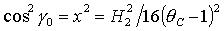 , , 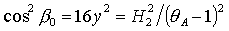 . .
Заметим,
что похожий результат имеет место в задаче о стационарных вращениях
осесимметричного спутника на круговой орбите [2].
4.
Достаточные условия устойчивости положений равновесия
Для получения достаточных условий устойчивости положений
равновесия спутника-гиростата воспользуемся интегралом энергии (4). Представим  , , 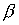 , , 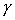 в виде в виде
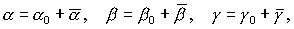 (22) (22)
где 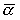 , , 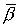 , , 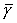 - малые отклонения от положения
равновесия спутника - малые отклонения от положения
равновесия спутника 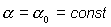 , , 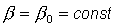 , , 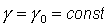 , удовлетворяющего системе уравнений (5). Тогда интеграл энергии может
быть представлен в виде , удовлетворяющего системе уравнений (5). Тогда интеграл энергии может
быть представлен в виде
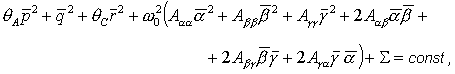 (23) (23)
где
символ  обозначает члены выше
второго порядка малости относительно обозначает члены выше
второго порядка малости относительно  , ,  , , 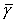 , ,
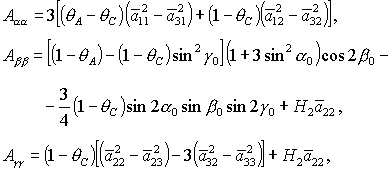
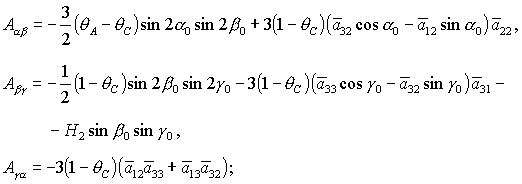
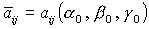 . .
Из теоремы Ляпунова следует, что решение 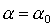 , , 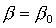 , , 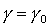 устойчиво, если квадратичная
форма устойчиво, если квадратичная
форма
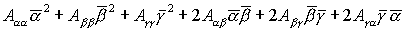
является
определенно-положительной. Опуская промежуточные выкладки, достаточные условия
устойчивости шести групп решений (16)-(21) запишем в следующем виде:
для решений (16)
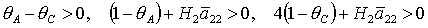 ;
(24) ;
(24)
для решений (18), которые
существуют при 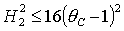 , ,
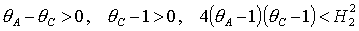 (25.1) (25.1)
либо
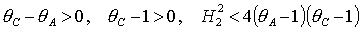 ; (25.2) ; (25.2)
для решений (20), которые
существуют при 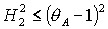 , ,
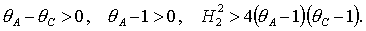 (26) (26)
Заметим,
что для решений (18) условие 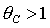 и условие
существования решения и условие
существования решения 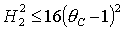 сводится к
единственному условию сводится к
единственному условию 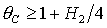 . Более того, при . Более того, при 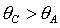 последнее условие
мажорируется неравенством последнее условие
мажорируется неравенством 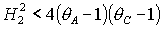 . Таким образом, достаточные условия устойчивости решения
(18) окончательно принимают вид . Таким образом, достаточные условия устойчивости решения
(18) окончательно принимают вид
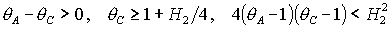 (27.1) (27.1)
либо
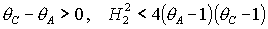 . (27.2) . (27.2)
Анализ условий (26) совместно с условием существования
решений (20) 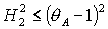 показывает, что они
сводятся к двум неравенствам показывает, что они
сводятся к двум неравенствам
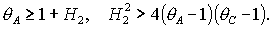 (28) (28)
При замене 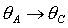 , , 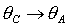 условия (24) для
решений (16) переходят в условия для решений (17), условия (27) для решений
(18) переходят в условия для решений (19), а условия (28) для решений (20) - в
условия для решений (21). Напомним также, что при исследовании областей, где
выполняются условия устойчивости положений равновесия гиростата, необходимо
учитывать условия физической реализуемости тела, т.е. «неравенства
треугольника» условия (24) для
решений (16) переходят в условия для решений (17), условия (27) для решений
(18) переходят в условия для решений (19), а условия (28) для решений (20) - в
условия для решений (21). Напомним также, что при исследовании областей, где
выполняются условия устойчивости положений равновесия гиростата, необходимо
учитывать условия физической реализуемости тела, т.е. «неравенства
треугольника» 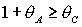 , , 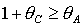 , , 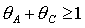 . Далее область в плоскости . Далее область в плоскости 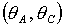 , где выполнены неравенства треугольника, будем называть
рабочей областью. , где выполнены неравенства треугольника, будем называть
рабочей областью.
Рассмотрим эволюцию областей выполнения достаточных условий
устойчивости положений равновесия спутника-гиростата в плоскости 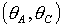 при изменении
величины безразмерного гиростатического момента при изменении
величины безразмерного гиростатического момента 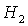 . Если . Если 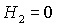 , то спутник-гиростат представляет собой твердое тело; при
этом решения (16)-(21) устойчивы в областях, показанных на рис. 2 (здесь и
далее на рисунках горизонтальная и вертикальная оси отвечают безразмерным
моментам инерции , то спутник-гиростат представляет собой твердое тело; при
этом решения (16)-(21) устойчивы в областях, показанных на рис. 2 (здесь и
далее на рисунках горизонтальная и вертикальная оси отвечают безразмерным
моментам инерции 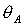 и и 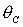 соответственно). Вся
область допустимых соответственно). Вся
область допустимых 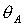 , , 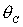 разбивается прямыми разбивается прямыми 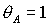 , , 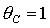 , , 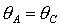 на 6 областей, в
каждой из которых выполняются достаточные условия устойчивости только одной
группы решений (на рисунке области обозначены номерами соответствующих
решений). на 6 областей, в
каждой из которых выполняются достаточные условия устойчивости только одной
группы решений (на рисунке области обозначены номерами соответствующих
решений).
При 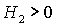 характер границ
областей изменяется. Прямые характер границ
областей изменяется. Прямые 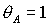 , , 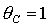 переходят в гиперболу переходят в гиперболу
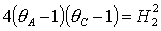 . Кроме того, для решений (16) и (17) имеет место следующая
особенность: области выполнения достаточных условий устойчивости решений,
отвечающих . Кроме того, для решений (16) и (17) имеет место следующая
особенность: области выполнения достаточных условий устойчивости решений,
отвечающих 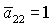 и и 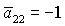 , не совпадают. На рис. 3 в областях, обозначенных (16) и
(17), условия выполняются для , не совпадают. На рис. 3 в областях, обозначенных (16) и
(17), условия выполняются для 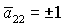 , а в областях, обозначенных (16)+ или (17)+ ,
условия выполняются только в случае , а в областях, обозначенных (16)+ или (17)+ ,
условия выполняются только в случае 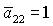 . .
С
ростом 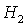 взаимное расположение
границ разбиения изменяется, а при двух бифуркационных значениях взаимное расположение
границ разбиения изменяется, а при двух бифуркационных значениях 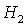 ( (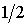 и и 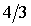 ) картина разбиения претерпевает качественные изменения (рис.
3-5). При первом бифуркационном
значении ) картина разбиения претерпевает качественные изменения (рис.
3-5). При первом бифуркационном
значении 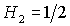 исчезают области (16)
и (17), а при втором бифуркационном значении исчезают области (16)
и (17), а при втором бифуркационном значении 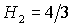 исчезают и области
(20), (21). исчезают и области
(20), (21).
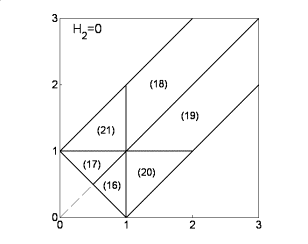
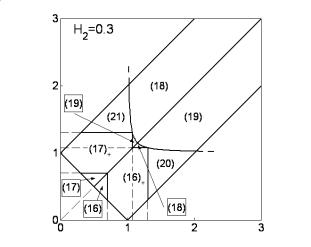
Рис. 2 Рис. 3
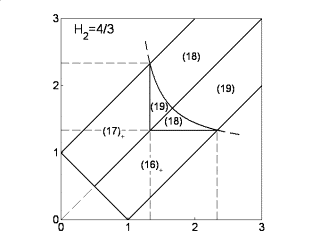
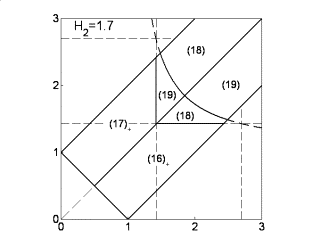
Рис.
4 Рис. 5
5. Необходимые условия устойчивости
Для
исследования необходимых условий устойчивости положений равновесия
спутника-гиростата линеаризуем систему уравнений (2)-(3) в окрестности решения 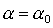 , , 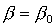 , , 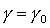 . После достаточно утомительных преобразований линеаризованная система
уравнений движения принимает следующий вид: . После достаточно утомительных преобразований линеаризованная система
уравнений движения принимает следующий вид:
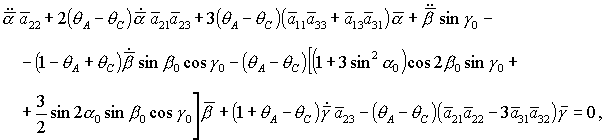
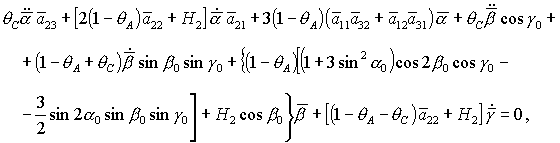 (29) (29)
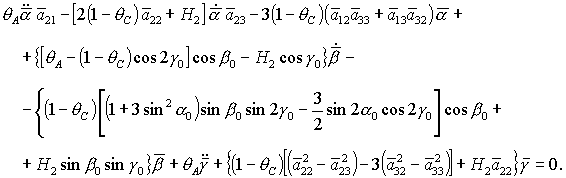
Здесь точкой обозначено
дифференцирование по безразмерному времени 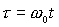 . .
Перейдем к рассмотрению конкретных
положений равновесия спутника-гиростата. Для решений (16) с учетом выражений
(1) для направляющих косинусов имеем 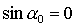 , , 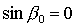 , , 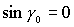 и линеаризованные
уравнения принимают вид и линеаризованные
уравнения принимают вид
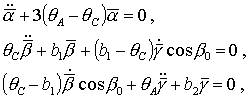 (30)
(30)
где
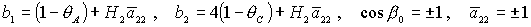 . .
Характеристическое уравнение системы (30)
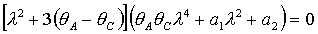
распадается на квадратное и биквадратное
уравнения. Здесь введены обозначения
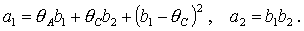
Поскольку необходимым
условием устойчивости является отсутствие корней характеристического уравнения
с положительными действительными частями, то в случае, когда в уравнении
присутствуют только четные степени 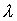 , надо потребовать, чтобы все корни были чисто мнимыми.
Другими словами, , надо потребовать, чтобы все корни были чисто мнимыми.
Другими словами, 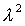 должно быть
вещественным и отрицательным. Таким образом, приходим к условиям должно быть
вещественным и отрицательным. Таким образом, приходим к условиям
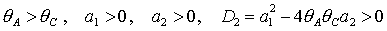 . (31) . (31)
Разумеется, наряду с (31) должны выполняться
и неравенства треугольника
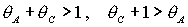 .
(32) .
(32)
Третье неравенство
треугольника 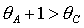 можно не учитывать,
т.к. при можно не учитывать,
т.к. при 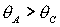 оно выполняется
автоматически. Обратим также внимание на то, что неравенство оно выполняется
автоматически. Обратим также внимание на то, что неравенство 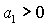 не может обращаться в
равенство на границе области выполнения необходимых условий устойчивости (31),
(32), поскольку при не может обращаться в
равенство на границе области выполнения необходимых условий устойчивости (31),
(32), поскольку при 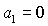 из условия из условия 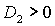 следует следует 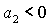 , что противоречит (31). , что противоречит (31).
Условие 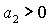 выполняется либо при выполняется либо при 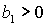 , ,  , либо при , либо при 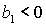 , , 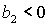 . В первом случае выполняются все достаточные условия
устойчивости (24). Очевидно, при этом выполняются также и все необходимые
условия (31), т.е. . В первом случае выполняются все достаточные условия
устойчивости (24). Очевидно, при этом выполняются также и все необходимые
условия (31), т.е. 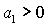 и и 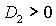 . Таким образом, приходим к области, в которой выполняются
необходимые и достаточные условия устойчивости решений (16), уже полученной в
предыдущем разделе. . Таким образом, приходим к области, в которой выполняются
необходимые и достаточные условия устойчивости решений (16), уже полученной в
предыдущем разделе.
Пусть теперь 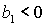 , , 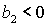 . Тогда достаточные условия нарушаются, а необходимые условия
принимают вид . Тогда достаточные условия нарушаются, а необходимые условия
принимают вид
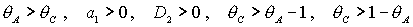 . (33) . (33)
На границе области
обращается в равенство по крайней мере одно из неравенств (33). При этом
равенство 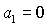 возможно только, если
одновременно возможно только, если
одновременно 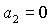 и и 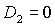 . Таким образом, область может быть ограничена прямыми . Таким образом, область может быть ограничена прямыми 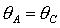 , , 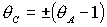 , , 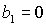 , , 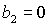 и кривой и кривой 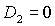 . Пример такой
области, а также все линии, на которых одно из неравенств (31) обращается в
равенство, показаны на рис. 6. Область, где выполнены необходимые и достаточные
условия устойчивости, выделена светло-серым цветом, область, где выполнены
только необходимые условия устойчивости, выделена темно-серым цветом. Отметим,
что кривая . Пример такой
области, а также все линии, на которых одно из неравенств (31) обращается в
равенство, показаны на рис. 6. Область, где выполнены необходимые и достаточные
условия устойчивости, выделена светло-серым цветом, область, где выполнены
только необходимые условия устойчивости, выделена темно-серым цветом. Отметим,
что кривая 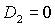 пересекает, а точнее,
касается прямой пересекает, а точнее,
касается прямой 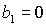 в точке в точке 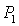 , где , где 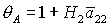 , , 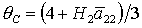 . Здесь же . Здесь же 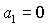 . Прямые . Прямые 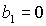 и и 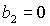 пересекаются в точке пересекаются в точке 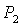 , где , где 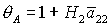 , , 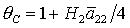 . Далее проанализируем отдельно случаи . Далее проанализируем отдельно случаи 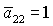 и и 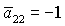 . .
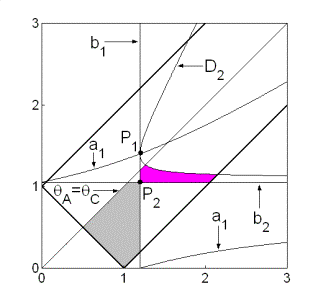
Рис. 6
Если 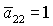 , то качественная смена формы области имеет место при таких
значениях , то качественная смена формы области имеет место при таких
значениях 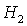 , когда точка , когда точка 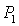 оказывается на прямой оказывается на прямой
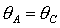 , либо когда точка , либо когда точка 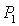 или или 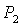 оказывается на прямой оказывается на прямой
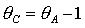 . Отсюда следуют бифуркационные значения . Отсюда следуют бифуркационные значения  , , 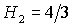 и и 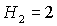 . При последнем значении безразмерного гиростатического
момента область вырождается в точку и при . При последнем значении безразмерного гиростатического
момента область вырождается в точку и при 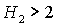 перестает
существовать. Эволюцию формы области иллюстрирует рис. 7, на котором показаны
области выполнения необходимых условий устойчивости решений (16) в случае перестает
существовать. Эволюцию формы области иллюстрирует рис. 7, на котором показаны
области выполнения необходимых условий устойчивости решений (16) в случае 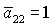 . .
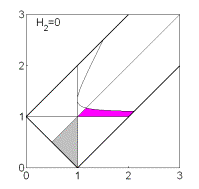
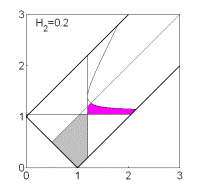
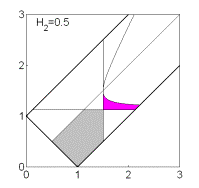
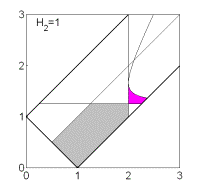
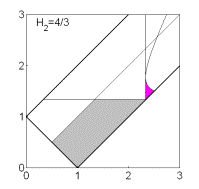
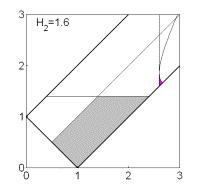
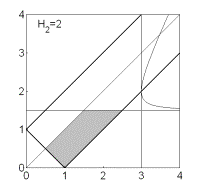
Рис. 7: Решения (16), 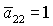 . .
Пусть теперь 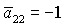 . На этот раз особая ситуация имеет место при . На этот раз особая ситуация имеет место при 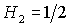 , когда прямая , когда прямая 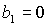 проходит через точку
пересечения границ проходит через точку
пересечения границ 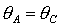 и и 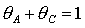 . В результате исчезает область выполнения достаточных
условий устойчивости. Область выполнения необходимых условий устойчивости
ограничена прямыми . В результате исчезает область выполнения достаточных
условий устойчивости. Область выполнения необходимых условий устойчивости
ограничена прямыми 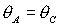 , , 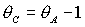 , , 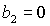 и кривой и кривой 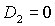 . Отметим, что граница . Отметим, что граница 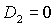 с ростом с ростом 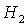 смещается вниз, если смещается вниз, если 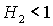 и вверх, если и вверх, если 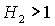 . При . При 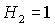 она вырождается в
прямую она вырождается в
прямую 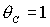 и происходит
очередное качест-венное изменение формы области. В этот момент точка
пересечения границ и происходит
очередное качест-венное изменение формы области. В этот момент точка
пересечения границ 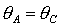 и и 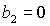 оказывается на прямой оказывается на прямой
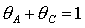 . В дальнейшем эта прямая также становится одной из границ области.
Наконец, при . В дальнейшем эта прямая также становится одной из границ области.
Наконец, при 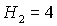 прямая прямая 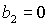 перестает быть одной
из границ области, и при перестает быть одной
из границ области, и при 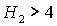 область выполнения
необходимых условий ограничена прямыми область выполнения
необходимых условий ограничена прямыми 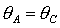 , , 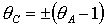 и кривой и кривой 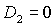 . На рис. 8 показаны соответствующие примеры областей
выполнения необходимых условий устойчивости решений (16) в случае . На рис. 8 показаны соответствующие примеры областей
выполнения необходимых условий устойчивости решений (16) в случае 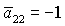 . .
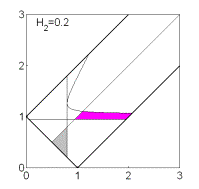
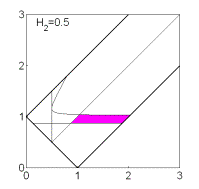
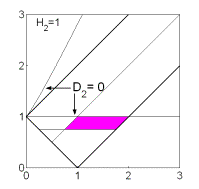
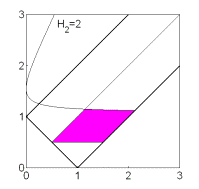
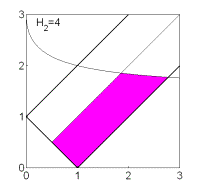
Рис. 8: Решения
(16), 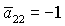 . .
Перейдем к решениям (18), для которых 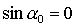 , , 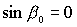 , , 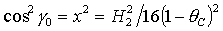 . В результате характеристическое уравнение системы (29)
приводится к виду . В результате характеристическое уравнение системы (29)
приводится к виду
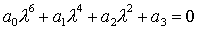 , (34) , (34)
где
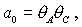
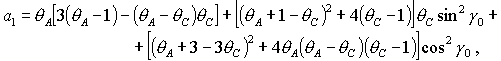
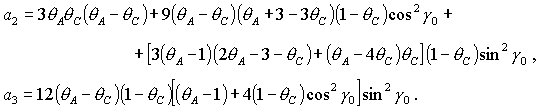
Необходимые условия устойчивости - условия
чистой мнимости корней уравнения (34) - представляют собой систему неравенств
[4]
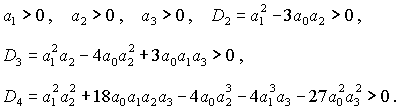 (35) (35)
Как и в предыдущем
случае, наряду с (35) должны выполняться неравенства треугольника. Кроме того,
дополнительно следует удовлетворить условие существования решений (18), т.е. 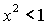 . .
Легко показать, что на границе области (35) равенство 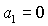 возможно только в
точках, где одновременно возможно только в
точках, где одновременно 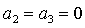 и и 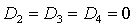 . Аналогично равенство . Аналогично равенство 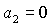 возможно, если возможно, если 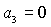 и и 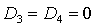 . Более того, численные исследования показали, что границами
области (35) могут быть только линии, на которых . Более того, численные исследования показали, что границами
области (35) могут быть только линии, на которых 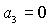 или или 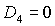 . .
Из вида 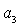 следует, что
равенство следует, что
равенство 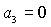 имеет место на прямых имеет место на прямых
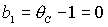 , , 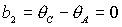 , , 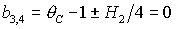 и на гиперболе и на гиперболе 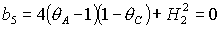 , причем прямую , причем прямую 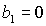  можно исключить,
поскольку решения (18) не существуют, если можно исключить,
поскольку решения (18) не существуют, если 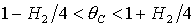 . Пример области в плоскости . Пример области в плоскости 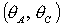 , где выполняются необходимые условия устойчивости,
представлен на рис. 9. Область выделена темно-серым цветом и ограничена прямыми , где выполняются необходимые условия устойчивости,
представлен на рис. 9. Область выделена темно-серым цветом и ограничена прямыми
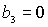 , , 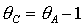 и кривой и кривой 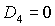 . Здесь же выделена светло-серым цветом область выполнения
необходимых и достаточных условий устойчивости, которая ограничена прямыми . Здесь же выделена светло-серым цветом область выполнения
необходимых и достаточных условий устойчивости, которая ограничена прямыми 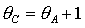 , , 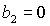 , , 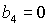 и гиперболой и гиперболой 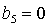 . .
Отдельные части области выполнения необходимых условий на
рис. 9 обозначены B, C и D. Область B ограничена прямыми 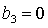 , , 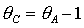 и кривой и кривой 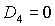 . Нижняя граница области B ( . Нижняя граница области B (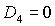 ) с ростом ) с ростом 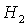 смещается вниз и при смещается вниз и при 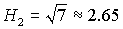 проходит через точку проходит через точку 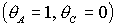 . Аналогично ведет себя и верхняя граница ( . Аналогично ведет себя и верхняя граница (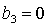 ), которая при ), которая при 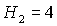 также проходит через
точку также проходит через
точку 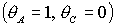 , после чего область перестает существовать. , после чего область перестает существовать.
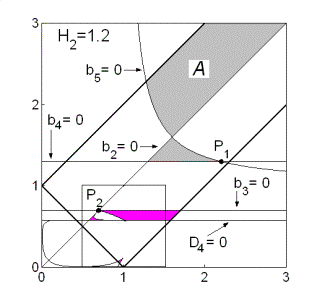 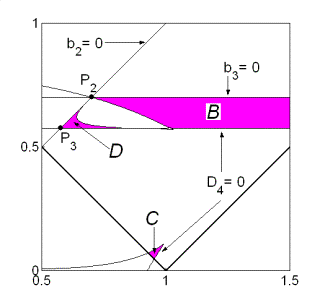
Рис. 9
Обратим
внимание на точку 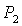 на пересечении прямых на пересечении прямых
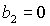 и и 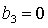 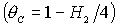 . В этой же точке . В этой же точке 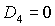 и и 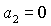 . При увеличении . При увеличении 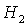 точка точка 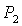 смещается вдоль
прямой смещается вдоль
прямой 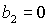 и выходит из рабочей
области, если и выходит из рабочей
области, если 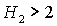 . .
Область С рождается при 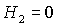 в точке в точке 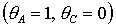 и образована границей
рабочей области и образована границей
рабочей области 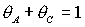 и кривой и кривой 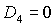 . .
Область D рождается при 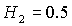 в точке в точке  . При увеличении . При увеличении 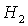 точка точка 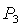 смещается вдоль
прямой смещается вдоль
прямой 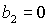 и выходит на границу
рабочей области и выходит на границу
рабочей области  при при
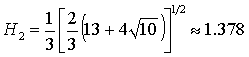 . .
Кроме
того, численные исследования показали, что при 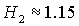 происходит смыкание
областей B и D, а при происходит смыкание
областей B и D, а при 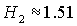 смыкаются области С и D. При смыкаются области С и D. При 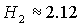 исчезает объединение
областей С и D. Напомним, что в
ходе анализа достаточных условий устойчивости было получено бифуркационное
значение исчезает объединение
областей С и D. Напомним, что в
ходе анализа достаточных условий устойчивости было получено бифуркационное
значение 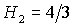 , при котором точка , при котором точка 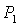 выходит на границу
рабочей области выходит на границу
рабочей области 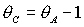 . .
Таким образом, качественная смена
формы областей устойчивости решений (18) происходит при следующих
бифуркационных значениях гиростатического момента:
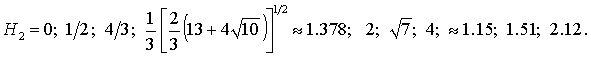
Соответствующие
области показаны на рис. 10, причем здесь основное внимание уделяется
областям выполнения только необходимых условий устойчивости, поскольку области
выполнения достаточных условий уже подробно обсуждались в предыдущем разделе.
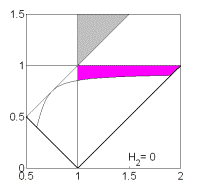
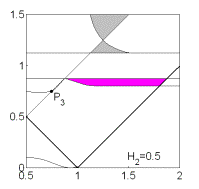
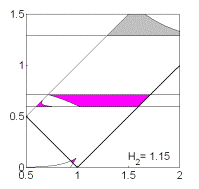
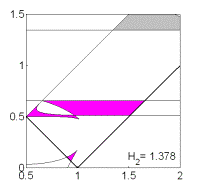
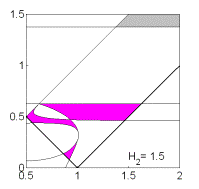
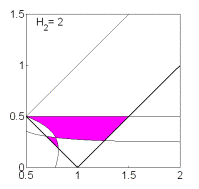
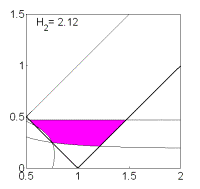
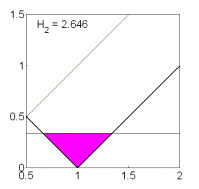
Рис. 10: Решения
(18).
Наконец, рассмотрим решения (20), для которых 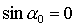 , , 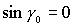 , , 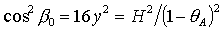 . Характеристическое уравнение снова имеет вид (34), где . Характеристическое уравнение снова имеет вид (34), где
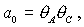
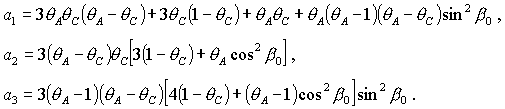
Анализ необходимых условий устойчивости, которые аналогичны (35),
приводит к выводу, что на границе области 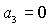 либо либо 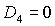 . Равенство . Равенство 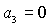 имеет место на прямых имеет место на прямых
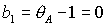 , , 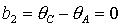 , , 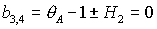 и на гиперболе и на гиперболе 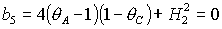 , причем прямую , причем прямую 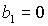 можно исключить, т.к.
при можно исключить, т.к.
при 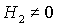 решения (20) не
существуют в полосе решения (20) не
существуют в полосе 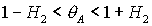 . .
Эволюция областей при изменении 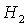 показана на рис. 11.
Области, где выполнены необходимые и достаточные условия устойчивости, выделены
светло-серым цветом и ограничены прямыми показана на рис. 11.
Области, где выполнены необходимые и достаточные условия устойчивости, выделены
светло-серым цветом и ограничены прямыми 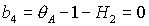 , , 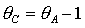 и гиперболой и гиперболой 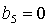 . Области, где выполнены только необходимые условия
устойчивости, выделены темно-серым цветом и образованы прямыми . Области, где выполнены только необходимые условия
устойчивости, выделены темно-серым цветом и образованы прямыми 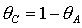 (граница рабочей
области), (граница рабочей
области), 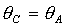 (на ней (на ней 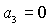 ) и кривой ) и кривой 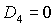 . Качественный вид областей зависит от положения двух
характерных точек: точки . Качественный вид областей зависит от положения двух
характерных точек: точки 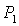 , в которой пересекаются линии , в которой пересекаются линии 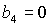 и и 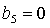 , и точки , и точки 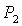 , где пересекаются линии , где пересекаются линии 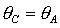 и и 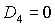 (заметим, что в этой
же точке (заметим, что в этой
же точке 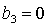 ). ).
Рис. 11.1 соответствует случаю твердого тела (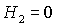 ). При ). При 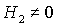 прямая прямая 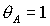 расщепляется на две
прямые расщепляется на две
прямые 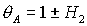 ( (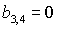 ). Полоса ). Полоса 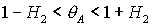 , в которой решения (20) не существуют, с ростом , в которой решения (20) не существуют, с ростом 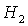 расширяется, и при расширяется, и при 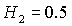 точка точка 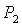 выходит на границу
рабочей области выходит на границу
рабочей области 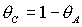 . При этом область выполнения необходимых условий
устойчивости вырождается в точку (рис. 11.3) и при . При этом область выполнения необходимых условий
устойчивости вырождается в точку (рис. 11.3) и при 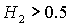 перестает
существовать. перестает
существовать.
Область необходимых и достаточных условий с ростом 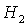 также сокращается и
при также сокращается и
при 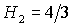 , когда , когда  выходит на границу
рабочей области выходит на границу
рабочей области 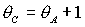 , вырождается в точку (рис. 11.4). При , вырождается в точку (рис. 11.4). При 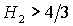 необходимые условия
устойчивости не выполняются ни в одной точке рабочей области. необходимые условия
устойчивости не выполняются ни в одной точке рабочей области.
 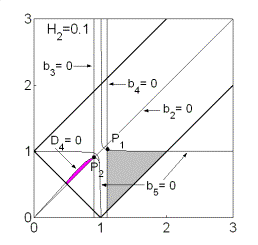
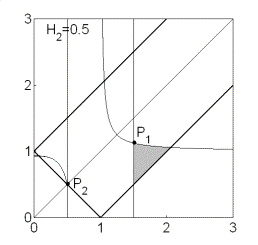 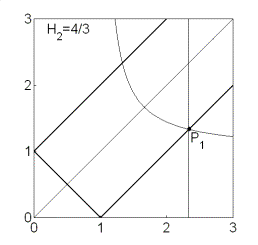
Рис. 11. Решения (20).
6.
Заключение
В
настоящей работе проведено исследование движения спутника-гиростата
относительно центра масс под действием гравитационного момента на круговой
орбите. Основное внимание при исследовании было
уделено определению положений равновесия для частного случая
спутника-гиростата, когда 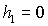 , , 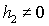 , , 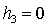 . Предложено новое, более простое по сравнению с полученным в
[5], решение этой задачи. Представлены в явном виде выражения для направляющих
косинусов в зависимости от параметров . Предложено новое, более простое по сравнению с полученным в
[5], решение этой задачи. Представлены в явном виде выражения для направляющих
косинусов в зависимости от параметров 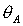 , , 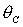 , , 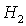 для шести групп
(16)-(21) положений равновесия гиростата. Доказано, что группы решений (16),
(18), (20) переходят соответственно в группы решений (17), (19), (21) при
замене для шести групп
(16)-(21) положений равновесия гиростата. Доказано, что группы решений (16),
(18), (20) переходят соответственно в группы решений (17), (19), (21) при
замене 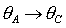 , , 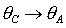 . С использованием теоремы Ляпунова получены в виде простых
неравенств достаточные условия устойчивости (24), (27), (28) положений
равновесия. Численно-аналитическим методом подробно исследована эволюция
областей необходимых условий устойчивости в плоскости параметров . С использованием теоремы Ляпунова получены в виде простых
неравенств достаточные условия устойчивости (24), (27), (28) положений
равновесия. Численно-аналитическим методом подробно исследована эволюция
областей необходимых условий устойчивости в плоскости параметров 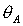 , , 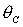 при различных
значениях параметра при различных
значениях параметра 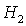 . Определены все бифуркационые значения . Определены все бифуркационые значения 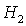 , при которых происходит качественное изменение вида областей
устойчивости. , при которых происходит качественное изменение вида областей
устойчивости.
Рассмотренной
здесь прямой задаче определения положений равновесия гиростата посвящено много
публикаций. Так, например, наиболее полное исследование всех положений
равновесия гиростата и их устойчивости проведено в [5] и [6] для случая 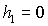 , , 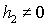 , , 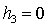 . Следует отметить также работы [7] и [8], где аналогичная
задача была решена применительно лишь к решению . Следует отметить также работы [7] и [8], где аналогичная
задача была решена применительно лишь к решению 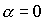 , ,  , , 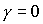 . Явный вид соотношений, определяющих все положения
равновесия (16)-(21) гиростата, и достаточные условия устойчивости, аналогичные
неравенствам (24), (27), (28), были получены в [9]. . Явный вид соотношений, определяющих все положения
равновесия (16)-(21) гиростата, и достаточные условия устойчивости, аналогичные
неравенствам (24), (27), (28), были получены в [9].
В общем
случае задачи о гиростате (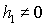 , , 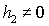 , , 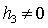 ) система уравнений (6) была, по-видимому, впервые приведена
в [5] и [10], решения (8) получены в [11]. В работе [12] система уравнений
(6)-(7) сведена к двум тригонометрическим уравнениям. И, наконец, в [3] с
использованием соотношений (8) была доказана возможность получения одного
алгебраического уравнения 12-го порядка, коэффициенты которого довольно сложно
зависят от 4 безразмерных параметров задачи. ) система уравнений (6) была, по-видимому, впервые приведена
в [5] и [10], решения (8) получены в [11]. В работе [12] система уравнений
(6)-(7) сведена к двум тригонометрическим уравнениям. И, наконец, в [3] с
использованием соотношений (8) была доказана возможность получения одного
алгебраического уравнения 12-го порядка, коэффициенты которого довольно сложно
зависят от 4 безразмерных параметров задачи.
Литература
1.
T.R. Kane, P.W. Likins, D.A. Levinson. Spacecraft Dynamics, 1983, McGraw-Hill.
2.
В.А. Сарычев. Вопросы
ориентации искусственных спутников, Итоги науки и техники. Серия “Исследование космического
пространства”, ВИНИТИ, т. 11, 1978.
3.
В.А. Сарычев, С.А. Гутник. К вопросу о положениях
относительного равновесия спутника-гиростата, Космические исследования, 1984, т. 22, №3, 323-326.
4.
А.М. Кац. К вопросу о критерии апериодической устойчивости, Приклад-ная математика и механика, 1951,
т. 15, №1, 120.
5.
R.W. Longman. The equilibria of orbiting
gyrostats with internal angular momenta along principal axes, Proc. of the Symposium on Gravity Gradient
Attitude Stabilization, El Segundo,
USA, 1968.
6.
R. Longman, P. Hagedorn, A. Beck. Stabilization due to
gyroscopic coupling in dual-spin
satellites subject to gravitational torques, Celestial Mechanics, 1981, Vol. 25, №4, 353-373.
7.
M.R.M. Crespo da Silva. Attitude
stability of a gravity-stabilized gyrostat satellite, Celestial Mechanics, 1970, Vol. 2, №2, 147-165.
8.
А.А. Анчев, В.А. Атанасов. Анализ необходимых и достаточных условий
устойчивости равновесия спутника-гиростата, Космические
исследования, 1990, т. 28, №6, 831-836.
9.
V.A. Sarychev, S.A. Mirer. Relative equilibria of a
gyrostat satellite with internal angular momentum along a principal axis, Acta Astronautica, 2001, Vol. 49, №11,
641-644.
10.
А.A. Анчев. Об устойчивости относительного
равновесия спутника с роторами, Българска
академия на науките, Известия на Математическия институт, 1968, т. 11, 149-158.
11.
В.А. Сарычев, Н.И. Яковлев. Исследование динамики
гравитационно-ориентированного спутника с маховиками, Препринт Института прикл. математики им. М.В. Келдыша АН СССР, 1973, №32.
12.
А.A. Анчев, Л. Лилов. Равновесни ориентации
на спътник-жиростат по кръгова орбита
при фиксирани вътрешни движения, Българска
академия на науките, Теоретична и приложна механика, 1978, т. 9, №4, 9-15.
|