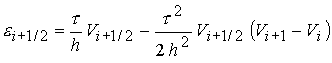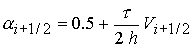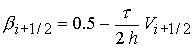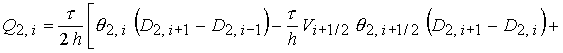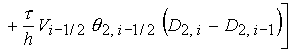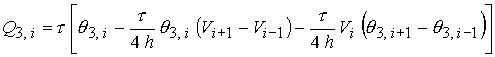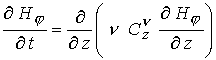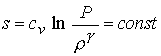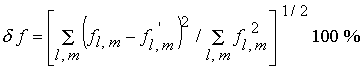В в е д е н и е
Данная
публикация посвящена выявлению качественных особенностей плазмодинамики,
связанных с новым направлением исследований, а именно,
исследований вращающихся потоков в каналах коаксиальных плазменных ускорителей
при наличии продольного магнитного поля. Дополнительное продольное магнитное
поле 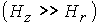 помимо традиционного
магнитного поля помимо традиционного
магнитного поля 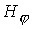 открывает новые возможности для управления
динамическими процессами. открывает новые возможности для управления
динамическими процессами.
Плазменный
ускоритель [1] схематично состоит из двух коаксиальных электродов,
подсоединенных к соответствующей электрической цепи. Между электродами по
плазме протекает ток 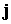 . В свою очередь протекающий по внутреннему электроду ток
порождает азимутальное магнитное поле . В свою очередь протекающий по внутреннему электроду ток
порождает азимутальное магнитное поле 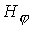 . В результате плазма ускоряется вдоль оси системы за счет амперовой силы . В результате плазма ускоряется вдоль оси системы за счет амперовой силы
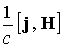 . Аналогично газодинамическому соплу в канале плазменного
ускорителя при правильной организации процесса реализуется трансзвуковое
течение так, что в середине канала с минимальной площадью поперечного сечения
происходит переход скорости потока через скорость магнитозвуковой волны. . Аналогично газодинамическому соплу в канале плазменного
ускорителя при правильной организации процесса реализуется трансзвуковое
течение так, что в середине канала с минимальной площадью поперечного сечения
происходит переход скорости потока через скорость магнитозвуковой волны.
Негативное
воздействие эффекта Холла приводит к недостатку ионов в прианодной области и,
как следствие, возникновению явления кризиса тока [1, 2]. Наряду с другими
менее существенными факторами это препятствует достижению больших скоростей в
плазменных ускорителях с непроницаемыми, сплошными электродами. Преодоление
явления кризиса тока возможно в системах типа двухступенчатого
квазистационарного плазменного ускорителя, предложенного А.И.Морозовым [3]. В ускорителях
данного типа осуществляется режим ионного токопереноса с проницаемыми
электродами. Эксперименты [4,5,6,7] подтвердили возможность
получения высокоскоростных потоков плотной плазмы (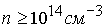 , , 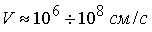 ). Такие возможности
обуславливают перспективность использования плазменных ускорителей в
космической технике в качестве электрореактивных двигателей, а также в
различных приложениях, включая термоядерные. ). Такие возможности
обуславливают перспективность использования плазменных ускорителей в
космической технике в качестве электрореактивных двигателей, а также в
различных приложениях, включая термоядерные.
Основам
теории аксиально симметричных течений плазмы посвящены обзор [8] и монография [1]. Заметная роль в
разработке квазистационарного плазменного ускорителя и понимании происходящих
процессов отводится математическим моделям [9]. Численным
исследованиям динамики плазмы и
ионизующегося газа в каналах ускорителей посвящены также обзор [10] и целый ряд других
публикаций ( см. например [11-13]). Теоретические и численные
исследования процессов в ускорителях для плотной плазмы проводятся в рамках
МГД-уравнений.
Наличие
продольного магнитного поля дает дополнительные возможности для реализации
трансзвуковых течений, позволяет исследовать течение плазмы во всем
многообразии процессов. Предшествующие двумерные численные исследования следует
рассматривать как частный случай, отвечающий динамике плазмы в отсутствии
вращения.
В работе [14] аналитически выявлено
влияние продольного магнитного поля на двумерные аксиально симметричные потоки
двухкомпонентной плазмы. Исследования проведены в рамках приближения плавного канала для уравнений идеальной
магнитной гидродинамики. Продольное поле усложняет течение, в частности,
приводит к вращению плазмы вокруг оси системы. Анализ важнейших свойств
плазменных потоков в этом случае показал, что благодаря продольному полю можно
существенно уменьшить влияние эффекта Холла и область прианодного потока.
В данной
работе представлена численная модель двумерного осе симметричного течения в
канале плазменного ускорителя при наличии продольного магнитного поля. В основу
модели положены МГД-уравнения с учетом эффекта Холла (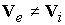 ), тензора проводимости среды и зависимости коэффициентов
переноса в магнитном поле от ), тензора проводимости среды и зависимости коэффициентов
переноса в магнитном поле от 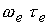 . Проведено
сопоставление результатов численного моделирования с результатами, полученными в
аналитической модели [14]. . Проведено
сопоставление результатов численного моделирования с результатами, полученными в
аналитической модели [14].
1. Уравнения двухжидкостной
магнитной газодинамики
В отсутствии диссипативных факторов уравнения
идеальной газодинамики для каждой из компонент плазмы получаются в пределе,
когда длина свободного пробега стремится к нулю и функция распределения
считается максвелловской. Коэффициенты переноса вычисляются в ряде работ,
разными методами и в разной форме. Во всех случаях предполагается, что
локальная функция распределения мало отличается от максвелловской.
Техника получения газодинамических уравнений из
кинетических была разработана Энскогом, Чепменом и Каулингом для
больцмановского столкновительного члена. Для случая столкновительного члена
Ландау эту технику развили С.И. Брагинский и Л. Спитцер.
Универсальность традиционных газодинамических уравнений
обесценивается тем, что входящие в них диссипативные величины не выражаются в
общем случае через гидродинамические параметры 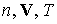 . .
В работе С.И .Брагинского [15] найдены явные выражения для
диссипативных членов в гидродинамических уравнениях. Следуя этой работе,
приведем систему уравнений переноса для двухкомпонентной простой плазмы,
состоящей из электронов и одного сорта ионов.
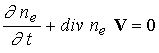 ; ; 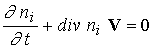 (1) (1)
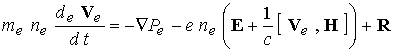  (2) (2)
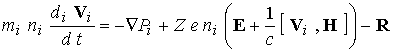  (3) (3)
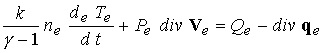 (4) (4)
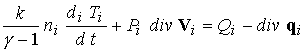 (5) (5)
где 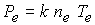 ; ; 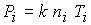 ; ; 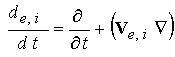
В данной системе уравнений
пренебрегаем вязкостью компонент плазмы в силу малости соответствующих диссипативных
членов по сравнению с другими слагаемыми. Для достаточно плотной среды можно
считать плазму квазинейтральной 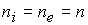 и пренебречь
инерцией электронов ( и пренебречь
инерцией электронов ( 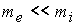 ). Соответственно из
(2) следует обобщенный закон Ома. В
рассматриваемом диапазоне параметров задачи стандартные оценки передачи тепла и
характерного времени обмена энергией между компонентами показывают, что ). Соответственно из
(2) следует обобщенный закон Ома. В
рассматриваемом диапазоне параметров задачи стандартные оценки передачи тепла и
характерного времени обмена энергией между компонентами показывают, что 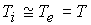 . Результаты численных экспериментов демонстрируют тот факт,
что на уравнение энергии не ложится сколько-нибудь существенной нагрузки в
общей картине динамики плазмы. Разница между температурами электронной и ионной
компонент может быть учтена в
последующих исследованиях. . Результаты численных экспериментов демонстрируют тот факт,
что на уравнение энергии не ложится сколько-нибудь существенной нагрузки в
общей картине динамики плазмы. Разница между температурами электронной и ионной
компонент может быть учтена в
последующих исследованиях.
Уравнения переноса замыкаются уравнениями Максвелла, в
которых пренебрегаем током смещения. Далее ограничимся исследованием динамики
водородной плазмы ( 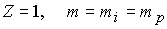 ), часто используемой
в экспериментах. ), часто используемой
в экспериментах.
В результате несложных преобразований исходных уравнений
переноса с учетом уравнения индукции магнитного поля и сделанных выше
предположений получим следующую систему уравнений:
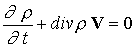 ; ; 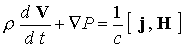 (6) (6)
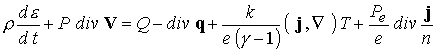 (7) (7)
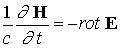 ; ; 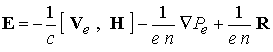 (8) (8)
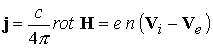 ; ; 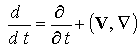 (9) (9)
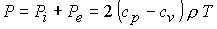 ; ; 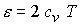 ; ; 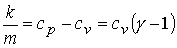
Здесь
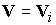 , , 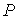 - суммарное
давление, - суммарное
давление, 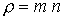 - плотность тяжелых
частиц, - плотность тяжелых
частиц, 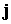 - электрический ток; - электрический ток; 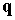 - тепловой поток. - тепловой поток.
2. Коэффициенты переноса.
Коэффициенты
переноса в магнитном поле зависят от 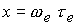 , где , где 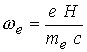 -циклотронная частота
электронов, -циклотронная частота
электронов, 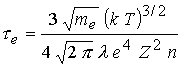 - электронное время
между столкновениями, - электронное время
между столкновениями, 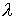 - кулоновский логарифм. - кулоновский логарифм.
Передача импульса
путем столкновений от
ионов к электронам 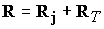 складывается из силы
трения складывается из силы
трения 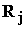 , обусловленной
наличием относительной скорости , обусловленной
наличием относительной скорости 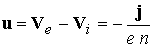 , и термосилы , и термосилы 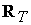 , связанной с
градиентом температуры. , связанной с
градиентом температуры.
В
соответствии с работой [15]
имеем
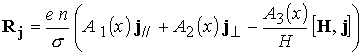 (10) (10)
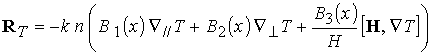 (11) (11)
Здесь
 и и 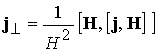 - компоненты вектора, параллельного и
перпендикулярного к магнитному полю; - компоненты вектора, параллельного и
перпендикулярного к магнитному полю;
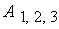 и и 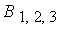 - известные функции переменной величины - известные функции переменной величины 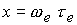 ; ;
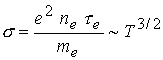 - электропроводность среды. - электропроводность среды.
Электронный
поток тепла также складывается из двух частей

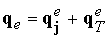 . Потоком тепла . Потоком тепла 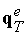 , обусловленным
градиентом температуры, можно пренебречь , обусловленным
градиентом температуры, можно пренебречь
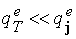 . Кроме того, ионный поток тепла существенно
меньше электронного и им также можно пренебречь ( . Кроме того, ионный поток тепла существенно
меньше электронного и им также можно пренебречь (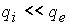 ). Поэтому ). Поэтому
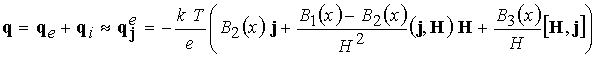
Суммарное
тепло, выделяющиеся вследствие столкновений, равно
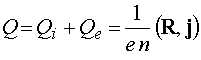 (12) (12)
3. Модифицированные МГД-уравнения в осесимметричном случае.
Уравнения (6) - (12)
преобразуем и запишем
в безразмерном виде.
В качестве единиц измерения
выберем размерные константы: 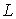 - длина канала; - длина канала; 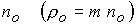 , , 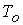 , , 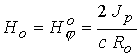 - характерные
значения концентрации, температуры и азимутальной составляющей магнитного поля
на входе в канал, где - характерные
значения концентрации, температуры и азимутальной составляющей магнитного поля
на входе в канал, где 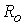 - радиус внешнего
электрода, - радиус внешнего
электрода, 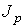 - разрядный ток в системе. С помощью
перечисленных величин формируются единицы : давления - - разрядный ток в системе. С помощью
перечисленных величин формируются единицы : давления - 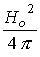 , скорости – , скорости – 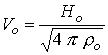 (характерная
альфвеновская скорость), времени - (характерная
альфвеновская скорость), времени - 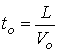 (’’пролетное” время),
напряженности электрического поля - (’’пролетное” время),
напряженности электрического поля - 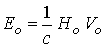 и плотности тока - и плотности тока - 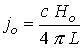 . Связь исходных размерных величин с безразмерными
параметрами, участвующими в задаче, определяется следующим образом: . Связь исходных размерных величин с безразмерными
параметрами, участвующими в задаче, определяется следующим образом: 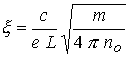 - локальный параметр
обмена, характеризующий роль эффекта Холла в двухжидкостной модели; - локальный параметр
обмена, характеризующий роль эффекта Холла в двухжидкостной модели; 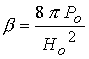 - отношение газового
и магнитного давлений на входе, где - отношение газового
и магнитного давлений на входе, где  ; ; 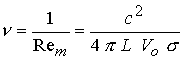 - магнитная вязкость, обратно пропорциональная
магнитному числу Рейнольдса с характерным значением спитцеровской
проводимости - магнитная вязкость, обратно пропорциональная
магнитному числу Рейнольдса с характерным значением спитцеровской
проводимости 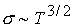 . Отсюда следует, что . Отсюда следует, что
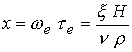 (13) (13)
При численном интегрировании многомерной МГД-задачи должно
быть выполнено условие бездивергентности магнитного поля (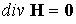 ). Существует несколько подходов для обеспечения
соленоидальности магнитного поля ( см., например, [16]). Самый простой
способ состоит в том, чтобы переписать уравнения с учетом векторного потенциала ). Существует несколько подходов для обеспечения
соленоидальности магнитного поля ( см., например, [16]). Самый простой
способ состоит в том, чтобы переписать уравнения с учетом векторного потенциала
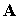 ( (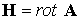 ). Такой подход становится особенно очевидным, если решается
осе симметричная задача ( ). Такой подход становится особенно очевидным, если решается
осе симметричная задача ( 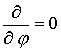 ). Действительно, в
цилиндрической системе координат имеем ). Действительно, в
цилиндрической системе координат имеем
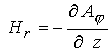 ; ; 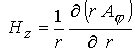 (14) (14)
где 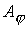 - тороидальная компонента векторного потенциала - тороидальная компонента векторного потенциала 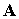 . Соотношения (14) в аксиально симметричном
случае обеспечивают точное выполнение условия . Соотношения (14) в аксиально симметричном
случае обеспечивают точное выполнение условия
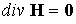 . Правда, в уравнениях импульсов нужно будет аппроксимировать
вторые производные векторного потенциала. Как показали результаты численного
моделирования рассматриваемой задачи, в расчетах не наблюдается выбросов в
распределении вторых производных и разворотов тока . Правда, в уравнениях импульсов нужно будет аппроксимировать
вторые производные векторного потенциала. Как показали результаты численного
моделирования рассматриваемой задачи, в расчетах не наблюдается выбросов в
распределении вторых производных и разворотов тока  . .
С учетом сделанных выше замечаний в осе
симметричном случае уравнения (6) – (9) в безразмерной форме можно записать в
терминах 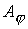 -компоненты векторного потенциала и -компоненты векторного потенциала и 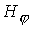 -компоненты магнитного поля
: -компоненты магнитного поля
:
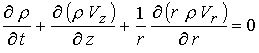 (15) (15)
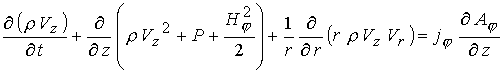 (16)
(16)
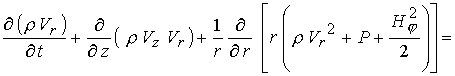
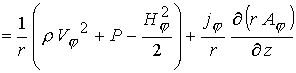 (17) (17)
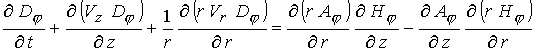 (18)
(18)

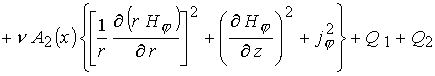 (19) (19)
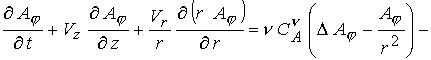
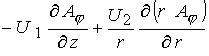 (20) (20)

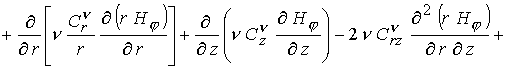
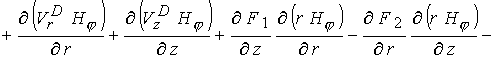
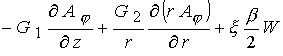 (21) (21)
В данных уравнениях
дополнительно введены следующие обозначения:
 , , 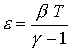 , , 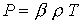 , ,
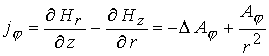 - тороидальная компонента тока, где - тороидальная компонента тока, где
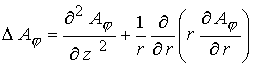
Коэффициенты
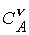 , , 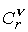 , , 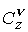 , , 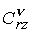 выражаются через
известные функции выражаются через
известные функции 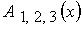 и и 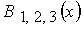 , в
которых параметр Холла , в
которых параметр Холла
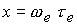 определяется
соотношением (13) : определяется
соотношением (13) :
  ; ; 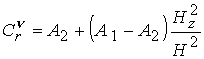 ; ;
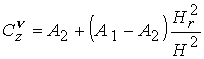 ; ; 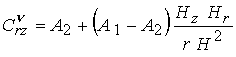
Согласно
экспериментальным данным [4 - 7]
безразмерные
параметры 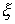 , , 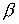 и и 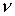 , как правило, существенно меньше единицы. Уравнения (15) – (21)
содержат функции , как правило, существенно меньше единицы. Уравнения (15) – (21)
содержат функции 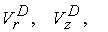 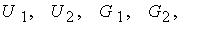  , зависящие от переменных задачи и пропорциональные
параметрам , зависящие от переменных задачи и пропорциональные
параметрам 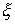 , , 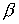 и и 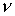 . Поэтому на гладких решениях все слагаемые в уравнениях, содержащие
указанные функции, можно рассматривать как маленькие добавки, не оказывающие
значительного влияния на динамику плазмы в целом. . Поэтому на гладких решениях все слагаемые в уравнениях, содержащие
указанные функции, можно рассматривать как маленькие добавки, не оказывающие
значительного влияния на динамику плазмы в целом.
Доступные
автору литературные источники указывают на то, что данное исследование можно
рассматривать как одну из первых попыток полномасштабного решения МГД-уравнений
с учетом вращения, тензора проводимости среды и зависимости коэффициентов
переноса в магнитном поле от 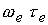 . Только этим может быть оправдана следующая
часть препринта : . Только этим может быть оправдана следующая
часть препринта :
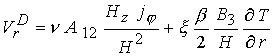 ; ; 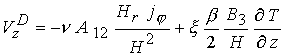 ; ;
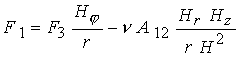 ; ; 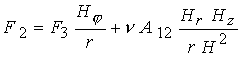 ; ;
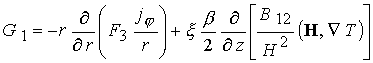 ; ;
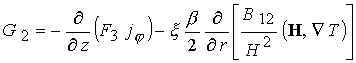 ; ;
 ; ; 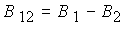 ; ; 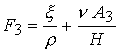 ; ;
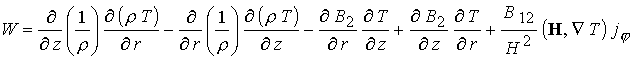
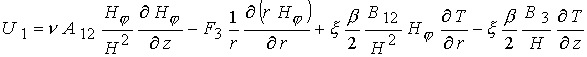 ; ;
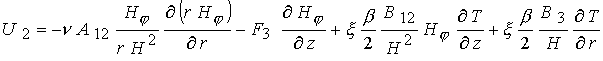 ; ;
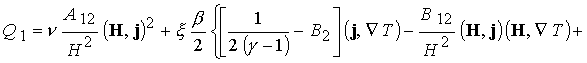
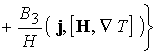 ; ;
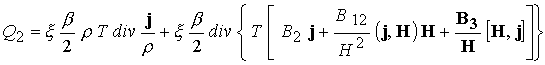
В уравнении энергии (19)
основной вклад в выделение энергии за счет трения вносит отдельно
представленное слагаемое 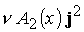 . В итоге имеем 7
уравнений для переменных . В итоге имеем 7
уравнений для переменных 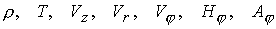 . .
4. Постановка задачи.
В данной работе динамика плазмы исследуется в предположении
аксиальной симметрии течения ( 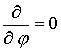 ). Уравнения (15) - (21) рассматриваются
в области переменных ). Уравнения (15) - (21) рассматриваются
в области переменных 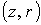 , соответствующей форме канала, изображенного на рис.1 .
Криволинейная расчетная область отображается на единичный квадрат с помощью
переменных , соответствующей форме канала, изображенного на рис.1 .
Криволинейная расчетная область отображается на единичный квадрат с помощью
переменных 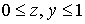 так, что так, что
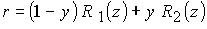 (22) (22)
где 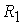 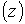 и и 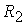 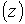 описывают форму
соответственно внутреннего и внешнего электродов. Производные по новым
координатам связаны с производными по старым координатам следующими
соотношениями: описывают форму
соответственно внутреннего и внешнего электродов. Производные по новым
координатам связаны с производными по старым координатам следующими
соотношениями: 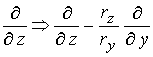 ; ; 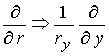 , где , где 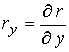 , , 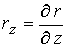 - соответствующие
производные функции (22). Используя их, уравнения переписывается в дивергентном
виде и численно интегрируется. Так, например, уравнение непрерывности (15)
записывается в виде - соответствующие
производные функции (22). Используя их, уравнения переписывается в дивергентном
виде и численно интегрируется. Так, например, уравнение непрерывности (15)
записывается в виде
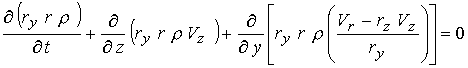
Уравнения и условия
на границах определяют динамику потока.
На входе в канале 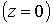 полагаем, что плазма
подается с известными значениями
плотности и температуры полагаем, что плазма
подается с известными значениями
плотности и температуры 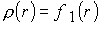 , ,  . .
Если не рассматривается дополнительное
уравнение электрической цепи [17], считаем, что ток поддерживается постоянным и на
входе поступает в систему только через электроды, т.е. 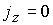 при при 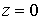 или или 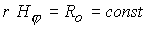 , где , где  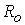 характерное значение радиуса. характерное значение радиуса.
Естественно
предположить, что подача плазмы осуществляется вдоль определенного направления,
например, вдоль координатных линий.
Азимутальную
скорость при 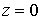 считаем равной
нулю считаем равной
нулю 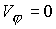 , т.е. плазма во
входном сечении не вращается. , т.е. плазма во
входном сечении не вращается.
Кроме
того, зададим на входе 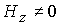 . Следуя работе [14], имеем при . Следуя работе [14], имеем при 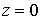 : : 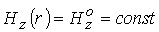 . Из (14)
получим . Из (14)
получим 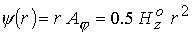 . .
На
выходе ( 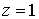 ) предполагается
свободное ( сверхзвуковое ) вытекание плазмы. ) предполагается
свободное ( сверхзвуковое ) вытекание плазмы.
Более
подробно рассмотрим граничные условия на электродах. Динамика плазмы в
ускорителях исследуется в разных
режимах токопереноса. В режиме электронного токопереноса линии тока ионной
компоненты плазмы лежат на поверхности
непроницаемых электродов: катода и анода. При этом, электроды не являются эквипотенциальными. Наоборот, в режиме
ионного токопереноса электроды
представляют собой эквипотенциальные поверхности. В этом случае они
должны быть прозрачными для плазмы, поступающей сквозь них в канал. В основе
большинства экспериментов [4-7] и соответственно моделей [9, 11, 12] лежит ионный токоперенос.
В данной
работе также предпочтем режим ионного токопереноса. Следуя экспериментам,
полагаем, что внешний электрод является анодом. На поверхности коаксиальных
электродов и соответствующих границах плазменного объема тангенциальная
составляющая электрического поля равна нулю 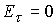 . Разность потенциалов между электродами определяется
динамикой плазмы внутри канала и процессами в электрической цепи. Вектор . Разность потенциалов между электродами определяется
динамикой плазмы внутри канала и процессами в электрической цепи. Вектор 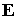 вычисляется с помощью
обобщенного закона Ома (8), имеющего в безразмерной форме следующий вид: вычисляется с помощью
обобщенного закона Ома (8), имеющего в безразмерной форме следующий вид:
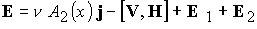 (23) (23)
 , ,
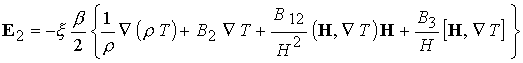
Обозначим 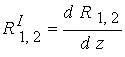 , где функции , где функции 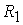 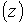 и и 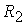 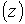 определяют профили
соответственно катода и анода.
Условие определяют профили
соответственно катода и анода.
Условие 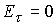 приводит к
соотношению приводит к
соотношению
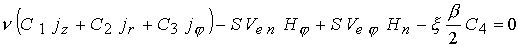 (24) (24)
где 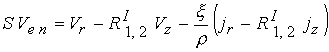 ; ; 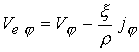 ; ;
 ; ; 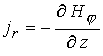 ; ; 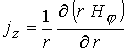 ; ;
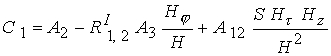 ; ;
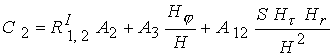 ; ; 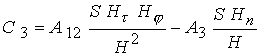 ; ;
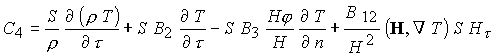 ; ;
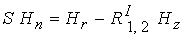 ; ; 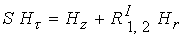 . .
При наличии продольного магнитного поля соотношение (24) на
электродах следует дополнить условием на магнитное поле. В магнитной
плазмодинамике 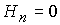 - типичное и естественное условие, связывающие компоненты магнитного
поля на границе плазма – проводник. Оно приводит, в частности, к сохранению
магнитного потока вдоль канала. Поэтому в рассматриваемом случае ионного
токопереноса данное условие также является одним из допустимых условий на
поверхности электродов. - типичное и естественное условие, связывающие компоненты магнитного
поля на границе плазма – проводник. Оно приводит, в частности, к сохранению
магнитного потока вдоль канала. Поэтому в рассматриваемом случае ионного
токопереноса данное условие также является одним из допустимых условий на
поверхности электродов.
Таким образом, простейшая постановка задачи предполагает,
что на электродах, ограничивающих исследуемый плазменный объем, выполнены по
крайней мере два условия: 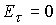 и и 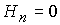 . .
Далее представлены некоторые соображения, позволяющие
определить минимальное количество граничных условий, необходимое для корректной
постановки задачи.
Переход к вектор потенциалу 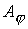 - это не только один
из способов исключения численного магнитного заряда. Такой переход сокращает
число уравнений : вместо двух уравнений
для - это не только один
из способов исключения численного магнитного заряда. Такой переход сокращает
число уравнений : вместо двух уравнений
для 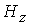 и и 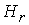 решается одно
уравнение для решается одно
уравнение для 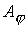 . Однако не следует
забывать, что по сути речь идет о решении традиционной системы МГД-уравнений,
которая в отсутствии диссипаций и в одно-жидкостном приближении превращается в
систему уравнений идеальной магнитной газодинамики, т.е. в гиперболическую
систему квазилинейных уравнений. . Однако не следует
забывать, что по сути речь идет о решении традиционной системы МГД-уравнений,
которая в отсутствии диссипаций и в одно-жидкостном приближении превращается в
систему уравнений идеальной магнитной газодинамики, т.е. в гиперболическую
систему квазилинейных уравнений.
Выберем направление 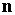 по нормали к поверхности электродов и
рассмотрим простейшую одномерную систему МГД-уравнений в этом направлении.
Решение соответствующего характеристического уравнения дает следующие
собственные значения по нормали к поверхности электродов и
рассмотрим простейшую одномерную систему МГД-уравнений в этом направлении.
Решение соответствующего характеристического уравнения дает следующие
собственные значения
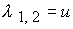 ; ; 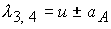 ; ; 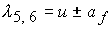 ; ; 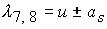 , где , где 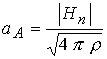 ; ;
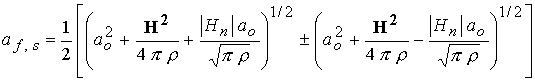
Здесь 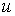 - скорость среды, - скорость среды, 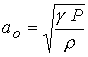 - скорость звука в среде при отсутствии
магнитного поля. Величины - скорость звука в среде при отсутствии
магнитного поля. Величины 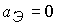 , , 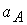 , , 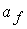 и и 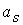 определяют
соответственно скорости распространения энтропийных, альфвеновских, быстрых и
медленных магнитозвуковых волн и возмущений относительно среды по направлению
нормали к поверхности электродов и в противоположном направлении. определяют
соответственно скорости распространения энтропийных, альфвеновских, быстрых и
медленных магнитозвуковых волн и возмущений относительно среды по направлению
нормали к поверхности электродов и в противоположном направлении.
Видно, что при условии 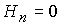 на поверхности
электродов соответствующие характеристические скорости вырождаются. В режиме
ионного токопереноса с ”прозрачными” электродами на поверхности
анода и
катода может происходить соответственно втекание и вытекание плазмы с очень
малой нормальной составляющей скорости на поверхности
электродов соответствующие характеристические скорости вырождаются. В режиме
ионного токопереноса с ”прозрачными” электродами на поверхности
анода и
катода может происходить соответственно втекание и вытекание плазмы с очень
малой нормальной составляющей скорости 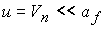 . Следовательно, на аноде две характеристики
являются входящими в область, и минимальное число граничных условий равно двум.
На катоде при условии . Следовательно, на аноде две характеристики
являются входящими в область, и минимальное число граничных условий равно двум.
На катоде при условии 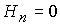 (одно граничное
условие) одна характеристика входит в область и необходимо поставить еще одно,
второе граничное условие, например, (одно граничное
условие) одна характеристика входит в область и необходимо поставить еще одно,
второе граничное условие, например, 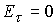 . .
Для того, чтобы сопоставить результаты численного
моделирования с аналитическим решением [14], на аноде, где происходит
втекание плазмы, помимо условий 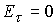 и и 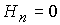 следует задать
значения плотности и азимутальной скорости следует задать
значения плотности и азимутальной скорости
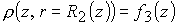 ; ; 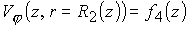
где функции 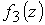 и и 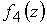 (также как (также как 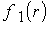 , , 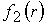 на входе)
определяются в аналитической модели. на входе)
определяются в аналитической модели.
5. Метод численного решения.
Численные исследования в плазмодинамике, как
правило, не ограничиваются решением гиперболической системы МГД-уравнений для
идеально проводящей плазмы. Диффузия в плазме играет существенную роль. Учет
диффузии предполагает решение параболических систем дифференциальных уравнений.
Кроме того, детальное моделирование таких процессов, как ионизация и
рекомбинация, приводит к необходимости использовать программы для решения
жестких систем дифференциальных уравнений.
В настоящее время разработано большое количество численных
методов, в частности, для решения систем уравнений гиперболического типа,
записанных в форме законов сохранения и в неконсервативном виде. К ним
относятся методы сквозного счета и методы с выделением разрывов, включая
использование само подстраивающихся сеток, методы различного порядка точности,
явные и неявные методы, методы коррекции потоков, монотонные схемы с не
возрастанием полной вариации и т.д.
В данной работе речь идет об исследовании процессов на
качественном уровне и решении новой, в физическом плане, задачи. В этом случае
достаточно ограничиться набором методов, хорошо зарекомендовавших себя, часто
используемых и вполне апробированных на рассматриваемом классе явлений.
Конкретный выбор методов обусловлен спецификой задачи и может зависеть от
вкусов пользователя.
Поиск решения модифицированной системы двумерных
нестационарных МГД-уравнений осуществляется в ограниченном объеме. При этом
граничные условия в полной мере определяют процессы не только в приграничных
областях, но и в основном потоке плазмы.
В данной
численной модели вращающихся осе симметричных
потоков проводится расщепление
по физическим факторам и координатам 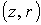 или или 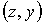 с учетом (22). с учетом (22).
В расчете переноса с коррекцией потоков воспользуемся
алгоритмом SHASTA-FCT [18-22]. Этот алгоритм применяется
к обобщенному уравнению переноса для величины уравнению переноса для величины 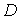 
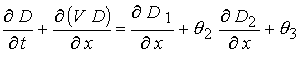 (25) (25)
Данный алгоритм достаточно
часто используется в практических расчетах (см., например, [23-24]
) и для
сравнения с результатами вычислений по новым методикам. Выпишем для
определенности разностную схему
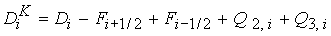 (26) (26)
где 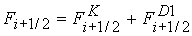 - разностная аппроксимация дивергентной части
(25), - разностная аппроксимация дивергентной части
(25), 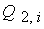 - аппроксимация
слагаемого - аппроксимация
слагаемого 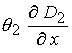 , , 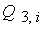 - соответственно источника - соответственно источника 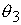 . Слагаемое . Слагаемое
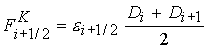 (27) (27)
отвечает конвективному
переносу, где
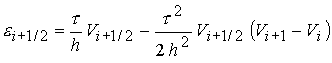
Кроме того,
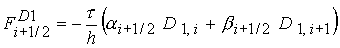 ; ;
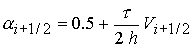 ; ; 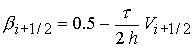 ; (28) ; (28)
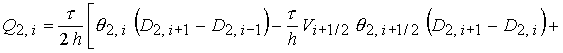
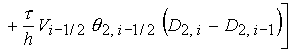 ; ;
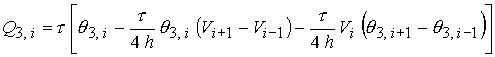
Здесь 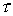 - шаг по
времени, - шаг по
времени, 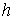 - шаг по координате. Для компенсации внесенной
численной вязкости и сохранения положительности решения добавляются
антидиффузионные потоки, которые не должны приводить к образованию новых
экстремумов и увеличивать уже существующие, - шаг по координате. Для компенсации внесенной
численной вязкости и сохранения положительности решения добавляются
антидиффузионные потоки, которые не должны приводить к образованию новых
экстремумов и увеличивать уже существующие,
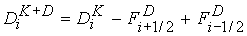 , (29) , (29)
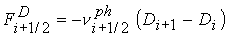 ; ; 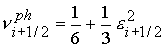
Далее осуществляется коррекция:
(30)
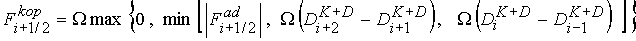
где 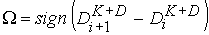 . В данной работе используется так называемая
фениксная коррекция и не скорректированный антидиффузионный поток равен . В данной работе используется так называемая
фениксная коррекция и не скорректированный антидиффузионный поток равен
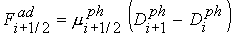 (31) (31)
где 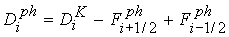 ; ;  ; ;
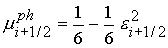 ; ; 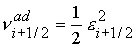
Окончательно имеем
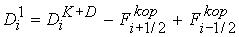 (32) (32)
Продвижение величины 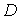 на следующий
временной слой осуществляется в несколько этапов. На первом этапе по формулам
(26) – (31) проводится расчет всех величин на на следующий
временной слой осуществляется в несколько этапов. На первом этапе по формулам
(26) – (31) проводится расчет всех величин на 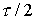 . Затем с их помощью пересчитываются коэффициенты в формулах
и осуществляется расчет с шагом . Затем с их помощью пересчитываются коэффициенты в формулах
и осуществляется расчет с шагом  . Такая процедура производится раздельно по координатам . Такая процедура производится раздельно по координатам 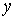 и и 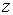 , т.е. используется покоординатное расщепление. Симметризация
( , т.е. используется покоординатное расщепление. Симметризация
(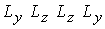 ) завершает переход
на следующий временной слой для всех величин. ) завершает переход
на следующий временной слой для всех величин.
Учет диссипативных факторов производится отдельно.
Теплопроводностью среды в данном исследовании можно пренебречь, а вот конечную
проводимость следует учитывать. Электропроводность плазмы вдоль и поперек
магнитного поля имеет разные значения. Это приводит к необходимости решать
уравнение параболического типа с различными коэффициентами вдоль и поперек
канала. Например, учет диффузии в уравнении (21) для 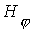 - составляющей магнитного поля в результате покоординатного
расщепления предполагает решение уравнения типа - составляющей магнитного поля в результате покоординатного
расщепления предполагает решение уравнения типа 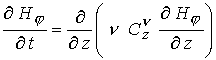 в продольном направлении.
Аналогичное уравнение решается в поперечном направлении с другим коэффициентом
диффузии. На данном этапе исследований возникновение больших градиентов не
ожидается. Тем не менее, применяется
потоковый вариант метода прогонки для разностных задач с сильно меняющимися
коэффициентами [25]. в продольном направлении.
Аналогичное уравнение решается в поперечном направлении с другим коэффициентом
диффузии. На данном этапе исследований возникновение больших градиентов не
ожидается. Тем не менее, применяется
потоковый вариант метода прогонки для разностных задач с сильно меняющимися
коэффициентами [25].
6. Сопоставление с аналитическим
решением.
В рамках представленной численной модели произведены
тестовые расчеты для сопоставления с имеющимся аналитическим решением [14]. В соответствии с экспериментальными
данными выберем в качестве характерных единиц задачи, например, следующие
значения концентрации 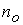 , температуры , температуры 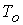 , разрядного тока , разрядного тока 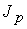 и длины канала: и длины канала:
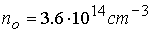 ; ; 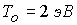 ; ;  ; ; 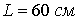
В этом случае безразмерные
параметры задачи равны
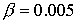 ; ; 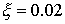 ; ; 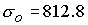 ; ;
При 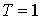 и и 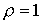 имеем имеем 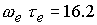 и и 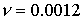 . В потоке плазмы
характерное значение спитцеровской проводимости зависит от температуры: . В потоке плазмы
характерное значение спитцеровской проводимости зависит от температуры: 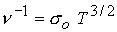 , а , а 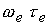 меняется согласно
(13). меняется согласно
(13).
Величина
продольного магнитного поля на входе в канал равна 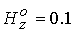 . Геометрия канала
задана профилями электродов . Геометрия канала
задана профилями электродов 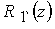 и и 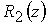 , приведенными на рис. 1 ,
и также соответствует работе [14]. Расчеты проведены на
сетке (21х21). В тестовых расчетах интегрирование уравнения энергии заменяется
предположением об изэнтропичности течения ( энтропия , приведенными на рис. 1 ,
и также соответствует работе [14]. Расчеты проведены на
сетке (21х21). В тестовых расчетах интегрирование уравнения энергии заменяется
предположением об изэнтропичности течения ( энтропия 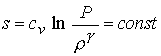 или в
безразмерных переменных или в
безразмерных переменных 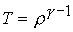 ). ).
Численное решение исходной нестационарной задачи
осуществляется до установления течения. Характерное время установления течения
по порядку величины равно единице времени
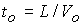 или характерному “пролетному” времени. или характерному “пролетному” времени.
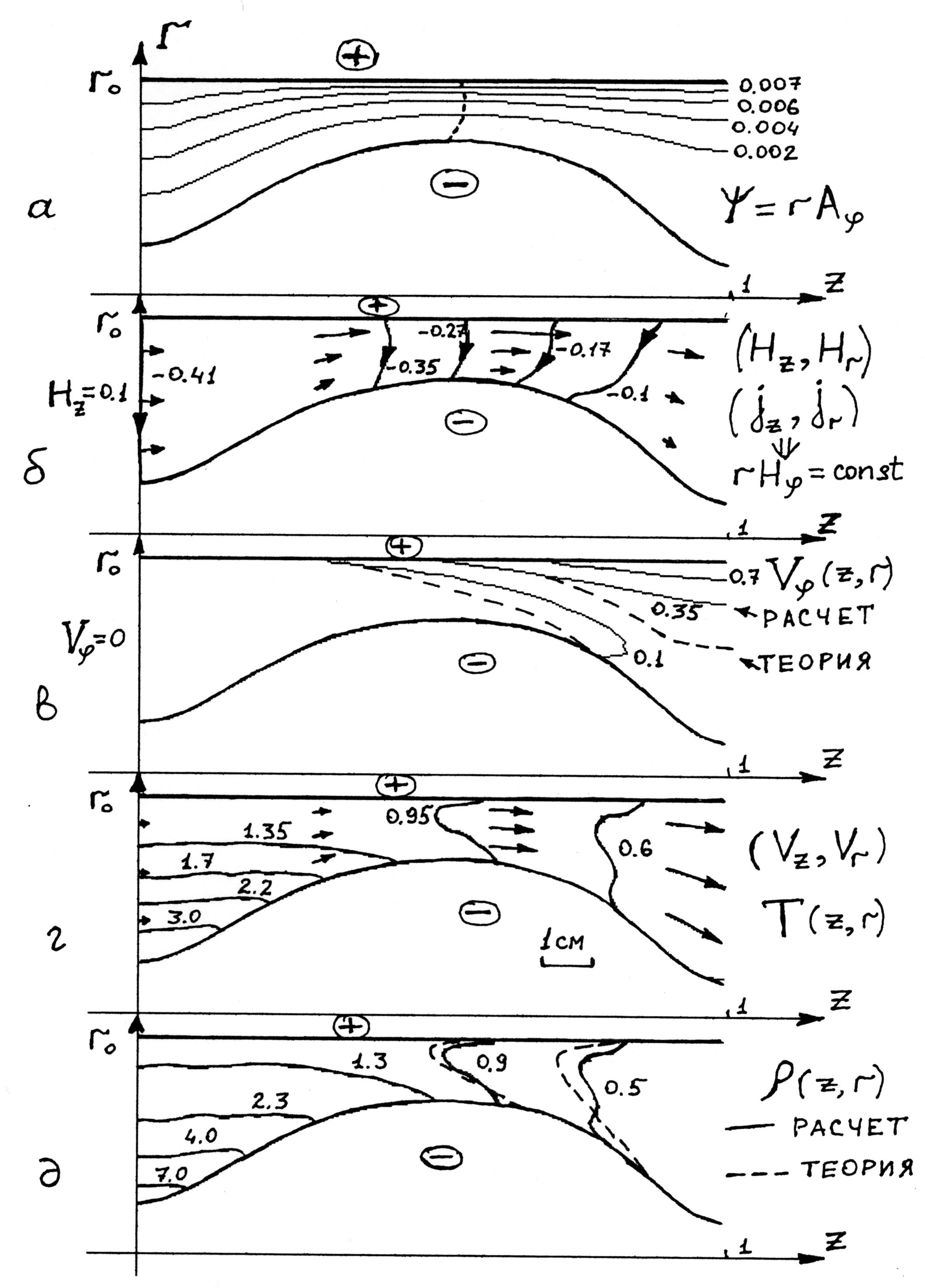
На рис.1 представлено установившееся трансзвуковое течение
в режиме ионного токопереноса при наличии продольного магнитного поля. Здесь
изображены: а – линии уровня
функции 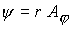 или магнитного
потока; б – электрический ток или магнитного
потока; б – электрический ток 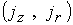 ( линии уровня
функции ( линии уровня
функции 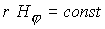 ) и векторное
распределение магнитного поля ) и векторное
распределение магнитного поля 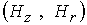 ; в
– азимутальная скорость ионов ( сплошные линии ); г – векторное поле скоростей ионной компоненты ; в
– азимутальная скорость ионов ( сплошные линии ); г – векторное поле скоростей ионной компоненты 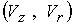 и распределение
температуры и распределение
температуры 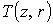 ; д – линии уровня
функции ; д – линии уровня
функции 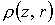 ( сплошные кривые ).
Длина векторов на рис. 1-г (в сантиметрах) равна безразмерному значению
скорости в данной точке. ( сплошные кривые ).
Длина векторов на рис. 1-г (в сантиметрах) равна безразмерному значению
скорости в данной точке.
Видно (пунктир на рис. 1-а ), что в середине канала
скорость потока переходит через местную скорость быстрой магнитозвуковой волны.
Азимутальная скорость (рис. 1-в) имеет максимальные значения в окрестности
анода ближе к выходу из канала ускорителя. В экспериментах при определенных
условиях в отсутствии продольного поля в этой области за счет эффекта Холла
возникает недостаток ионов, сопровождающийся явлением кризиса тока и срывом
процесса ускорения. Решение этой проблемы возможно, в частности, путем введения
в систему небольшого продольного магнитного поля и благодаря возникающему
вращению плазмы, ее отжатию к аноду за счет “центробежных”
сил.
Далее сопоставим результаты расчета установившегося течения
плазмы и аналитическое решение. Эти решения не обязаны совпадать, поскольку
аналитическая модель [14] построена в приближении плавного канала для
МГД-уравнений идеальной двухкомпонентной холодной ( 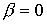 ) плазмы. ) плазмы.
Наиболее заметные отличия аналитической модели
характеризуются на рис. 1 штриховыми
линиями, соответствующими ближайшим сплошным линиям уровня искомых функций в
полной МГД-модели. Принципиальных качественных отличий двух решений не
наблюдается, а идеального количественного совпадения и не должно быть.
Количественной характеристикой сопоставления двух моделей
может служить разница двух решений в норме 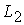 . Для искомых
переменных задачи соответствующие среднеквадратичные отклонения равны: . Для искомых
переменных задачи соответствующие среднеквадратичные отклонения равны:
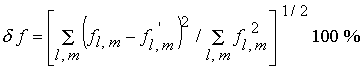
|
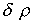
|
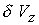
|
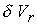
|
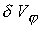
|
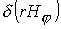
|
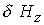
|
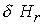
|
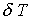
|
|
6.8
|
9.4
|
34.1
|
31.7
|
7.1
|
3.1
|
26.9
|
5.2
|
Данные результаты также говорят об удовлетворительном
соответствии двух моделей.
В дальнейших публикациях будут представлены более детальные
исследования в рамках полной МГД-модели для различных параметров задачи и
условий подачи плазмы на входе и аноде.
Выводы и заключение
Разработана двумерная численная модель для исследования
вращающихся осе симметричных потоков плазмы на основе МГД-уравнений с учетом
эффекта Холла и тензора проводимости среды. Результаты расчетов в данной модели
соответствуют полученному ранее аналитическому решению [14].
Литература
1.
Морозов А.И. Физические основы космических электрореактивных
двигателей. М.: Атомиздат, 1978.
2.
Энциклопедия низкотемпературной плазмы. / Под ред. В.Е.Фортова. М.: Наука, 2000, т. III, с. 389.
3.
Морозов А.И. Принципы коаксиальных
(квази)стационарных плазменных
ускорителей (КСПУ). // Физика плазмы, 1990, т.16, вып. 2, с. 131-146.
4.
Волошко А.Ю., Гаркуша И.Е., Морозов А.И., Соляков Д.Г., Терешин В.И.,
Царенко А.В., Чеботарев В.В. Исследование локальной картины течения плазмы
в двухступенчатом КСПУ. // Физика плазмы, 1990, т.
16, вып. 2, с. 168-175.
5. Белан В.Г.,
Золотарев С.П., Левашов В.Ф., Майнашев В.С., Морозов А.И., Подковыров В.Л.,
Скворцов Ю.В. Экспериментальное исследование квазистационарного плазменного
ускорителя, питаемого от индуктивного и емкостного накопителей. //
Там же, с. 176-185.
6.
Ананин С.И., Асташинский В.М., Баканович Г.И.,
Костюкевич Е.А., Кузмицкий А.М., Маньковский А.А., Минько Л.Я., Морозов А.И.
Исследо-вание процессов формирования плазменных потоков в квазистационарном
сильноточном плазменном ускорителе (КСПУ). // Там же, с. 186-196.
7. Alexandrov
V.A., Dyakonov G.A., Popov G.A., Tikhonov V.B., Tyutin V.K. Research of the
influence of acceleration channel geometry and external magnetic field on modes
of plasma flow in quasistationary plasma accelerator (QSPA) P-50A. // II-nd German-Russian conference on electric
propulsion engines and their technical applications. Moscow Aviation Institute,
1993, c. 10.
8.
Морозов А.И., Соловьев Л.С. Стационарные течения плазмы в
магнитном
поле.// В сб. ’’ Вопросы теории
плазмы’’ под ред. Леонтовича М.А., М.:
Атомиздат, 1974, вып. 8 , с.
3-87.
9.
Брушлинский К.В., Заборов А.М., Козлов А.Н., Морозов А.И., Савельев
В.В. Численное моделирование течений плазмы в КСПУ. // Физика плазмы, 1990, т.
16, вып. 2, с. 147-157.
10. Брушлинский К.В.,
Морозов А.И. Расчет двумерных течений плазмы в каналах. // В сб. ’’ Вопросы теории плазмы’’ под ред. Леонтовича М.А., М.: Атомиздат, 1974, вып. 8 , с. 88-163.
11. Брушлинский
К.В., Козлов А.Н., Морозов А.И. Численное исследование двумерных течений
плазмы и ионизующегося газа методом пробных частиц. // Физика плазмы,
1985, т. 11, вып. 11, с. 1358-1367.
12. Козлов А.Н.
Особенности динамики плазмы в КСПУ в процессе установления течения. // Физика плазмы,
1992, т. 18, вып. 6, с.714-723.
13. Kozlov
A.N. Ionization
and recombination kinetics in a plasma accelerator channel. //
Fluid Dynamics, 2000, v. 35, N 5, pp. 784-790.
14. Kozlov
A.N. Influence
of a longitudinal magnetic field on the Hall effect in the plasma accelerator
channel. // Fluid Dynamics, 2003, v. 38,
N 4, pp.
653-661.
15. Брагинский С.И.
Явление переноса в плазме . В сб. ’’Вопросы теории плазмы’’ под ред. Леонтовича М.А., М.: Госатомиздат, 1963, вып. 1 , с.
183-272.
16. Куликовский А.Г.,
Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения
гиперболических систем уравнений. М.: Физматлит, 2001.
17. Козлов А.Н.
Моделирование двумерных течений ионизующегося газа и плазмы в коаксиальном
ускорителе с учетом теплопроводности, излучения и процессов в электрической
цепи. Препринт ИПМ им. М.В.Келдыша АН СССР,
№ 186, 1985.
18. Boris
J.P., Book D.L. Flux-corrected transport. I. SHASTA, a fluid transport
algorithm that works. J. Comput. Phys.,1973, v. 11, N 1, pp.38-69.
19. Boris
J.P., Book D.L., Hain K. Flux-corrected transport. II. Generalization of the
method. J. Comput. Phys.,1975, v. 18, N 3, pp.248-283.
20. Boris
J.P., Book D.L. Flux-corrected transport. III. Minimal-error FCT algorithm. J.
Comput. Phys.,1976, v. 20, N 4, pp.397-431.
21. Борис Д.П., Бук Д.Л.
В сб. “Управляемый термоядерный синтез”
под ред. Дж. Киллина, М.: Мир, 1980, с.92-140.
22. Оран Э., Борис Д.П. Численное моделирование
реагирующих потоков . М.: Мир , 1990.
23. Савельев В.В.
МГД-задача о динамике входа плазменной струи в антипробочную ловушку. Препринт
ИПМ им. М.В.Келдыша РАН, № 89, 1992.
24. Toropin
Y.M., Toropina O.D., Savelyev V.V., Chechetkin V.M., Lovelace R.V.E. Spherical
bondi accretion onto a magnetic dipole. Astrophysical Journal, 1999, 517, pp.
906-918.
25. Дегтярев Л.М.,
Фаворский А.П. Потоковый вариант метода
прогонки для разностных задач с сильно меняющимися коэффициентами . ЖВМ и МФ,
1969, т. 9, N 1,
c. 211-218.
|
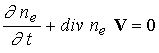
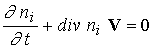
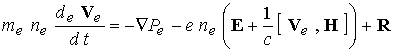
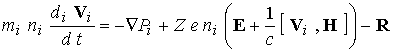
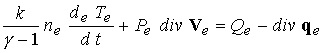
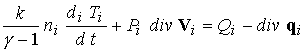
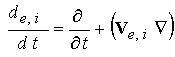
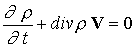
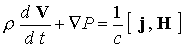
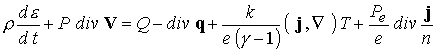
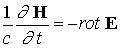
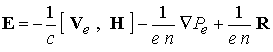
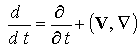
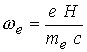
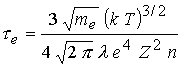
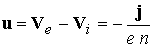
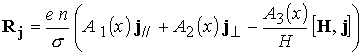
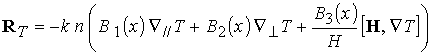

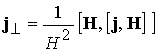
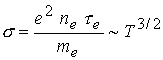
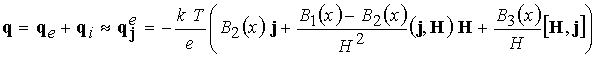
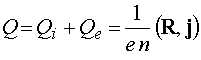
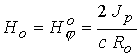
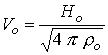
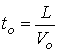
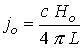 . Связь исходных размерных величин с безразмерными
параметрами, участвующими в задаче, определяется следующим образом:
. Связь исходных размерных величин с безразмерными
параметрами, участвующими в задаче, определяется следующим образом: 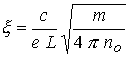
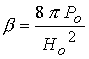
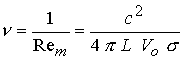
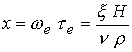
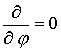
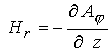
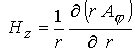
 .
.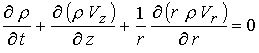
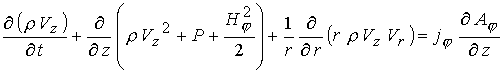
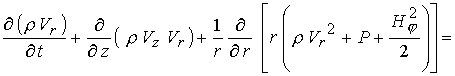
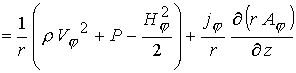
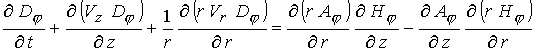

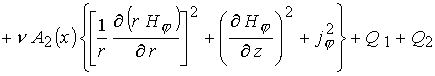
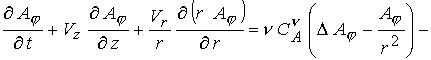
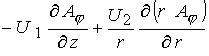

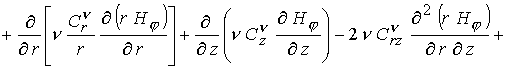
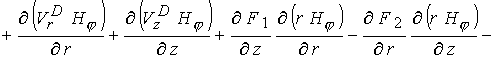
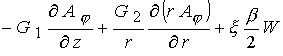
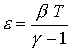
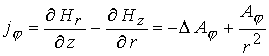
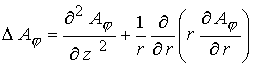

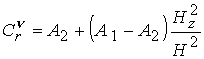
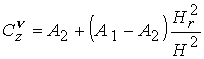
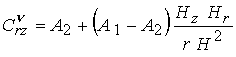
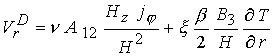 ;
;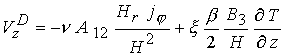
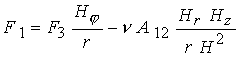
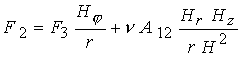
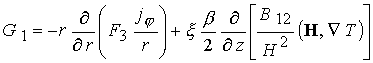
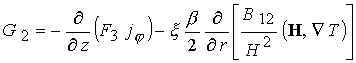
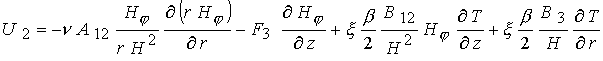
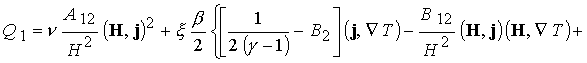
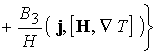
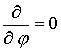
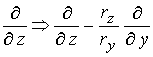 ;
;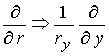 ,
,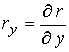 ,
,

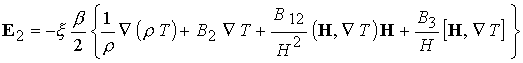
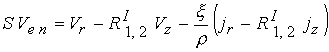
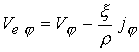
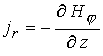
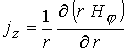
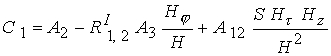
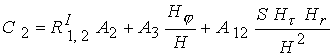 ;
;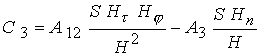 ;
;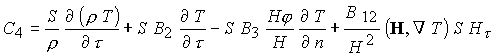
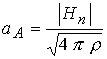 ;
; 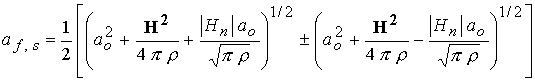
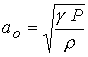
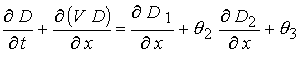
 ,
,