Аннотация
Исследована динамика спутника, движущегося в центральном ньютоновом силовом поле на круговой
орбите под действием гравитационного и аэродинамического моментов. В частном случае, когда
центр давления аэродинамических сил расположен на одной из главных центральных осей инерции
спутника, определены все положения равновесия. Для каждой равновесной ориентации получены как
достаточные, так и необходимые условия устойчивости в удобном для анализа виде. Подробно
исследована эволюция областей выполнения условий устойчивости для каждого из положений
равновесия в зависимости от параметров задачи. Определены все бифуркационные значения
параметров, при которых происходит качественная смена формы областей устойчивости.
Abstract
The dynamics of the setellite moving in a central Newtonian force field in a circular orbit
under action of the gravitational and aerodynamic moments is investigated. In specific case,
when the center of pressure of aerodynamic forces is located on one of the principal central
axes of inertia of the satellite, all equilibrium orientations are determined. Necessary and
sufficient conditions of stability are obtained for each equilibrium orientation. Evolution of
domains where stability conditions take place is investigated in detail depending on parameters
of a problem. All bifurcational values of parameters corresponding to qualitative change of
domains of stability are determined.
1.
Введение
Одним из важных направлений развития
космической техники является создание систем ориентации искусственных спутников
Земли. В зависимости от поставленных задач ориентация спутника может быть
осуществлена с использованием активных или пассивных методов. При разработке
пассивных систем ориентации можно использовать свойства гравитационного и
магнитного полей, эффект сопротивления атмосферы и давления солнечного
излучения, гироскопические свойства вращающихся тел и др. Важное свойство
пассивных систем ориентации спутников заключается в том, что эти системы могут
функционировать продолжительное время без расходования энергии или рабочего
тела.
На круговых или
слабоэллиптических орбитах в диапазоне высот от 250 км до 500 км для ориентации
оси симметрии спутника по набегающему потоку воздуха, направление которого мало
отличается от направления касательной к орбите, можно использовать
аэродинамический момент. Если спутник аэродинамически устойчив, то при
нарушении нормальной ориентации возникает восстанавливающий аэродинамический
момент по тангажу и рысканию, стремящийся совместить продольную ось спутника с
вектором набегающего потока.
Существует значительное число работ,
посвященных исследованию динамики спутника, подверженного действию
гравитационного и аэродинамического моментов. Идея использования
аэродинамического момента для ориентации спутника и простейшие результаты
исследования были приведены в работах [1-5]. Более глубокие исследования
влияния аэродинамического момента на движение спутника около центра масс
проведены в [6-9]. Положительные и отрицательные эффекты воздействия
сопротивления атмосферы на динамические характеристики гравитационной системы
ориентации спутник-стабилизатор проанализированы в [10, 11].
Первая успешная
реализация аэродинамической системы ориентации была осуществлена советскими
учеными на спутниках Космос-149 (1967 г.) и Космос-320 (1970 г.). Система
ориентации состоит из аэродинамического стабилизатора и гиродемпфера.
Аэродинамический стабилизатор выполнен из тонкой жести в виде боковой
поверхности усеченного конуса и установлен на четырех длинных (4-6 м)
полых стержнях, соединенных с корпусом спутника (рис. 1). Аэродинамический
стабилизатор приводит к появлению восстанавливающих аэродинамических моментов
по тангажу и рысканию, стремящихся совместить продольную ось спутника с
направлением набегающего потока воздуха. Гиродемпфер (два двухстепенных
интегрирующих гироскопа, установленные по схеме V-рыскание) обеспечивает демпфирование собственных колебаний спутника и
появление восстанавливающих гироскопических моментов по рысканию и крену.
Основные проблемы динамики спутника с аэродинамической системой ориентации были
исследованы в [12-17].
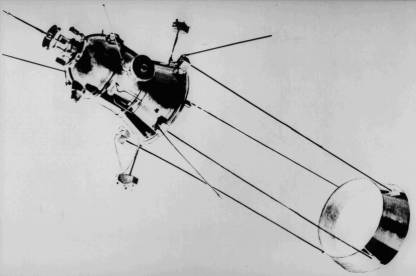
Рис.1
Еще один пример
использования аэродинамического момента для ориентации спутников –
разработанный американскими учеными малый спутник PAMS (проект GAMES) [18-20]. Демпфирование
собственных колебаний этого спутника реализовано с помощью магнитных
гистерезисных стержней. Спутник был запущен на орбиту с борта Space Shuttle в мае 1996 г.
Значительный цикл работ
посвящен исследованию влияния аэродинамического момента на динамику движения
находящихся в режиме гравитационной ориентации орбитальных станций Салют-6 и
Салют-7, обладающих большими солнечными батареями [21-25].
В работах [26, 27]
проведен анализ влияния неконсервативной компоненты аэродинамического момента
на устойчивость положений равновесия спутника. Более подробно и глубоко эта
задача рассмотрена в [28] применительно к исследованию вращательного движения
орбитальной станции Салют-7 под действием гравитационного, аэродинамического и
диссипативного моментов. Проведено оригинальное численно-аналитическое
исследование, позволяющее объяснить основные характеристики самопроизвольно
устанавливающегося режима гравитационной ориентации орбитальной станции
Салют-7.
В работе [29]
исследовано движение спутника на круговой орбите под действием гравитационного
и аэродинамического моментов. В случае, когда центр давления расположен на
главной центральной оси инерции спутника, определены все положения равновесия в
орбитальной системе координат и получены достаточные условия их устойчивости.
Настоящая статья
является продолжение работы [29]. Основное внимание уделено исследованию
устойчивости положений равновесия спутника. Полученные в [29] достаточные
условия устойчивости упрощены и записаны в удобном для анализа виде.
Рассмотрены необходимые условия устойчивости, когда характеристическое
уравнение для линеаризованных в окрестности положения равновесия уравнений
движения спутника имеет лишь мнимые корни. В решаемой задаче доказано наличие
симметрии, позволяющей ограничиться исследованием устойчивости лишь трех из
шести групп положений равновесия. Результаты численно-аналитического
исследования представлены в виде серии графиков, где в плоскости двух безразмерных
инерционных параметров при различных значениях безразмерного аэродинамического
параметра приведены области выполнения как достаточных, так и необходимых
условий устойчивости положений равновесия спутника.
2.
Уравнения движения
Рассмотрим задачу о
вращательном движении на круговой орбите спутника, подверженного действию
гравитационного и аэродинамического моментов. Введем две правые декартовы
системы координат с началом в центре масс 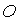 спутника. спутника.
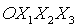 - орбитальная система
координат. Ось - орбитальная система
координат. Ось 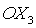 направлена вдоль
радиуса-вектора, соединяющего центры масс Земли и спутника; ось направлена вдоль
радиуса-вектора, соединяющего центры масс Земли и спутника; ось 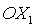 направлена вдоль
вектора линейной скорости центра масс направлена вдоль
вектора линейной скорости центра масс 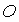 . .
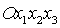 - связанная со
спутником система координат; - связанная со
спутником система координат; 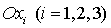 суть главные
центральные оси инерции спутника. суть главные
центральные оси инерции спутника.
Определим ориентацию
системы координат 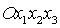 относительно
орбитальной системы координат углами относительно
орбитальной системы координат углами 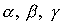 с последовательностью
поворотов 2-3-1 [30]. Первый поворот системы координат с последовательностью
поворотов 2-3-1 [30]. Первый поворот системы координат 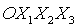 осуществляется на
угол осуществляется на
угол 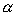 в плоскости в плоскости 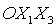 (вокруг оси (вокруг оси 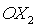 ), второй поворот – на угол ), второй поворот – на угол 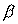 в плоскости в плоскости 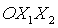 (вокруг оси (вокруг оси 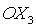 ), третий поворот – на угол ), третий поворот – на угол 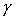 в плоскости в плоскости 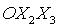 (вокруг оси (вокруг оси 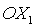 ). Тогда направляющие косинусы осей ). Тогда направляющие косинусы осей 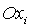 в орбитальной системе
координат в орбитальной системе
координат 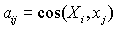 задаются выражениями задаются выражениями
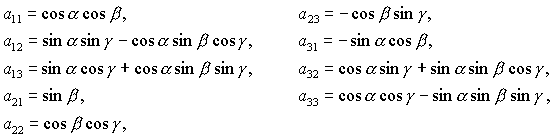 (1) (1)
а уравнения движения спутника относительно
его центра масс записываются в виде [29]
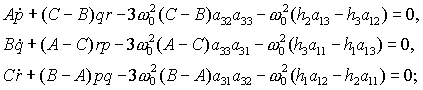 (2) (2)
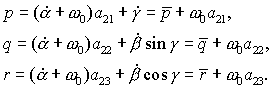 (3) (3)
В уравнениях (2), (3)
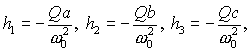
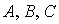 - главные центральные
моменты инерции спутника; - главные центральные
моменты инерции спутника; 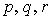 - проекции абсолютной
угловой скорости спутника на оси - проекции абсолютной
угловой скорости спутника на оси 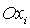 ; ; 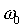 - угловая скорость
движения центра масс спутника на круговой орбите; - угловая скорость
движения центра масс спутника на круговой орбите; 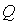 - действующая на
спутник сила сопротивления; - действующая на
спутник сила сопротивления; 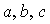 - координаты центра
давления спутника в системе координат - координаты центра
давления спутника в системе координат 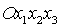 . Точкой обозначено дифференцирование по времени . Точкой обозначено дифференцирование по времени 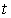 . .
Для системы уравнений
(2), (3) справедлив обобщенный интеграл энергии
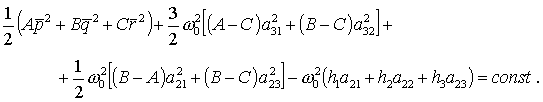 (4) (4)
3.
Положения равновесия спутника
Положив в (2) и (3) 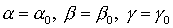 ( (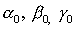 - постоянные величины), получим уравнения - постоянные величины), получим уравнения
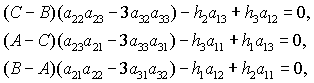 (5) (5)
позволяющие определить положения равновесия спутника в орбитальной системе
координат. Вместо системы (5) удобнее использовать эквивалентную ей систему
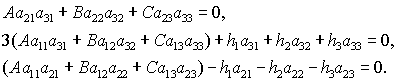 (6) (6)
C учетом
(1) систему (6) можно трактовать как систему трех уравнений с неизвестными 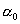 , ,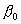 , ,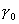 . Другой способ замыкания уравнений (6)
заключается в добавлении условий ортогональности направляющих косинусов . Другой способ замыкания уравнений (6)
заключается в добавлении условий ортогональности направляющих косинусов
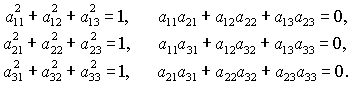 (7) (7)
Далее
будем исследовать положения равновесия гиростата, используя системы (6) и (7).
Как показано в [29], при
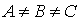 систему уравнений
(6), (7) можно разрешить относительно систему уравнений
(6), (7) можно разрешить относительно 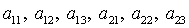 . В результате получим . В результате получим
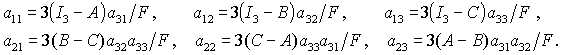 (8) (8)
Здесь 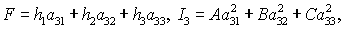 а направляющие
косинусы а направляющие
косинусы 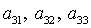 определяются
уравнениями определяются
уравнениями
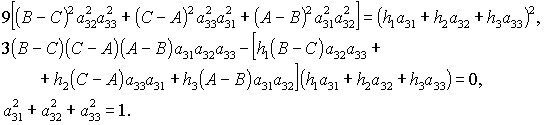 (9) (9)
После решения системы (9) формулы (8) позволяют определить оставшиеся шесть
направляющих косинусов. Отметим, что решения (8) существуют лишь в том случае,
когда из трех направляющих косинусов 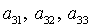 никакие два
одновременно не обращаются в нуль. Случаи никакие два
одновременно не обращаются в нуль. Случаи 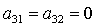 , , 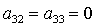 , , 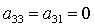 для предлагаемого
метода решения задачи являются особыми и их следует рассматривать
непосредственно обращаясь к системе уравнений (6)-(7). для предлагаемого
метода решения задачи являются особыми и их следует рассматривать
непосредственно обращаясь к системе уравнений (6)-(7).
Используя идеи работы
[31], можно показать, что после введения новых неизвестных 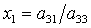 , , 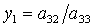 первые
два уравнения системы (9) с использованием понятия результанта сводятся к
одному алгебраическому уравнению 12-го порядка (например, относительно первые
два уравнения системы (9) с использованием понятия результанта сводятся к
одному алгебраическому уравнению 12-го порядка (например, относительно 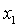 ) с действительными коэффициентами. Число его действительных
корней четно и не превышает 12. Подставляя значение действительного корня ) с действительными коэффициентами. Число его действительных
корней четно и не превышает 12. Подставляя значение действительного корня 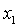 алгебраического
уравнения в первые два уравнения системы (9), найдем совпадающий корень алгебраического
уравнения в первые два уравнения системы (9), найдем совпадающий корень 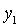 этих уравнений. Для
каждого решения этих уравнений. Для
каждого решения 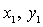 из последнего
уравнения системы (9) можно определить два значения из последнего
уравнения системы (9) можно определить два значения 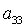 , а затем и соответствующие им величины , а затем и соответствующие им величины 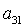 и и 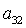 . Таким образом, каждому действительному корню
алгебраического уравнения соответствуют два набора значений . Таким образом, каждому действительному корню
алгебраического уравнения соответствуют два набора значений 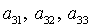 , которые в силу (8), однозначно определяют остальные
направляющие косинусы , которые в силу (8), однозначно определяют остальные
направляющие косинусы 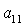 , , 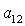 , , 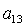 , , 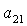 , , 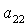 , , 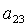 . Из приведенных соображений следует, что спутник
на круговой орбите, находящийся под действием гравитационного и
аэродинамического моментов, может иметь не более 24 положений равновесия. . Из приведенных соображений следует, что спутник
на круговой орбите, находящийся под действием гравитационного и
аэродинамического моментов, может иметь не более 24 положений равновесия.
Далее,
как и в [29], будем рассматривать частный случай, когда центр давления
расположен на оси 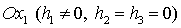 . Тогда система (9) после перехода к безразмерным параметрам . Тогда система (9) после перехода к безразмерным параметрам 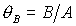 , , 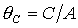 , , 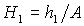 принимает
вид принимает
вид
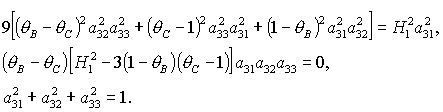 (10) (10)
Заметим, что достаточно
ограничиться рассмотрением положительных 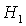 , поскольку случай , поскольку случай 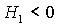 сводится к случаю сводится к случаю 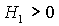 заменой направления
осей заменой направления
осей 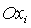 связанной системы
координат на противоположные. связанной системы
координат на противоположные.
Из второго уравнения
системы (10) следует
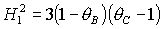 (11)
(11)
или
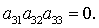 (12) (12)
Можно показать, что при
выполнении условия (11) системе (10) удовлетворяют 8 однопараметрических
семейств решений. Свойства этих решений подробно исследованы в [29].
Пусть теперь 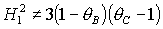 . Тогда второе уравнение (10) примет вид (12). В результате
поочередного рассмотрения случаев . Тогда второе уравнение (10) примет вид (12). В результате
поочередного рассмотрения случаев 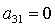 , , 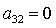 , , 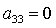 получаем
следующие группы изолированных решений (приведены лишь отличные от нуля направляющие
косинусы) [29]: получаем
следующие группы изолированных решений (приведены лишь отличные от нуля направляющие
косинусы) [29]:
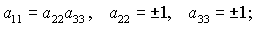 (13)
(13)
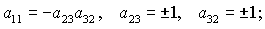 (14)
(14)
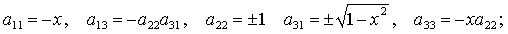 (15)
(15)
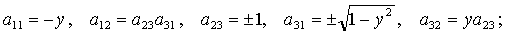 (16)
(16)
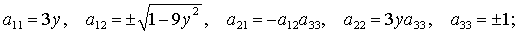 (17)
(17)
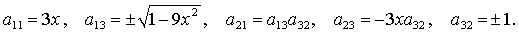 (18)
(18)
Здесь 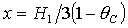 , , 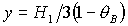 . Отметим, что каждая группа (13)-(18) состоит из
четырех решений, соответствующих одному из четырех вариантов выбора знаков . Отметим, что каждая группа (13)-(18) состоит из
четырех решений, соответствующих одному из четырех вариантов выбора знаков 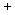 и и 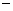 . .
Решения (13) и (14)
существуют при любых значениях параметров рассматриваемой задачи, решения (15)
– при 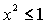 , решения (16) – при , решения (16) – при 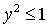 , решения (17) – при , решения (17) – при 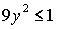 , решения (18) – при , решения (18) – при 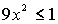 . Условия существования решений (13)-(18) выделяют
в плоскости . Условия существования решений (13)-(18) выделяют
в плоскости 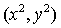 9 областей с
фиксированным числом положений равновесия в каждой области (рис. 2).
Разумеется, при 9 областей с
фиксированным числом положений равновесия в каждой области (рис. 2).
Разумеется, при 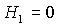 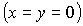 решения
(13) – (18) совпадают с известными 24 равновесными ориентациями спутника –
твердого тела в орбитальной системе координат на круговой орбите. решения
(13) – (18) совпадают с известными 24 равновесными ориентациями спутника –
твердого тела в орбитальной системе координат на круговой орбите.
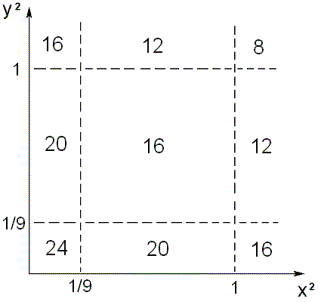
Рис. 2
Следует обратить
внимание на то, что решения (13), (15) и (17) переходят соответственно в
решения (14), (16) и (18), если другим способом определить связанную систему
координат. А именно, введем вместо 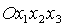 систему
координат систему
координат 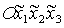 , получающуюся из , получающуюся из 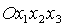 поворотом
вокруг оси поворотом
вокруг оси 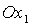 на угол на угол 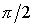 . Ясно, что оси . Ясно, что оси 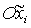 по-прежнему являются главными центральными осями инерции
спутника-гиростата, но их порядок и направления отличаются от по-прежнему являются главными центральными осями инерции
спутника-гиростата, но их порядок и направления отличаются от 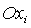 . Фактически переход от осей . Фактически переход от осей 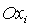 к осям к осям 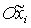 эквивалентен замене эквивалентен замене 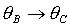 , , 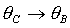 (при этом,
как следствие, (при этом,
как следствие, 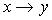 , , 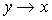 ). ).
Рассмотрим,
например, решение (15). В системе координат  оно
принимает вид оно
принимает вид
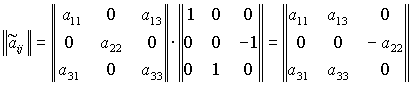 , ,
откуда
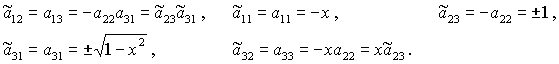
Полученные
выражения с учетом того, что 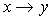 , действительно совпадают с (16). , действительно совпадают с (16).
Таким
образом, можно ограничиться анализом устойчивости решений (13), (15) и (17), а
соответствующие области для решений (14), (16) и (18) будут симметричны им
относительно прямой 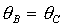 . .
Что касается
геометрического смысла полученных решений, то для четырех решений (13)
одноименные оси орбитальной и связанной систем координат параллельны или
антипараллельны друг другу. При этом ось 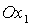 направлена
по вектору линейной скорости (оси направлена
по вектору линейной скорости (оси 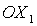 ), если ), если 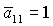 , и противоположно направлена, если , и противоположно направлена, если 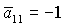 . .
Решения (15) и (17) могут быть получены из (13) путем поворота
вокруг оси 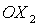 и и 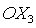 на углы на углы 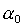 или или 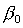 соответственно, причем значения углов поворота определяются
соотношениями соответственно, причем значения углов поворота определяются
соотношениями 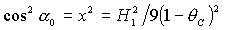 , , 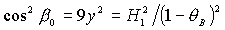 . .
4.
Достаточные условия устойчивости
положений равновесия
Для получения
достаточных условий устойчивости положений равновесия (13) – (18) можно
воспользоваться интегралом энергии (4). Вводя замену переменных
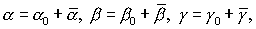 (19) (19)
где 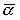 , , 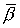 , , 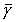 - малые
отклонения от положения равновесия спутника - малые
отклонения от положения равновесия спутника 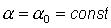 , , 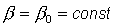 , , 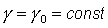 , удовлетворяющего системе уравнений (5). Тогда
интеграл энергии может быть представлен в виде [29] , удовлетворяющего системе уравнений (5). Тогда
интеграл энергии может быть представлен в виде [29]
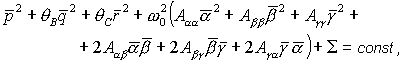 (20) (20)
где символом 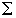 обозначены члены выше
второго порядка малости относительно обозначены члены выше
второго порядка малости относительно 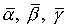 , ,
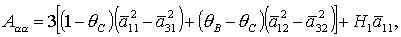
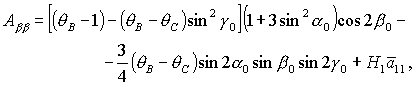
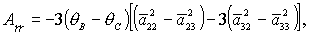
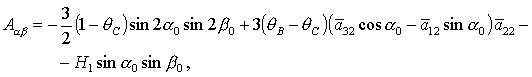
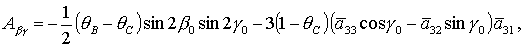
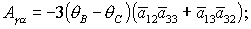
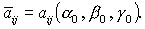
Из теоремы Ляпунова следует, что решение 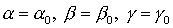 устойчиво, если
квадратичная форма устойчиво, если
квадратичная форма

является определенно-положительной. Опуская промежуточные выкладки,
достаточные условия устойчивости для каждой из шести групп решений (13)-(18) и
условия их существования запишем в следующем, более простом, чем в [29], виде:
для решений (13)
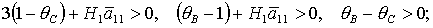 (21)
(21)
для решений (15), которые
существуют при 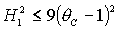 , ,
 (22) (22)
для решений (17), которые
существуют при 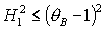 , ,
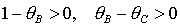 . (23) . (23)
При
замене 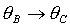 , , 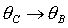 условия
(21) для решений (13) переходят в условия для решений (14), условия (22) для
решений (15) переходят в условия для решений (16), а условия (23) для решений
(17) - в условия для решений (18). Заметим, что последнее неравенство (22)
может быть отброшено, поскольку при выполнении первых двух неравенств (22) и
условия существования решения условия
(21) для решений (13) переходят в условия для решений (14), условия (22) для
решений (15) переходят в условия для решений (16), а условия (23) для решений
(17) - в условия для решений (18). Заметим, что последнее неравенство (22)
может быть отброшено, поскольку при выполнении первых двух неравенств (22) и
условия существования решения 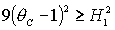 оно всегда
удовлетворяется. В самом деле, оно всегда
удовлетворяется. В самом деле,
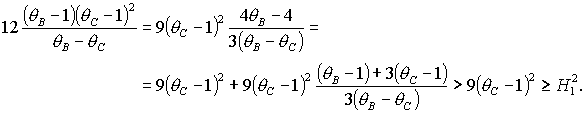
Напомним
также, что при исследовании областей, где выполняются условия устойчивости
положений равновесия спутника, необходимо учитывать условия физической
реализуемости тела, т.е. «неравенства треугольника»
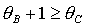 , , 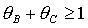 , , 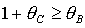 .
(24) .
(24)
Рассмотрим
эволюцию областей выполнения достаточных условий устойчивости положений
равновесия спутника в плоскости 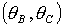 при
изменении величины безразмерного параметра при
изменении величины безразмерного параметра 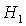 . За формирование областей устойчивости в общем
случае отвечают восемь прямых. Для удобства изложения присвоим каждой прямой
свой индекс . За формирование областей устойчивости в общем
случае отвечают восемь прямых. Для удобства изложения присвоим каждой прямой
свой индекс
1.
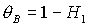 ,
5.
,
5.
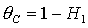 , ,
2.
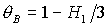 ,
6.
,
6.
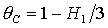 , ,
3. 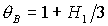 ,
7. ,
7.
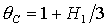 , (25) , (25)
4. 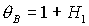 , 8. , 8. 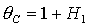 . .
Если 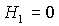 , то получаем спутник, на который действует только
гравитационный момент; при этом решения (13)-(18) устойчивы в областях,
показанных на рис. 3 (здесь и далее на рисунках горизонтальная и вертикальная
оси отвечают безразмерным моментам инерции , то получаем спутник, на который действует только
гравитационный момент; при этом решения (13)-(18) устойчивы в областях,
показанных на рис. 3 (здесь и далее на рисунках горизонтальная и вертикальная
оси отвечают безразмерным моментам инерции 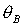 и и 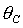 соответственно). Вся область допустимых соответственно). Вся область допустимых 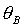 , , 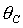 разбивается прямыми разбивается прямыми 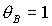 , , 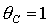 , , 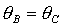 на 6
областей, в каждой из которых выполняются достаточные условия устойчивости
только одной группы решений (на рисунке области обозначены номерами
соответствующих решений). на 6
областей, в каждой из которых выполняются достаточные условия устойчивости
только одной группы решений (на рисунке области обозначены номерами
соответствующих решений).
При 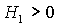 характер
границ областей изменяется. Границы областей устойчивости теперь определяются
прямыми (24). Кроме того, для решений
(13) и (14) имеет место следующая особенность: области выполнения достаточных
условий устойчивости решений, отвечающих характер
границ областей изменяется. Границы областей устойчивости теперь определяются
прямыми (24). Кроме того, для решений
(13) и (14) имеет место следующая особенность: области выполнения достаточных
условий устойчивости решений, отвечающих 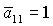 и и 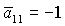 , не совпадают. На рис. 4 в областях, обозначенных
(13) и (14), условия выполняются для , не совпадают. На рис. 4 в областях, обозначенных
(13) и (14), условия выполняются для 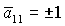 , а в областях, обозначенных (13)+ или
(14)+ , условия выполняются только в случае , а в областях, обозначенных (13)+ или
(14)+ , условия выполняются только в случае 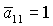 . .
С ростом 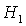 взаимное
расположение границ разбиения изменяется, а при двух бифуркационных значениях взаимное
расположение границ разбиения изменяется, а при двух бифуркационных значениях 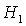 ( (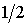 и и 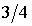 ) картина разбиения претерпевает качественные
изменения (рис. 5-6). При первом
бифуркационном значении ) картина разбиения претерпевает качественные
изменения (рис. 5-6). При первом
бифуркационном значении 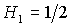 исчезают
области (17) и (18), а при втором бифуркационном значении исчезают
области (17) и (18), а при втором бифуркационном значении 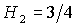 исчезают области (13) и
(14). исчезают области (13) и
(14).
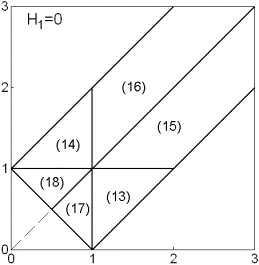 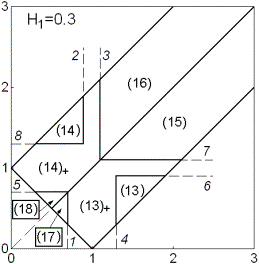
Рис. 3 Рис. 4
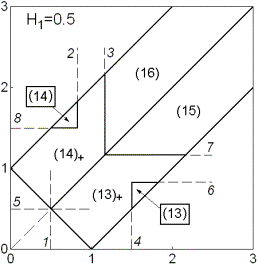 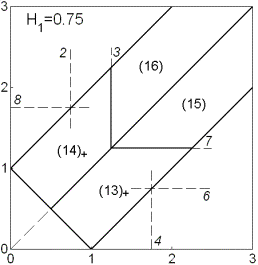
Рис.
5 Рис. 6
5. Необходимые условия устойчивости
Для
исследования необходимых условий устойчивости положений равновесия
спутника-гиростата линеаризуем систему уравнений (2)-(3) в окрестности решения 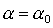 , , 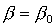 , , 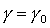 . После достаточно утомительных преобразований линеаризованная система
уравнений движения принимает следующий вид: . После достаточно утомительных преобразований линеаризованная система
уравнений движения принимает следующий вид:
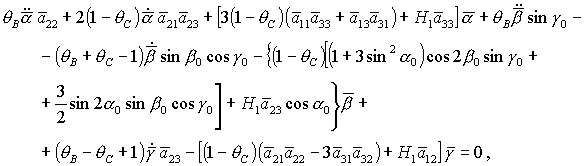
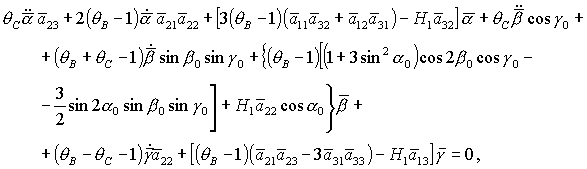 (26) (26)
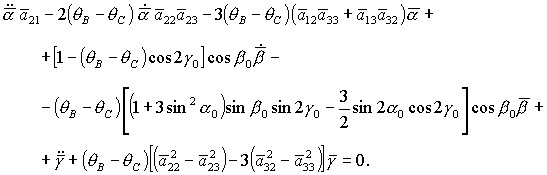
Здесь точкой обозначено дифференцирование по безразмерному времени 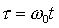 . .
Перейдем к рассмотрению
конкретных положений равновесия спутника. Для решений (13) с учетом выражений
(1) для направляющих косинусов имеем 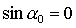 , , 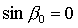 , , 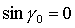 и
линеаризованные уравнения принимают вид и
линеаризованные уравнения принимают вид
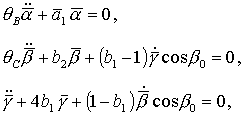 (27)
(27)
где
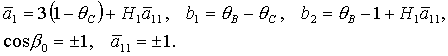
Характеристическое уравнение
системы (27)
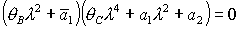
распадается
на квадратное и биквадратное уравнения. Здесь введены обозначения

Поскольку
необходимым условием устойчивости является отсутствие корней
характеристического уравнения с положительными действительными частями, то в
случае, когда в уравнении присутствуют только четные степени 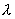 , надо потребовать, чтобы все корни были чисто
мнимыми. Другими словами, , надо потребовать, чтобы все корни были чисто
мнимыми. Другими словами, 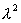 должно
быть вещественным и отрицательным. Таким образом, приходим к условиям должно
быть вещественным и отрицательным. Таким образом, приходим к условиям
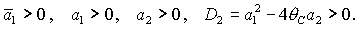 (28) (28)
Разумеется,
наряду с (28) должны выполняться и неравенства треугольника (24).
Обратим внимание на то, что неравенство 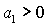 не может
обращаться в равенство на границе области выполнения необходимых условий
устойчивости (28), поскольку при не может
обращаться в равенство на границе области выполнения необходимых условий
устойчивости (28), поскольку при 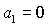 из условия из условия
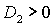 следует следует 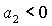 , что противоречит (28). , что противоречит (28).
Условие
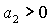 выполняется либо при выполняется либо при 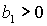 , , 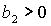 , либо при , либо при 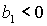 , , 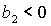 . В первом случае выполняются все достаточные
условия устойчивости (21). Очевидно, при этом выполняются также и все
необходимые условия (28), т.е. . В первом случае выполняются все достаточные
условия устойчивости (21). Очевидно, при этом выполняются также и все
необходимые условия (28), т.е. 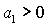 и и 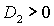 . Таким образом, приходим к области, в которой
выполняются необходимые и достаточные условия устойчивости решений (13), уже
полученной в предыдущем разделе. . Таким образом, приходим к области, в которой
выполняются необходимые и достаточные условия устойчивости решений (13), уже
полученной в предыдущем разделе.
Пусть теперь 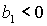 , , 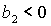 . Тогда достаточные условия нарушаются, а
необходимые условия принимают вид . Тогда достаточные условия нарушаются, а
необходимые условия принимают вид
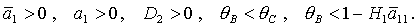 (29) (29)
Причем,
из системы (24) можно исключить третье неравенство, так как при 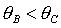 оно автоматически
выполняется. оно автоматически
выполняется.
На
границе области обращается в равенство по крайней мере одно из неравенств (29).
При этом равенство 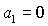 возможно
только, если одновременно возможно
только, если одновременно 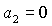 и и 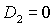 . Таким образом, область может быть ограничена
прямыми . Таким образом, область может быть ограничена
прямыми 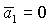 , , 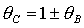 , , 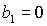 , , 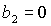 и кривой и кривой 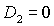 . Пример такой области и образующих ее границ
приведен на рис. 7 ( . Пример такой области и образующих ее границ
приведен на рис. 7 (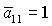 ). Область, где выполнены необходимые и достаточные условия
устойчивости, выделена светло-серым цветом, область, где выполнены только
необходимые условия устойчивости, выделена темно-серым цветом. Отметим, что
кривая ). Область, где выполнены необходимые и достаточные условия
устойчивости, выделена светло-серым цветом, область, где выполнены только
необходимые условия устойчивости, выделена темно-серым цветом. Отметим, что
кривая 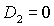 пересекает, а точнее, касается прямой пересекает, а точнее, касается прямой 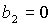 в точке в точке 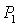 , через которую проходит также и кривая , через которую проходит также и кривая 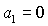 . Прямые . Прямые 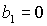 и и 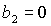 пересекаются в точке пересекаются в точке 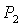 , где , где 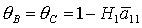 . Далее проанализируем отдельно случаи . Далее проанализируем отдельно случаи 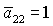 и и 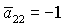 . .
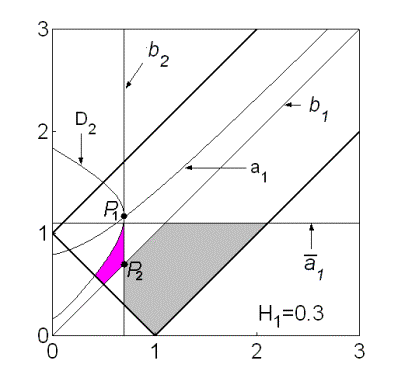
Рис. 7
Если 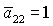 , то качественная смена формы области имеет место
при таких значениях , то качественная смена формы области имеет место
при таких значениях 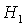 , когда точка , когда точка 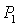 оказывается
на прямой оказывается
на прямой 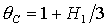 и на пересечении
прямых и на пересечении
прямых 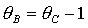 и и 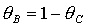 , либо когда точка , либо когда точка 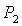 оказывается на прямой оказывается на прямой 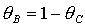 . Отсюда следует существование бифуркационных
значений . Отсюда следует существование бифуркационных
значений 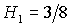 , , 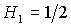 и и 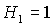 . При последнем значении безразмерного параметра . При последнем значении безразмерного параметра 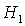 область
выполнения необходимых условий устойчивости вырождается в точку и при область
выполнения необходимых условий устойчивости вырождается в точку и при 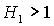 перестает
существовать. Эволюцию формы области иллюстрирует рис. 8, на котором показаны
области выполнения необходимых условий устойчивости решений (13) в случае перестает
существовать. Эволюцию формы области иллюстрирует рис. 8, на котором показаны
области выполнения необходимых условий устойчивости решений (13) в случае 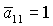 . .
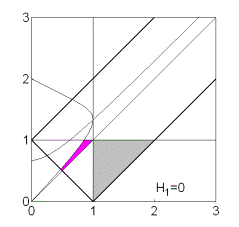
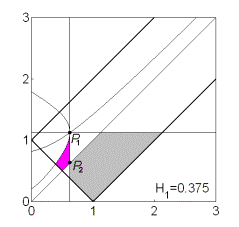
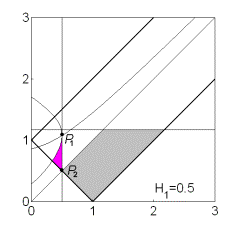
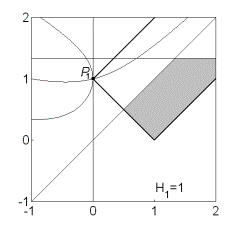
Рис. 8
Пусть теперь 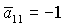 . Область выполнения необходимых условий
устойчивости, ограниченная прямыми . Область выполнения необходимых условий
устойчивости, ограниченная прямыми 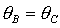 , , 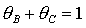 , , 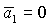 и кривой и кривой 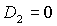 , с ростом параметра , с ростом параметра 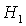 уменьшается вследствие сближения кривой уменьшается вследствие сближения кривой 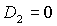 и прямой и прямой 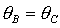 . Кроме того, смещается точка . Кроме того, смещается точка 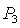 пересечения пересечения 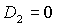 и и 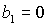 , в которой одновременно имеет место , в которой одновременно имеет место 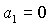 . Качественная смена формы области происходит при . Качественная смена формы области происходит при 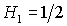 и при и при 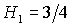 . .
При 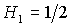 точка точка 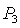 ложится на
границу рабочей области ложится на
границу рабочей области 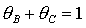 и с этого момента
область необходимых условий устойчивости ограничивается только линиями и с этого момента
область необходимых условий устойчивости ограничивается только линиями 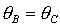 , , 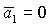 и и 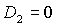 . При . При 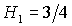 точка точка 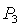 оказывается на прямой оказывается на прямой 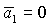 . В результате область необходимых условий устойчивости
вырождается в точку и перестает существовать. Напомним, что при этом же
значении . В результате область необходимых условий устойчивости
вырождается в точку и перестает существовать. Напомним, что при этом же
значении 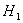 вырождается в точку и перестает существовать также и область
достаточных условий устойчивости. Таким образом, при вырождается в точку и перестает существовать также и область
достаточных условий устойчивости. Таким образом, при 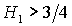 для
решений (13) при для
решений (13) при 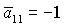 не
существует областей, где выполняются необходимые и (или) достаточные условия
устойчивости. На рис. 9 показаны соответствующие примеры областей для решений
(13) в случае не
существует областей, где выполняются необходимые и (или) достаточные условия
устойчивости. На рис. 9 показаны соответствующие примеры областей для решений
(13) в случае  . .
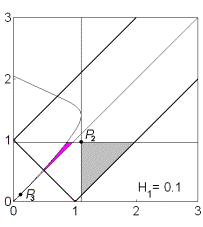
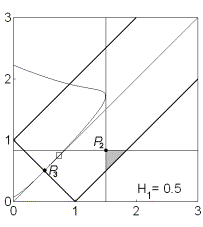
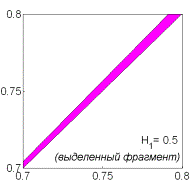
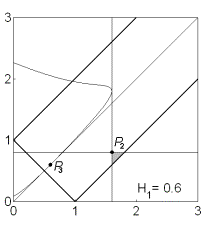
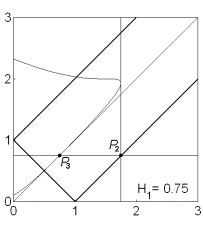
Рис. 9
Перейдем к решениям
(15), для которых 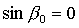 , , 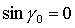 , , 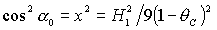 . В результате
система (26) приводится к виду . В результате
система (26) приводится к виду
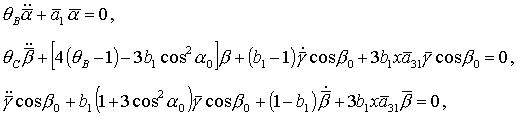 (30) (30)
где
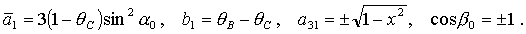
Характеристическое уравнение
системы (30)
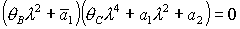
распадается
на квадратное и биквадратное уравнения. Здесь введены обозначения
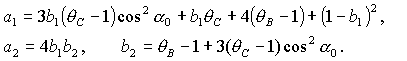
Необходимые
условия устойчивости имеют вид (28). Кроме того, дополнительно следует
удовлетворить условие существование решений (15), т.е. 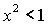 . Легко показать, что неравенство . Легко показать, что неравенство 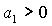 не может обращаться в
равенство на границе области выполнения необходимых условий устойчивости. Из
вида не может обращаться в
равенство на границе области выполнения необходимых условий устойчивости. Из
вида 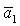 следует, что
равенство следует, что
равенство 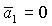 имеет место на прямых имеет место на прямых
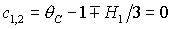 и и 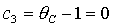 , причем последнюю прямую можно исключить, поскольку решения
(15) не существуют, если , причем последнюю прямую можно исключить, поскольку решения
(15) не существуют, если 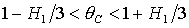 , а первые две прямые являются границами области
существования решений (15). , а первые две прямые являются границами области
существования решений (15).
Условие
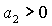 выполняется либо при выполняется либо при 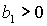 , , 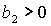 , либо при , либо при 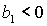 , , 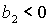 . В первом случае выполняются все достаточные
условия устойчивости (22). Очевидно, при этом выполняются также и все
необходимые условия (28), т.е. . В первом случае выполняются все достаточные
условия устойчивости (22). Очевидно, при этом выполняются также и все
необходимые условия (28), т.е. 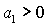 и и 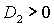 . Таким образом, приходим к области, в которой
выполняются необходимые и достаточные условия устойчивости решений (15), уже
полученной в предыдущем разделе. . Таким образом, приходим к области, в которой
выполняются необходимые и достаточные условия устойчивости решений (15), уже
полученной в предыдущем разделе.
Пусть теперь 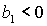 , , 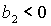 . Тогда достаточные условия нарушаются, а
необходимые условия принимают вид . Тогда достаточные условия нарушаются, а
необходимые условия принимают вид
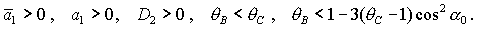 (31)
(31)
Отметим,
что из системы (24) можно исключить третье неравенство, так как при 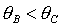 оно автоматически
выполняется. Пример области в
плоскости оно автоматически
выполняется. Пример области в
плоскости 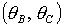 , где выполняются необходимые условия
устойчивости, представлен на рис. 10. Область выделена темно-серым цветом и
ограничена кривыми , где выполняются необходимые условия
устойчивости, представлен на рис. 10. Область выделена темно-серым цветом и
ограничена кривыми 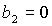 , , 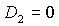 , , 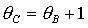 и прямой и прямой 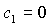 . Здесь же выделена светло-серым цветом область
выполнения необходимых и достаточных условий устойчивости, которая ограничена
прямыми . Здесь же выделена светло-серым цветом область
выполнения необходимых и достаточных условий устойчивости, которая ограничена
прямыми 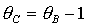 , , 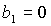 и и 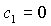 . .
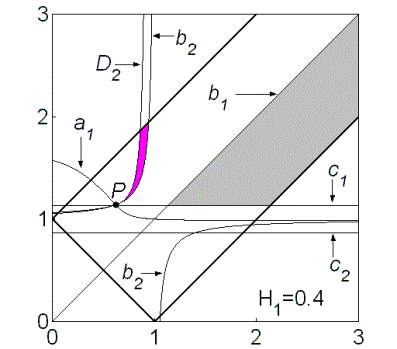
Рис. 10
Кривые 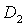 , , 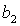 и и 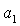 пересекаются в общей точке пересекаются в общей точке 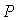 (точнее,
кривая (точнее,
кривая 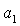 проходит
через точку касания кривых проходит
через точку касания кривых 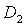 и и 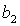 ). При малых значениях параметра ). При малых значениях параметра 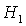 точка точка 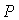 лежит между прямыми лежит между прямыми 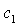 и и 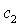 . .
Первое бифуркационное
значение 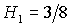 имеет
место, когда имеет
место, когда 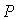 ложится на
прямую ложится на
прямую 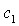 . При . При 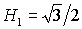 точка точка 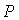 оказывается на границе рабочей области оказывается на границе рабочей области 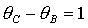 . В результате область выполнения необходимых
условий устойчивости вырождается в точку и при . В результате область выполнения необходимых
условий устойчивости вырождается в точку и при 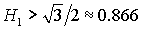 перестает
существовать. На рис. 11 показаны соответствующие примеры областей
выполнения необходимых условий устойчивости решений (15) . перестает
существовать. На рис. 11 показаны соответствующие примеры областей
выполнения необходимых условий устойчивости решений (15) .
Наконец, рассмотрим
решения (17), для которых 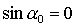 , , 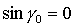 , , 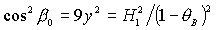 . В этом
случае характеристическое уравнение системы (25) приводится к виду . В этом
случае характеристическое уравнение системы (25) приводится к виду
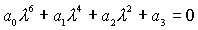 , (32) , (32)
где
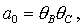
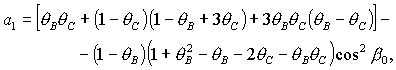
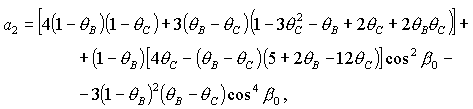
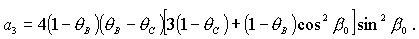
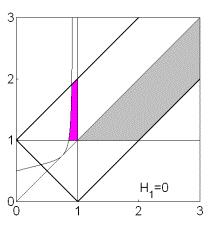
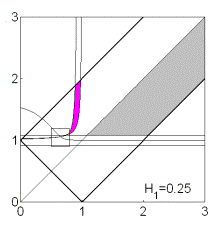
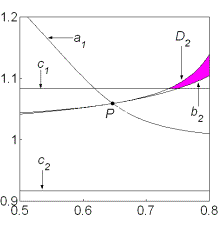
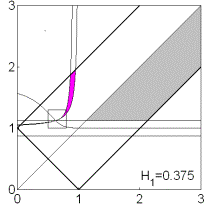
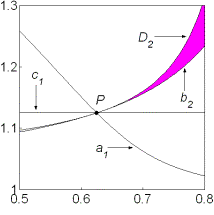
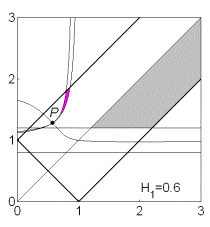
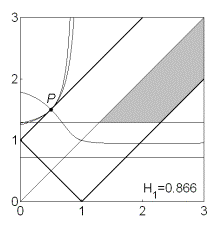
Рис.11
Необходимые условия устойчивости -
условия чистой мнимости корней уравнения (32) - представляют собой систему
неравенств [32]
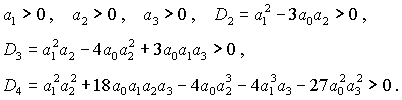 (33) (33)
Как и в предыдущих
случаях, наряду с (33) должны выполняться неравенства треугольника (24). Кроме
того, дополнительно следует удовлетворить условие существования решений (17),
т.е. 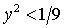 . .
Легко показать, что на
границе области (33) равенство 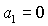 возможно
только в точках, где одновременно возможно
только в точках, где одновременно 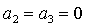 и и 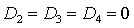 . Аналогично, равенство . Аналогично, равенство 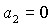 возможно,
если возможно,
если 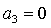 и и 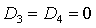 . Более того, численные исследования показали, что
границами области (33) могут быть только линии, на которых . Более того, численные исследования показали, что
границами области (33) могут быть только линии, на которых 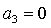 или или 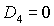 . .
Из вида 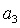 следует,
что равенство следует,
что равенство 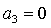 имеет
место на прямых имеет
место на прямых 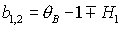 , , 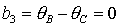 и на
гиперболе и на
гиперболе 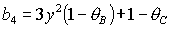 . Прямую . Прямую 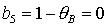 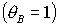 можно
сразу исключить из рассмотрения, поскольку решения (17) не существуют, если можно
сразу исключить из рассмотрения, поскольку решения (17) не существуют, если 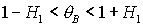 . Пример области в плоскости . Пример области в плоскости 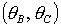 , где выполняются необходимые условия
устойчивости, представлен на рис. 12. Область выделена темно-серым цветом и ограничена
прямыми , где выполняются необходимые условия
устойчивости, представлен на рис. 12. Область выделена темно-серым цветом и ограничена
прямыми 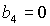 , , 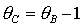 и кривой и кривой 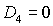 . Здесь же выделена светло-серым цветом область
выполнения необходимых и достаточных условий устойчивости, которая ограничена
прямыми . Здесь же выделена светло-серым цветом область
выполнения необходимых и достаточных условий устойчивости, которая ограничена
прямыми 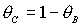 , , 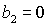 и и 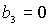 . Кривые . Кривые 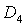 , , 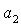 и прямые и прямые 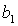 и и 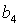 пересекаются в общей точке пересекаются в общей точке 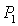 . Этот факт легко устанавливается исходя из
уравнения этих кривых. Кроме того,
можно найти координаты этой точки, как функции параметра . Этот факт легко устанавливается исходя из
уравнения этих кривых. Кроме того,
можно найти координаты этой точки, как функции параметра 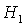 : : 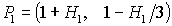 . .
Эволюция областей при
изменении 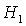 показана
на рис. 13. Рис. 13.1 соответствует случаю, когда аэродинамический момент
отсутствует ( показана
на рис. 13. Рис. 13.1 соответствует случаю, когда аэродинамический момент
отсутствует (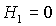 ). При ). При 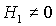 прямая прямая 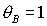 расщепляется на две прямые расщепляется на две прямые 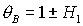 ( (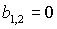 ). Полоса ). Полоса 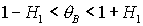 , в которой решения (17) не существуют, с ростом , в которой решения (17) не существуют, с ростом 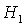 расширяется, и при расширяется, и при 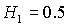 точка точка 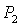 выходит на
границу рабочей области выходит на
границу рабочей области 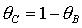 . При этом область выполнения необходимых и
достаточных условий устойчивости вырождается в точку (рис. 13.3) и при . При этом область выполнения необходимых и
достаточных условий устойчивости вырождается в точку (рис. 13.3) и при 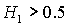 перестает
существовать. перестает
существовать.
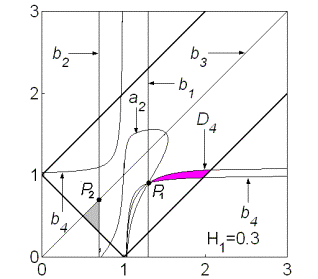
Рис.12
Область необходимых
условий устойчивости с ростом 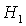 также
сокращается и при также
сокращается и при  , когда , когда 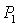 выходит
на границу рабочей области выходит
на границу рабочей области 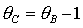 , вырождается в точку (рис. 13.4). При , вырождается в точку (рис. 13.4). При 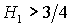 необходимые условия устойчивости не выполняются ни в одной точке
рабочей области. необходимые условия устойчивости не выполняются ни в одной точке
рабочей области.
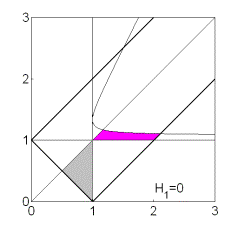
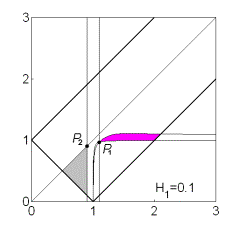
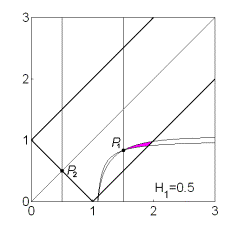
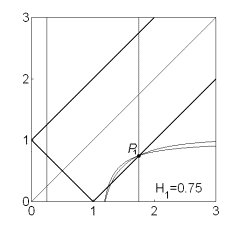
Рис.13
6. Заключение
В
растоящей работе проведено исследование движения спутника относительно центра
масс под действием гравитационного и аэродинамического моментов на круговой
орбите. Основное внимание уделено определению положений равновесия спутника в
орбитальной системе координат и анализу их устойчивости. В общем случае (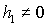 , , , ,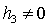 ) предложен численный метод определения всех положений
равновесия спутника. При ) предложен численный метод определения всех положений
равновесия спутника. При 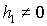 , , 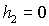 , ,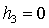 представлены в явном виде выражения для направляющих
косинусов в зависимости от параметров представлены в явном виде выражения для направляющих
косинусов в зависимости от параметров 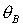 , , 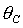 , , 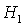 для шести групп
(13)-(18) положений равноввесия. Доказано, что группы решений (13), (15), (17)
переходят соответственно в группы решений (14), (16), (18) при замене для шести групп
(13)-(18) положений равноввесия. Доказано, что группы решений (13), (15), (17)
переходят соответственно в группы решений (14), (16), (18) при замене 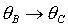 , , 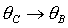 . С использованием теоремы Ляпунова получены в виде простых
неравенств достаточные условия устойчивости положений равновесия. В заключительной
части работы численно-аналитическим методом подробно исследована эволюция
областей, где выполняются необходимые условия устойчивости, в плоскости
параметров ( . С использованием теоремы Ляпунова получены в виде простых
неравенств достаточные условия устойчивости положений равновесия. В заключительной
части работы численно-аналитическим методом подробно исследована эволюция
областей, где выполняются необходимые условия устойчивости, в плоскости
параметров ( , , 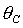 ) при различных значениях параметра ) при различных значениях параметра 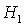 . Определены все бифуркационные значения . Определены все бифуркационные значения  , при которых происходит качественное изменение вида областей
устойчивости. , при которых происходит качественное изменение вида областей
устойчивости.
Работа
выполнена при финансовой поддержке Российского фонда фундаментальных
исследований (проект № 03-01-00652) и Португальского Фонда по науке и технике.
Литература
1.
R.E. Roberson.
Attitude control of a satellite – an outline of the problems,
7th
International Astronautical Congress, 1957, Barcelona, Spain (Proceedings, 1958, pp. 317-339).
2.
D.B. DeBra. The effect of
aerodynamic forces on satellite attitude, Journal
of Astronautical Sci., 1959, Vol. 6, No. 3, pp. 40-45.
3.
J.K. Wall. The feasibility of
aerodynamic attitude stabilization of a satellite vehicle, American Rocket Soc. Preprints, 1959, No. 787.
4.
D.M. Schrello. Aerodynamic
influences on satellite librations, ARS
Journal, 1961, Vol. 31, No. 3, pp. 442-444.
5.
D.M. Schrello. Dynamic stability
of aerodynamically responsive satellites, Journal
of Aerospace Sci., 1962, Vol. 29, No. 10, pp. 1145–1155, 1163.
6.
В.В. Белецкий. Движение искусственного
спутника относительно центра масс, М.,
«Наука», 1965.
7.
L. Meirovitch, F.B. Wallace,
Jr. On the effect of aerodynamic and gravitational torques on the attitude
stability of satellites, AIAA Journal,
1966, Vol. 4, No. 12, pp. 2196–2202.
8.
V.J. Modi, S.K. Shrivastava. On the
limiting regular stability and periodic solutions of a gravity oriented system
in the presence of the atmosphere, C.A.S.I.
Transactions, 1972, Vol. 5, No. 1, pp. 5-10.
9.
В.А. Сарычев, М.Ю. Овчинников.
Динамика спутника с пассивной аэродинамической системой ориентации, Космические исследования, 1994, т. 32, №
6, с. 561-575.
10. В.А. Сарычев. Влияние сопротивления атмосферы на систему гравитационной
стабилизации искусственных спутников Земли, Космические
исследования, 1964, т. 2, № 1, с. 23-32.
11.
V.A. Sarychev.
Dynamics of a satellite gravitational stabilization system with consideration
of atmosphere resistance, 11th
International Congress on Applied Mechanics, 1964, Munich, FRG
(Proceedings, Springer-Verlag, 1965, pp. 429-435).
12. V.A. Sarychev. Aerodynamic stabilization system of the satellite, Proceedings of the International Conference
on Attitude Changes and Stabilization of satellites, 1968, pp. 177-183,
Paris, France.
13. В.А. Сарычев. Условия устойчивости системы гравитационной стабилизации спутника
с гиродемпфированием, Astronautica Acta, 1969, Vol. 14, Nº
4, pp. 299-310.
14. В.А. Сарычев, Ю.А. Садов. Анализ динамики спутника с гиро-аэродинамической
системой ориентации, Сборник «Космическая
стрела. Оптические исследования атмосферы», М., «Наука», 1974,
с. 71-88.
15. В.И. Драновский, В.Н. Зигунов, Н.Г. Новоселова, Л.В. Соколов. Математическая нелинейная модель гироаэродинамической
системы ориентации, Сборник «Космическая
стрела. Оптические исследования атмосферы», М., «Наука», 1974, с. 47-54.
16.
В.А. Сарычев. Вопросы ориентации искусственных
спутников, Итоги науки и техники. Серия «Исследование космического пространства», ВИНИТИ, т. 11, 1978.
17. В.А. Сарычев, С.А. Мирер, В.А. Златоустов. Оптимальные параметры аэрогироскопической системы ориентации
спутников, Космические исследования,
1984, т. 22, № 3, с. 369-380.
18.
L. Pacini,
D. Skillman. A passive aerodynamically stabilized satellite for low Earth
orbit, AAS Paper 95-173, Feb. 1995,
pp. 625-630.
19.
R.R. Kumar,
D.D. Mazanek, M.L. Heck. Simulation and Shuttle Hitchhiker validation
of passive satellite aerostabilization, Journal
of Spacecraft and Rockets, 1995, Vol. 32, No. 5, pp. 806-811.
20.
R.R. Kumar,
D.D. Mazanek, M.L. Heck. Parametric and classical resonance in
passive satellite aerostabilization, Journal
of Spacecraft and Rockets, 1996, Vol. 33, No. 2, pp. 228-234.
21.
V. A. Sarychev, V. V. Sazonov. Gravity gradient
stabilization of large space stations, Acta
Astronautica, 1981, Vol. 8, No. 5-6, pp. 549-573.
22. В.А. Сарычев, В.В. Сазонов. Влияние сопротивления атмосферы на одноосную гравитационную
ориентацию искусственного спутника, Космические
исследования, 1982, т. 20, № 5, с. 659-673.
23.
V.A. Sarychev, V.V. Sazonov. Gravity gradient stabilization of the Salyut - Souz orbital
complex, Acta Astronautica, 1984,
Vol. 11, No. 7-8, pp. 435-447.
24. Г.М. Гречко, В.А. Сарычев, В.П. Легостаев, В.В. Сазонов, И.Н. Гансвинд. Гравитационная ориентация орбитального комплекса «Салют-6»-«Союз», Космические исследования, 1985, т. 23, №
5, с. 659-675.
25.
V.A. Sarychev, V.P. Legostaev,
V.V. Sazonov, M.Yu. Belyaev, I.N. Gansvind, T.N. Tyan. The
passive attitude motion of the orbital stations Salyut-6 and Salyut-7, Acta Astronautica, 1987, Vol. 15, No. 9,
pp. 635-640.
26.
G.S. Nurre.
Effects of aerodynamic torques on an asymmetric, gravity stabilized satellite, Journal of Spacecraft and Rockets, 1968,
Vol. 5, No. 9, pp.1046-1050.
27.
M.A. Frik.
Attitude stability of satellites subjected to gravity gradient and aerodynamic
torques, AIAA Journal, 1970, Vol. 8,
No. 10, pp. 1780-1785.
28. В.В. Сазонов. О механизме потери устойчивости в гравитационно-ориентированном
спутнике, Космические исследования,
1989, т. 27, № 6, с. 836-848.
29.
V.A. Sarychev,
S.A. Mirer. Relative equilibria of a satellite subjected to gravitational
and aerodynamic torques, Celestial
Mechanics and Dynamical Astronomy, 2000, Vol 76, No. 1, pp. 55-68.
30.
T.R. Kane,
P.W. Likins, D.A. Levinson. Spacecraft
Dynamics, 1983, McGraw-Hill.
31. В.А. Сарычев, С.А. Гутник. К вопросу о положениях относительного равновесия
спутника-гиростата, Космические
исследования, 1984, т. 22, № 3, с. 323-326.
32. А.М. Кац. К вопросу о критерии апериодической устойчивости, Прикладная математика и механика, 1951, т. 15, № 1, с. 120.
|