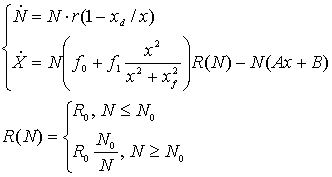Математическое моделирование экономико-демографических процессов в аграрном обществе
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
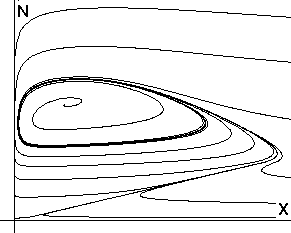
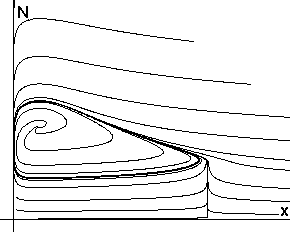
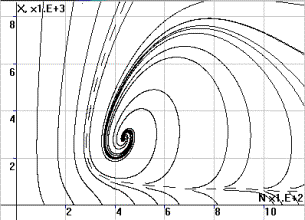
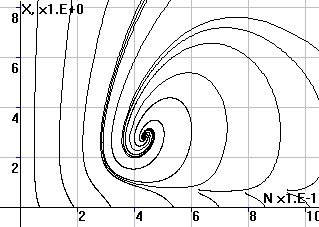
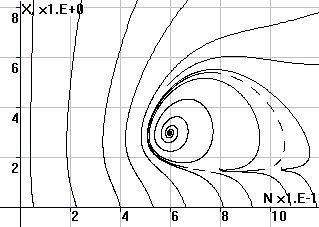
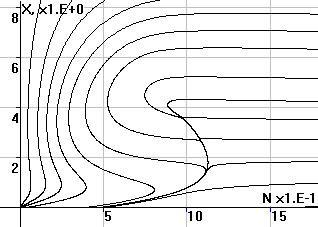
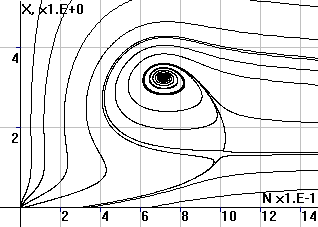
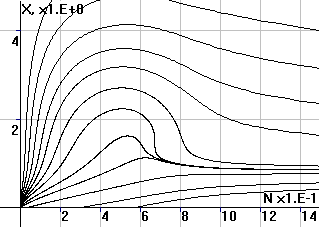
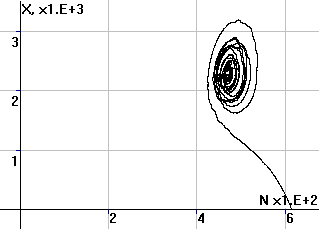
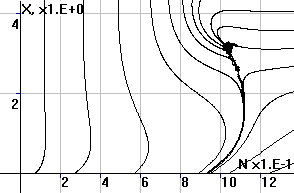
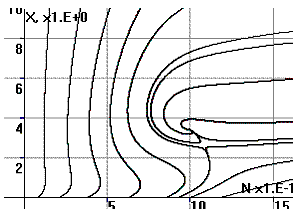
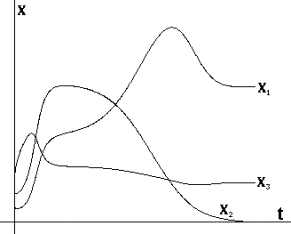
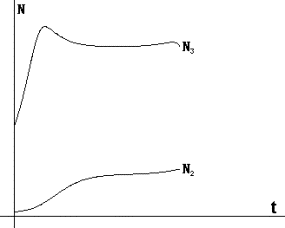
Рис.2. Фазовый портрет
системы в координатах (X,N) |
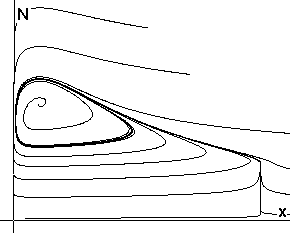
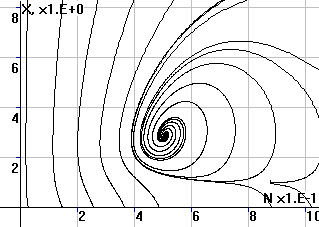
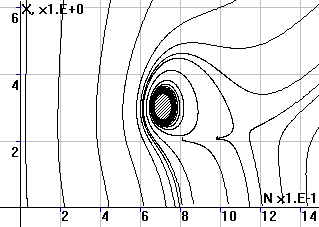
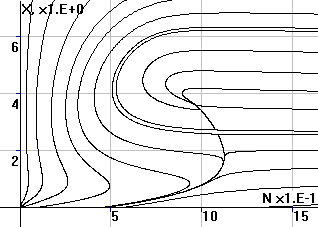
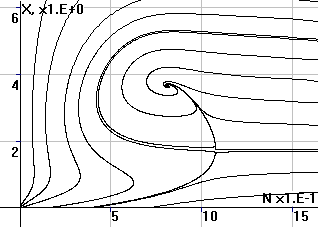
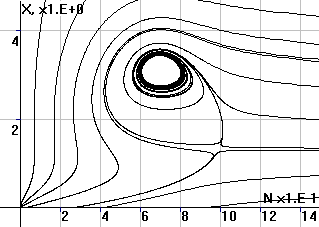
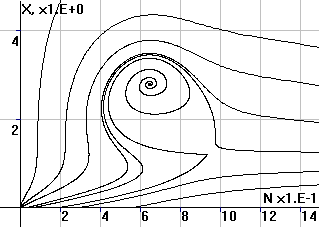
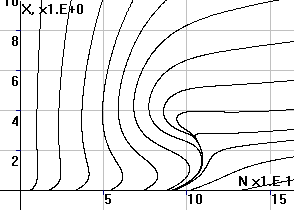
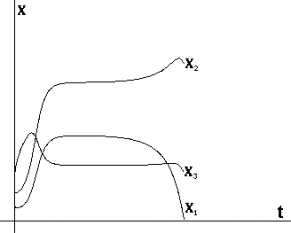
Рис.3. Фазовый портрет
системы в координатах (x,N) |
|
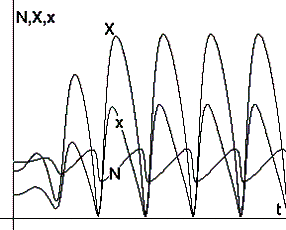
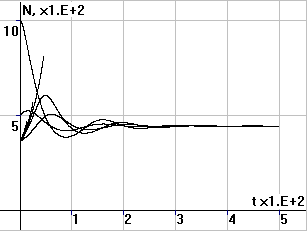
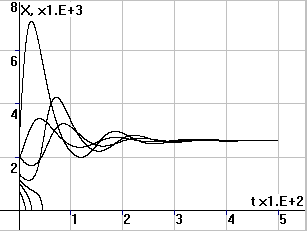
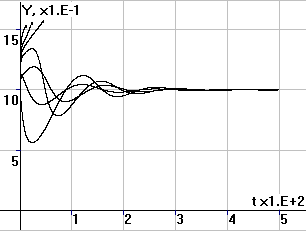
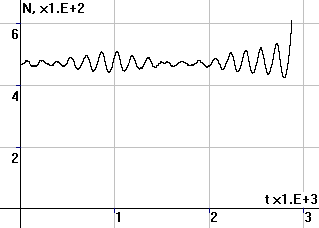
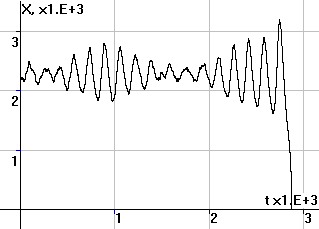
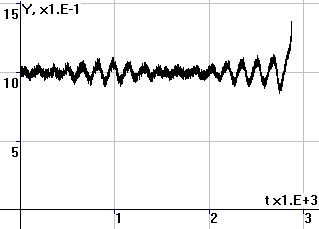
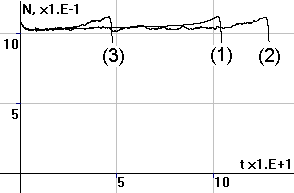
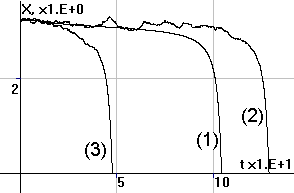
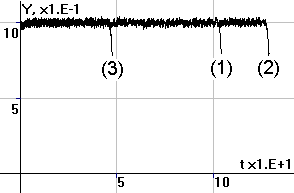
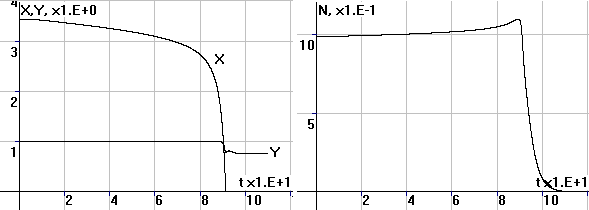
Рис.4. Периодические
колебания численности N, суммарных накоплений X и удельных накоплений x |
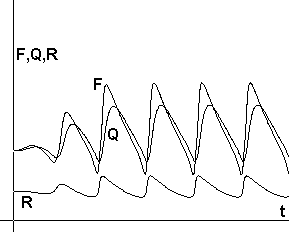
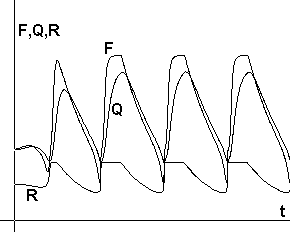
Рис.5. Площадь
обрабатываемой земли R, доход F и потребление Q на одного
крестьянина |
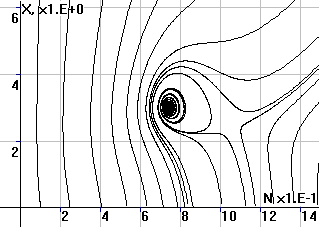
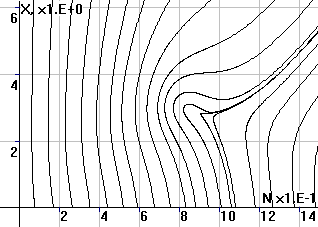
На рисунках 6 – 9 приведены фазовые траектории системы (7) при тех же значениях параметров за исключением f0 : значение f0 уменьшено с 1.7 до 1.2. Величина f0 зависит от природно-климатических условий в регионе (естественного плодородия почв, температурно-влажностного режима и т.п.). Ее уменьшение означает переход в более суровую климатическую зону.
|
|
Рис.7. Фазовый портрет
системы в координатах (x,N) |
|
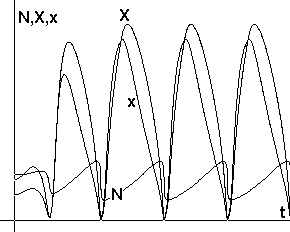
Рис.8. Периодические
колебания численности N, суммарных накоплений
X и удельных накоплений x |
Рис.9. Площадь
обрабатываемой земли R, доход F и потребление Q на одного
крестьянина |
Видно, что длительность демографических циклов увеличивается, появляется некоторый период стабильного развития: участки с R ~ const и F ~ const. Эти участки соответствуют постепенному освоению ранее заброшенных земель (пустошей) при умеренных темпах роста населения.
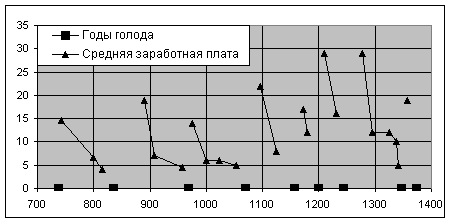
Интересно сравнить результаты расчетов с реальными историческими данными. К сожалению, возможности реконструкции экономических показателей аграрных обществ на больших временных интервалах (сотни лет) крайне ограничены, поэтому приходится пользоваться косвенной информацией. В [9] приведены данные по средней дневной заработной плате неквалифицированных рабочих в средневековом Египте (см. рис.10). Если предположить, что потребление неквалифицированных рабочих (соответствующее их заработной плате) коррелирует с потреблением крестьян, то можно сопоставить приведенные данные с рассчитанной по модели функцией Q(t) (см. соответствующий график на рис.5).
|
Рис.10. Средняя заработная
плата неквалифицированных рабочих в Египте в литрах зерна в день |
Указанное сопоставление демонстрирует неплохое качественное соответствие расчетов по модели с реальной исторической картиной в период приблизительно с 700 по 1100 г.г. н.э. На этом этапе модель вполне применима, поскольку в этот период в Египте преобладала государственная собственность на землю, а налоги собирались, исходя из площади имеющейся у крестьянина земли, что позволяет считать коэффициент f0 в (7) постоянным. Дальнейшие расхождения по-видимому связаны с тем, что в государстве, в конце концов, установилась феодальная система, существенно изменившая структуру социально-экономических взаимоотношений. Потому приведенная модель перестает быть адекватной.
2.2. Базовая модель аграрного общества с преобладанием
государственной собственности на землю
Рассматривается социальная система, основными составляющими которой являются сельскохозяйственные производители – крестьяне и собственник земли – государство. Такие социальные системы были достаточно широко распространены в докапиталистическую эпоху в Северной Африке, на Ближнем и Дальнем Востоке. Модель, описывающая такую систему, в отличие от модели (7), наряду с демографическими и производственными процессами учитывает социальное взаимодействие крестьян и государства.
2.2.1. Описание модели
Модель является усложненной версией модели "феодал-производитель" [5,6] и строится следующим образом.
Как уже упоминалось выше, предполагается, что общество состоит из производителей аграрного продукта (крестьян) и военно-административной элиты, стоящей на службе у государства и живущей за счет изъятия продукта на собственные нужды у производителей. Произведенный продукт расходуется на потребление как непосредственно (продукты питания), так и в преобразованной форме (ремесленная продукция, услуги и т.п.). Кроме того, государство может расходовать определенные средства на стимулирование и повышение эффективности сельскохозяйственного производства (что сказывается на появлении зависимости производительности крестьян от экономического состояния государства), а также тратит определенные средства на удержание производителей в повиновении, чтобы обеспечить себе возможность дальнейшего изъятия продукта.
В соответствии с (1) две выделенные группы - крестьяне и государство - характеризуются в модели величинами X1, N1 ≡ 1, X2, N2. Для удобства обозначим: X=X1, N=N2, Y=x2=X2/N2. Таким образом, состояние государства характеризуется величиной X – суммарным накоплением материальных благ (государственная казна), выраженным в единицах обобщенного продукта. Крестьяне характеризуются величинами Y и N, где Y - средние накопления материальных благ у одного крестьянина и N - численность крестьян в рассматриваемом аграрном государстве. При сделанных предположениях производство и перераспределение продукта, а также демографические процессы в обществе могут быть в соответствии с (1) описаны следующей системой дифференциальных уравнений:
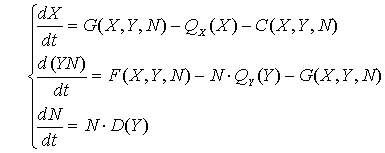 (8)
(8)
Здесь:
G(X, Y, N) - суммарное количество продукта, изымаемое государством у крестьян в единицу времени (например, за год) посредством налогов и различных поборов;
QX(X) и QY(Y) - функции потребления государства и крестьян, соответственно, показывающие, какое количество продукта потребляется ими в единицу времени. Функция QX(X) включает в себя расходы на содержание чиновничества, на развитие инфраструктуры, охрану внешних границ и т.п.;
F(X,Y,N) - производственная функция, характеризующая совокупное сельскохозяйственное производство в государстве;
C(X,Y,N) - функция затрат государства на управление (на обеспечение повиновения крестьянства);
D(Y) - функция прироста населения.
В первом приближении можно считать, что функция G(X, Y, N) пропорциональна X, Y и N:
G(X, Y, N) = a∙X∙Y∙N. (9)
Аналогичное приближение может быть принято и для функций потребления:
QX(X) = AX ∙X, (10)
QY(Y) = AY ∙Y. (11)
Допустим, что функция C(X,Y,N) затрат на управление не зависит явно от X. Если границы государства стабильны, то допустимо считать, что C(X,Y,N) линейна по N. С другой стороны, она должна возрастать как при Y → 0 (поскольку обнищание населения усиливает недовольство и сопротивление власти), так и при Y → ∞ (так как у состоятельного населения возникает стремление добиваться независимости от центральной власти). В соответствии с этим в модели принимается, что
![]() . (12)
. (12)
Производственная функция может быть представлена в виде
F(X,Y,N) = N∙f(X)∙R(N), (13)
где R(N) – площадь обрабатываемой одним крестьянином земли, а функциональная зависимость f(X) отражает вклад государства в производительность труда (строительство дамб и каналов, проведение ирригационных работ, обеспечение порядка).
В соответствии с
(5) 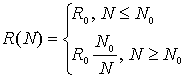 ,
,
В модели используется гладкое приближение этой функции:
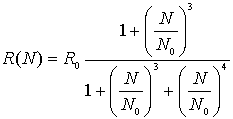 , (14)
, (14)
в соответствии с которым R(N) ~ const = R0 при N → 0 и R(N) ~ R0∙(N0/N) при N → ∞.
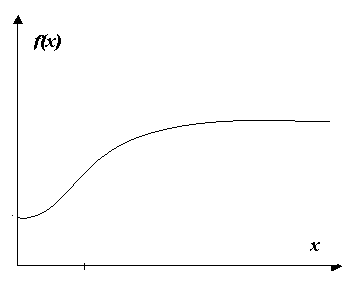
Предполагается, что производительность труда f(X) – монотонно возрастающая функция, выходящая на насыщение при X → ∞. В модели принято:
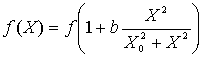 , (15)
, (15)
где b и X0 – некоторые постоянные. Таким образом, вид функции аналогичен представленному на рис.1. Предполагается, что средства X, прямо или косвенно расходуемые государством на повышение производительности труда крестьян, входят составной частью в функцию потребления государства QX(X).
Функция прироста
населения, как и в предыдущей модели, предполагается равной D(x) = r ∙(1 − Y0/Y).
В итоге имеем систему:
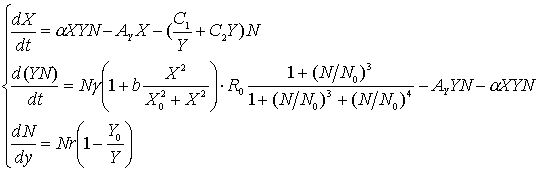 (16)
(16)
Раскрыв ![]() , получим:
, получим:
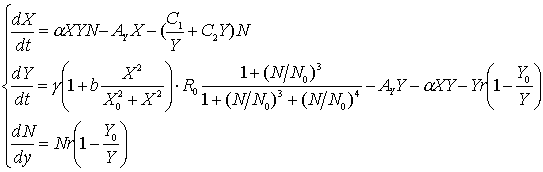 (17)
(17)
В полученной системе двенадцать коэффициентов. От некоторых из них можно избавиться, введя нормировку X, Y, N и t.
Положив 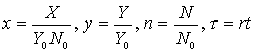 , получим:
, получим:
 (18)
(18)
где β = a∙Y0∙N0/r, ax = Ax/r, ay = Ay/r, c1 = C1/(r ∙Y02), c2 = C2/r, F = f∙R0/(r ∙Y0), x0 = X0/(Y0∙N0). Здесь единица численности N0 – численность населения, при которой обрабатывается вся пригодная земля; единица времени – минимально возможный период (при условии y >> 1), за который население увеличится в e раз.
В дальнейшем, в основном, будет использоваться система в виде (18). Иногда, для большей наглядности, результаты будут приводиться для системы (17).
2.2.2. Результаты численного
моделирования
Результаты численного решения системы показали, что
при различных наборах параметров наблюдаются следующие режимы:
1) система сильно нестабильна, то есть не
существует устойчивой или неустойчивой точки равновесия (X*, Y*, N*) в фазовом
пространстве системы при положительных значениях X*, Y* и N*. Такая система быстро разрушается, то есть хотя бы одно из значений X(t), Y(t), N(t), характеризующих систему, обращается в ноль;
2) в фазовом пространстве существует точка
неустойчивого равновесия типа “фокус” или “центр”. Система разрушается за
конечное время. Однако, если начальные условия близки к точке равновесия,
система может довольно долго существовать не разрушаясь даже при наличии
флуктуаций;
3) существует точка устойчивого равновесия типа
“фокус” или “центр” и соответствующая область притяжения данного аттрактора в
фазовом пространстве (X, Y, N);
4) существует предельный цикл с соответствующей
областью притяжения.
В двух последних случаях система теоретически может
существовать неограниченно долго. Однако для устойчивости системы необходимо,
чтобы изменения ее параметров вследствие каких-либо внешних или внутренних
причин не выводили систему за границу области притяжения. В соответствии с
этим, представляет большой интерес исследование влияния параметров системы на
размеры и форму области притяжения существующих аттракторов.
При достаточно широких вариациях значений параметров
система имеет точку равновесия типа «устойчивый фокус», имеющую определенную
область притяжения. Типичный вид траекторий системы в таком случае представлен
на рис.11(a)-(d)
(значения коэффициентов: a = 0.0003, AX = 0.1, AY = 0.7, C1 = C2 = 0.1,
f = 1, X0 = 500, b = 0.5,
r = 0.04, Y0 = 1, R0 = 1, N0 = 1000).
На рисунке 11(а) пунктиром показана граница области притяжения при значениях y, близких к y = 1.
|
Рис.11(a).
Траектории системы в координатах X, N при y = 1. |
Рис.11(b).
Зависимость N(t) для различных начальных условий. |
|
Рис.11(c).
Зависимость X(t) для различных начальных условий. |
Рис.11(d).
Зависимость Y(t) для различных начальных условий. |
|
Представляет интерес то, каким образом поведение системы зависит от значений параметров.
Зависимость устойчивости системы
от затрат на управление
На рис.12(a)-(f) в нормированных координатах показаны траектории при разных значениях параметров c1 и c2, характеризующих затраты правящего класса на управление и поддержание порядка. Как видно из графиков, при росте затрат равновесное значение n сначала увеличивается. При этом равновесное значение x почти не изменяется, но область притяжения сужается (см. рис.12(a)-(d)). Наконец, при достаточно больших c1 и c2 фокус становится неустойчивым (рис.12(e)) и при дальнейшем росте коэффициентов исчезает совсем (рис.12(f)).
|
Рис.12(a). Траектории системы в координатах x, n
при с1 = с2 = 2.5 |
Рис.12(b).
Траектории системы в координатах x, n при с1 = с2 = 3.75 |
|
Рис.12(c).
Траектории системы в координатах x, n при с1 = с2 = 5.0 |
Рис.12(d).
Траектории системы в координатах x, n при с1 = с2 = 6.0 |
|
Рис.12(e).
Траектории системы в координатах x, n при с1 = с2 = 6.25 |
Рис.12(f).
Траектории системы в координатах x, n при с1 = с2 = 6.7 |
Зависимость устойчивости системы
от способа перераспределения продукта
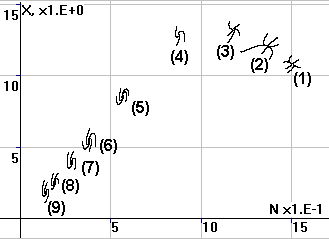
Рассмотрим для системы с нормированными коэффициентами, как зависит положение точки устойчивого равновесия от коэффициента b, определяющего долю изымаемого у крестьян продукта. С уменьшением b координаты аттрактора (x*, n*) растут (см. рис.13), причем зависимость между x* и n* близка к линейной. При n близких к единице (N* близких к N1) эта зависимость нарушается, и с дальнейшим уменьшением b система теряет устойчивость. Это объясняется тем, что при n > 1 (N > N0) рост N уже не приводит к увеличению выпуска суммарного продукта (т.к. вся пригодная к сельскохозяйственной обработке земля уже используется), а лишь к снижению удельного (на одного крестьянина) выпуска.
|
Рис.13. Положение аттрактора системы при различных
значениях β (F = 37.5). (1) – β = 2.125, (2) – β = 2.25. (3) – β = 2.5, (4) – β = 3.25, (5) – β = 5.0, (6) – β = 7.5, (7) – β = 10.0, (8) – β = 15.0, (9) – β = 17.5 |
Эволюция фазовой картины с изменением параметра β для значений коэффициентов: ax = 0.1, ay = 1, c1 = c2 = 0.05, F = 0.75, b = 1.0, x0 = 1.0 представлена на рис.14(a)–(h). При β, меньших определенного критического значения аттрактор отсутствует, однако существует неустойчивая точка равновесия типа «узел» (см. рис.14(a)). С ростом β узел приобретает устойчивость, и область притяжения при этом уже довольно велика (см. рис.14(b)). В дальнейшем узел переходит в фокус (рис.14.(c),(d)). Потом фокус теряет устойчивость, и возникает предельный цикл (рис.14(e)). Область притяжения изменяется незначительно, но предельный цикл расширяется, подходя все ближе к ее границам (рис.14(f)), после чего разрушается (рис.14(g)), и аттрактор исчезает (рис.14(h)).
|
Рис.14(a).
Фазовый портрет системы при β = 0.128 |
Рис.14(b).
Фазовый портрет системы при β = 0.13 |
|
Рис.14(c).
Фазовый портрет системы при β = 0.15 |
Рис.14(d).
Фазовый портрет системы при β = 0.17 |
|
Рис.14(e).
Фазовый портрет системы при β = 0.175 |
Рис.14(f).
Фазовый портрет системы при β = 0.1875 |
|
Рис.14(g).
Фазовый портрет системы при β = 0.19 |
Рис.14(h).
Фазовый портрет системы при β = 0.25 |
Учет внешних факторов
Если предположить, что внешние воздействия относительно малы и имеют несистематический характер, можно представить их как случайные флуктуации параметров, и введя в модель, проследить, как изменится поведение системы.
Интересно исследовать, как влияет на поведение системы наличие флуктуаций параметра f. Этот параметр характеризует производительность труда крестьян (урожайность), которая зависит от применяемой технологии обработки земли. При этом она в значительной мере определяется также и климатическими, погодными факторами, экологической обстановкой и т.п. И, если остальные параметры системы могут оставаться почти неизменными на протяжении десятилетий, а то и столетий, то урожайность может сильно изменяться из года в год.
Для учета влияния внешних факторов на производительность была введена зависимость параметра f от времени: f(t) = f0(1 + dfi), где dfi – случайная величина, равномерно распределенная на отрезке [−Δf, Δf] (Δf > 0) и сохраняющаяся постоянной в течение времени (T0 + dT∙i) ≤ t < (T0 + dT∙(i + 1)), где T0 > 0, dT > 0, i = 0, 1, 2, …
Сравнение результатов расчетов при f = const и f = f(t) показывает, что при различных соотношениях параметров область устойчивости системы может остаться практически неизменной, или, напротив, значительно измениться, либо исчезнуть вообще.
Если параметры системы далеки от критических значений, а вариации коэффициента f(t) не слишком велики, то фазовый портрет системы меняется несущественно. Совсем иная ситуация складывается, если параметры системы околокритические. Рассмотрим случай, когда производительность низка, но у правящего класса еще остается возможность изменять долю изымаемого продукта, не нарушая устойчивости всей системы (интервал значений a, при которых существует точка устойчивого равновесия, еще достаточно широк). При значениях параметров, соответствующих системе, фазовый портрет которой изображен на рис.12(d), область устойчивости невелика, а затухание возмущений происходит медленно. Потому система, будучи выведена из равновесия даже относительно слабыми воздействиями (Δf = 0.1, dT = 1), не успевает вернуться в прежнее состояние, и с каждой новой флуктуацией оказывается все дальше и дальше от равновесного положения, пока не попадает, наконец, в зону неустойчивости (рис.15(a)–(d)).
|
Рис.15(a). Траектория системы в координатах X,
N. |
Рис.15(b). Зависимость N(t). |
|
Рис.15(c). Зависимость X(t). |
Рис.15(d). Зависимость Y(t). |
Следует заметить, что при меньших a (и неизменных прочих параметрах) система с введением флуктуаций остается устойчивой. Однако для того, чтобы общество сознательно изменило значение коэффициента, нужно суметь вовремя предсказать приближающуюся катастрофу. Это трудно, поскольку в рассматриваемой ситуации система может оставаться относительно стабильной достаточно долго, и может создаться впечатление, что так будет продолжаться и в дальнейшем. Однако рано или поздно устойчивость все равно будет потеряна.
Аналогичная ситуация внезапного
разрушения системы после длительного периода относительной стабильности может
реализоваться и в отсутствие внешних воздействий, а именно – в случае, когда
система попадает в состояние неустойчивого равновесия. Фазовый портрет,
соответствующий данной ситуации, изображен на рис.16. Видно, что существует
точка равновесия, которая является притягивающей для траекторий из достаточно
обширной фазовой области, и система, приближаясь к этой точке, будет достаточно
долго находиться в ее окрестности без существенного изменения своих
характеристик. Однако, затем величина государственной казны X, характеризующая
в том числе их возможности удерживать крестьян в повиновении, резко падает до
нуля – наступает кризис (траектория (1) на рис.16). Реально это приводит к
смутам, гражданским войнам, массовым миграциям населения, что в конце концов
может завершиться завоеванием страны соседями, или разделением ее на более
мелкие государства, или сменой государственного устройства на более
эффективное.
Моделирование показывает, что такое поведение системы может реализоваться тогда, когда b > 0 (см. уравнение (15)), то есть когда государство играет существенную роль в повышении эффективности производства. Это может выражаться в организации общественных работ, направленных на повышение плодородия (мелиорация, ирригация, строительство плотин и каналов), развитие транспортной инфраструктуры, поддержание порядка внутри страны, защиту от внешних врагов, борьбу со стихийными бедствиями. В таком случае усиление государства стабилизирует систему, а ослабление – после некоторого периода относительно слабых изменений приводит к глубокому кризису (см. рис.16(с)), который сопровождается резким обнищанием населения (рис.16(d)) и депопуляцией (рис.16(b)) (реальные исторические аналогии этому легко найти, например, в многовековой истории Китая или в истории России XVII и XX веков).
|
(a) |
(b) |
|
(c) |
(d) |
|
Рис.16. Фазовые траектории и временные зависимости x(t), y(t), n(t) в системе с параметрами β = 1.28,
ax = 1.0, ay = 10.0, c1 = c2 = 0.5, F = 7.5, b = 1.0, x1 = 1.0,
(1): Δf
= 0, (2),(3):
Δf = 0.1, dT = 0.04 |
|
Следует отметить, что подобная картина сохраняется и при наличии флуктуаций параметра f(t) (траектории (2) и (3) на рис.16): в этом случае изменяется лишь момент начала катастрофы, но не сам характер процесса. При этом система может долго не проявлять явных признаков нестабильности, и общество скорее всего окажется не готовым к приближающемуся кризису.
Влияние флуктуаций параметров проявляется в том, что одновременно с их скачкообразным изменением также скачком меняется форма и размеры области притяжения аттрактора, и дальнейшее поведение системы зависит от того, окажется ли она в этот момент внутри или вне новой области притяжения. Если же параметры системы изменяются медленно и непрерывно, то область притяжения, как правило, меняется плавно, и система будет устойчива до тех пор, пока эта область существует.
Рассмотрим пример, когда медленно уменьшается уровень производства F. Это может происходить как в результате глобального изменения климата, так и в результате чрезмерно интенсивной хозяйственной деятельности, приводящей к постепенному исчерпанию природных ресурсов и/или к ухудшению экологической обстановки. На рис.17 изображена эволюция системы при постепенном уменьшении значения F. Зависимость F от времени полагается линейной: F = 7.5 – 10-3∙τ. В данном случае наблюдается быстрый выход системы из стационарного состояния при исчезновении области устойчивости.
|
Рис.17(a). Фазовый портрет системы при F = 7.5 |
Рис.17(b). Фазовый портрет системы при F = 7.4 |
|
Рис.17(c). Изменение x(t), y(t), n(t) при уменьшении
значения F. |
|
2.3. Модель аграрного государства феодального типа
В предыдущей
модели военно-административная элита отожествлялась с институтом государства.
Однако, как известно из истории, конфликты и социальное взаимодействие могут
происходить не только между государством и народом, но и внутри властных
структур, что приводит к многообразию различных форм правления и политической
организации. В приведенной далее модели элита и государство представлены не как
единое целое, а как отдельные элементы системы, взаимодействующие между собой.
Итак, в соответствии с (1), введем в рассмотрение крестьянское сословие, землевладельцев-феодалов и институт центральной власти. Вертикальной мобильностью, в условиях сословного средневекового общества практически отсутствующей, можно пренебречь, т.е. D’ji = 0. Таким образом, имеем систему из пяти уравнений для величин: X1 – государственная казна, N1 º 1, X2 и N2 – материальные накопления и численность феодалов, X3 и N3 – материальные накопления и численность крестьянства соответственно.
Предположим, что взаимоотношения между выбранными группами построены следующим образом. Основным (и, при сделанных упрощениях, – единственным) производителем материальных благ (в данном случае – сельскохозяйственной продукции) являются крестьяне. Землевладельцы и государство силой изымают продукцию у крестьян, а государство, также, – у землевладельцев, встречая при этом некоторое сопротивление и неся расходы на его преодоление. Помимо того, государство и землевладельцы косвенно вносят определенный вклад в повышение выпуска сельскохозяйственной продукции (инвестиции I), что выражается в организации и проведении ирригационных работ, охране территории и т.п.
Положим: F1 = F2 º 0 и
 , (19)
, (19)
где R(N3) – площадь обрабатываемой земли, приходящейся на крестьянина (за единицу принимается максимальная площадь, которую способен обрабатывать один крестьянин).
Будем, как и прежде, в первом приближении считать, что функции G, Q, I пропорциональны соответствующим накоплениям Xi. Тогда коэффициенты системы (1) примут вид:
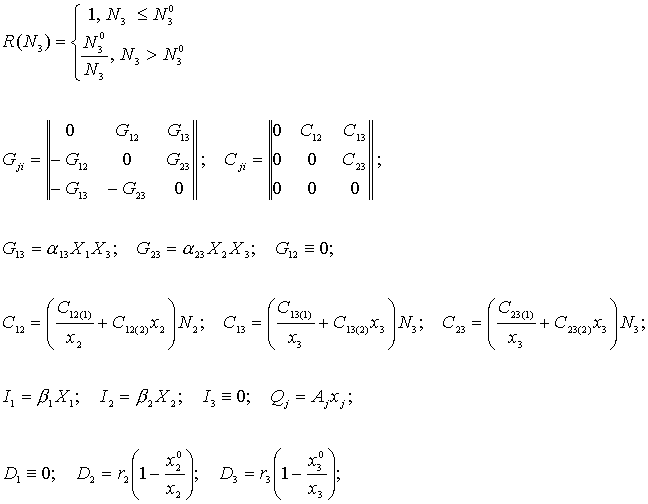
Определив таким образом коэффициенты, мы в данном
случае считаем, что:
а) затраты государства на управление
землевладельческой элитой и крестьянами, и землевладельцев – на управление
крестьянами, имеют минимум при некотором значении удельных накоплений
управляемой группы, и возрастают как при их росте, так и при падении;
б) и государство, и землевладельцы изымают
продукт непосредственно у крестьян (G12 º 0, G13 > 0,
G23 > 0);
в) рождаемость
Dj ® rj
при xj ® +¥,
и Dj ® -¥
при xj ® 0.
Полученная система является более сложной, чем система
(8), и имеет множество различных решений в зависимости от количественного
соотношения параметров модели.
|
|
|
|
Рис.18(а). Зависимость Nj = Nj(t) при a23 = 0,001065 |
Рис.18(b).
Зависимость Xj = Xj(t) при a23 = 0,001065 |
|
|
|
|
Рис.19(а). Зависимость Nj = Nj(t) при a23 = 0,001066 |
Рис.19(b).
Зависимость Xj = Xj(t) при a23 = 0,001066 |
На рисунках 18 и 19 представлены зависимости накоплений (рис.18(b), 19(b)) и численностей социальных групп (рис.18(a), 19(a)) от времени при начальных условиях X1(t=0) = 50, X2(t=0) = 100, X3(t=0) = 100, N2(t=0) = 10, N3(t=0) = 100 и незначительно различающихся значениях коэффициента a23 (a23 = 0,001065 (рис.18), a23 = 0,001066 (рис.19)).
Параметры модели приняты в соответствии с таблицей:
|
A1 |
0,1 |
a13 |
0,0015 |
C12(1) |
0,05 |
C13(1) |
0,001 |
C23(1) |
0,001 |
b1 |
0,1 |
|
A2 |
0,1 |
a23 |
|
C12(2) |
0,05 |
C13(2) |
0,001 |
C23(2) |
0,001 |
b2 |
0,1 |
|
A3 |
0,1 |
|
|
|
|
|
|
|
|
|
|
|
f1 |
1 |
b1 |
100 |
N30 |
100 |
r2 |
0,1 |
x20 |
10 |
|
|
|
f2 |
1 |
b2 |
100 |
|
|
r3 |
0,1 |
x30 |
1 |
|
|
|
f3 |
0,1 |
|
|
|
|
|
|
|
|
|
|
Из рисунков
видно, что данных значениях параметров система имеет точку неустойчивого
равновесия, покинув которую, она может перейти в одно из двух принципиально разных
для рассматриваемой социальной системы состояний. Изображенные на рисунках графики
можно интерпретировать как отражение течения конфликта между центральной
властью и элитой, который в первом случае (рис.18) заканчивается победой одной,
а во втором (рис.19) - другой стороны. То есть государство из состояния со
сбалансированным управлением в результате приходит либо к авторитаризму (первый
случай: численность и накопления элиты обращаются в нуль), либо к олигархии
и/или феодальной раздробленности (второй случай: накопления государства
обращаются в нуль).
Конечно,
приведенный пример расчета довольно условен. Зависимости параметров модели от
динамических переменных, безусловно, имеют более сложный характер. Данный
пример служит лишь для иллюстрации того, что с помощью представленного подхода
можно моделировать и наблюдать экономические и социальные кризисы, революции,
смены форм производственных отношений, форм правления и т.п.
Заключение
В работе изложена математическая модель для описания аграрного общества, учитывающая демографические процессы и взаимодействие различных социальных слоев. Показано, что общество может иметь качественно разные пути развития в зависимости от внешних условий, начального состояния и параметров системы. Обсуждены различные возможности возникновения кризисных ситуаций, рассмотрены некоторые механизмы потери устойчивости рассматриваемого общества. Несмотря на свою простоту, модель позволяет описать некоторые особенности эволюции социальных систем. В дальнейшем предполагается использовать данную модель для анализа закономерностей социальной динамики в конкретных государствах, для определения условий стабильного развития аграрных обществ.
Литература
1. Капица С.П., Курдюмов С.П., Малинецкий Г.Г. Синергетика и прогнозы будущего. - М.: Наука, 1997.
2. Малинецкий Г.Г. Нелинейная динамика и историческая механика // Общественные науки и современность, 1997, №2, с.99.
3. Turchin P. Historical Dynamics: Why States Rise and Fall,
Princeton University Press, Princeton, NJ, 2003.
4. Нефедов С.А. Опыт моделирования демографического цикла // Информационный бюллетень
Ассоциации "История и компьютер", №29, 2002, с.131-142.; Теория демографических циклов и социальная
эволюция древних и средневековых обществ Востока // Восток, 2003, №3, с.5-22.
5. Малков С.Ю.,
Ковалев В.И., Малков А.С. История человечества и стабильность
(опыт математического моделирования) // Стратегическая стабильность, 2000, №3,
с.52-66.
6. Малков С.Ю.,
Малков А.С. История в свете математического моделирования // История
за и против истории, книга 2. - М.: Центр общественных наук, 2000, с.54-76.
7. Малков С.Ю.
Математическое моделирование исторических процессов // Новое в синергетике:
Взгляд в третье тысячелетие / Под ред. Г.Г.Малинецкого, С.П.Курдюмова. - М.:
Наука, 2002, с.291-323.
8. Малков С.Ю.,
Коссе Ю.В., Бакулин В.Н.,
Сергеев А.В. Социально-экономическая и демографическая динамика в
аграрных обществах // Математическое моделирование, 2002, т.14, №9,
с.103-108.
9. Нефедов С.А. О демографических циклах в истории средневекового Египта [http://hist1.narod.ru/Science/Egipt/EgiptSV.htm];
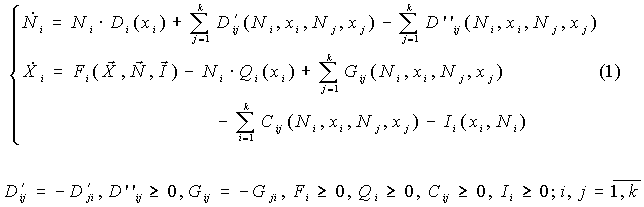
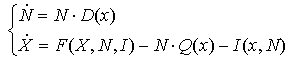
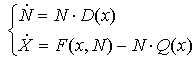
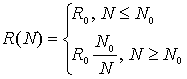
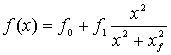 .
.