Abstract
The concise look at the Difference Potentials Method and at the causes of new possibilities
which are provided by this method; three examples of solved applied problems and also the notes
about connections between Calderon-Seely and new potentials.
Àííîòàöèÿ
Îáùèé âçãëÿä íà ìåòîä ðàçíîñòíûõ ïîòåíöèàëîâ è íà ïðè÷èíû íîâûõ âîçìîæíîñòåé, êîòîðûå äàåò ýòîò
ìåòîä; òðè ïðèìåðà èç ÷èñëà ðåøåííûõ ïðèêëàäíûõ çàäà÷; çàìå÷àíèÿ î ñâÿçÿõ ìåæäó íîâûìè
ïîòåíöèàëàìè è ïîòåíöèàëàìè Êàëüäåðîíà-Ñèëè.
The method of difference potentials (DPM) is intended for digital
simulation and numerical solution of some problems of mathematical physics DPM
was proposed by the author in his doctoraite (D. Sc.) thesis in 1969 and was
significantly developed at Keldysh Institute Russian Academy of Sciences, at
the Department of Computational Mathematics of the Moscow Institute of Physics
and Technology, at the Institute for Mathematics Modeling of the Russian
Academy of Sciences, at ICASE (NASA Lengley Reserch Center) as well as some
other Institutes.
This report will be necessarily
fragmentary. The almost modern state-of-the art of the DPM is reflected in [1].
There (in [1]) are also named others
people who take part in developing of DPM. Here I would like to mention only
Professor Semeon Tsynkov, whose participation was very bright and significant.
The new possibilities provided by the
DPM originate from the fact, that DPM combines several advantages of the
classical potentials and Calderon’s-type potentials with the universality and
constructively of difference schemes.
The main advantage of classical
potential method for discretisation and numerical solution the different
problems of mathematical physics (Laplas and Helmholtz equations, the Lame,
Stocks, Maxwell, Cauhy-Riemann systems) is
the possibility to digitize the potentials and boundary integral
equations by means of quadratures. But the kernels of integral operators of
this kind are constructed by means of fundamental solutions, which must be
sufficiently simple. Therefore the field of applicability of classical
potentials method is bounded, to say the least, by equations with constant
coefficients, and can’t be used for
equations with variable coefficients.
A.P.Calderon [2] and R.T.Seeley [3]
have constructed and studied the pseudodifferential potentials, boundary
pseudodifferential equations with projectors for elliptic equations with
variable coefficients. But Calderon-Seeley equations can’t be digitized by
means of quadratures, because they do not contain any integrals.
We have constructed some simple
auxiliary boundary problems which are used instead of using symbols of differential
operators. These modified potentials are defined not only for elliptic
equations, they have similar properties, but they also can’t be digitized by
means of quadratures because they also do not contain the integrals. However,
we have constructed earlier the difference potentials. Those can be used for
discrete approximation of new potentials and boundary pseudodifferential
equations with projectors, connected with them. It is possible to say that the
difference potentials play the role of non-classic quadratures for modified
Calderon-Seeley potentials.
Thus the modified Calderon-Seeley
potentials can be used for discrete simulation and numerical solution of
different problems of mathematical physics, not only elliptic.
Note, however, that really the
difference potentials were proposed much earlier then modification of
Calderon-Seeley potentials was made (1983). This modification was made firstly
to close the constructions of difference potentials when grid step tends to
zero.
The difference potentials can be used
also for discrete simulation and numerical solution of different problems
directly, without using the modified Calderon-Seeley potentials.
Note also, that theory of DPM is
mainly algebraic and algorithmic. The general metric properties of new
potentials are studied only partially (see [1], part I-III). We will speak here
below only about one sort of difference potentials, namely, about the so-called
difference potentials of Cauchy-type and about three examples of applications
of DPM to some numerical problems.
I. The constructions and properties of
Cauchy-type difference potentials.
The
difference potentials of Cauchy-type and more general potentials are
constructed for solutions of linear system of difference equations of general
form. But we will speak here only about difference potentials of Cauchy-type,
using the Poisson equation 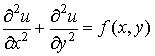 and its simplest
difference analogue and its simplest
difference analogue
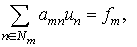
where
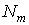 is five-point stencil
of difference scheme. Namely, we use grid is five-point stencil
of difference scheme. Namely, we use grid 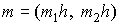 , with step h; , with step h; 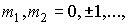 and stencil and stencil 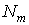 , which contain following five points: , which contain following five points:

I. 1.
The auxiliary difference problem.
To construct the
difference potentials we use the following auxiliary difference problems.
Let 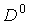 be a bounded domain
in the xy-plane. We will assume that be a bounded domain
in the xy-plane. We will assume that 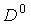 is some square, whose
sides are lying on grid line x=kh, or y=lh, where k and l are any integers (Fig.1). is some square, whose
sides are lying on grid line x=kh, or y=lh, where k and l are any integers (Fig.1).
Let M0 be the set
of points 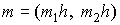 , which belong to interior part of square , which belong to interior part of square  (the black points on
Fig.1). We consider the following difference equation (the black points on
Fig.1). We consider the following difference equation
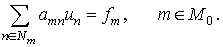 (1) (1)
Obviously,
the left-hand side of this equation is meaningful for the functions 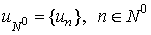 , whose grid domain , whose grid domain 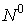 is is 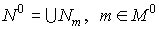 . We add some linear homogeneous condition to the difference
equation (1). For example we assume . We add some linear homogeneous condition to the difference
equation (1). For example we assume
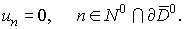
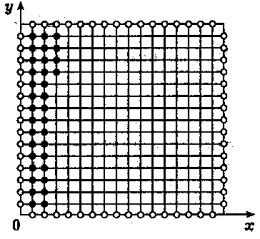
Fig.1.
We can rewrite
these boundary conditions as inclusion
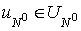 (2) (2)
where
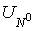 is the space of all
functions is the space of all
functions 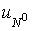 , which equal to zero on boundary , which equal to zero on boundary 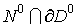 . .
I. 2. The grid boundary and Cauchy-type potential with jump.
Let 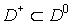 be given subdomain of be given subdomain of
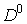 (Fig.2). By (Fig.2). By 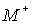 we denote the set of
points m lying in the interior of we denote the set of
points m lying in the interior of 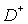 or on its boundary or on its boundary 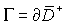 , and consider the equation , and consider the equation
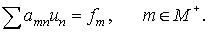 (3) (3)

Fig.2.
The
left-hand side of this equation is meaningful only for the functions 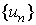 , defined on the set , defined on the set
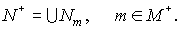
By 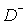 we denote the domain we denote the domain 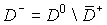 and by and by  the set of grid
points lying in the set of grid
points lying in 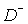 : :
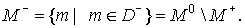
We
consider system
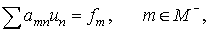 (4) (4)
on
the set 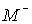 . The left-hand side of system (4) is meaningful for the
function . The left-hand side of system (4) is meaningful for the
function 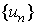 that are defined on
the set that are defined on
the set
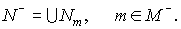
Thus
system (1) splits into two subsystems (3) and (4) whose solutions are defined
on 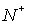 and and 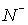 respectively. respectively.
Let us define the boundary g between grid domains 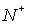 and and 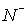 , by setting , by setting
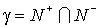 (see Fig.3). (see Fig.3).
We shall speak that
functions 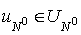 from space from space 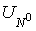 are regular. are regular.
Let 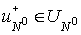 and and 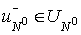 be two arbitrary
regular functions. We define the piecewise-regular function be two arbitrary
regular functions. We define the piecewise-regular function  , by setting , by setting
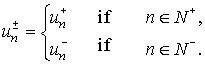 (5) (5)
Let
us introduce the linear space 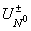 all functions of the
form (5). The function (5) takes two values all functions of the
form (5). The function (5) takes two values  and and 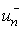 at each point at each point 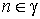 of the grid boundary g. of the grid boundary g.
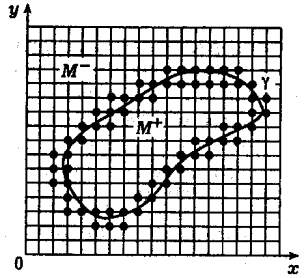
Fig.3.
A single-value function  , defined at the points , defined at the points  by the formula by the formula
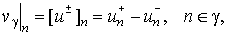
will
be called a jump of the piecewise-regular function  on the grid boundary g.
The piecewise-regular function (5) will be called a piecewise-regular solution
of the problem on the grid boundary g.
The piecewise-regular function (5) will be called a piecewise-regular solution
of the problem
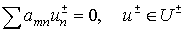 (6) (6)
if
the functions 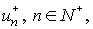 and and 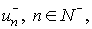 satisfy the
homogeneous equations satisfy the
homogeneous equations
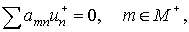
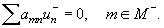
Theorem. Let
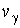 be an arbitrary
function which is defined on g.
There exists one and only one piecewise-regular solution be an arbitrary
function which is defined on g.
There exists one and only one piecewise-regular solution 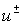 of the problem (6)
with jump of the problem (6)
with jump 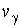 . .
Definition.
The piecewise-regular solution 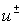 of problem (6) with
given jump of problem (6) with
given jump 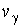 will be called a
difference potential will be called a
difference potential 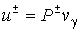 with density with density 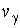 . .
I. 3. An analogy between the Cauchy-type difference potential and the
classical Cauchy-type integral.
Suppose that G is
a non-self-intersecting closed contour that divides the complex plane z=x+iy into the bounded part 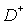 and the complimentary
unbounded part and the complimentary
unbounded part 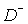 . The classical Cauchy-type integral . The classical Cauchy-type integral
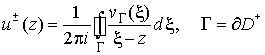 (7) (7)
can
be determined as a piecewise analytic function tending to zero at infinity and
exhibiting the jump 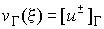 on the contour G.
Here on the contour G.
Here 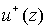 and and 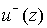 are the values of the
Cauchy-type integral (7) for are the values of the
Cauchy-type integral (7) for 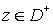 and and  accordingly. accordingly.
A Cauchy-type integral can be
interpreted as a potential for the solutions of the Cauchy-Riemann system
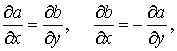
connecting
the real and imaginary parts of an analytic function.
Thus the Cauchy-type
difference potentials
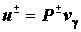 plays the same role for solutions of general linear difference equations
as the Cauchy-type integral plays for solutions of the Cauchy-Riemann system. plays the same role for solutions of general linear difference equations
as the Cauchy-type integral plays for solutions of the Cauchy-Riemann system.
II. The examples of applications of DPM.
The difference Cauchy-type potentials
play the same role for general difference schemes as Cauchy-type integral play
for Cauchy-Riemann system. The
Cauchy-type integral has many applications to different problems, which are
connected with Cauchy-Riemann system. Therefore it is naturally to expect, that
the difference Cauchy-type potentials must have many applications to the
different and distant one to other problems. Really, it is so.
We give here several examples of
applications of DPM.
These and many others ones are
reflected in the book [1] and many papers.
II. 1. Artificial boundary conditions for
stationary problems.
A typical example of
problem requiring the construction of artificial boundary conditions is the
problem of calculating the velocity and pressure of the air flow around a body,
usually in the close vicinity of the body. However, for computation we have to
take considerably larger neighborhood.
The DPM gives the
possibilities to construct the nonlocal artificial boundary conditions on the
external boundary of the finite computational subdomain, which demonstrate some
advantages in comparison with ordinary classical artificial boundary
conditions. It was demonstrated by means of some NASA tests ([1], part V).
II. 2. Nonreflecting
artificial boundary conditions for long-time calculations of acoustic and
electromagnetic waves propagation.
Let we need to calculate a table of
values some function u(t,x,y,z)
on grid of points 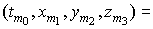 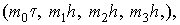 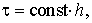 h>0, h>0, 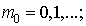 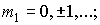 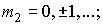  which are lying
inside of the unique sphere which are lying
inside of the unique sphere
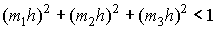
on the time-levels 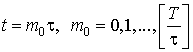 and T can be arbitrary great number.
Obviously, the amount of grid points, where we have to find function u(t,x,y,z) has the order of and T can be arbitrary great number.
Obviously, the amount of grid points, where we have to find function u(t,x,y,z) has the order of 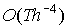 . Therefore there is no method, which requires less then . Therefore there is no method, which requires less then 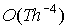 arithmetic operations
to calculate this table. arithmetic operations
to calculate this table.
We consider now this problem in case when function u(t,x,y,z) is the solution of the following
problem
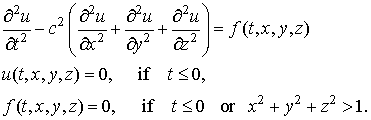
The calculation by means of ordinary difference scheme with grid mech h
for x,y,z and 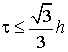 for t requires for t requires  arithmetic operations
and becomes impossible even for not very large values of T. arithmetic operations
and becomes impossible even for not very large values of T.
But using the lacunas of wave equation
in 3 dimensional space x,y,z together
whit DPM we constructed algorithm which
takes only 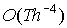 and which therefore
can’t be improved. and which therefore
can’t be improved.
Recently this result was obtained also
for solution 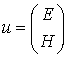 Maxwell system,
namely, were constructed non-reflecting artificial boundary conditions for
change the Maxwell system in vacuum out computational subdomain Maxwell system,
namely, were constructed non-reflecting artificial boundary conditions for
change the Maxwell system in vacuum out computational subdomain 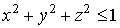 . These results valid also, if inside sphere . These results valid also, if inside sphere 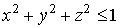 there are some
scattering, cavities or any non linearity. there are some
scattering, cavities or any non linearity.
These results can be used for
long-time calculations of some problems of acoustic and electrodynamics (see
[1], part VII).
II. 3. Difference simulating of active shielding problem.
We will consider following problem,
which describes single-frequency harmonic sound
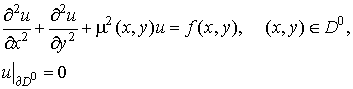 (8) (8)
on
domain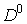 (see Fig.2). We will assume that (see Fig.2). We will assume that 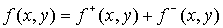 , where , where
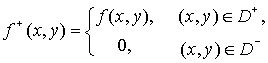
is a
density of useful sound of sources, and function
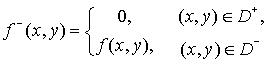
is a density of noise sources accordingly. We
will assume also, that neither f(x,y)
nor u(x,y) is given. We know only two functions 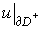 and and 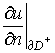 on boundary on boundary  , which reflect the sum either the useful sound and noise. , which reflect the sum either the useful sound and noise.
The problem of active shielding the
subdomain 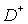 against sources,
which are located outside against sources,
which are located outside 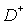 , we are setting in the following way: to construct function g(x,y), , we are setting in the following way: to construct function g(x,y), 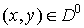 , in order that the solution v(x,y) of the problem , in order that the solution v(x,y) of the problem
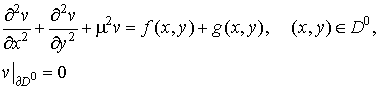 (9) (9)
and
the solution w(x,y) of the problem
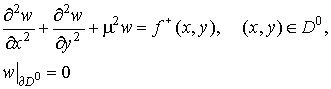 (10) (10)
were
coinciding on domain  : :
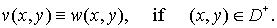
The
function g(x,y) in this case will be
called the active suppress of noise.
We will construct now digital simulation of this problem
and give its general solution.
Instead of problem (8) we consider its
five-points difference analogue (Fig.2)
 (11) (11)
We
consider the difference analogue of problem (9)
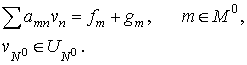 (12) (12)
where
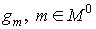 , is an arbitrary grid function. , is an arbitrary grid function.
We also consider the problem
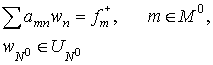
where
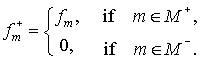
The
grid function will be called active digital suppress function, if the following
equality is valid:
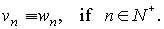
Theorem. All
active suppress digital functions 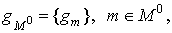 have the form have the form
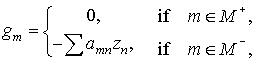 (13) (13)
where
 is an arbitrary
function from is an arbitrary
function from 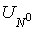 which coincides with
given which coincides with
given 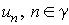 : :
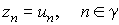 (14) (14)
on
the grid boundary g.
Note that the function 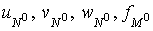 are unknown. We know
only are unknown. We know
only 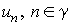 which can be measured.
And we know, that influence of active suppress function which can be measured.
And we know, that influence of active suppress function 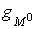 has the same effect
as if we switch off all noise sources, i.e. change has the same effect
as if we switch off all noise sources, i.e. change 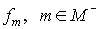 , supposing , supposing
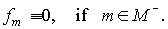
About the more general
setting and solution of active shielding problem see [1], part VIII.
III. On some properties of modified Calderon
potentials and approximation of these
potentials by means of difference potentials.
The
general scheme of modified Calderon-Seeley potentials is based on using of
auxiliary boundary-value problems instead of the symbols of differential
operators. The modified in accordance with this general scheme potentials save
the main properties of Calderon-Seeley potentials and have some additional
useful characteristics. Namely, modified potentials contains some unrestraint
of choice of the auxiliary problems, which can be taken in attention of the
particularity of problem we have to consider. The modified Calderon-Seeley
potential can be approximated by difference potential and then can be used for
numerical solution of the original problem.
The examples of application of DPM
given above and many other ones, which book [1] contains or reflects, allow to
say that DPM is one among other numerical methods.
At the same time the book [1] contains mainly the algebraic and
algorithmic parts of theory DPM, but metric part is developed much less.
Maybe it would be interesting to
obtain the theorems about metric characteristics of modified Calderon-Seeley
potentials and accordance pseudo-differential boundary projectors for different
classes of differential equations like that, as it is made for Calderon
potentials and boundary pseudodifferential projectors of elliptic equations by
Seeley [3].
Maybe it would be interestingly
also to obtain some theorems about metric characteristics of difference
potentials and about approximation of modified Calderon’s potential by means of
difference ones, when mesh step tends to zero.
The example of similar investigation
contains in the part I of book [1], where
the problems, which are connected with Poisson equation and
corresponding fife point difference scheme, were considered .
REFERENCES
[1]
V.S. Ryaben’kii, Method of Difference Potentials and Its Applications,
Springer-Verlag, 2002, p.538.
[2]
A.P.Calderon (1964), Boundary-value problems of elliptic equations. In:
Proceedings of Sovief-American Symposium in Partial Differential Equations,
Novosibirsk, Fizmatgiz, Moscow, pp.303-304.
[3]
R.T.Seeley (1966), Singular integrals and boundary-value problems. Amer. J.
Math., 88, No. 4, pp.781-809.
|