1. Введение

В настоящей работе моделируется взаимодействие рентгеновского излучения, которое образуется в результате микровзрыва дейтерий-тритиевой мишени, с первой стенкой камеры термоядерного реактора в рамках концепции FIHIF тяжелоионного синтеза (Fast Ignition Heavy Ion Fusion). Эта концепция была сформулирована в работах [1-4] и развивалась далее в [5-7]. Специально для нее авторами данной работы была предложена конструктивная схема реакторной камеры, в которой происходит микровзрыв, а также общая структура бланкета, поглощающего нейтронное излучение. Описание камеры и первые качественные оценки ее отклика на тепловое и динамическое воздействие термоядерного микровзрыва содержатся в [4-6].

         Отклик первой стенки камеры на микровзрыв определяется в основном двумя физическими процессами: тепловым разогревом потоком нейтронов и абляцией защитной пленки теплоносителя под действием рентгеновского излучения. Характерные времена этих процессов различаются более чем на порядок: нейтроны достигают первой стенки через 70-80 наносекунд после микровзрыва, причем характерная продолжительность нейтронного импульса всего несколько наносекунд, тогда как продолжительность рентгеновского излучения доходит до микросекунды (излучение фактически сопровождает разлет мишени до стадии поглощения осколков в защитной пленке). Поэтому поведение защитной пленки под воздействием рентгеновского излучения может быть рассмотрено отдельно от отклика первой стенки и всего бланкета на нейтронный нагрев.

В настоящей работе представлено подробное описание одномерного гидродинамического кода, на основе которого были получены новые результаты моделирования взаимодействия рентгеновского излучения с первой стенкой камеры, уточняющие оценки [5, 6]. Частично эти результаты были приведены в нашей предыдущей работе [8], посвященной анализу концепции FIHIF в целом. Здесь же мы ограничимся только рассмотрением задачи испарения жидкой пленки, защищающей первую стенку реактора, под воздействием рентгеновского излучения. Эта проблема является ключевой в оценке работоспособности реактора как энергетической установки. Взаимодействием излучения и защитной пленки определяется первоначальная масса испаренного материала защиты, его температура, механический импульс, идущий внутрь стенки камеры.

Сложность задачи состоит в том, что в литературе в настоящее время достаточно подробно описано влияние короткодействующего импульса длительностью порядка нескольких наносекунд [9]. У нас, как следует из данных, приведенных далее на рисунке 1, другой случай: интервал действия импульса приближается к микросекунде. За такое время уже происходит течение испаряемого вещества, однако режим течения нестационарный, и сам временной профиль импульса влияет на формирование теплового и динамического откликов, что существенно отличается от «мгновенных» воздействий. Разработка физической модели в данных условиях, насколько известно авторам, является новой задачей, а создание соответствующего расчетного кода для реального вещества имеет и практическую ценность.

Отметим, что существует большое количество работ по описанию термомеханического воздействия рентгеновского излучения на преграду. Во многих практически важных случаях [10] эта преграда твердая, однако качественная классификация типов воздействий может быть распространена и на жидкую преграду, поскольку поведение вещества определяется в основном отношением максимальной удельной поглощенной энергии в материале к удельной энергии испарения. Если это отношение велико, что имеет место и в нашем случае, то в области поглощения формируется низкотемпературная плазма. В результате поглощение излучения в наружных слоях вещества уменьшается, глубина энерговыделения увеличивается и становится существенным учет электронной теплопроводности. При детальном анализе формирования механического воздействия на вещество существенно также отношение характерной глубины прогрева к расстоянию, проходимому волной разгрузки за время воздействия рентгеновского излучения.

Моделирование процесса испарения вещества на фоне затухающего рентгеновского импульса и с учетом собственного движения среды, которое описывается уравнениями вязкой гидродинамики с добавлением реального уравнения состояния, составляет тему настоящего исследования.

2. Исходные данные

В наших расчетах мы будем использовать данные об энерговыделении в цилиндрической DT-мишени [3, 7], полученные М.М. Баско. Согласно расчетам [7], полное энерговыделение в рассматриваемой мишени составляет 750 MДж, т.е. коэффициент усиления мишени приблизительно равен . Распределение энергии между продуктами синтеза следующее:

- Рентгеновское излучение – 17 MДж.

- Осколки мишени (ионы) – 153 MДж.

- Нейтроны – 580 MДж.

Одной из существенных особенностей рассматриваемой концепции является растянутый во времени импульс рентгеновского излучения. Это обусловлено использованием тяжелой оболочки мишени, тепловое излучение которой можно считать равновесным (планковским) с меняющейся во времени температурой. Профиль излучения приведен ниже на рисунке 1 согласно данным [7]. Теплофизические параметры теплоносителя приведены в таблице 1.

Рис. 1. Временной профиль импульса рентгеновского излучения в результате микровзрыва. Пунктирная линия – температура, сплошная линия – мощность излучения, точечная линия – выделившаяся энергия. Данные [7].

Таблица 1. Теплофизические параметры теплоносителя Li₁₇Pb₈₃ [20, 21].

  3. Физическая постановка задачи

Физическая модель распространения возмущений в пленке и ее частичного испарения в результате поглощенной энергии рентгеновского излучения опирается на законы сохранения массы, импульса и энергии. Изменение этих величин во времени описывается уравнениями гидродинамики. Для замыкания системы необходимо сделать предположения об уравнении состояния рассматриваемого вещества (эвтектики LiPb). Мы будем считать, что основной вклад в давление и внутреннюю энергию вносит свинец. Соответствующие реальные барическое и калорическое уравнения состояния возьмем из широкодиапазонной модели А.Б. Медведева [11, 12] с учетом ионизации. Эта модель обобщает классическое уравнение состояния Ван-дер-Ваальса.

Считаем, что на границе жидкой пленки с первой стенкой из SiC поддерживаются равновесные параметры. Это предположение опирается на оценки характерных времен распространения возмущений в среде эвтектики LiPb по сравнению с длительностью импульса рентгеновского излучения.

Считаем также, что в начальный момент возмущения в среде отсутствуют, а все теплофизические параметры в пленке отвечают равновесному состоянию.

Скорость звука в жидкой пленке оценивается величиной 2000 м/с (дальнейшие расчеты подтверждают эту оценку). Это важный параметр, т.к. он позволяет оценить характерное время, в течение которого отклик пленки можно считать в приближении бесконечного слоя, пренебрегая влиянием собственно первой стенки:

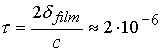                                   с.                                           (3.1)

Коэффициент температуропроводности жидкой пленки равен, согласно данным таблицы 1, величине

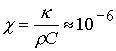                                                       м²/с.                                      (3.2)

Тогда за время действия рентгеновского излучения  = 700 нс тепловой фронт продвинется вглубь пленки за счет теплопроводности на расстояние

                                                      2,6  мкм,                                   (3.3)

а ударная волна, распространяясь со скоростью звука, – на расстояние порядка 1,4 мм. Поскольку длительность импульса рентгеновского излучения  примерно в 3 раза меньше , а толщина пленки много больше , то в этих условиях допустима упрощенная постановка задачи об испарении защитной пленки в приближении бесконечного слоя. Поскольку же толщина пленки, в свою очередь, много меньше радиуса камеры, то задачу можно решать в приближении плоского слоя.

         На границе жидкой пленки и камеры ставится условие нулевого потока тепла. Это предложение основывается на том, что, хотя равновесная плотность пара в камере много меньше плотности пленки, в этом паре все же происходит частичное поглощение рентгеновского излучения, в результате чего удельная массовая плотность энерговыделения в камере и пленке одинакова. Это условие является важным, поскольку оно показывает, что испарение защитной пленки происходит только под действием внутри нее объемного источника энерговыделения, определяемого поглощением рентгеновского излучения.

         Итак, мы описали условия и предположения, на основе которых будет проводиться расчет испарения жидкой пленки в течение действия рентгеновского импульса.

При описании теплопроводности в жидкой пленке учитывается также электронная теплопроводность в ионизованной среде, согласно [13]:

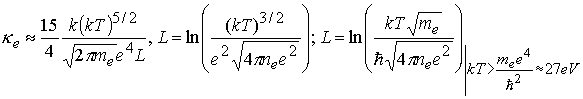(3.4) 

Теплопроводность пара в камере, помимо электронной, имеет также лучистую  и «собственно газовую» составляющие. Последнюю мы возьмем согласно модели газа твердых сфер [13]:

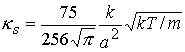                                        ,                                             (3.5)

где  – постоянная Больцмана,  м.

Расчет глубины поглощения рентгеновского излучения в среде Li₁₇Pb₈₃ основывается на спектральных данных лаборатории NIST [14].

4. Математическая постановка задачи

         Построим расчетную модель испарения жидкой пленки под действием рентгеновского излучения заданной мощности и температуры. Исходные данные возьмем из расчетов М.М. Баско [7], согласно которым длительность рентгеновского импульса составляет около 700 нс, средняя температура 30 эВ. Тогда средняя поверхностная плотность излучения равна 88 кДж/м². 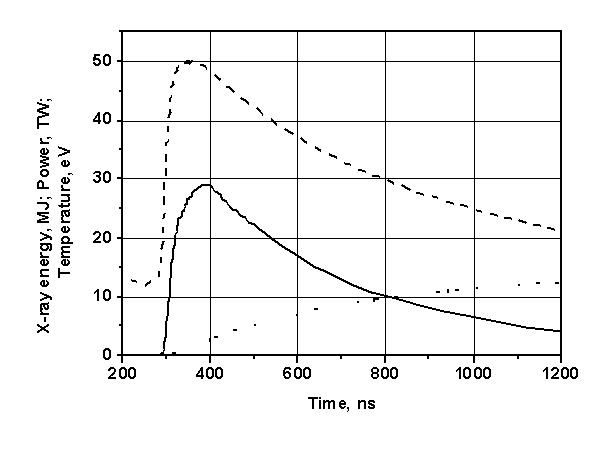Спектр рентгеновского излучения определяется тепловым излучением горячей плазмы, образующейся в результате термоядерной реакции, поэтому частотное распределение аппроксимируется планковским с некоторой эффективной температурой , которая меняется с течением времени (см. Рис. 1). Пусть  – энергия излучения [эВ]. Тогда

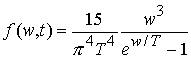                                 .                                                   (4.1)

Максимум распределения приходится на значение энергии , а среднее значение энергии излучения равно .

         Введем спектральную плотность мощности излучения  на глубине  проникновения в жидкую пленку:

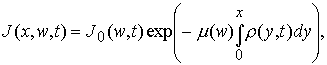                                                        (4.2)

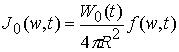                                   .                                                   (4.3)

Первоначальная мощность источника  задана на Рис. 2, функция распределения Планка определяется выражением (4.1). Тогда объемная плотность энерговыделения на глубине  равна

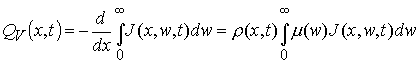                .                   (4.4)

Формулы (4.3), (4.4) описывают поглощение излучения посредством ионизации нейтральных атомов. Характерное время ионизации составляет 5∙10^-17 с, что много меньше длительности импульса . Поэтому можно считать, что коэффициент поглощения  не зависит от времени.

Формула (4.4) определяет источниковый член в уравнениях гидродинамики, описывающих движение вещества пленки. Считая излучение сферически симметричным, а пленку – тонкой, ограничимся при описании пленки одномерным плоским случаем. Запишем постановку задачи сначала в эйлеровой форме (см. [15]). Обозначения:  – плотность,  – скорость,  – плотность внутренней энергии,  – давление,  – плотность энтальпии. Коэффициенты вязкости  и теплопроводности  берем из таблицы 1. Коэффициент  определен в (3.4), так что суммарная теплопроводность в пленке определяется коэффициентом .

Записываем уравнения законов сохранения массы, импульса и энергии в виде:

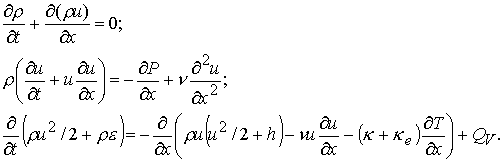                  (4.5)

Начальные условия:

           (4.6)

Здесь 10^-2 Па – давление насыщенного пара в камере,  определяется по соответствующей концентрации 10¹⁸ м^-3. На границе «камера/пленка» приняты условия:

.                                                                                           (4.7)

На «бесконечности», т.е. на границе «пленка/стенка», приняты условия

,                                                                                             (4.8)

а плотность и давление связаны между собой по уравнению состояния.

Поставленная задача (4.5)-(4.8) решалась численно в лагранжевых координатах. Обсуждению построенного кода и особенностям решения данной конкретной задачи будет посвящена отдельная работа. Здесь мы приведем только общую постановку задачи и некоторые важные для дальнейшего результаты. Следуя [15, 16], вводится лагранжева координата

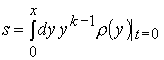                                               ,                                          (4.9)

где k = 1, 2, 3. Скорость определяется как . Системе (4.5) тогда отвечают уравнения

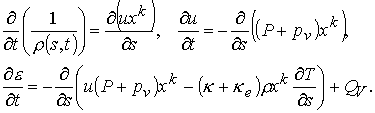                                           (4.10)

Здесь  – диссипативные члены с вязкостью. Начальные и граничные условия модифицируются аналогично.

         Далее мы приводим описание расчетного кода и результаты расчетов для вышеописанных начальных условий. Мы ограничились однократной ионизацией, первый потенциал ионизации для свинца  эВ.

5. Уравнение состояния для свинца

         Широкодиапазонное уравнение состояния для свинца представляет обобщение модели Ван-дер-Ваальса и имеет вид [11, 12]:

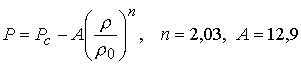      ГПа,  г/см³.                 (5.1)

Параметр  (давление отталкивания) определяется из трансцендентного уравнения как функция температуры и плотности:

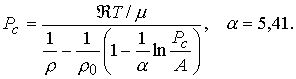                                                              (5.2)

Здесь  – газовая постоянная, а  – молярная масса свинца. Это уравнение имеет единственное решение относительно  при всех действительных значениях параметров . Перейдем к безразмерным величинам температуры, плотности и давления:

                                   .                         (5.3)

Тогда уравнение состояния (5.1) примет вид:

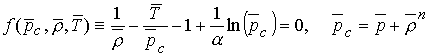                 .                (5.4)

Для табулирования и визуализации зависимости , определяемой неявным уравнением (5.4), мы используем метод Ньютона. Табуляцию функции  начинаем с области малых значений  и больших значений , где хорошо работает приближение идеального газа. Тогда начальным приближением служит тройка

                                               .

Вводя далее приращения плотности и температуры, так что , организуем итерационный процесс нахождения для определения соответствующего давления отталкивания :

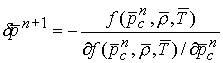                                          .                                   (5.5)

Учтем в модели (5.1), (5.2) K-кратную ионизацию согласно [11]. Получаем:

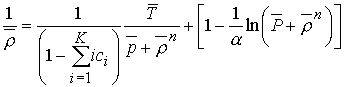                               ,                    (5.6)

где  – концентрации ионов i-кратной ионизации, которые можно найти (в предположении равновесия) из системы уравнений

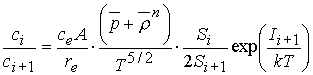                                   ,                      (5.7)

где  – потенциал ионизации, ,  – внутренняя статистическая сумма, . Потенциалы ионизации для свинца, эВ [17], равны:

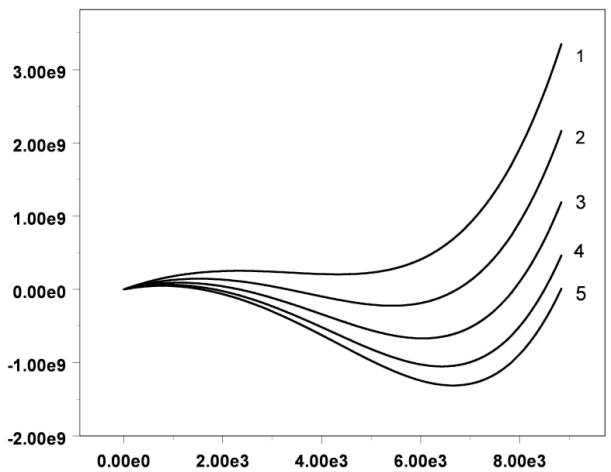
         Ниже на Рис. 4.1.1 приведены изотермы для свинца, рассчитанные по этой модели.

Давление, Па

                                                                                                      Плотность, кг/м³

Рис. 2. Изотермы модели (5.1)-(5.2). Температуры: 1- 6000К, 2- 5000К, 3- 4000К, 4- 3500К, 5- 3000К.

Барическому уравнению состояния (5.6) соответствует следующее калорическое уравнение состояния:

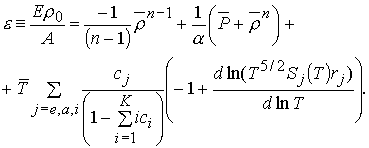                                              (5.8)

Здесь , .

Равновесная кривая  находится из условия равенства температур, давлений и потенциалов Гиббса паровой () и жидкой () фаз:

                                                                  (5.9)

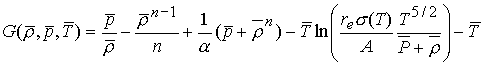   .                (5.10)

Для численного нахождения  стартуем с известных точек на равновесной кривой , соответствующих температуре . Тогда приращению  отвечают приращения   и . В паровой и жидкой фазах справедливо также и барическое уравнение состояния. Тогда систему уравнений (5.6), (5.9) приближенно записываем в виде (штрих означает производную):

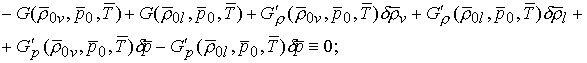
                        (5.11)                 

Используя систему (5.11), организуем итерационный процесс:

                                 (5.12)

Приращения находятся по формулам (температуру в аргументах опускаем)

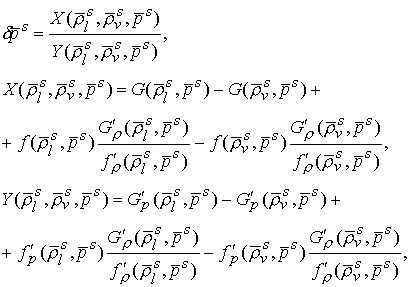 (5.13) .          

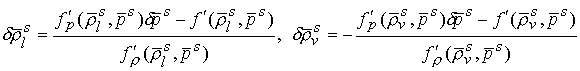За исходную точку итерационного процесса берем критические значения .

         Расчетная кривая равновесия пар-жидкость приведена на Рис. 3. Мы выносим ее на отдельный рисунок, поскольку на графиках барического уравнения состояния (Рис. 2) она занимает очень незначительную область в окрестности ниже значения давления 300 МПа.

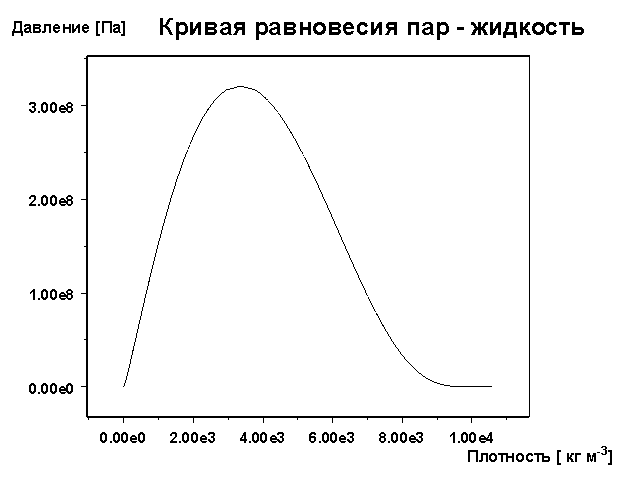
Рис. 3. Расчетная кривая равновесия фаз теплоносителя.

Критическая температура для свинца – 6025 K. Поэтому при высокой интенсивности энерговложения в жидкую пленку возможен эффект испарения по кривой, проходящей выше критической точки, т.е. вне двухфазной области. Результаты расчетов отклика жидкой пленки по уравнениям гидродинамики, приведенные в п. 7, показывают наличие такого эффекта.

6. Описание расчетного гидродинамического кода

В настоящее время имеется много численных кодов для решения уравнений движения жидкостей и газов, причем в многомерных случаях. Если в эту систему добавляется учет теплопроводности, то имеющиеся коды требуют замены, что сопряжено с серьезными трудностями, которые обсуждаются, например, в недавней работе А.В. Острика и Е.А. Ромадиновой [18]. Одной из таких трудностей является использование калорического уравнения состояния , которое должно быть согласовано с барическим . В [18] предлагается расщепить решение по физическим процессам и решать задачи собственно гидродинамики отдельно от задачи теплопроводности. Это позволяет не изменять «гидрокод», но зато решать на каждом временном шаге две задачи определения температуры: сначала без учета теплопроводности, но с включенной динамикой, а потом с выключенной динамикой, но с учетом теплопроводности и источников. Однако там же отмечается, что такой подход достаточно хорошо работает в случае слабого энерговыделения, а для высоких энергий он неэффективен. Поскольку у нас реализуется именно случай интенсивного источника тепла, то мы пошли по пути создания кода по совместному решению всех трех уравнений движения сплошной среды, когда используется согласованное уравнение состояния.

Приведем схему численного решения задачи (4.10). Величину  обозначаем далее для краткости через , общий коэффициент теплопроводности – через . Тогда получаем

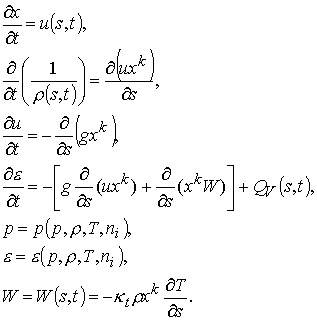                                                          (6.1)

Система (6.1) аппроксимировалась на двух взаимосвязанных сетках: на основной сетке  с шагом (вообще говоря, неравномерным)  (т.е. , m=1,…, M-1),  и промежуточной (, m=0,…, M), причем основная сетка служит для аппроксимации величин , а промежуточная – для .

Следуя [16], для аппроксимации системы (6.1) была использована  двухслойная (с шагом t), чисто неявная, полностью консервативная схема. Избегая громоздкости формул, в величинах на промежуточной сетке будем использовать целочисленные индексы, так что, например, g_m означает g_m+1/2 . Вводим оператор

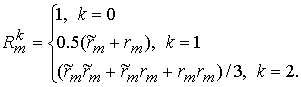                                                             (6.2)

Тильда означает, что данное значение берется с искомого слоя по времени. Тогда расчетный алгоритм описывается следующими формулами:

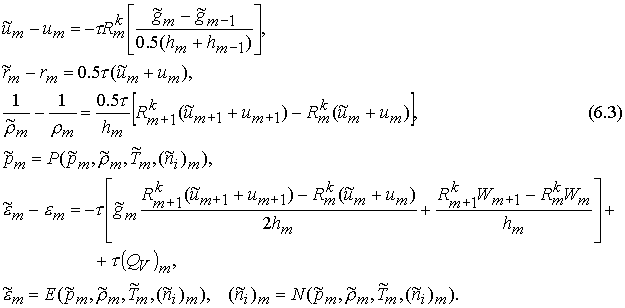
Система разностных уравнений (6.3) задает общую схему численного решения системы. Общим методом ее решения служит метод раздельных прогонок [16], когда система (6.3) делится на две группы: «динамическую» и «тепловую». Каждая из них решается отдельно некоторым итерационным методом (причем величины из другой группы считаются замороженными), с последующими итерациями между группами.

Рассмотрим, например, «динамическую» группу для k=0. Величина , определяющая псевдовязкое давление, имеет вид

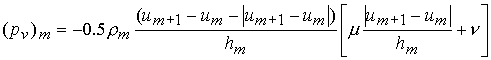      ,             (6.4)

а уравнение состояния определено в (5.6), (5.8). Итерационный процесс в этой группе организован следующим образом. Разностное уравнение для скорости

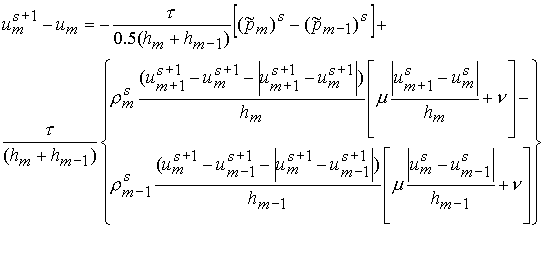         (6.5)

решается с помощью прогонки. Тогда находятся значения пары величин на следующем слое:

                                            (6.6)

По известным значениям  давление  находится из уравнения состояния с помощью итерационного метода Ньютона. Если при этом  пересекает кривую равновесия (использовалась табулированная кривая на 10000 точек, полученная по описанной выше методике – см. п. 5), то выбирается значение давления в точке пересечения.

Для решения «тепловой» части запишем формулу для энергии (в приближении однократной ионизации) в виде:

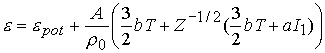                              ;                         (6.7)

,        ,

                                               .       

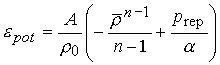Теперь, опуская для краткости индекс m в правой части, получаем:

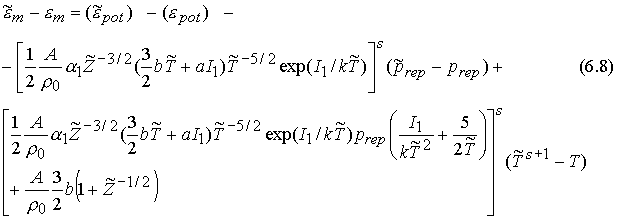
Верхний индекс s здесь относится только к температуре (также и в функции ). Подставив эту формулу в соответствующее уравнение системы (6.3), получим разностное уравнение относительно , решаемое прогонкой.

7. Результаты расчетов

7.1. Расчет источника тепловыделения.

Расчеты по формулам (4.1)-(4.4) дают значения объемной плотности энергии рентгеновского излучения, поглощенной в парах теплоносителя внутри камеры и в защитной пленке, приведенные ниже на рисунках 4-5. Видно, что поглощение излучения внутри камеры на 4 порядка ниже, чем в пленке, в связи с малой плотностью насыщенного пара.

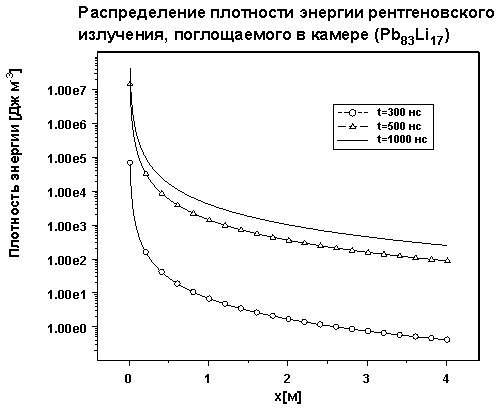
Рис. 4. Объемная плотность энергии поглощенного излучения в камере.

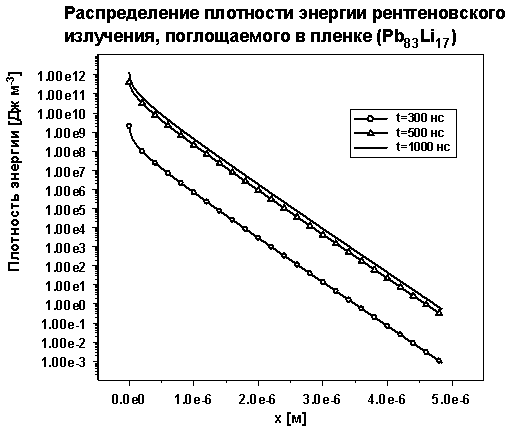
Рис. 5. Зависимость объемной плотности энергии поглощенного излучения в пленке от глубины проникновения излучения в пленку.

         Данные, приведенные на Рис. 5, определяют источник энерговыделения  в правой части уравнения переноса тепла в системе (6.1).

7.2. Испарение защитной пленки.

         Гидродинамический код, описанный в п. 6, был применен нами для расчетов воздействия рентгеновского излучения (его профиль приведен на Рис. 1) на жидкую защитную пленку первой стенки реактора. Полученные расчетные результаты приведены на Рис. 6-15.

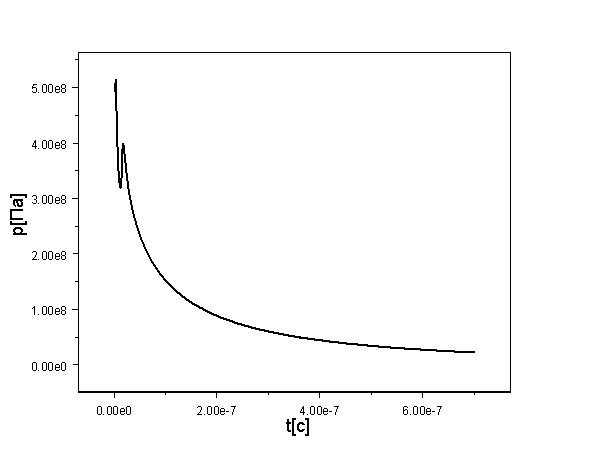
Рис. 6. Зависимость давления в расчетной лагранжевой ячейке пленки на фронте испарения от времени. Толщина ячейки – 10 нм.

Отчетливо видимый на Рис. 6 зигзаг в начале теплового воздействия на ячейку обусловлен изменением режима испарения (см. также Рис. 7): сначала испарение идет поверх кривой равновесия, а затем по мере снижения тепловыделения возникает характерная для фазовых переходов двухфазная область. Толщина этой области не превосходит 0,1 от толщины ячейки и расположена приблизительно посередине. Слева от двухфазной области находится пар, справа – жидкость. Таким образом, движение двухфазной области по расчетным ячейкам является достаточно надежным индикатором, показывающим положение фронта испарения пленки (см. Рис. 8). Адекватность расчетного кода и модели иллюстрируется на Рис. 9, на котором равновесная кривая испарения согласно модели [11] и кривая, построенная по расчетным данным на фронте испарения, расположены достаточно близко. Динамика испарения пленки в лагранжевых координатах представлена на Рис. 10.

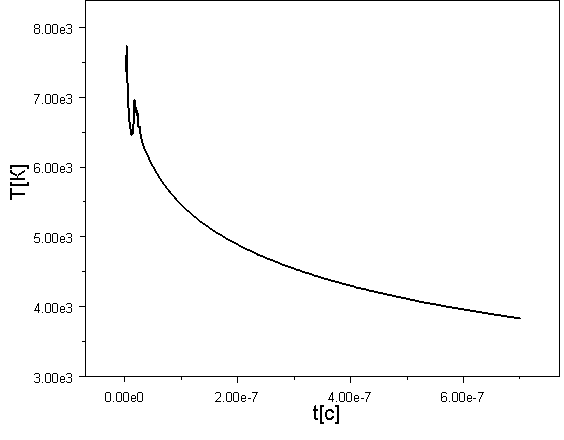
Рис. 7. Зависимость температуры в расчетной лагранжевой ячейке пленки на фронте испарения от времени. Толщина ячейки – 10 нм.

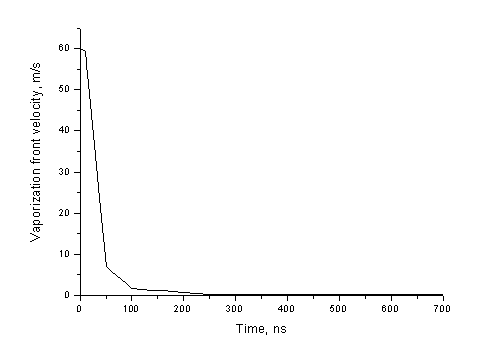
Рис. 8. Зависимость скорости фронта испарения от времени.

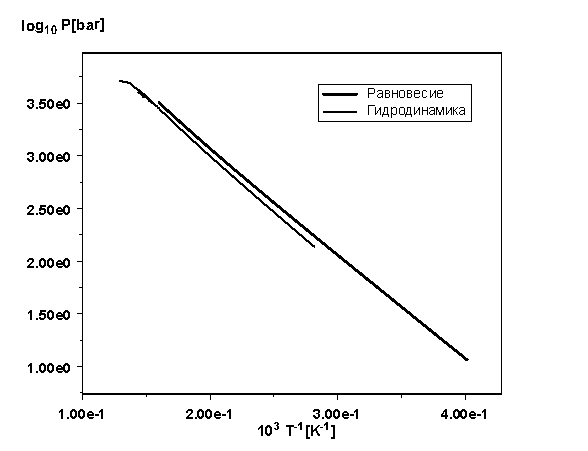
Рис. 9. Сравнение равновесной кривой испарения (А.Б. Медведев, [11]) с данными на фронте испарения, рассчитанными по нашей программе.

Согласно проведенным расчетам, за время действия рентгеновского импульса (700 нс) испарится 1,42 кг жидкой пленки. Динамика испарения пленки приведена ниже на Рис. 10-11. Испаренный слой имеет внешнюю разреженную корону, нагретую до нескольких миллионов градусов, и внутреннюю более плотную часть (вблизи пленки), имеющую температуру около 6000 K. Средняя температура «пара» 15 эВ, плотность 7∙10^-5 г/см³. Подчеркнем, что эта температура завышена, т.к. учитывалась только однократная ионизация. Скорость движения лагранжевых ячеек и распределение температуры в них приведены на Рис. 12-13. Распределение температуры в испаренном слое приведено на Рис. 14. Видно, что толщина пара к моменту окончания воздействия рентгеновского излучения составляет около 7 см. Далее на Рис. 15 показано распределение скоростей в паровом слое: внешние области движутся со скоростями, сопоставимыми с движением осколков мишени (10⁵ м/с), а внутренние слои движутся медленнее. Зависимость скорости от расстояния до фронта испарения практически линейная. Знак « – » у расстояния и скорости на графиках 12-13 означает, что расстояние отсчитывается влево от фронта испарения, т.е. внутрь камеры, и туда же направлено и движение испаренного слоя. Расстояние вправо (внутрь пленки) считается положительным.

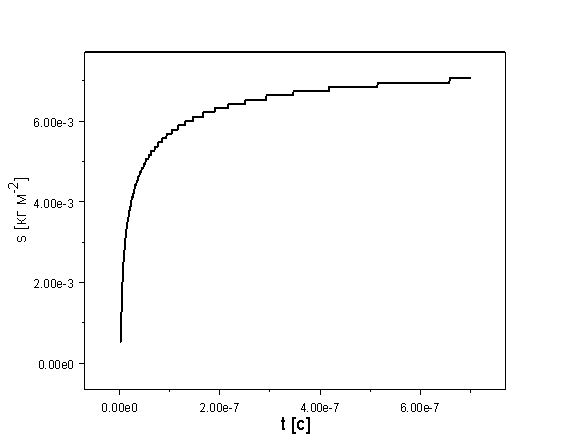
Рис. 10. Зависимость лагранжевой координаты испаренной части пленки от времени.

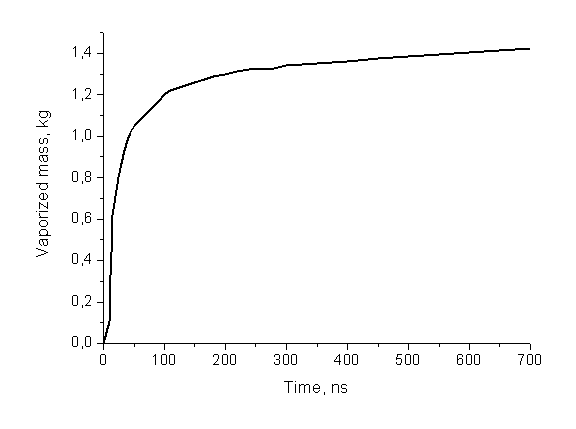
Рис. 11. Зависимость испаренной массы теплоносителя от времени.

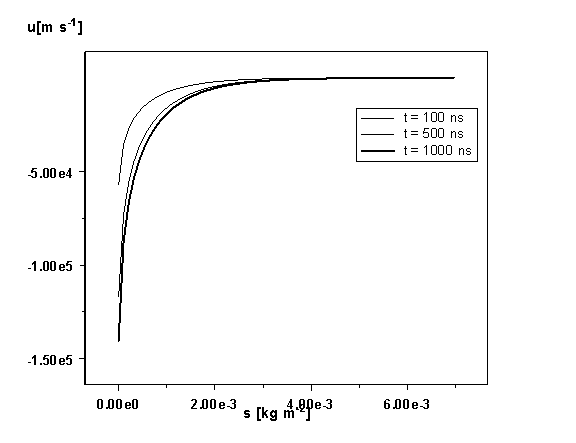
Рис. 12. Скорость движения лагранжевых ячеек в различные моменты времени.

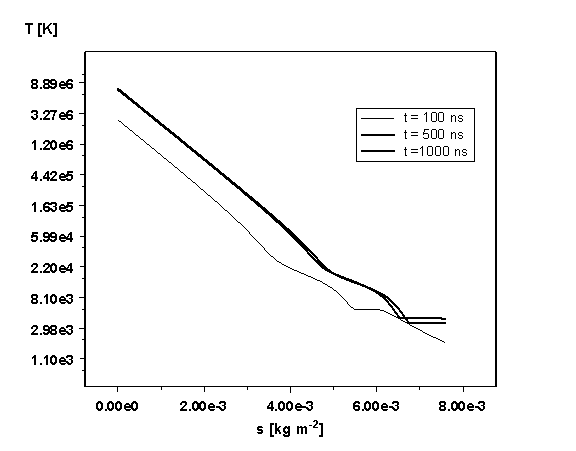
Рис. 13. Температура лагранжевых ячеек в различные моменты времени.

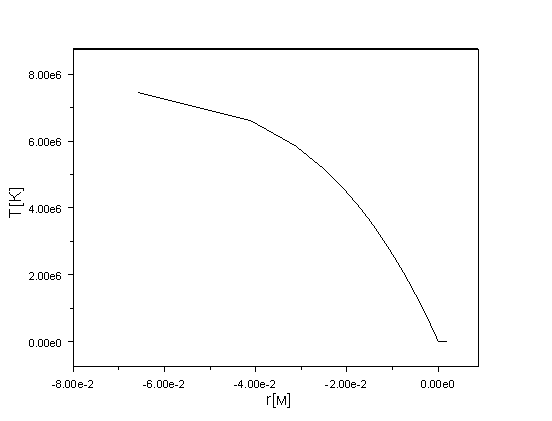
Рис. 14. Профиль температуры в испарившемся слое теплоносителя в физических координатах на момент окончания рентгеновского импульса.

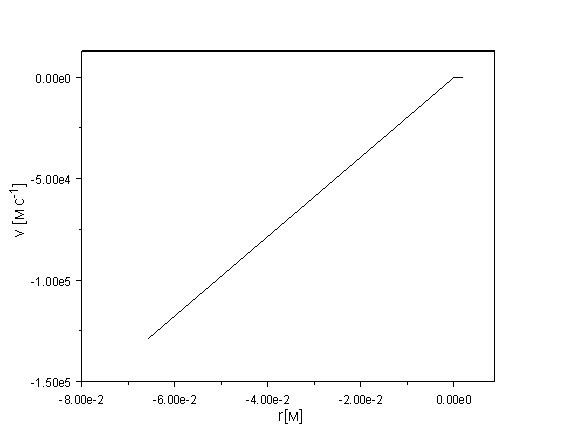
Рис. 15. Распределение скоростей в испарившемся слое теплоносителя в физических координатах на момент окончания рентгеновского импульса.

7.3. Распространение возмущений в жидкой пленке.

Испарение пленки сопровождается также импульсом давления, идущим внутрь камеры со скоростью звука. Расчетное распределение давления и плотности в пленке на момент окончания рентгеновского излучения приведено на Рис. 16-18. Воздействие генерируемой ударной волны на стенку SiC будет описано в отдельной работе. Эта ударная волна, отразившись от стенки, может привести к разрыву пленки и образованию капель теплоносителя. Однако можно предположить, что эти капли сыграют положительную роль в ускорении процесса конденсации, т.к. поверхность конденсации в результате этого увеличится. Возможно также, что капли полностью испарятся после того, как температура образованного на первом этапе испаренного слоя теплоносителя еще более возрастет после поглощения в нем осколков мишени.

Сделаем сначала качественную оценку величины импульса отдачи, считая импульс излучения «ступенькой» и используя вышеприведенные результаты. На нагрев до температуры кипения (при равновесном давлении насыщения) и испарение 1,42 кг теплоносителя требуется, согласно данным таблицы 2.3.1, около 1,7 МДж. На однократную ионизацию этого количества пара потребуется еще 4,8 МДж, итого – 6,5 МДж. Тогда полная кинетическая энергия пара  будет не больше, чем 17 – 6,5 = 10,5 МДж. Тогда импульс отдачи при испарении будет иметь величину порядка

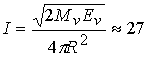                                      Па×с.                                     (7.1)

Для оценки соответствующего давления надо взять характерный интервал воздействия. Из Рис. 1 оцениваем его величиной порядка 250-300 нс. Тогда

                                                MПа.                                            (7.2)

Эта оценка, как показывают дальнейшие расчеты (Рис. 16-17), занижена, т.к. реальный импульс имеет достаточно высокий пик. После воздействия в пленке формируется ударная волна, давление на фронте которой понижается по мере продвижения вглубь. На момент окончания импульса оно равно 250 МПа. Ударная волна прошла к этому времени путь около 1,3 мм, что совпадает с качественной оценкой, сделанной в п.3.

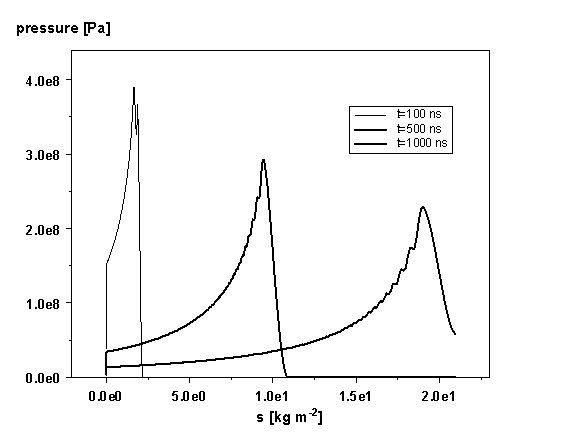
Рис. 16. Распределение давления по толщине защитной пленки в разные моменты времени в лагранжевых координатах.

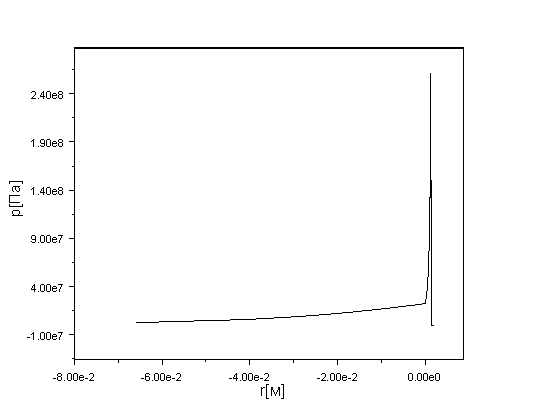
Рис. 17. Распределение давления по толщине защитной пленки в физических координатах на момент окончания рентгеновского импульса (700 нс).

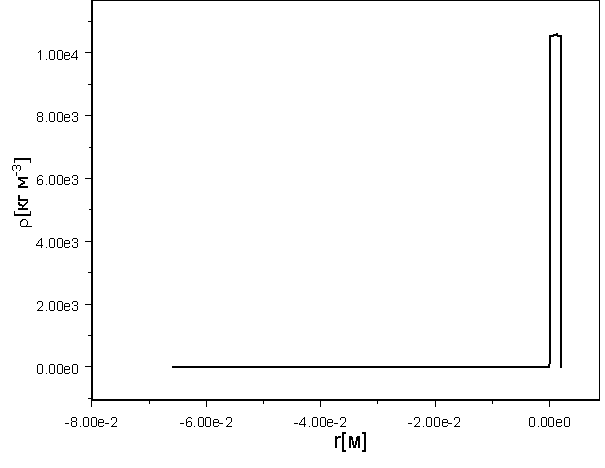
Рис. 18. Распределение плотности теплоносителя в паре и жидкой пленке на момент окончания рентгеновского импульса.

Поскольку скорость фронта испарения почти на два порядка меньше скорости движения ударной волны, то на Рис. 16 левые концы этих волн начинаются практически в одной точке. На Рис. 18 видно незначительное утолщение на узкой части ступеньки, которое отвечает положению ударной волны, бегущей по пленке. Отрицательная область (внутренность камеры) заполнена расширяющимся паром.

Итак, в данной работе мы описали постановку задачи и алгоритм решения для взаимодействия высокоинтенсивного рентгеновского излучения с жидкой пленкой, защищающей первую стенку камеры реактора. Приведенные в работе результаты расчетов для некоторого типичного режима горения термоядерной микромишени хорошо согласуются друг с другом и имеют ясную интерпретацию в соответствии с общими физическими представлениями о процессе, что свидетельствует о достаточной достоверности разработанного кода. Дальнейшее его развитие будет включать описание собственно камеры в сферической геометрии, а затем и неоднородность излучения в силу цилиндрической структуры мишени, т.е. переход к 2D-коду. 1D-приближение необходимо для возможности качественного тестирования выбранного подхода.

         В заключение авторы выражают глубокую признательность всем своим коллегам – членам Совета РАН по физико-техническому анализу энергетических систем, инициировавшим эту работу, в особенности его председателю академику РАН В.И. Субботину, а также академику РАН В.П. Смирнову, чл.-корр. РАН А.В. Забродину, профессорам Б.Ю. Шаркову, М.В. Масленникову и С.Л. Недосееву, многократные обсуждения с которыми различных аспектов модели принесли авторам неоценимую помощь. Мы благодарим также Федеральное Агентство по атомной энергии, которое поддерживает развитие этого направления в ГНЦ РФ ИТЭФ.

         Авторы благодарят Фонд «Human Capital Foundation», чья спонсорская поддержка позволила выполнить эти исследования.

Литература.

1. Koshkarev D.G. Charge-Symmetric Driver for Heavy-Ion Fusion. // IL Nuovo Chimento, Vol.106 A, No.11, p.1567-1573. 1993.

2. Koshkarev D.G., Korenev I.L., Yudin L.A. Conceptual Design of Linac for Power HIF Driver. /  CERN 96-05, VI, p.423-426. 1996.

3. Чуразов M.Д., Аксенов A.Г., Забродина E.A. Зажигание термоядерных мишеней пучком тяжелых ионов. // ВАНТ, Сер. Математические модели физических процессов, Вып. 1, №.20. 2001.

4. Medin S.A. et al. Evaluation of a power plant concept for fast ignition heavy ion fusion // Laser and Particle Beams, 2002. V.20. P.419-423.

5. Medin S.A. et al. Reactor Chamber and Balance-of-Plant Characteristics for Fast-Ignition Heavy-Ion Fusion Power Plant // Fusion Science and Technology, 2003. V.43. No.3. P.437-446.

6. Medin S.A., et al. Conceptual Analysis of Energy Conversion in Power Plant for Fast Ignition Heavy Ion Fusion / 30-th EPS Conference on Controlled Fusion and Plasma Physics. Russia, S-Petersburg, July 7-11, 2003.

7. Basko M. M., Churazov M. D. and  Aksenov A. G. Prospects of heavy ion fusion in cylindrical geometry. // Laser and Particle Beams, 2002. V.20.P.411-414.

8. Медин С. А., Орлов Ю. Н., Паршиков А.Н., Суслин В. М. Моделирование отклика первой стенки камеры и бланкета реактора ИТС на микровзрыв. / Препринт ИПМ им. М.В. Келдыша РАН, № 41, 2004.

9. Peterson R.R. et al. Chamber dynamic research with pulsed power. // Nuclear Instr. and Meth. in Phys. Res. A, 2001. V.464. P. 172-179.

10. Острик А.В. Термомеханическое действие рентгеновского излучения на многослойные гетерогенные преграды в воздухе. М.: НТЦ «Информтехника», 2003.

11. Копышев В.П., Медведев А.Б. Термодинамическая модель сжимаемого коволюма. Саров: РФЯЦ-ВНИИЭФ, 1995.

12. Медведев А.Б. Модификация модели Ван-дер-Ваальса для плотных состояний. / В сб.: Ударные волны и экстремальные состояния вещества. Под ред. В.Е. Фортова, Л.В. Альтшулера, Р.Ф. Трунина и А.И. Фунтикова. М.: Наука, 2000.

13. Силин В.П. Введение в кинетическую теорию газов. М.: Наука, 1971.

14. Hubbell J.H., Seltzer S.M. Tables of X-Ray Mass Attenuation Coefficients. NIST, 1996.

15. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика, Т.VI. Гидродинамика. М.: Наука, 1988.

16. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М.: Наука, 1980.

17. Никифоров А.Ф., Новиков В.Г., Уваров В.Б. Квантово-статистические модели высокотемпературной плазмы и методы расчета росселандовых пробегов и уравнений состояния. М.: Физматлит, 2000.

18. Острик А.В., Ромадинова Е.А. Учет химических реакций и теплопроводности в современных гидродинамических кодах. / Тезисы докладов V Международной конференции по неравновесным процессам в соплах и струях (NPNJ-2004), с. 160. Июль 5 – 10, Самара, 2004.