Аннотация
Описан алгоритм расчета распада разрыва для трехтемпературной модели газовой динамики. В случае
задания уравнений состояния компонент в форме двучленов может быть получено точное решение.
Это достигается введением неопределенных коэффициентов в обобщенное уравнение состояния среды
и их подбором в ходе специального итерационного процесса.
Получаются изменения давления и внутренней энергии отдельно для каждой из трех
компонент среды. В сумме автоматически реализуется закон изменения полной энергии. При
разностной реализации все три компоненты становятся равноправными участниками вычислительного
процесса, как и в дифференциальной модели.
Abstract
Algorithm of Riemann problem for three-temperature model of gas dynamics is described.
In case the component equation of state can be present in two-term view the exact solution is
obtained. A special iterative process is used for selection of undefined in advance coefficients
in generalized equation of state.
Pressure and inner energy are modified separately for each of three medium components. The law
of total energy preservation is true automatically. During numerical procedure all thee
components are equitable as in differential model.
Содержание
Введение
3
§ 1. Уравнения
трехтемпературной газовой динамики……………….
4
§ 2. Характеристики
трехтемпературных уравнений………………… 6
§ 3. Задача о распаде
произвольного разрыва………………………… 8
§ 4. Конструирование
общего уравнения состояния среды…………..
12
§ 5. Алгоритм расчета
распада разрыва……………………………….. 17
§ 6. О разностных
законах изменения внутренней энергии для
отдельных компонент
среды…………………………….………… 23
Заключение …...………………………………………………………….
25
Литература ……………………………………………………………….
27
Введение
В работе [1] рассматривались методические
вопросы, связанные с построением физически адекватной модели и созданием комплекса
программ для моделирования процессов в микромишенях при экстремальных условиях
сжатия и нагрева.
Как отмечалось в
[2] (см. стр. 17-18), широко известны два общих подхода к
макроскопическому описанию плазмы. В первом подходе плазма рассматривается как
совокупность взаимно проникающих друг в друга заряженных газов (или
«жидкостей»), представляющих смесь одного или нескольких сортов ионов и
электронов. Каждый из них описывается своей системой уравнений. Такие модели
принято называть двухжидкостными, трехжидкостными и т.д.
Во втором подходе плазма описывается как один газ (или
«жидкость») с единой плотностью частиц, скоростью и плотностью электрического
тока. Такая модель обычно называется одножидкостной. Она может быть как
однотемпературной, когда температуры всех частиц предполагаются равными друг
другу, так и двухтемпературной или трехтемпературной, если они предполагаются
различающимися между собой. Последний подход представляется особенно
плодотворным, благодаря прежде всего широкой области применимости
соответствующих уравнений. Кроме того, очевидно, что в математическом плане
такая модель проще рассматриваемой при первом подходе. Как будет видно из
последующего, при ее реализации может быть существенно использован опыт,
накопленный в обычной однотемпературной газовой динамике.
Итак, в рассматриваемой модели среда (плазма)
предполагается состоящей из трех видов частиц: ионов, электронов и фотонов (так
условно названы частицы, ответственные за перенос энергии излучения). Она
описывается как газ (или «жидкость») с единой плотностью частиц и общим
вектором их скорости. Однако температура, давление и удельные внутренние
энергии (для единицы массы среды) предполагаются различающимися между собой для
ионов, электронов и фотонов в каждой точке пространства и времени.
При конструировании и реализации вычислительного алгоритма
на каждом временном шаге нестационарного процесса осуществляется расщепление по
физическим процессам. На одном из них (обычно выполняемом первым) реализуется
численное интегрирование системы дифференциальных уравнений трехтемпературной
газовой динамики.
Для обычной газовой динамики при построении разностной
схемы успешно применяется предложенная С.К.Годуновым идея использования точных
решений уравнений с кусочно-постоянными начальными данными – «распадов
разрывов» (см., напр., [3]). Эта идея получила широкое распространение и для
других гиперболических систем (см, напр., [4]).
Некоторый вариант приближенного решения задачи о распаде
разрыва был использован и в рассматриваемой трехтемпературной модели. Он описан
в упомянутой работе [1]. Однако по ряду причин целесообразно рассмотреть
другой, более совершенный вариант реализации задачи о распаде разрыва. Его
изложение является основной целью настоящей работы.
§ 1. Уравнения трехтемпературной
газовой динамики.
Систему дифференциальных уравнений для газодинамического
этапа расчета в рассматриваемой трехтемпературной модели, как и в работе [1],
выпишем в следующей форме:
(1.1)
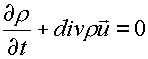 , ,
(1.2)
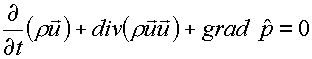
(1.3i) 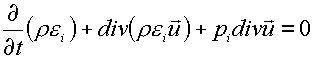
(1.3e)
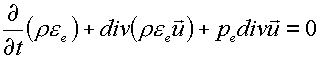
(1.3f)
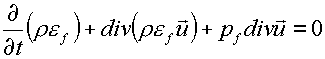
Здесь r - единая плотность частиц,
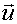 - общий вектор
скорости частиц, - общий вектор
скорости частиц,
pk ; k=i,e,f, - давление ионов, электронов и фотонов
соответственно,
ek , k=i,e,f, - их удельные внутренние энергии.
В векторном уравнении
(1.2) для импульса участвует 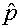 - суммарное давление частиц: - суммарное давление частиц:
(1.4) 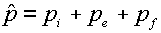
Система
уравнений (1.1)-(1.3) замыкается заданием уравнений состояния для всех трех
компонент среды. Временно, до §4, будем предполагать их заданными в простейшей
двучленной форме:
(1.5)
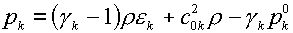 , k=i,e,f
, , k=i,e,f
,
где 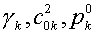 - некоторые
константы, свои для каждой из компонент. - некоторые
константы, свои для каждой из компонент.
Введем в рассмотрение суммарную удельную внутреннюю
энергию:
(1.6) 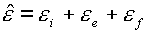 . .
Сложив
три уравнения (1.3i), (1.3e), (1.3f), получим для описания ее изменения уравнение:
(1.7) 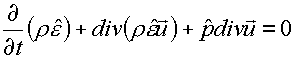
Как и в обычной газовой динамике, из уравнений (1.1) и
векторного уравнения импульса (1.2) получается в качестве следствия:
(1.8) 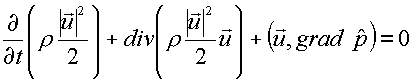
Оно описывает изменение
кинетической энергии.
Если
использовать тождество:
(1.9) 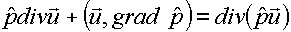 , ,
то после сложения (1.7)
и (1.8) получается дивергентная форма закона изменения полной энергии:
(1.10) 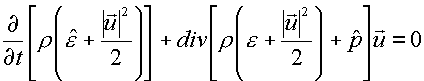
Система законов сохранения массы, импульса и полной энергии
оказалась бы замкнутой, если бы существовало общее уравнение состояния среды в
форме явной или неявной зависимости
(1.11) 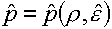 или или 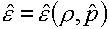
Это позволило бы использовать алгоритмические разработки
однотемпературной газодинамической модели, в том числе и решение задачи о
распаде произвольного разрыва. В работе [1] было отмечено, что попытки получить
такое уравнение состояния не дали приемлемого результата. Поэтому, как отмечено
во введении, был использован некоторый вариант приближенного решения, описанный
в [1] на стр. 6-13. Разработка более совершенного алгоритма решения задачи о
распаде разрыва будет предметом последующего изложения.
§2. Характеристики
трехтемпературных уравнений.
В
простейшей форме система уравнений (1.1)-(1.3) для одномерного случая может
быть записана в виде:
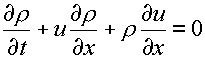
(2.1)
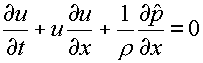
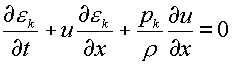 (k=i,e,f) (k=i,e,f)
Анализ характеристического уравнения для этой системы, описанный, напр., в
[1] на стр. 8, обнаруживает следующее. Все корни характеристического уравнения
вещественны, причем два из них суть:
(2.2) 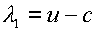 , , 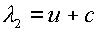 , ,
и один корень является
трехкратным и отвечает траектории частиц: 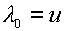 . .
Величина с определяется
формулами:
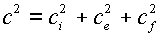 , ,
(2.3) 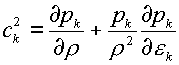 (k=i,e,f) (k=i,e,f)
В случае двучленных
уравнений состояния (1.5), как легко проверить, будем иметь:
(2.4) 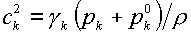
По
аналогии с обычной газовой динамикой величина с именуется
скоростью звука.
Соотношения на трехкратной
характеристике – траектории – позволяют для каждой из трех компонент среды (ионов,
электронов и фотонов) ввести свою энтропийную функцию:
(2.5) 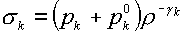 (k=i,e,f) (k=i,e,f)
Для гладкого решения энтропия каждой из трех компонент остается постоянной
вдоль трактории:
(2.6) 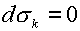 , , 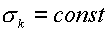 для для 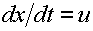 . .
Вдоль двух других («звуковых») характеристик выполнены
соотношения:
(2.7) 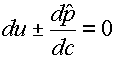 для для 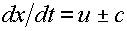 . .
В обычной (однотемпературной) газовой динамике для газа с
двучленным уравнением состояния
(2.8) 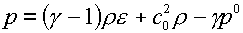
соотношения (2.7)
удается проинтегрировать в явном виде. Поскольку (2.7) удается переписать в
виде:
 , ,
получаются хорошо
известные римановы инварианты:
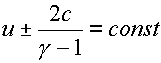 для для 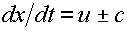 . .
К сожалению, такого замечательного результата не удается
достигнуть в трехтемпературной модели: соотношение (2.7), в котором скорость
звука определяется формулой (2.3), в явном виде проинтегрировать не удается
даже в простейшем случае (2.4).
§ 3. Задача о распаде
произвольного разрыва.
Описанная
выше структура характеристик для трехтемпературной модели (с единой плотностью
и скоростью среды) позволяет воспользоваться аналогией с обычной
однотемпературной газовой динамикой. Задача о распаде разрыва в рассматриваемой
ситуации представляет следующее.
Пусть в начальный момент времени t=0 левое полупространство (x<0)
заполнено средой с параметрами:
(3.1) rI, uI, (p,e,T)i,I, (p,e,T)e,I, (p,e,T)f,I,
а правое – средой с
параметрами:
(3.2) rII, uII, (p,e,T)i,II, (p,e,T)e,II, (p,e,T)f,II,
Присутствие,
кроме давлений р и удельных внутренних энергий e, температуры Т для всех трех компонент среды бывает
необходимо в случаях, если уравнения состояния задаются не в простейшей
двучленной форме (1.5). Достаточно типичной является, например, ситуация, когда
давление и внутренняя энергия задаются в виде зависимостей от плотности и
температуры.
Описанные
две среды разделены перегородкой х=0,
которая мгновенно убирается в момент t=0. Две
среды начинают взаимодействовать между собой. Автомодельную конфигурацию для t>0, возникающую после распада такого разрыва, естественно представлять такой
же, как в обычной газовой динамике: волна (ударная или разрежения), бегущая по
первой (левой) среде, волна (ударная или разрежения), бегущая по второй
(правой) среде, и контактный разрыв между ними. В случае волны разрежения
волновой фронт представляет «веер характеристик». Его границы определяются
расчетом.
Математическое
рассмотрение алгоритма расчета проведем по аналогии с его описанием в [3] на
стр. 102-117. Начнем со случая ударной волны. Как следствие уравнений (1.1),
(1.2) и (1.10), на ней должны быть выполнены соотношения:
(3.3) 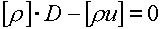
(3.4)
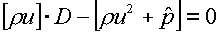
(3.5) 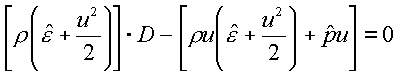 . .
Здесь D – скорость ударной волны, u –
нормальная компонента вектора скорости среды, r - плотность среды, 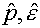 - суммарные давление
и энергия, определенные формулами (1.4)-(1.6). [ ] обозначается разрыв
величины, заключенной в скобки, т.е. разность ее значений за и перед волновым
фронтом. - суммарные давление
и энергия, определенные формулами (1.4)-(1.6). [ ] обозначается разрыв
величины, заключенной в скобки, т.е. разность ее значений за и перед волновым
фронтом.
Введем в рассмотрение, как делается в схеме С.К.Годунова,
«большие» величины за фронтом волны в отличие от «малых» величин перед фронтом.
Тогда
для левой ударной волны (если она таковой является) соотношение (3.3) можно
переписать так:
(3.6) 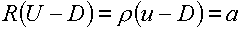 , ,
а затем соотношение
(3.4) - в виде:
(3.7) 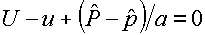
(Чтобы не загромождать
изложение, индексы I «левых» величин до окончания рассмотрения левой волны
будут опускаться).
В свою очередь, из (3.6) и (3.7) для величины а ,
называемой обычно массовой скоростью ударной волны, получается формула:
(3.8) 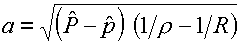 . .
Важно отметить, что выбор знака +
перед квадратным корнем обусловлен при этом требованием, чтобы в ударной волне
реализовалось возрастание энтропии.
Соотношение
(3.5) для изменения полной энергии после вычитания (3.7), умноженного на 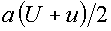 , и использования очевидного тождества , и использования очевидного тождества
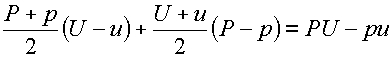 , ,
которое можно
рассматривать как разностный аналог тождества (1.9), переписывается в виде:
(3.9) 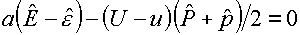
Используя
(3.7)-(3.8), получаем равенство:
(3.10)
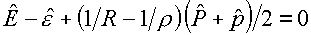
Заслуживает быть отмеченным, что с
учетом определения энтропии
(3.11)
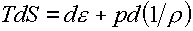
равенство (3.10) можно
рассматривать как разностную альтернативу на ударной волне условию сохранения
энтропии на гладком решении. В качестве следствия выводится известный факт, что
скачок (положительный!) энтропии на ударной волне слабой интенсивности является
малой величиной третьего порядка по сравнению со скачком давления (см., напр.,
[5], на стр. 460).
Требование неубывания энтропии разрешает ударные волны
сжатия и запрещает ударные волны разрежения, обеспечивая единственность решения
задачи о распаде разрыва (при выполнении некоторых требований к уравнению
состояния). В противном случае легко строятся примеры неединственности (см.,
напр., [3], стр.115-117).
Обратим теперь внимание, что следствием (3.9) на
ударной волне можно заменить соотношение (3.5), выражающее сохранение полной
энергии. В свою очередь (3.9) возникает, если вместо уравнения (1.10), имеющего
дивергентную форму, использовать уравнение (1.7). В силу аддитивной формы
соотношений (3.9) и (3.10) представляется совершенно естественным, что в
трехтемпературной модели уравнения, описывающие изменения энергии трех сортов
частиц, на ударной волне следует аппроксимировать соотношениями:
(3.12)
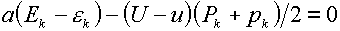 (k=i,e,f) (k=i,e,f)
В
качестве их следствий будем иметь три соотношения:
(3.13)
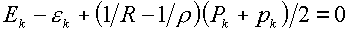 (k=i,e,f) (k=i,e,f)
Суммирование
(3.12) по индексу k
автоматически дает соотношение (3.9), а суммирование (3.13) – соотношение
(3.10).
Важно
отметить, что пока не использовалось уравнение состояния среды. В случае
однотемпературной газовой динамики использование уравнения состояния позволяет
исключить величину энергии Е и
получить выражение для плотности R. Для случая уравнения
состояния в форме двучлена (2.8) это удается реализовать в явном виде и
получить так называемую адиабату Гюгонио:
(3.14) 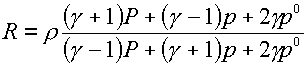
Сложнее обстоит дело в
трехтемпературном случае. Использование уравнений состояния для компонент в
простейшей двучленной форме (1.5) после подстановки Ek в соотношения (3.13) позволяет получить равенства, связывающие величины Pk и R:
(3.15) 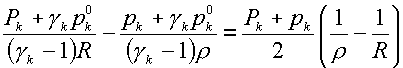
Представляется
естественным получить из них выражения для давлений компонент Pk через общую величину плотности R:
(3.16) 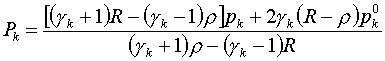 (k=i,e,f) (k=i,e,f)
В случае, если левая волна является волной разрежения, уже упоминалась
возможность введения для каждой из трех компонент среды своей энтропийной
функции (2.5), сохраняющейся вдоль траектории. Это приводит к соотношениям:
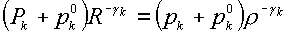 (k=i,e,f) (k=i,e,f)
Они дают формулы для давлений компонент Pk через общую величину плотности R в случае волны разрежения:
(3.17)
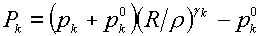 (k=i,e,f) (k=i,e,f)
Напомним, что пока рассматривалась левая волна (ударная или разрежения).
Рассмотрение правой волны осуществляется аналогичным образом (конечно, с
использованием величин с индексом II, описывающих правую среду) и
отличается только знаками в соотношениях (3.6) и (3.7). Мы не будем на этом
останавливаться. Формулы (3.15)-(3.17) сохраняют свой вид и для правой среды.
Рассмотрим ситуацию, когда в результате распада разрыва
образуются две ударные волны. После исключения давлений компонент Pk,I и Pk,II (k=i,e,f), своих для среды слева и справа от контактного
разрыва, и величины скорости U
получается уравнение, содержащее две общие для компонент, но различные слева и
справа плотности RI и RII . (В однотемпературном случае исключались плотности и получалось одно нелинейное уравнение для общего давления P на контактном разрыве.) Второе уравнение для этих
величин получаем, исходя из требования равенства суммарных давлений:
(3.18) 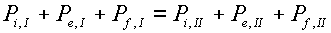 . .
Разработка
алгоритма для решения возникающей (только в случае образования двух ударных
волн) системы двух нелинейных уравнений возможна, но не представляется целесообразной.
Как уже упоминалось в конце §2, в случае возникновения волны разрежения
соответствующие уравнения даже выписать в явном виде не удается.
§ 4. Конструирование общего
уравнения состояния среды.
Для преодоления описанных трудностей прибегнем к процедуре
введения общего уравнения состояния для трехтемпературной среды. Воспользуемся
следующим приемом, описанным в [6], стр. 14-15.
Пусть пока уравнения состояния компонент задаются в
двучленной форме (1.5):
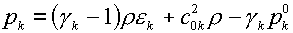 . .
Введем в рассмотрение
величины:
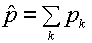 , , 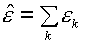 , , 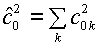
(4.1)  , , 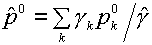
Тогда после суммирования (1.5) по индексу k будем
иметь:
(4.2) 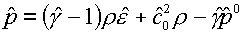
Если величины 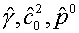 после их вычисления
по конкретным локальным значениям величин ek, pk «заморозить», то (4.2) можно рассматривать как общее уравнение состояния
среды в форме двучлена. после их вычисления
по конкретным локальным значениям величин ek, pk «заморозить», то (4.2) можно рассматривать как общее уравнение состояния
среды в форме двучлена.
Заметим,
что формулы (4.1) могли быть и иными. Например, с точки зрения получения
правильного значения скорости звука с, согласно формулам (2.3)-(2.4) следовало бы полагать:
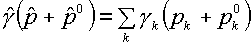 . .
Отсюда
естественно напрашивается 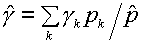 , т.е. получение показателя адиабаты , т.е. получение показателя адиабаты 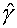 усреднением по
давлениям, а не по энергиям. Такой вариант рассматривался в [6] на стр.14 и был
забракован, поскольку соответствующая ему формула для параметра усреднением по
давлениям, а не по энергиям. Такой вариант рассматривался в [6] на стр.14 и был
забракован, поскольку соответствующая ему формула для параметра 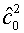 не гарантировала его
положительности. не гарантировала его
положительности.
С этой
точки зрения формулы (4.1) для всех трех параметров 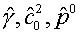 безупречны. Правда,
как следствие только что изложенного, придется мириться с тем, что для общей
скорости звука с формула безупречны. Правда,
как следствие только что изложенного, придется мириться с тем, что для общей
скорости звука с формула 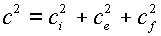 , вообще говоря, не будет выполняться даже локально, в
рассматриваемой точке. , вообще говоря, не будет выполняться даже локально, в
рассматриваемой точке.
Реализовав процедуру получения (4.2) в задаче
о распаде разрыва независимо для «левой» и «правой» среды, как уже отмечалось
выше, мы получаем возможность осуществить расчет конфигурации распада разрыва,
например, по алгоритму, описанному в [7], обобщающему изложенный в [3] на стр.
102-117.
При этом будут получены величины P=P*, U, RI, RII .
Далее по формулам (3.16) в случае ударной волны или (3.17) в случае волны
разрежения вычисляются величины Pk,I и Pk,II (k=i,e,f) давлений для отдельных компонент среды. Заметим, что вопрос о том,
является ли волна ударной или волной разрежения, и соответствующий выбор
расчетных формул решается путем сравнения величин давления P* и 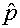 или плотностей R и r за и перед фронтом волны сразу для всех компонент среды. или плотностей R и r за и перед фронтом волны сразу для всех компонент среды.
То обстоятельство, что параметры 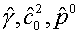 уравнения состояния
(4.2) «замораживались», естественно приводит к тому, что полученный результат
можно рассматривать только в качестве приближенного решения задачи о распаде
разрыва. Это проявится прежде всего в том, что вместо равенства (3.18) величины уравнения состояния
(4.2) «замораживались», естественно приводит к тому, что полученный результат
можно рассматривать только в качестве приближенного решения задачи о распаде
разрыва. Это проявится прежде всего в том, что вместо равенства (3.18) величины
(4.3) 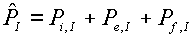 , ,
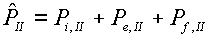 , ,
как правило, будут
различаться между собой и отличаться от величины 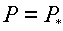 , полученной при описанном выше расчете: , полученной при описанном выше расчете:
(4.4) 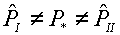
Исправление ситуации возможно следующим путем. В работе [8]
для получения точного решения задачи о распаде разрыва со сложными уравнениями
состояния в обычной (однотемпературной) газовой динамике предложено введение
дополнительных неопределенных коэффициентов в аппроксимирующие такие уравнения
состояния двучленные уравнения. Коэффициенты должны быть в процессе расчета
подобраны так, чтобы решение задач о распаде разрыва для двучленных и исходных
(«настоящих») уравнений состояния совпадали. Метод введения неопределенных
коэффициентов, предложенный в [8], по мнению его авторов оказался весьма удобным
и эффективным. Его аналог может быть использован для получения точного решения
задачи о распаде разрыва и в трехтемпературном случае.
Сущность метода состоит в следующем. Уравнение состояния
(4.2) для левой среды запишем в виде:
(4.5) 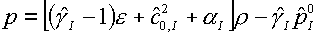 , ,
а для правой среды – в
аналогичном виде:
(4.6) 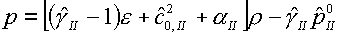
Здесь aI , aII – неопределенные пока коэффициенты.
Параметры 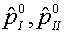 назначаются с учетом
конкретных значений aI, aII : назначаются с учетом
конкретных значений aI, aII :
(4.7) 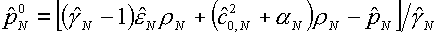 ( N=I,II). ( N=I,II).
Они пересчитываются при
изменении aI и aII .
Заметим, что в работе [8] введение неопределенного
коэффициента a осуществлялось в несколько иной форме:
(4.8) 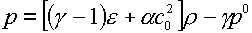 . .
При этом теряется работоспособность такого коэффициента в
случае с0=0. Поскольку
такой случай находится в сфере наших интересов, форма (4.8), где a
является сомножителем при 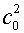 , заменена на
«аддитивную» (4.5)-(4.6). При этом коэффициенты aN становятся размерными (имеют
размерность удельной энергии или квадрата скорости звука), что следует
учитывать при их вариации. , заменена на
«аддитивную» (4.5)-(4.6). При этом коэффициенты aN становятся размерными (имеют
размерность удельной энергии или квадрата скорости звука), что следует
учитывать при их вариации.
Выбор формы (4.8) или (4.5)-(4.6) для введения
дополнительного неопределенного параметра a не случаен. Он обусловлен тем обстоятельством, что формула (3.17) для
волны разрежения и ударная адиабата Гюгонио (3.14) зависят от параметров
двучленного уравнения состояния g и р0, но не зависят
от параметра с0. Это в
свою очередь связано с тем, что для двучленного уравнения состояния (2.8):
(4.9) 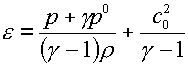 . .
При подстановке в (3.10)
последнее постоянное слагаемое исключается, что и приводит к упомянутому
результату.
Выбранный способ введения дополнительного параметра
сводится к замене 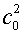 на на 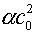 в случае (4.8) или
замене в случае (4.8) или
замене 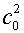 на на 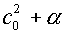 в случае (4.5)-(4.6).
В обоих вариантах ударная адиабата (3.14) будет сохранена (но с другими
значениями параметра р0,
что и позволяет варьировать получаемые результаты). в случае (4.5)-(4.6).
В обоих вариантах ударная адиабата (3.14) будет сохранена (но с другими
значениями параметра р0,
что и позволяет варьировать получаемые результаты).
При конкретных значениях параметров aI и aII для сред с уравнениями
состояния (4.5)-(4.6) давление на контактной границе, которое обозначим P=P*, можно
найти из уравнения вида:
(4.10) 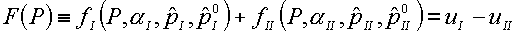 . .
Выражения fI и fII определяются конфигурацией, возникающей при распаде разрыва, и приведены в
[3], [7].
Из (4.10) следует, что 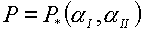 . .
Как уже описывалось в §3, после этого могут быть вычислены
значения плотностей RI и RII по формуле (3.14). Затем вычисляются
давления компонент среды по формулам (3.16) или (3.17). Их суммирование
(4.3) дает величины 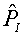 и и 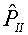 . Очевидно, что . Очевидно, что 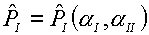 , , 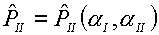 . Роль параметров aI , aII состоит в том, чтобы посредством их подбора добиться выполнения условий: . Роль параметров aI , aII состоит в том, чтобы посредством их подбора добиться выполнения условий:
(4.11)
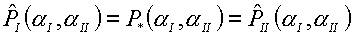 . .
Их
можно рассматривать как два уравнения для определения параметров aI , aII.
Вопрос о существовании искомых параметров в ситуации,
рассматривавшейся в работе [8], определялся фактом единственности решения
задачи о распаде произвольного разрыва для сред со сложными уравнениями
состояния, подчиненными определенным ограничениям.
Для рассматриваемой нами ситуации положение сложнее. С
точки зрения здравого смысла представляется целесообразной реализация
некоторого итерационного процесса, в ходе которого параметры aI , aII подбираются, исходя из требований достижения минимальных
значений величин погрешностей
(4.12) 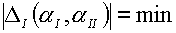 , , 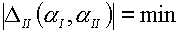 , ,
где DI , DII представляют невязки
уравнений (4.11):
(4.13) 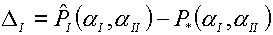
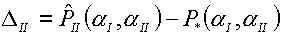
С
вычислительной точки зрения по-видимому предпочтительнее в качестве таких
величин выбрать безразмерные величины относительных погрешностей, определив
(4.14) 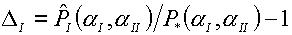
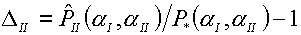
Если
удается достигнуть нулевых значений этих величин, можно будет говорить о
выполнении условий (4.11) и, следовательно, о точном решении задачи о распаде
разрыва для трехтемпературной среды, компоненты которой удовлетворяют
двучленным уравнениям состояния (1.5). Итерационный процесс по подбору
параметров aI , aII естественно основывать на методах типа стрельбы или секущих, как это
предлагалось и в работе [8].
Прежде,
чем переходить к рассмотрению соответствующих алгоритмов, остановимся еще на
одном вопросе.
Уравнения
состояния в двучленной форме (1.5) представляют лишь простейший случай. В
практике расчетов, как правило, в качестве уравнений состояния привлекаются
гораздо более сложные зависимости, зачастую задаваемые в параметрической или
табличной форме. В обычной (однотемпературной) газовой динамике преодоление
возникающих алгоритмических трудностей (в частности, при решении задач о
распаде разрыва) успешно достигается с помощью локальной аппроксимации
уравнений состояния общего вида двучленными уравнениями. В случае задания
уравнения состояния в виде функциональной зависимости p=p(r,e) три
константы g,р0,с0 определяются формулами (см., напр., [6], стр. 9, или [4], стр. 177):
(4.15) 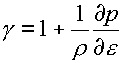 , , 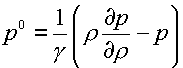 , , 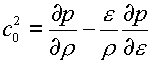 . .
Эти формулы были
предложены А.В.Забродиным.
Легко проверить, что при подстановке этих формул в
двучленное уравнение состояния они превращают его в тождество. Кроме того,
отметим, что формулы (2.3) и (2.4) дают одинаковую величину скорости звука для
«настоящего» уравнения состояния и для аппроксимирующего его двучлена
(локально, в рассматриваемой точке).
В случае задания уравнения состояния в параметрической
форме
(4.16) 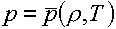 , , 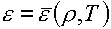
можно считать их
определяющими неявную функцию 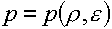 . Тогда будем иметь . Тогда будем иметь
(4.17) 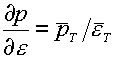 , , 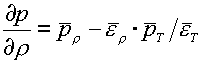
Пример таких уравнений представляет «газ с учетом
излучения»:
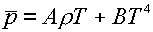 , , 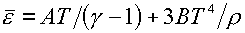
с заданными константами А,В,g.
Еще один пример – для описания плазмы с неполной ионизацией
изучался в [6]. Необходимость выполнения термодинамического тождества (3.11),
определяющего энтропию, накладывает на уравнения состояния в форме (4.16)
определенные ограничения: они должны удовлетворять условию:
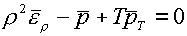 . .
Отметим, что необходимым элементом алгоритма при
использовании (4.16) является вычисление температуры Т при заданных значениях 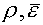 (или (или 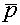 ). Если это не удается выполнить по явным формулам,
приходится привлекать специальные итерационные процедуры. ). Если это не удается выполнить по явным формулам,
приходится привлекать специальные итерационные процедуры.
Использование
локальных аппроксимаций для уравнений состояния отдельных компонент
трехтемпературной среды вносит дополнительные сложности в обоснование
описываемого алгоритма расчета задачи о распаде разрыва и является дополнительным
аргументом в пользу постановки задачи в форме (4.12).
§ 5. Алгоритм расчета распада
разрыва.
Предлагаемый
алгоритм расчета распада разрыва для трехтемпературной среды представляется
следующим.
1. Если среди
уравнений состояния компонент среды есть более сложные, чем двучленные вида
(1.5), то для каждого из них осуществляется локальная аппроксимация двучленным
уравнением состояния. В случае задания уравнения состояния в форме p=p(r,e) ее
параметры g, 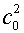 вычисляются по формулам: вычисляются по формулам:
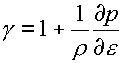 , , 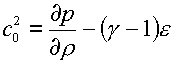 . .
В
случае параметрического задания (4.16) нужные производные вычисляются по (4.17)
после предварительного вычисления Т.
Возможны и другие формы задания уравнений состояния (например, табличная).
2. Вычисляются
значения параметров 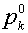 для левой и правой
сред по формулам: для левой и правой
сред по формулам:
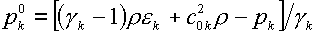 (k=i,e,f) (k=i,e,f)
3. Для
левой и правой сред вычисляются параметры общих уравнений состояния 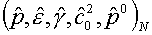 , N=I,II, по формулам (4.1). , N=I,II, по формулам (4.1).
4. Назначаются
коэффициенты aI , aII. В качестве исходных выбираются, как правило, aI=aII=0. В
противном случае сразу исправляются параметры 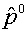 для левой и правой сред: для левой и правой сред:
(5.1)
 , N=I,II. , N=I,II.
5.
Решается задача о распаде разрыва с газодинамическими параметрами
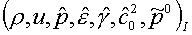 для левой среды, для левой среды,
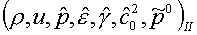 для правой среды, для правой среды,
в предположении
двучленных уравнений состояния. Она подробно изучалась в [3], [7]. Решение
уравнения для давления находится итерациями на основе метода касательных
(Ньютона), имеющего в окрестности искомого корня квадратичную скорость
сходимости.
Как указывалось в [8], из анализа свойств этого уравнения
при любой конфигурации распада разрыва следует, что для его численного решения
можно применить и метод обратной параболической интерполяции, описанный в [9]
на стр.297.
Суть
его состоит в том, что в итерационном процессе используется корень уравнения
параболы, принимающей заданные значения на концах текущего интервала и нужное
значение производной на одном из его концов. В уравнении параболы меняются роли
абсциссы и ординаты. Авторы [8] успешно применили этот метод и, по их мнению,
результаты расчетов задачи о распаде произвольного разрыва подтвердили
преимущество метода обратной параболической интерполяции по сравнению с методом
Ньютона.
Метод обратной параболической интерполяции требует для
своей реализации вычисления производных функции F(P) в уравнении (4.10) только
первого порядка (как и метод касательных Ньютона), но имеет кубическую скорость
сходимости.
Процесс
решения уравнения (4.10) методом касательных или обратной параболической
интерполяции будем называть внутренними итерациями.
Как уже
отмечалось в §4, выбранный способ введения неопределенного параметра позволяет
сохранить ударную адиабату (3.14), а следовательно и весь алгоритм внутренних
итераций. Единственное исключение может касаться назначения исходного
приближения для искомого давления Р.
Представляется целесообразным использовать для этого результат, который был
получен для предыдущих значений параметров 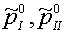 . .
6. При
доведении процесса внутренних итераций до требуемой степени сходимости будет
получено значение P* давления на контактном разрыве.
Как уже отмечалось в
§3 и §4, после этого последовательно вычисляются плотности RI, RII,
давления компонент среды Pk,I, Pk,II (k=i,e,f),
суммарные давления 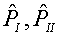 и, наконец, их
относительные погрешности и, наконец, их
относительные погрешности
(5.2) 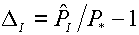 , , 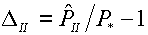 . .
Если при назначенном
уровне погрешностей d>0 выполнены условия
(5.3) 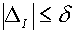 и и 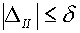 , ,
то процесс расчета
распада разрыва считаем завершенным.
В противном случае приступаем к процессу подбора
неопределенных коэффициентов aI , aII, который назовем внешними итерациями. Как уже упоминалось, для этого будут использованы методы типа
стрельбы и метода секущих.
7. Описывать процесс
внешних итераций во всех подробностях нецелесообразно, поскольку вполне
возможны его усовершенствования в ходе практической эксплуатации (как это было
в свое время с упомянутыми выше внутренними итерациями). Тем не менее для
полноты изложения остановимся на его основных деталях.
Присвоим внешним итерациям номер-индекс j.
Пусть 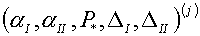 - величины,
полученные на j-ой
внешней итерации. Для решения вопроса об изменении параметров aI , aII привлекаем кроме них
аналогичные величины, полученные на предыдущей (j-1)-ой
итерации. - величины,
полученные на j-ой
внешней итерации. Для решения вопроса об изменении параметров aI , aII привлекаем кроме них
аналогичные величины, полученные на предыдущей (j-1)-ой
итерации.
Для каждого из номеров сред N=I,II независимо проводится
следующее рассмотрение.
Пусть ситуация настолько «хорошая», что величины 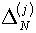 и и 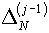 имеют разные знаки,
т.е. выполнено условие имеют разные знаки,
т.е. выполнено условие
(5.4)
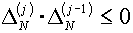 . .
Тогда естественно
ожидать, что параметр aN «захвачен в вилку»
между 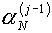 и и 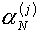 . (Хотя возможно это и не так – в силу далекого от
правильного значения другого из параметров aN). Согласно методу секущих в качестве
следующего приближения напрашивается результат линейной интерполяции величин . (Хотя возможно это и не так – в силу далекого от
правильного значения другого из параметров aN). Согласно методу секущих в качестве
следующего приближения напрашивается результат линейной интерполяции величин 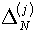 и и 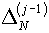 на нулевое значение: на нулевое значение:
(5.5)
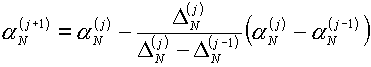 . .
Теперь рассмотрим
«плохую» ситуацию. Если условие (5.4) не достигнуто, т.е.
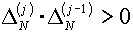 , ,
то вариацию
параметра 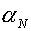 будем осуществлять исходя из следующих
соображений. Результат вычисления по формуле (5.5) будет представлять не
интерполяцию, а экстраполяцию на нулевое значение. Поэтому его прямое использование опасно возможным
появлением численной неустойчивости. Рассмотрим два случая. будем осуществлять исходя из следующих
соображений. Результат вычисления по формуле (5.5) будет представлять не
интерполяцию, а экстраполяцию на нулевое значение. Поэтому его прямое использование опасно возможным
появлением численной неустойчивости. Рассмотрим два случая.
а) Если 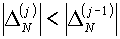 , то естественно предполагать, что процесс движется в
«правильном» направлении. Если изменение , то естественно предполагать, что процесс движется в
«правильном» направлении. Если изменение 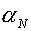 по формуле (5.5) не
слишком велико, а именно по формуле (5.5) не
слишком велико, а именно
 , ,
то назначаем 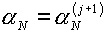 , вычисленное по формуле (5.5). , вычисленное по формуле (5.5).
В противном случае
полагаем:
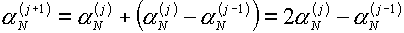 . .
б) В случае, если 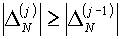 , полагаем «неправильным» выбранное ранее направление
изменения параметра. Если изменение , полагаем «неправильным» выбранное ранее направление
изменения параметра. Если изменение 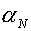 по формуле (5.5) не
слишком велико, а именно: по формуле (5.5) не
слишком велико, а именно:
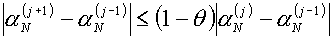 , ,
то назначаем 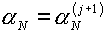 , вычисленное по формуле (5.5). , вычисленное по формуле (5.5).
В противном случае
полагаем:
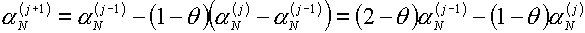 . .
Здесь 0<q<1 –
задаваемая константа, роль которой – избежать возможного возврата к ранее
рассматривавшимся значениям искомых параметров и обеспечить численную
устойчивость итерационного процесса.
Таким образом, описано автоматизированное назначение новых
значений параметров aN для
всех случаев. Как уже отмечено, оно выполняется для N=I,II
независимо. После этого для новых значений повторяется описанный выше расчет,
начиная с пункта 4. Его результатом
будет получение величин  . .
В монографии [10] на стр. 419-420 под названием «метода
вилки» для решения одного нелинейного уравнения рекомендуется после достижения
условия (5.4) и вычислений для проинтерполированного значения (5.5), чтобы
сохранить условие вилки, завершать итерацию отбором одного из двух отрезков, на
концах которого получаются противоположные знаки невязки решаемого уравнения. В
наших условиях это означает, что перед началом следующей внешней итерации в качестве
исходных задаются:
в случае, если 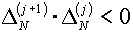 , - величины , - величины  , ,
а в противном случае –
величины 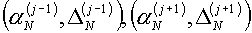 . .
Заметим, что для каждого
N из N=I,II это делается независимо.
После всего изложенного осталось неопределенным только
назначение параметров для первой итерации (для расчета с параметрами aI = aII=0 будем считать j=0).
Исходя
из (4.5)-(4.6), сделаем это назначение формулами:
(5.6)
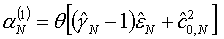 , (N=I,II), , (N=I,II),
воспользовавшись тем же
параметром q (чтобы не загромождать входную информацию лишними параметрами).
Отметим важность назначений (5.6), в значительной степени
предопределяющих ход процесса внешних итераций). Если исходные шаги (5.6)
слишком велики, может возникнуть опасность численной неустойчивости. В качестве
контрольной меры можно предложить следить за поведением величины P*.
Естественно ожидать, что она должна сходиться к некоторому пределу. Поэтому в
случае, если в ходе внешних итераций обнаружится, что
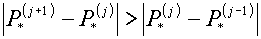 , ,
это должно быть поводом
для беспокойства.
Можно рекомендовать в этом случае уменьшить управляющий
параметр q. Может быть, целесообразно начинать процесс внешних итераций сначала или
продолжить с того момента, когда достигнутые значения 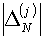 были наименьшими. были наименьшими.
С другой стороны, описанные формулы вариации параметров aN
целенаправленно не допускают превышения исходных шагов в ходе итерационного
процесса. Поэтому, если шаги (5.6) слишком малы, для экономии вычислительной
работы желательно их увеличить. В силу «благополучного» хода процесса
обнаружить это можно было бы методом стрельбы, пробуя увеличивать q, но не
допуская возникновения «неприятностей». Поэтому рекомендация сводится к тому,
чтобы не назначать сразу слишком малых значений q. Более четкие рекомендации могут быть сформулированы по мере накопления
практического опыта.
В частности, формула (5.6) для назначения параметра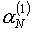 на первой итерации, по-видимому, может быть
усовершенствована, например, присвоением знака этой величине с учетом величины на первой итерации, по-видимому, может быть
усовершенствована, например, присвоением знака этой величине с учетом величины 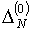 , полученной для
значения , полученной для
значения 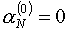 . Это позволило бы сразу задать правильное направление
изменения параметра. К сожалению, слишком сложный нелинейный характер
зависимости величины P* от параметров aN затрудняет
аналитическое обоснование таких рекомендаций. . Это позволило бы сразу задать правильное направление
изменения параметра. К сожалению, слишком сложный нелинейный характер
зависимости величины P* от параметров aN затрудняет
аналитическое обоснование таких рекомендаций.
Еще одно замечание связано с тем обстоятельством, что
параметры aN могут
оказаться и отрицательными. Двучленное уравнение состояния предполагает, что р+р0>0. В противном
случае, например, невозможно введение скорости звука формулой (2.4). Поскольку 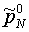 определяется формулой
(5.1), требование определяется формулой
(5.1), требование 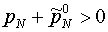 приводит к
ограничениям приводит к
ограничениям
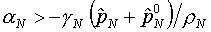 (N=I,II). (N=I,II).
В ходе
итераций необходимо это контролировать во избежание аварийных ситуаций
(«авостов»).
Наконец, в качестве последнего замечания необходимо
напомнить, что факт существования и тем более единственности искомых параметров
не обоснован. Поэтому в ходе внешних итераций контролируются условия (4.12), а
условия (5.4) могут и не реализоваться. Ничего страшного в этом, по-видимому,
нет. Напомним по аналогии, что в обычной газовой динамике в случае слишком
больших скоростей разлета может образоваться зона вакуума. В [7] и в монографии
[4] на стр. 175 для таких случаев предусматриваются некоторые специальные меры.
Главная забота состоит в том, чтобы процесс был полностью автоматизирован и для
любой ситуации выдавал «разумный» ответ.
Предусматриваются
также ограничения для количества внешних итераций.
В связи с возможностью таких ситуаций заметим также, что и
в обычной (однотемпературной) газовой динамике альтернативой точному решению
задачи является приближенное. Такие методы экономичнее и в ряде случаев дают
вполне удовлетворительную точность. В монографии [4] им уделено достаточно
много внимания. Однако в ряде ситуаций необходимость точного решения задачи о
распаде разрыва становится весьма желательной. Особенно это касается расчета
движения контактных границ между двумя средами, описываемыми различными
уравнениями состояния.
§ 6. О разностных законах
изменения внутренней энергии для
отдельных компонент среды.
В работе [1] для приближенного решения задачи о распаде
разрыва был предложен алгоритм, который был основан на идее замены «настоящей»
среды некоторой искусственной, удовлетворяющей двучленному уравнению состояния.
При этом привлекались предположения о том, что для ионов и электронов
показатели адиабаты g одинаковы, учитывалась структура фронта ударной волны в магнитной плазме с
неполной ионизацией, исследованная в [2], специально выбирались параметры для
правильной аппроксимации скорости звука в случае волны разрежения. При
реализации разностной схемы для расчета
газодинамического этапа искусственно выделялась роль ионов предположением, что
перенос кинетической энергии осуществляется только ионами. В результате
расчетные формулы, основанные на законах сохранения, для энергии ионной
компоненты оказывались отличными от аналогичных формул для электронов и
фотонов.
Предлагаемый усовершенствованный алгоритм расчета распада
произвольного разрыва позволяет отказаться от этих предположений и ограничений.
Выше, в §3, была описана и обоснована процедура, позволяющая получить изменение
давлений и энергий в ударной волне или волне разрежения отдельно для каждой из
трех компонент среды. В работе [1]
на стр. 16 разностные законы для расчета значений удельной внутренней энергии
электронов и фотонов в отдельной ячейке разностной сетки для случая плоского
течения выписывались в виде:
(6.1)
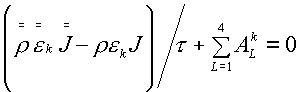 (k=e,f). (k=e,f).
Здесь t - шаг по времени t, 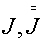 - площади
ячейки на нижнем и верхнем слое соответственно, - площади
ячейки на нижнем и верхнем слое соответственно, 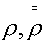 - значения
плотности в центрах ячеек, - значения
плотности в центрах ячеек, 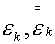 - значения внутренней
энергии. Величины - значения внутренней
энергии. Величины 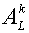 представляют потоки
энергии через четыре боковые грани пространственно-временной ячейки в
направлении вектора внешней нормали в единицу времени. Эти потоки выписываются
в виде: представляют потоки
энергии через четыре боковые грани пространственно-временной ячейки в
направлении вектора внешней нормали в единицу времени. Эти потоки выписываются
в виде:
(6.2) 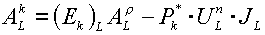 . .
Здесь 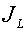 - длина ребра ячейки, - длина ребра ячейки,
 - поток массы через
ребро, - поток массы через
ребро, 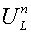 - составляющая
вектора скорости, нормальная по отношению к ребру, - составляющая
вектора скорости, нормальная по отношению к ребру, 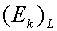 = получаемые из
задачи о распаде разрыва вспомогательные «большие» величины энергии на ребре.
Вопрос о величинах давлений = получаемые из
задачи о распаде разрыва вспомогательные «большие» величины энергии на ребре.
Вопрос о величинах давлений 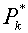 заслуживает
специального обсуждения. В соответствии с изложенным в §3 обоснованием
соотношений (3.9) и затем (3.12), предлагается задавать их формулой: заслуживает
специального обсуждения. В соответствии с изложенным в §3 обоснованием
соотношений (3.9) и затем (3.12), предлагается задавать их формулой:
(6.3)
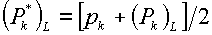 . .
Здесь pk – давление в центре ячейки на
«нижнем» слое по времени, 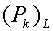 - «большая» величина
давления для компоненты k, полученная
в задаче о распаде разрыва для ребра с номером L. - «большая» величина
давления для компоненты k, полученная
в задаче о распаде разрыва для ребра с номером L.
Заметим, что при этом становится излишним обсуждавшийся в
[1] на стр.16 вопрос о том, использовать ли в качестве 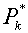 давление pk в центре ячейки на «нижнем»
слое или, с точки зрения устойчивости, предпочесть еще не известное давление давление pk в центре ячейки на «нижнем»
слое или, с точки зрения устойчивости, предпочесть еще не известное давление 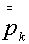 на верхнем слое.
Последнее вносит определенные усложнения в расчетные формулы, особенно в случае
не двучленных уравнений состояния для компонент. на верхнем слое.
Последнее вносит определенные усложнения в расчетные формулы, особенно в случае
не двучленных уравнений состояния для компонент.
Между тем использование формулы (6.3) очень естественно
вписывается в алгоритм.
Соотношения (6.1)-(6.3) представляют разностную
аппроксимацию дифференциальных уравнений (1.3e) и (1.3f),
содержащих недивергентные члены 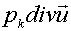 . Точно такую же форму имеет и уравнение (1.3i) для
ионов. Естественно и для него использовать такие же формулы (6.1)-(6.3),
полагая индекс k=i. . Точно такую же форму имеет и уравнение (1.3i) для
ионов. Естественно и для него использовать такие же формулы (6.1)-(6.3),
полагая индекс k=i.
Новый алгоритм расчета распада разрыва позволяет это
сделать. В случае двучленных уравнений состояния для всех компонент
суммирование (6.1) по индексу k с
привлечением разностной аппроксимации законов изменения массы и импульса в
качестве следствия автоматически дает разностный закон изменения полной
энергии. При этом отпадает необходимость в приписывании ионам переноса всей
кинетической энергии. (Это ранее
делалось, исходя из того, что массой электронов можно пренебречь по сравнению с
массой ионов, а фотоны вообще считаются не имеющими массы).
Таким образом, при разностной реализации все три компоненты
(ионы, электроны и фотоны) становятся совершенно равноправными участниками
вычислительного процесса, как это и должно быть в силу математического
содержания рассматриваемой модели.
Еще одно замечание касается расчета газодинамических задач
в осесимметричных координатах. В этом случае в системе дифференциальных
уравнений появляются ненулевые правые части (например, давление р в двумерном уравнении для импульса).
Очевидно, что аппроксимацию этих членов желательно
выполнить так, чтобы суммирование формул изменения энергии для отдельных
компонент и изменения кинетической энергии автоматически давало закон изменения
полной энергии. Как описано выше, в декартовых координатах эта цель
достигается.
Заключение
В настоящей работе описан алгоритм расчета распада
произвольного разрыва для трехтемпературной модели. Для случая, когда уравнения
состояния всех трех компонент задаются в форме двучленов, алгоритм позволяет
получить точное решение этой задачи. Это достигается путем использования
обобщенного уравнения состояния среды в форме двучлена, введения в него неопределенных
коэффициентов и последующего их подбора в ходе специального итерационного
процесса. При этом удовлетворяются заданные двучленные уравнения состояния
каждой из компонент или локально аппроксимированные заданные «настоящие»
уравнения состояния компонент.
Полученный результат позволяет получить изменение давления
и внутренней энергии отдельно для каждой из трех компонент среды несмотря на
недивергентную форму уравнений. Их суммирование с привлечением закона изменения
импульса автоматически реализует закон изменения полной энергии.
При разностной реализации все три компоненты (ионы,
электроны и фотоны) становятся равноправными участниками вычислительного
процесса, как и в дифференциальной модели. При использовании прежнего
приближенного алгоритма расчета распада разрыва приходилось прибегать к
дополнительным предположениям, например, приписывать ионам перенос всей
кинетической энергии (на том основании, что масса электрона мала по сравнению с
массой иона, а фотоны вообще не имеют массы). Отпадает необходимость и в
некоторых других предположениях, перечисленных в начале §6.
Метод введения неопределенного коэффициента в уравнение
состояния в работе [8] был использован для получения точного решения задачи о
распаде разрыва в случае «сложного» уравнения в однотемпературной газовой
динамике. Следовательно, принципиально этого можно достигнуть и в
рассматриваемой трехтемпературной модели.
Практическая сложность состоит прежде всего в том, что
число таких «сложных» уравнений состояния может варьироваться от нуля до шести.
Последнее будет иметь место в задаче о распаде разрыва на контактной границе,
если каждая из трех компонент слева и справа от разрыва не описывается
«двучленным» уравнением состояния. В такой ситуации естественно для каждой из
них вводить свой неопределенный коэффициент. Подбор их становится слишком уж
обременительной процедурой, надежность которой трудно обосновать.
Можно попытаться обойтись и двумя введенными параметрами,
дополнив изложенный алгоритм расчета распада разрыва пересчетом в ходе внешних
итераций локальных параметров по формулам, описанным в начале §5. При этом
придется в обязательном порядке ориентироваться лишь на выполнение условий
(4.12), рискуя попасть в ситуацию, которая наглядно иллюстрируется русской
пословицей: «За двумя зайцами погонишься – ни одного не поймаешь».
Остановимся еще на одной ситуации, важной с
производственной точки зрения. При решении практических задач для расчета
процессов, протекающих в сложных геометрических конструкциях, производится их
разрезание на расчетные области (см., напр., [3]). Число их может быть
достаточно большим и карта взаимного расположения достаточно сложной. По целому
ряду причин, на обсуждении которых останавливаться не будем, возможны ситуации,
когда лишь в некоторых областях используется трехтемпературное приближение. В
других же областях может использоваться двухтемпературная или однотемпературная
модель. С точки зрения рассматривавшейся задачи о распаде разрыва это означает,
что на границах между такими областями возникает необходимость проведения
расчета, когда для сред I и II слева и справа от разрыва количество компонент для
моделирования среды может быть различным. Описанный алгоритм пригоден и для
таких ситуаций. Необходимо лишь при конструировании общего уравнения состояния
соответствующей среды по формулам (4.1) производить суммирование по индексу k для фактических компонент моделируемой среды.
(Заметим, что их число может быть и более трех).
Автор признателен Л.А.Плинер, которая ознакомилась с
рукописным вариантом работы, сделала несколько ценных замечаний и реализовала
алгоритм на ЭВМ.
Автор также выражает благодарность М.С.Гавреевой за помощь
в оформлении работы.
Литература
1. Забродин А.В., Прокопов Г.П. Методика численного моделирования двумерных
нестационарных течений теплопроводного газа в трехтемпературном приближении.//
Препринт ИПМ им.М.В.Келдыша РАН, 1998, №25, 24 стр.
2. Имшенник В.С., Боброва Н.А. Динамика столкновительной плазмы.//
Энергоатомиздат, М, 1997, 320 стр.
3. Численное решение многомерных задач газовой динамики. Под ред. С.К.Годунова// М,
Наука, 1976, 400 стр.
4. Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы
численного решения гиперболических систем уравнений.// М, Физматлит, 2001, 608
стр.
5. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. Теоретическая физика. 6.// М,
Наука, 1986.
6. Прокопов Г.П. О задании уравнений состояния при моделировании неполностью
ионизованной плазмы.//Вопросы атомной науки и техники. Сер.: Матем. моделир.
физ. процессов, 2000, вып.3, С.45-63.
7. Прокопов Г.П. Расчет распада разрыва для пористых сред и сплошных сред с
двучленными уравнениями состояния.// Вопросы атомной науки и техники. Сер.
Методики и прогр. числ. реш. задач матем. физики. 1982, вып. 2(10), с. 32-40.
8. Кобзева Т.А., Моисеев Н.Я. Метод неопределенных коэффициентов для решения
задачи о распаде произвольного разрыва.// Вопросы атомной науки и техники. Сер.
Матем. моделир. физ. процессов. 2003, вып.1, с.3-9.
9. Коллатц Л. Функциональный анализ и вычислительная математика.// М, Мир,
1969, 447 стр.
10.
Бахвалов Н.С. Численные методы (анализ, алгебра,
обыкновенные дифференциальные уравнения).// Гл.ред.физ.-мат.лит. изд-ва
«Наука». М, 1973, 632 стр.
|