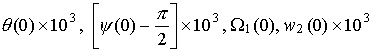
Исследование эволюции режима закрутки спутника в плоскости орбиты
|
|
|
Матрицу перехода от системы Ox1x2x3
к системе Oy1y2y3
обозначим ||bij
|| 3i,j=1 ,
где bij - косинус угла между осями Oyi и Oxj.
Элементы этой матрицы выражаются в функции углов gc, ac
и bc,
на которые надо повернуть систему Oy1y2y3
последовательно вокруг осей Oy2, Oy3 и Oy1,
чтобы перевести ее в систему Ox1x2x3.
Соответствующие выражения имеют вид
|
|
В уравнениях движения спутника относительно центра масс
будем учитывать гравитационный и восстанавливающий аэродинамический моменты.
Компоненты гравитационного момента в системе Ox1x2x3
имеют вид [2]
|
|
Здесь w0 - среднее движение спутника (орбитальная частота), Ii - моменты инерции спутника относительно осей Oxi.
При выводе выражений для аэродинамического момента внешнюю
оболочку спутника считаем эллипсоидом, который в системе координат Oy1y2y3
задается уравнением
|
Атмосферу полагаем неподвижной в абсолютном пространстве, а
ее плотность r
вдоль орбиты спутника постоянной. Пусть спутник неподвижен относительно
набегающего аэродинамического потока и молекулы воздуха при столкновении со
спутником испытывают абсолютно неупругий удар. Тогда компоненты
аэродинамического момента в системе Ox1x2x3
имеют вид
|
|
|
Здесь v - геоцентрическая скорость точки O. Эти формулы пригодны и в случае, когда угловая скорость спутника не очень велика по сравнению с w0.
Исходные уравнения движения спутника относительно центра масс возьмем в виде динамических уравнений Эйлера для компонент Wi абсолютной угловой скорости спутника в системе координат Ox1x2x3 и кинематических уравнений для углов y, q и j. Компоненты угловой скорости будем измерять в единицах w0, в качестве единицы измерения времени t примем w0-1. Орбитальный период при этом равен 2p. Уравнения движения имеют вид
|
|
|
|
|
|
|
Здесь точкой обозначено дифференцирование по времени. По своему физическому смыслу e ≥ 0, параметры l и m должны удовлетворять неравенствам |m| < 1, 0 < l < 2/(1-m). Неравенства для l и m следуют из "неравенств треугольника" для моментов инерции спутника. Правые части выписанных уравнений являются 2p-периодическими функциями j.
3. Закрутка спутника в плоскости орбиты. Интегральная
поверхность ориентированного движения. Предположим, что спутник близок к
осесимметричному с осью материальной симметрии Ox1 и что
влияние на него аэродинамического момента мало. Иными словами, |m| << 1, eE
<< 1, E=maxLiLj|dk| (i,j,k=1,2,3).
Для упрощения формул оставим только один малый параметр m, приняв e = me1, e1E ~ 1. Вместо
переменных W2,W3
введем переменные
|
Величины w2,w3 представляют собой проекции абсолютной угловой скорости спутника на оси Резаля, получающиеся из осей Ox2 и Ox3 при j = 0.
В новых переменных уравнения движения спутника принимают вид
|
|
| (1) |
|
|
Здесь
|
|
|
причем переменные W2, W3 должны быть выражены через w2, w3. Правые части уравнений (1) периодически зависят от j с периодом 2p и аналитически зависят от m в окрестности точки m = 0.
При m = 0 (ось Ox1 является осью материальной
симметрии спутника, и аэродинамический момент отсутствует) уравнения (1)
принимают вид
| (2) |
|
| (3) |
|
В силу второго уравнения (2) W1=const, и не зависящие от j уравнения (3) образуют замкнутую систему, в которую W1 входит как параметр. Система (3) описывает движение оси оси Ox1 относительно орбитальной системы координат, уравнения (2) описывают движение спутника вокруг этой оси.
Система (3) допускает стационарные решения
|
(4) |
которые принимаются в качестве невозмущенных движений осесимметричного спутника в режиме закрутки в плоскости орбиты. Для практического использования стационарных решений (4) необходимо, чтобы они были устойчивы. Поскольку уравнения (3) инвариантны относительно замены переменных y → -y, W1 → -W1, w3 → - w3, ограничимся описанием свойств устойчивости решения (4), в котором y = p/2.
Уравнения (3) допускают обобщенный интеграл энергии,
используя который в качестве функции Ляпунова, можно найти достаточные условия
устойчивости решения (4) при y = p/2
[2,3]:
|
(5) |
Необходимые условия устойчивости этого решения получаются из
анализа соответствующей линеаризованной системы
| (6) |
|
Здесь Dy = y-p/2.
Характеристическое уравнение системы (6) имеет вид
|
(7) |
|
Оно биквадратное, поэтому решения системы (6) ограниченны
только в том случае, когда все корни уравнения (7) - чисто мнимые и простые, т.
е. при d1 > 0, d2 > 0, d12-4d2
> 0. Последние неравенства выражают необходимые условия устойчивости решения
(4), в котором y
= p/2. Эти
условия удовлетворяются при выполнении неравенств (5) или неравенств [2]
|
(8) |
Описываемые ниже числовые расчеты проводились при l = 0.7, что примерно соответствует орбитальной станции Мир в последние годы ее полета. Для такого l неравенства (5) выполнены при W1 > 2.7143, неравенства (8) выполнены на интервалах W1 < -1.8770 и 1.42462 < W1 < 1.42857. Последний интервал практического значения не имеет, а движения с W1 > 2.7143 и W1 < -1.8770 были реализованы [4,5].
Решению (4) в случае y = p/2 отвечает двухпараметрическое семейство
решений полной системы уравнений (2), (3)
|
(9) |
|
с параметрами j0 и W1. Если W1 удовлетворяет неравенствам (5) (неравенствам (8)), то решения (9) устойчивы (устойчивы в первом приближении) по переменным W1, q, y, w2 и w3.
Семейство (9) при m
≠
0 порождает двумерную интегральную
поверхность системы (1), которая может быть построена методом Н.Н.Боголюбова -
Ю.А.Митропольского [6] в виде формальных рядов по целым неотрицательным
степеням m:
|
| (10) |
|
Коэффициенты этих рядов суть 2p-периодические функции x. Изменение
переменных x
и h, т.е.
движение по поверхности, определяется уравнениями
| (11) |
Построение рядов (10), (11) выполняется так. Подставим эти
ряды в уравнения (1), разложим левые и правые части получившихся равенств в
ряды, аналогичные рядам (10), и приравняем коэффициенты при одинаковых степенях
m слева и
справа. Получим цепочку линейных неоднородных дифференциальных уравнений
относительно коэффициентов искомых рядов. Можно доказать, что при выполнении
условия
|
(12) |
такая цепочка имеет единственное 2p-периодическое по x решение,
удовлетворяющее соотношениям
| (13) |
Далее полагаем, что именно это решение использовано в качестве коэффициентов рядов (10), (11).
Условие (12) здесь является главным. Оно означает, что вращение спутника вокруг оси Ox1 не должно находиться в резонансе с колебаниями этой оси по углам q и y, описываемыми уравнениями (6). Условие (12) выполнено, в частности, при l = 0.7, h < -1.8770 или h > 2.7143. Условия (13) нужны только для единственности решения цепочки, и хотя они использованы ниже, их, в принципе, можно опустить (с потерей единственности) или заменить какими-либо другими условиями.
Будем считать, что решения (10), (11) описывают невозмущенные движения спутника в режиме закрутки вокруг нормали к плоскости орбиты. По этой причине интегральную поверхность (10) назовем интегральной поверхностью ориентированного движения. Наибольший интерес в соотношениях (10), (11) представляет второе уравнение (11), описывающее вековое изменение угловой скорости вращения спутника вокруг оси Ox1. Чтобы получить представление о таком изменении, достаточно найти первый отличный от тождественного нуля коэффициент Bk(h).
4. Численное исследование интегральной поверхности
ориентированного движения. Для сокращения записи воспользуемся векторными
обозначениями. Введем вектор1 z=[q, y, w2,
w3] и запишем систему (1) в виде
| (1ў) |
|
Векторная запись системы (3): [(z)\dot]=F0(W1,z). Ее стационарное решение (4), в котором y = p/2, обозначим z0. В последующих выкладках учитываем равенство g(z0)=-1.
Соотношения (10), (11) представим в виде
| (10ў) |
| (11ў) |
Тот факт, что система (1 ′ ) допускает решения вида (10 ′), (11 ′) выражается тождествами
|
|
|
Здесь x и h
- равноправные независимые переменные, и выписанные соотношения представляют
собой уравнения в частных производных относительно u, v и f.
В предыдущем разделе был описан способ построения формального решения этих
уравнений в виде рядов по степеням m. Построенное решение 2p-периодически зависит от x и удовлетворяет
соотношениям (ср. (13))
| (13ў) |
Теперь пойдем другим путем. Отбросим в выписанных уравнениях члены m2B ∂ (...)/ ∂ h. В результате получим дифференциальные уравнения с одной независимой переменной x, т.е. обыкновенные, в которых h является параметром. По-прежнему будем искать решения этих уравнений, зависящие от x и h, причем от x - периодически с периодом 2p, и удовлетворяющее соотношениям (13 ′). Полученные усеченные уравнения и условия, определяющие их искомое решение, запишем используя исходные переменные системы (1) и обозначения a=mA, b=mB. В результате придем к краевой задаче
|
|
(14) |
|
|
Здесь x - независимая переменная, h - параметр, j, W1 и z - неизвестные функции, a и b - неизвестные постоянные.
Задачу (14) будем решать методом Пуанкаре. При m = 0 эта задача имеет решение j = x, W1=h, z=z0, a=b=0. Линеаризация соотношений (14) в окрестности указанного решения приводит к линейной краевой задаче
|
|
|
|
|
|
относительно функций Dj = j-x, DW1=W1-h, q, Dy, w2, w3 и постоянных a, b. Можно доказать, что при выполнении условия (12) выписанная задача имеет только тривиальное решение. Следовательно, в окрестности точки m = 0 краевая задача (14) имеет единственное решение j = j*(x,h,m), W1=W1*(x,h,m), z=z*(x,h,m), a=a*(h,m), b=b*(h,m), аналитически зависящее от m и удовлетворяющее соотношениям j*(x,h,0)=x, W1*(x,h,0)=h, z*(x,h,0)=z0, a*(h,0)=b*(h,0)=0.
Функции j*(x,h,m), W1*(x,h,m) и z*(x,h,m), продолженные с отрезка 0 ≤ x ≤ 2p на всю действительную ось 2p-периодически по x, удовлетворяют вместе с постоянными a*(h,m) и b*(h,m) дифференциальным уравнениям в (14). Эти функции представляются рядами вида (10), коэффициенты которых удовлетворяют соотношениям (13), а постоянные a*(h,m) и b*(h,m) представляются рядами, аналогичными рядам, стоящим в правых частях уравнений (11). Если Bm(h) - первый отличный от тождественного нуля коэффициент второго ряда (11), то коэффициенты при первых m степенях m в рядах (10), (11) и в рядах, представляющих рассматриваемое решение задачи (14), совпадают. Более того, b*(h,m)=mm Bm(h)+mm+1Bm+1(h)+O(mm+2). Это соотношение позволяет использовать краевую задачу (14) для приближенного численного расчета правой части второго уравнения (11).
Численное интегрирование второго уравнения (11) можно выполнить двухцикловым методом [7]. Метод называется так потому, что включает два цикла интегрирования - внешний и внутренний. Внешний цикл состоит в интегрировании уравнения (11) каким-либо численным методом, внутренний заключается в расчете правой части этого уравнения посредством решения краевой задачи (14). В [8] описанный вариант двухциклового метода был применен в очень похожей на рассматриваемую задаче исследования режима одноосной гравитационной ориентации спутника.
Прежде чем перейти к более подробному описанию метода
интегрирования упростим задачу (14). Заменим в ней краевое условие и
интегральное соотношение для переменной j краевыми условиями j(0)=0, j(2p)=2p. Получившуюся
краевую задачу назовем задачей (14 ′). Используя описанную выше схему метода Пуанкаре, можно
доказать, что при выполнении условия (12) задача (14′) имеет в окрестности точки m = 0
единственное решение [^(j)](x,h,m), [^(W)]1(x,h,m), [^(z)](x,h,m), [^(a)](h,m), [^(b)](h,m), аналитически
зависящее от m
и удовлетворяющее соотношениям [^(j)](x,h,0)=x, [^(W)]1(x,h,0)=h, [^(z)](x,h,0)=z0,
[^(a)](h,0)=[^(b)](h,0)=0. Решения
задач (14) и (14â)
связаны между собой соотношениями
|
|
где x0(h,m)
- корень уравнения j*(x,h,m)=0,
удовлетворяющий условию2 x0(h,0)=0 или, что
то же самое,
|
В задаче (14′) перейдем к новой независимой переменной - времени t. Новую задачу будем решать на отрезке 0 ≤ t ≤ T, T=2p(h-1+a)-1 при h > 1 и на отрезке T ≤ t ≤ 0 при h < 1. Эта задача имеет вид
|
| (15) |
|
|
Здесь j, W1
и z - неизвестные функции, T и b - неизвестные постоянные.
В окрестности точки m
= 0 задача (15) имеет единственное решение
|
(16) |
|
аналитически зависящее от m и удовлетворяющее соотношениям j*(t,h,0)=(h-1)t, W1*(t,h,0)=h, z*(t,h,0)=z0, T*(h,0)=2p(h-1)-1, b*(h,0)=0.
Посредством численного решения задачи (15) решение (16) было построено в явном виде и исследовано в функции параметра h. Значения h менялись на равномерной сетке с шагом 0.01. В каждом узле сетки задача (15) решалась методом пристрелки. Неизвестными параметрами были W1(0), z(0), T и b. Краевые условия в точке t=T и интегральное условие служили уравнениями для их определения. Система таких уравнений решалась методом Ньютона. Вычисление частных производных функций, задающих эти уравнения, по определяемым параметрам (кроме T) сводилось к интегрированию уравнений в вариациях для дифференциальных уравнений в (15). В процессе вычислений узлы сетки проходились последовательно, начиная с узла с максимальным значением |h|. Начальное приближение в этом узле бралось в виде W1(0)=h, z(0)=z0, T=2p(h-1)-1, b=0. Во всех остальных узлах начальным приближением служило решение, найденное в предыдущем узле.
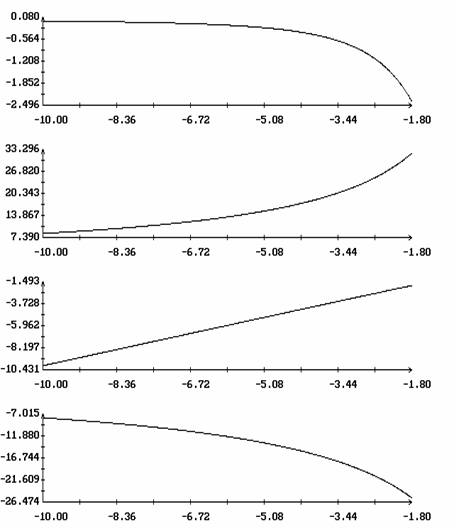
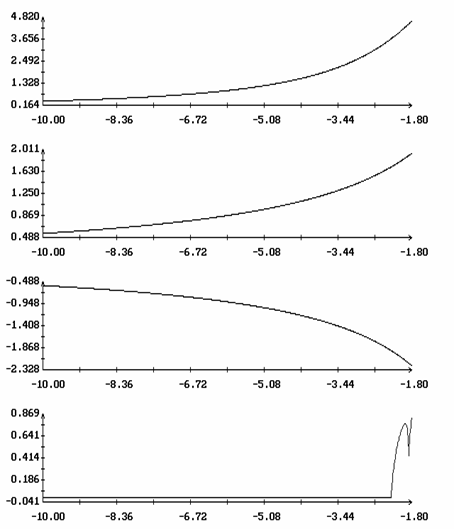
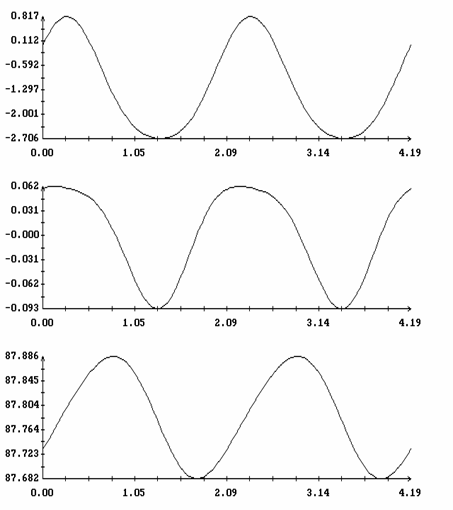
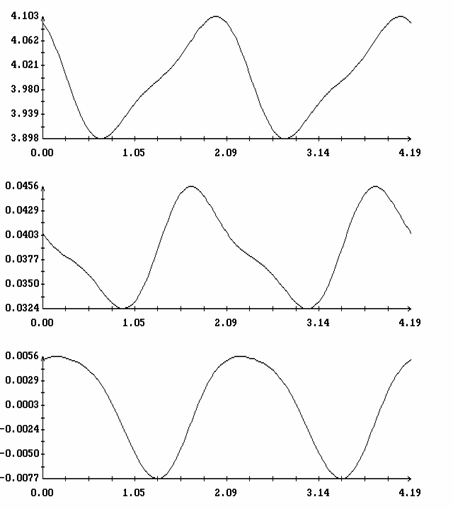
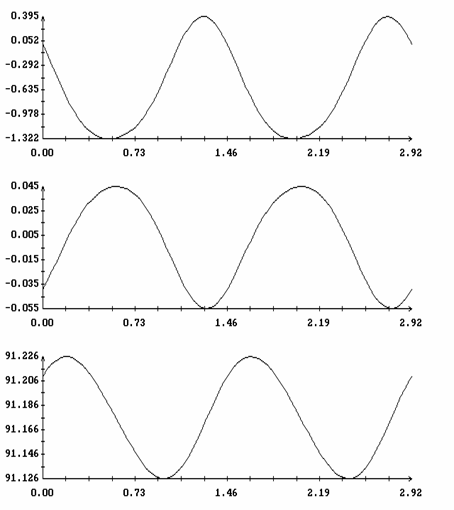
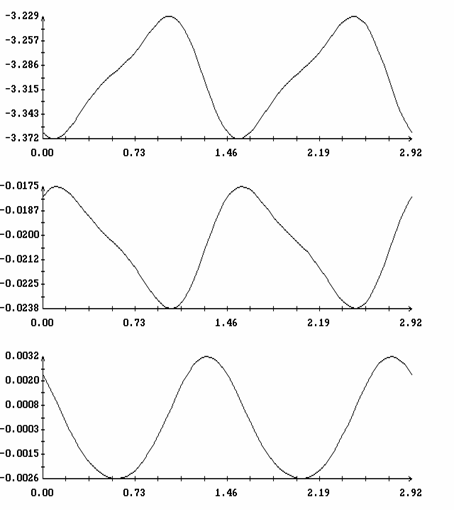
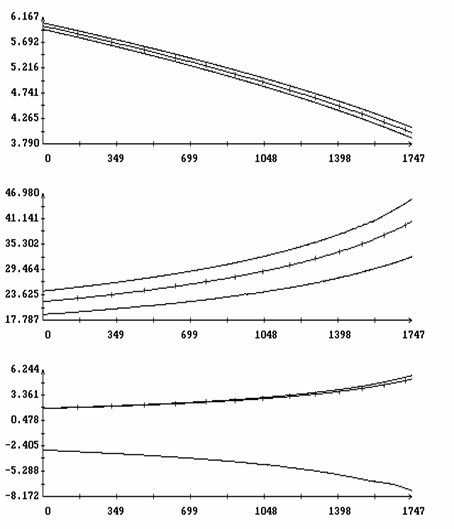
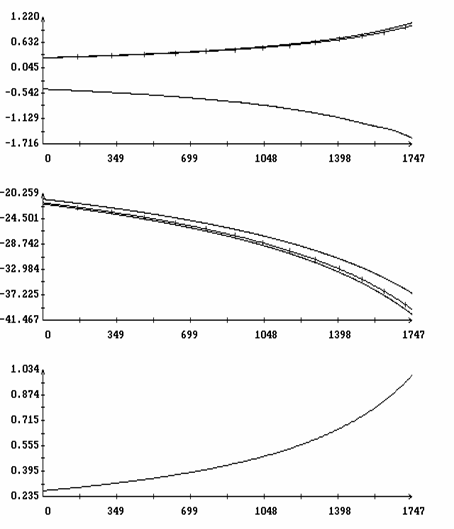
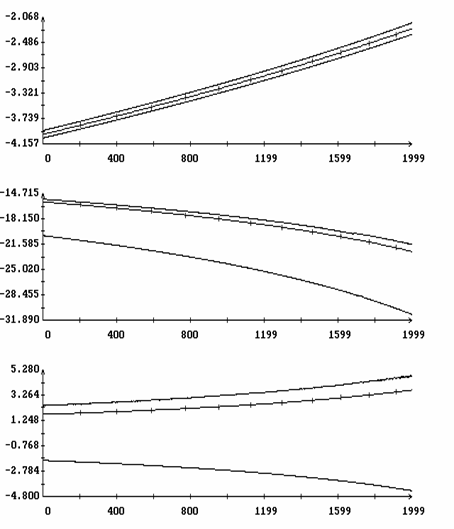
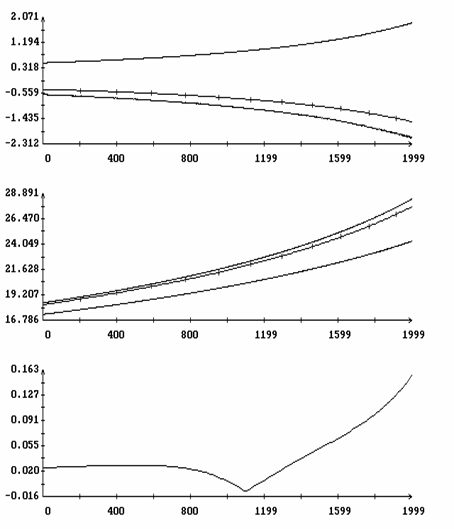
Расчеты проводились при l = 0.7, m = 0.1, gc=0.01, ac=-0.15, bc=0.025, L1=16 м, L2=14 м, L3=12 м, d1=-0.5 м, d2=d3=1 м, e = 3·10-4 м-3. В этом случае рассматриваемый спутник может служить грубой моделью станции Мир на орбите с высотой около 330 км. Отвечающее такой высоте значение e получено с использованием статической модели атмосферы [9]. Найденные решения задачи (15) представлены на рис. 1, 2 графиками зависимости от h величин W1(0), z(0), T и b. Кроме того, здесь представлен график функции d=d(h), характеризующей свойства устойчивости интегральной поверхности ориентированного движения (см. ниже). Найденные решения распадаются на две ветви. Одна ветвь отвечает значениям h > 1, другая - значениям h < 1. Эти ветви не были продолжены в область малых значений |h-1|, поскольку в этой области найденные решения оказались неустойчивы. Примеры решений краевой задачи (15) приведены на рис. 3, 4. Здесь эти решения представлены графиками функций Dj(t)=j(t)-2pT-1t, q(t), y(t), W1(t), w2(t) и w3(t), построенными на отрезках 0 ≤ t ≤ 2|T|. Как видно из графиков, отклонения оси Ox1 от оси OX2 в этих решениях весьма малы, т.е. интегральная поверхность, описываемая найденными решениями, обоснованно названа интегральной поверхностью ориентированного движения.
Исследуем вопрос об устойчивости какого-либо решения j ° (t), W1 ° (t), z°(t), T°, b° краевой задачи (15). Под устойчивостью будем понимать устойчивость неподвижной точки [W1 °(0),z °(0)] преобразования пространства R5[W1,z], задаваемого решениями дифференциальных уравнений в (15) при b=b °. А именно, решение j(t), W1(t), z(t) с начальными условиями j(0)=0, W1(0)=W ′ 1, z(0)=z ′ задает преобразование точки [W ′ 1,z ′ ] в точку [W"1,z" ], если в некоторый момент времени T выполнены соотношения W"1=W1(T), z"=z(T), j(T)=2p. В окрестности указанной выше неподвижной точки такое преобразование, называемое преобразованием Пуанкаре, определено.
Устойчивость исследовалась следующим образом. Пусть dj(t), dW1(t)
dz(t)
- решение системы уравнений в вариациях для решения j°(t), W1
°
(t),
z°(t),
T°,
b°
краевой задачи (15). Построим вектор
|
Обозначим через xi (i=1,2,...,5) такие векторы x, вычисленные при dj(0)=0 и [dW1(0),dz(0)]=[1,0,...,0], [0,1,0,...,0], ... [0,...,0,1]. Составим 5×5 - матрицу X=(x1,x2,...,x5). В случае T ° > 0 необходимое условие устойчивости неподвижной точки [W1 ° (0),z ° (0)] состоит в том, что модули всех собственных чисел матрицы X должны быть ≤ 1. В случае T ° < 0 для устойчивости этой неподвижной точки необходимо, чтобы модули всех собственных чисел матрицы X были ≥ 1. Представленная на рис. 1, 2 величина d определяется следующим образом. Пусть r1 и r2 - минимум и максимум модулей собственных чисел матрицы X. Тогда d=r1-1 при T ° > 0, d=r2-1-1 при T ° < 0. В терминах величины d необходимое условие устойчивости выражается неравенством d ≤ 0.
Как показало вычисление функции d(h), все найденные решения задачи (15) неустойчивы. Однако при h > 3.93 (рис. 1) и h < -2.26 (рис. 2) эта неустойчивость весьма слаба - выполнено неравенство d < 10-3. На графиках функции d(h) участки слабой неустойчивости выглядят как горизонтальные прямые. Такая слабая неустойчивость встречается во многих задачах вращательного движения спутников, в которых учитывается аэродинамический момент, и обусловлена непотенциальностью этого момента [10]. При h < 3.93 и h > -2.26 неустойчивость решений задачи (15) ярко выражена (см. рис. 1, 2). В обоих семействах решений функция d(h) реализуется действительными собственными числами матрицы X. К тому же, эта неустойчивость возникает при значениях h, лежащих достаточно далеко от границ интервалов устойчивости решения (4) в случае l = 0.7 (см. раздел 3), поэтому ее трудно связать с этими границами.
Вернемся к двухцикловому методу численного интегрирования
уравнения [(h)\dot]=b*(h,m). Заменим его
эквивалентным уравнением
|
(17) |
которое будем интегрировать методом трапеций на сетке по параметру h в процессе продолжения по этому параметру решений краевой задачи (15). Результаты такого интегрирования будем сравнивать с результатами непосредственного интегрирования уравнений (1). Начальные условия сравниваемых решений: для уравнения (17) h(0)=h0, для системы (1) j(0)=0, W1(0)=W1*(0,h0,m), z(0)=z*(0,h0,m).
Сравнение проведем так. Для решения системы (1) определим последовательности чисел
|
|
|
|
|
|
Эти последовательности будем представлять графически ломаными. Например, последовательности {W1N′} и {W1N ′′ } будем изображать ломаными, проходящими соответственно через точки (N,W1N ′) и (N,W1N ′′ ) (N=1,2,...) в плоскости (N,W1). Две такие ломаные в единых координатных осях дают представление о пределах изменения переменной W1 на длительном интервале времени. В тех же координатных осях представим график решения h(t) уравнения (17), причем связь между N и t зададим формулой t=2pN, а ось h отождествим с осью W1. Аналогичным образом последовательности {Dy′N} и {Dy"N} будем представлять в единых координатных осях со второй компонентой векторной функции z*[t,h(t),m]-z0 и т.д. Такие тройки графиков дают наглядное представление о близости решений системы (1) к интегральной поверхности ориентированного движения.
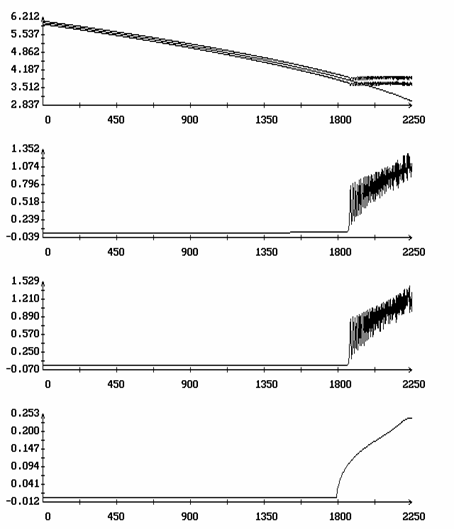
Сравнение решений системы (1) и уравнения (17) представлено на рис. 5, 6. Помимо указанных выше графиков на этих рисунках приведены еще графики функции d[h(t)], которые характеризуют свойства устойчивости решений, лежащих на интегральной поверхности ориентированного движения. Графики функций h(t) и z*[t,h(t),m]-z0 отмечены маркерами. Как видно из рисунков, двухцикловой метод правильно описывает эволюцию решений системы (1), лежащих в окрестности интегральной поверхности ориентированного движения. Точность описания сохраняется до тех пор, пока неустойчивость решений краевой задачи (15) при h = h(t) остается слабой, т.е. до тех пор, пока значения функции d[h(t)] малы.
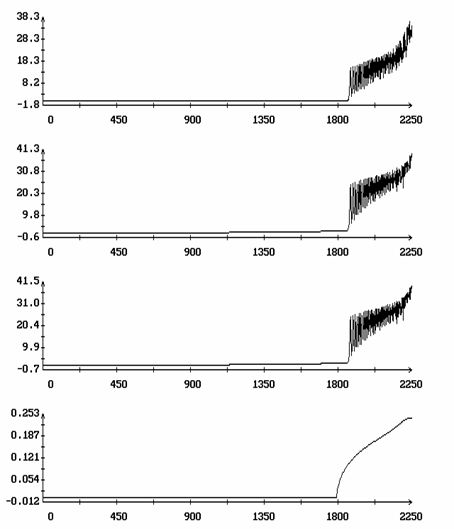
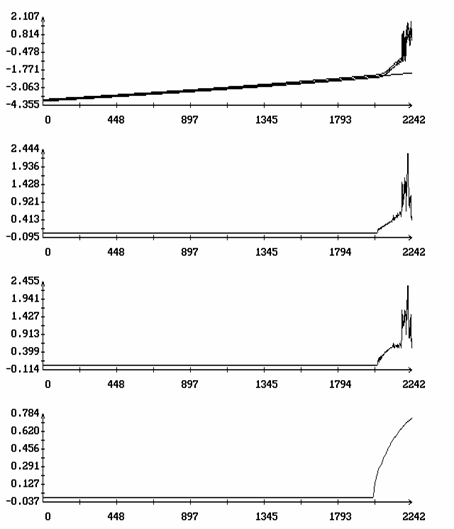
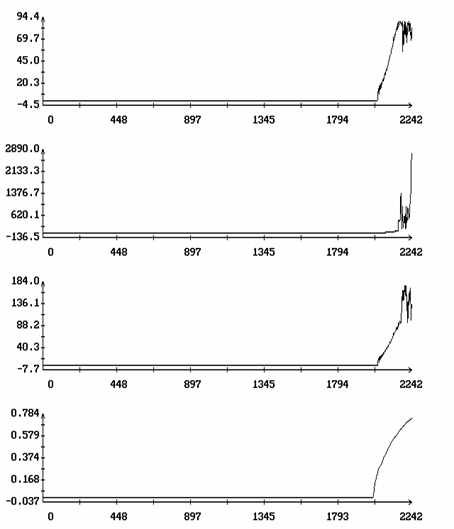
Нарушение точности после возникновения сильной
неустойчивости показано на рис. 7, 8. На этих рисунках представлены те же
решения, что и на рис. 5, 6, но на более продолжительном интервале времени.
Способ представления несколько изменен. Во-первых, в плоскостях (N,w2),
(N,w2), (N,q) и (N,Dy) приведены только ломаные,
отвечающие последовательностям
|
|
вычисленным вдоль решения системы (1). Во-вторых, добавлена
новая ломаная, характеризующая последовательность
|
Здесь L - угол между осями Ox1 и OX2. Этот угол также вычисляется для решения системы (1). В третьих, для удобства анализа график функции d[h(t)] приведен дважды. Как видно из рисунков, резкое возрастание функции d[h(t)] сопровождается резким возрастанием последовательностей {[^(w)]2N}, {[^(w)]3N}, {[^(q)]N}, {D[^(y)]N} и {[^(L)]N}, т. е. развитием сильной неустойчивости. При этом резко ухудшается точность описания эволюции последовательностей {W′1N}, {W"1N} решением уравнения (17). На рис. 7, 8 маркеры отсутствуют, но сравнение этих рисунков с рис. 5, 6 позволяет легко установить происхождение кривых в плоскости (N,W1).
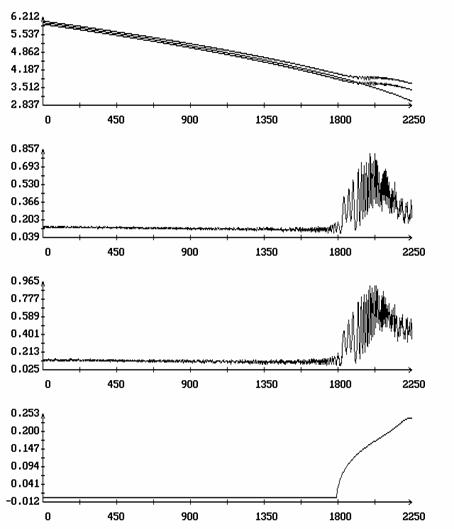
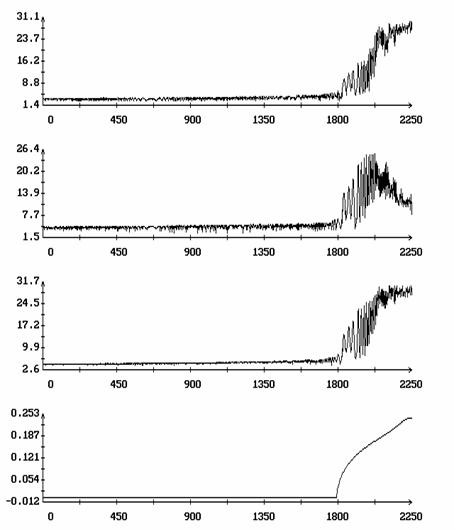
На рис. 7 резкое возрастание последовательностей {[^(w)]2N}, {[^(w)]3N} и т.п. заметно запаздывает по сравнению с резким подъемом функции d[h(t)]. Это известное явление задержки развития неустойчивости, объясняемое весьма слабыми возмущениями ориентированного движения спутника. После возникновения неустойчивости эти возмущения нарастают экспоненциально, но должно пройти некоторое время прежде, чем они станут заметны в привычном масштабе изучения данной задачи. Для сравнения на рис. 9 приведены такие же графики, полученные для решения системы (1) с возмущенными начальными условиями - к значению w2(0), задаваемому третьей компонентой вектора z*(0,h0,m), было добавлено возмущение 0.1. Теперь запаздывание практически исчезло, а точность описания эволюции последовательностей {W′1N}, {W"1N} функцией h(t) практически не изменилась.
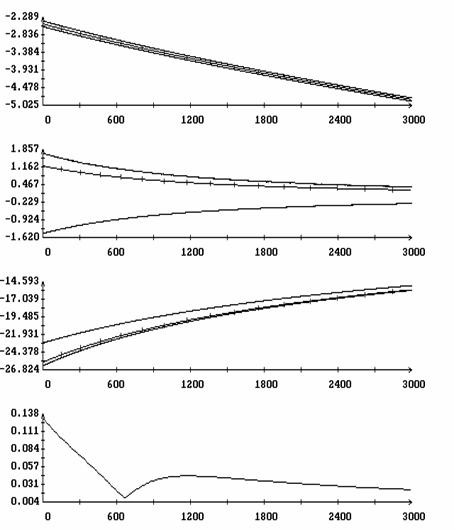
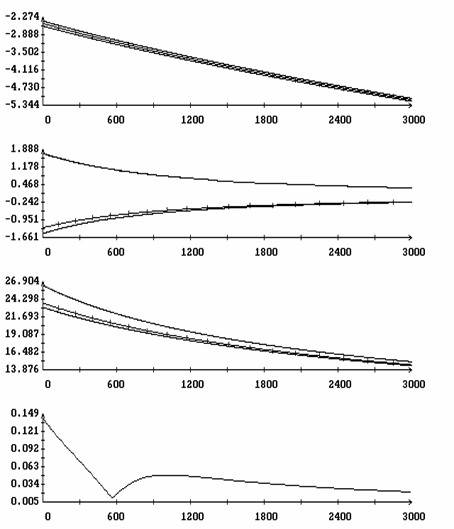
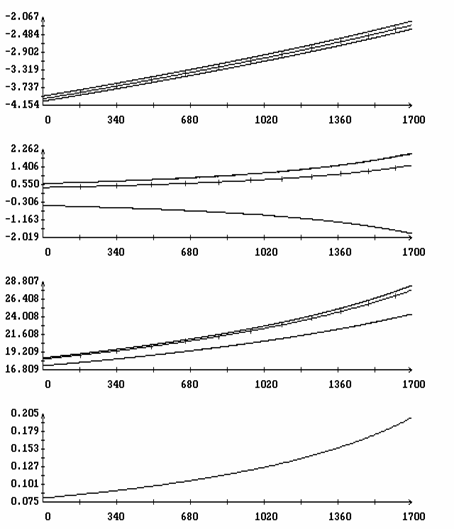
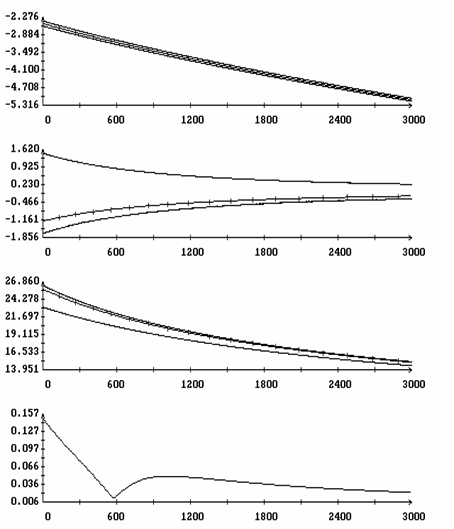
Исследуем влияние параметров спутника на эволюцию решений, лежащих на интегральной поверхности ориентированного движения. Для этого повторим описанные выше расчеты решений системы (1) и уравнения (17), изменив знак одного из параметров d1, d2, d3, gc, ac и bc. Результаты четырех таких расчетов, отвечающих сменам знака d1, d2, d3 и ac, приведены на рис. 10, 11. Каждого расчет представлен графиками функций h(t), d[h(t)] и первых двух компонент векторной функции z*[t,h(t),m]-z0, а также ломаными для последовательностей {W′1N}, {W"1N}, {q′N}, {q"N}, {Dy′N} и {Dy"N}. Это сокращенный вариант графиков, приведенных на рис. 5, 6. Как видно из рисунков, изменение знака одного из параметров d1, d2, ac меняет направление эволюции - торможение вращения спутника сменяется его раскруткой (рис. 10 и 11б). Изменение знака одного из параметров d3, gc и bc к изменению направления эволюции не приводит. В случае параметра d3 этот факт иллюстрируется рис. 11а.
5. Еще один способ отыскания решений, лежащих на интегральной поверхности ориентированного движения. Во время выполнения работы [7] уровень развития вычислительной техники был таким, что только применение двухциклового метода (или какой-либо его альтернативы) позволяло исследовать эволюцию движения спутников на длительных интервалах времени. В настоящее время ситуация существенно иная, и краевая задача (15) вместе с уравнением (17) интересны главным образом тем, что позволяют лучше понять устройство решений системы (1), лежащих на интегральной поверхности ориентированного движения. Кроме того, начальные условия решений краевой задачи (15) дают весьма точное приближение начальных условий ориентированного движения спутника.
Недостаток использованного варианта двухциклового метода
состоит в том, что он пригоден только для систем с одной быстрой переменной. В
частности, им нельзя исследовать интегральную поверхность ориентированного
движения уравнений (1), если в последних учесть эллиптичность орбиты спутника и
периодическое изменение плотности атмосферы вдоль орбиты. Существует однако
простой метод, который позволяет справиться с трудностью такого рода. Согласно
этому методу поиск начальных условий ориентированного движения сводится к
минимизации интеграла
| (18) |
по начальным условиям z(0)=p=[q0,y0,...] при j(0)=0 и заданном значении W1(0). Здесь t - достаточно большое положительное число. Решения системы (1), доставляющие при таких условиях минимум интегралу (18), будем называть минималями.
Минимизация функции J=J(p) сводилась к
решению уравнения ∂J(p)/
∂p=0
методом Гаусса-Ньютона. Рсчет производных
∂J(p)/
∂p и
∂2
J(p)/∂p2
выполнялся по формулам вида
|
Производные ∂z/ ∂q0 и т.п.вычислялись посредством интегрирования уравнений в вариациях для системы (1).
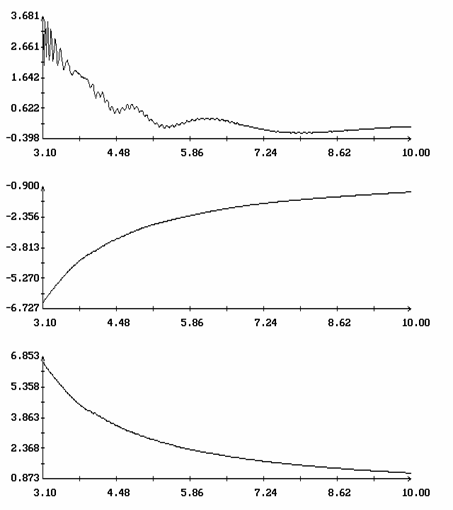
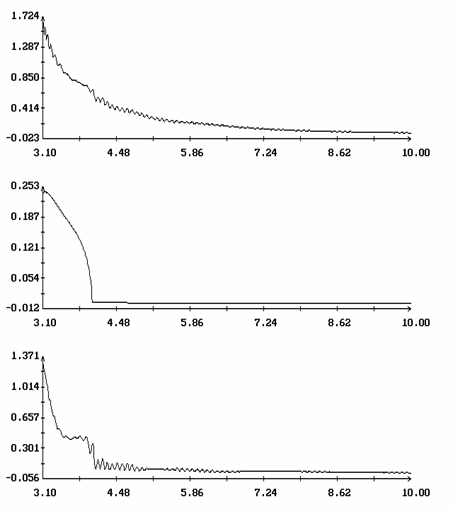
Начальные условия минималей в случае t = 30p приведены на рис. 12. Здесь приведены также графики зависимости от W1(0) величин d и e, которые характеризуют преобразование Пуанкаре пространства R5[W1,z], задаваемое решениями системы (1) из окрестности найденных минималей. А именно, решение j(t), W1(t), z(t) с начальными условиями j(0)=0, W1(0)=W′1, z(0)=z′ задает преобразование точки [W′1,z ′ ] в точку [W"1,z" ], если в некоторый момент времени T выполнены соотношения W"1=W1(T), z"=z(T), j(T)=2p. Пусть точка [W1 ° ,z ° ] задает начальные условия минимали и переходит при таком преобразовании в точку [W1*,z*]. Тогда e= √ {(W1*-W1 ° )2+||z*-z ° ||2}. Величина e характеризует смещение точки [W1 ° ,z ° ] под действием введенного преобразования. При e=0 эта точка была бы неподвижной. Величина d, характеризует устойчивость преобразования Пуанкаре в окрестности точки [W1 ° ,z ° ]. Она определяется по линеаризации этого преобразования тем же способом, каким одноименная величина была определена для решений краевой задачи (15). В целом графики на рис. 12 похожи на графики, приведенные на рис. 1. Функция d[W1(0)]) ведет себя очень похоже на функцию d(h).
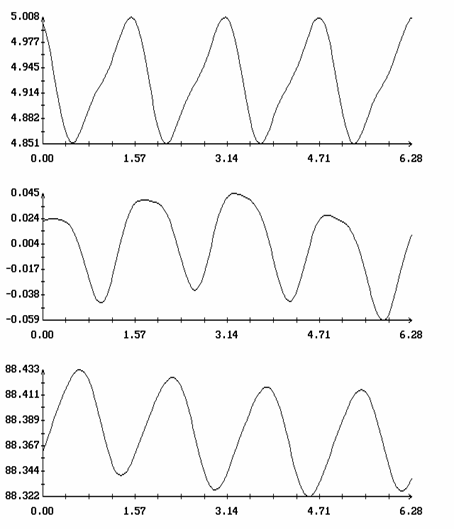
Пример минимали приведен на рис. 13. На рис. 13а изображены графики функций W1(t), q(t) и y(t) (0 ≤ t ≤ 2p), из которых видно, что на минимали отклонения оси Ox1 от оси OX2 весьма малы, т.е. минималь лежит в окрестности интегральной поверхности ориентированного движения. На рис. 13б для той же минимали показаны ломаные, описывающие последовательности {W′1N}, {W"1N}, {[^(q)]N} и {D[^(y)]N}. Как видно из рисунка, при достижении величинами W′1N и W"1N окрестности точки резкого возрастания функции d[W1(0)] (примерно при W1=3.92) происходит быстрое разрушение ориентированного движения (ср. рис. 7).
Данная работа выполнена при поддержке РФФИ (проект 02-01-00323).
[1]
Бозюков А.Ю., Сазонов В.В. Об одном способе гравитационной ориентации вращающегося спутника. Препринт Института прикладной математики РАН, 2004, N 24.
[2]
Белецкий В.В. Движение искусственного спутника относительно центра масс. М., Наука, 1965.
[3]
Черноусько Ф.Л. Об устойчивости регулярной прецессии спутника. Прикладная математика и механика, 1964, т. 28, вып. 1, с. 155-157.
[4]
Бабкин Е.В., Беляев М.Ю., Ефимов Н.И., Сазонов В.В., Стажков В.М. Неуправляемое вращательное движение орбитальной станции Мир. Космические исследования, 2001, т. 39, N 1, с. 27-42.
[5]
Бабкин Е.В., Беляев М.Ю., Ефимов Н.И., Сазонов В.В., Стажков В.М. Неуправляемое вращательное движение орбитальной станции Мир в последние месяцы ее полета. Космические исследования, 2003, т. 41, N 3, с. 285-294.
[6]
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М., Физматгиз, 1963.
[7]
Охоцимский Д.Е., Энеев Т.М., Таратынова Г.П. Определение времени существования искусственного спутника Земли и исследование вековых возмущений его орбиты. Успехи физических наук, 1957, т. 63, N 1а, с. 33-50.
[8]
Сазонов В.В., Петров А.Л. Эволюция режима гравитационной ориентации вращающегося спутника под действием непотенциального аэродинамического момента. Космические исследования, 1987, т. 25, N 4, с. 508-522.
[9]
Навигационное обеспечение полета орбитального комплекса Салют-6 - Союз - Прогресс. М., Наука, 1985.
[10]
Сарычев В.А. Вопросы ориентации искусственных спутников. Итоги науки и техники. Исследование космического пространства, т. 11. М., ВИНИТИ, 1978.
1 Запись [x1,...,xn] означает вектор-столбец с соответствующими компонентами.
2 Поскольку j*(0,h,0)=0 и dj*(0,h,0)/dx = 1, по теореме о неявной функции в окрестности точки m = 0 такой корень существует и единствен.
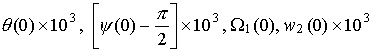
![]()

![]()
![]()
Рис. 1. Интегральная
поверхность ориентированного движения.
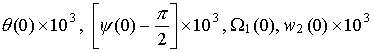
![]()
![]()
![]()
Рис. 2. Интегральная
поверхность ориентированного движения.
![]() (град.)
(град.) ![]()
![]()
![]()
Рис. 3. Решение на интегральной
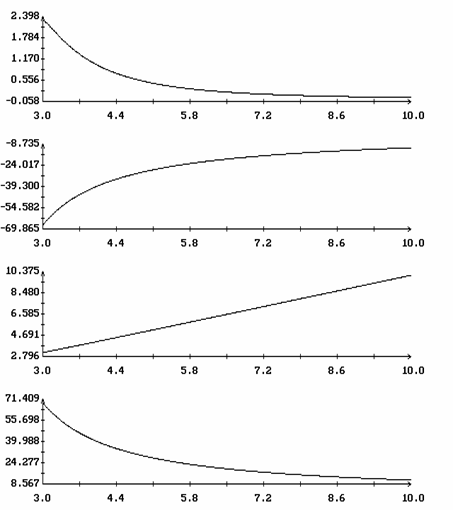
поверхности ориентированного движения; ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() (град.)
(град.) ![]()
![]()
![]()
Рис. 4. Решение на интегральной
поверхности ориентированного движения; ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]()
![]() ,
,
![]() (витки)
(витки) ![]() (витки)
(витки)
Рис. 5. Движение вдоль интегральной
поверхности ориентированного движения, ![]() .
.
![]()
![]() ,
,
![]() (витки)
(витки) ![]() (витки)
(витки)
Рис. 6. Движение вдоль интегральной
поверхности ориентированного движения, ![]() .
.
![]()
![]() (град.),
(град.), ![]()
![]() (витки)
(витки)
![]() (витки)
(витки)
Рис. 7. Движение вдоль
интегральной поверхности с последующей потерей устойчивости, ![]() .
.
![]()
![]() (град.),
(град.), ![]()
![]() (витки)
(витки)
![]() (витки)
(витки)
Рис. 8. Движение вдоль
интегральной поверхности с последующей потерей устойчивости, ![]() .
.
![]()
![]() (град.),
(град.), ![]()
![]() (витки)
(витки)
![]() (витки)
(витки)
Рис. 9. Движение вдоль
интегральной поверхности с последующей потерей устойчивости, ![]() .
.
В начальное условие ![]() системы (1) внесена
ошибка:
системы (1) внесена
ошибка: ![]() .
.
![]()
![]()
![]() (витки)
(витки) ![]() (витки)
(витки)
(а)
(б)
Рис. 10. Движение вдоль интегральной
поверхности, ![]() ; (а)
; (а) ![]() , (б)
, (б) ![]()
![]()
![]()
![]() (витки)
(витки) ![]() (витки)
(витки)
(а)
(б)
Рис. 11. Движение вдоль интегральной
поверхности; (а) ![]() ,
, ![]() , (б)
, (б) ![]() ,
, ![]() .
.
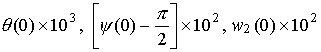
![]()
![]()
![]()
Рис. 12. Результаты минимизации
интеграла (18).
![]()
![]()
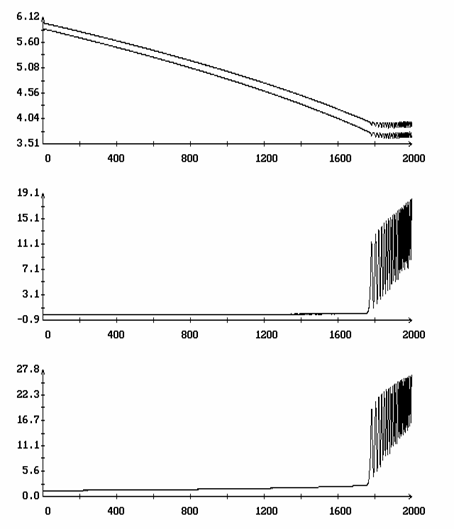
![]()
![]() (витки)
(витки)
(а)
(б)
Рис. 13. Решение,
минимизирующее интеграл (18) при ![]() .
.
File translated from TEX
by TTH, version
3.40.
On 14 Feb 2005, 13:42.