Численное моделирование МГД - течений, возникающих при движении проводящей плоскости в идеальнопроводящей плазме
( The simulation of the MHD-flows which generated by moving of the conductive plane in the perfect conductive plasma
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Еленина Т.Г., Устюгова Г.В.
(T.G.Yelenina, G.V.Ustyugova)

ИПМ им. М.В.Келдыша РАН

Москва, 2004
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проекты №№ 03-01-00461, 03-02-16548)

Аннотация

Работа посвящена исследованию и численному моделированию течений, возникающих при движении проводящей плоскости перпендикулярно силовым линиям магнитного поля в идеальнопроводящей плазме. Построено аналитическое решение этой задачи и проведено его сравнение с результатами численного интегрирования. Возникающее течение является комбинацией ударной волны и простой автомодельной волны разрежения, за которой следует область постоянного течения или вакуума. Ударная волна может быть либо гидродинамической, либо магнитогидродинамической волной включения, в зависимости от соотношения величин альфвеновской скорости и скорости звука в плазме. Исследована зависимость решения от величины поверхностной магнитной вязкости.

Abstract

The aim of the paper is the investigation and simulation the flows that generated in the perfect conductive plasma when conductive plane were moving across the magnetic field lines. The analytical solution was found and it was compared with the numerical simulations results.

1  Введение

Настоящая работа посвящена исследованию и численному моделированию магнитогидродинамического течения, возникающего при движении проводящей плоскости в идеальнопроводящей плазме. В частном случае идеальнопроводящей плоскости задача аналогична задаче о движении идеальнопроводящего поршня [Kul]. Плоскость обладает поверхностной электрической проводимостью l = const и соответствующей поверхностной магнитной вязкостью z = c2 / 2pl. Поверхностная магнитная вязкость имеет размерность скорости, поэтому в задаче нет масштабов длины и времени, её решение является автомодельным и зависит от переменной x / t. Возникающее течение является комбинацией ударной волны и простой автомодельной волны разрежения, за которой следует область постоянного течения или вакуума. Ударная волна может быть либо гидродинамической, либо магнитогидродинамической волной включения, в зависимости от соотношения величин альфвеновской скорости и скорости звука в плазме.

Авторы благодарны М.П. Галанину, А.В. Колдобе и С.Д. Устюгову за многочисленные полезные обсуждения и консультации.

2  Постановка задачи

Рассматривается задача о движении проводящей плоскости в идеальнопроводящей плазме, заполняющей все пространство. Плазма является однородной и покоится в однородном магнитном поле. В начальный момент времени проводящая плоскость, расположенная перпендикулярно силовым линиям магнитного поля, начинает перемещаться параллельно себе с постоянной скоростью.
Направление невозмущенного магнитного поля принимается за ось x, положение плоскости за x=0, а направление ее движения - за ось y. Величина невозмущенного магнитного поля есть Bx0 (для определенности Bx0 > 0), скорость плоскости - V.
Возникающее в результате перемещения плоскости МГД-течение очевидно является одномерным, все величины зависят от координаты x и времени t. При этом x-компонента магнитного поля остается неизменной вследствии соленоидальности магнитного поля.
Очевидно, что при движении плоскости вдоль оси y не возникают z-компоненты скорости и магнитного поля, то есть векторы u и B лежат в плоскости XY. Соответственно не возникают альфвеновские волны, которые могли бы вывести векторы u , B из этой плоскости.
Таким образом, течение плазмы описывается системой уравнений идеальной МГД, которая в дивергентном виде имеет вид
 U
t
 +  F(U)
x
 =0,
(1)
с "вектором" плотностей
U= м
н
о 		r,ru,rv, By, r  u2
2
 +  p
g-1
 +  B2y
8p
 ь
э
ю
и "вектором" потоков
F= м
н
о 		ru,ru2+ p-  B2x0
4p
 +  B2
8p
 , ru v-  Bx0By
4p
 , u By - v Bx0, ru w-  v Bx0 By
4p
 ь
э
ю 		.
Здесь u=(u,v) - скорость, B=(Bx0,By) - магнитная индукция, p - давление, r - плотность, u2=u2+v2, B2=B2x0+B2y, w = u2/2+c2/(g-1)+a2y - полная энтальпия, g - показатель адиабаты, c=Ц{gp / r} - газодинамическая скорость звука, a=Ц{a2x+a2y} - альфвеновская скорость, ax=Bx0/Ц{4pr} - нормальная компонента альфвеновской скорости, ay=By/Ц{4pr} - тангенциальная компонента альфвеновской скорости.
В начальный момент времени t=0 плазма однородна r = r0, p=p0 и покоится (u=0) в однородном магнитном поле B=(Bx0, 0).
Прежде, чем переходить к формулировке условий сопряжения на проводящей плоскости, отметим, что течение обладает определенной симметрией. А именно, в любой момент времени r(-x)=r(x), p(-x)=p(x), u(-x)=-u(x), v(-x)=v(x), By(-x)=- By(x). То есть термодинамические переменные и тангенциальная к плоскости компонента скорости - четные функции x, а нормальная скорость и тангенциальная компонента магнитного поля - нечетные.

3  Условия сопряжения на проводящей плоскости

Примем, что для поверхностных токов в плоскости выполнен закон Ома в форме
i = lEўp  ,
(2)
где i - поверхностная плотность тока, Eўp - тангенциальные к плоскости компоненты напряженности электрического поля в системе отсчета, связанной с рассматриваемым элементом плоскости, l - поверхностная электрическая проводимость плоскости.
Поскольку предполагается, что плазма, окружающая плоскость, является идеальнопроводящей, то напряженность электрического поля в лабораторной системе отсчета на границе плоскость - плазма составляет
E=-  1
c
 [u,B]   к
к

x=0 
  ,
где u - скорость плазмы, B - магнитная индукция при x=0. В дальнейшем не указываем, что x=0.
Так как при переходе через границу двух сред тангенциальные компоненты электрического поля непрерывны, то последняя формула дает величину электрического поля в плоскости в лабораторной системе отсчета. Переходя к сопутствующей системе отсчета, получаем
Eўp=-  1
c
 [u-V,B] ,
где V - скорость плоскости.
Закон Ома (2) принимает вид
i=-  l
c
 [u-V,B].
(3)
Поверхностные токи, текущие по плоскости (x=0), приводят к разрыву тангенциальной к плоскости компоненты вектора магнитной индукции. При этом выполнено соотношение [LL]
[n,B1-B0]=  4p
c
 i,
(4)
где B1, B0 - магнитное поле по обе стороны плоскости, n - единичный вектор нормали, направленный внутрь области 1 (Рис. ).
Figure 1:

Так как предполагается, что картина МГД-течения симметрична относительно плоскости, и задача рассматривается в верхнем полупространстве, то
B0=-B1=B
и соотношение (4) принимает вид
[n,B]+  2p
c
 i=0.
Подставляя сюда (3), окончательно получается
 c2
2pl
 [n,B]-[u-V,B]=0
или
[u-V-zn,B]=0,
(5)
где z = c2/2pl, n=(-1, 0). В этом соотношении имеет смысл только тангенциальная к плоскости компонента. Приравнивая нулю тангенциальную компоненту векторного произведения (5), получаем при x=0
(u+z)By-(v-V)Bx=0.
(6)
Отметим, что если движущаяся плоскость является идеальнопроводящей, то рассматриваемая здесь проблема может быть сведена к задаче о распаде МГД-разрыва специального вида, которая была изучена Базером в [Baz]. В этой работе исследовались МГД-течения, возникающие в результате распада разрыва скорости в однородной идеальнопроводящей плазме, находящейся в однородном магнитном поле, перпендикулярном плоскости разрыва. В наших обозначениях единственной величиной, претерпевающей в начальный момент времени разрыв при x=0, была y-компонента скорости: v(x > 0)=v0, v(x < 0)=-v0. Остальные переменные постоянны: u=0, r = r0, p=p0, Bx=Bx0, By=0. Ясно, что при одинаковых фоновых значениях плотности r0, давления p0 и продольного поля Bx0 решение задачи о движении идеальнопроводящей плоскости с точностью до перехода в систему отсчета, в которой плоскость покоится, совпадает при x > 0 с решением задачи Базера о распаде разрыва тангенциальной скорости, если v0=V. Более того, указанная аналогия решений может быть перенесена и на общий случай с конечной электрической проводимостью.
Пусть функции u(t,x), v(t,x), p(t,x), r(t,x), By(t,x) являются решением задачи о распаде разрыва тангенциальной скорости. Рассмотрим для простоты случай, когда в возникающем течении не образуется зона вакуума. Такое же течение (с точностью до перехода в систему отсчета, в которой плоскость покоится) может быть реализовано в области x > 0 при движении через плазму проводящей плоскости. Так как решения обеих задач зависят только от автомодельной переменной x = x/t, то значения МГД-переменных в плоскости x=0 не зависят от времени. Пусть v(0), By(0) - тангенциальная скорость и магнитная индукция, возникающие при распаде тангенциального разрыва скорости, при x = 0 (то есть при x = 0). Тогда в системе отсчета, в которой невозмущенная плазма покоится, скорость плазмы при x = 0 составляет [^(u)]=0, [^(v)]=v(0)-v0, а индукция [^(B)]y=By(0).
Пусть проводящая плоскость обладает поверхностной магнитной вязкостью z. Установим, какова должна быть скорость плоскости, чтобы на ней удовлетворились условия сопряжения (6). Имеем (так как [^(u)]=0)
(
^
v
 
 -V)Bx0-z
^
B
 
y 
 =0,
откуда
V=
^
v
 
 -
z
^
B
 
y 
Bx0
 =v(0)-v0-  zBy(0)
Bx0
 .
(7)
При такой величине скорости проводящей плоскости возникающее в полупространстве x > 0 течение содержит МГД-волны того же типа и интенсивности, что и при распаде тангенциального разрыва скорости с v(t=0)=±v0 (с теми же p0, r0, Bx0).

4  Построение автомодельного решения

Как уже отмечалось, задача о распаде тангенциального разрыва скорости в идеальнопроводящей плазме подробно исследована в [Baz]. Решение содержит (при x > 0) быструю ударную волну и следующую за ней медленную центрированную волну разрежения. В зависимости от соотношения между скоростью плазмы v0, газодинамической скоростью звука c0 и альфвеновской скоростью ax0 в невозмущенной плазме быстрая ударная волна может быть либо газодинамической ударной волной, в которой не возникает тангенциальная компонента вектора магнитной индукции, либо ударной волной включения. В первом случае y-компонента магнитного поля возникает в медленной волне разрежения. Во втором случае тангенциальная компонента возникает в ударной волне и скорость вещества за ударной волной включения в системе отсчета, связанной с фронтом ударной волны, равна нормальной компоненте альфвеновской скорости за ударной волной (условие Жуге).
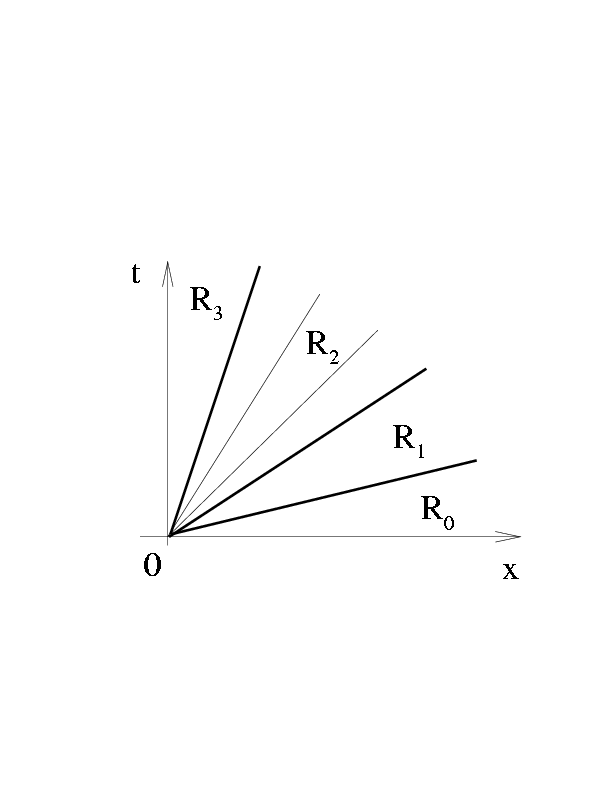region01.png
Figure 2: Области решения задачи
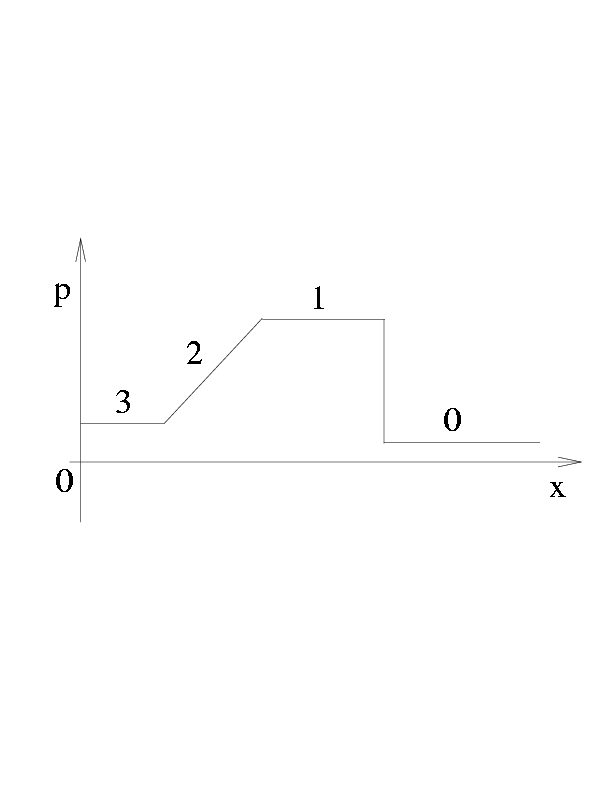region02.png
Figure 3: Характерный вид точного решения для давления p(x,t)
На рис. 2 показана качественная картина решения на (x,t) - плоскости (рассматриваем область x > 0). Здесь R0 - область невозмущенной плазмы справа от ударной волны, R1 - область постоянного течения слева за ударной волной, R2 - область, охваченная медленной центрированной простой волной разрежения, R3 - область постоянного течения, следующая за задним фронтом простой волны. На рис. 3 показано качественное поведение решения, например, давления p(x,t) при x > 0.
Алгоритм построения решения задачи о движении проводящей плоскости состоит в следующем. Считаем заданными МГД-переменные в начальный момент времени:
p(t = 0)=p0, r(t=0)=r0, Bx0, u(t = 0)=0, v(t=0)=0.
Ясно, что единственной существенной величиной является отношение газодинамической скорости звука c0 к альфвеновской скорости ax0. В других терминах - плазменный параметр b = 8pp0/Bx02.
Задаем интенсивность быстрой ударной волны. В качестве величины, параметризующей интенсивность, а заодно и семейство решений, удобно принять плотность вещества за ударной волной r1 или безразмерное отношение a = r1/r0 > 1.
Согласно [Baz] быстрая ударная волна будет газодинамической, если давление за ней p1 удовлетворяет условию
 p1
p0
 і 1+  2g
g-1
 ж
и 		 ax02
c02
 -1 ц
ш 		.
При выполнении обратного неравенства ударная волна будет волной включения.
Для определения типа быстрой ударной волны находим величину
pgas=p0  r0+r1-g(r0-r1)
r0+r1+g(r0-r1)
 =p0  (g+1)a-(g-1)
(g+1)-(g-1)a
 ,
имеющую смысл давления за газодинамической ударной волной данной интенсивности. Если выполняется неравенство
 pgas
p0
 і 1+  2g
g-1
 (  ax02
c02
 -1),
то реализуется течение с газодинамической ударной волной, если выполнено обратное неравенство - с волной включения.
В первом случае МГД-величины за ударной волной определяются по формулам Гюгонио
U=c0   ж
Ц
 2r1
r0+r1+g(r0-r1)
 
 = c0   ж
Ц
 2a
(g+1)-(g-1)a
 
  ,
u0=0,    u1=c0   ж
Ц
 2a
(g+1)-(g-1)a
 
 ж
и 		1-  1
a
 ц
ш 		 ,
p1=pgas=p0  (g+1)a-(g-1)
(g+1) -(g-1)a
  ,
где p0, r0, c0 - невозмущенные величины давления, плотности и газодинамической скорости звука.
Во втором случае, так как за ударной волной включения выполнено условие Жуге, то
r0 U=r1 ax1=  Bx0r1

Ц
4 pr1
 .
Используя это соотношение, находим скорость ударной волны и оставшиеся неизвестные величины
U=ax1a = ax0
Ц
 
a
 
 ,     u0=0,    u1=U-ax1=ax1(a-1),
By12=Bx02(1-a)[2(1+a+ga) -gb],
p1=pmhd=p0 ж
и 		2+  a-1
b
 (2+2(1+a+ga)-gb) ц
ш 		,
v12=ax12(1-a)[2(1+a+ga)-gb] ,
где p0, r0, Bx0, ax0 - невозмущенные величины давления, плотности, продольного магнитного поля и альфвеновской скорости.
При заданных давлении p0 в невозмущенной плазме и интенсивности ударной волны a давление p1 за фронтом ударной волны определяется величиной продольного магнитного поля Bx0. На рис. показан график зависимости p1 от Bx0 при p0=1, a = 2, g = 5/3. При Bx0 < BA=5.6 давление за фронтом ударной волны не зависит от величины продольного магнитного поля, то есть реализуется газовая ударная волна и тангенциальное магнитное поле возникает в волне разрежения. При Bx0 і BA возникает МГД-волна включения и давление p1 зависит от величины Bx0.
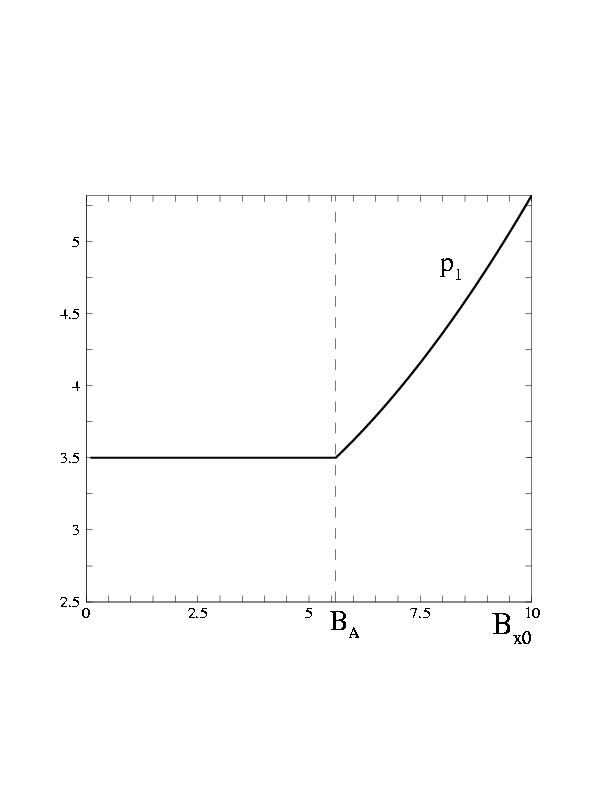fgmhd5.png
Figure 4: Функция p1(Bx0), в точке BA=5.6.
Для расчета распределения МГД-переменных в центрированной простой волне (область R2 на рис. 2) удобно вместо уравнения энергии использовать уравнение для энтропии, так как энтропия S=ln(p/rg), а также любая непрерывная функция от неё, остается постоянной в такой волне.
Для системы квазилинейных уравнений
 U
t
 + A(U)  U
x
 = 0
решение типа центрированной волны представляется в виде U(x, t)=U(x), где x = x/t. При подстановке такого U в систему получаем
(A-xI )  dU
d x
 =0,
таким образом x - является собственным числом матрицы A, d U/d x - соответствующий ему правый вектор:
м
п
н
п
о
x =  x
t
 = l(U),
 d U
d x
 = В(U).
(8)
Для системы уравнений идеальной МГД с уравнением энергии в энтропийной форме
 rS
t
 +  
x
 ru S=0
правый вектор, соответствующий распространяющейся направо медленной магнитозвуковой волне, есть [KPS]
В= м
н
о 		1,  u+cS,  v+  e1
e2
  cF, -   ж
Ц
 4p
r
 
  c    e1
e2
 ,  S ь
э
ю 		,
где c2F, S=(a2+c2 ±Ц{(a2+c2)2-4c2a2x0})/2 - квадрат быстрой (или соответственно медленной) магнитозвуковой скорости, e12/e22=(c2 -cS2)/(cF2-c2).
После некоторых преобразований система (8) принимает вид [Kul]
м
п
п
п
п
н
п
п
п
п
о
 d By2
d r
 = 8 p(cS2-c2),
 d u
d r
 =  cS
r
 ,
 d v
d r
 = -  Bx0(cS2-c2)
rcS By
 ,
 d S
d r
 = 0 .
Система уравнений (8) имеет следующие интегралы [Polov]:
I1=  r
(q-1)d
 +d у
х 		 d q
q2(q-1)d+1
  ,     I2=u+  1
g
 у
х 		 Цq
r
  d r,
I3=v -  1
g
 у
х
c
Ц
q-1
r
Ц
rq-1
  d r,    I4=S=lnp/rg.
(9)
Здесь r=c2/ax02 є 4pp/Bx02, d = g/(2-g), q=cS2/c2.
Однако проще реализовать её численное интегрирование методом Рунге - Кутта с "начальными" данными:
u(r1)=u1, v(r1)=v1, By(r1)=By1, S=S1=const.
Интегрирование проводится до некоторого r = r2, такого что u(r2)=0. Интегралы (9) использовались для проверки точности численного интегрирования как системы (8), так и нестационарных уравнений идеальной МГД.

5  Численный метод

Для численного интегрирования уравнений идеальной МГД (1) использовалась консервативная квазимонотонная разностная схема годуновского типа, допускающая вырождение характеристик в случае отсутствия тангенциального поля. Разностная схема при исчезновении y-компоненты магнитного поля содержит неопределенности вида 0/0. Возникновение неопределенностей связано с вырождением собственных чисел матрицы соответствующей квазилинейной системы [Kol].
Разностная схема строится для гиперболической системы уравнений (1) с "векторами" U, F, определенными выше. Система (1) может быть записана в квазилинейном виде:
 U
t
 + A(U)  U
x
 = 0.
(10)
Поскольку система (10) гиперболическая, член A(U) U/x можно представить в виде суперпозиции волн
A(U)  U
x
 =
е
a 
 la Вa < La,  U
x
 > ,
где суммирование проводится по всем собственным числам (с учетом кратности) матрицы A. Гиперболичность (10) означает, что матрица A(U)= F/U имеет полный набор левых La и правых Вa собственных векторов, соответствующих действительным собственным числам la. Базисы, заданные системами векторов La и Вa, предполагаются сопряженными, то есть
< La, Вb > =
е
k 
 La,k Вb,k = dab,    dab - символ Кронекера .
Собственные числа la имеют смысл скоростей распространения МГД-волн, Aa = < La,U/x > - амплитуды соответствующих волн.
По переменной x введем равномерную разностную сетку, состоящую из интервалов, разделенных узлами. Интервалы сетки будем нумеровать целыми индексами, узлы - полуцелыми. Сеточные функции для "вектора" U будем относить к интервалам сетки, нумеруемым целыми индексами, и обозначать Ui, сеточные функции для F - к узлам с полуцелыми индексами и обозначать Fi+1/2.
Разностная схема годуновского типа имеет вид:
 Uin+1-Uin
Dt
 +  Fi+1/2 - Fi-1/2
Dx
 = 0,
(11)
где Dx - шаг по пространству, Dt - шаг по времени.
Проблема состоит в вычислении потоков Fi+1/2 таким образом, чтобы схема обладала заданными качествами: требуемым порядком аппроксимации, монотонностью и т.п. Для учета характеристических свойств уравнений используется подход, аналогичный [Roe]. Получающиеся при этом квазимонотонные разностные схемы первого порядка аппроксимации далее преобразуются к квазимонотонной схеме повышенного порядка аппроксимации в соответствии с методикой [Fav], [Elen].
В данной работе дискретные потоки вычисляются по формулам:
Fi+1/2 =  F(Ui) + F(Ui+1)
2
 -  1
2
е
a 
 (| la | Вa
~
A
 
a 
 )i+1/2 .
(12)
Собственные числа la, правые векторы Вa и амплитуды волн [(A)\tilde]a определяются из дифференциальной задачи. Переход к разностной схеме осуществляется формальной заменой Aa в формулах для амплитуд и интерполяцией сеточных функций в узлы сетки по формулам, аналогичным [Roe]. Условия монотонности в данном случае аналогичны условиям для подобных схем газовой динамики. Точность схемы повышается с помощью процедуры, описанной в [Fav], [Elen]. Амплитуды волн [(A)\tilde]a вычисляются по формуле
~
A
 
a, i+1/2 
 = Aa, i+1/2 + limiter(d1, d2) = Aa, i+1/2 - ma, i+1/2Aa, i+1/2,
где d1=Aa, i+1/2, d2=Aa, i-1/2 при la і 0 или d2=Aa, i+3/2 при la < 0. Функция ma=m(Da), Da=d2/d1 - анализатор гладкости для волны типа a (магнитозвуковой, альфвеновской, энтропийной).
limiter(d1,d2) = м
п
н
п
о
0,    d1 d2 Ј 0,
0.5(1-k)d1,    |d2| < 2/(1-k)|d1| ,
d1,     |d2| і 2/(1-k)|d1|,
где k < 1 - число Куранта. Функция m(D), соответствующая указанной функции limiter(d1,d2), показана на рисунке .
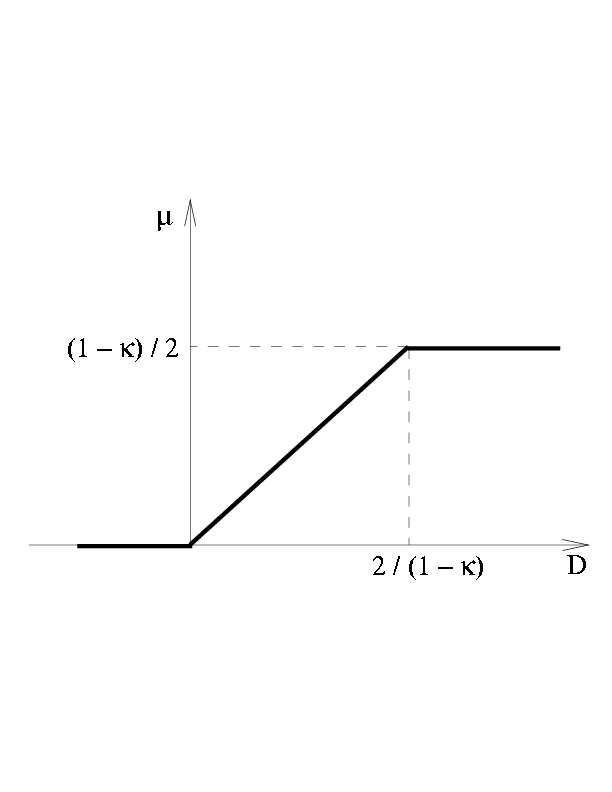nulim101.png
Figure 5: Лимитер m(D), k - число Куранта.
Корректная постановка начально-краевой задачи задачи для гиперболической системы уравнений требует задания такого числа граничных условий, сколько характеристик выходит с рассматриваемого участка границы. Кроме того, если этот участок границы является характеристическим многообразием (в одномерном случае - характеристикой), на нем должны быть выполнены соответствующие соотношения.
В данной работе рассматриваются МГД-течения такие, что на правой границе расчетной области - интервала 0 < x < L - сохраняется начальное невозмущенное состояние. Точнее, рассматриваются только такие моменты времени, в которые МГД-волны, вызванные движением проводящей плоскости x=0, не достигают правой границы. Поэтому на границе при x=L поддерживаются исходные значения МГД-переменных. Эта постановка граничных условий корректна независимо от числа уходящих с этой границы характеристик, так как амплитуды всех волн равны нулю.
Так как на левой границе вещество покоится u(x=0)=0, то с неё выходит две характеристики, соответствующие быстрой и медленной магнитозвуковым волнам, распространяющимся направо. Поэтому здесь следует задать два граничных условия.
Одно из граничных условий выражает закон Ома для поверхностных токов и имеет вид
f1=(u+z)By-(v-V)Bx=0.
(13)
Второе граничное условие имеет вид
f2=u=0.
(14)
Кроме того, линия x=0 в (x,t)-плоскости является в силу (14) энтропийной характеристикой, поэтому на ней должно быть выполнено соотношение
 S
t
 =0.
(15)
Дифференцируя (13), (14) по t, получаем два линейных уравнения,которым должен удовлетворять "вектор" Ut
< Yk, Ut > = 0,    Yk =  fk
U
 ,   k=1,2.
(16)
Соотношение (15) имеет такую же форму.
Таким образом, при x=0 "вектор" Ut удовлетворяет трем уравнениям (16) с "векторами" Yk следующего вида
Y1={0, By, -Bx0,u+z, 0},   Y2={0, 1, 0, 0,0},  Y3={0, 0, 0, 0, S}.
Недостающие уравнения получаются из системы уравнений (1), записанной в квазилинейной форме (10). Умножая (10) на векторы La, соответствующие характеристикам, приходящим на границу, получаем недостающие уравнения для определения вектора Ut
< La, Ut > + la < La, Ux > = 0,    для   la Ј 0 .
(17)
Решение уравнений (16), (17) ищем в виде
Ut =
е
a 
 ha Вa .
Очевидно ha = < La, Ut > . Из (17) сразу получаем, что коэффициенты ha, соответствующие la Ј 0, есть
ha = - la < La, Ux > .
Подставляя эти ha в (16), получаем для оставшихся ha линейную систему

е
la <  0 
 < Yk, Вa > ha =
е
la і  0 
 < Yk, Вa > ha,   k = 1,2,
где слева стоит сумма по a таким, что la < 0, справа сумма по a таким, что la і 0.

6  Результаты расчетов

Численное интегрирование уравнений идеальной МГД (1) проводилось на равномерной сетке, содержащей L=200 интервалов с пространственным шагом Dx=1. Шаг по времени Dt вычислялся из условия Куранта - Фридрихса - Леви по формуле: Dt=kDx/max|la|, где максимум в знаменателе берется по всем ячейкам и типам МГД-волн. Величина k варьировалась, в представленных расчетах k = 0.5. Использовалась разностная схема повышенного порядка аппроксимации с "лимитером", показанном на рис. 5.
Ниже на рисунках приведены результаты численного и аналитического решений данной задачи. Приведены рисунки для Bx0=1 и Bx0=10 для случаев идельнопроводящей при z = 0 и конечнопроводящей z = 0.01 и z = 1 плоскости.
Расчеты проводились при g = 5/3, p0=1, r0=1, r1=2.1 для волны включения, r1=1.4 для газодинамической волны.
Как следует из результатов расчетов, численные решения, полученные при разных величинах поверхностной магнитной вязкости z (и соответственно для разных начальных скоростей плоскости V) совпадают, что соответствует теоретическим выводам, сделанным в данной работе. При одних и тех же начальных данных задачи, в которых скорость V и поверхностная магнитная вязкость z связаны соотношением (7), имеют одинаковые решения.
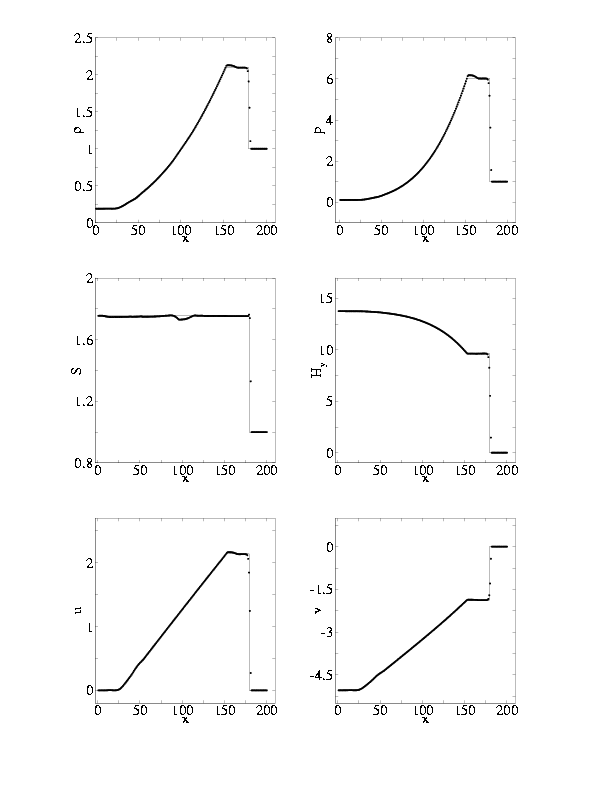
pic005.png
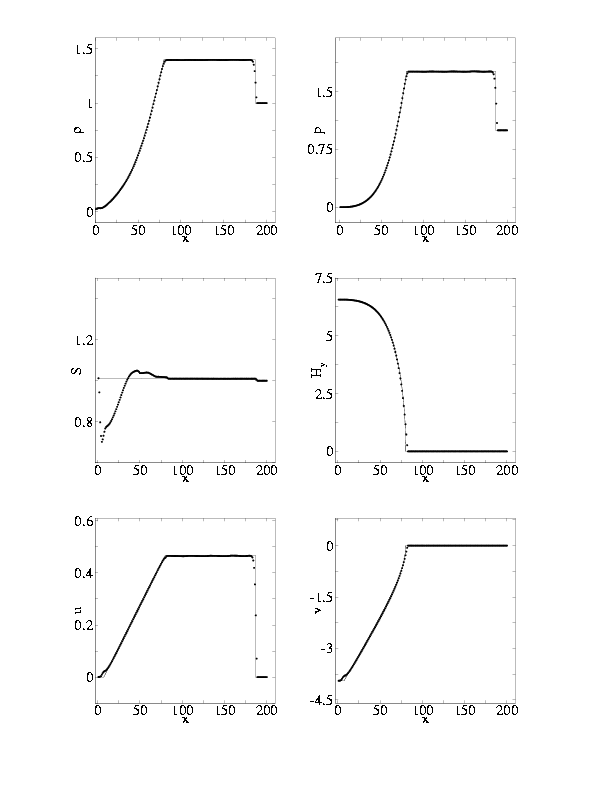
Рис. 6. Профили переменных на момент времени t=44.8 при z = 1, Bx0=10
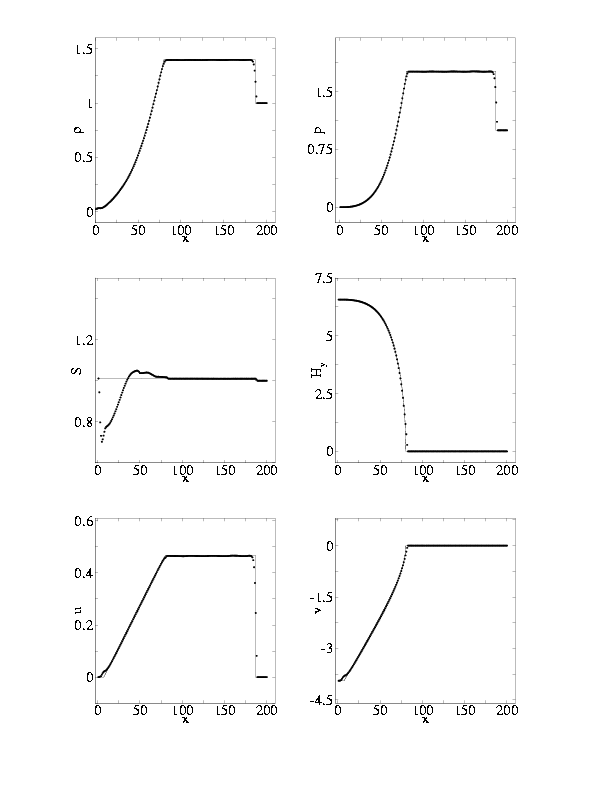
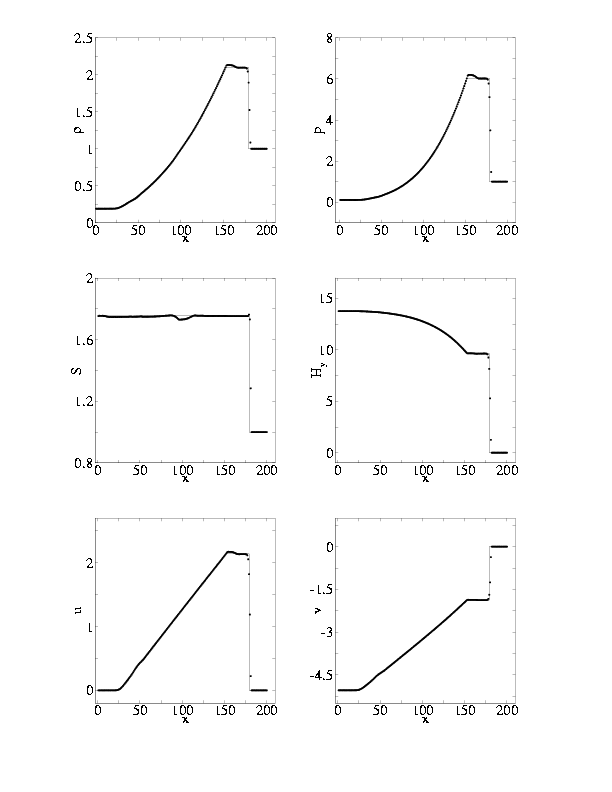
pic001.png
Рис. 7. Профили переменных на момент времени t=44.8 при z = 0.01, Bx0=10
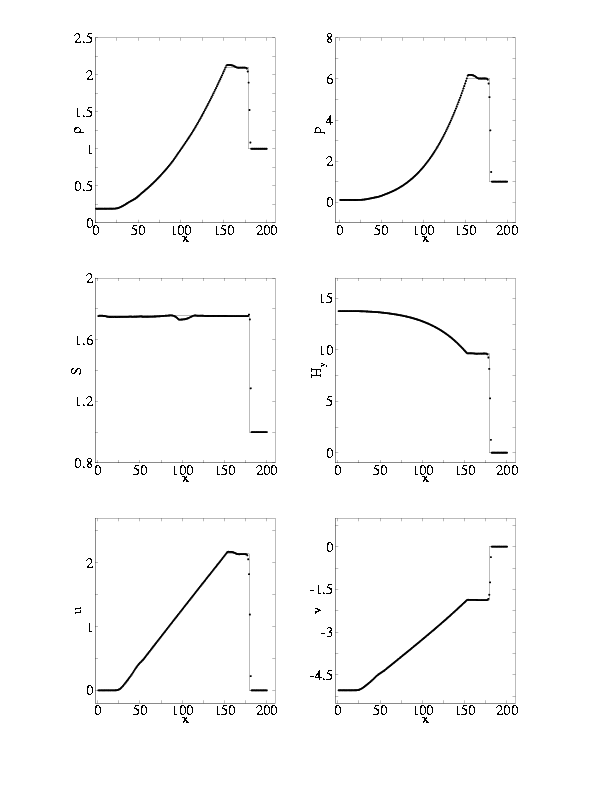
pic002.png
Рис. 8. Профили переменных на момент времени t=44.8 при z = 0, Bx0=10
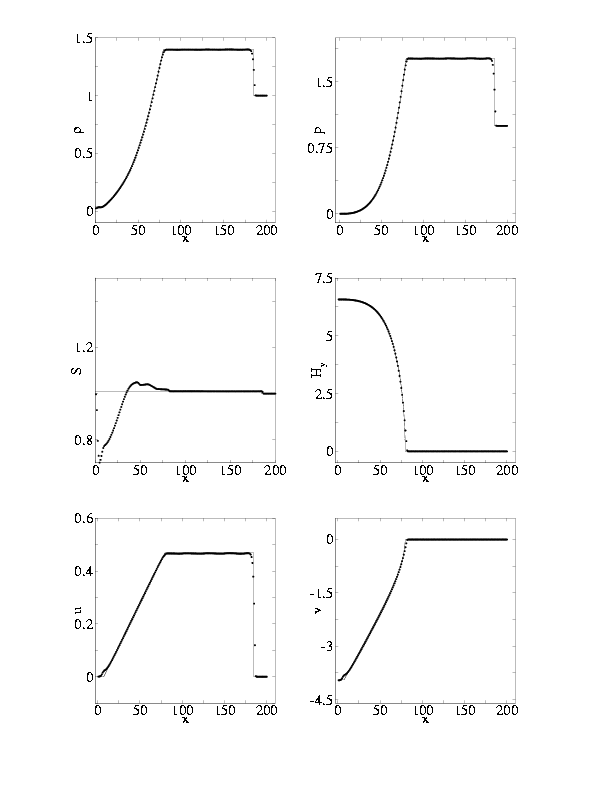
pic006.png
Рис. 9. Профили переменных на момент времени t=112.6 при z = 1, Bx0=1
pic003.png
Рис. 10. Профили переменных на момент времени t=112.6 при z = 0.01, Bx0=1
pic004.png
Рис. 11. Профили переменных на момент времени t=112.6 при z = 0, Bx0=1

References

[Kul]
Куликовский А.Г., Любимов Г.А. Магнитная гидродинамика. М., Физматгиз, 1962, 248 с.
[LL]
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. Том VII, М., Наука, 1982, 620 с.
[Baz]
Bazer J. Resolution of an initial shear-flow discontinuity in one-dimentional hydromagnetic flow. Astrophysical Journal, 1958, V.128, N 3, p. 686-712.
[KPS]
А.Г. Куликовский, Н.В. Погорелов, А.Ю. Семенов Математические вопросы численного решения гиперболических систем уравнений. М.: ФИЗМАТЛИТ, 2001, 608 с.
[Polov]
Р.В. Половин. К теории простых магнитогидродинамических волн. Журнал экспериментальной и теоретической физики, 1960, Т. 39, вып. 2(8), с. 463-470.
[Kol]
А.В. Колдоба, Г.В. Устюгова. Разностные схемы для уравнений МГД в эйлеровых перменных (случай кратных корней). Препринт ИПМ им. М.В. Келдыша РАН, 1996, N 42, 25 с.
[Roe]
Roe P.L. Characteristic-based schemes for the Euler equations. Ann. Rev. Fluid Mech., 1986, V.18, p. 337-365.
[Fav]
Вязников К.В., Жорняк Н.С., Тишкин В.Ф., Фаворский А.П. О методе построения квазимонотонных схем повышенного порядка аппроксимации. Препринт ИПМ АН СССР, 1989, N 141, 19 с.
[Elen]
Галанин М.П., Еленина Т.Г. Нелинейная монотонизация разностных схем для линейного уравнения переноса. Препринт ИПМ им. М.В. Келдыша РАН, 1999, N 44, 30 с.


File translated from TEX by TTH, version 3.40.
On 28 Apr 2005, 18:52.